Altitude Correction of an UAV Assisted by Point Cloud Registration of

LiDAR Scans

Marcus Davi Forte

, Polycarpo Souza Neto

, George Andr

e Pereira Th

and Fabricio Gonzalez Nogueira

Department of Electrical Engineering, Federal University of Ceara, Fortaleza CEP 60455-970, Brazil

Department of Teleinformatic Engineering, Federal University of Ceara, Fortaleza CEP 60455-970, Brazil

Keywords:

Unmanned Aerial Vehicle, Localization, Laser Scanning, Generalized Iterative Closest Point, Fast Point

Cloud Registration, Stockpile Mapping.

Abstract:

This paper presents an online localization estimation of an Unmanned Aerial Vehicle (UAV) by fusing data

provided by the on-board ﬂight controller and a LiDAR (Light Detection and Ranging) carried by the UAV.

Pose estimations solely obtained by the UAV are often corrupted by noise or instrumentation limitation, which

may lead to erroneous mapping of the environment. To correct potential estimation errors, the LiDAR scans

are assembled into a local point cloud history and matched against a partial map of the environment using

a proposed point cloud registration method, similar to a Simultaneous Localization and Mapping (SLAM)

approach. The resulting correction is incorporated into the estimation of the UAV using an asynchronous

Kalman Filter implementation. For this work, only the altitude errors are corrected by the registration. We

conducted tests on a local thermal power plant which contained three large coal stockpiles. We chose one of

them as our Region of Interest (ROI).

1 INTRODUCTION

The mapping procedure and modeling of three dimen-

sional objects is a subject of interest of various ap-

plications, for example precision agriculture (Lin and

Habib, 2021). The precise reconstruction of real sur-

faces has become a challenge and has been deeply

studied over last years (Vacca et al., 2018), and the

use of UAV (Unmanned Aerial Vehicle) as a remote

sensing platform has shown promising results.

It is essential that the UAV carrying sensory in-

strumentation such as cameras or Light Detection

and Ranging (LiDAR) sensors provides accurate es-

timates for its three dimensional pose. The sensory

data provided by the on-board instrumentation is usu-

ally associated to the pose of the aircraft. Any uncer-

tainty present in the pose estimation directly affects

the quality of the information inferred from the sen-

sor (Mughal et al., 2021). UAV often relies on Global

Navigation Satellite System (GNSS) combined with

Inertial Measuring Units (IMU). However, GNSS sig-

nals are vulnerable to noise and IMU is not reliable

for long-term estimations. Consequently, whenever a

GNSS signal suffers from some interference, it affect

the entire pose estimation of the UAV. A less noisy es-

timation alternative is the use of Real Time Kinematic

(RTK) equipment, which is able to offer estimations

with less than 5 cm error. Such solutions, however,

are much more expensive than GNSS solutions.

These drawback motivates the use of the on-board

instrumentation of the UAV to help correct estima-

tion errors that arise from the localization sensors.

In (Mughal et al., 2021) a deep learning technique is

used on image from cameras to localize an UAV based

on geotagged images. The approach is, however, un-

able to provide real time estimates and require train-

ing data before usage. On the other hand, LiDAR sen-

sors are able to provide common landmarks between

scans so that the motion of the aircraft is success-

fully estimated in real time, as explored in (Chiang

et al., 2017). This technique is usually integrated into

a Simultaneous Localization and Mapping (SLAM)

framework. The scan matching between frames is

achieved by applying what is known as point cloud

registration.

In this work, we will explore the use of point cloud

registration for estimating the error on the altitude of

an UAV in real time. We will present experimen-

tal results and an implementation of an asynchronous

Kalman ﬁlter for integrating the estimations.

Forte, M., Neto, P., Thé, G. and Nogueira, F.

Altitude Correction of an UAV Assisted by Point Cloud Registration of LiDAR Scans.

DOI: 10.5220/0010583004850492

In Proceedings of the 18th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2021), pages 485-492

ISBN: 978-989-758-522-7

485

2 LITERATURE REVIEW

2.1 UAV-based Laser Scanning

LiDAR based UAV scanning system is an alternative

solution to the classical photogrammetry method of

acquiring a 3D model of surfaces. The laser meth-

ods can be applied to mitigate gaps and acquire a pre-

cise point cloud image (Huang et al., 2019). It can

offer a centimeter accuracy and the data capture can

be performed either aerial or terrestrial (Amann et al.,

2001). It has been shown that such approach produces

slightly superior accuracy results comparing to pho-

togrammetry methods (He et al., 2019).

Recent works have been utilizing LiDAR sensors

to acquire 3D point clouds of bulk material stock-

piles. The works (Zhang et al., 2020; He et al., 2019)

present solutions for the laser scan measurement of

stockpiles using mobile hand-held devices that needs

to be carried along with the entire stockpile surround-

ing. This technique has the limitation that it can only

capture a side view from the stockpile, essentially

missing information about the top side of higher piles.

In addition, the data acquisition is a slow process and

can cause physical stress for the person carrying the

scanner system the whole stockpile, not to mention

that the carrier is exposed to perilous conditions dur-

ing the acquisition procedure due to the existing coal

particulates and pile collapse risk.

Equipping a similar system to a UAV overcomes

several of these difﬁculties. The aerial systems have

the advantage of covering large areas or places that

are not easily accessible for terrestrial systems. Some

works have successfully integrated LiDAR sensors

into UAVs in order to construct 3D point cloud data.

In (Wallace et al., 2012) a low-cost UAV-LiDAR sys-

tem was developed for managing forest inventories.

Data fusion algorithms that combine Global Position-

ing System (GPS), IMU and video camera images

are employed to UAV position and posture estimation

during the ﬂight.

In (Beland et al., 2019) is presented the use of a

LiDAR sensor in an airborne covering large areas and

acquiring a large amount of data. Airborne LiDAR

remote sensing systems must be able to provide ac-

curate aircraft position information. Otherwise, the

formed point cloud will present unreliable informa-

tion. Measurement errors and attitude ﬂuctuations af-

fect the accuracy of laser points, and the impacts of

these problems are discussed in (Wang et al., 2011),

(Wang et al., 2018), and (Hauser et al., 2016).

2.2 Point Cloud Registration

The Iterative Closest Point (ICP) algorithm was pro-

posed in (Besl and McKay, 1992) and aims at ﬁnding

a transformation that optimizes a rotation and trans-

lation in two point clouds. The algorithm uses one

of the data sets a reference and applies rotations and

translations to the other set. This is repeated itera-

tively until the convergence occurs, that is, the small-

est difference between the gradient of two successive

iterations. Although it is widely used in the literature,

as it has an iterative method and depends on an initial

guess, it is quite susceptible to local minimums. In

(Chen and Medioni, 1992), an improvement is made

in the ICP, where we now have information on the

surface normal, called the point to plane ICP. How-

ever, this approach fails to deal with clouds of dif-

ferent densities, with many outliers or noise, which

somehow affects the calculation of the normal.

An efﬁcient approach to registration dense clouds

is the GICP (Segal et al., 2009). This probabilis-

tic version of the ICP is based on the probabilistic

Maximum Likelihood Estimation model (MLE). The

method explores local planar patches in both point

clouds. For this case, we say that the metric here is a

generalization of the point to point and point to plane

metrics, with the concept of plane to plane being in-

troduced. As a failure, the GICP has a reasonably

high computational cost compared to other ICP vari-

ants.

In the search for an alternative to conventional

sampling methods and the attempt to reduce ambi-

guities, computational cost and obtain better align-

ment, the Cloud Partitioning ICP (CP-ICP) method

was proposed in (Souza Neto et al., 2018). Basi-

cally, the two clouds involved in the process are parti-

tioned into the same number of slices, with each pair

(slices of the same index) subject to registration and

the best alignment among the various pairs, represents

the rigid transformation that best corrects the entire

clouds (since which are rigid bodies).

In view of the problems found in the classic al-

gorithms, sometimes the quality of the alignment, in

other situations due to the high computational cost,

this work proposes the utilization of a modiﬁed ver-

sion of CP-ICP algorithm with the purpose of correct-

ing erroneous height estimates provided by an UAV

pose estimation in real time. We will see more details

in the following section.

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

486

3 PROPOSED MATCHING

3.1 Cloud Partitioning Generalized ICP

(CP-GICP)

Recently, it was proposed a subsampling stage of

point clouds, where two sets of data, both were par-

titioned into k parts, in order to reduce the computa-

tional cost for the alignment step.(Souza Neto et al.,

2018). This partitioning step is previous to the align-

ment, performed on the partitions by the ICP algo-

rithm (Besl and McKay, 1992). In summary, the par-

titions of the source cloud (S) are aligned with those

of the target cloud (M), where the rigid transforma-

tion that results from this alignment is replicated in

the complete source cloud, correcting its pose in rela-

tion to the reference. The equation that represents the

alignment of the partitions, using the CP-ICP method

in (Souza Neto et al., 2018) can be seen in Eq. 1.

(Ψ)

ICP

∑

i=1

k ~m

− Ψ

k, (1)

where j they are the indexes of the partitions being

aligned, N it is the number of points,

it is i-th vector

related to the source point cloud, ~m

the i-th vector

related to the target point cloud and Ψ it is the rigid

transformation (4 x 4 matrix) obtained from ICP in

the alignment core.

In this paper, we propose some changes to the pre-

viously mentioned algorithm, in order to adapt it to

the purpose of this work. In the current version of the

algorithm, the ﬁrst modiﬁcation we added a density

equalization step, as a ﬁrst level of sampling. After

that, will be separate only one of the point clouds into

smaller parts hereinafter referred to as sub-clouds,

and then perform the registration process for each par-

tition with the other entire cloud, until a simple deci-

sion criterion (here the lowest possible RMSE com-

pared to a criterion decided a previously) is reached.

It is worth mentioning that this variant of the al-

gorithm with a second modiﬁcation, intrinsic to the

needs of the application, where here, the alignment

core is Generalized ICP (Segal et al., 2009), suitable

for the alignment of outdoor scenarios. The equation

that describes the proposed alignment method is seen

in Eq. 2.

(Ψ)

GICP

∑

i=1

(Ψ)

(Σ

+ ΨΣ

)

−1

(Ψ)

(2)

where d

(Ψ)

they are point to point distances of the

correspondences, Σ

and Σ

are covariances of the

local point neighborhoods of j-th source sub-cloud

and target point cloud, respectively.

The choice to partition only one of the clouds is

due to the size discrepancy between the data involved

in the process; in relation to the alignment core, GICP

error metric that generalizes over point to point and

point to plane, it uses covariances of the local point

neighborhoods in order to align the underlying sur-

faces rather than the points themselves (Holz et al.,

2015). The classic ICP, used in the variant improved

CP-ICP is known for its susceptibility to the problem

of local minimums. Because it is an iterative method,

it requires an initial guess, without which the algo-

rithm can easily get stuck in a local minimum (Yang

et al., 2016). If this occurs, the solution may be far

from the optimal solution, resulting in an incorrect es-

timate. This interpretation of the above can be seen in

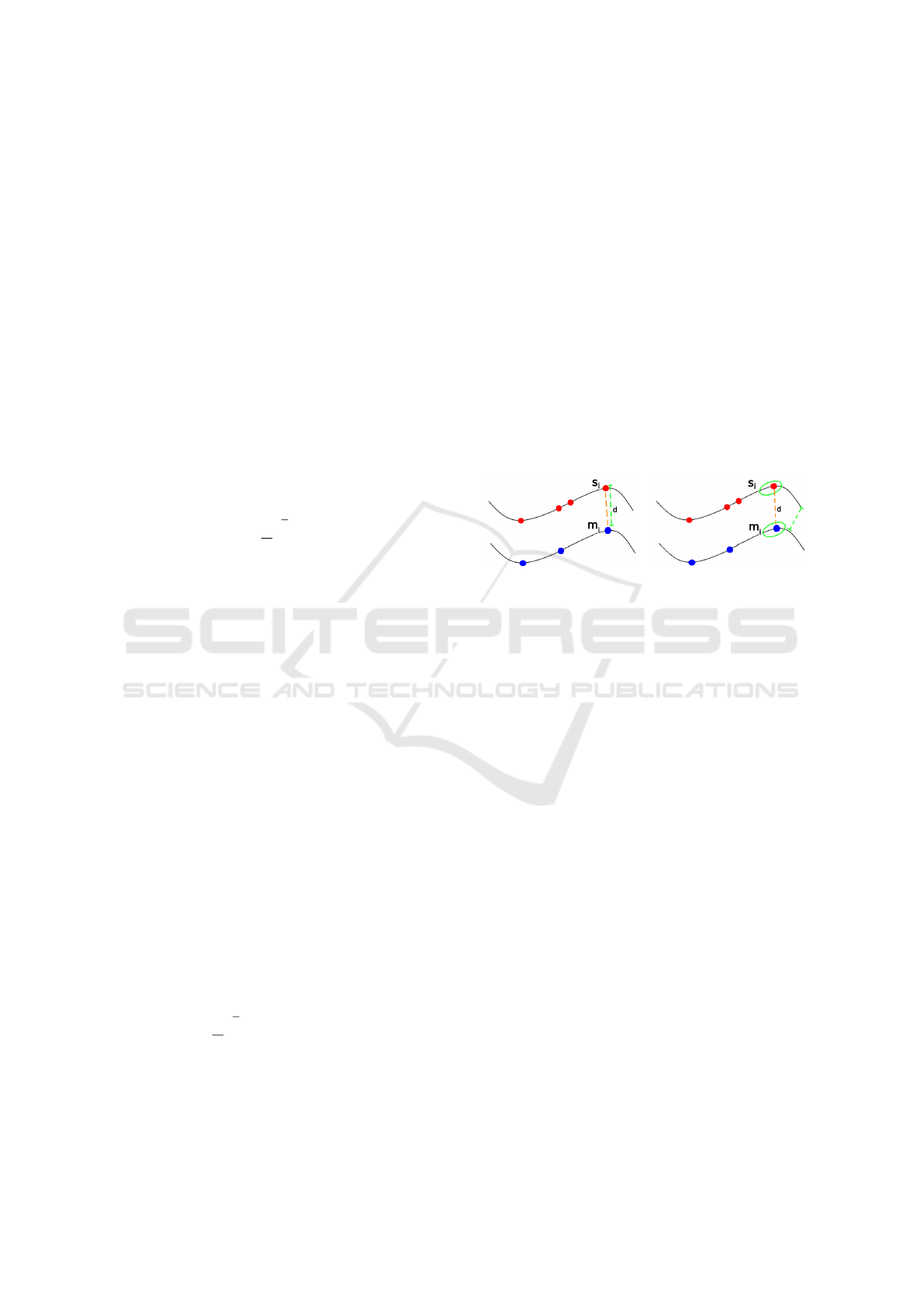
Figure 1(a) and 1(b).

(a) (b)

Figure 1: Error metrics and transformation estimators. In

(a) point to point erro metric and (b) Generalized ICP or

plane to plane error.

3.2 Sufﬁcient Registration

Consider two point clouds: an source point cloud and

a target point cloud. The goal is to successfully per-

form a registration procedure, which means matching

the input point cloud to the target one. Let is see the

steps:

1. Initially, we performed density equalization of the

point clouds, using a voxel grid algorithm;

2. Subdivide one of the datasets (the source) in k

sub-clouds;

3. For each of the k iterations, solve the Generalized

ICP algorithm for the partition and the entire tar-

get cloud:

• Apply the achieved transformation to the source

point cloud;

• The source cloud post GICP is then compared to

the target point cloud, using RMSE error at each

iteration;

• If the RMSE value achieved in a given iteration is

acceptable (when it compares to a stop criterion)

the algorithm stops and the ideal transformation

has been found.

Altitude Correction of an UAV Assisted by Point Cloud Registration of LiDAR Scans

487

4 LASER-BASED UAV SCANNER

SYSTEM

The aerial scanning system is mainly composed of an

industrial UAV and an embedded computer which im-

plements the proposed pose compensation system.

The DJI Matrice 100 is a fully programmable

quad-copter. It features an Onboard Software Devel-

opment Kit (OSDK) which allows sensor data sam-

pling in real-time, setting missions and waypoints,

and creating ﬂight reports. Its weight is around 2.5

kg and can carry an additional 1.1 kg as payload.

It comes with IMU and GPS to estimate its posi-

tion and orientation. The provided SDK allows di-

rect integration with the ROS framework. Any ROS-

Supported embedded computer is able to communi-

cate with the Matrice 100 though a serial port made

available within the drone frame.

Once SDK is installed in the embedded computer,

it provides an application that offers topics contain-

ing useful information, among them, the most impor-

tant are the fused geographic coordinate and the fused

orientation data. The coordinates are the result of a

proprietary data fusion algorithm that combines data

from IMU and GPS. The resulting data is also a geo-

graphic coordinate, containing more accurate latitude,

longitude, and altitude information. Coming from the

IMU, and magnetic compass, a fused orientation is

also provided. Both 3D coordinate and 3D orienta-

tion data are published in topics with a programmable

frequency of up to 50 Hz.

The chosen embedded computer is an Asus Tinker

Board S with a Debian-based distribution which sup-

ports ROS framework. It is powered by a quad-core

ARM based processor, with 16 GB eMMC storage,

2 GB of LPDDR3 dual-channel memory, and oper-

ates at frequencies up to 1.8 GHz. Its main role is to

act as an interface between the drone and the LiDAR

sensor to assemble the point cloud data.

The used LiDAR is a SICK LD-MRS420201 de-

signed for outdoor applications. It has IP69K enclo-

sure rate protection and weights 0.77 kg. Its scanning

range stands under 150 m and 50 m for objects up

to 90% and 10% remission, respectively. And coal

is a material with low levels of remission. Therefore

the LiDAR is expected to work with a range of up to

50 m. The sensor possesses ROS drivers for integra-

tion with ROS applications, which are essential for

point cloud models assembly. The sensor is attached

beneath the drone and points towards the ground dur-

ing the ﬂight.

5 REGISTRATION-ASSISTED

LOCALIZATION ESTIMATION

This section details the proposed system for correct-

ing measurements using point cloud registration.

The UAV is able to provide a full pose estima-

tion using inertial sensors, GNSS localization and the

model of the drone itself. As stated in the documen-

tation of the equipment, this estimation contains an

estimation error of about a few meters. We propose a

Kalman ﬁlter structure which models the noise error

and receives the correction of the point cloud registra-

tion as an update variable.

Figure 2 illustrates the estimation process. First,

the map is constructed using the pose from the UAV

instrumentation. The map construction performed

using frame transformations from an inertial frame,

whose origin is set to the take off position. and the

laser frame. As the UAV ﬂies above the surface, the

laser point clouds are transformed to the map frame

and added to the previous ones. Notice that during

this step, it is not possible to correct the UAV pose.

As soon as the UAV detects an overlap between

the current laser scan and the map, it is assumed that

the overlap is enough to provide a correction estima-

tion. The registration process is then triggered and the

output transformation matrix is used to provide the

height correction. Subsequent laser scans are added

to the current map but with the corrected pose.

We included a parameter χ, deﬁned as the local

point cloud history, which controls how many laser

scans are included in the source point cloud used for

the registration.

5.1 Asynchronous Kalman Filter

A Kalman ﬁlter structure is modeled to account for

the asynchronous registration corrections and the es-

timation provided by the DJI proprietary fusion so-

lution. The term asynchronous refer to that fact that

the corrections occur at a variable sampling rate, in

contrast to the predictions which occur at a constant

sampling rate. The equations remain the same, but the

implementation is slightly different. Instead of exe-

cuting both predictions and corrections in a single it-

eration, the correction step is called only upon receiv-

ing the updating states provided by the point cloud

registration. Moreover, it is possible to use multiple

corrections models, each with its own measurement

matrix and sampling rate (Shabani et al., 2015).

Since we do not have access to the UAV estima-

tion internal model, the proposed Kalman Filter treats

the incoming data from the UAV estimation as an up-

date measurement. The corresponding measurement

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

488

Figure 2: Flowchart of registration-assisted localization.

noise covariance is then computed through the accu-

racy given by the equipment data sheet.

The correction transformation estimation is also

treated as an update measurement. Note that the trans-

formation matrix is an 4×4 matrix, composed of a ro-

tation component and a translation component. This

work will focus only on the translational z component.

This correction is extracted from the resulting regis-

tration matrix and fed into the Kalman ﬁlter update

equation.

Therefore, the states which will be estimated by

the ﬁlter are given by

x =



x y z δz



, (3)

where x,y and z is the three dimensional pose of

the UAV and δz is the measurement error on z.

The Kalman Filter algorithm is implemented in

two steps, the prediction and the update. We assume

that the process and measurements noises are mod-

eled by a Gaussian distribution with zero mean. The

computation of the state prediction is given by

ˆx

−

= A ˆx

k−1

+ Bu, (4)

−

= AP

k−1

+ Q

, (5)

where x is the estimated state, A is the state transi-

tion model, B is the input model, u is the input vector,

P is the covariance of the estimation error and Q

the covariance of the process noise. The computation

of the state updates, or state innovation, is given by

˜e

= y

−C ˆx

−

(6)

= CP

−

+ R

(7)

= P

−

−1

(8)

ˆx = ˆx

−

+ K

˜e

(9)

= (I − K

C)P

−

, (10)

where ˜e

is the prediction error, y

is the measured

output, C is the output model matrix, R

is the mea-

surement covariance matrix and K

is the Kalman gain

matrix.

5.2 Implementation

Our implementation of the Kalman ﬁlter contains two

separate update steps, one from the estimated pose in-

coming from the sensory instrumentation of the UAV

and another from the registration correction. Thus,

we compose two different C matrices





1 0 0 0

0 1 0 0

0 0 1 −1





, (11)

which models the estimation and includes the al-

titude model error δz compensated in the measured z,

and



0 0 0 1



, (12)

which yields the estimated altitude error δz.

For this particular case, the prediction step (4) is

not performed. We compute only the update in the es-

timated covariance error (5) according to the noise co-

variance Q

which models the instrumentation noise.

This computation is calculated every time the pose is

updated.

At the same time, update equations (6)-(10) cor-

responding to C

is computed. This step uses its own

measurement noise covariance R

As soon as the registration subsystem outputs its

correction estimate, the same update equations (6)-

(10) are computed, this time using the corresponding

noise R

The measurement covariance matrix R

is related

to the UAV instrumentation, while matrix R

is re-

lated to the performance of the registration and how

much time has passed without any correction, since

we assume the uncertainty increases with the time.

For this work, we assume it to be a constant matrix

scaled by the time between registration corrections.

Altitude Correction of an UAV Assisted by Point Cloud Registration of LiDAR Scans

489

6 EXPERIMENTAL RESULTS

The developed system was evaluated through ﬁeld

tests carried out in a real stockyard (Figure 3) with

a coal stock capacity of approximately 600 thousand

tons. The plant is located in the state of Cear

a –

Brazil and is part of the Pecem Thermoelectric Com-

plex (Pecem TC), with an installed capacity of 1080

MW of active power. There are a total of three stock-

piles within the power plant. We chose one of the for

our experiments.

Figure 3: UAV in a thermal power plant.

The UAV was programmed to ﬂy over the chosen

stockpile by setting four waypoints to be tacked by

the ﬂight controller, as shown in Figure 4.

150 m

Waypoint 2

Waypoint 3

Waypoint 1

Waypoint 4

Home

Point

Figure 4: Home point and waypoints used on the experi-

ments.

During the tracking of Waypoint 1 towards Way-

point 2, the UAV was set to build the map using only

the estimates from the instrumentation, without any

registration correction, since there is still no overlap-

ping region between scans and a map. During the

tracking of Waypoint 3 towards Waypoint 4, we en-

able the registration procedure. During this period,

the local point cloud history is matched against the

previously acquired map in order to estimate devia-

tion in the altitude. The correction is then applied to

the current altitude and the frame of the UAV is up-

dated. The resulting corrections are shown in Figure

Notice how the altitude error varies over time and

Figure 5: Result of registration-assisted altitude correction.

may reach up to 3.5 m. The error be better visualized

in Figure 6.

6.1 Comparison between Registration

Algorithms

We implemented a variant registration approach to

CP-ICP, in C ++, with the aid of the PCL library, with-

out code optimization, and we conduct experiments of

alignment, simulating accumulation of data in three

different sizes of histories, thus comparing the pro-

posed method to CP-ICP and other classic algorithms,

focused on the alignment of outdoor scenes.

The comparison with the state of the art is car-

ried out between the point to point and point to plane

ICP variants, the Generalized ICP, CP-ICP and the

proposed method. The metrics used for comparison

are the smallest possible rotation and displacement to

be achieved, ε

= arccos(∆R − I)/2 (in degree) and

= µ

−µ

(where µ

and µ

are respectively the cen-

troides of the registered source cloud and the original

source cloud) and the time (in seconds), which for ap-

plications in real time must be as small as possible.

Table 1 synthesizes the rotation, translation and

cost time performance of the various registration ap-

proaches; as it is clear from the results, the proposed

method achieved top performance for each 3D model

aligned. A good performance of the proposed ap-

proach conﬁrms to some extent the expectations about

computational cost reduction due to partitioning and

density reduction through sampling with voxel grid,

a correct alignment by changing the alignment core,

performing small rotations, since the rotation error

here should be close to zero, in addition to a perfect

altitude correction. When compared to the others, we

conclude that the classic ICP make mistakes due to

bad estimates, as well the CP-ICP itself. Among those

used for comparison, only the GICP can achieve very

close results, however two orders of magnitude are

more costly.

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

490

(a) (b)

Figure 6: Side view of a history registration. In (a) the initial pose, with difference in altitude and in (b) alignment with the

proposed method.

Table 1: Table with comparison metrics for the Stockpiles scenes registration.

Scan 1 Scan 2 Scan 3

(o) ε

(m) t (s) ε

(o) ε

(m) t (s) ε

(o) ε

(m) t (s)

ICP

p2pt

59.1370 3.8866 6.8892 43.9945 1.2401 13.0223 42.2599 0.9203 19.2812

ICP

p2pl

50.488 4.3514 3.3678 40.0173 2.5921 5.1246 35.9679 2.4285 6.7039

GICP 0.7244 2.1613 60.1746 0.7593 1.7940 61.5916 1.2170 1.5967 70.1895

CP-ICP 27.4122 0.7217 1.4764 26.6329 -0.1478 2.8011 28.3209 -0.9307 4.1855

Proposed 0.6370 1.9936 0.5744 0.8080 1.7688 0.6042 0.2676 1.5011 0.6377

More deeply evaluating the algorithms, some fac-

tors, as the parameters set can inﬂuence. Particularly

we can mention as a factor of the choice of the GICP

instead of the ICP (for alignment core) the low tuning

sensitivity of the maximum distance for correspon-

dence. Generally, if this value is very small, the prob-

ability of convergence to an undesired local minimum

is high and the number of iterations to correct the pose

can increase. If this distance is too high, the transfor-

mation estimation may suffer with a loss of accuracy.

In the present work, our main problem is the altitude

correction, which contemplates this failure of the ICP.

In Figure 6, we have an example of a side view

of a clearly misaligned history, in 6(a), and the result

of the pose correction by the proposed algorithm, in

6(b).

6.2 Volume Estimation

Stockpile inventory control is an extremely important

process of the thermal power plant. The plant must

know how much coal they posses before issue any

purchase, selling or usage in the plant itself. The point

cloud generated by our experiments may be used to

give such important estimate. This estimate will also

be used to evaluate the performance of the mapping

and the impact caused by misaligned point clouds.

Figure 7 shows the top view of a cropped point cloud

corresponding to satellite image from Figure 4. A

ROI (Region of Interest) cropping was applied over

part of the stockpile.

Figure 7: Top View of ROI.

The volume was computed using an algorithm that

applies a gridding process and sums the volume dif-

ferences between the highest point in the cloud and an

arbitrary ground surface. We then set the same ground

plane for the resulting point clouds of the mapping

with and without registration and computed the cor-

responding volumes, as shown in Table 2.

Table 2: Estimated volumes.

Point Cloud Volume (m

)

Without Altitude Correction 60243.67

With Altitude Correction 54467.18

Notice that the misaligned point cloud yields a

volume error over 10%. This is a signiﬁcant amount,

considering that erroneous stockpile estimates may

heavily affect the purchase and usage of the material

within the power plant.

Altitude Correction of an UAV Assisted by Point Cloud Registration of LiDAR Scans

491

7 CONCLUSION

Among the contributions of this work, we present an

approach for the registration of point cloud of external

scenarios. The proposed algorithm takes the General-

ized ICP to a new use, aligning doubly subsampled

data. In comparison with other algorithms, the low

computational cost derives from the reduction of den-

sity by the voxelgrid and the space of the sub-clouds

of one of the sets. In terms of accuracy, changing the

alignment core, using the Generalized ICP instead of

the classic ICP (as in CP-ICP), we avoid convergence

to local minimums. We then use the proposed reg-

istration approach for correcting the altitude of the

UAV in real time. The corrections allowed the sub-

sequent mapping to be aligned to the existing map,

which helps constructing a more reliable dataset that

represents the actual stockpile surface.

ACKNOWLEDGEMENTS

This study was ﬁnanced in part by the Coordenac¸

de Aperfeic¸oamento de Pessoal de N

ıvel Superior-

Brazil(CAPES)-Finance Code 001; Financial support

from Energia Pecem and ANEEL under the grant

number PD-07267-0016/2018.

REFERENCES

Amann, M.-C., Bosch, T. M., Lescure, M., Myllylae, R. A.,

and Rioux, M. (2001). Laser ranging: a critical re-

view of unusual techniques for distance measurement.

Optical Engineering, 40(1):10 – 19 – 10.

Beland, M., Parker, G., Sparrow, B., Harding, D., Chas-

mer, L., Phinn, S., Antonarakis, A., and Strahler, A.

(2019). On promoting the use of LiDAR systems in

forest ecosystem research. Forest Ecology and Man-

agement, 450:117484.

Besl, P. J. and McKay, N. D. (1992). Method for registration

of 3-d shapes. IEEE Transactions on Pattern Analysis

and Machine Intelligence.

Chen, Y. and Medioni, G. (1992). Object modelling by reg-

istration of multiple range images. Image and vision

computing, 10(3):145–155.

Chiang, K., Tsai, G., Li, Y., and El-Sheimy, N. (2017). De-

velopment of LiDAR-based UAV system for environ-

ment reconstruction. IEEE Geoscience and Remote

Sensing Letters, 14(10):1790–1794.

Hauser, D., Glennie, C., and Brooks, B. (2016). Calibration

and accuracy analysis of a low-cost mapping-grade

mobile laser scanning system. Journal of Surveying

Engineering, 142(4):04016011.

He, H., Chen, T., Zeng, H., and Huang, S. (2019). Ground

control point-free unmanned aerial vehicle-based pho-

togrammetry for volume estimation of stockpiles car-

ried on barges. Sensors, 19(16):3534.

Holz, D., Ichim, A. E., Tombari, F., Rusu, R. B., and

Behnke, S. (2015). Registration with the point cloud

library: A modular framework for aligning in 3-d.

IEEE Robotics & Automation Magazine, 22(4):110–

124.

Huang, R., Jiang, L., Wang, H., and Yang, B. (2019). A

bidirectional analysis method for extracting glacier

crevasses from airborne LiDAR point clouds. Remote

Sensing, 11:2373.

Lin, Y.-C. and Habib, A. (2021). Quality control and crop

characterization framework for multi-temporal uav li-

dar data over mechanized agricultural ﬁelds. Remote

Sensing of Environment, 256:112299.

Mughal, M. H., Khokhar, M. J., and Shahzad, M. (2021).

Assisting uav localization via deep contextual image

matching. IEEE Journal of Selected Topics in Applied

Earth Observations and Remote Sensing, 14:2445–

2457.

Segal, A., Haehnel, D., and Thrun, S. (2009). Generalized-

icp. In Robotics: science and systems, volume 2, page

435.

Shabani, M., Gholami, A., and Davari, N. (2015). Asyn-

chronous direct kalman ﬁltering approach for under-

water integrated navigation system. Nonlinear Dy-

namics, 80(1):71–85.

Souza Neto, P., Pereira, N. S., and Th

e, G. A. P. (2018).

Improved Cloud Partitioning Sampling for Iterative

Closest Point: Qualitative and Quantitative Compar-

ison Study. In 15th International Conference on In-

formatics in Control, Automation and Robotics.

Vacca, G., Furfaro, G., and Dessi, A. (2018). The use of the

uav images for the building 3d model generation. The

International Archives of the Photogrammetery, Re-

mote Sensing and Spatial Information Sciences, pages

217–223.

Wallace, L., Lucieer, A., Watson, C., and Turner, D. (2012).

Development of a UAV-LiDAR system with applica-

tion to forest inventory. Remote Sensing, 4(6):1519–

1543.

Wang, J., Xu, L., Fan, Y., Liu, X., Tian, Z., Wang, X.,

and Cheng, Y. (2018). A method for compensating

platform attitude ﬂuctuation for helicopter-borne Li-

DAR: Performance and effectiveness. Measurement,

125:37–47.

Wang, J., Xu, L., Li, X., and Tian, X. (2011). Simulation

on impact of random attitude measurement errors on

point cloud and 3D image of ALS. In 2011 IEEE In-

ternational Conference on Imaging Systems and Tech-

niques, pages 60–64.

Yang, J., Li, H., Campbell, D., and Jia, Y. (2016). Go-

ICP: A Globally Optimal Solution to 3D ICP Point-

Set Registration. IEEE Transactions on Pattern Anal-

ysis and Machine Intelligence.

Zhang, W., Yang, D., Li, Y., and Xu, W. (2020). Portable

3D laser scanner for volume measurement of coal pile.

In Communication, Signal Processing, and Systems.

Lecture Notes in Electrical Engineering, volume 517,

pages 340–347.

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

492