Identiﬁcation of Critical Links within Complex Road Networks using

Centrality Principles on Weighted Graphs

Nirupam Bidikar

1 a

, Yunpeng Zhang*

,2 b

and Fengxiang Qiao

3 c

Dept. of Computer Science, University of Houston, Houston, U.S.A.

Dept. of Information and Logistics Technology, University of Houston, Houston, U.S.A.

Innovative Transportation Research Institute, Texas Southern University, Houston, U.S.A.

Keywords:

Resilience, Graphs, Roadway Infrastructure, Geographic Information Systems, Centrality, Betweeness, Node

Criticality, Link Criticality.

Abstract:

Building resilient infrastructure has become a necessity in modern times. If a system can efﬁciently deal

with failures, it is considered resilient. Roadways are some of the most vital infrastructures in the world. Their

collapse due to unprecedented calamities would disrupt the normal functioning of society and cause signiﬁcant

ﬁnancial loss. To minimize trafﬁc jams and keep trafﬁc ﬂowing during such times, it is essential to identify

important roads within a network and plan alternate routes to divert trafﬁc. This study aims to ﬁnd critical links

in a road network and study their relationships with important nodes in the same network. It also highlights

some traditional approaches and applies graph-theory concepts to measure node and edge importance within

a network. An approach based on variable centrality is proposed. We have implemented our proposed system

and evaluated its performance on multiple networks including a large scale statewide road network in Texas.

Our preliminary experiments show promising results.

1 INTRODUCTION

Transportation networks are vital components in as-

sessing a country or state’s planning and infrastruc-

ture capabilities. They also play a crucial role in the

region’s economy and ﬁnancial standing as they are

one of the essential means of trade. Natural calami-

ties and disasters are some of the events that mas-

sively affect (Mattsson and Jenelius, 2015) transporta-

tion infrastructure. Due to their sudden and unpre-

dictable nature, no amount of preparation is sufﬁcient

to tackle them. (Karagyozov et al., 2012) showcased

that around 44 million euros worth of damage had

been generated on Bulgaria’s transportation infras-

tructure as a result of natural disasters. In such sit-

uations, most people take alternate shortest routes to

reach their destination. This may lead to users choos-

ing roads which are unable to accommodate this new

inﬂux of vehicles causing blockages and trafﬁc jams.

This effect can cascade over through the network and

can compromise multiple roads making them inop-

https://orcid.org/0000-0002-3452-4094

https://orcid.org/0000-0001-6208-9571

https://orcid.org/0000-0001-9074-0288

erable. To tackle such situations and be prepared to

lessen their impacts, there is a need for effective meth-

ods to identify critical links or roads within a given

network. Through proper planning, trafﬁc has to be

properly rerouted through these critical links which

are able to function at a greater operating capacity

until the primary roads are restored to their original

state.

Road networks can be essentially represented as

giant graphs, with intersections or cities being the

nodes and roadways being the edges. Converting

geospatial data like road networks into functional

structures like graphs requires signiﬁcant preprocess-

ing to address topological errors resulting from, e.g.,

discretized digital coordinate systems. Once that hur-

dle is overcome, one can obtain a network where all

concepts from graph theory like centrality can be di-

rectly applied. Finding alternate routes between a

source and destination can be solved as k-shortest

paths problem using routing algorithms like Djikstra’s

Algortihm or Bellman-Ford Algorithm. These algo-

rithms don’t necessarily give routes which consider

trafﬁc volume and sudden change in ﬂow of trafﬁc.

The critical links we seek should consider the overall

connectivity and the operating capacity of the edge

542

Bidikar, N., Zhang, Y. and Qiao, F.

Identiﬁcation of Critical Links within Complex Road Networks using Centrality Principles on Weighted Graphs.

DOI: 10.5220/0010583605420549

In Proceedings of the 16th International Conference on Software Technologies (ICSOFT 2021), pages 542-549

ISBN: 978-989-758-523-4

which can be calculated though graph properties such

as centrality.

Traditional methods of ﬁnding centrality and node

importance are not relevant in weighted and directed

graphs (Opsahl et al., 2010). Recently, researchers

have developed many metrics to represent these prop-

erties for weighted graphs accurately. On road net-

works, not all links have the same functional capac-

ity and importance, and it is crucial to incorporate

this distinction within analyses. This paper shows

how essential links can be identiﬁed within complex

road networks using centrality principles on weighted

graphs. It also gives precedence to the structural prop-

erties of the network which has a signiﬁcant impact on

the proposed centrality metric. Road transport metrics

like edge capacity and daily trafﬁc value are consid-

ered as edge weights to analyze networks better on a

higher level.

The paper is organized as follows. Section 2 high-

lights some of the research done in this ﬁeld. Sec-

tion 3 introduces several metrics used to quantify con-

nectivity within a network. Section 4 describes data

collection and processing methodology used to per-

form analyses. Section 5 shows the impact of destroy-

ing edges within a network using a synthesised graph

and a real world graph. We also propose a solution

to identify critical links in the network and demon-

strate its performance on real world graphs. Finally

we present conclusions of our work and future direc-

tion of our research.

2 RELATED WORK

(Gauthier et al., 2018) performed stress tests on links

to ﬁnd out critical connections in networks. The au-

thors experimented with real-world scenarios, includ-

ing trafﬁc ﬂows. They compared results with topo-

logical methods, which have a more signiﬁcant com-

putational overhead, showing that the criticality of

links depends on the metric being evaluated. This

method seems to be a viable option to determine crit-

ical links. While their research was limited to a small

net work, their results look promising. (Almotahari

and Yazici, 2020) introduced link criticality index for

ranking connections. They used network ﬂows to

evaluate the criticality of a link using readily avail-

able sensor and trafﬁc data. They were able to ﬁnd

critical links in the network using only the top 20% of

the origin-destination pairs. This approach might not

fare well for all kinds of network structures. Network

topology dramatically affects the performance of this

algorithm. (Furno et al., 2018) proposed a framework

to identify vulnerable nodes in large scale road net-

works. Road networks are modelled as graphs and big

data techniques were used to improve performance.

Betweenness centrality metric is used to evaluate the

critical nodes. Resilience metrics - Vulnerability, ef-

ﬁcient information exchange were used to evaluate

their procedure. City scale networks were represented

as undirected graphs independent of contextual traf-

ﬁc data. (Li et al., 2020) proposes a “Trafﬁc Flow

Betweenness index”(TFBI) to identify critical links

in a network. The index is determined by shortest

travel path, trafﬁc ﬂow, and origin-destination de-

mand. Critical links determined using TFBI are se-

lected and masked from the network to assess their

impact. Compared to the traditional methods, their

approach is computationally less intensive. However,

their method does not consider non-linear effects due

to degradation of connectivity in a sub-network af-

fecting the rest of the network. (Herrera et al., 2016)

analyzed the resilience of water distribution networks

using graph concepts. Their approach involved calcu-

lating redundant paths between nodes and generating

ﬂow graphs to analyze edge operating capacity and

maximum ﬂow through the system. This approach is

suitable for analyzing networks with a threshold for

edge capacity and can scale for large networks.

(Bhatia et al., 2015) studied the Indian railway

network, ﬁnding out critical links using percolation

theory. They selected the giant component (largest

connected part of the network) from the network to

perform their analysis and established a metric ”crit-

ical functionality” which is the ratio of nodes in gi-

ant component to that in the original network. Later

they experimented by removing individual nodes and

routes and observing the overall connectivity of the

network. (Singh et al., 2015) developed a service built

using PostGIS and pgRouting, which helps calculate

alternate shortest paths in the event of a natural disas-

ter or any similar incident that compromises an edge.

(Henning et al., 2017) developed a method to

identify critical networks within small city networks

using the centrality indices of edges. They propose a

function that depends on the centrality indices, which

classiﬁes each edge as critical or non-critical. This pa-

per serves as an essential basis for our solution as we

are interested in analyzing the relation between node

and edge importance in large-scale networks.

(Opsahl et al., 2010) published a study in which

they have conducted extensive work to generalize

centrality measures for weighted graphs networks and

ﬁnd the shortest paths among such networks. (Pas-

sos and Cardoso, 2020) followed up on the previously

mentioned paper and suggested improvements to the

metrics. They suggested that using logarithmic ratios

to calculate variable node centrality would minimize

Identiﬁcation of Critical Links within Complex Road Networks using Centrality Principles on Weighted Graphs

543

errors and extend the range of varying parameter (α)

as shown in the equations below.

log,α

(u) = log(

) ∗ α + log(k

) (1)

log,α

(u) = log(

(u)

) ∗ α + log(C

(u)) (2)

where, C

represents degree centrality, C

represents

closeness centrality, s

is strength of a node, and k

the degree of a node.

Most of the research done in this ﬁeld is based on

either topology alone or edge weights. As seen from

the study by (Opsahl et al., 2010), we can see how

both these factors are essential to determine central-

ity measures in a weighted graph. Our approach aims

to solve this problem by extending the research done

by (Passos and Cardoso, 2020) and apply it to large

real world networks like road transportation systems.

We also study the relation between node and edge im-

portance in a complex network and how variable cen-

trality is affected by changing the precedence given to

weighted centrality.

3 METRICS FOR

CONNECTIVITY AND

IMPORTANT COMPONENTS

In this section we introduce deﬁnitions of various

metrics relevant to assessing the connectivity and re-

silience of a graph.

3.1 Average Shortest Path

It is the average distance between all possible pairs

of points along the shortest possible paths. This met-

ric gives an idea about how the network is connected

overall and the effort it takes to transmit information

among nodes.

3.2 Flow

Flow networks are graphs which showcase connectiv-

ity based an edge’s capacity. Every edge has a ﬂow

parameter which constitutes to the operating limits

of the particular edge. The ﬂow of an edge is ﬁxed

and cannot change. During operation, the informa-

tion ﬂow cannot exceed the set limit deﬁned by the

edge.

3.3 Closeness Centrality

Closeness Centrality depends on distance between a

pair of nodes. Smaller the distance of a node with re-

maining nodes in a network, the greater it’s centrality.

3.4 Betweenness Centrality

This metric measures the importance of a node in the

network. It depends on the number of shortest paths

passing through a vertex for a given pair of start and

end points. Higher the centrality, greater is the inﬂu-

ence of the node on the network meaning it’s disrup-

tion can cause signiﬁcant problems.

3.5 Service Area

A service area deﬁnes a region accessible from a start-

ing point given a distance using the network. A test

was performed on the highway network of Texas us-

ing the major cities as starting points and the output is

shown in Figure 1.

Figure 1: Service area for 100 KM.

3.6 Origin-destination Cost Matrix

OD cost matrix calculates shortest paths between

pairs of nodes within a network. The distance cal-

culated can be euclidean or along the polylines in the

network. This metric is used in GIS for routing prob-

lems involving multiple origins and destinations.

4 DATA COLLECTION AND

PREPROCESSING

The datasets used in this paper were collected for

performing analysis in ESRI Shapeﬁle format (ESRI

and PaperdJuly, 1998) which consists of polylines

and points. The Highway Performance Monitor-

ing System (HPMS) data (TxDOT, 2019) contains

highway performance metrics for the roadway net-

work like average daily trafﬁc volume and maximum

ICSOFT 2021 - 16th International Conference on Software Technologies

544

operating capacity. Texas roads were taken from

TIGER/Line dataset (Bureau, 2020) which shows the

major road system of the state. Texas cities data was

obtained from Open Data Portal (Portal, 2020) hosted

by TxDOT which is a repository for many geospa-

tial datasets. We chose to add in another dataset for

road network obtained from (Survey, 2014) to verify

the effect of topography on our results. This graph is

more generalized and less complex than the TIGER

dataset.

The data was compiled together in a PostgreSQL

database and a spatial index was created for fast

retrieval and processing. Using the PostGIS and

pgRouting extensions, the shapeﬁles were checked

for topological errors like dangles, self loops, and par-

allel vectors, and shape length for each line segment

was also calculated. The cities database was ﬁltered

based on population of city from year 2010. Top 30

cities were selected for analysis. Giant component

(Bollob

as, 2001) of the Texas road network was taken

to exclude broken links as the network is too com-

plex to manually repair. All analysis was done using

QGIS (QGIS Development Team, 2021) toolbox and

PyQGIS library for custom scripts.

5 IMPACT OF EDGE REMOVAL

IN NETWORKS

In this section, we present details of our empirical

work which show the effect of edge removal within

a network.

5.1 Experiments with Dummy Graph

Networks

Initial experiments proceed with generating graph

structures with one of them being poorly connected

and the other being well connected. We start remov-

Figure 2: Well connected

graph (WCG).

Figure 3: Poorly con-

nected graph (PCG).

ing edges and calculate the metric “average shortest

path length”. In Figure 4, the blue line represents

the poorly connected graph shown in Figure 3 and

the yellow line represents the well-connected graph

shown in Figure 2. The test was performed with both

graphs having 30 nodes each. We chose to take the

Figure 4: Edges removed vs (avgshortest pathlength)

−

inverse of the metric because the poorly connected

graph gets split into multiple components as we keep

removing nodes there by making the average shortest

path length inﬁnity. We can observe from Figure 4

that this value drastically drops for PCG whereas the

decline is smoother for the WCG.

5.2 Experiments with Real Road

Networks

A separate view was created by removing different

highway systems. The shortest routes for an un-

touched network can be seen in Figure 5. These were

plotted using Dijkstra’s algorithm.

Figure 5: Regular Shortest Paths.

Removing interstate highways created measur-

able change in shortest paths between destinations as

shown below in Figure 6. The extreme left of the state

is cut off from the rest based on the our given network.

Identiﬁcation of Critical Links within Complex Road Networks using Centrality Principles on Weighted Graphs

545

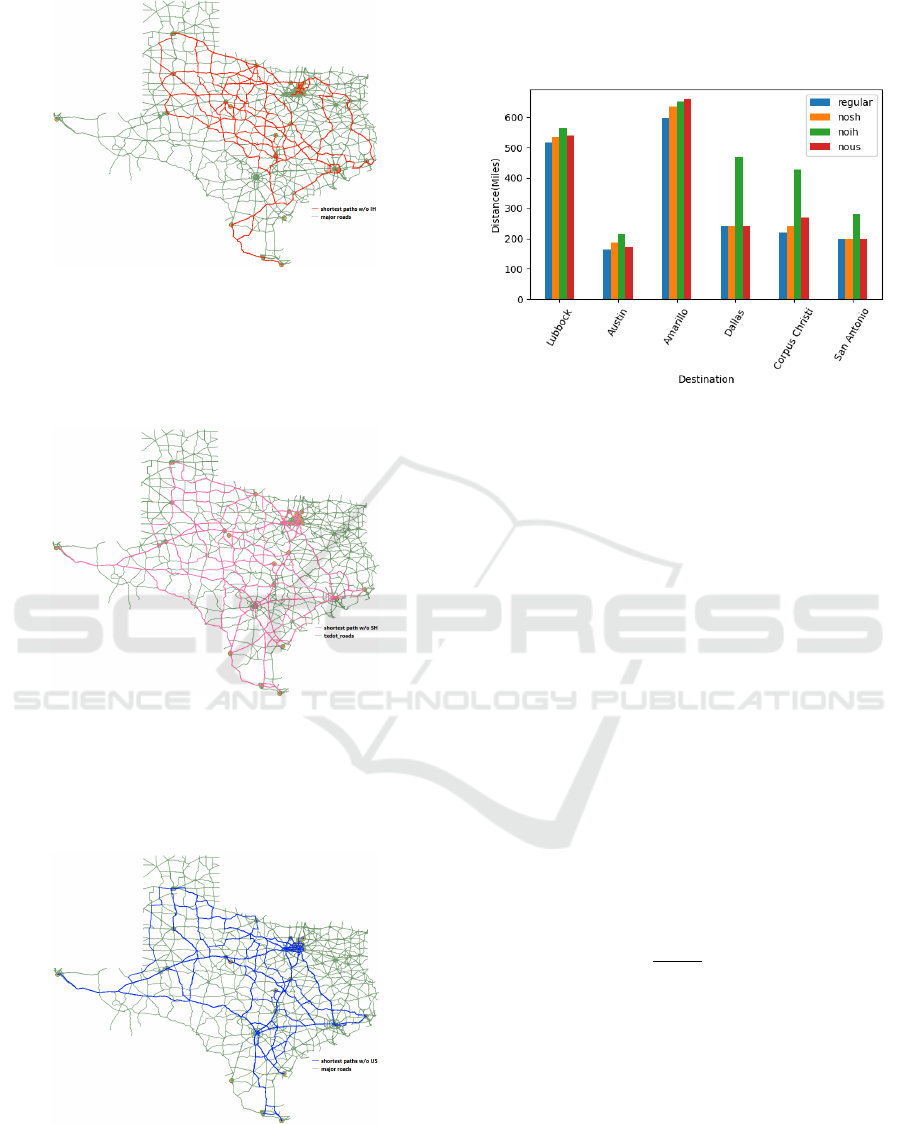
Figure 6: Shortest Paths without Interstate Highways.

Disabling state highways did not have as drastic of

an effect as removing interstate highways as shown in

Figure 7 hinting towards the apparent importance of

Interstate highways.

Figure 7: Shortest Paths without State Highways.

Removal of US highways did not affect the end

to end connectivity much but it did considerably in-

crease the cost of travel between destinations as seen

from Figure 8.

Figure 8: Shortest Paths without US Highways.

Based on the empirical observations from the ex-

periments so far, we considered OD cost matrix as a

basis to study road network deterioration. We gener-

ated tables for all 4 views and selected Houston, Texas

as the origin and 6 other cities as destinations which

are spread across the state to highlight end to end con-

nectivity which is shown in Figure 9 below.

Figure 9: Shortest Path Variation on edge removal.

We can see that for major cities like Corpus Cristi,

San Antonio, and Dallas, Interstate Highways play a

crucial role in fast connectivity. For Austin, alternate

routes almost have the same distance as the original

shortest path which indicates disrupting the direct link

to Austin would not affect overall travel time to that

city.

6 PROPOSED SOLUTION

We propose a procedure to assess criticality of an

edge based on the importance of the nodes it con-

nects using local characteristics of the node and its

connectivity with the remaining network. The nodes

are evaluated using the variable centrality metric and

is also indirectly used to ﬁnd out critical links. Initial

exploratory analysis with variable closeness central-

ity did not show favorable results, which led us to try

Betweenness, as deﬁned in Equation 3.

log,α

(u) = log(

(u)

) ∗ α + log(C

(u)) (3)

Variable Betweeness centrality C

log,α

(u) depends

on weighted betweeness centrality C

(u) which takes

into account the impact of an edge and regular be-

tweeness centrality C

(u) which considers connectiv-

ity of a given node with rest of the network.

We begin with calculating centrality metrics for

the weighted and unweighted networks. Then we

compute the variable centralities using Equation 3 by

varying α for different views on the network based on

the node’s individual and global impact.

The nodes are ranked based on C

log,α

(u), and the

ICSOFT 2021 - 16th International Conference on Software Technologies

546

top 900 are selected. We combine the different short-

est path views as shown in section 5.2 and a spatial

join is performed to check the percentage of nodes

that lie on these edges in shortest paths between the

cities. (Br

ohl and Lehnertz, 2019) showcases the rela-

tionship between node-edge importance based on the

centrality metrics. Their study shows that around 60%

of the critical nodes ranked using betweenness cen-

trality lie on the network’s shortest paths. Inspired by

this approach, we choose the shortest paths to validate

our critical nodes and also extract critical edges based

on this approach. Attributes like path length, average

daily trafﬁc volume, maximum operating capacity are

used as edge weights to calculate centrality metrics.

7 RESULTS

Not all edges within a network have the same level of

importance. The statistics such as daily trafﬁc volume

and maximum operating capacity suggest that some

roads are more important than others. We observed

how ranking using different centrality metrics would

change edge identiﬁcation.

7.1 Complex Graph

Out of 12,118 nodes in our network, around 4,614 lie

on the shortest paths between the selected 30 cities.

The top 900 nodes in intervals of 100, are selected

based on the centrality metrics. In each value range,

we check the percentage of nodes lying on the short-

est paths, which are shown in Figure 10. Between-

Figure 10: Plot showing percentage of nodes lying on

Shortest Paths with respect to top 900 Nodes.

ness gives a higher rank to nodes with better local

connectivity and the maximum number of shortest

paths passing through them irrespective of edge im-

portance. Variable Centralities (α > 1, α < 1) show

a more realistic output considering the entire network

while evaluating the node.

Figure 11: Edges covered when certain number of nodes are

selected.

A plot to show edge coverage as ranking range

(top 100 - 900 nodes) was increased is shown in Fig-

ure 11. From this plot, we can observe that the met-

ric with a steeper line covers greater edges within the

shortest paths. Increasing α makes variable centrality

very selective about the nodes it chooses. This leads

to the solution missing out on some edges with rea-

sonable properties (as seen from Figure 12).

Figure 12: Average accumulated edge weight with respect

to top 900 Nodes.

When no preference is given to weighted central-

ity, we fall back to our original Betweenness metric.

This has less node and edge coverage due to main

ranking factor being local connectivity. Overall, when

0 < α < 1, our metric performs the best, having re-

spectable node, edge coverage, and reasonable aver-

age edge weights.

Identiﬁcation of Critical Links within Complex Road Networks using Centrality Principles on Weighted Graphs

547

7.2 Simpliﬁed Graph

The simpliﬁed graph has 15,309 nodes and 16,662

edges. There are no multiple edges between any two

pairs of nodes in this graph. We could not join the

weights from the HPMS dataset to this graph for a

similar metric analysis. Hence, we focus only on the

topology and how it affected our results.

6,762 nodes lie on the shortest paths, and there ex-

ist 7,281 edges that belong to the shortest path among

the 30 cities. From Figure 13, we can see that it is

consistent with the deﬁnition of betweenness. All of

Figure 13: Percentage of nodes lying on Shortest Paths with

respect to top 900 Nodes.

the top 200 nodes ranked by betweenness lie on the

shortest paths. Similarly, if we look at Figure 14, the

number of edges covered increases almost linearly as

the range of nodes increases.

Figure 14: Edges covered in Shortest Paths with respect to

top 900 Nodes.

Comparing the results of this graph with those in

Section 7.1, we can see the effect that the topology

has on the centrality and its subsequent effect on edge

importance.

8 CONCLUSIONS

Identifying critical links within road networks is ex-

tremely important for transportation and planning.

Our research has shown the impact of disabling ma-

jor highway links on inter-city travels within a State.

We also showcased a method to rank critical nodes

based on variable centrality and extract respective

edges originating or terminating on them under the

assumption that edge criticality is directly dependent

on node criticality. Below we list other insights from

our research and the future direction.

Topology has had a considerable inﬂuence on the

experiment results. The Complex graph had many

illegal values for the variable centrality metric due

to topological errors and disconnected components in

several places. This made our approach very sensitive

towards even the smallest error. In future research,

we aim to experiment using more real-world road net-

works and develop ways to handle these errors. Our

approach currently works by considering the network

as a single mode network (Opsahl et al., 2010). We

would like to extend our research by viewing it as a

two mode network and testing variable centrality on

it.

Inferring edge centrality in a complex network

from node centrality is a challenging problem. The

prevalent edge ranking algorithms need signiﬁcant

improvement to predict the shortest path links when

the network is complex. Variable centrality ranking

often (incorrectly) better ranks nodes not lying on

the shortest paths. We can also infer that there exist

other shortest paths with similar weighted distances

but a different route within the network. Our future

research would improve the variable centrality met-

ric by considering additional graph properties cover-

ing the entire network. Our procedure used a metric

similar to recall (Van Rijsbergen, 2004) for evaluat-

ing edge ranking algorithms that assess the number of

correctly guessed links on the shortest path. Another

assessment of interest would be precision (Van Rijs-

bergen, 2004) like metric, which would quantify the

number of irrelevant links ranked higher than correct

links. We are also interested in theoretically inves-

tigating the limitations of the existing ranking algo-

rithms since they rely on very myopic information

about the graph. We also would like to explore ﬂow

analysis within trafﬁc networks and combine it with

variable centrality to validate the results. Measuring

trafﬁc ﬂow through extracted critical edges can be a

good metric to determine criticality of those links.

ICSOFT 2021 - 16th International Conference on Software Technologies

548

ACKNOWLEDGMENT

This work is funded by Acquisition of an Advanced

Trafﬁc Management Systems for Cyber and Physical

Security Research, UH High Priority Area Research

Equipment Award, University of Houston, U.S.A.

REFERENCES

Almotahari, A. and Yazici, A. (2020). Practice friendly

metric for identiﬁcation of critical links in road

networks. Transportation Research Record, page

0361198120925475.

Bhatia, U., Kumar, D., Kodra, E., and Ganguly, A. R.

(2015). Network science based quantiﬁcation of re-

silience demonstrated on the indian railways network.

PloS one, 10(11):e0141890.

Bollob

as, B. (2001). The evolution of random graphs—the

giant component. In Random graphs, volume 184,

pages 130–59. Cambridge university press Cam-

bridge.

ohl, T. and Lehnertz, K. (2019). Centrality-based iden-

tiﬁcation of important edges in complex networks.

Chaos: An Interdisciplinary Journal of Nonlinear Sci-

ence, 29(3):033115.

Bureau, U. C. (2020). Tiger/line shapeﬁles.

ESRI, U. and PaperdJuly, W. (1998). Esri shapeﬁle techni-

cal description. Comput. Stat, 16:370–371.

Furno, A., El Faouzi, N.-E., Sharma, R., Cammarota, V.,

and Zimeo, E. (2018). A graph-based framework

for real-time vulnerability assessment of road net-

works. In 2018 IEEE International Conference on

Smart Computing (SMARTCOMP), pages 234–241.

IEEE.

Gauthier, P., Furno, A., and El Faouzi, N.-E. (2018). Road

network resilience: how to identify critical links sub-

ject to day-to-day disruptions. Transportation re-

search record, 2672(1):54–65.

Henning, S., Biemelt, P., Abdelgawad, K., Gausemeier,

S., Evers, H. H., and Tr

achtler, A. (2017). Method-

ology for determining critical locations in road net-

works based on graph theory. IFAC-PapersOnLine,

50(1):7487–7492.

Herrera, M., Abraham, E., and Stoianov, I. (2016). A

graph-theoretic framework for assessing the resilience

of sectorised water distribution networks. Water Re-

sources Management, 30(5):1685–1699.

Karagyozov, K., Razmov, T., Todorova, M., Varadinova, J.,

and Dzhaleva-Chonkova, A. (2012). Impact of nat-

ural disasters on transport systems–case studies from

bulgaria. Report from the International Panel of the

WEATHER project funded by the European Commis-

sion’s 7th framework programme. Soﬁa.

Li, F., Jia, H., Luo, Q., Li, Y., and Yang, L. (2020). Identi-

ﬁcation of critical links in a large-scale road network

considering the trafﬁc ﬂow betweenness index. Plos

one, 15(4):e0227474.

Mattsson, L.-G. and Jenelius, E. (2015). Vulnerability and

resilience of transport systems–a discussion of recent

research. Transportation Research Part A: Policy and

Practice, 81:16–34.

Opsahl, T., Agneessens, F., and Skvoretz, J. (2010). Node

centrality in weighted networks: Generalizing degree

and shortest paths. Social networks, 32(3):245–251.

Passos, R. S. and Cardoso, D. O. (2020). Extrema anal-

ysis of node centrality in weighted networks. arXiv

preprint arXiv:2011.00429.

Portal, T. O. D. (2020). Texas cities.

QGIS Development Team (2021). QGIS Geographic Infor-

mation System. QGIS Association.

Singh, P. S., Lyngdoh, R. B., Chutia, D., Saikhom, V.,

Kashyap, B., and Sudhakar, S. (2015). Dynamic short-

est route ﬁnder using pgrouting for emergency man-

agement. Applied Geomatics, 7(4):255–262.

Survey, U. G. (2014). National atlas of the united states.

TxDOT (2019).

Van Rijsbergen, C. J. (2004). The geometry of information

retrieval. Cambridge University Press.

Identiﬁcation of Critical Links within Complex Road Networks using Centrality Principles on Weighted Graphs

549