Searching & Generating Discrete-Event Systems

T. J. Helliwell

, B. Morgan

and M. Mahfouf

Automatic Control & Systems Engineering Department, University of Sheffield, Sheffield, England

Advanced Manufacturing Research Center (AMRC), University of Sheffield, Sheffield, England

Keywords: Generative Models, Discrete-Event Systems, Variable Structures, Event Calculus, Metaprogramming.

Abstract: In this paper we introduce a new method for the automatic generation and computer experimentation of

Discrete-Event Systems (DES). We introduce the concept that DES descriptions may be used to define a

searchable configuration space. Configuration instances in this space a represented as a permutation encoding

which shows the number-of and types-of resources in a given configuration. Each instance is checked that the

number of resources does not exceed a maximum and whether a fixed set of processes (a decomposed goal of

uncertain time intervals drawn from a Gaussian distribution) can be logically completed on the given set of

resources. If the permutation instance satisfies these constraints, it is subsequently constructed as a simulation

model to quantify completion through global features of makespan and total processing time. We claim this

is the basis for a powerful tool in high-level informed design of these types of systems that have hitherto

avoided autonomous description or have been previously individually designed using time consuming

manually defined programs.

1 INTRODUCTION

The fields of engineering and computing have

synergistically supported one another in providing

tools to enhance humanities ability to shape our

world. Various forms of ‘Electronic Design

Automation’ (EDA), including optimisation of

hypotheticals in the broadest sense under the context

of Model Driven Engineering (MDE), have allowed

engineering tasks to be presented in appropriate

mathematical structures to be utilised by computer

programs. As a result of the ability of computers to

inform design decisions, the computer becomes a part

of the engineer’s cognitive process allowing

engineers to sit at a higher level of abstraction –

typically defining the system constraints and goals. It

is inevitable this trend will accelerate, EDA being one

of the most established software disciplines to utilise

design automation. In a broader-still context,

Generative Modelling has emerged as software

process in which a program assists in the design

modelling of a wide range of mediums including

sound, images, animations and products. In this work

we show how Discrete-Event Systems (DES) that can

be generalised as a ‘logical graph structure’ which

defines a constrained space of sub-DES. These

instances can be generated autonomously using a

functional-style programming approach and then

simulated using non-deterministic processing time

intervals to quantify their performance. The program

itself is inspired by the metaprogramming capabilities

of the LISt Processing (LISP) programming language

but written in MATLAB

DES express phenomena that can only be

described through two distal model-theoretic

viewpoints; on the one hand, by considering their

logical graph structure (a computer-science

theoretical approach, in which analogies to Cellular

Automata (CA), Markov Logic Networks (MLN),

message passing networks, or even representation of

a Chess board, in which places - squares - are

resources) or on the other hand, through statistical

modelling of the dynamic (i.e. time-focused)

evolution of the system, which draws somewhat

predictably from the fields of a simulation, computer

programming and statistics.

The former is related to the state space definition

as a disjoint sum, as opposed to the Cartesian

product, which removes the necessity to declare

variables not required as simply undefined. There

have been little to no attempts to unify or understand

these two aspects of the DES field explicitly in a

coherent framework, despite the fact that they are

inextricably linked – the structure, and discrete-time

Helliwell, T., Morgan, B. and Mahfouf, M.

Searching Generating Discrete-Event Systems.

DOI: 10.5220/0010584302030210

In Proceedings of the 18th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2021), pages 203-210

ISBN: 978-989-758-522-7

203

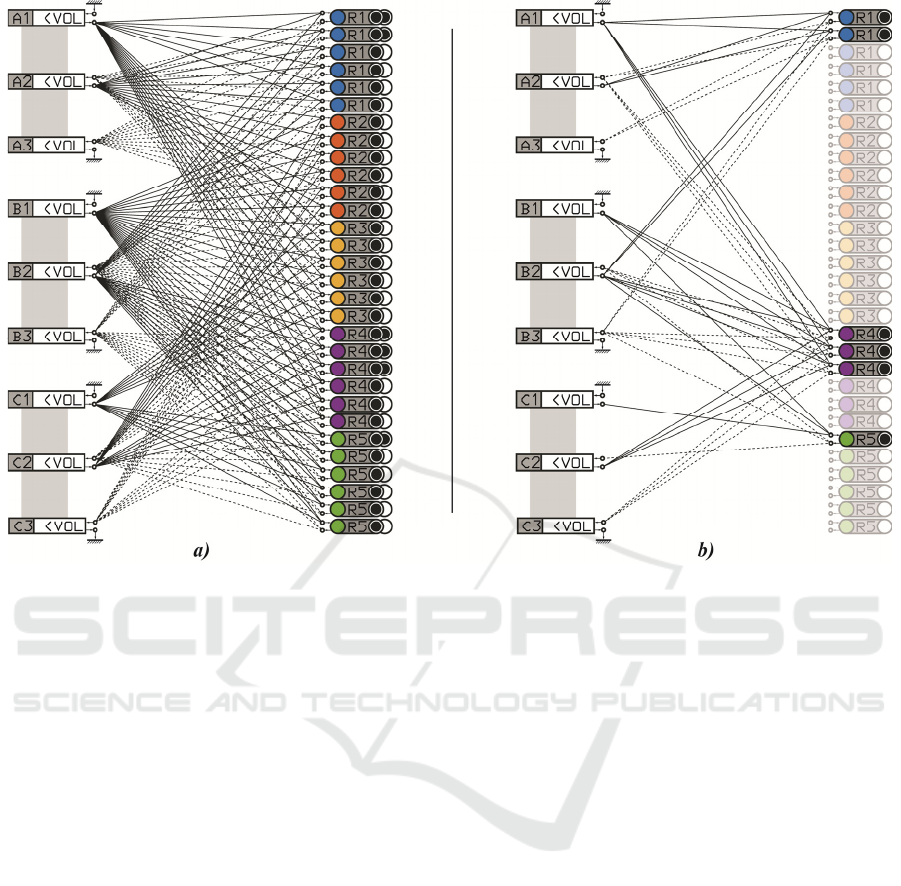
Figure 1: Discrete-Event Systems; in a) we have all possible DES configurations together, which can be seen by the high

number of relations between processes that are queued on the left and their respective resources on the right. In b) we show

the ‘highest performing’ configuration: it logically completes the processing; it satisfies the constraint of a maximum of 6

resources; when it is generated and simulated it is found to be the most performant.

process viewpoint allows us to both consider a

‘space’ of possible structural DES configurations and

subsequently establish how they stand in relation to

one another when actualised through simulation and

statistical uncertainty propagation. As shown in this

paper, statistical information indicates that logical

graph structure has an unequivocally fundamental

and exploitable impact on system dynamics and

consequentially has many applications in many real-

world systems. An accessible approach to enable

computers to explore this configuration space is a

powerful and useful tool in the discrete or

combinatorial optimisation of many highly

commercially valuable systems, allowing supply

chains, logistical systems and manufacturing systems

to be brought into the fold of EDA in a design

perspective, and move towards ideals of Industrie 4.0

in regards to control.

1.1 Previous Work

There is very little previous work to be found though

searching for automatic generation of DES

specifically. However, on a more general level, early

work oriented around modelling theory and how DES

stands in relation to automation and Artificial

Intelligence (AI). As early as 1984, Klir, as part of a

holistic approach to systems modelling architectures,

focused on techniques for inductive System

Identification (SI) of systems with variable structures.

Whereas Zeigler, also in 1984, who coined the

term ‘variable structure model’, was primarily

concerned with capturing this phenomena through

simulation – computer programs. (Uhrmacher &

Arnold, 1994), explored a constructive view of

autonomous agents in which hierarchical,

compositionally organised, internal models that

describe an agent-environment coupling are

fundamentally discrete-event structures, and are

thereby central to progress in AI. The term processors

is seen here also, and uses an analogy of ‘hiring’ and

‘firing’ to indicate processor instantiation under

response to different workloads and development of

strategies to undertake them. (Barros, 1995), and

previously in (Barros, Mendes, & Zeigler, 1994),

introduce the concept of ‘dynamic structure’

computer modelling [presumably inspired by

Variable Structure Modelling in (Zeigler, Kim, &

Lee, 1991) and (Zeigler & Praehofer, 1989) neither of

which are accessible] which extended the original

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

204

Discrete-Event System Specification (DEVS)

formalism that assumes a static structure of the

system with a formalism known as Dynamic

Structure Discrete Event System Specification

(DSDEVS), extending DEVS via a special model

called a network executive. (Uhrmacher, 2001) states

the motivation and necessity for capturing structural

changes via variable structure models originated in

sociological and ecological applications.

Recent formalisation work by (Ay, 2020) defines

characteristics of robustness is in ‘invariance of their

function against the removal of some of their

structural components’. We argue that the advent of

Industrie 4.0 – the information age – decentralised

multi-agent technological systems will begin to

reflect these same properties. It is broadly agreed that

autonomous systems or agents must model

concurrent dynamics in actions, interactions,

composition and robust behaviour that features the

appearance, disappearance and movement of entities.

Most closely to this work, Aspenti & Busi in 1996

(Asperti & Busi, 2009) [appeared as a technical report

in 1996, but later published in 2009] presented Mobile

Petri Nets (MPN) that use join-calculus to support a

change of coupling between nodes; and Dynamic

Petri Nets (DPN) that support additions of new Petri

Net components, both via firing of transitions on a

higher level to create new complete net structures –

new models – in which is thus a DSDEVS.

(Perrica, Fantuzzi, Grassi, & Goldoni, 2010)

discussed in detail requirements surrounding DES

experiments and design of such experiments in

regards to interactions between samples drawn from

probability distributions. Perrica made some

important points about ‘proper configuration’ of

simulation experiments, namely; a great deal of

attention is paid to model development, verification

and validation steps [see (Van Tendeloo &

Vangheluwe, 2019) for a brilliantly clear tutorial

exposition of these steps], whereas comparatively

little attention is paid to what might be summarised as

Design of Experiments (DoE).

Although the generality of DES will affect the

necessity to focus on one aspect or another, for

example; some work primarily use DES formalisms

to address logical graph structures only by omitting

consideration of time as a variable completely, and

instead, only consider ordering or sequencing of

events. In description of a DES, a ‘global’

understanding of state space, state transitions and

output function is required, so we broadly support this

argument, and it is reflective in this work that model

development, verification and validation is not only

time consuming - making a strong argument for its

automation - but also may help to address the need for

more attention (vis-a-vis researcher time) to statistical

analysis by defining the logical graph structure only.

(Cai & Wonham, 2010) consider a top-down

approach by a decomposition of a monolithic

(centralised) for supervisory control in pre-defined

DES systems. Wonham, developer of foundational

work in DES (Ramadge & Wonham, 1989), has

focused primarily on synthesis of supervisory control

as opposed to establishing theory surrounding scalar

comparisons between different DES. That said, the

ability to control DES systems is severely complex

and any statements regarding their overall

performance must be restricted to global feature

summaries using typical initial states and goal states

[as it is here], in the form of a ‘job-shop scheduling’

problem formulation.

(Jiao, Gan, Xiao, & Wonham, 2020), [with prior

work in (Jiao, Gan, Yang, & Wonham, 2016) and

(Macktoobian & Wonham, 2017)] discuss an

approach for reduction in the computational

complexity by grouping together identical processes

and ‘achieve controller reduction by suitable

relabelling of events’ to exploit symmetry inherent to

many DES. In addition to describing a computational

model of DES, in the final part of (Van Tendeloo &

Vangheluwe, 2019)’s work, a queueing system is

considered, and they undertake performance analysis

regarding how the number of resources stands in

relation to the average and maximum queuing times.

In defining a ‘maximum queuing time’, a constraint

is defined, and they discover that 2 resources is the

minimum to satisfy this constraint, whilst it is

speculated that 3

would be quantifiably optimal based

on the future definition of a cost function that trade-

off the waiting of jobs to the cost of adding additional

resources.

2 METHODOLOGY

DES are defined by a discrete state space

representation and asynchronous discrete events. It is

evident that a variable structure model could be

represented in such a way that a static structure is used

to fully enfold all possible variable or dynamic

structural change and associated possible state space

by exploiting either model-based conditionals [See

Fig. 1. a)] or hardcoding intricate conditional

structures as mentioned by (Uhrmacher, 2001).

It is unfeasible for large models, and applications

such as the one outlined in this work, in which the

purpose is to automate the process of model

construction and simulation, to approach the problem

Searching Generating Discrete-Event Systems

205

in this inefficient and less elegant manner. We

consider instead a stochastically searched

configuration space of sub-DES, represented as a

sequence of real-valued integers, called a

permutation, that is constrained by the maximum

total number of resources (in this example, 6) in

which each unique structure is generated [Fig. 1. b)

shows instead how the present treatment illustrates an

instance of a structure]. This is checked first for

logical feasibility in regards to completing the

workload (an exemplar set of processes) and then

simulated (i.e. a trajectory through time or

simulation) with uniformly probable random routing,

inclusion of processing time interval uncertainty, and

asymmetric context (process) switching time

intervals for resources. By defining a DES instance in

a procedural sequence, the workflow is undertaking

an epistemic action, taking the role of the higher-level

‘network executive’. As with (Uhrmacher, 2001), we

have been inspired by Ferber’s concept of

“reflectivity” (Ferber & Carle, 1991), (Ferber, 1999),

defined as “the ability of a computational system to

Table 1: Model Input Data.

Resource

Type

PROCESS TIME INTERVALS

CST – FROM

MEAN VAR

A1 A2 B2

100 100 0 4 5

400 150 8 0 9

600 200 10 19 0

RESOURCE TYPE 2 A2 B1 C2

500 100 0 7 4

200 50 4 0 5

300 75 8 12 0

RESOURCE TYPE 3 A1 B1 B1

100 50 0 8 6

250 100 18 0 14

150 25 7 5 0

RESOURCE TYPE 4 A1 B1 B2 C2

70 30 0 12 15 10

300 50 5 0 7 5

550 200 8 5 0 12

350 20 11 14 12 0

RESOURCE TYPE 5 B1 B2 C1

400 50 0 15 10

550 100 4 0 5

125 50 17 8 0

a. Context Switching Time (CST) ‘from’ being the current state or mode.

Figure 2: General Layout of a DES in a scheduling format.

represent, control and modify its own behaviour”.

Strictly speaking, this encapsulates many of the

automated tools seen in EDA for MDE (as discussed

in the introduction), but in the context of DES

structures specifically leads to a recursive definition

of models.

Metaprogramming for simulation allows for the

labelling of variables and functions in a manner that

partially avoids the requirement of hardcoding

intricate case structures. Inspired by the LISP

language, the program generates its structure by

selecting the number of instances of each processor

(0 ≤ 6) , then recording the ‘events’ (i.e. state

transitions) as a dynamically generated list of variable

length and content. That list is then used as a typical

mapping that relates events and entities in simulation.

The term Uncertainty Quantification (UQ) is used

in many different contexts to classify those

methodologies that integrate and propagate

uncertainties into mathematical and computer models

where they are used to generate data that is typically

used in forecasting or prediction. Models are

fundamentally limited on account of epistemic

uncertainty regarding a limit on understanding of a

modelled system [and its consequential complexity]

and secondly, on the intractability of complex

models.

2.1 System Architecture

Resources are used by processes over time intervals.

The main thesis is that connections [in this case,

events] between processes and resources are the

fundamental source of structure in defining

possibility. In this context, connections are couplings

of atomic propositions that represent concurrent state

transitions, but could equally be seen as a simple

function - namely - unitary decrement of a process

token from the origin node and increment at the target

node.

Jobs, tasks and processes are similar,

interchangeable concepts and are held in process

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

206

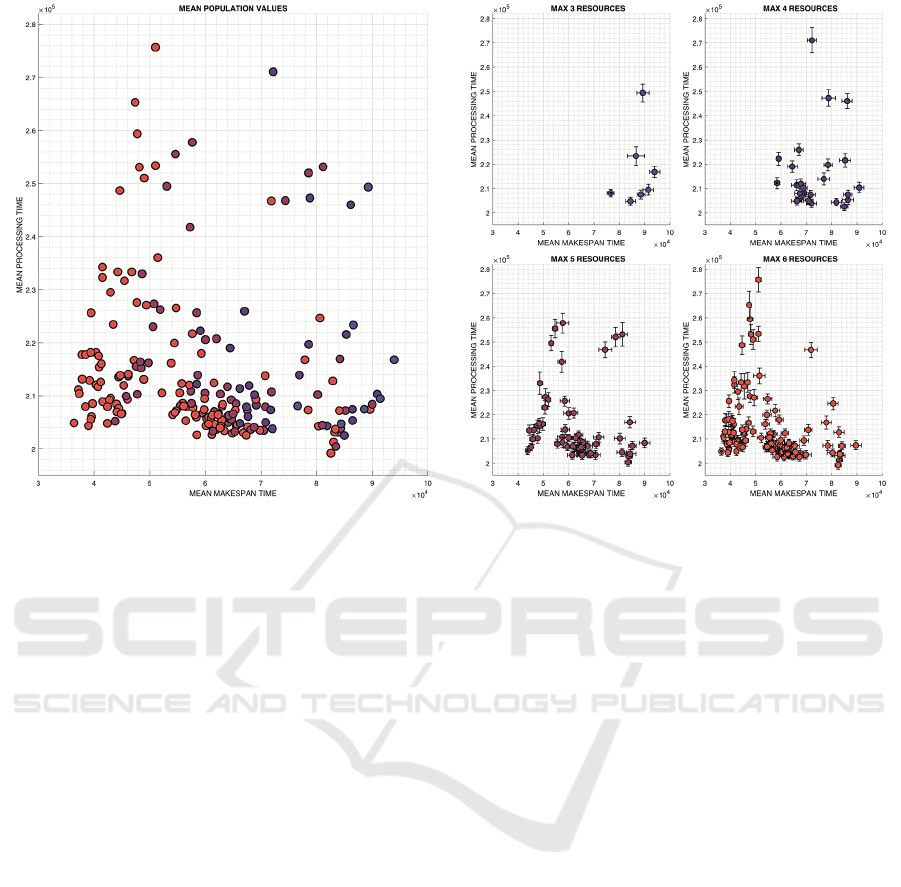
Figure 3: Mean permutation performances data; shown in relation to one another on the left-half; on the right-half, organised

in classes using sub-plots by total number of resources where the error bars show the standard deviation and the dotted

instance is the highest performing configuration of that class.

queue nodes, which are rectangular on the left hand

side of Fig. 2. Identical instances of processes are

held together within one node, categorically labelled

as ‘Process Type’ with a unique encoding and the

number of processes within a node is shown.

Actualisation involves the instantiation of a uniquely

labelled process-resource coupling upon assignment;

an event. External events (perhaps via a supersystem)

can be used to instantiate or inject new process tokens

to their respective process queue, or remove

finished/completed processes. Resources are nodes

on the right hand side which are instantiated as part

of the model construction process. Each has a label or

name indicating its type and index. Nodes of process

and resource types are connected by events of two

types; uncontrolled and controlled, which are dotted

and solid respectively. The possibility of assignment

between processes and resources (and vice-versa) is

dictated by these connections. A lower-level policy

must be used when selecting between (𝑛  1)

possible assignments. Once an assignment is made,

the nondeterministic time interval from a Gaussian

distribution with a specific mean and variance of the

resultant process-resource coupling is generated from

the input data in Table 1.

Depending on the current state or mode of the

resource, the Context Switching Time (CST) which is

asymmetrical and deterministic, [for instance, if a

type R4 resource was in mode C2, and switched to

A1, it takes 10 units of time, whereas in reverse it will

take 11]. Process-resource couplings persist,

addressing the ‘frame’ problem through

circumscription. Requalifying the proposition is

achieved through scheduled firing of uncontrolled

events in future. Because process-resource couplings

(also known as fluents) have the quality of qualitative

reasoning, process models can be described using

natural language, and like language systems, have a

syntax - rules of structure dictated by their

configuration.

2.2 Program Structure & Parameters

Table 1 shows the logical relations between

processes (A1, A2, …, C3) and respective resources

(R1, R2, …, R5). A workload is a set of processes. In

this experiment we only consider one workload;

comprised of 100 A, B and C process tokens each. A1,

A2, A3 are sub-states of the processes – A1 state

would indicate unprocessed, A2, partially processed

and A3 is completed – processed. The performance is

judged on two primary features; the processing time

and makespan. Processing time indicates the literal

amount (scalar sum total) of processing required,

since this relates to important second-order resources,

e.g. energy. The makespan gives a scalar value that is

Searching Generating Discrete-Event Systems

207

indicative of system global performance; the total

processing time of all processes from first process

start to last process finish. Because a given control

policy (e.g. intelligent task sequencing/routing or

load balancing) can vary the local features; process

queue volume and/or associated waiting times, this

consequentially hides global system performance

from evaluation. This phenomena is pervasive in real-

life systems, and it is exceptionally difficult to

perceive, since local control policies are deployed to

avoid bottlenecks at a cost of overall performance (it

can be conceptualised as performance lowering to the

point at which evidence of bottlenecks is removed).

2.3 Results

The system discovered 221 unique configurations

that feasibly process this workload with a maximum

of 6 resources. The logically minimum resource

number is 3, as the workload required 3 different

resource types for completion. Fig. 3. shows the

majority of permutations (outliers were omitted for

clarity) and their respective total number of resources

(as different coloured classes), the respective mean

makespan time and mean processing time [in X-Y

respectively] calculated from a population of 400

simulations. It can be seen that the number of

resources has a significant impact on performance;

and within each class there is also an optimal resource

configuration. It is suggestive in the data that clusters

appear in certain regions, opening the possibility to

discover some heuristic to help inform the selection

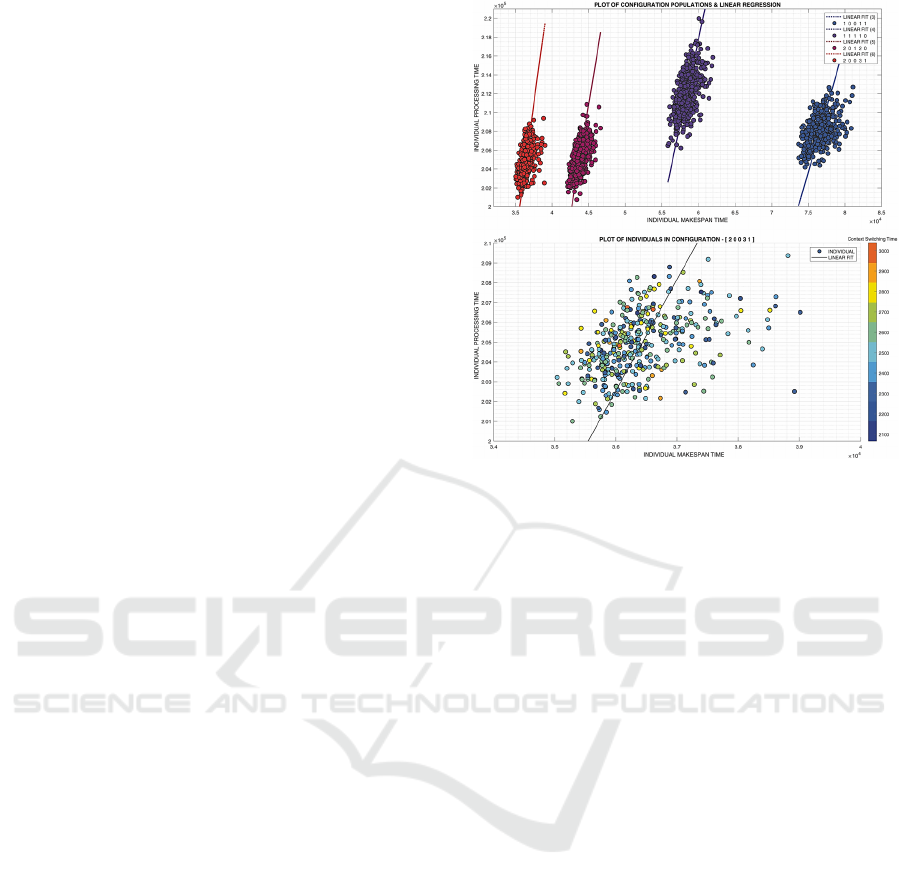
of new configurations in larger problems. In Fig. 4.

(upper) the highest performing configurations of each

class are shown with their simulation results.

It is notable that fewer resources show a greater

relation between total processing time and makespan,

as indicated by linear regression fit. In Fig. 4. (lower),

the highest performing configuration is shown once

again, with inclusion of the total Context Switching

Time (CST). Note the highest performing

configuration is visually represented in Fig. 1 b).

3 FUTURE WORK

The routing policy used is likely to be creating

second-order un-modelled effects on simulation,

impacting generated behavior data and performance,

alleviated by; 1) detection using a hybridization of

global and local performance features for evaluation

and/or 2) a more systematic simulation. Using purely

exploratory stochastic search, the discovery of

configurations in larger spaces that are both feasible

Figure 4: Performances – top; best in each class, bottom;

best overall.

and high-performing is unacceptably inefficient

without exploitation. Further development will

feedback high performing features [performance

result(s) of the forward model] from an initial

population to a selection mechanism for

configurations of new populations. An obvious

candidate could be a derivative of the canonical

Genetic Algorithm (GA), via a mixed-integer

encoding, since the permutation itself has no

particular structure. In addition to establishing useful

heuristics to the user about this particular problem, an

interesting avenue of research would be a

metaheuristic algorithm where the generation of new

permutations are limited to features inherent to

clusters of high performing configurations in the

existing population. Software experience limits this

work in regards understanding how variable structure

modelling is manifest in other application contexts.

However, the ability to construct structurally variable

models is growing in applicability to both well

established and contemporary use cases – in systems

that adapt online to variation in requirements. Many

computational workloads involve the fault-tolerant

decomposition, processing and recomposition of

processes or tasks and the allocation of these

subproblems to computer systems that are

increasingly interconnected, hierarchical and

heterogeneous. The internet has enabled macro-scale

workload distribution through cloud computing,

whilst at processing scale, we see a continuous

growth in multi-processor Central Processing Units

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

208

(CPU), a growth in the use of Graphical Processing

Units (GPU), and new specialised systems, such as

the Intelligence Processing Unit (IPU)(Mohan et al.,

2020)(Jia, Tillman, Maggioni, & Scarpazza,

2019)(Ortiz, Pupilli, Leutenegger, & Davison, 2020)

and Tensor Processing Unit (TPU) (Jouppi, Young,

Patil, & Patterson, 2018). The advent of Industrie 4.0

demands that these systems can adaptively self-

organise so that large workloads are distributed

between specialised resources in real time.

The design or operational control manufacturing

systems is an obvious candidate, and was anticipated

by (Uhrmacher, 2001); “in factories where machines

are capable of being dynamically reconfigured for

different products”. Typically in the design and

control of manufacturing systems, the time interval

distribution of jobs, the types of resources unto which

the jobs can be executed, how they are sequenced and

context switching in the form of tool changeovers are

all known or estimated. In which case a project is to

establish a globally optimal manufacturing system

design based on exemplar workloads which satisfies

the demands of the supply chain. It appears that DES

models or structures undertake a form of automatic

reification in order to provide a closed domain of

discourse a la constructivism. Machine Learning

(ML) and metamodeling has approaches for

modelling that encapsulates different structures

numerically, removing the requirement to create or

omit entities. Most evident is the property of linear

separability in classical Perceptrons and ‘dropout’ in

contemporary Neural Networks (NN) in which

variables between layers are contextually

disconnected by reaching zero weight. This suggests

generality is a property of models that in some way

manifest reconfigurablity.

ACKNOWLEDGEMENTS

The authors would like to acknowledge Finneran, S.

in his early observations regarding the value of

automatic generation of Discrete-Event System

models in the manufacturing industry.

REFERENCES

Uhrmacher, A.M. and Arnold, R. (1994). Distributing and

maintaining knowledge: Agents in variable structure

environments. Proceedings of the 5th Annual

Conference on AI, Simulation, and Planning in High

Autonomy Systems: Distributed Interactive Simulation

Environments, AIHAS 1994, pp. 178–184.

Barros, F.J. (1995). Dynamic Structure Discrete Event

System Specification: A New Formalism for Dynamic

Structure Modelling & Simulation. Proc. 1995 Winter

Simul. Conf. ed. C.

Barros, F.J., Mendes, M.T. and Zeigler, B.P. (1994).

Variable DEVS - Variable Structure Modelling

Formalism An Adaptive Computer Architecture

Application. Fifth Annu. Conf. AI Plan. High Auton.

Syst.

Zeigler, B.P., Kim, T.G. and Lee, C. (1991). Variable

structure modelling methodology: an adaptive

computer architecture example. Trans. Soc. Comput.

Simul. Int., vol. 7, no. 4, pp. 291–319.

Zeigler, B.P., and Praehofer, H. (1989). Systems Theory

Challenges in the Simulation of Variable Structure and

Intelligent Systems. CAST Comput. Syst. Theory, pp.

41–51.

Uhrmacher, A.M. (2001). Dynamic Structures in Modeling

and Simulation: A Reflective Approach. ACM Trans.

Model. Comput. Simul., vol. 11, no. 2, pp. 206–232.

Ay, N. (2020). Ingredients for robustness. Theory Biosci.,

vol. 139, no. 4, pp. 309–318.

Asperti, A. and Busi, N. (2009). Mobile Petri nets. Math.

Struct. Comput. Sci., vol. 19, no. 6, pp. 1265–1278,

Perrica, G., Fantuzzi, C., Grassi, A. and Goldoni, G. (2010).

Automatic experiments design for discrete event

system simulation. Proc. - 2nd Int. Conf. Adv. Syst.

Simulation, SIMUL 2010, pp. 7–10.

Tendeloo, Y and Vangheluwe, H. (2019). Discrete event

system specification modeling and simulation. Proc. -

Winter Simul. Conf., vol. 2018-Decem, pp. 162–176.

Cai, K. and Wonham, W.M. (2010). Supervisor

localization: A top-down approach to distributed

control of discrete-event systems. IEEE Trans.

Automat. Contr., vol. 55, no. 3, pp. 605–618.

Ramadge, P.J.G. and Wonham, W.M. (1989). The control

of discrete event systems. Proceedings of the IEEE, vol.

77, no. 1. pp. 81–98.

Jiao, T., Gan, Y., Xiao, G. and Wonham, W.M. (2020).

Exploiting Symmetry of Discrete-Event Systems by

Relabeling and Reconfiguration. IEEE Trans. Syst.

Man, Cybern. Syst., vol. 50, no. 6, pp. 2056–2067.

Jiao, T., Gan, Y., Yang, X. and Wonham, W.M. (2016).

Exploiting symmetry of discrete-event systems with

parallel components by relabeling. IEEE Reg. 10 Annu.

Int. Conf. Proceedings/TENCON, vol. 2016-Janua, pp.

0–3.

Macktoobian, M. and Wonham, W.M. (2017). Automatic

reconfiguration of untimed discrete-event systems.

2017 14th Int. Conf. Electr. Eng. Comput. Sci. Autom.

Control. CCE 2017.

Ferber, J. and Carle, P. (1991). Actors and agents as

reflective concurrent objects: A Mering IV perspective.

IEEE Trans. Syst. Man Cybern., vol. 21, no. 6, pp.

1420–1436.

Ferber, J. (1999). Multi-Agent Systems: An Introduction to

Distributed Artificial Intelligence.

Mohan, L.R.M. et al. (2020). Studying the potential of

Graphcore IPUs for applications in Particle Physics.

Jia, Z., Tillman, B., Maggioni, M. and Scarpazza, D.P.

Searching Generating Discrete-Event Systems

209

(2019). Dissecting the graphcore IPU architecture via

microbenchmarking. https://arxiv.org/abs/1912.03413.

Ortiz, J., Pupilli, M., Leutenegger, S. and Davison, A.J.

(2020). Bundle Adjustment on a Graph Processor.

Proc. IEEE Comput. Soc. Conf. Comput. Vis. Pattern

Recognit., pp. 2413–2422.

Jouppi, N., Young, C., Patil, N. and Patterson, D. (2018).

Motivation for and Evaluation of the First Tensor

Processing Unit. IEEE Micro, vol. 38, no. 3, pp. 10–19.

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

210