On the Issue of Modeling the Factor of Economic Development:

Environmental Factor

Karolina V. Ketova

and Daiana D. Vavilova

Department of Applied Mathematics and Information Technologies, Kalashnikov Izhevsk State Technical University,

Studencheskaya Street, Izhevsk, Russia

Keywords: Mathematical Modeling, Socio-Economic System, Ecological Factor, Environment, Atmospheric Air, Water

Resources, Land Resources.

Abstract: The article is proposed a mathematical model of the ecological factor dynamics. Modeling of the

environmental factor is carried out by types of costs aimed at environmental measures and activities leading

to the rational using of natural resources. The work is considered investments, an attack on the protection of

atmospheric air, water resources and land resources. The model of the ecological factor ensures the

effectiveness of environmental protection measures. The calculation of the ecological factor is carried out on

the basis of statistical data for the Udmurt Republic. Given the cumulative character of the negative impact

of poor environmental conditions on human health, the long available period 1996-2019 is chosen. For the

calculations statistical data on the annual indicators of pollution and purification of atmospheric air, water and

land resources of the Udmurt Republic are used and information on current annual costs of environmental

activities of the Udmurt Republic are reviewed. Calculations are shown that environmental pollution (air,

water and land resources in the complex) in the region occurs at an average annual rate 0.48%. The estimated

efficiency of environmental protection measures for atmospheric air is about 25.0%, for water resources is

47.5%, for land resources is 38.2%.

1 INTRODUCTION

Now a driving force of growth and a prerequisite for

the sustainable development of regions is a set of

qualitative population characteristics of the health,

the intelligence, the education, the ability to master

modern knowledge. Of course, the quantitative

component of the population in regions is also

important: the demographic one. These

characteristics determine the quality of human

capital, which in the context of rapidly changing

technology, with the development of the components

of an innovative economy, is necessary condition for

ensuring social progress (Dubiei, 2021; Amanova,

Turysbekova, Tazhibayeva, Izatullaeva and

Kaltayeva, 2017; Ketova, Rusyak and Derendyaeva,

2013).

In terms of the influence degree on the economy,

the most important components of human capital are

health, education and culture. In this work, we study

https://orcid.org/0000-0001-7143-1930

https://orcid.org/0000-0002-2161-4402

the environmental factor that directly affects the

health status of the population and on its demographic

indicators such as life expectancy, fertility, mortality.

To improve the state of the environment, the

government needs to direct financial resources and

plan financial strategies (D’Orazio and Valente,

2019), since investments in the environment of health

care reduce the levels of morbidity and mortality and

extend the working life period (Yang, Zheng and

Zhao, 2021; Seixas, Regier, Bryan and Mitton, 2021).

Good health of the population is the greatest value

and benefit, it is the high importance for increasing

the rate of socio-economic growth of society and the

practical implementation of new innovative

development paradigms (Tandon, Cain, Kurowski,

Dozol and Postolovska, 2020; Lu, Chen, Hao, Wang,

Song and Mok, 2017). The state of health determines

the capabilities of the person during labor activity and

the degree of his participation in it. A healthy person

fully realizes himself, health problems limit him.

Ketova, K. and Vavilova, D.

On the Issue of Modeling the Factor of Economic Development: Environmental Factor.

DOI: 10.5220/0010586000530058

In Proceedings of the International Scientiﬁc and Practical Conference on Sustainable Development of Regional Infrastructure (ISSDRI 2021), pages 53-58

ISBN: 978-989-758-519-7

Measures aimed at improving health status increase

the potential of the labor force and reduce the

economic losses from demographic losses (Ketova,

2007; Rusyak and Ketova, 2008).

Recently, humanity is paid special attention to the

state of the environment around it. Scientists around

the world are actively engaged in the analysis of

issues related to environmental problems and the

search for their solutions. An overview of the

progress of modern research by scientists around the

world is presented, for example, in the work (Fan, He,

Hou and Meng, 2020). Comparative analysis of the

environmental pollution problem in the past, present,

and forecasts for the future are assessed in the

research (Huang, 2018).

The quality of the natural environment decreases

as a result of active changes in people’s lives:

processes of industrialization and urbanization are

taking place, traditional sources of energy and raw

materials are being depleted, ecological balances in

nature are disrupted, species of animals and plants are

being destroyed, etc. Progress is far from the desired,

the demographic “load” on nature is gradually

increasing.

The direct objects of pollution are the atmosphere,

water and soil. All living organisms are indirect

objects of pollution. Failure to take measures to

prevent environmental pollution can lead humanity to

an environmental disaster. In this regard, the issues of

constructing and implementing the concepts of

environmentally oriented progress in order to

preserve natural resources (Mcinnes and Roemer-

Mahler, 2017) and the implementation of

international cooperation on environmental problems

(Fedulova, Korchagina, Vik and Martyanov, 2017;

Gasanov, Kolotov and Kadnikova, 2017) are relevant.

In this situation, the environmental factor is the

most important condition for economic development.

Thus, investments in environmental protection are

becoming priority sources of positive economic

dynamics in the regions (Danilova, Podoprigora and

Ufimtseva, 2020; Maher, Fenichel, Schmitz and

Adamowicz, 2020). In this regard, the urgency of

studying and modeling the environmental factor, as

well as evaluating the effectiveness of environmental

protection measures, is obvious.

Since the ecological factor in the deteriorating

environment is an one of factors of the successful

development of socio-economic systems, therefore

we need to consider ecological factor when

constructing strategies for optimal management of

these systems (see, for example, (Belenky and

Ketova, 2006; Ketova, Rusyak and Derendyaeva,

2013; Ketova, Rusyak, Saburova and Vavilova,

2020). The process of constructing strategies for

optimal management of territories involves the using

mathematical and computer modeling tools (Gertsev

and Gertseva, 2004; Bravo de la Parra and Poggiale,

2005). In this regard, it becomes necessary to build

mathematical models to study the environmental

factor in order to be able to further take it into account

in models of economic dynamics. As a rule, when

describing the processes of the ecological systems

dynamics, differential equations are used (Vincenot,

Giannino, Rietkerk, Moriya and Mazzoleni, 2011).

This research is devoted to the mathematical

model construction of the ecological factor dynamics,

which allows to estimate the magnitude and compare

the change in time of this factor for three basic

components of the environment: atmospheric air,

water resources and land resources.

2 RESEARCH MATERIALS AND

METHODS

Let’s define the ecological factor as the percentage of

the volume of the environment that does not need

cleaning to its total volume, and denote it

 . The

measure of environmental pollution determines the

degree of deterioration of the environmental factor.

We divide the ecological factor according to the

types of costs aimed at environmental protection and

rational using natural resources: investments directed

to the protection of atmospheric air, water resources

and land resources. The total value of the

environmental factor is determined by linear

combination:

)()()()(

332211

tttt 















)

where





the corresponding terms proportion in

the total volume of the factor;





1,0





;





i

)

values











are measured as a percentage,

calculated as part of an unpolluted natural resource in

its total volume; index

1i

corresponds to the

component of atmospheric air,

2i

– component of

water resources,



– component of land resources

of the natural environment.

To describe the dynamics of the

i component of

the ecological factor, we use an equation of the form:

ISSDRI 2021 - International Scientiﬁc and Practical Conference on Sustainable Development of Regional Infrastructure



iiii

tkZ 



(3)

where



operating costs for measures taken to

environmental protection and activities for rational

using of natural resources;



coefficient of

conversion of the value, expressed in monetary units,

into the amount of refined resources;



t

intensity

of pollution of the

i

component of the

environmental factor.

Note that dynamic equation of the form (3) is easy

to integrate into models of economic dynamics. This

is due to the internal logic of building these models.

The functioning of regional economic systems is a

dynamic system of financial, material and

information flows, within the framework of which the

produced final product is formed. Expressed in

monetary terms, the final product is divided into

parts: investments in production activities, in the

social sphere, in improving the environment, in the

field of increasing production efficiency, etc. This

distribution should be carried out in an optimal way,

based on their criteria for increasing the efficiency of

the functioning of the regional economy. An optimal

strategy can be constructed using a mathematical

apparatus that includes the L.S. Pontryagin and

R. Bellman’s optimality principle (Pontryagin, 1961;

Belenky, 2007; Ioffe, 2020). The possibility of using

this mathematical apparatus presupposes the presence

of dynamic equations for the development factors of

the economic system of the form (3).

The initial condition at

tt 

looks like:

iii

ktZt )()(



(4)

where

)(

a known value from statistical data.

The dynamics equation (3) with initial data (4) is

the Cauchy problem. The solution can be carried out

by the numerical three-stage Runge-Kutta method of

the 3rd order.

Let’s introduce a variable

grid with a step

We consider the set of points

,...2,1,0,



 nnh

For calculating the formulas are:





3211

iii

FFF





(5)

  

 

















)2(η

)

(

213

inininii

inini

hFhFttktZF

ttktZF

(6)

3 RESEARCH RESULTS

We consider the regional socio-economic system of

the Udmurt Republic. Let’s analyse the development

of the ecological situation using its example. To do

this, we use the proposed mathematical model of the

form (1)-(4) and the solution methods (5) and (6). We

fill the mathematical model with the statistical data

necessary to solve the problem. Since the

environmental factor is characterized by a long-term,

deferred effect of exposure, we use a long time

interval for analysis. We have the opportunity to

analyze the indicator under study for the period 1996-

2019.

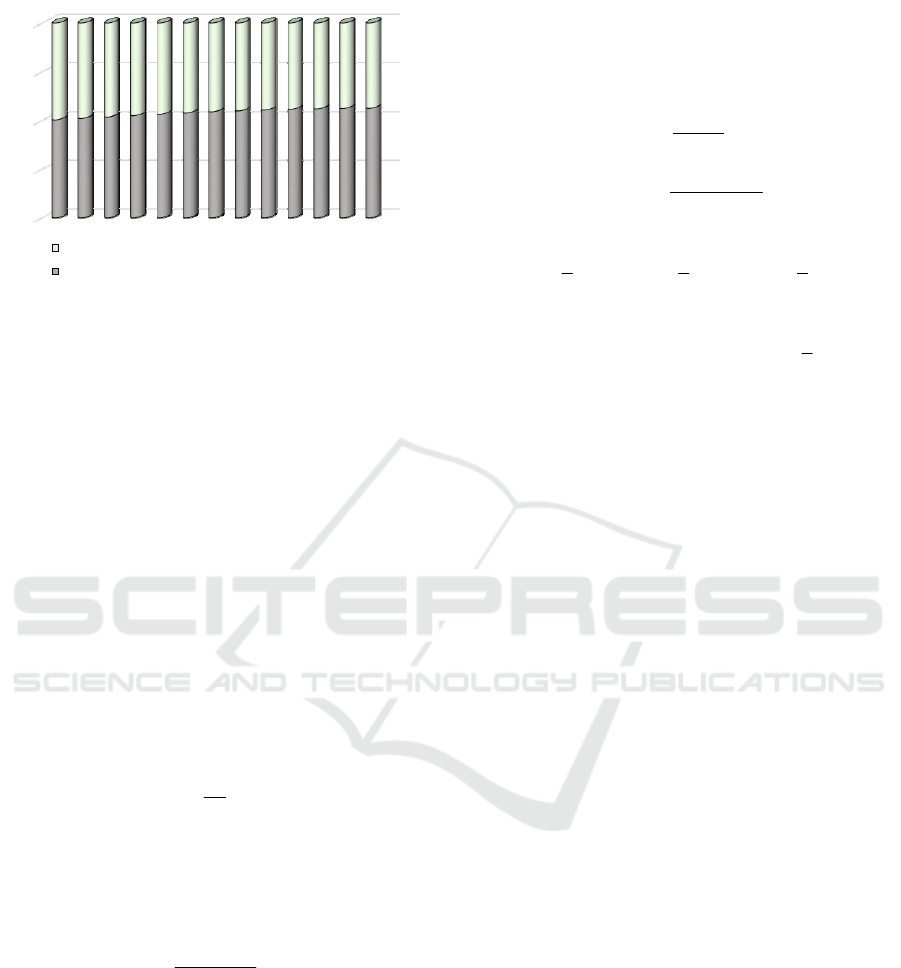
The dynamics of the ecological factor of the UR,

which characterizes atmospheric air, water resources

and land resources, for the period 1996-2019, is

shown in Figure 1. In this paper, the environment is

the totality of atmospheric air, water and land

resources. In this regard, in terms of the entire

environment as a combination of these three

components, we get the graph shown in Figure 2. It

displays the degree of environmental pollution in

dynamics over the years for the period under study.

1996 2000 2004 2008 2012 2016 2019

Атмосферный воздух Водные ресурсы Земельные ресурсы

t, year



, %

Atmospheric air Water re sources Land resources

Figure 1: Ecological factor dynamics of the UR,

characterizing atmospheric air, water resources and land

resources.

It is obtained that the average rate of pollution in

the region of atmospheric air was 0.64%, water –

0.73%, land resources – 0.31% (Figure 1). The share

of the environment, which requires the using of

cleaning measures, on average for the period 1996-

2019 in UR was 53.9%. The change over the 23-year

period under study is from 50.3% to 56.4% (Figure

2). The most intense was pollution of the atmosphere

and water resources. The soil is polluted less

intensively, but, nevertheless, production and

economic activities cause significant damage to the

nature of this cumulative nature of this phenomenon.

On the Issue of Modeling the Factor of Economic Development: Environmental Factor

100

1996 2000 2004 2008 2012 2016 2019

Доля окружающей среды, находящаяся в нормальном состоянии, %

Доля окружающей среды, требующая проведения очистных мероприятий, %

t, year

The share of the environment in a normal state, %

The share of the environment requiring cleaning activities, %

Figure 2: Change in the percentage of polluted environment

of the UR.

The calculated dynamics of the environmental

factor are shown that the rate of pollution has

decreased. This is due to the strengthening of

measures aimed at combating environmental

pollution in the region in the last decade. This

government policy is carried out within the

framework of the state program of the Russian

Federation “Environmental Protection”. In the future,

the policy of respect for the environment should be

continued.

The value of the environmental factor directly

depends on the effectiveness of environmental

protection measures. Let’s analyze this indicator. We

designate the effectiveness of environmental

protection measures



; it is the reciprocal of the

intensity of environmental pollution











(7)

Based on (3), we determine the intensity of

environmental pollution by the formula:









(8)

Let’s determine the value of conversion

coefficient

, expressed in monetary units, into the

amount of refined resources. To do this, we calculate

the ratio of the cleaned volume resource

U of the to

the current costs of protecting this resource

. Next,

we use information on the annual indicators of

pollution and purification of atmospheric air, water

and land resources of the UR for the period 1996-

2019 and information on the current costs of

environmental protection of the UR for the period

1996-2019 (in the calculations, the current financial

costs for the possibility of comparing the obtained

results are adjusted to 2019 prices):

)(



2019,1996,3,1

___

 ji

)

Average value of the coefficient for each

resource:

144.0



021.0



014.0



Further, we calculate the values of the coefficients for

converting the components of the environmental

factor into monetary terms, as a ratio

)(t



to the

known values of the total volume of these resources.

Then

105.3



k

104.3



k

103.3



k

. As a result of calculations for the studied period

1996-2019 for UR, the following values of pollution

intensity are obtained, in accordance with formula

(8): for atmospheric air –

00023.001.0





, for

water resources –

00006.0003.0







, for land

resources –

00057.001.0







Based on the values of the annual pollution

indicators and purification of atmospheric air, water

and land resources of the UR for the period 1996-

2019 and the estimated rate of change in the

percentage of environmental pollution, the values of

the proportionality coefficients from formula (7) for

the three resources (air, water, land):

003.0

a

001.0



004.0



The efficiency of environmental protection

measures, determined by formula (7), for atmospheric

air is about 25.0%, for water resources – 47.5%, for

land resources – 38.2%.

4 CONCLUSIONS

The authors have proposed a mathematical model of

the environmental factor in this research. Modeling of

the environmental factor is carried out by types of

costs aimed at measures taken to environmental

protection and activities for rational using of natural

resources. In the model of the environment, three

components appear, which are presented in

combination: water, air and land resources.

The presented in the article mathematical model

allows solving the problem of calculating the

ISSDRI 2021 - International Scientiﬁc and Practical Conference on Sustainable Development of Regional Infrastructure

environmental factor dynamics, taking into account

the effectiveness of environmental protection

measures. The solution to the problem of the

environmental factor modeling is found using a

combination of analytical and numerical methods.

The mathematical model of the ecological factor

dynamics is built in the form of a differential equation

of this type, which allows taking into account the

ecological factor in the models of economic

dynamics, as well as when constructing strategies for

optimal control of socio-economic systems using the

L.S. Pontryagin and R. Bellman’s optimality

principle.

The calculation of the environmental factor is

carried out using the example of the Udmurt

Republic. For this, statistical data on the annual

indicators of pollution and purification of

atmospheric air, water and land resources of the UR

and information on the current annual costs for

measures to protect the environment of the UR are

used. Since the environmental factor is characterized

by a delayed impact, the long available period 1996-

2019 was chosen.

It has been established that environmental

pollution in the region occurs at an average annual

rate of 0.48%. However, over the past decade, there

is a decrease in the rate of environmental pollution.

The estimated efficiency of environmental protection

measures for atmospheric air is about 25.0%, for

water resources is 47.5%, for land resources is 38.2%.

This state of affairs leads us to the need to strengthen

measures aimed at improving the state of the

environment in the region.

REFERENCES

Amanova, G., Turysbekova, G., Tazhibayeva, R.,

Izatullaeva, B., Kaltayeva, S. (2017). Human capital as

a determining factor of increasing the competitiveness.

Espacios, 38(42): 27.

Belenky, V.Z., Ketova, K.V. (2006). The complete

analytical solution of the macro-model of regional

development for the exogenous demographic

prognosis. In

Economics and Mathematical Methods,

42(4): 85-95.

Belenky, V.Z. (2007).

Optimization models of economic

dynamics. Conceptual apparatus. One-dimensional

models.

Nauka. Moscow.

Bravo de la Parra, R., Poggiale, J.-C. (2005). Theoretical

ecology and mathematical modelling: Problems and

methods. In

Ecological Modelling, 188(1): 1-2.

doi:10.1016/j.ecolmodel.2005.05.005.

Danilova, M., Podoprigora, Y., Ufimtseva, E. (2020).

Investment Ensuring Process of Rational Environmental

Management as Factor of a Sustainable Development of

the Territory. In

IOP Conference Series: Materials

Science and Engineering, 753(7): 072014.

doi:10.1088/1757-899X/753/7/072014.

Dubiei, Yu.V. (2021). Interrelation between human capital

and innovation in the context of technical and

technological development of a country. In

Naukovyi

Visnyk Natsionalnoho Hirnychoho Universytetu

, 6:

148-154.

D’Orazio P., Valente, M. (2019). The role of finance in

environmental innovation diffusion: An evolutionary

modeling approach. In

Journal of Economic Behavior

& Organization

, 162: 417-439.

doi:10.1016/j.jebo.2018.12.015.

Fan, X., He, P., Hou, L., Meng, X. (2020). Review of

International Research Progress on Ecological

Threshold. In

Research of Environmental Sciences,

33(3): 691-699.

Fedulova, E.A., Korchagina, I.V., Vik. S.V., Kalinina, O.I.,

Martyanov, V.L. (2017). International Cooperation in

Environmental Management and Rational Use of

Natural Resources. In

IOP Conference Series: Earth

and Environmental Science, 50(1): 012023.

doi:10.1088/1755-1315/50/1/012023.

Gasanov, M. A.. Kolotov, K. A., Demidenko, K. A.,

Podgornaya, E. A., Kadnikova, O. V. (2017). The

Concept of Ecologically Oriented Progress and Natural

Resource Preservation. In

IOP Conference Series: Earth

nd Environmental Science, 50(1): 012025.

doi:10.1088/1755-1315/50/1/012025.

Gertsev, V.I., Gertseva, V.V. (2004). Classification of

mathematical models in ecology. In

Ecological

Modelling

, 178: 329-334.

doi:10.1016/j.ecolmodel.2004.03.009.

Huang, S. (2018). Air pollution and control: Past, present

and future. In

Chinese Science Bulletin, 63(10): 895-

919.

Ioffe, A. D. (2020). An Elementary Proof of the Pontryagin

Maximum Principle. In

Vietnam Journal of

Mathematics

, 48(3): 527-536.

Ketova, K. V. (2007). A mathematical economic model of

the manpower resource potential and cost

characteristics of demographic losses. In

Expert Syst.

Appl.

, 3 (7): 80-94.

Ketova, K. V., Rusyak, I. G., Derendyaeva, E. A. (2013).

Solution of the problem of optimum control regional

economic system in the conditions of the scientific and

technical and social and educational progress. In

Mathematical modelling

, 10 (25): 65-78.

Ketova, K. V., Rusyak, I. G., Saburova, E. A., Vavilova, D.

D. (2020). Regional socio-economic parameters

modeling and system analysis by means of

programming and computing suite. In

IOP Conference

Series: Materials Science and Engineering

. Vol.

862(5): 52044. doi:10.1088/1757-899X/862/5/052044.

Lu, Z., Chen. H., Hao, Yu., Wang, J., Song. X., Mok. T.

(2017). The dynamic relationship between

environmental pollution, economic development and

public health: Evidence from China. In

Journal of

On the Issue of Modeling the Factor of Economic Development: Environmental Factor

Cleaner Production, 166: 134-147.

doi:10.1016/j.jclepro.2017.08.010.

Mcinnes, C., Roemer-Mahler, A. (2017). From security to

risk: Reframing global health threats. In

International

Affairs

, 93(6): 1313-1337.

Maher. S. M.. Fenichel. E. P.. Schmitz. O. J.. Adamowicz.

W. L.. (2020). The economics of conservation debt: a

natural capital approach to revealed valuation of

ecological dynamics. In

Ecological Applications, 30(6):

02132. doi:10.1002/eap.2132.

Pontryagin. L. S. (1961).

Mathematical theory of optimal

processes. Nauka. Moscow. (in Russ.).

Rusyak, I. G., Ketova, K. V. (2008). Analysis of

Demographic Losses Economic Characteristics. In

Tomsk State University Journal, 310: 153-160. (in

Russ.).

Seixas, B. V., Regier, D. A., Bryan, S., Mitton, C. (2021).

Describing practices of priority setting and resource

allocation in publicly funded health care systems of

high-income countries. In

BMC Health Services

Research

, 21((1)90). doi:10.1186/s12913-021-06078-

Tandon, Aj., Cain. Je., Kurowski, Ch., Dozol, A.,

Postolovska. I. (2020). From slippery slopes to steep

hills: Contrasting landscapes of economic growth and

public spending for health. In

Social Science &

Medicine

, 259: 113171.

doi:10.1016/j.socscimed.2020.113171.

Vincenot, C. E., Giannino. Fr., Rietkerk, M., Moriya, K.,

Mazzoleni, S. (2011). Theoretical considerations on the

combined use of System Dynamics and individual-

based modeling in ecology. In

Ecological Modelling,

222(1). doi:10.1016/j.ecolmodel.2010.09.029.

Yang, Y., Zheng, R., Zhao, L. (2021). Population aging,

health investment and economic growth: Based on a

cross-country panel data analysis. In

International

Journal of Environmental Research and Public Health

Vol. 18(4) No 1801: 1-16.

doi:10.3390/ijerph18041801.

ISSDRI 2021 - International Scientiﬁc and Practical Conference on Sustainable Development of Regional Infrastructure