
A Novel Recommender System based on Two-level Friendship Ties
within Social Learning
Sonia Souabi, Asmaâ Retbi, Mohammed Khalidi Idrissi and Samir Bennani
RIME TEAM-Networking, Modeling and e-Learning Team, MASI Laboratory, Engineering 3S Research Center,
Mohammadia School of Engineers (EMI), Mohammed V University in Rabat, Morocco
Keywords: Social Networks, Recommendation System, Correlation, Co-occurrence, Community Detection, Two-level
Friendship Ties.
Abstract: Nowadays, social networks are starting to emerge as a huge part of e-learning. Indeed, learners are more
attracted to social learning environments that foster collaboration and interaction among learners. To enable
learners to handle their time and energy more effectively, recommendation systems tend to address these
issues and provide learners with a set of recommendations appropriate to their needs and requirements. To
this end, we propose a recommendation system based on the correlation and co-occurrence between the
activities performed by the learners on one hand, and on the other hand, based on the community detection
based on two-level friendship ties. The idea is to detect communities based on friends and friends of friends,
and then generate recommendations for each community detected. We test our approach on a database of
3000 interactions and it turns out that the two-level recommendation system based on friendships reaches a
high accuracy and performs better results than the recommendation system based one level friendship ties in
terms of precision as well as accuracy. It turns out that expanding the detected communities to generate new
communities leads to more relevant and reliable results.
1 INTRODUCTION
In the midst of several difficulties in face-to-face
learning, distance learning is a necessity, especially
when face-to-face learning is no longer possible
(Aboagye et al., 2020). In this case, it is highly
preeminent to focus on distance learning and the
proper monitoring of online learners. With the
emergence of the social networking and social
learning mode, learners are increasingly turning to
social learning as it promotes collaboration and
interaction with other learners (Tartari et al., 2019;
Tosun, 2018). Being part of an online social
environment is one of the finest options available to a
learner. In order to streamline learners' tasks and
improve the management of information and content,
recommendation systems are among the most optimal
solutions as long as they manage the large amount of
information a learner is confronted with and the
associated time and energy (Rezvanian et al., 2019).
All of these elements are counted among the key
benefits of recommendation systems, hence their
importance within learning environments. In the
literature, many recommendation systems have been
proposed for distance learning (Panagiotakis et al.,
2020 ; Ansari et al., 2016; George, 2019), but not
much importance has been dedicated to social
learning and social learning networks. Many
researchers are limited to considering explicit
feedback from learners and their direct evaluations in
order to generate recommendations (Salehi, 2013),
but implicit feedback should also be included in the
recommendation process. On the other hand, there are
recommendation systems that can meet the
requirements of social networks, but are developed in
other contexts besides e-learning. All these points
render a recommendation system's work incomplete
in the distance learning context, hence the need to re-
propose a recommendation system taking into
account both implicit feedbacks in particular and
considering community detection according to a
reliable and relevant criterion since we are dealing
with social networks. A learner needs above all a
learning atmosphere that encourages interaction and
collaboration, and to achieve that, he needs to receive
all the support he truly requests, including a relevant
recommendation system providing recommendations
based on his interactions and implicit feedbacks.
566
Souabi, S., Retbi, A., Idrissi, M. and Bennani, S.
A Novel Recommender System based on Two-level Friendship Ties within Social Learning.
DOI: 10.5220/0010599605660573
In Proceedings of the 16th International Conference on Software Technologies (ICSOFT 2021), pages 566-573
ISBN: 978-989-758-523-4
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

In our work, we propose a recommender system
considering implicit feedbacks, i.e. activities carried
out by the learners, and going beyond communities
based on one-level friendships to reach two-level
friendships. Our recommendation system is therefore
based on several points: (1) Integrating learner
activities by considering the two notions of
correlation and co-occurrence, (2) Detecting
communities based on friendships and then
broadening the scope of communities to include
friends of friends, and (3) generating
recommendations for each detected community.
The article is divided into several parts. The
second part outlines a general overview of
community detection and recommendation systems
based on community detection. The third part deals
with the recommendation approach proposed in
details. The fourth part concerns the tests performed
and the results obtained. The final part summarizes
the article in general and the next directions to pursue.
2 BACKGROUND
2.1 Community Detection Algorithms
In order to analyse the structure of the relationships
between entities, regardless of the nature of these
entities, they are generally visualized by graphs. In e-
learning, for example, it is possible to model the
relationships and interactions between different
learners. Learners are modelled by vertices and
interactions are presented in the shape of edges. A
graph is therefore made up of several communities,
and a community is made up of vertices strongly
linked to each other than to the other vertices of the
graph. We can decide on the type of graph based on
several criteria (Beauguitte, 2010):
• The orientation of the graph: There are two
types of graph concerning the orientation,
oriented graph or non-oriented graph. The
direction of the links judges the orientation of
a graph. The symmetry of the corresponding
adjacent matrix most often depends on the
nature of the graph; whether it is oriented or
not.
• The type of links existing between nodes: It is
possible to distinguish several types of graphs
based on the nature of the links; binary graphs
whose links express the presence of
interaction or relationship between two nodes,
and non-binary graphs whose links not only
reveal the presence of a relationship, but also
its intensity.
• The number of sets of vertices: If the graph
consists of a single set of vertices, we would
call it a unipartite graph. If the graph
contains two different sets of vertices and
each set belongs to a specific category, we
talk about a bipartite graph.
To detect communities, many algorithms are
available. Among those we will explore in our work,
there are four:
• Louvain (Blondel et al., 2008): The Louvain
algorithm is based on several phases. First of
all, each node is considered as an individual
community. Then, each node is associated
with its closest neighbours and the gain in
modularity is calculated (Equation 1), then it
is inserted into the community which provides
the maximum value of modularity. Finally, the
process is performed several times until the
modularity gain converges.
∆𝑄=
∑
+
𝑏
,
2𝑝
−
∑
+𝑏
2𝑝
−
∑
2𝑝
−
∑
2𝑝
−
𝑏
2𝑝
Equation 1. Modularity gain in Louvain
𝑆
is the weight of the edge between nodes 𝑖 and 𝑗
• InfoMap (Rosvall et al., 2009): This
algorithm is based on an equation called the
map equation (Equation 2). The principle is
straightforward, just minimizing the random
walk within the graph. In other words, if a
random walk keeps the same connections, it
is due to the fact that the vertices linked to
these connections are part of the same
community.
𝑀𝑎𝑝 𝑒𝑞𝑢𝑎𝑡𝑖𝑜𝑛=
𝑤↷)log (𝑤↷)−2↷log𝑤
↷ − 𝑤
log
(
𝑤
)
+𝑤
↷+𝑤
log𝑤
↷+𝑤
Equation 2. The map equation
𝑀: Network with 𝐾 objects (𝑘=1,,𝐾) et 𝐽 groups
(𝑗=1,,𝐽)
𝑤
: The weight of all connections of i.
𝑤
: The sum of the weights of all connections of the
objects belonging to k.
𝑤
↷ : The sum of the weights of all the connections
of the objects of k leaving the group.
𝑤↷ : The sum of the weights of all the connections
of the objects belonging to
• Walktrap (Pons & Latapy, 2005): Walktrap is
part of the family of algorithms based on
random walks. The concept is to minimize
A Novel Recommender System based on Two-level Friendship Ties within Social Learning
567

random walks within the same community and
maximize them between communities. Like
Louvain, the algorithm starts by considering
each node as an individual community. Then,
the distance between one community and
another is computed (Equation 3), and
merging the communities having the minimal
distance between them, the process is repeated
until the algorithm converges.
∆𝜎
(
𝐶
,𝐶
)
=
1
𝑛
⎝
⎜
⎛
𝑟
∈
−𝑟
−𝑟
∈
∈
⎠
⎟
⎞
Equation 3. Random walk variation
• Edge Betweenness (Cuzzocrea et al., 2012):
This is another measure of the centrality of a
vertex in a graph. The centrality of a vertex
is expressed as follows (Equation 4):
𝑔
(
𝑝
)
=
𝜎
(𝑝)
𝜎
∈
∈
Equation 4. Edge centrality
𝑆=<𝑉,𝑃> : Non oriented connected graph.
𝑣
,𝑣
: Two nodes in 𝑆.
𝑝: An edge part of 𝑉.
𝜎
(
𝑝
)
: The number of shortest paths between
𝑣
𝑎𝑛𝑑 𝑣
.
2.2 Related Studies
Gasparetti et al. provide a review of the general
literature on social recommendation systems based on
community detection (Gasparetti et al., 2020). The
main objective is to clarify research directions
regarding community detection and its relation to
recommendation systems. A recommender system
based on community detection therefore requires
several steps:
• Data collection.
• Content extraction and tie recognition.
• The reduction of dimensionality.
• Detection of communities.
• Recommendations.
It is worth mentioning from this work that
recommender systems based on the community
detection still require efforts and new avenues to
generate more relevant recommendations. Boussaadi
et al. focus on recommendation systems based on
supervised learning in a purely academic learning
context (Boussaadi et al., 2020). Indeed, the approach
focuses on two main steps. The first step is to group
researchers who are likely to be engaged in the same
topic. Then, communities are detected in each cluster
identified beforehand. The purpose is to reduce the
time in terms of generating recommendations and
provide more prominent results. The results highlight
the importance of integrating community detection to
generate articles for researchers. As several works
performed, Parimi and Caragea aim at combining
community detection with the adsorption algorithm to
generate recommendations in the form of articles
(Parimi & Caragea, 2014). The preferences of the
considered users are rather implicit. Integrating the
detection of communities as a preliminary step
facilitates the task for the adsorption algorithm and
detects the closest neighboring users. The test was
performed on two datasets: at DBLP level and at
Book Crossing level. It turns out that the community
detection improves the performance of the adsorption
algorithm. Several recommendation systems are
based solely on traditional collaborative filtering
techniques. Cao et al. propose an improved version of
collaborative filtering; a version that integrates
community detection as well. In a first step, the
evaluation matrix leads to the similarities obtaining
the network (Cao et al., 2015). Then, communities are
detected based on the network and an optimization
algorithm. Finally, recommendations are generated
for each community. Lalwani et al. propose in this
paper is to integrate the detection of communities
(Lalwani et al., 2015). Communities are detected
through social interactions between users. The system
goes through several steps:
• Detect communities based on the friendships
between users.
• Generate recommendations in each
community using collaborative filtering.
The experiments were carried out based on
MovieLens and Facebook data, and involve social
interactions in the shape of friendships between users.
3 THE PROPOSED APPROACH
In this section, we propose another vision of
recommendation systems based on social interactions
through friendships; a vision based not exclusively on
friends, but also on friends of friends. That is, instead
of applying a unique level of friendship, we add
another level of friendship considering friends and
friends of friends. This will broaden the size of
communities and the scope of recommendation
systems. The concept is straightforward, just add one
more step to the previous recommendation system
ICSOFT 2021 - 16th International Conference on Software Technologies
568
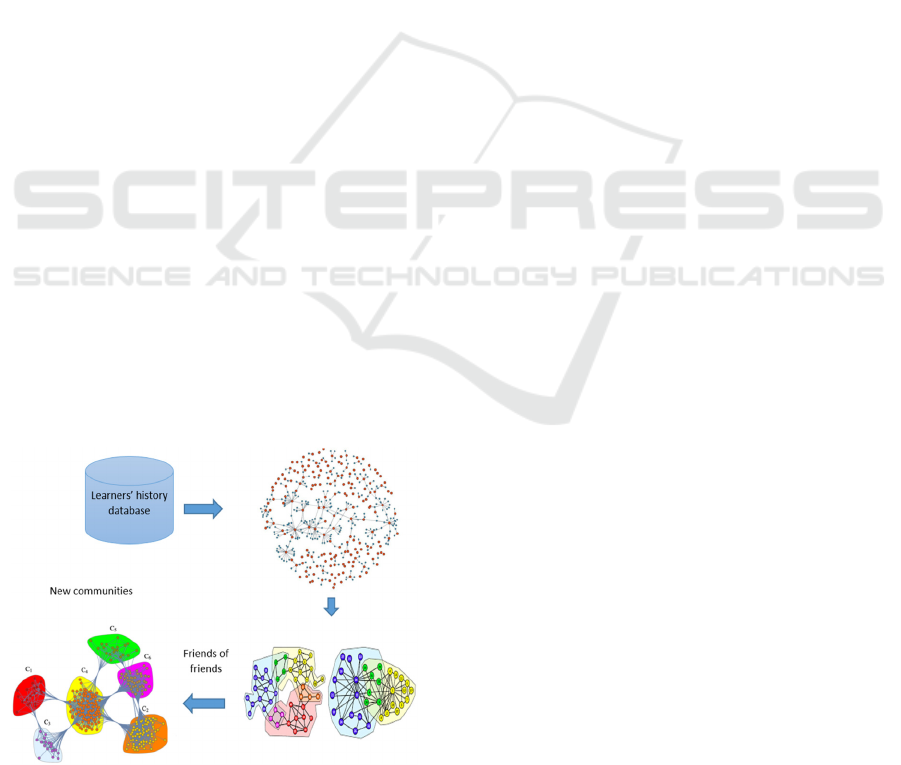
based on social interactions. This says that from the
communities detected by social interactions, we
identify the friends of members of the same
community and then we integrate these new members
with the old members of the same community. In this
way, the community is enlarged and the calculation
of recommendations might be more relevant. We can
summarize the general process in the following steps:
• Identify social interactions between
individuals through friendship ties.
• Detecting communities based on social
interactions through friendship ties.
• Identify friends of individuals who are
members of the same community.
• Identify new communities based on social
interactions across two levels (friends and
friends of friends).
• Calculate recommendation scores for each
new community identified.
• Generate recommendations for each new
community identified.
3.1 First Phase
The first phase consists in detecting communities
based on friendship ties existing between the different
learners. We are going to test several algorithms to
opt for the optimal one: Louvain, InfoMap, Walktrap
and Edge Betweenness.
3.2 Second Phase
After detecting communities based on friendship
links, the next step is to identify the friends of
members who are part of the same community, and
thus obtain new communities including friends and
friends of friends as shown in figure 1.
Figure 1: Schematic synthesis of the two-level friendship
links process in the recommendation system.
3.3 Third Phase
When new communities have been detected, and
which hold more members than the original
communities, we reach the main step of calculating
recommendations. Our calculation approach consists
in defining the correlation and co-occurrence existing
between the different activities performed by the
learners. In our previous work, we have already
developed the part of the calculation of
recommendations based on correlation and co-
occurrence (Souabi et al., 2020; S. Souabi et al.,
2020). First of all, we identify the actions performed
by the learners that are associated with the
recommendations (primary action directly associated
with the recommendations and secondary actions in
the second). The idea is to calculate the correlation
scores (Equation 7) from the correlation matrix
(Equation 5) and the co-occurrence scores (Equation
6) from the co-occurrence matrix, and finally
generate the total scores from the two previous scores.
All these operations are performed for each
community individually.
𝑓
,𝑓
,…,𝑓
: Learning objects to recommend.
𝑐
,𝑐
,…,𝑐
: The activities performed by the
learners such as 𝑎
is the primary activity and
𝑎
,…,𝑎
are secondary activities.
𝑟
,…,𝑟
,…,𝑟
,…,𝑟
: History of
activities performed by learners regarding each
learning object.
𝑅
,…,𝑅
,…,𝑅
,…,𝑅
: Co-
occurrence history of the activities performed by the
learners regarding each learning object.
𝑪𝒐𝒓𝒓𝒆𝒍𝒂𝒕𝒊𝒐𝒏 𝒔𝒄𝒐𝒓𝒆 𝒎𝒂𝒕𝒓𝒊𝒙=
𝑟
𝑟
…𝑟
𝑟
𝑟
…𝑟
⋮⋮⋮
×
1𝑐𝑜𝑟(𝑐
,𝑐
) … 𝑐𝑜𝑟(𝑐
,𝑐
)
=
𝑐𝑜𝑟𝑟𝑒𝑙𝑎𝑡𝑖𝑜𝑛 𝑠𝑐𝑜𝑟𝑒 (𝑓
) … 𝑐𝑜𝑟𝑟𝑒𝑙𝑎𝑡𝑖𝑜𝑛 𝑠𝑐𝑜𝑟𝑒 (𝑓
)
Equation 5. The correlation matrix score
𝑪𝒐 − 𝒐𝒄𝒄𝒖𝒓𝒓𝒆𝒏𝒄𝒆 𝒔𝒄𝒐𝒓𝒆 𝒎𝒂𝒕𝒓𝒊𝒙=
𝑅
𝑅
…𝑅
𝑅
𝑅
…𝑅
⋮⋮⋮
×
1𝑐𝑜−𝑜𝑐𝑐(𝑐
,𝑐
) … 𝑐𝑜− 𝑜𝑐𝑐(𝑐
,𝑐
)
=
𝑐𝑜− 𝑜𝑐𝑐 𝑠𝑐𝑜𝑟𝑒 (𝑓
) .. 𝑐𝑜 − 𝑜𝑐𝑐 𝑠𝑐𝑜𝑟𝑒 (𝑓
)
Equation 6. The co-occurrence matrix score
𝑻𝒐𝒕𝒂𝒍 𝒔𝒄𝒐𝒓𝒆 𝒎𝒂𝒕𝒓𝒊𝒙=
𝑐𝑜 − 𝑜𝑐𝑐𝑢𝑟𝑟𝑒𝑛𝑐𝑒 𝑠𝑐𝑜𝑟𝑒 𝑚𝑎𝑡𝑟𝑖𝑥
+ 𝑐𝑜𝑟𝑟𝑒𝑙𝑎𝑡𝑖𝑜𝑛 𝑠𝑐𝑜𝑟𝑒 𝑚𝑎𝑡𝑟𝑖𝑥=
𝑐𝑜 −𝑜𝑐𝑐 𝑠𝑐𝑜𝑟𝑒 (𝑓
) … 𝑐𝑜− 𝑜𝑐𝑐 𝑠𝑐𝑜𝑟𝑒 (𝑓
)
+
𝑐𝑜𝑟𝑟𝑒𝑙𝑎𝑡𝑖𝑜𝑛 𝑠𝑐𝑜𝑟𝑒 (𝑓
) … 𝑐𝑜𝑟𝑟𝑒𝑙𝑎𝑡𝑖𝑜𝑛 𝑠𝑐𝑜𝑟𝑒 (𝑓
)
A Novel Recommender System based on Two-level Friendship Ties within Social Learning
569

Equation 7. The total scores of recommendation
After having detected the new communities, it
remains to calculate the recommendations for each
new community detected.
4 TESTS AND RESULTS
A Under the proposed approach, we suggest
considering two levels of social interactions so that
more relevant and precise recommendations can be
generated. Therefore, in addition to adding a
preliminary step of community detection, we propose
to integrate social interactions with two levels, i.e.,
integrating friends and friends of friends in the same
community.
The database we will focus on in our experiment
is a dataset extracted from a video-based educational
experience using a social and collaborative platform.
1
The interdisciplinary learning activity is carried out
between students in computer engineering and media
and communication. The collaborative social network
is divided into groups, each group including students
in computer engineering and media and
communication. We opted for this database because
it perfectly matches our context and expectations, and
it supports all the activities carried out by the learners
within the social network while providing them with
several supports, such as: documents, videos,
presentations. Students have a workspace where they
can share files, images and various resources, as well
as messages to interact with other students. The
exchange therefore consists of sharing several types
of educational material. The database holds 3000
learner interactions containing their activities within
the learning network (Martín et al., 2015).
To highlight the performance of this
recommendation system and the importance of
merging two-tier friendship with recommendation
generation, we compare the performance of the one-
tier social interaction-based system with the two-tier
social interaction-based recommendation system.
4.1 Community Detection
After testing the four algorithms: Louvain, InfoMap,
Walktrap and Edge Betweenness, we realize that the
most optimal algorithm in terms of modularity and
execution time is the Louvain algorithm with the
following results (Table 1). We also showcase the
1
http://dx.doi.org/10.13140/RG.2.1.2316.7521
communities obtained by the Louvain algorithm in
Figure 2.
Table 1: Modularity and execution time according to the
chosen algorithm.
Algorithm Modularity Execution
time
Number of
communities
Louvain 0,64 0,03 s 9
InfoMa
p
0,17 0,03 s 32
Walktra
p
0,62 0,03 s 11
Edge
Betweenness
0,63 0,03 s 11
Figure 2: Communities obtained in Louvain algorithm.
4.2 Friends of Friends
This step consists in detecting the friends of the
members of each community in order to acquire the
following new communities (Table 2).
Table 2: Communities detected by Louvain algorithms and
new communities generated by the approach proposed.
Community Number of
members’
original
communities
Number of
members’ new
communities
Communit
y
1 6 learners 12 learners
Communit
y
2 9 learners 16 learners
Communit
y
3 9 learners 11 learners
Communit
y
4 15 learners 32 learners
Communit
y
5 10 learners 14 learners
Communit
y
6 10 learners 15 learners
Communit
y
7 12 learners 18 learners
Communit
y
8 6 learners 8 learners
Communit
y
9 7 learners 18 learners
ICSOFT 2021 - 16th International Conference on Software Technologies
570

By shifting from one-level to two-level social
interactions, the number of individuals increases
tremendously and can reach twice the initial number.
This implies that the initial size of each community
will be multiplied by twice, and therefore more data
to process and more data to consider in generating
recommendations.
4.3 Evaluating Recommendations
Results
To properly evaluate our proposal, we compare the
results of the recommendation system based on one-
level social interactions with the results of the
recommendation system based on two-level social
interactions. The evaluation measures included are:
accuracy and precision. To evaluate the
recommendation system, we made a distribution of
the database according to the 20/80 law, which means
that we dedicate 80% to create the recommendation
model and 20% to test the recommendation model
and compare the actual preferences to the predicted
recommendations. After detecting the communities,
we apply the 20/80 rule for each community.
Many activities have been recorded in this database.
We restricted our analysis to those relevant actions
according to recommendations generated. Indeed, the
video is a very practical support to illustrate certain
notions. It is one of the soundest learning techniques
as it is supported by images and sound, and these two
elements fully attract the learner's attention.
Since the correlation between the primary activity is
associated with the recommendations and the other
secondary activities, as well as the co-occurrence, the
primary activity must be identified in addition to the
secondary activities whose relevance comes after:
The primary activity: Learner evaluation of
videos (fivestar).
The secondary activity: Creating a comment
for a video.
Precision:
To measure the relevance of the recommendation
system based on two-level social interactions, we
resort to precision in the first instance (Equation 8).
Considering the same previous communities, the
measures are represented in the following table with
RSSI1 is the recommendation system based on two-
level friendship ties and RSSI2 is the
recommendation system based on one level
friendship ties (Table 3).
𝑃𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛=
𝑇𝑃
𝑇𝑃+ 𝐹𝑃
Equation 8. Precision of recommender system
Where:
TP: Number of preferred items that are
recommended.
FP: Number of preferred items that are not
recommended.
Table 3: Precision obtained for RS1 and RS2.
𝐶
𝐶
𝐶
𝐶
𝐶
𝐶
𝐶
𝐶
𝐶
Precision
of RSSI1
1 1 1 1 1 1 1 1 1
Precision
of RSSI2
1 1 0 0 1 0 1 1 1
We thus visualize the box plot to view the accuracy
of the two types of recommendations (RSSI1 and
RSSI2) in figure 3. We note that the precision of
RSSI1 significantly exceeds the precision of RSSI2
since it reaches a value of 1 for all communities
versus values that vary between 0 and 1 for the second
recommendation system based on one-level
friendship ties (Figure 3).
Figure 3: Box plot presenting the variation of precision
according to the type of recommender system.
Accuracy :
Secondly, with a view to assessing the relevance of
the recommendation system, we measure the
accuracy of the two recommendation systems (RSSI1
and RSSI2) for the same communities in Table 4 by
using the equation 9:
𝐴𝑐𝑐𝑢𝑟𝑎𝑐𝑦=
𝑇𝑃+ 𝑇𝑁
𝑇𝑃+𝐹𝑃+ 𝑇𝑁+ 𝐹𝑁
Equation 9. Accuracy measure in the recommender
system
Where:
TP: Number of preferred items that are
recommended.
FP: Number of preferred items that are not
recommended.
TN: Number of non-preferred items that are not
recommended.
A Novel Recommender System based on Two-level Friendship Ties within Social Learning
571

FN: Number of non-preferred items that are
recommended.
Table 4: Accuracy according to RS1 and RS2.
𝐶
𝐶
𝐶
𝐶
𝐶
𝐶
𝐶
𝐶
𝐶
Accuracy
of RSSI1
1 1 1 1 1 1 1 1 1
Accuracy
of RSSI2
0,92
1
0,88 0,9
1
0,91
1 1 1
The box plot, reporting the variation in accuracy for
the two recommendation systems (RSSI1 and
RSSI2), shows the stability of the first
recommendation system, as well as its accuracy. The
value remains within 1 (Figure 4). As for the second
recommendation system based one level friendship
ties, one quarter of the values are between 0.88 and
0.91, while three quarters of the data are between 0.88
and 1.
Figure 4: Box plot emphasizing the variation of accuracy
according to the type of recommender system.
4.4 Discussion
Based on the findings, the recommendation system
based on two-level social interactions seems to
produce more appealing results than the
recommendation based on one-level friendship ties,
whether in terms of precision, or accuracy (Table 5).
An average precision of 1 is registered for the
recommender approach based on two-level friendship
ties against only 0.66 for the recommender approach
based on one-level friendship ties. This is due to the
recognition of the two-level friendship relations
instead of generating recommendations based on one
level friendship interactions. Adding an additional
level to the level of social interactions leads to more
meaningful and relevant results. We obtain a
precision and accuracy that reaches a value of 1,
which reveals the great added value of social
interactions in two levels. The larger the number of
friends, the more relevant the generated
recommendations are, and the larger the number of
data is counted as well. If the number of friends is
restricted, the data remains limited and the
recommendations may lose their relevance and
reliability. It is therefore important to consider social
interactions within recommendation systems, but
attention must be devoted to the number of friends to
be counted within each community.
Table 5: Average precision and accuracy obtained
according to the type of recommender system.
Recommender
system
Average
precision
Average
accuracy
RSSI1 1 1
RSSI2 0,66 0,956
5 CONCLUSION
This work addresses a very prominent topic in e-
learning: Recommender systems in social learning.
Our proposal consists of several core components: (1)
Detecting communities based on friendships, (2)
Identifying the friends of all members belonging to
each community and then building new communities
composed of members and friends of members, and
(3) generating recommendations for each new
community individually based on the correlation and
co-occurrence of events performed by learners. This
process is developed and requires the use of
community detection and matrix computation
algorithms. After testing the approach on a database
of several learners, it turns out that the
recommendation system based on two-level
friendship links is more efficient than the one based
one level friendship links in terms of precision and
accuracy. We thus contributed by proposing a hybrid
recommendation system based on two-level
friendship links within social learning, which is
perceived as a major strength, mainly because
community detection is not properly addressed at the
social learning level and social learning is not
adequately addressed in general. In upcoming
research, we intend to:
• Test our approach on a database within our
university with the intention of highlighting
the importance of community detection in the
management of recommendations.
• Dig deeper into the discipline of community
detection in online learning; which means to
address new aspects of community detection
in terms of recommendations not only on
social links, but also on other indicators.
ICSOFT 2021 - 16th International Conference on Software Technologies
572

REFERENCES
Aboagye, E., Yawson, J. A., & Appiah, K. N. (2020).
COVID-19 and E-Learning: The Challenges of
Students in Tertiary Institutions. Social Education
Research, 109–115. https://doi.org/10.37256/ser.12202
0422
Ansari, M. H., Moradi, M., NikRah, O., & Kambakhsh, K.
M. (2016). CodERS: A hybrid recommender system for
an E-learning system. 2016 2nd International
Conference of Signal Processing and Intelligent
Systems (ICSPIS), 1–5. https://doi.org/10.1109/
ICSPIS.2016.7869884
Beauguitte, L. (2010). Graphes, réseaux, réseaux sociaux:
Vocabulaire et notation. 8.
Blondel, V. D., Guillaume, J.-L., Lambiotte, R., &
Lefebvre, E. (2008). Fast unfolding of communities in
large networks. ArXiv:0803.0476 [Cond-Mat,
Physics:Physics]. https://doi.org/10.1088/1742-5468/
2008/10/P10008
Boussaadi, S., Aliane, H., Abdeldjalil, O., Houari, D., &
Djoumagh, M. (2020). Recommender systems based on
detection community in academic social network. 2020
International Multi-Conference on: “Organization of
Knowledge and Advanced Technologies” (OCTA), 1–
7. https://doi.org/10.1109/OCTA49274.2020.9151729
Cao, C., Ni, Q., & Zhai, Y. (2015). An Improved
Collaborative Filtering Recommendation Algorithm
Based on Community Detection in Social Networks.
Proceedings of the 2015 Annual Conference on Genetic
and Evolutionary Computation, 1–8. https://doi.org/
10.1145/2739480.2754670
Cuzzocrea, A., Papadimitriou, A., Katsaros, D., &
Manolopoulos, Y. (2012). Edge betweenness centrality:
A novel algorithm for QoS-based topology control over
wireless sensor networks. Journal of Network and
Computer Applications, 35(4), 1210–1217.
https://doi.org/10.1016/j.jnca.2011.06.001
Gasparetti, F., Sansonetti, G., & Micarelli, A. (2020).
Community detection in social recommender systems:
A survey. Applied Intelligence. https://doi.org/
10.1007/s10489-020-01962-3
George, G. (2019). Review of ontology-based recommender
systems in e-learning. 18.
Lalwani, D., Somayajulu, D. V. L. N., & Krishna, P. R.
(2015). A community driven social recommendation
system. 2015 IEEE International Conference on Big
Data (Big Data), 821–826. https://doi.org/
10.1109/BigData.2015.7363828
Martín, E., Gértrudix, M., Urquiza‐Fuentes, J., & Haya, P.
A. (2015). Student activity and profile datasets from an
online video‐based collaborative learning experience.
British Journal of Educational Technology, 46(5), 993–
998. https://doi.org/10.1111/bjet.12318
Panagiotakis, C., Papadakis, H., & Fragopoulou, P. (2020).
Unsupervised and supervised methods for the detection
of hurriedly created profiles in recommender systems.
International Journal of Machine Learning and
Cybernetics, 11(9), 2165–2179. https://doi.org/
10.1007/s13042-020-01108-4
Parimi, R., & Caragea, D. (2014). Community Detection on
Large Graph Datasets for Recommender Systems. 2014
IEEE International Conference on Data Mining
Workshop, 589–596. https://doi.org/10.1109/ICDMW.
2014.159
Pons, P., & Latapy, M. (2005). Computing communities in
large networks using random walks. 20.
Rezvanian, A., Moradabadi, B., Ghavipour, M., Daliri
Khomami, M. M., & Meybodi, M. R. (2019). Social
Recommender Systems. In A. Rezvanian, B.
Moradabadi, M. Ghavipour, M. M. Daliri Khomami, &
M. R. Meybodi, Learning Automata Approach for
Social Networks (Vol. 820, pp. 281–313). Springer
International Publishing. https://doi.org/10.1007/978-
3-030-10767-3_8
Rosvall, M., Axelsson, D., & Bergstrom, C. T. (2009). The
map equation. The European Physical Journal Special
Topics, 178(1), 13–23. https://doi.org/10.1140/
epjst/e2010-01179-1
S. Souabi, A. Retbi, M. K. Idrissi, & S. Bennani. (2020). A
Recommendation approach based on Correlation and
Co-occurrence within social learning network. 2020 5th
International Conference on Cloud Computing and
Artificial Intelligence: Technologies and Applications
(CloudTech), 1–6. https://doi.org/10.1109/CloudTech
49835.2020.9365874
Salehi, M. (2013). Application of implicit and explicit
attribute based collaborative filtering and BIDE for
learning resource recommendation. Data & Knowledge
Engineering, 87, 130–145. https://doi.org/10.1016/
j.datak.2013.07.001
Souabi, S., Retbi, A., Idrissi, M. K., & Bennani, S. (2020).
A Recommendation Approach in Social Learning
Based on K-Means Clustering. 2020 International
Conference on Intelligent Systems and Computer
Vision (ISCV), 1–5. https://doi.org/10.1109/
ISCV49265.2020.9204203
Tartari, E., Tartari, A., & Beshiri, D. (2019). The
Involvement of Students in Social Network Sites
Affects Their Learning. International Journal of
Emerging Technologies in Learning (IJET), 14(13), 33.
https://doi.org/10.3991/ijet.v14i13.10453
Tosun, N. (2018). Social Networks as a Learning and
Teaching Environment and Security in Social
Networks. Journal of Education and Training Studies,
6(11a), 194. https://doi.org/10.11114/jets.v6i11a.3817
A Novel Recommender System based on Two-level Friendship Ties within Social Learning
573
