
Side Channel Counter-measures based on Randomized AMNS
Modular Multiplication
Christophe Negre
1,2
1
DALI, Universit
´
e de Perpignan, France
2
LIRMM, Universit
´
e de Montpellier and CNRS, France
Keywords:
Exponentiation, DSA, Scalar Multiplication, ECC, Randomization, AMNS, Side Channel Analysis,
Counter-measure.
Abstract:
The paper presents counter-measures based on dynamic randomization against side channel analysis like dif-
ferential and correlation power analysis. The building block of the proposed counter-measure is a randomiza-
tion of the modular multiplication in AMNS for a prime p. We use this randomized modular multiplication to
inject randomization during the whole computation in DSA exponentiation and Co-Z elliptic curve scalar mul-
tiplication. We analyze the level of randomization injected and, through implementations results, we evaluate
the penalty in terms of performance of the proposed counter-measures.
1 INTRODUCTION
Modern cryptographic protocols like Digital Signa-
ture Algorithm (DSA), Elliptic Cryptography (ECC)
or post-quantum SIDH (Jao and Feo, 2011) necessi-
tate to perform hundreds of multiplications modulo
a prime integer p. Such modular multiplications in-
volve quite large integers : 256 to 500 bits for ECC
and SIDH and 2000 bits to 8000 bits for DSA. Com-
puting a multiplication modulo p consists in com-
puting a product of integers C = A ×B which pro-
duces C of size p
2
, the product C is reduced to an
integer R of size p by subtracting a multiple of p
which clears out parts of the bits of C. Indeed, in Bar-
rett approach (Barrett, 1987) computing R = C − pQ
clears out the most significant bits of C, whereas in
Montgomery approach (Montgomery, 1985) comput-
ing R = C − pQ clears out the least significant bit,
in this latter case the output is R/φ ≡ ABφ
−1
mod p
where φ is a power 2.
Alternative number system can be used to improve
such modular multiplication. Indeed, in the Adapted
Modular Number System (Bajard et al., 2004) for a
prime p, the elements are represented with a larger
radix γ modulo p than the usual 2
w
-radix for multi-
precision integer representation. The initial goal of
the ANMNS was to simplify carry propagation in in-
teger multiplications and reductions. Recently in (Di-
dier et al., 2019), it was shown that the Montgomery-
like approach for modular multiplication in AMNS
was competitive compared to state of the art ap-
proaches.
Cryptographic protocols can be threaten by side
channel analysis when they are executed on an em-
bedded device. Indeed when monitoring either power
consumption (Kocher et al., 1999), electronic em-
anation or computation time, it is possible to re-
cover part of the secret data involved in the com-
putation. For example Differential Power Analysis
(DPA) (Kocher et al., 1999) or Correlation Power
Analysis (CPA) (Brier et al., 2004) guess some secret
bits, and they check if this guess leads to data cor-
related to leaked out power consumption. The main
strategy to counteract these attacks consists in ran-
domizing the data involved in cryptographic computa-
tion, which reduces the correlation between the secret
data and the power consumption or electronic emana-
tion. The main methods for randomizing data (i.e. the
integer modulo p or the exponent in DSA) consists in
masking data with additive mask (Tunstall and Joye,
2010; Clavier et al., 2010) or multiplicative mask, but
this induces additional computations and penalty in
terms of performance. In 2016, the method proposed
in (Lesavourey et al., 2016) combines Montgomery
and Barrett modular multiplication to induces mul-
tiplicative mask of the form 2
t
with random t. The
interest of this approach is that it is almost free of
computation, and it produces a mask which randomly
changes during the whole computation.
Negre, C.
Side Channel Counter-measures based on Randomized AMNS Modular Multiplication.
DOI: 10.5220/0010599706110619
In Proceedings of the 18th International Conference on Security and Cryptography (SECRYPT 2021), pages 611-619
ISBN: 978-989-758-524-1
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
611

Contributions. In this paper we extend the approach
presented in (Lesavourey et al., 2016) to the case
of modular arithmetic in AMNS for a prime p. We
provide a randomized version of both Montgomery-
like (resp. Barrett-like) multiplication in AMNS
producing multiplicative mask φ
−1
γ
−s
(resp. γ
−s
)
for a random s. Afterwards we present modular
exponentiation for DSA and scalar multiplication on
elliptic curve both using the proposed randomized
multiplication to produce multiplicative random
mask during the whole computation. We evaluate
the level of randomization produced by the proposed
approach and also present implementation results.
Organization of the Paper. In Section 2 we review
Barrett-like and Montgomery-like modular multipli-
cation in an AMNS. In Section 3 we present a strat-
egy to randomized Barrett-like and Montgomery-like
modular multiplication in AMNS. In Section 4 and 5
we adapt the Montgomery ladder for modular expo-
nentation and scalar multiplication in order to use
the proposed randomized AMNS multiplications. Fi-
nally, in Section 6, we give some concluding remarks.
2 ARITHMETIC IN ADAPTED
MODULAR NUMBER SYSTEM
In this section we review the Adapted Modular Num-
ber System and related algorithms for multiplication
modulo a prime integer p.
2.1 Definition
Arithmetic of integers are generally based on radix
representation : in radix β an integer A is expressed
as A =
∑
n−1
i=0
a
i
β
i
where 0 ≤ a
i
< β. On computers the
radix β is generally chosen as β = 2
w
where w is the
word size of the computer. In (Bajard et al., 2004)
the authors introduced the Adapted Modular Number
System (AMNS) to represent integers modulo p (cf.
Definition 1). This system somehow extends the radix
representation to a larger set of radix γ ∈{0,1, .. ., p −
1}.
Definition 1 (AMNS (Bajard et al., 2004)). An
Adapted Modular Number System B = (p,n,ρ, γ,λ)
is such that
i) p is prime integer.
ii) n is the number of coefficients of the system.
iii) ρ the upper bound of the absolute value of the
coefficients.
iv) γ is the radix of the system and λ is a small integer
such that
γ
n
= λ mod p. (1)
v) Any integer A modulo p can be written as
A ≡
n−1
∑
i=0
a
i
γ
i
mod p with |a
i
| < ρ.
The elements of an AMNS are seen as degree n −1
polynomials A(X) =
∑
n−1
i=0
a
i
X
i
in X with coefficients
smaller that ρ. To get their integer expression we have
to evaluate A(X) at γ modulo p.
2.2 AMNS Lattice and Short
Polynomial
Given an AMNS B = (p,n, γ,λ) the authors in (N
`
egre
and Plantard, 2008) define the following rank n lattice
L
p,n,ρ,γ,λ
= {V (X) ∈ Z[X] s.t. degV (X) < n
and V (γ) ≡ 0 mod p}
.
A lattice can be seen as integer linear combinations of
vector in Z
n
. Below we provide a basis of the lattice
L
p,n,ρ,γ,λ
:
B =
p 0 0 0 .. . 0
−γ 1 0 0 .. . 0
−γ
2
0 1 0 .. . 0
.
.
.
.
.
.
.
.
.
−γ
n−2
0 0 .. . 1 0
−γ
n−1
0 0 .. . 0 1
← p
← X −γ
← X
2
−γ
2
.
.
.
← X
n−2
−γ
n−2
← X
n−1
−γ
n−1
The above basis tells us that the volume of the lattice
is
det(B) = p.
With Minkowsky’s inequality, the authors (N
`
egre and
Plantard, 2008) then obtained a short non-zero vector
(or polynomial) in L
p,n,ρ,γ,λ
by applying a reduction
algorithm such as LLL or BKZ:
M = m
0
+ m
1
X +···+ m
n−1
X
n−1
(2)
such that kMk
∞
∼
=
n
q
det(L
p,n,γ,λ
) =
n
√
p and M(γ) = 0
mod p.
2.3 Montgomery-like Multiplication in
AMNS
The condition iv) on γ in Definition 1 is meant to ease
the multiplication modulo p in the AMNS. Indeed,
let us call E(X ) the polynomial X
n
−λ: this means
that, from condition iv) in Definition 1, γ is a root of
the polynomial E(X) in Z/pZ. As described in (Ba-
jard et al., 2004) a multiplication of two elements in
SECRYPT 2021 - 18th International Conference on Security and Cryptography
612

AMNS consists of a polynomial multiplication mod-
ulo E(X) = X
n
−λ
C(X ) = A(X) ×B(X ) mod E(X)
and a reduction of the coefficients. Since
kAk∞,kBk
∞
< ρ, the coefficients of C lie in the in-
terval ] −nρ
2
λ,nρ
2
λ[, they must be reduced such that
they have absolute value smaller than ρ.
A first method to reduce the coefficients was pro-
posed in (N
`
egre and Plantard, 2008), this approach
uses the short polynomial M(X) of (2) which satisfies
M(γ) = 0 mod p and kMk
∞
is small. This method is
depicted in Algorithm 1: it computes Q such that the
lower parts of the coefficient (C + Q ×M) mod E are
all zero (or equivalently are equal to 0 modulo φ = 2
k
).
But adding Q ×M modulo E does not change the
value modulo p since M(γ) = 0 mod p and E(γ) = 0
mod p. At the end the polynomial
R = (C + Q ×M mod E)/φ
evaluated at γ leads to
R(γ) = C(γ)φ
−1
mod p = A(γ) ×B(γ)φ
−1
mod p.
Algorithm 1: AMNS MonMul.
Require: A,B ∈ B = AMNS(p, n,γ,λ,ρ) with E =
X
n
−λ M such that M(γ) ≡ 0 (mod p) an inte-
ger φ and M
0
= −M
−1
mod (E,φ)
Ensure: R such that R(γ) = A(γ)B(γ)φ
−1
mod p
1: C ← A ×B mod E
2: Q ←C ×M
0
mod (E,φ)
3: R ←(C + Q ×M mod E)/φ
The authors in (N
`
egre and Plantard, 2008) showed
that the above algorithm outputs R in the AMNS (i.e.
with kRk
∞
< ρ) under the following condition
ρ > 2|λ|nσ and φ > 2|λ|nρ
2.4 Barrett-like Multiplication in
AMNS
A second approach to perform the reduction of the
coefficients in an AMNS multiplication was proposed
in (Plantard, 2005). This method adapts the Barrett
method (Barrett, 1987) to the case of multiplication
in an AMNS. This approach use the short polynomial
M defined in (2) to reduce the upper part of the coef-
ficients of the following polynomial:
C = A(X) ×B(X ) mod E(X).
The method of (Plantard, 2005) is shown in Algo-
rithm 2, this method computes a polynomial Q such
Algorithm 2: AMNS BarMul.
Require: A(X),B(X ) two elements in an AMNS
(p,n,ρ,γ, λ), a radix β, a polynomial M such
that M(γ) = 0 mod p and V = b(M
−1
mod E)×
β
2k
e
Ensure: R such that R(γ) = A(γ) ×B(γ) mod p.
1: C ← (A ×B) mod E
2: U ← bC/β
k−1
e
3: W ← (U ×V ) mod E
4: Q ←bW /β
k+1
e
5: R ←C −((Q ×M) mod E)
6: return (R)
that in C −((Q×M) mod E) the most significant bits
of the coefficients are set to zero. In the sequel we will
assume β = 2, indeed, in this case a division by power
of β is just a right shift.
If we assume
ρ > 2n
2
λ
2
kMk
∞
and kAk
∞
,kBk
∞
< ρ
then, the polynomial R output by Algorithm 2 satisfies
kRk
∞
< ρ and R(γ) = A(γ) ×B(γ) mod p.
3 RANDOMIZED MODULAR
MULTIPLICATION IN AMNS
In this section we present a randomization of modu-
lar multiplication in an AMNS(p,n,ρ,γ, λ). We will
use it later to randomise modular exponentiation and
scalar multiplication. For the remaining of the paper,
we assume that:
λ = 2. (3)
3.1 Randomized Polynomial
Multiplication Modulo E
We propose to change Step 1 in AMNS MonMul and
AMNS BarMul with
C ← 2 ×(A ×B)/X
s
mod E. (4)
for s ∈ {0, ...,n −1}. Let us first see how to compute
C in (4). We consider the product U(X) = A(X ) ×
B(X), then we rewrite 2 ×U(X ) as follows:
2 ×U(X) = (
s−1
∑
i=0
2u
i
X
i
)
| {z }
U
0
+(
n+s−1
∑
i=s
2u
i
X
i
)
| {z }
U
1
+(
2n−1
∑
i=n+s
2u
i
X
i
)
| {z }
U
2
.
Then using (3), we have 2 ≡ X
n
mod E(X), we can
replace each 2 with X
n
in U
0
and we can also replace
each X
n
with 2 in U
2
. We get:
2 ×U(X) ≡ (
∑
n−1
i=s
(2u
i
+ 4u
i+n
)X
i
)
+(
∑
n+s−1
i=n
(2u
i
+ u
i−n
)X
i
) mod E
Side Channel Counter-measures based on Randomized AMNS Modular Multiplication
613

Which leads to the following
(2U(X))X
−s
mod E = (
∑
n−s−1
i=0
(2u
i+s
+ 4u
i+n+s
)X
i
)
+(
∑
n−1
i=n−s
(2u
i+s
+ u
i+s−n
)X
i
)
(5)
Complexity of Randomized Multiplication. The costs
of non-randomized and randomized multiplication are
show in Table 1. The shifts are due to the multiplica-
tions by 2 or 4 in a reduction modulo E.
Table 1: Complexity of randomized and non-randomized
multiplication mod E.
Operation # mul. # add. # shifts
A ×B mod E n
2
n
2
n
(A ×B)/X
s
mod E n
2
n
2
2n −s
We can notice that a randomized multiplication has a
complexity close to a non-randomized multiplication:
we just have a penalty of n −s shifts.
3.2 Randomized AMNS-Montgomery
and AMNS-Barret Multiplication
We can use this randomized multiplication mod-
ulo E(X) to randomize AMNS MonMul multipli-
cation. To reach this goal we replace the first
step of AMNS MonMul with C ← (A ×B)/X
s
mod
E. We show in Algorithm 3 the resulting random-
ized AMNS MonMul. The proposed modification
changes the output of the algorithm. The output of
Rd AMNS MonMul is:
R = C + Q ×M mod E
= ((A ×B) +W ×E)/X
s
+ Q ×M +W
0
×E
where in the last expression W (X) and W
0
(X) are due
to the reduction by E(X). If we evaluate the above
expression of R at γ the terms Q ×M, W ×E, and
W
0
×E vanish since M(γ) = 0 and E(γ) = 0. This
leads to the following:
R(γ) = A(γ)B(γ)φ
−1
γ
−s
mod p.
Algorithm 3: Rd AMNS MonMul.
Require: A,B ∈ B = AMNS(p, n,γ,λ,ρ) with E =
X
n
−λ and λ = 2, s a randomizing integer, M a
polynomial such that M(γ) ≡0 (mod p), an inte-
ger φ and M
0
= −M
−1
mod (E,φ)
Ensure: R such that R(γ) = A(γ)B(γ)φ
−1
γ
−s
mod p
1: C ← (A ×B)/X
s
mod E
2: Q ←C ×M
0
mod (E,φ)
3: R ←(C + Q ×M mod E)/φ
4: return R
We can do the exact same modification in
AMNS BarMul. The only change is on the output of
the algorithm which in this case produce a polynomial
R(X) satisfying:
R(γ) = A(γ)B(γ)γ
−s
mod p
The resultatin algorithms are shown in Algorithm 3
and 4.
Algorithm 4: Rd AMNS BarMul.
Require: A,B ∈ B = AMNS(p, n,γ,λ,ρ) with E =
X
n
−λ and λ = 2, s a randomizing integer, M such
that M(γ) = 0 mod p, V = b(M
−1
mod E) ×
β
2k
e.
Ensure: R such that R(γ) = A(γ) ×B(γ)γ
−s
mod p
1: C ← (A ×B)/X
s
mod E
2: U ← bC/β
k−1
e
3: W ← (U ×V ) mod E
4: Q ←bW /β
k+1
e
5: R ←C −((Q ×M) mod E)
6: return R
3.3 Implementation Results
We implemented in C Algorithm 3 and 4 along with
non-randomized Algorithm 1 and 2.We used the fol-
lowing strategies for large and small fields:
• Small fields: F
p
with p of bit-length 256 and 500
bits. AMNS elements are stored in an arrays of n
64-bit word integers. Polynomial multiplication is
done using schoolbook method using 64-bits inte-
ger multiplication instruction of the processor.
• Larger fields: F
p
with p of bit-length 2048 bits,
3096 bits. AMNS elements are stored in arrays of
n 128-bit word integers in order to keep n small.
We implemented multiplication of unsigned 128
bits integers through several 64-bit instructions.
This approach reduces the efficiency of Barrett
multiplication compared to Montgomery multipli-
cation since it involves more signed 128 integer
multiplications which are, in this case, less effi-
cient.
We compiled our C code with gcc 9.3.0, and run it
on an Ubuntu 20.04 and an Intel Westmere processor.
The timings are averages of 2000 multiplications with
randomized input.
The above timing results show that for larger
fields, the penalty due to signed 128 bits multipli-
cation render non-randomized and randomized Bar-
ret AMNS multiplication significantly slower. On
small fields one can notice that the randomization on
AMNS BarMul and AMNS MonMul reduce slightly
SECRYPT 2021 - 18th International Conference on Security and Cryptography
614

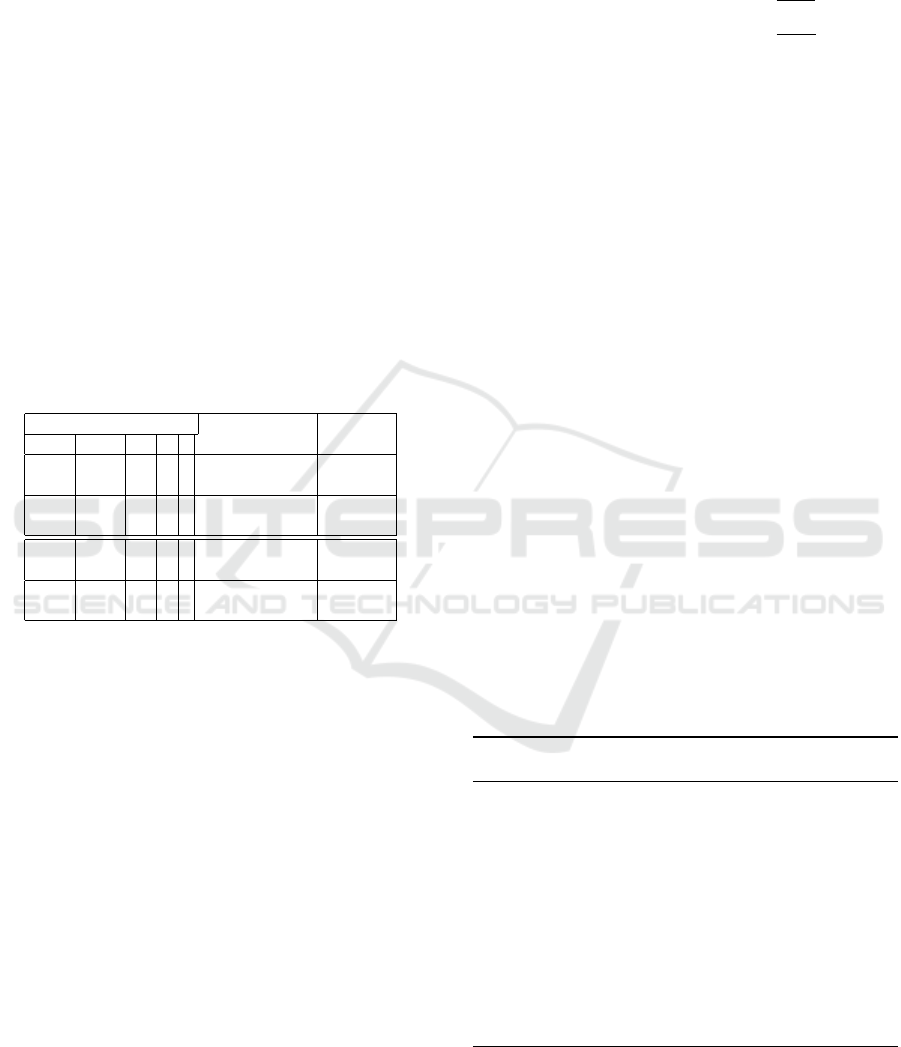
Table 2: Timings of AMNS multiplication.
Field and AMNS Algorithm #CC
log
2
(p) ρ n λ
3040 2
110
30 2
AMNS MonMul 75527
Rd AMNS MonMul 74930
AMNS BarMul 107429
Rd AMNS BarMul 107625
2020 2
109
20 2
AMNS MonMul 33372
Rd AMNS MonMul 34334
AMNS BarMul 47661
Rd AMNS BarMul 47624
510 2
53
10 2
AMNS MonMul 1041
Rd AMNS MonMul 1176
AMNS BarMul 1507
Rd AMNS BarMul 1632
256 2
57
5 2
AMNS MonMul 207
Rd AMNS MonMul 230
AMNS BarMul 201
Rd AMNS BarMul 228
their efficiency compared to non-randomized counter
parts.
4 RANDOMIZED DSA
EXPONENTIATION
We consider in this section the modular expo-
nentiation involved in Digital Signature Algorithm
(DSA (NIST.FIPS.186.4, 2012)). We present a ran-
domized exponentiation based on the randomized
Montgomery and Barrett multiplications in AMNS
introduced in Subsection 3.2.
4.1 Background on DSA and Side
Channel Analysis
DSA security is based on the difficulty of the discrete
logarithm problem. Given a prime p, and an element
G of order q in the finite field F
p
, then, computing
the discrete logarithm of R ∈ hGi in base G consists
in finding the exponent E such that R = G
E
mod p.
For a security level larger than 128-bit the prime p
has a bit-length is larger than 2048 bits and q has a
bit-length larger than 256 bits.
The main computation in DSA is an exponentia-
tion modulo p. Specifically, we have to compute:
R = G
E
mod p (6)
where G has order q|(p −1) and E ∈ [0,q −1]. The
basic approach to compute the modular exponentia-
tion in (6) consists in a sequence of squares and mul-
tiplications in order to reconstruct from the most sig-
nificant bits to the least significant bits the exponent
E = (e
`−1
,. ..,e
0
)
2
of R (cf. Algorithm 5).
Algorithm 5: Square-and-multiply.
Require: G ∈ F
p
and E = (e
`−1
,. ..,e
0
)
2
a positive
integer.
Ensure: R such that R = G
E
mod p
R ← 1
for i = 0 to ` do
R ← R
2
×G
e
i
mod p
return R
Side Channel Analysis. Sensitive computation on
an embedded device can be threaten by side channel
analysis. Indeed, such attacks use either power con-
sumption, electromagnetic emanation or computation
time to recover part of the secret data involved in the
computation. An example of such attacks is the sim-
ple power analysis (SPA) on Square-and-multiply ex-
ponentiation: assuming that multiplication consume
more power than a square we can identify on the
power trace the loop iteration involving a multiplica-
tion, which are loop iteration corresponding to e
i
= 1.
The basic protection against SPA consists in ren-
dering the sequence of squares and multiplications of
the exponentiation independent to the bits of the ex-
ponent. A popular approach to reach this goal is the
Montgomery ladder (Algorithm 6) which uses two
intermediate variables R
0
corresponding to R in the
Square-and-multiply exponentiation and R
1
always
satisfying R
1
= R
0
×G mod p. At each loop itera-
tion we have a multiplication followed by a square,
which then does not leak out the corresponding bit e
i
of E.
Algorithm 6: Montgomery-ladder (Joye and Yen, 2002).
Require: An base GF
p
and an exponent E =
(e
`−1
,. ..,e
0
)
2
Ensure: R
0
= G
E
mod N
1: R
0
← 1, R
1
← G
2: for i from 0 to ` −1 do
3: R
1−e
i
← R
0
×R
1
mod p
4: R
e
i
← R
2
e
i
mod p
5: return R
0
There are more powerful attacks like the Differential
Power Analysis (DPA) (Kocher et al., 1999) which
guesses a bit of the exponent and correctly predict
power consumption of a loop iteration. Or the Cor-
relation Power Analysis (CPA) (Brier et al., 2004)
which recovers a bit of exponent by correlating power
consumption of two consecutive loop iterations. To
counteract these attacks the main strategy consists in
randomizing the data involved in the exponentiation
(the exponent E and intermediate variables R
0
and
R
1
).
Side Channel Counter-measures based on Randomized AMNS Modular Multiplication
615

Specifically, one strategy to randomize the data
is the base blinding:. This strategy was proposed
in (Coron, 1999) and consists in multiplying G with a
random α, assuming that β = α
E
mod p is precom-
puted. Then we have
G
0
= G ×α mod p ⇒G
0E
(β
−1
) mod p = G
E
mod p
In (Lesavourey et al., 2016) the authors propose to
randomly update the multiplicative mask α with the
Montgomery factor induced by Montgomery multi-
plication. Their randomization is limited by the fact
that this random mask should be equal to 1 at the end
of the exponentiation and then is reduced to a small
set of values.
4.2 Randomized Montgomery Ladder
for DSA
Our approach consists in running the Montgomery
ladder with input given in an AMNS (p,n,ρ,γ,λ). At
each loop iteration we pick two random bits t
i
and
s
i
and then the two modular multiplications are com-
puted as follows:
• If t
i
= 1 we apply Rd AMNS MonMul with ran-
domizing parameter s
i
, in this case the output has
a multiplicative mask equal to φ
−1
×γ
−s
i
.
• If t
i
= 0 we apply Rd AMNS BarMul with ran-
domizing parameter s
i
, in this case the output has
a multiplicative mask equal to γ
−s
i
.
The resulting randomized Montgomery ladder is
shown in Algorithm 7.
Algorithm 7: Randomized Montgomery Ladder.
Require: G of order q in F
p
where q of bit-length `,
an exponent E = (e
`−1
,.., e
1
e
0
)
2
, w the bit-length
of the computer words, an AMNS (p,n, ρ,γ,λ)
with λ = 2 and precomputed data u ← b(p −
1)/2
`
c,v ←(p −1) mod 2
`
and β = γ
−u
mod p.
Ensure: R = G
E
mod p
1: T ←Random(0,..., b(v/(nw)c)
2: S ← v −nwT
3: R
0
(X) ← AMNS(1 ×β mod p)
4: R
1
(X) ← AMNS(G mod p)
5: for i = ` −1 to 0 do
6: if t
i
= 1 then
7: R
e
i
← Rd AMNS MonMul(R
e
i
,R
1−e
i
,s
i
)
8: R
1−e
i
← Rd
AMNS MonMul(R
e
i
,R
e
i
,s
i
)
9: else
10: R
e
i
← Rd AMNS BarMul(R
e
i
,R
1−e
i
,s
i
)
11: R
1−e
i
← Rd AMNS BarMul(R
e
i
,R
e
i
,s
i
)
12: R ←R
0
(γ) mod p
13: return R
At each iteration of the above algorithm R
0
R
1
are
multiplied by a factor which can be 1, φ
−1
, γ
−1
or
φ
−1
γ
−1
. These multiplications contribute to randomly
modify a multiplicative mask on R
0
and R
1
providing
a protection against side channel analyses like DPA
or CPA. But this mask should be equal to 1 at the end
of the exponentiation in order to have R
0
equal to the
correct output G
E
mod p. Steps 1 and 2 of the al-
gorithm set the necessary conditions on the random
bits in t
i
and s
i
which ensure that the random mask
induced by the factors φ
−t
i
γ
−s
i
and β is equal to 1 at
the end. This is shown in the following lemma.
Lemma 1. Algorithm 7 correctly outputs R = G
E
mod p.
Proof. Let us first unroll the algorithm to understand
how the random mask evolves during the exponentia-
tion:
• After loop i = ` −1 we have
R
0
=β
2
G
e
`−1
(γ
−1
)
s
`−1
(φ
−1
)
t
`−1
,
R
1
=β
2
G
e
`−1
+1
(γ
−1
)
s
`−1
(φ
−1
)
t
`−1
.
• After loop i = ` −2 whe have
R
0
=β
4
G
2e
`−1
+e
`−2
(γ
−1
)
2s
`−1
+s
`−2
(φ
−1
)
2t
`−1
+t
`−2
,
R
1
=β
4
G
2e
`−1
+e
`−2
+1
(γ
−1
)
2s
`−1
+s
`−2
(φ
−1
)
2t
`−1
+t
`−2
.
• ...
• After loop i = 0, we have
R
0
=β
2
`
G
E
(γ
−1
)
S
(φ
−1
)
T
, R
1
=β
2
`
G
E+1
(γ
−1
)
S
(φ
−1
)
T
.
We consider the last multiplicative mask of R
0
β
2
`
(γ
−1
)
S
(φ
−1
)
T
we use the fact that β = γ
−u
and φ = 2
w
and 2 = γ
n
mod p which leads to
β
2
`
(γ
−1
)
S
(φ
−1
)
T
= 2
−2
`
u
γ
−S
2
−wT
= γ
−(2
`
u+S+nwT )
= γ
−(2
`
u+v)
= γ
−(p−1)
= 1
Level of Randomization. At the beginning of the
Montgomery ladder there are no random mask on R
0
and R
1
(β is a public value), but the random mask is
growing by one bits after each iteration. This means
that the level of randomization injected at the end is
2
`
which correspond to the size of the random data T .
This is a larger level of dynamic randomization than
the one of (Lesavourey et al., 2016).
SECRYPT 2021 - 18th International Conference on Security and Cryptography
616
4.3 Implementation Results
We implemented in C the randomized and non-
randomized form of Montgomery ladder using
AMNS modular multiplication. We considered DSA
exponentiation for the two cryptographic size 2048
bits and 3096 bits for p. We also considered (non-
DSA) exponentiation on small field from 256 bits and
500 bits since for these size AMNS Barrett multipli-
cations is as efficient as their AMNS Montgomery
counter-parts. The resulting timing results are re-
ported in Table 3.
We notice that for large fields, the use of slow
AMNS Barrett multiplication render the proposed ap-
proach not efficient. For smaller fields, particularly
for field of size 256-bits the randomized approach
is competitive. This means that if we could im-
prove signed 128-bit multiplication we could get ran-
domized exponentiation on large field with smaller
penalty.
Table 3: Timings of exponentiation.
Field and AMNS Algorithm #CC
log
2
(p) log
2
(q) ρ n λ
3040 300 2
110
30 2
Mont. Ladder 46036405
Rand. Mont. Ladder 57285659
2020 256 2
109
20 2
Mont. Ladder 15911757
Rand. Mont. Ladder 21920264
510 510 2
53
10 2
Mont. Ladder 1211894
Rand. Mont. Ladder 1662200
256 256 2
57
5 2
Mont. Ladder 106877
Rand. Mont. Ladder 116832
5 RANDOMIZED SCALAR
MULTIPLICATION
We present in this section a strategy to dynamically
randomize data in scalar multiplication on an elliptic
curve E(F
p
). First, we provide the necessary back-
ground on elliptic curve and related algorithms.
5.1 Background on Elliptic Curve
An elliptic curve E(F
p
) is the set of points (x, y) ∈
F
2
p
, along with a point at infinity O, which satisfy an
equation of the form:
y
2
= x
3
+ ax + b where a,b ∈ F
p
with ∆ = −16(4a
3
+ 27b
2
) 6= 0. There is a additive
group law on E(F
p
) which is derived from the chord
and tangent rules: a line crossing two points P,Q on
the curve intersects the curve on a third point R
0
, then
R = P + Q is defined as the x-axis symmetric of R
0
.
The coordinates of R = (x
3
,y
3
) can be computed with
a few operations in F
p
from the coordinates of P =
(x
1
,y
1
) and Q = (x
2
,y
2
)
x
3
=λ −x
1
−x
2
y
3
=y
1
−λ(x
3
−x
1
)
with λ =
(
y
1
−y
2
x
1
−x
2
if P 6= Q
3x
2
1
+a
2y
1
if P = Q
To improve the efficiency of these operations, a var-
ious set of projective coordinate system was used in
order to avoid costly inversions. Among them there is
the Jacobian coordinates (X,Y,Z) which corresponds
to affine coordinates (x,y) = (X/Z
2
,Y /Z
3
).
Definition 2. Two points given in Jacobian coordi-
nates are equivalent (X ,Y, Z) ∼ (X
0
,Y
0
,Z
0
) if there is
β ∈ F
p
such that
(X
0
,Y
0
,Z
0
) = (X β
2
,Y β
3
,Zβ)
these two Jacobian coordinates correspond to
the same affine point (x, y) = (X /Z
2
,Y /Z
3
) =
(X
0
/Z
02
,Y
0
/Z
03
).
The use of Jacobian coordinates avoids inversion
in F
p
but, in counterpart, this increases the number
of multiplications per point operation. In the litera-
ture, several improvements were proposed to simplify
these Jacobian formula. We will focus here on the
co-Z formula for addition which was first proposed
in (M
´
eloni, 2007) and then extended in (Goundar
et al., 2011) to a few other co-Z point operations.
Co-Z point formula take as input two points in Ja-
cobian coordinates sharing the same Z coordinate.
In (M
´
eloni, 2007) they show that this simplifies Jaco-
bian addition and leads to the formula shown in Algo-
rithm 8. The last operations in Step 8 of Algorithm 8
are meant to update the input P such that it shares the
same Z coordinate as R = P + Q.
Algorithm 8: Co-Z addition with update
(ZADDU) (M
´
eloni, 2007).
Require: P = (X
1
,Y
1
,Z) and Q = (X
2
,Y
2
,Z)
Ensure: (R,P
0
) such that R = P + Q and P
0
∼ P
1: C ← (X
1
−X
2
)
2
2: W
1
← X
1
C, W
2
← X
2
C
3: D ←(Y
1
−Y
2
)
2
, A
1
←Y
1
(W
1
←W
2
)
4: X
3
← D −W
1
−W
2
5: Y
3
← (Y
1
−Y
2
)(W
1
−X
3
) −A
1
6: Z
3
← Z(X
1
−X
2
)
7: X
1
←W
1
, Y
1
← A
1
, Z
1
← Z
3
8: R ←(X
3
,Y
3
,Z
3
),P
0
← (X
1
,Y
1
,Z
1
)
9: return R,P
0
In (Goundar et al., 2011) the authors adapt the
ZADDU approach to the computation of P + Q and
P−Q with shared Z. They use the fact that most com-
putation for P + Q and P −Q are the same, unless for
Side Channel Counter-measures based on Randomized AMNS Modular Multiplication
617

P −Q we have to negate the Y coordinate of Q. This
leads to ZADDC algorithm ouputing P+Q and P −Q
with shared Z.
In (Goundar et al., 2011) the authors take advan-
tage of ZADDU and ZADDC to get a variant of the
Montgomery ladder for scalar multiplication. Indeed,
the two operations R
1−b
← R
b
+ R
1−b
and R
b
← 2R
b
in the Montgomery ladder can be done as follows:
(R
1−b
,R
b
)←ZADDC(R
b
,R
1−b
)
= (R
b
+ R
1−b
,R
b
−R
1−b
),
(R
b
,R
1−b
)←ZADDU (R
1−b
,R
b
)
= (R
b
+ R
1−b
+ R
b
−R
1−b
,R
b
−R
1−b
)
= (2R
b
,R
b
+ R
1−b
).
5.2 Randomized Scalar Multiplication
on Elliptic Curve
Jacobian coordinates can be used to randomly mask
a point. Indeed, given a point P = (X,Y,Z),
we randomly pick β ∈ F
p
then we compute P
0
=
(Xβ
2
,Y β
3
,Zβ) which are equivalent Jacobian coordi-
nates of the affine point (X/Z
2
,Y /Z
3
).
We propose to use Rand AMNS BarMul to dy-
namicly randomize the coordinates of the points R
0
and R
1
during the scalar multiplication. We first focus
on randomizing the ZADDU curve operation. Given
a randomizing integer t, we perform all multiplica-
tions involved in ZADDU with Rd AMNS BarMul
with parameter s = t, only, the square in Step 3 is
computed with parameter s = 2t. This approach is
shown in Algorithm 9.
Algorithm 9: Randomized Co-Z addition with update
(Rand ZADDU).
Require: P
0
= (X
0
1
,Y
0
1
,Z
0
) and Q
0
= (X
0
2
,Y
0
2
,Z
0
) with coor-
dinates in an AMNS (p,n, ρ, γ,λ) with λ = 2.
Ensure: (R
0
,P
0
) such that R = P + Q and P
0
∼
=
P
1: C
0
← Rd AMNS BarMul((X
0
1
−X
0
2
),(X
0
1
−X
0
2
),t)
2: W
0
1
← Rd AMNS BarMul(X
0
1
,C
0
,t),
3: W
0
2
← Rd AMNS BarMul(X
0
2
,C
0
,t)
4: D
0
← Rd AMNS BarMul((Y
0
1
−Y
0
2
),(Y
0
1
−Y
0
2
),2t)
5: A
0
1
← Rd AMNS BarMul(Y
0
1
,(W
0
1
−W
0
2
),t)
6: X
0
3
← D
0
−W
0
1
−W
0
2
7: Y
0
3
← Rd AMNS BarMul(Y
0
1
−Y
0
2
),(W
0
1
−X
0
3
),t) −A
0
1
8: Z
0
3
← Rd AMNS BarMul(Z
0
,(X
0
1
−X
0
2
),t)
9: X
00
1
←W
0
1
, Y
00
1
← A
0
1
, Z
00
1
← Z
0
3
10: R
0
← (X
0
3
,Y
0
3
,Z
0
3
),P
00
← (X
0
1
,Y
0
1
,Z
0
1
)
11: return R
0
,P
00
Let us show that the two points R
0
and P
00
output by
Algorithm 7 have Jacobian coordinates equivalent to
the points R and P output by ZADDU. We assume
that the input points P
0
and Q
0
are equivalent to P and
Q. Which means for P
0
that there exists β such that
Z
0
= Zβ,X
0
1
= X
1
β
2
and Y
0
1
= Y
1
β
3
and the same β applies for the equivalence between
Q
0
and Q. Now, one can notice that:
C
0
= (X
0
1
−X
0
2
)
2
γ
−t
= Cβ
4
γ
−t
,
W
0
1
= X
0
1
C
0
γ
−t
= X
1
Cβ
6
γ
−2t
= W
1
β
6
γ
−2t
W
0
2
= X
0
2
C
0
γ
−t
= X
2
Cβ
6
γ
−2t
= W
2
β
6
γ
−2t
D
0
= (Y
0
1
−Y
0
2
)
2
γ
−2t
= Dβ
6
γ
−2t
A
0
1
= (Y
0
1
−Y
0
2
)(W
0
1
−W
0
2
)γ
−t
= A
1
β
9
γ
−3t
Then we can express the coordinates of R
0
in terms of
the ones of R:
X
0
3
= Dβ
6
γ
−2t
−W
1
β
6
γ
−2t
−W
2
β
6
γ
−2t
= X
3
β
6
γ
−2t
,
Y
0
3
= (Y
0
1
−Y
0
2
)(W
0
1
−X
0
3
)γ
−t
−A
0
1
= (Y
1
−Y
2
)(W
1
−X
3
)β
9
γ
−3t
−A
1
β
9
γ
−3t
,
= Y
3
β
9
γ
−3t
Z
0
3
= Z
0
(X
0
1
−X
0
2
)γ
−t
= Z
3
β
3
γ
−t
,
But the above equations show that R
0
∼ R with β
0
=
β
3
γ
−t
. Similarly for P
00
we have
X
00
1
= W
0
1
= W
1
β
6
γ
−2t
Y
00
1
= A
0
1
= A
1
β
9
γ
3t
which means that the Jacobian coordinates P
00
are
equivalent to the ones of P
0
output by ZADDU with
β
0
= β
3
γ
−t
.
The same strategy can be applied to the conjugate
addition ZADDC leading to the same Jacobian coor-
dinates factor β
3
γ
−t
. Now using these Rand ZADDU
and Rand ZADDC we can randomize the co-Z Mont-
gomery ladder as shown in Algorithm 10.
Algorithm 10: Randomized co-Z Montgomery ladder.
Require: P = (x
P
,y
P
) ∈ E(F
p
) and e =
(e
`−1
,. ..,e
0
) ∈ N with e
`−1
= 1.
Ensure: Q = eP
1: (R
1
,R
0
) ← DBLU(P)
2: (t
2`−1
,. ..,t
0
)
3
← Random(3
2`
)
3: for i = ` −1 to 0 do
4: b ← k
i
5: (R
1−b
,R
b
) ← Rand ZADDC(R
b
,R
1−b
,t
2i+1
)
6: (R
b
,R
1−b
) ← Rand ZADDU(R
1−b
,R
b
,t
2i
)
7: return Jac2a f f (R
0
)
From the analysis on Rand ZADDU and
Rand ZADDC we know that they output points
equivalent to non-randomized ZADDU and ZADDC,
which means that the randomized Co-Z Montgomery
ladder correctly output the point R = eP.
Level of Randomization. At each loop iteration the
random multiplicative mask β evolves as β
3
×γ
−t
i
for Rand ZADDC and Rand ZADDU. Since t
i
is in
{0,1, 2}, this sequence of operations for i = ` −1,...0
SECRYPT 2021 - 18th International Conference on Security and Cryptography
618

consists in a cube and multiply exponentiation of γ.
Which means that in loop i, the random factor is
β = γ
−T
i
for some T
i
of size ∼ 3
2(`−i)
and at the end
we have β = γ
−T
for t ∼ 3
2`
.
In other words, the level of randomization is low
during the first loops of the algorithm but it grows
quickly and it is really large at the end. The lack of
randomization at the beginning can be overcome by
picking an random β and compute an equivalent Jaco-
bian coordinates R
0
0
and R
0
1
with factor β at just after
Step 1 in Algorithm 9.
5.3 Implementation Results
Our implementation are done in C using our code for
randomized and non-randomized AMNS multiplica-
tion presented in Subsection 3.3. The timings of ran-
domized scalar multiplication are reported in Table 4.
For field size 510 bits, the proposed randomization
is significantly slower, but we don’t know what is
the reason for that. But for field size 256 bits the
proposed randomization is competitive with the non-
randomized version.
Table 4: Timings of scalar multiplication.
Field and AMNS Algorithm #CC
log
2
(p) ρ n λ
510 510 2
53
10 2
co-Z Mont. Ladder 8891506
Rd. co-Z Mont. Ladder 12683841
256 256 2
57
5 2
co-Z Mont. Ladder 939424
Rd. co-Z Mont. Ladder 885270
6 CONCLUSION
In this paper we considered randomization for DSA
exponentiation and elliptic curve scalar multiplica-
tion. Our randomization take advantage of the modu-
lar multiplication in AMNS. We then presented a ran-
domized AMNS multiplication using modified poly-
nomial reduction and random choice between Bar-
rett and Montgomery multiplication. This leads to
a randomizing factor φ
−t
γ
−s
for some t ∈ {0, 1} and
s ∈ {0,... ,n − 1}. We then presented randomized
DSA exponentiation and co-Z elliptic curve scalar
multiplication using these modified AMNS multipli-
cations. This improves the level of randomization,
with, in the best case, a limited loss of performance.
REFERENCES
Bajard, J., Imbert, L., and Plantard, T. (2004). Modular
Number Systems: Beyond the Mersenne Family. In
SAC 2004, volume 3357 of LNCS, pages 159–169.
Springer.
Barrett, P. (1987). Implementing the Rivest Shamir and
Adleman Public Key Encryption Algorithm on a Stan-
dard Digital Signal Processor. In CRYPTO ’86, pages
311–323. Springer.
Brier, E., Clavier, C., and Olivier, F. (2004). Correlation
Power Analysis with a Leakage Model. In CHES
2004, volume 3156 of LNCS, pages 16–29. Springer.
Clavier, C., Feix, B., Gagnerot, G., Roussellet, M., and
Verneuil, V. (2010). Horizontal Correlation Analysis
on Exponentiation. In ICICS 2010, volume 6476 of
LNCS, pages 46–61. Springer.
Coron, J.-S. (1999). Resistance against Differential Power
Analysis for Elliptic Curve Cryptosystems. In CHES,
pages 292–302.
Didier, L.-S., Dosso, F.-Y., Mrabet, N. E., Marrez, J., and
V
´
eron, P. (2019). Randomization of arithmetic over
polynomial modular number system. In ARITH 2019,
pages 199–206. IEEE.
Goundar, R. R., Joye, M., Miyaji, A., Rivain, M., and
Venelli, A. (2011). Scalar multiplication on Weier-
straß elliptic curves from Co-Z arithmetic. J. Cryp-
togr. Eng., 1(2):161–176.
Jao, D. and Feo, L. D. (2011). Towards Quantum-Resistant
Cryptosystems from Supersingular Elliptic Curve Iso-
genies. In Post-Quantum Cryptography 2011, volume
7071 of LNCS, pages 19–34. Springer.
Joye, M. and Yen, S. (2002). The Montgomery Powering
Ladder. In CHES 2002, volume 2523 of LNCS, pages
291–302. Springer.
Kocher, P. C., Jaffe, J., and Jun, B. (1999). Differen-
tial Power Analysis. In Advances in Cryptology,
CRYPTO’99, volume 1666 of LNCS, pages 388–397.
Springer.
Lesavourey, A., N
`
egre, C., and Plantard, T. (2016). Efficient
Randomized Regular Modular Exponentiation using
Combined Montgomery and Barrett Multiplications.
In SECRYPT 2016, pages 368–375. SciTePress.
M
´
eloni, N. (2007). New Point Addition Formulae for ECC
Applications. In WAIFI 2007, volume 4547 of LNCS,
pages 189–201. Springer.
Montgomery, P. (1985). Modular Multiplication Without
Trial Division. Math. Computation, 44:519–521.
N
`
egre, C. and Plantard, T. (2008). Efficient Modular Arith-
metic in Adapted Modular Number System Using La-
grange Representation. In ACISP 2008, volume 5107
of LNCS, pages 463–477. Springer.
NIST.FIPS.186.4 (2012). Digital Signature Standad (DSS).
Standard, NIST.
Plantard, T. (2005). Arithm
´
etique modulaire pour la cryp-
tographie. PhD thesis, Montpellier 2 University,
France.
Tunstall, M. and Joye, M. (2010). Coordinate blinding over
large prime fields. In CHES 2010, volume 6225 of
LNCS, pages 443–455. Springer.
Side Channel Counter-measures based on Randomized AMNS Modular Multiplication
619
