Estimating Territory Risk Relativity for Auto Insurance Rate Regulation

using Generalized Linear Mixed Models

Shengkun Xie

, Chong Gan

and Clare Chua-Chow

Global Management Studies, Ted Rogers School of Management, Ryerson University, Toronto, Canada

Department of Mathematics and Statistics, University of Guelph, Guelph, Canada

Keywords:

Generalized Linear Mixed Models, Rate-making, Insurance Rate Regulation, Business Data Analytics.

Abstract:

Territory risk analysis has played an essential role in auto insurance rate regulation. It aims to obtain a set

of regions to estimate their respective relativities to reﬂect the regional risk. Cluster as a latent variable has

not yet been considered in modelling the regional risk of auto insurance. In this work, spatially constrained

clustering is ﬁrst applied to insurance loss data to form such regions. The generalized linear mixed model

is then proposed to derive the risk relativities for obtained clusters and then for each basic rating unit. The

results are compared to the ones from generalized linear models. The Forward Sortation Area (FSA) grouping

to a speciﬁc region by spatially constrained clustering is to reduce the insurance rate heterogeneity caused by

some smaller number of risk exposures. The spatially constrained clustering and risk relativity estimation help

obtain a set of territory risk benchmarks, which can be used in rate ﬁlings within the regulation process. It

also provides guidance for auto insurance companies on rate-making. The proposed methodologies could be

helpful and applicable in many other ﬁelds, including business data analytic.

1 INTRODUCTION

Auto insurance rate regulation plays a vital role in

insurance premium rate changes. The rate regulation

is through a rate ﬁling review process. To apply

for a rate change, an insurance company needs

a detailed justiﬁcation of the use of rate-making

methodologies and risk analysis at the company

level. From insurance regulators’ perspectives, to

make meaningful decisions on applications of rate

changes by insurance companies, an overview of how

rate-making methods work and how they impact the

overall risk at the industry level is required. This

may imply that a set of benchmark estimates as key

metrics used in the review process are essential.

Within auto insurance rate-making, territory risk

analysis is considered one of the most important

aspects due to the dominance of territory as a risk

factor in pricing. Therefore, the classiﬁcation of

territorial risk and its relativity associated with

each territorial level requires considerable effort, in

particular, for rate regulation purposes. Because of

this, a fair amount of the work in territory analysis

has been done. (Brubaker, 1996; Xie, 2019; Zhang

and Miljkovic, 2019).

The generalized linear model (GLM) has been

widely used in rate-making and is now becoming a

standard approach in deriving risk relativity for a risk

factor at a given level (McClenahan, 2014; Xie and

Lawniczak, 2018). The main beneﬁt of using GLM is

the statistical soundness and its superiority to many

other traditional methods such as linear models and

the minimum bias procedure (Brown, 1988). In fact,

auto insurance companies have widely used GLM for

rate-making and predictive modelling of insurance

risk (Antonio and Beirlant, 2014). However, GLM

aims at capturing the ﬁxed effect contributed by the

risk factor at a given level, which may not be sufﬁ-

cient to fully explain the variation for the response

variable. Although in many applications, explaining

data variation through an estimate of ﬁxed effect

sufﬁces, there are still some concerns in estimating

risk relativity for regulation purposes. In this work,

we try to address this issue within the domain of auto

insurance rate-making and rate regulation.

In territory risk analysis, the residential informa-

tion such as postal codes or zip codes is used as a

basic pricing unit (Yao, 2008). The risk relativity can

be calculated by determining the ratio of the loss cost

per rating unit and the overall average of all rating

units. The risk relativity is then used to calculate

insurance premiums. In rate regulation, often, postal

Xie, S., Gan, C. and Chua-Chow, C.

Estimating Territory Risk Relativity for Auto Insurance Rate Regulation using Generalized Linear Mixed Models.

DOI: 10.5220/0010601003290334

In Proceedings of the 10th International Conference on Data Science, Technology and Applications (DATA 2021), pages 329-334

ISBN: 978-989-758-521-0

329

codes or zip codes are further grouped to form a

more prominent territorial region to contain more

risk exposures. This can better reﬂect the actual loss

pattern and stabilize the risk relativities to minimize

the ﬂuctuation among the calculations using data

from different accident years. A spatial clustering

does this, and a more suitable number of clusters

to be formed to act as new pricing units. Since

postal codes or zip codes are nested in the city or

town, there may be another effect based on different

cities or towns. Those potential effects on insurance

loss may be, in fact, due to some factors associated

with the city or town. For instance, in a city where

commuting buses lack or public transportation is

relatively limited, people tend to drive more to work.

In this work, we propose a method of using Gen-

eralized Linear Mixed Models (GLMM) (Antonio

and Beirlant, 2007) to derive the risk relativity for

different clusters produced by a spatially constrained

clustering(Xie, 2019). GLMM is an extension of

GLM in which the model contains both ﬁxed and

random effects. GLMM can further capture the

impact due to differences among cities or towns

such that the difference in risk relativity associated

with different cities can be better reﬂected. GLMM

has been successfully used in actuarial science as a

non-life rate-making technique(Jeong et al., 2017),

and a model for credibility(Antonio and Beirlant,

2007). It has also been applied to spatial analysis of

disease spread (Kleinschmidt et al., 2001). We apply

GLMM to model territorial risk in a novelty way and

estimate regional risk relativities. It is considered to

be an extension of the current approach that appeared

in(Xie and Lawniczak, 2018) by further addressing

the impact from other correlated factors on the

territorial risk relativities estimates.

This paper is organized as follows. In Section

2, the data and its basic processing are brieﬂy intro-

duced. In Section 3, the proposed generalized linear

mixed models is discussed. In Section 4, the summary

of the main results are presented. In Section 5, we

conclude our ﬁndings and provide further remarks.

2 DATA

In this work, we apply our proposed method to a real

dataset coming from an auto insurance regulator in

Canada. This dataset includes the reported loss in-

formation from all auto insurance companies within

a province for accident years 2009 to 2011. It con-

sists of geographical loss information including postal

codes, cities, reported average loss cost and earned

exposures. The geographical information refers to the

residential places of insured drivers who had reported

the loss, rather than the place where the insured suf-

fered the accident. The reported average loss cost

is the projected ultimate expected loss. The earned

exposures refer to the total number of insured vehi-

cles within a policy year. In this dataset, we ﬁrst re-

trieved all postal codes that are associated with the

same FSA, where FSA is the ﬁrst three characters of

postal codes. For each FSA, the postal codes were

further geo-coded using a geo-coder. The obtained

geo-coding contains both latitude and longitude val-

ues that are used to represent the center of a given

FSA. The centroid of FSA is used to identify its loca-

tion.

3 METHODS

This work’s main objective is to estimate each clus-

ter’s risk relativity obtained from a spatial clustering.

At a given level, the relativity of a risk factor is the

risk level relative to the overall averages for all levels

that we consider. In this work, the loss cost at a given

level is divided by the average loss cost across all lev-

els within a risk factor to calculate the risk relativity.

Here we consider the territory risk. The level of terri-

tory risk is at the FSA level, and we try to derive the

relativity associated with each FSA. Data input to the

spatial clustering is three-dimensional, consisting of

normalized lost cost, normalized latitude and normal-

ized longitude. Although the optimal number of clus-

ters is important, it has been fully addressed in (Xie,

2019) using an entropy-based approach. This work is

considered a follow-up study after a spatial clustering

of loss data to determine each FSA’s relativity.

In rate-making, Generalized Linear Models

(GLM) have been widely used because an exponen-

tial family distribution is a better choice for the error

distribution instead of a normal distribution assump-

tion, which is the case in linear models. The main idea

of using GLM for territory risk analysis is to model a

transformation of the expected value of loss cost so

that the predictors have a linear relationship with the

transformed loss cost values. In territory analysis, the

loss cost is deﬁned as the average loss level per vehi-

cle for a deﬁned basic rating unit such as the postal

code. In this work, we extend GLM to the general-

ized linear mixed model (GLMM) (Antonio and Beir-

lant, 2007) to further explain the random effect from a

considered rating variable. Since a city has its own in-

frastructure and public transportation, the underlying

risk of causing accidents is dependent of a city. To

explain the GLMM, let us assume that the loss data

DATA 2021 - 10th International Conference on Data Science, Technology and Applications

330

has been spatially clustered to N clusters, and in total,

there are M different cities associated with this insur-

ance loss cost data. Therefore, the loss cost associ-

ated with cluster i and City j is deﬁned as L

i j

, where

i = 1, 2, . . . , N and j = 1, 2, . . . , M. We further deﬁne

the expected value of loss cost as µ

i j

= E(L

i j

). This

expected value is then transformed by a given func-

tion g and deﬁned as η

= g(µ

i j

). This transformation

function is called the link function. The model that

is used to explain the transformation function g is a

linear mixed effect model that contains both ﬁxed and

random effects, and it can be written as follows:

g(µ

i j

) = β

+ β

+ v

, (1)

where x

represents the ﬁxed effect of the ith cluster,

and v

represents the random effect of City. In gener-

alized linear model, the variance of model residual ε

i j

is assumed to have the following functional relation-

ship with the mean response:

Var(ε

i j

) =

φV (µ

i j

)

i j

, (2)

where V (x) is called a variance function. This is an

immediate result of the fact that the error distribution

belongs to the exponential family distribution. The

parameter φ scales the variance function V (x), and

i j

is a constant assigning a weight. The case when

V (x) = 1 implies a normal distribution. If V (x) = x,

then the distribution is Poisson. If V (x) = x

, then it

is a gamma distribution, and if V (x) = x

, then it is

an inverse Gaussian distribution. These are the dis-

tributions used in this work. They are considered to

be some special cases of Tweedie distribution that of-

ten used in the actuarial domain(Xacur and Garrido,

2015).

To derive the relativities for each FSA, we ﬁrst de-

termine the relativity of ﬁxed effect of clusters, which

is exp{

} for the ith ﬁxed effect. The purpose of

this is because the log link function is used there. The

estimate of v

is the conditional mode, which is the

difference between the average predicted response for

a given set of ﬁxed-effect values and the response pre-

dicted for a particular individual. Technically speak-

ing, they are the solutions to a penalized weighted

least-squares estimation procedure. We can think of

these as individual-level effects, i.e. how much does

any individual lost cost differ from the population due

to the jth City? Because of this, the relativity corre-

sponding to jth City becomes exp{ ˆv

}. Therefore, the

relativities due to both ﬁxed and random effect are

then calculated as exp{

+ ˆv

}, and then normalized

by the mean value of exp{

+ ˆv

Figure 1: The empirical estimate of the risk relativities for

the obtained ﬁve clusters.

4 RESULTS

In this section, we discuss the results of relativities us-

ing empirical, GLM and GLMM models. The method

of spatially constraint K-means clustering was ﬁrst

carried out to group the territories. To investigate how

the number of clusters (K) affects the results of rela-

tivities, we let K take the values of 5, 10, 15 and 20,

respectively. Note that to avoid the non-contiguous

points, the clusterings below have applied the Delau-

nay triangulation approach. After ﬁnding the clus-

ter index for each FSA as the covariate, we apply

the generalized linear model and generalized linear

mixed model with spatially correlated random effects

”City”, weighted by risk exposures to ﬁt the loss cost.

Table 1 shows an example of modelling loss cost

by 5 clusters, using Gaussian, Poisson, Gamma and

Inverse Gaussian as the error function in the GLM

model. We can observe that the estimates of rela-

tivities are consistent among different distributions.

It is interesting to see that the error distributions in

GLM will not contribute signiﬁcant inﬂuences to each

cluster’s relativities. When considering only two dec-

imal places, the risk relativities do not depend on the

given model’s error distribution. However, consider-

ing the goodness of the ﬁt, the Gaussian error distri-

bution achieves the lowest AIC and BIC, which may

due to the loss data not following a heavy-tailed distri-

bution so that we can rely more on the Gaussian GLM

model. After that, we conducted a similar analysis on

the rest of the K and GLMM models, and we obtained

the same ﬁndings and conclusions

Recall that the empirical risk relativity is calcu-

lated by the overall ratio of average loss within each

cluster, relatively to the grand average loss. It can

be treated as the benchmark to compare the perfor-

Estimating Territory Risk Relativity for Auto Insurance Rate Regulation using Generalized Linear Mixed Models

331

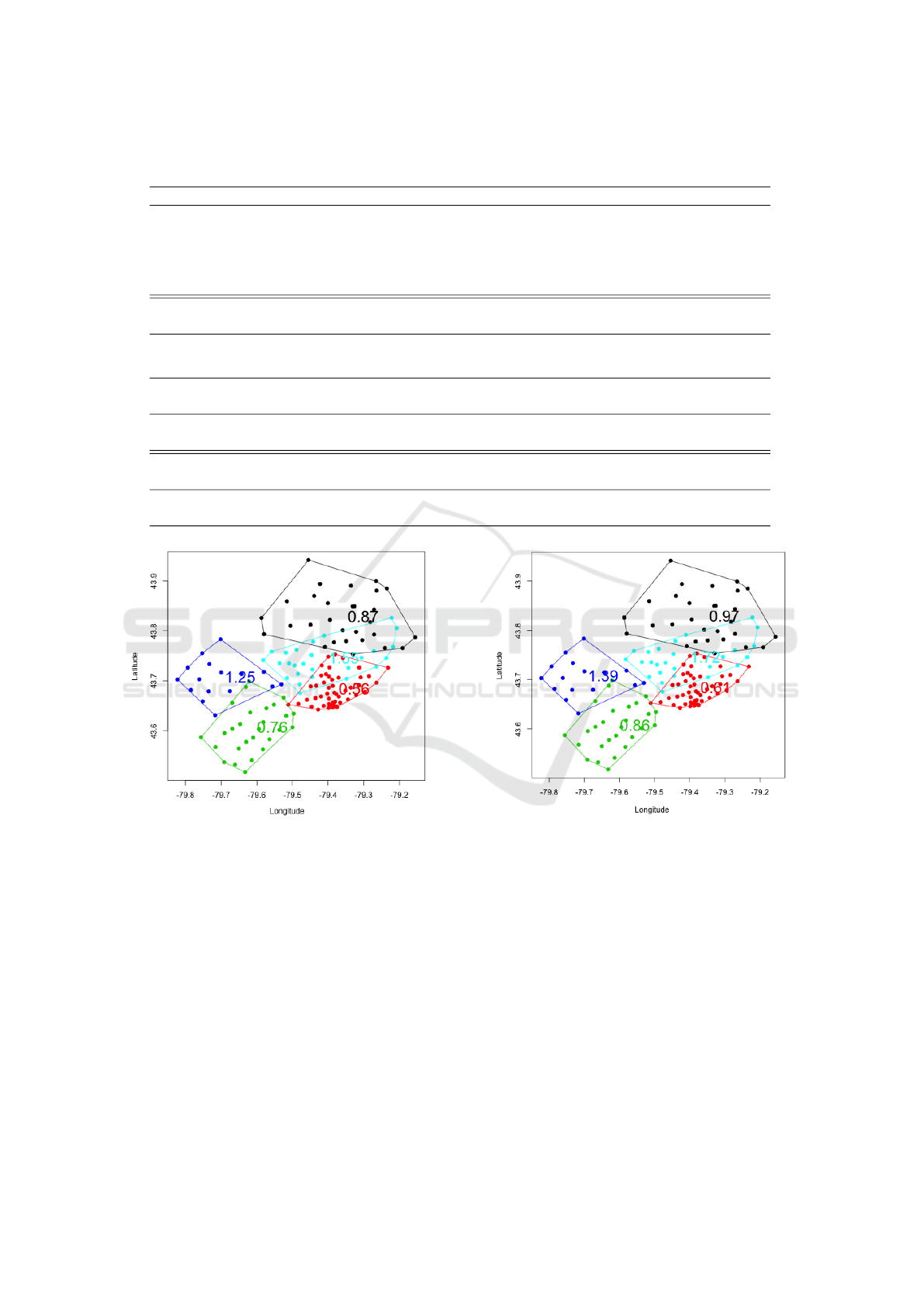
Table 1: The GLM estimates of risk relativities for the obtained ﬁve clusters, using Gaussian, Poisson, Gamma, inverse

Gaussian error function, along with AICs and BICs.

Relativity Gaussian Poisson Gamma Inverse Gaussian

cluster 1 0.87 0.87 0.87 0.87

cluster 2 0.56 0.56 0.56 0.56

cluster 3 0.76 0.76 0.76 0.76

cluster 4 1.25 1.25 1.25 1.25

cluster 5 1.55 1.55 1.55 1.55

AIC 2403.75 324546794.5 30078415.55 31491160.07

BIC 2421.82 324546809.5 30078433.62 31491178.14

Table 2: RMSE and MAD of the relativity for selected number of clusters 5, 10, 15, 20, using GLM and GLMM models.

GLM model

Number of Clusters 5 10 15 20

RMSE 0.0405 0.0464 0.0717 0.0731

MAD 0.0360 0.0383 0.0443 0.0494

GLMM model

Number of Clusters 5 10 15 20

RMSE 0.1254 0.1886 0.0729 0.0862

MAD 0.1120 0.1620 0.0443 0.0576

Figure 2: The GLM estimate of risk relativities for the ob-

tained ﬁve clusters.

mance of pricing among different models and the dif-

ferent number of clusters. Table 2 lists the RMSE

and MAD of the relativities for K = 5, 10, 15, 20, us-

ing GLM and GLMM models. Overall, the empirical

and estimated relativities do not differ much, which

shows that our proposed methods are reliable and con-

sistent with the benchmark estimate. The difference

of relativity between the empirical and GLM models

is slightly smaller than GLMM models, while the in-

crease of K in the GLMM model reversely improves

the performance. Among the K values we consider,

GLMM produce a more realistic number of clusters

in terms of a smaller RMSE or MAD. Table 2, we ob-

serve that when K=15, RMSE or MAD is the smallest.

Figure 3: The GLMM estimate of risk relativities for the

obtained ﬁve clusters. Cluster has ﬁxed effect and City is

considered as a random effect.

To visualize the grouping structures and estimated

relativities of obtained clusters, we produce the plots

displayed in Figures 1 - 6. Within the Figures, the x

axis represents longitude, and the y axis represents lat-

itude. Through K-means clustering, the points within

the same cluster boundary are homogeneous, sharing

the common information of relativities. Figure 1 - 3

displays the results for K = 5, using empirical, GLM,

GLMM models, while Figure 4 - 6 displays the clus-

ters and relativities for K = 10. Again, comparing

the estimated relativities among these three methods,

we can ﬁnd that there are no signiﬁcant differences,

and the estimated values seem reasonable. For exam-

DATA 2021 - 10th International Conference on Data Science, Technology and Applications

332

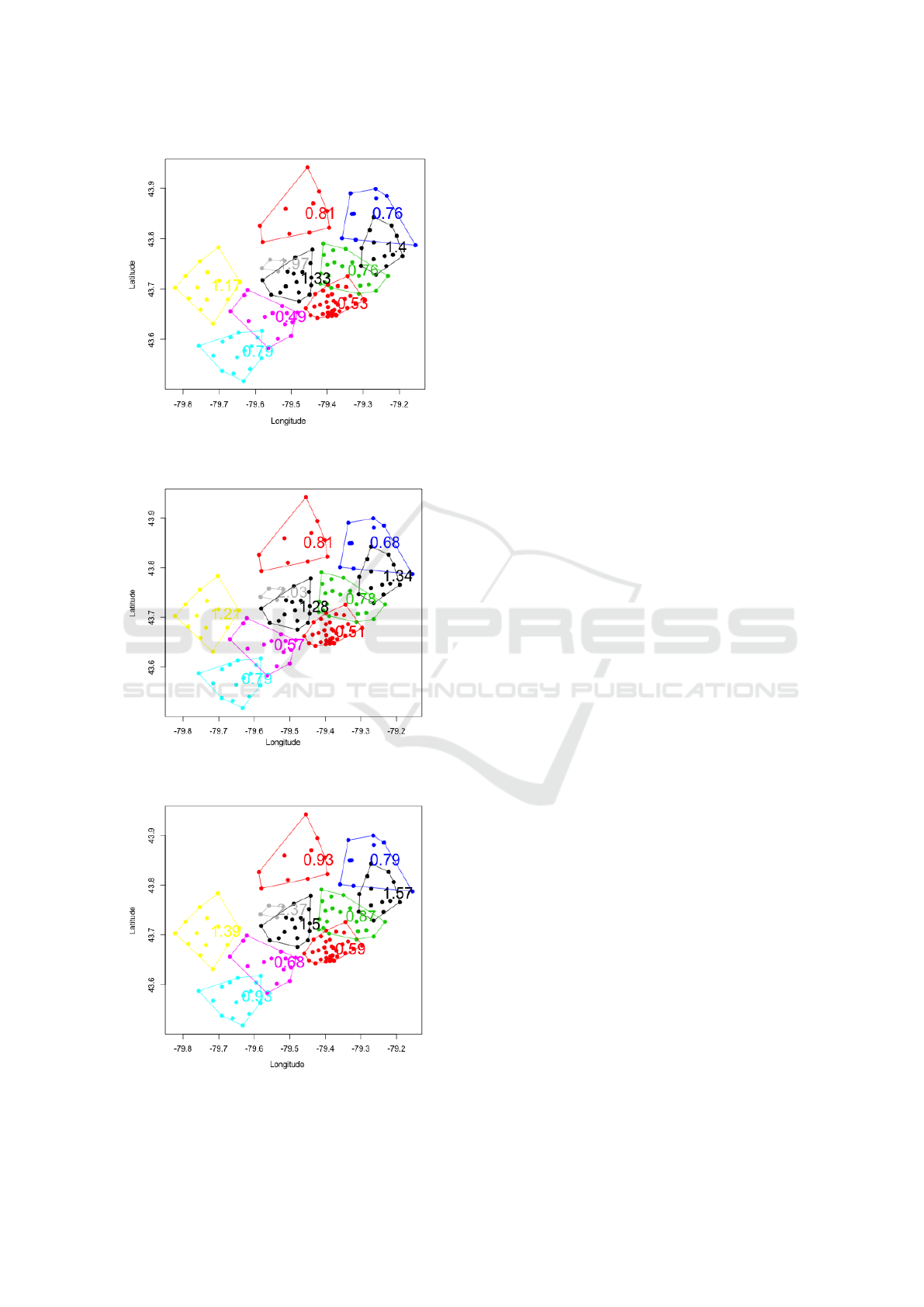
Figure 4: The empirical estimate of risk relativities for the

obtained ten clusters.

Figure 5: The GLM estimate of risk relativities for the ob-

tained ten clusters.

Figure 6: The GLMM estimate of risk relativities for the

obtained ten clusters. Cluster has ﬁxed effect and City is

considered as a random effect.

ple, in the case of K = 5, relativities in the blue and

light blue clusters are higher than those of red and

blue clusters, which indicates that the region of North

York and Brampton has a higher risk than Etobicoke

and Mississauga. It can be explained by the differ-

ent driving behaviours and trafﬁc volumes in differ-

ent districts. However, the generalized linear mixed

model gave slightly higher relativities in each cluster,

which may lead to the overestimation of the pure pre-

mium, but this method considers the spatial random

effect of cities. With the increase of numbers of clus-

ters, the risk assessment can be more accurate and ex-

plicit in response to small cluster boundaries. That is,

some points (FSAs) are not necessary to evaluate in

the same risk. For example, the black cluster in Fig-

ure 2 (K = 5) is partitioned into several clusters in Fig-

ure 5 (K = 10). In Figure 5, red includes the regions

of Thornhill and Richmond hill while blue represents

Markham’s area. It is reasonable to have the differ-

ent relativities in these two clusters. Another impor-

tant ﬁnding is that as the number of clusters increases,

there are fewer overlaps between clusters. We prefer

the separated clusters because it has a more practical

meaning that we can easily deﬁne the relativities of

other FSAs within the cluster boundaries. However, if

we allow a too large number of clusters, it will over-

ﬁt the data and become meaningless to let each FSA

have its own risk relativity. It is important for a regu-

lator to consider the trade-off between the complexity

of clusters and geographical information. Often the

selection of the optimal number of clusters is based on

the sum of squares data variation, but our experiments

show that the sum of squares-based methods produces

a small number of clusters which has no meaning in

the actual application of territory risk classiﬁcation.

5 CONCLUDING REMARKS

Generalized linear models and generalized linear

mixed models are now gaining signiﬁcant attention in

insurance pricing and many other ﬁelds involving pre-

dictive modelling techniques, particularly for auto in-

surance rate-making. GLMs and GLMMs have been

discussed as actuarial statistical techniques in the cur-

rent literature, but they are not being widely used

for regulatory purposes. In this work, we proposed

a GLMM to estimate risk relativities after obtaining

spatial clusters for a given set of spatial loss data. Our

study illustrated the suitableness of using GLMMs to

estimate the risk relativities for obtained spatial clus-

ters so that the risk relativity of a basic rating unit

(such as FSA) can be calculated, for auto insurance

regulation purposes. The spatially constrained clus-

Estimating Territory Risk Relativity for Auto Insurance Rate Regulation using Generalized Linear Mixed Models

333

tering aims to produce more homogeneous groups.

The GLMM is used to model the loss cost by explain-

ing the variation of the loss cost through both ﬁxed

and random effects. The obtained results suggest that

GLMM is promising in estimating the risk relativity

for spatially constrained clustering. Our future study

will investigate how it differs when moving from hard

clustering (e.g. K - means clustering) to soft clus-

tering (Fuzzy C-means clustering) and the impact of

fuzzy computing on the estimate of territory risk rel-

ativities. We will also investigate how risk relativities

can be integrated to the part of the criterion for de-

termining the optimal number of clusters in spatially

constrained clusterings.

REFERENCES

Antonio, K. and Beirlant, J. (2007). Actuarial statistics with

generalized linear mixed models. Insurance: Mathe-

matics and Economics, 40(1):58–76.

Antonio, K. and Beirlant, J. (2014). Risk classiﬁcation in

nonlife insurance. Wiley StatsRef: Statistics Reference

Online.

Brown, R. L. (1988). Minimum bias with generalized lin-

ear models. In Proceedings of the Casualty Actuarial

Society, volume 75, pages 187–217. Citeseer.

Brubaker, R. E. (1996). Geographic rating of individual

risk transfer costs without territorial boundaries. In

Casualty Actuarial Society Forum, pages 97–127.

Jeong, H., Valdez, E. A., Ahn, J. Y., and Park, S. (2017).

Generalized linear mixed models for dependent com-

pound risk models. Available at SSRN 3045360.

Kleinschmidt, I., Sharp, B., Clarke, G., Curtis, B., and

Fraser, C. (2001). Use of generalized linear mixed

models in the spatial analysis of small-area malaria in-

cidence rates in kwazulu natal, south africa. American

journal of epidemiology, 153(12):1213–1221.

McClenahan, C. L. (2014). Ratemaking. Wiley StatsRef:

Statistics Reference Online.

Xacur, O. A. Q. and Garrido, J. (2015). Generalised lin-

ear models for aggregate claims: to tweedie or not?

European Actuarial Journal, 5(1):181–202.

Xie, S. (2019). Deﬁning geographical rating territories

in auto insurance regulation by spatially constrained

clustering. Risks, 7(2):42.

Xie, S. and Lawniczak, A. (2018). Estimating major risk

factor relativities in rate ﬁlings using generalized lin-

ear models. International Journal of Financial Stud-

ies, 6(4):84.

Yao, J. (2008). Clustering in ratemaking: Applications in

territories clustering. Casualty Actuarial Society Dis-

cussion Paper Program Casualty Actuarial Society-

Arlington, Virginia, pages 170–192.

Zhang, J. and Miljkovic, T. (2019). Ratemaking for a

new territory: Enhancing glm pricing model with a

bayesian analysis.

DATA 2021 - 10th International Conference on Data Science, Technology and Applications

334