Selective Owner-side Encryption in Digital Data Markets:

Strategies for Key Derivation

Sara Foresti

and Giovanni Livraga

Computer Science Department, Universit

a Degli Studi di Milano, Via Celoria 18, Milano, Italy

Keywords:

Digital Data Market, Selective Encryption, Key Derivation.

Abstract:

The combined adoption of selective encryption and smart contracts deployed on blockchains allows data own-

ers to maintain control over their data when traded on digital data market platforms. Selective encryption,

combined with key derivation techniques, guarantees that only customers who are entitled to access a resource

can read its content. The adoption of smart contracts deployed on a blockchain permits to regulate the in-

terplay among parties, the possible economic incentives to be paid to the owners, and the exchange of the

information necessary for resource decryption (i.e., updates to the key derivation structure) upon payment.

However, operations on blockchains have a cost. In this paper, we propose two approaches for updating the

key derivation structure to enable customers to access resources, while limiting access times to resources and

the cost of write operations on the blockchain to enforce purchases.

1 INTRODUCTION

A great deal of interest is paid nowadays towards

the development of spaces and platforms where data

can be easily shared among interested subjects. Such

spaces, typically called digital data markets, repre-

sent virtual places where data owners, acting as data

producers, offer datasets, and customers, acting as

data consumers, can access (parts of) these datasets.

The creation of these platforms, enabling data sharing

among different subjects, can have a positive impact

on the creation of knowledge based on the analysis of

heterogeneous data, with clear societal beneﬁts.

One of the main concerns that can hamper the

diffusion of data-driven innovation is the (perceived)

lack of control suffered by owners when they resort

to these platforms. Completely delegating to a third

party (such as the market provider) the storage and

management of data, while relieving overhead at the

owners’ side, inevitably requires complete trust in the

market provider, as it should be trusted to i) access

all data; ii) maintain them conﬁdential and not dis-

close them improperly to others; iii) correctly route

the payment to the owner, if a price is to be paid to

the owner for sharing a dataset with a customer. How-

ever, market providers are third parties that can more

https://orcid.org/0000-0002-1658-6734

https://orcid.org/0000-0003-2661-8573

realistically (in line with traditional data outsourcing

scenarios) be considered honest-but-curious, meaning

trusted for correctly managing data but not trusted

for accessing their content. Hence, ensuring proper

protection to the data shared in digital data markets,

and maintaining owners in control over the customers

with which data are shared, are key requirements for

enabling a wide adoption of digital data markets.

To address these issues, a recent proposal

combines selective owner-side encryption and

blockchain (De Capitani di Vimercati et al., 2019).

With selective owner-side encryption, data are stored

in encrypted form. Encryption uses different keys,

which are then distributed to the interested customers

according to possible restrictions set by the owners.

In this way, encrypted data can be possibly stored

directly on the premises of the data market, if avail-

able, or more generally of economically-convenient

cloud platforms with the guarantee that unauthorized

subjects (including the market/cloud provider) cannot

access the data content. When an interested customer

requests access to a certain data collection of a given

owner, their interaction and the possible economic

transaction are managed via smart contracts deployed

and executed on a blockchain. In this way the request,

the payment, and the willingness of the owner to

grant access to such data collection to that customer

remains logged in the tamper-proof ledger of the

blockchain, ensuring transparency and accountability.

620

Foresti, S. and Livraga, G.

Selective Owner-side Encryption in Digital Data Markets: Strategies for Key Derivation.

DOI: 10.5220/0010603506200627

In Proceedings of the 18th International Conference on Security and Cryptography (SECRYPT 2021), pages 620-627

ISBN: 978-989-758-524-1

The combined adoption of blockchain and selec-

tive owner-side encryption should however be care-

fully regulated. Selective owner-side encryption re-

quires in fact the deﬁnition of encryption keys and

of tokens enabling the derivation (i.e., computation)

of one key starting from another one. The catalog of

the tokens is publicly stored on the blockchain so that

key derivation can be executed in accordance with the

restrictions imposed by the owners. At every pur-

chase request by a customer, the key derivation struc-

ture (and hence the token catalog) needs to be up-

dated to reﬂect and enforce the new granted access.

However, writing on a blockchain inevitably implies

an economic cost, and hence the updates to the key

derivation structure should be carefully managed. In

this paper, we investigate this issue and, after a brief

discussion of basic concepts (Section 2), we investi-

gate strategies (Section 3) that aim at minimizing the

overall number of tokens in the system (Section 3.1)

on the one hand, and which aim at minimizing the

number of additional tokens needed to grant an access

(Section 3.2), along with further optimizations (Sec-

tion 3.3), on the other. We then discuss related works

(Section 4) and present our conclusions (Section 5).

2 PRELIMINARIES

We consider a data market scenario, characterized by

different data owners O={o

, . . . , o

} who are willing

to sell their data (represented as a set R ={r

, . . . , r

}

of resources) to interested customers C ={c

, . . . , c

}

through a platform made available by a data market

provider.

To enable data owners to regulate access to re-

sources by customers who paid for them, without the

need of relying on the (curious) market provider, we

adopt selective encryption as proposed in (De Capi-

tani di Vimercati et al., 2019). Intuitively, selective

encryption consists in encrypting (at the owner-side)

different resources with different encryption keys, and

in distributing encryption keys to customers in such a

way that each customer can decrypt all and only the

resources she is authorized to access. To limit the

number of keys that customers need to manage, while

preventing resource replication, selective encryption

is typically combined with key derivation approaches.

Key derivation enables the computation of the value

of an encryption key k

, leveraging the knowledge of

another encryption key k

through a publicly avail-

able token t

i, j

⊕h(k

), where h is a deterministic

non-invertible encryption function, ⊕ is the bitwise

xor operator, and l

is a public label associated with

(Atallah et al., 2009). Graphically, key derivation

a b c

cde

abc

Figure 1: An example of key derivation hierarchy.

structures can be represented as graphs having a node

for each encryption key and an edge from k

to k

there is a token t

i, j

enabling the derivation of k

start-

ing from k

. Any path in the graph represents a (direct

or indirect) derivation relationship among encryption

keys. In the remainder of this paper, for simplicity,

we will denote with i or with k

interchangeably the

node representing key k

To enforce access restrictions reﬂecting purchases

(i.e., each customer can access in plaintext all and

only the resources she purchased), each data owner o

selectively encrypts her resources before storing them

in the data market and distributes keys to customers

according to purchases. The solution proposed in (De

Capitani di Vimercati et al., 2019) is based on the def-

inition of a key derivation structure with at least a key

for each customer c, a key k

for each resource r,

and a set of tokens enabling each customer to derive

the keys of the resources that she purchased. Speciﬁ-

cally, the structure is assumed to have a key for each

set representing the capability list cap(c) of a cus-

tomer c (i.e., the set of resources that the customer

purchased). The node of each customer c is con-

nected, in the hierarchy, to the node representing her

capability list cap(c). The node of each capability list

cap(c) is connected (through a token) to other nodes

in the key derivation structure in such a way that it is

possible to (directly or indirectly) reach all and only

the nodes representing the resources in the capability

list (i.e., for each r∈cap(c) there is a path from cap(c)

to r in the structure). This guarantees that each cus-

tomer can derive the keys of all and only the resources

in her capability list. To illustrate, consider a market

storing ﬁve resources R ={a, . . . , e} owned by a sin-

gle data owner, and four customers C ={α,β,γ,δ} who

purchased access to {a, b, c}, {c, d, e}, {a}, and {d}

respectively (i.e., cap(α) = {a, b}, cap(β) = {c, d, e},

cap(γ) = {a}, and cap(δ) = {d}). Figure 1 illustrates

a key derivation hierarchy enabling customers to de-

crypt all and only the resources they purchased. For

instance, from her key k

, customer α can derive k

abc

with token t

α,abc

(edge (α, abc) in the ﬁgure). From

key k

abc

, she can then derive keys k

, k

and use

these keys to decrypt resources a, b, and c, respec-

tively. In the ﬁgure, we denote nodes representing

Selective Owner-side Encryption in Digital Data Markets: Strategies for Key Derivation

621

customers’ keys with a gray background, to distin-

guish them from the nodes representing resources (or

sets thereof), and omit commas and brackets (i.e., abc

stands for {a, b, c}).

3 MINIMIZATION STRATEGIES

Data market scenarios are characterized by data own-

ers joining the market to publish their resources, and

by customers purchasing resources. The accommoda-

tion of the changes in the set of resources and access

privileges requires the adaptation of the key deriva-

tion structure, and hence of the corresponding token

catalog. Clearly, re-building the key derivation hier-

archy from scratch at every purchase would be too

expensive for the data owner, and would imply exces-

sively long waiting times for customers. We therefore

propose to update the hierarchy to accommodate pur-

chases. Such updates should however be handled with

care, for two main reasons: i) a large token catalog

implies a higher response time for customers when

accessing resources (due to the search for the tokens

necessary for the access), and ii) write operations on

the blockchain imply a cost and should then be per-

formed with care. In this section, we propose two so-

lutions aimed at limiting the impact of purchases on

the token catalog. Section 3.1 illustrates an approach

to minimize the overall number of token in the cata-

log. Section 3.2 focuses on minimizing the number of

additional tokens for managing purchases (i.e., write

operations on the blockchain). Section 3.3 presents

some considerations to further reduce the number of

tokens necessary for purchase management.

3.1 Minimize the Overall Number of

Tokens

To limit response time for customers when access-

ing resources they have purchased, the size of the

token catalog should be kept limited. Every access

request implies a sequence of search operations in

the catalog, for retrieving the tokens along the path

connecting the node representing the requesting cus-

tomer c with the node representing the resource r of

interest. The size of the catalog has then a clear im-

pact on response times. The problem of computing

a key derivation hierarchy that minimizes the number

of tokens is NP-hard (De Capitani di Vimercati et al.,

2010). We therefore propose an heuristic approach

aimed at locally modifying the key derivation hierar-

chy to accommodate the purchase, while keeping the

number of tokens in the catalog low.

Let H (K ,T ) be the key derivation hierarchy, with

K the set of keys and T the set of tokens. The hier-

archy needs to be updated when: i) a new customer

c joins the data market, ii) a new resource r is pub-

lished in the market, and iii) a customer c purchases a

resource r. The insertion of a customer implies only

the creation of a new node c, whose key is agreed be-

tween the owner and the customer. Such a key is how-

ever not connected to the rest of the structure since her

capability list is initially empty. Similarly, the publi-

cation of a new resource only implies the creation of a

new node r, whose key is used to encrypt the resource,

but which is not connected to the derivation structure

by any token, since it does not belong to any capabil-

ity list. The purchase of a resource r by a customer

c requires instead a restructuring of the hierarchy, to

guarantee the existence of a path from c to r.

Let us consider, for generality, the purchase of a

set R of resources by a customer c. To keep the num-

ber of tokens in the system low, our solution is based

on the idea of leveraging existing nodes and tokens

to enable the derivation of the key used to encrypt

each resource r∈R starting from the key of customer

c. Let k

old

be the node in the hierarchy representing

the capability list of the customer before the purchase

(i.e., cap(c)), and k

new

be the node representing the

capability list of the customer after the purchase (i.e.,

cap(c)∪R). To enforce the purchase of R by c, it is

necessary to substitute the token enabling c to derive

old

from k

with a new token that permits her to de-

rive k

new

from k

. For instance, with reference to the

example in Figure 1, if γ purchases resources b and c,

the token enabling the derivation of k

from k

needs

to be substituted with a token enabling the derivation

of k

abc

from k

, as illustrated in Figure 2(a).

We note however that k

new

might not belong to the

key derivation structure and, in this case, it needs to

be created and properly connected to the structure.

In other words, it is necessary to insert into the hi-

erarchy node k

new

and a set of tokens enabling to

derive k

from k

new

for each r∈cap(c)∪R. To this

aim, we connect k

new

to a set K of nodes in hierarchy

that represent subsets of cap(c)∪R and that guaran-

tee complete coverage of such a set of resources (i.e.,

∀k

∈ K, X ⊆ cap(c)∪R and

∈K

X = cap(c) ∪R).

Clearly, we aim at keeping the number of nodes in

K low, to minimize the number of tokens in the sys-

tem. The minimum coverage problem is NP-hard and

we therefore propose a heuristic approach aimed at

identifying a coverage for cap(c)∪R while limiting

the number of nodes necessary for the coverage. To

this purpose, we populate K starting from the larger

subsets of cap(c)∪R in the hierarchy, until all the re-

sources in cap(c)∪R are covered by at least a node in

K. For instance, with reference to the example in Fig-

SECRYPT 2021 - 18th International Conference on Security and Cryptography

622

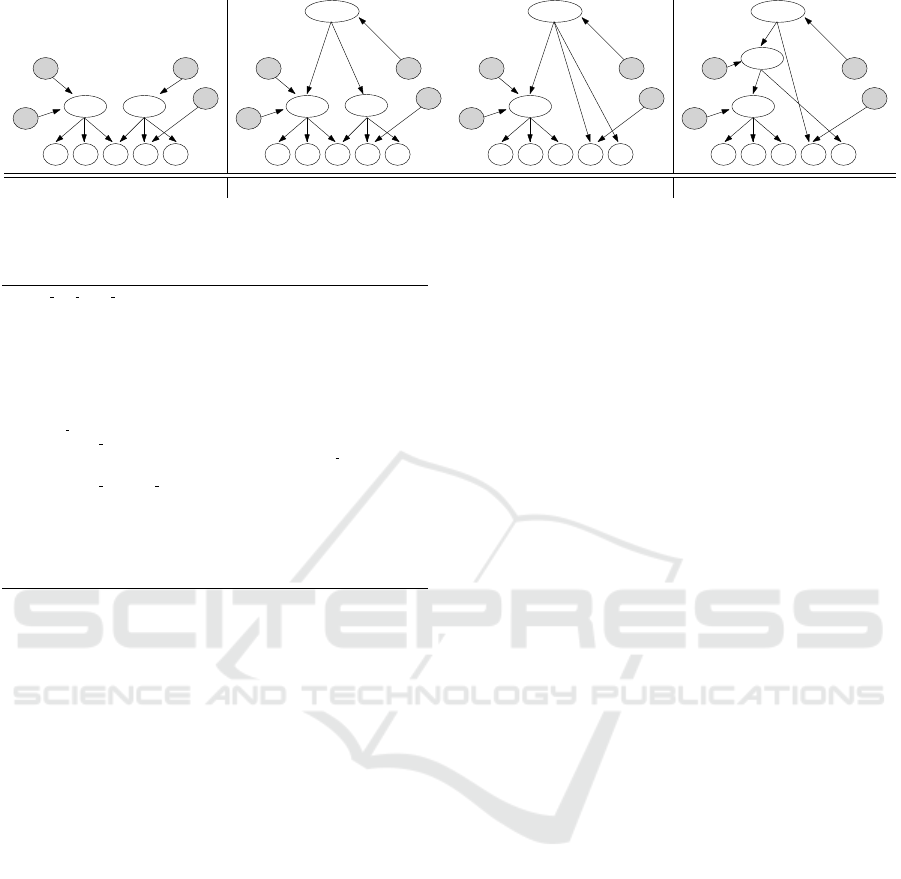
a b c

cde

abc

a b c

cde

abc

abcde

a b c

abc

abcde

a b c

abc

abcde

abce

(a) γ buys b and c (b) β buys a and b (c) α buys e

Figure 2: Evolution of the key derivation hierarchy in Figure1 to enforce a sequence of purchases minimizing the overall

number of tokens.

Purchase Min Token Catalog(c,R)

1: let Desc be the descendants of k

cap(c)

and Anc be the ancestors of k

cap(c)

2: if @c

6= c ∈ C s.t. cap(c )=cap(c

) AND |Desc| · |Asc| > |Desc| + |Asc|

4: then remove k

cap(c)

and all its incident edges from H

5: connect each node in Anc with each node in Desc via a set of tokens

6: else remove the token from k

to k

cap(c)

7: if k

cap(c)∪R

6∈K

8: then generate k

cap(c)∪R

and insert it into K

9: let K = {k

∈ K : X ⊆ cap(c ) ∪ R }

10: to cover := cap(c) ∪ R

11: while to cover6=

0 do

12: let k

be the largest set of resources in K s.t. X ∩ to cover 6=

13: K := K\{k

}

14: to cover := to cover\X

15: connect k

cap(c)∪R

to k

via a token

16: connect k

to k

cap(c)∪R

via a token

17: for each k

∈K s.t. cap(c)∪R⊂X do

18: let T be the tokens that are redundant if k

is connected to k

cap(c)∪R

19: if |T | > 2

20: then remove T from T and connect k

to k

cap(c)∪R

via a token

Figure 3: Management of resource purchase aimed to min-

imize the overall number of tokens.

ure 2(a), let us assume that β purchases a and b. It is

ﬁrst necessary to insert into the hierarchy a node rep-

resenting cap(β) = {a, b, c, d, e}. According to our

heuristics, such a node is then connected through a to-

ken to nodes abc and cde, as illustrated by the struc-

ture on the left hand side in Figure 2(b).

To reduce the number of tokens in T , we note

that node k

old

can be possibly removed from the key

derivation structure, if: i) no other customer shares

the same capability list with c; and ii) the removal of

old

reduces the number of tokens in T . Indeed, the

removal of k

old

requires to directly connect all its an-

cestors with its all its descendants. For instance, con-

sidering the purchase of a and b by β, node cde can

be removed from the key derivation structure (see the

structure on the right hand side of Figure 2(b)), sav-

ing one token with respect to the structure on the left

hand side in Figure 2(b). The insertion of node k

new

can also be leveraged to further reduce the number of

tokens in the hierarchy. To this purpose, it is possible

to analyze each node k

in the hierarchy represent-

ing a superset of cap(c)∪R. If such a node can be

connected to k

new

removing its connection to at least

two of its descendants, as they become redundant, we

enforce such a change. For instance, considering the

hierarchy in Figure 2(b), assume that customer α pur-

chases resource e. The new node representing cap(α)

can become direct descendant of node abcde, saving

one token in the structure (see Figure 2(c)).

Figure 3 illustrates the pseudo-code of the proce-

dure enforcing the purchase of a set R of resources by

a customer c, aimed at minimizing the overall number

of tokens in the catalog. Note that the procedure can

manage the purchase of a single resource r, by simply

setting R to the singleton set {r} of resources.

3.2 Minimize the Number of Additional

Tokens

The strategy illustrated in Section 3.1, while effective

in limiting the cost for customers in accessing data,

implies an economic cost for the data owner propor-

tional to the number of tokens inserted and deleted

from the catalog. Indeed, both insertion and dele-

tion of tokens imply a write operation on the cata-

log, and hence on the blockchain. In this section,

we propose an alternative approach for managing pur-

chases, aimed at minimizing the operations on the

blockchain. To this aim, we propose to prevent to-

ken deletion (the removal of tokens is not necessary

for the enforcement of purchases) and minimize the

number of additional tokens.

Let us consider the purchase of a set R of re-

sources by a customer c. The capability list of c needs

to be updated to include also the resources in R, that

is cap(c) ∪R. Therefore, we need to connect the node

of c with a node in the hierarchy representing the set

cap(c) ∪ R of resources. If such a node already be-

longs to the hierarchy, we can simply add a token en-

abling the derivation of k

cap(c)∪R

from k

, as showed

by the structure in Figure 4(a) illustrating the structure

in Figure 1 updated to accommodate the purchase of b

and c by γ: since the structure already contains a node

for the new capability list abc of γ, it is sufﬁcient to

create a token enabling the derivation of k

abc

from k

(note that in the ﬁgure, for the sake of readability, we

did not report the old token connecting γ to a). On the

Selective Owner-side Encryption in Digital Data Markets: Strategies for Key Derivation

623

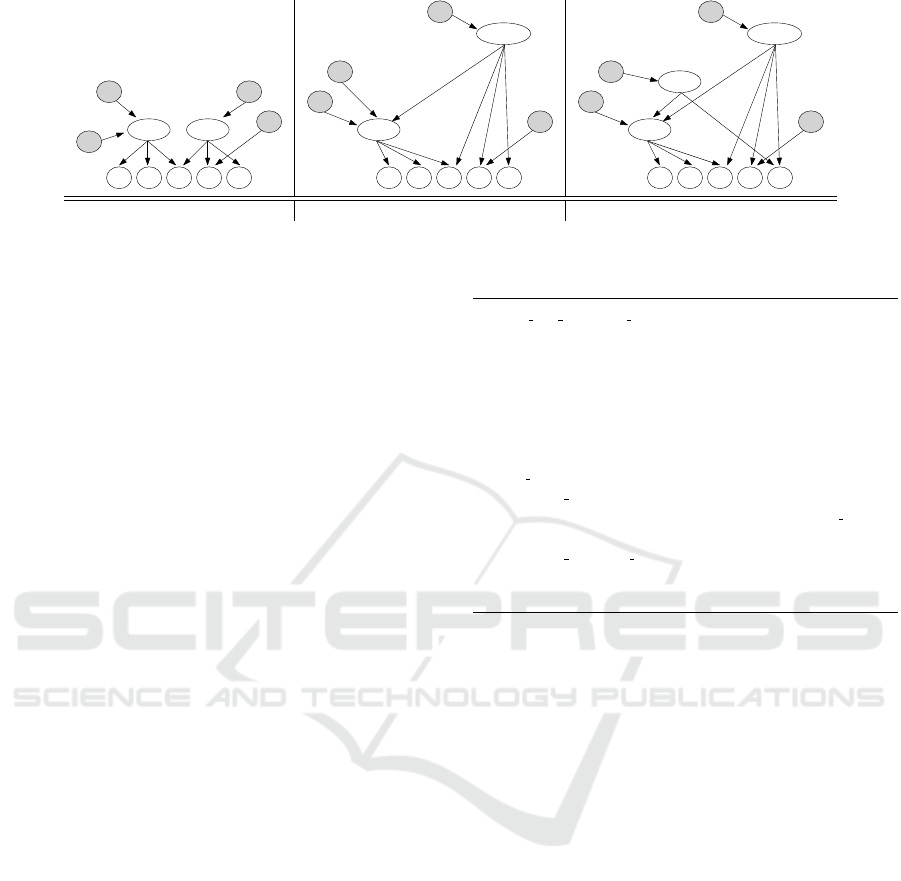
a b c

cde

abc

a b c

abc

abcde

a b c

abc

abcde

abce

(a) γ buys b and c (b) β buys a and b (c) α buys e

Figure 4: Evolution of the key derivation hierarchy in Figure1 to enforce a sequence of purchases minimizing the number of

additional tokens.

contrary, if such a node does not exist, we envision

the following two possible scenarios.

• New node: insert a node in the hierarchy repre-

senting cap(c) ∪ R and connect it to the node rep-

resenting cap(c) (and hence indirectly to the cor-

responding resources) and, directly or indirectly,

to the nodes of the resources in R.

• Rename node: connect (directly or indirectly) the

node representing cap(c) to the nodes of the re-

sources in R (i.e., node representing cap(c) is re-

labeled to represent cap(c) ∪ R). This strategy

saves the insertion and deletion of one token (the

one from k

to k

cap(c)∪R

, as it already exists) com-

pared to the previous strategy, but it is not always

viable. Speciﬁcally, this approach can be adopted

only if the following two conditions hold: i) no

other customer c

shares the (old) capability with

c, since otherwise c

too would be granted ac-

cess to R without being authorized; and ii) all

the ancestors of the node represent a superset of

cap(c) ∪ R, since otherwise this could enable cus-

tomers who can derive the ancestors of the node

to access R without paying for such resources.

For instance, consider the purchase of resources a and

b by β illustrated in Figure 2(b), starting from the hier-

archy in Figure 2(a). This purchase can be managed

by renaming node cde into abcde (see Figure 4(b))

paying the insertion of 2 tokens, in contrast to the in-

sertion of 4 tokens and the removal of 4 tokens payed

by the solution in Figure 2(b). On the contrary, the

purchase by α of e cannot be managed with a simple

renaming of node abc, since γ would gain access to e

without paying for such a resource. The structure is

then updated inserting a new node, representing abce,

connected to abc and to e (see Figure 4(c)).

Independently from the strategy chosen for having

a node representing cap(c) ∪ R in the hierarchy, such

a node (which is already connected to the resources

in cap(c)) needs to be connected to the resources in

R. A straightforward solution consists in adding a to-

ken enabling the derivation of the key k

used to en-

Purchase Min Additional Tokens(c,R)

1: if k

cap(c)∪R

6∈K

2: let Anc be the ancestors of k

cap(c)

3: if @c

6= c ∈ C s.t. cap(c

)=cap(c) AND ∀k

∈Anc, cap(c) ∪ R ⊂ X

4: then relabel k

cap(c)

as k

cap(c)∪R

5: else generate k

cap(c)∪R

and insert it into K

6: connect k

cap(c)∪R

to k

cap(c)

via a token

7: let K = {k

∈ K : X ⊆ cap(c) ∪ R}

8: to cover := R

9: while to cover6=

0 do

10: let k

be the largest set of resources in K s.t. X ∩ to cover 6=

11: K := K\{k

}

12: to cover := to cover\X

13: connect k

cap(c)∪R

to k

via a token

14: connect k

to k

cap(c)∪R

via a token

Figure 5: Management of resource purchase aimed to min-

imize the additional number of tokens.

crypt each resource r∈R from k

cap(c)∪R

. This simple

solution implies the creation of |R| new tokens. We

note however that, if the hierarchy already includes

a node representing R, node cap(c) ∪ R can be di-

rectly connected to it, enabling the derivation of k

∀r ∈ R, paying one token only. In general, if the hi-

erarchy includes a set K composed of less than |R|

nodes representing subsets of cap(c) ∪ R (and hence

also of R) that completely cover R, the number of ad-

ditional tokens can be reduced to |K| by connecting

cap(c) ∪ R with each of the nodes in K. Clearly, we

aim at minimizing the number of nodes in K. We then

follow a strategy similar to the one discussed in Sec-

tion 3.1, and ﬁrst consider nodes covering larger sub-

sets of R as candidates for insertion into K. For in-

stance, with reference to our running example, node

abcde is connected to node abc, which completely

covers the set R = {a, b} of resources purchased by β

(see Figure 4(b)). Indeed, connecting abcde to each

purchased resource would cost one additional token.

Figure 5 illustrates the pseudo-code of the func-

tion enforcing the purchase of a set R of resources by

a customer c, aimed at minimizing the number of to-

kens inserted into the catalog for the purchase.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

624

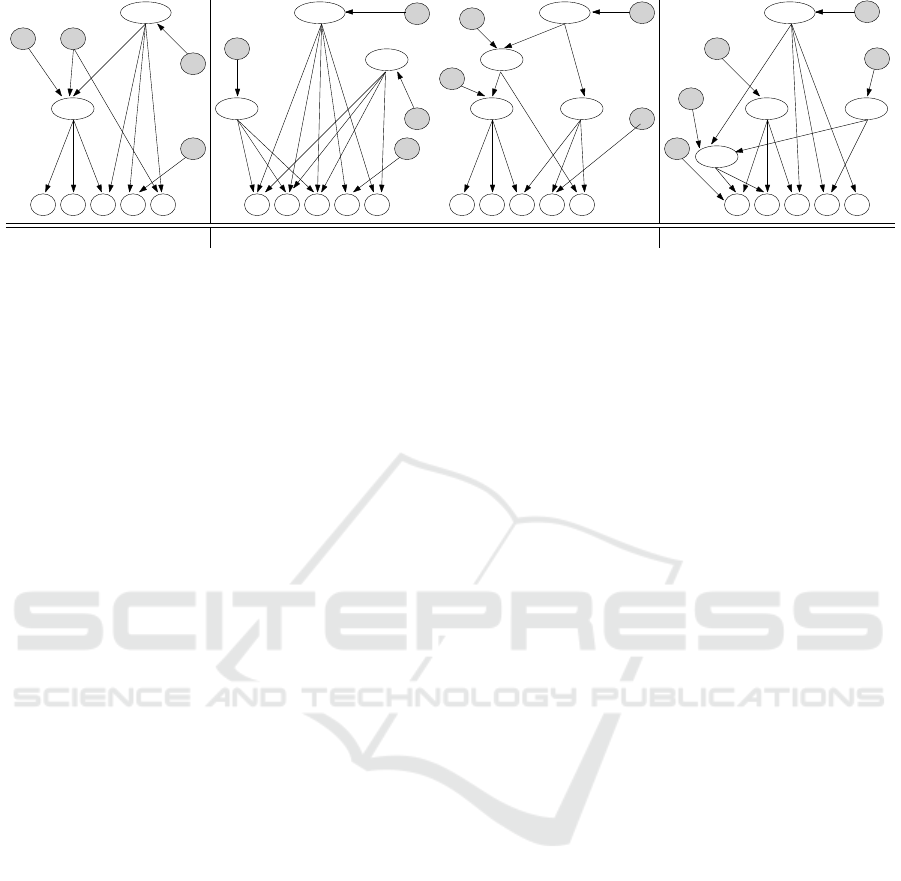
a b c

abc

abcde

a b c

abc

abce

abcde

a b c

abc cde

abce

abcde

a b c

abc abd

abcde

(a) no capability nodes (b) batch of purchases (d) additional nodes

Figure 6: Evolution of the key derivation hierarchy, considering the optimizations.

3.3 Discussion

The strategy illustrated in Section 3.2 can take advan-

tage of additional considerations that can possibly fur-

ther reduce the number of tokens inserted into the cat-

alog to enforce purchases. In this section, we discuss

further optimizations that could be adopted.

• Remove the assumption of having a node repre-

senting the capability list of each customer. Hav-

ing a node representing the capability list of each

customer implies the rename or the creation of a

new node at each purchase of a resource (or set

thereof). Removing this assumption could reduce

the number of tokens that need to be inserted into

the catalog to manage a purchase operation. Con-

sider, as an example, a customer c with capability

list cap(c), and assume that c purchases access to

a set R of resources and that the key derivation hi-

erarchy already includes a key k

. If we do not

require the presence of a node representing the set

cap(c) ∪ R of resources, it is sufﬁcient to create a

token enabling the derivation of k

from k

. On

the contrary, the need for node cap(c)∪R implies

the insertion of at least two tokens in the hierar-

chy: one enabling the derivation of k

cap(c)∪R

from

, and another one enabling the derivation of k

from k

cap(c)∪R

. Also, if cap(c) ∪ R is not repre-

sented by a node in the hierarchy, it is also neces-

sary to insert a token from k

cap(c)∪R

to k

cap(c)

(i.e.,

three tokens). For instance, with reference to our

running example, Figure 6(a) illustrates the key

derivation hierarchy obtained managing the pur-

chases of our running example, according to this

optimization strategy. This solution saves the in-

sertion of 3 tokens for the management of the pur-

chase of e by α. Note that we did not manage

the purchase of a and b by β and of b and c by

γ connecting directly the customer’s node to the

resources’ nodes since this would not provide any

cost reduction.

• Manage purchases in batch. The solutions illus-

trated in this section implicitly assume that pur-

chases are managed when they are submitted to

the data owner, who is expected to accommo-

date each purchase independently from the oth-

ers. However, the management of purchases in

batches could provide considerable advantages

for the data owner. As a ﬁrst advantage, the data

owner would not need to be always available to

manage resource purchases, but decide (in agree-

ment with customers) to enforce changes to the

key derivation hierarchy periodically (e.g., once

a day). As a second advantage, the management

of multiple purchases, by the same or by multiple

customers over one or more resources, could pro-

vide advantages also in terms of the management

of the key derivation hierarchy, enabling higher

economic savings for the write operations in the

blockchain. Intuitively, the data owner can op-

erate all the optimizations on the sub-hierarchy

necessary for managing the purchases in the batch

and possibly reduce the number of tokens with re-

spect to the management of each purchase singu-

larly taken. Clearly, there is an advantage in man-

aging together a batch of purchases by multiple

customers if they refer to the same resource (or

set thereof). Consider, as an example, three cus-

tomers c

, c

, and c

who all purchase resources

and r

. In this case, it would be convenient for

the data owner to create a node representing the

set {r

} of resources and connect c

, c

, and c

to such a node, which is in turn connected to r

and r

. This strategy implies the insertion of 5 to-

kens in the key derivation hierarchy. If the three

purchases were managed in sequence, at their sub-

mission time, the cost would be of 6 tokens (2

for each customer for connecting their node to the

node of each of the 2 resources). Intuitively, the

data owner could locally perform the optimiza-

tions illustrated in Section 3.1 on the portion of

the hierarchy affected by the batch of purchases

Selective Owner-side Encryption in Digital Data Markets: Strategies for Key Derivation

625

to be managed, and then connect it to the public

key derivation structure when the number of ad-

ditional tokens has been reduced as much as pos-

sible. For instance, with reference to our running

example, Figure 6(b) illustrates on the left the key

derivation hierarchy obtained managing, in the or-

der, the purchase of a by β, of c by γ, of b by β,

of e by α, and of b by γ starting from the initial

conﬁguration in Figure 1. Figure 6(b) illustrates

on the right the key derivation hierarchy obtained

managing the same purchases in batch. While the

ﬁrst strategy implies the addition of 8 tokens, the

second one costs only 6 additional tokens.

• Additional nodes. The data owner might con-

sider, when managing purchases, to insert addi-

tional nodes in the hierarchy to possibly reduce

the number of tokens that will be needed in the

future. Indeed, the presence of a node in the hi-

erarchy representing a set R of resources could be

proﬁtably used by any customer buying a superset

of R, saving in the number of tokens. Indeed, if

at least two customers buy a superset of R, there

is an advantage in having R in the hierarchy, in

terms of the number of tokens payed by the data

owner to manage the two purchases by the two

customers. The data owner can therefore decide,

when a customer buys a set R of resources, to ma-

terialize the node representing R, if she is conﬁ-

dent on the fact that other customers will be inter-

ested in the same set. The data owner pays an ad-

ditional token when ﬁrst inserting R, but she may

experience a saving in the future. For instance,

with reference to the initial conﬁguration of the

key derivation hierarchy in Figure 1, to manage

the purchase of resources a and b by β, the data

owner might decide to create a new node ab pay-

ing 3 tokens. If, after some time, also δ and ε buy

these resources, it would be sufﬁcient to insert a

token from k

abd

to k

for δ and from k

to k

for ε, saving on the number of tokens inserted to

manage the three purchases (7 tokens instead of

9 tokens). Figure 6(c) illustrates the resulting key

derivation hierarchy.

4 RELATED WORK

The adoption of selective encryption for enforcing ac-

cess restrictions in digital data market scenarios, cou-

pled with smart contracts deployed on a blockchain,

has ﬁrst been proposed in (De Capitani di Vimercati

et al., 2019). Our solution, while sharing with the

proposal in (De Capitani di Vimercati et al., 2019) the

use of selective encryption and key derivation for en-

abling data owners to maintain control over their re-

sources in the data market, nicely complements it. In-

deed, our techniques for minimizing the size of the to-

ken catalog and for limiting the number of additional

tokens implied by the management of each purchase

can be used in combination with the protocols for re-

source purchase presented in (De Capitani di Vimer-

cati et al., 2019).

The adoption of selective encryption, possibly

combined with key derivation, has been widely

adopted in data outsourcing scenarios, which are

characterized by data owners storing their resources

on the premises of non fully trusted cloud providers

(e.g., (Bacis et al., 2016; De Capitani di Vimercati

et al., 2010; De Capitani di Vimercati et al., 2016)).

These approaches however operate in a different sce-

nario and aim at enforcing a (quite static) authoriza-

tion policy deﬁned by the data owner. Also, the key

derivation hierarchy is organized to model the access

control lists of resources (i.e., nodes represent groups

of users), in contrast to capability lists. Changes in the

authorization policy can imply both grant and revoke

of privileges as decided by the data owner, who is in-

terested in limiting her intervention to enforce policy

updates.

Other lines of work close to ours are re-

lated to the adoption of blockchain and smart

contracts for data management and access control

(e.g., (Di Francesco Maesa et al., 2017; Kokoris-

Kogias et al., 2020; Nguyen et al., 2019; Nguyen

et al., 2021; Shafagh et al., 2017; Zichichi et al., 2020;

Zyskind et al., 2015)), and privacy and security in

cloud computing (e.g., (Donida Labati et al., 2020;

Zhang et al., 2020)). These approaches are however

complementary to ours, as they do not consider selec-

tive encryption and key derivation for enforcing ac-

cess restrictions to traded resources, and do not con-

sider the peculiarities of data markets.

5 CONCLUSIONS

We studied the management of purchases of resources

in a data market scenario, by properly modifying the

key derivation structure used to enforce access restric-

tions. We proposed two alternative solutions, aimed

at minimizing the overall number of tokens and the

number of additional tokens necessary to support each

purchase, respectively. We also discussed improve-

ments for further reducing the number of tokens nec-

essary to enforce purchases. Our work leaves room to

future works, aimed at comparing the two strategies in

a real world environment to determine which solution

should be preferred in different application scenarios.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

626

ACKNOWLEDGMENTS

This work was supported in part by the EC within the

H2020 Program under projects MOSAICrOWN and

MARSAL.

REFERENCES

Atallah, M., Blanton, M., Fazio, N., and Frikken, K. (2009).

Dynamic and efﬁcient key management for access hi-

erarchies. ACM TISSEC, 12(3):18:1–18:43.

Bacis, E., De Capitani di Vimercati, S., Foresti, S.,

Paraboschi, S., Rosa, M., and Samarati, P. (2016).

Mix&Slice: Efﬁcient access revocation in the cloud.

In Proc. of ACM CCS, Vienna, Austria.

De Capitani di Vimercati, S., Foresti, S., Jajodia, S., Para-

boschi, S., and Samarati, P. (2010). Encryption poli-

cies for regulating access to outsourced data. ACM

TODS, 35(2):12:1–12:46.

De Capitani di Vimercati, S., Foresti, S., Livraga, G., and

Samarati, P. (2016). Practical techniques building on

encryption for protecting and managing data in the

cloud. In Ryan, P., Naccache, D., and Quisquater, J.-

J., editors, The New Codebreakers: Essays Dedicated

to David Kahn on the Occasion of His 85th Birthday.

Springer-Verlag Berlin Heidelberg.

De Capitani di Vimercati, S., Foresti, S., Livraga, G., and

Samarati, P. (2019). Empowering owners with control

in digital data markets. In Proc. of IEEE CLOUD,

Milan, Italy.

Di Francesco Maesa, D., Mori, P., and Ricci, L. (2017).

Blockchain based access control. In Proc. of DAIS,

Neuch

atel, Switzerland.

Donida Labati, R., Genovese, A., Piuri, V., Scotti, F., and

Vishwakarma, S. (2020). Computational intelligence

in cloud computing. In Kov

acs, L., Haidegger, T., and

Szak

al, A., editors, Recent Advances in Intelligent En-

gineering: Volume Dedicated to Imre J. Rudas’ Seven-

tieth Birthday. Springer International Publishing.

Kokoris-Kogias, E., Alp, E. C., Gasser, L., Jovanovic, P.,

Syta, E., and Ford, B. (2020). CALYPSO: Private

data management for decentralized ledgers. PVLDB,

14(4):586–599.

Nguyen, D. C., Pathirana, P. N., Ding, M., and Seneviratne,

A. (2019). Blockchain for secure EHRs sharing of

mobile cloud based E-Health systems. IEEE Access,

7:66792–66806.

Nguyen, L. D., Leyva-Mayorga, I., Lewis, A. N., and

Popovski, P. (2021). Modeling and analysis of data

trading on blockchain-based market in IoT networks.

IEEE IoT-J, 8(8):6487–6497.

Shafagh, H., Burkhalter, L., Hithnawi, A., and Duquennoy,

S. (2017). Towards blockchain-based auditable stor-

age and sharing of IoT data. In Proc. of CCSW, Dallas,

TX, USA.

Zhang, Y., Deng, R. H., Xu, S., Sun, J., Li, Q., and Zheng,

D. (2020). Attribute-based encryption for cloud com-

puting access control: A survey. ACM CSUR, 53(4).

Zichichi, M., Ferretti, S., and D’Angelo, G. (2020). A

framework based on distributed ledger technologies

for data management and services in intelligent trans-

portation systems. IEEE Access, 8:100384–100402.

Zyskind, G., Nathan, O., et al. (2015). Decentralizing pri-

vacy: Using blockchain to protect personal data. In

Proc. of IEEE SPW, San Jose, CA, USA.

Selective Owner-side Encryption in Digital Data Markets: Strategies for Key Derivation

627