Genetic Programming based Constructive Algorithm with Penalty

Function for Hardware/Software Cosynthesis of Embedded Systems

Adam Górski and Maciej Ogorzałek

Department of Information Technologies, Jagiellonian University in Cracow,

Prof. Stanisława Łojasiewicza 11, Cracow, Poland

Keywords: Artificial Intelligence, Embedded Systems, Genetic Programming, Penalty Function, Hardware/Software

Co-Synthesis.

Abstract: In this work we present a constructive genetic programming method with penalty function for hw/sw

cosynthesis of embedded systems. The genotype is a tree which contains in its nodes system construction

options. Unlike existing solutions in this approach individuals which violate time constrains are investigated

during evolution process. Therefore the algorithm is even more able to escape local minima of optimizing

parameters.

1 INTRODUCTION

Artificial intelligence (AI) (Shastri et al. 2021) is

widely used in computer science. Method of AI like:

evolution algorithms and multi-agent systems (Jin et

al. 2021) were applied to solve many problems. One

of those are optimization problems like: hardware

design (Dick et al. 1998), traveling salesman problem

(Lust and Teghem 2010) Multi-skill resource-

constrained project scheduling problem (Lin et al.

2020), and many others.

Embedded system (Martins et al. 2020) is

a computer system consisted of hardware elements

optimized to execute appropriate tasks. According to

De Michelli and Gupta (De Michelli and Gupta 1997)

embedded system design can be divided onto three

phases: modelling, verification and implementation.

In (Górski and Ogorzałek 2016) authors propose

another phase – assignment of unexpected tasks.

Hardware/software co-syntesis (Yen and Wolf 1995,

Oh and Ha 2002) is a process of concurrent

generation of an architecture of embedded system and

its software. The goal of the process is to find optimal

architecture with optimal task assignment. The

architecture can be composed of two groups of

resources: Processing Elements (PEs) which are

responsible for tasks execution and Communication

Links (CLs) which provide communication between

connected PEs.. There are two kinds of PEs:

Programmable Processors (PPs) able to execute more

than one task and Hardware Cores (HCs) which are

specialized to execute only one task. Most of co-

synthesis algorithms can be divided on two groups –

constructive (Deniziak and Górski 2008, Górski and

Ogorzałek 2014a, Srinivasan and Jha 1995) and

iterative improvement (Oh and Ha 2002, Górski and

Ogorzałek 2021). Constructive algorithms build

system step by step making decisions separately for

each part. They have low complexity but are able to

stop in local minima of optimizing parameters.

Iterative improvement algorithms start from

suboptimal solution and by local changes try to

improve the quality of the system. The initial solution

in such methods is usually the fastest implementation

of all the tasks. In such a solution every task is usually

executed by another HC. Genetic algorithms (Conner

et. al 2005) were also applied to co-synthesis

problem. They can provide an acceptable result in

reasonable time and are able to escape local minima

of optimizing parameters. However the disadvantage

of those methods is that obtained results are sensitive

to change of genetic parameters. Very good results

were obtained using genetic programming (GP)

(Górski and Ogorzałek 2021). In (Deniziak and

Górski 2008) authors propose a constructive GP

method. One of the biggest disadvantages of the

method was that every generated individual could not

violate time constrains. Therefore the algorithm had

smaller chance to escape local minima of optimizing

parameters. The time of computation was also

Górski, A. and Ogorzałek, M.

Genetic Programming based Constructive Algorithm with Penalty Function for Hardware/Software Cosynthesis of Embedded Systems.

DOI: 10.5220/0010605005830588

In Proceedings of the 16th International Conference on Software Technologies (ICSOFT 2021), pages 583-588

ISBN: 978-989-758-523-4

583

increasing. In (Górski and Ogorzałek 2014b) an

iterative improvement algorithm for co-synthesis

problem was proposed. The algorithm builds initial

population by starting from the fastest

implementation. The next generations are obtained

using genetic operators: mutations, cloning and

crossover. However this method also do not use

a penalty function. Therefore only valid individuals

are used to generate the final solution. In this paper

we present a Genetic Programming method to

hardware/software co-synthesis of distributed

embedded system which uses the penalty function

during generation of the results. Unlike other

algorithms our method during evolution process

investigates also individuals which violate time

constrains. Therefore it is a greater chance that

algorithm will not stop in local minima of optimizing

parameters.

The paper is organized as follows: section 2

describes genetic programming – types and

application. In section 3 the representation of

embedded system is presented. Section 4 includes the

description of the algorithm. Experimental results are

given in section 5. The last section summarize the

paper and indicates the direction of future work.

2 GENETIC PROGRAMMING

Genetic Programming (Suganuma et al. 2020) is an

extension of Genetic Algorithm (Nayak and Panda,

2020). The main difference between those

methodologies is that in GP genotype is a tree. The

tree, in its nodes, includes functions.

In linear genetic programming (Zhang et al. 2020)

the tree is represented in linear form.

In cartesian genetic programming (Miller, 2011)

the genotype is a graph. Thus the genetic operators

needed to be modified.

Multigene Genetic Programming (Riahi-Madvar

et al. 2019) evolve strings of genes. However every

gene is a tree in which nodes are functions.

Developmental Genetic Programming (DGP)

(Koza et al. 1997) starts with embryo. Embryo is the

first node in genotype tree. Every other node contains

function which modifies the embryo. This type of GP

is often used for hardware design (Deniziak and

Górski 2008, Górski and Ogorzałek 2017, Górski and

Ogorzałek 2021). This kind of GP was also used in

this paper.

3 PRELIMINARIES

Embedded system is represented as a task graph G =

(T, E). This representation is one of the most popular.

In the representation each node T

in a graph is a task

executed by the system. Each edge describes an

amount of data (d

) that need to be transferred

between two connected tasks T

and T

. On figure 1

the example of task graph is presented.

T6 T7

T5 T4

Figure 1: Example of task graph.

The example consists of eight tasks: T0, T1, T2,

T3, T4, T5, T6 and T7. Tasks T1, T2 and T4, T5, T6,

T7 are parallel. Tasks T1 and T2 can start their

execution after finishing of T0 execution. Tasks T3

and T5 can be started only if T2 is finished. Tasks T6

and T7 can be executed after T3.

The transmission time t

i,j

is dependent on the

bandwidth (b

) of a communication link used to

connected PEs. It is described by the following

formula:

(1)

The execution of a task is characterized by the cost

include all times and cost of execution for every tasks

on every PEs is given. The database also contains cost

of each PE and cost of connection PEs using each

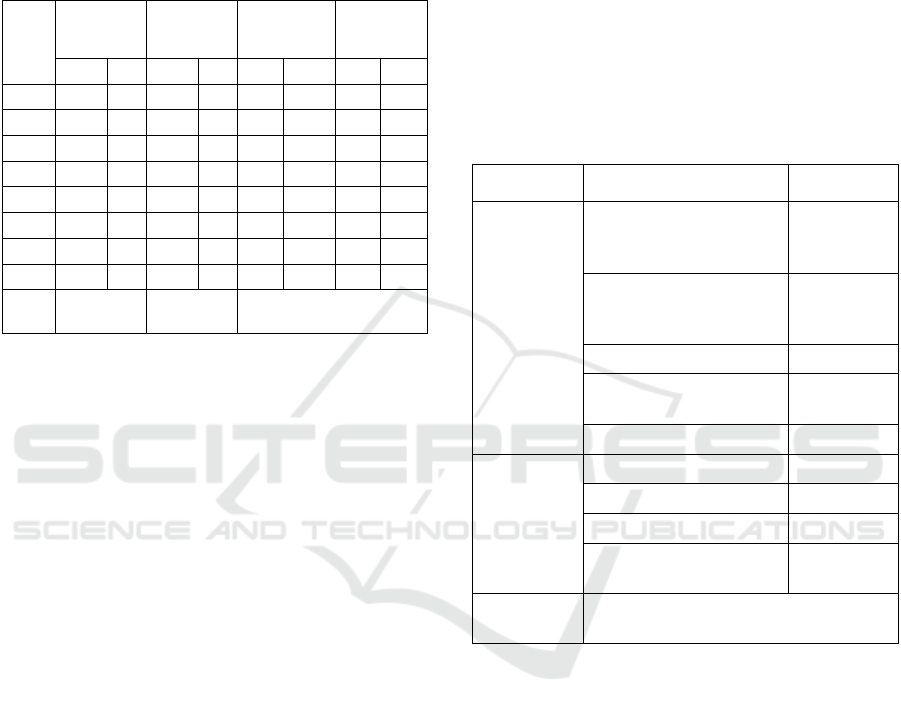
CLs. In table 1 the example of database for a graph

from figure 1 is presented. In the example there are

four kinds of possible PEs. Two of them are PPs and

two of them are HCs. The cost (C) of PP1 is 100, the

cost of PP2 is 300. The cost of HCs is added to a cost

of tasks’ execution. PEs can be connected using one

CL. The bandwidth of the CL is 13. Cost of

connection of PP1 to CL1 is equal to 6. The cost of

ICSOFT 2021 - 16th International Conference on Software Technologies

584

connection of PP2 is equal to 3. The costs of

connection of every HCs to CL1 are equal to 25. If

one or more PEs execute more than one task, then

those tasks need to be scheduled. We decided to use

list scheduling.

Table 1: Example of resource database.

Task

PP1

C=100

PP2

C=300

HC1 HC2

t c t c t c t c

T0 12 6 15 4 10 200 3 160

T1 11 8 23 10 7 90 12 80

T2 30 2 21 8 6 100 5 140

T3 18 4 20 3 4 150 1 350

T4 26 10 22 5 3 200 2 240

T5 22 5 36 12 6 90 8 70

T6 34 11 44 9 11 88 13 80

T7 45 15 30 16 9 180 10 190

CL1,

b=13

c=6 c=3 c=25

To estimate the quality of individuals we use the

fitness function (F). We decided that during evolution

process, to avoid stopping in local minima of

optimizing parameters, every generated individuals

can be used. Therefore every individuals which

violate the time constrains must be given a penalty.

The penalty is depended on the violation time. The

function is depended on time of the solution (t), its

cost (C

) and given penalty (PF). It is described by the

following formula:

PptlCkF *** ++=

(2)

Parameters k, l and p are given by the designer.

There are no dependencies between the parameters k,

l and p. The time of the solution is a time after which

the last task finishes its execution. The cost of

embedded system can be calculated as:



====

++=

PCCL

PEs

yuz

ccCC

(3)

Where n is a number of tasks in a task graph, m is

a number of PP in solution, u is a number of CLs

connected to v PEs.

Penalty can be calculated as follows:

)(

max

ttP

−=

(4)

where t

max

is a time constrain and t is a time of

execution of all the tasks for investigated solution.

4 THE ALGORITHM

The algorithm which is presented in this paper is

constructive method. Therefore design decisions are

made for each task separately. The genotype is a tree.

To be sure that every task is executed the genotype is

a spanning tree of given task graph. The first node in

the tree is embryo. Embryo is a random

implementation of the first task. The rest of nodes

contains genes. In our solution genes are system

construction options. The options are presented in

table 2.

Table 2: Options for building system.

Step Option Probability

a. The fastest

implementation of the

task

0.2

b. The cheapest

implementation of the

task

0.2

c. min (t*c) 0.2

d. The same as

predecessor

0.2

e. The rarest used PP 0.2

CL a. The fastest CL 0.2

b. The cheapest CL 0.2

c. The rarest used 0.3

d. The same as

predecessor

0.3

Task

scheduling

list scheduling

Unlike others constructive methods (Deniziak and

Górski 2008) our algorithm do not separate options

for used PEs and options for allocating new ones. The

algorithm independently makes a decision if it is

necessary to allocate a new PE.

The number of individuals in each population is

described by the following formula:

e*n* =

(5)

where n is number of tasks (nodes in the task

graph), e is possible number of embryos.

After generating an initial population the

algorithm builds new individuals using genetic

operators: selection, crossover, mutation and cloning.

In this paper we decided to use rank selection. Every

generated individuals are ranked by the minimum

value of fitness function. The individuals have

Genetic Programming based Constructive Algorithm with Penalty Function for Hardware/Software Cosynthesis of Embedded Systems

585

probability (P) depended on the position on the rank

list (r):

−Π

(6)

The probability describes the chance that every

individual will be used during evolution process.

Individuals with lower value of fitness function have

greater probability of being selected, however the

solutions with higher value are not necessary rejected.

Mutation randomly selects (using selection

operator) Ὠ individuals:

ΠΩ *=

(7)

For each individual one node is selected

randomly. Mutation substitutes the option in selected

node on another using available options (from table

2).

Crossover chooses Ψ individuals. Selected

individuals are connected in pairs. Then a crossing

point is selected randomly. The point is the same for

both individuals in each pair. The operator substitutes

subtrees between the solutions. The number of

individuals created by crossover is equal to the

following formula:

ΠΨ *=

(8)

Cloning operator copies Φ individuals to the next

population. formula:

ΠΦ *=

(9)

To have the same number of individuals in each

population must be satisfied the condition:

β + γ + δ = 1

(10)

The algorithm stops if in ε next generations better

individual was not found.

5 FIRST RESULTS

To check the quantity of presented algorithm we

decided to use benchmarks with 10, 20 and 30 nodes.

The results are presented in table 3 below. For each

graph 10 runs were made and the best obtained results

were put in table 3. They were compared with Genetic

Programming algorithm proposed by Deniziak and

Górski (Deniziak and Górski 2008) which is also

a developmental genetic programming constructive

method. The parameters were set as follows: α=2,

β=0.2, γ= 0.7, δ=0.1, ε=3, k=8, l=1, p=4.

Table 3: The results.

Algorithm Graph t c Gen. F

DGP08 10 479 1667 3 13815

20 970 3575 9 29570

30 1273 6323 28 51857

DGP2021 10 531 2095 15 17322

20 937 2749 29 22929

30 937 6035 44 49217

The time constrains for each graph were set as

follows: graph with 10 nodes – 500, graph with 20

nodes – 1000, graph with 30 nodes – 1300. As it can

be observed in table 3 the results obtained by the

presented algorithm are much better in most of cases

than obtained by DGP08. Only for a graph with 10

nodes the best solution obtained by presented

algorithm has fitness function equal to 17322,

meanwhile the best solution obtained by DGP08 has

fitness function equal to 13815. For graphs with 20

nodes presented algorithm generated results with

fitness function equals to 22929. For that graph

presented algorithm generated individual with better

value of time (937) and cost (2749) than DGP08 (cost

equal to 3575, and time equal to 970). What is worth

to underline using the presented approach during the

evolution process despite the fact that in some of the

generations best individuals violated time constrain,

the final solution has time under maximum value. The

same situation can be observed for graph with 30

nodes. The time of a final solution obtained by

presented algorithm (937) does not violate time

constrains. It is also lower than time obtained using

DGP08 (1273). The solution generated by presented

approach has also lower value of cost (6035) than

result obtained by DGP08 (6323). This suggest that

algorithm presented in this paper has greater ability to

escape local minima of optimizing parameters.

6 CONCLUSIONS AND FUTURE

WORK

In this paper a constructive genetic programming

method for hardware/software cosynthesis of

distributed embedded system was presented. The

method uses a penalty function. Some of the

individuals in each generation can violate time

constrains. Therefore those individuals can be used to

construct next generations. Thus the algorithm is

more able to escape local minima of optimizing

parameters. The first experimental results indicates

ICSOFT 2021 - 16th International Conference on Software Technologies

586

bigger effectiveness of presented algorithm than

DGP08. Only in one case better results were

generated by DGP08 algorithm – for graph with 10

nodes. However more experiments must be

performed using presented algorithm to be sure why

in such a case the results were worse. Maybe with

different value of genetic parameters or another

values of probability of system construction options

results could be better even for graph with 10 nodes.

Therefore more experiments are needed to find the

best values of genetic operators. In future work we

also plan to check another combination of system

construction options and different genetic operators

and their impact on final results.

REFERENCES

Shastri B. J., Tait A. N., De Lima T. F., Pernice W. H. P.,

Bhaskaran H., Wright C. D., Prucnal P. R, 2021.

Photonics for artificial intelligence and neuromorphic

computing. In Nature Photonics, vol. 15, no. 2,

pp. 102–114, (online), available: https://doi.org/

10.1038/s41566-020-00754- .

Jin X., Lü S. Yu J., 2021. Adaptive NN-Based Consensus

for a Class of Nonlinear Multiagent Systems With

Actuator Faults and Faulty Networks. In IEEE

Transactions on Neural Networks and Learning

Systems, doi: 10.1109/TNNLS.2021.3053112.

Dick R. P., Jha N. K., 1998. MOGAC: a multiobjective

Genetic algorithm for the Co-Synthesis of

Hardware-Software Embedded Systems. In IEEE

Trans. on Computer Aided Design of Integrated

Circiuts and systems, vol. 17, No. 10.

Lust, T. Teghem J, 2010 The multiobjective traveling

salesman problem: a survey and a new approach. In

Advances in Multi-Objective Nature Inspired

Computing. Springer. p. 119-141.

Lin J, Zhu L, Gao K., 2020. A genetic programming hyper-

heuristic approach for the multi-skill resource

constrained project scheduling problem. In Expert Syst

Appl 140. https://doi.org/10.1016/j.eswa.2019.112915.

Martins J., Tavares A., Solieri M., Bertogna M., Pinto S.,

2020. Bao: A lightweight static partitioning hypervisor

for modern Multi-Core Embedded Systems. In

Workshop on Next Generation Real-Time Systems.

De Micheli, G., Gupta, R., 1997. Hardware/software

co-design. In Proceedings IEEE 95.3 (Mar). IEEE.

Górski, A., Ogorzałek, M.J., 2016. Assignment of

unexpected tasks in embedded system design process.

Microprocessors and Microsystems, Vol. 44,

pp. 17-21, Elsevier.

Yen, T., Wolf, W., 1995. Sensivity-Driven Co-Synthesis of

Distributed Embedded Systems. In Proceedings of the

International Symposium on System Synthesis.

Srinivasan, S., Jha, N.K., 1995. "Hardware-Software Co-

Synthesis of Fault-Tolerant Real-Time Distributed

Embedded Systems", In Proceedings European Design

Automation Conference. pp. 334-339.

Oh, H., Ha, S., 2002. Hardware-software cosynthesis of

multi-mode multi-task embedded systems with real-

time constraints. In Proceedings of the International

Workshop on Hardware/Software Codesign,

pp. 133–138.

Górski, A., Ogorzałek, M.J., 2021. Genetic programming

based iterative improvement algorithm for HW/SW

cosynthesis of distributted embedded systems. In

Proceedings of the 10th International Conference on

Sensor Networks.

Deniziak, S., Górski, A., 2008. Hardware/Software Co-

Synthesis of Distributed Embedded Systems Using

Genetic programming. In Proceedings of the 8th

International Conference Evolvable Systems: From

Biology to Hardware, ICES 2008. Lecture Notes in

Computer Science, Vol. 5216. SPRINGER-VERLAG.

Górski, A., Ogorzałek, M.J., 2014a. Adaptive GP-based

algorithm for hardware/software co-design of

distributed embedded systems. In Proceedings of the

4th International Conference on Pervasive and

Embedded Computing and Communication Systems,

Lisbon, Portugal.

Górski, A., Ogorzałek, M.J., 2014b. Iterative improvement

methodology for hardware/software co-synthesis of

embedded systems using genetic programming. In

Proceedings of the 11th Conference on Embedded

Software and Systems (Work in Progress Session),

Paris, France.

Conner, J., Xie, Y., Kandemir, R., Link, G., Dick, R., 2005.

FD-HGAC: A Hybrid Heuristic/Genetic Algorithm

Hardware/Software Co-synthesis Framework with

Fault Detection. In Proceedings of Asia South Pacific

Design Automation Conference (ASP-DAC), pp. 709-

712.

Suganuma M., Shirakawa S., Nagao T., 2020. Designing

Convolutional Neural Network Architectures Using

Cartesian Genetic Programming. In Iba H., Noman N.

(eds) Deep Neural Evolution. Natural Computing

Series. Springer, Singapore. https://doi.org/10.1007/

978-981-15-3685-4_7

Nayak S., Panda M., 2020. Hardware Partitioning Using

Parallel Genetic Algorithm to Improve the Performance

of Multi-core CPU. In: Mohanty M., Das S. (eds)

Advances in Intelligent Computing and

Communication. Lecture Notes in Networks and

Systems, vol 109. Springer, Singapore.

https://doi.org/10.1007/978-981-15-2774-6_55

Zhang Y., Chen Y., Hu T., 2020. Classification of Autism

Genes Using Network Science and Linear Genetic

Programming. In: Hu T., Lourenço N., Medvet E.,

Divina F. (eds) Genetic Programming. EuroGP 2020.

Lecture Notes in Computer Science, vol 12101.

Springer, Cham. https://doi.org/10.1007/978-3-030-

44094-7_18

Górski, A., Ogorzałek, M.J., 2017. Adaptive iterative

improvement GP-based methodology for HW/SW co-

synthesis of embedded systems. In Proceedings of the

7th International Joint Conference on Pervasive and

Genetic Programming based Constructive Algorithm with Penalty Function for Hardware/Software Cosynthesis of Embedded Systems

587

Embedded Computing and Communication Systems,

Madrid, Spain.

Miller J.F., 2011 Cartesian Genetic Programming. In:

Miller J. (eds) Cartesian Genetic Programming. Natural

Computing Series. Springer, Berlin, Heidelberg.

https://doi.org/10.1007/978-3-642-17310-3_2

Riahi-Madvar, H., Dehghani, M., Seifi, A.; Singh, V.P.,

2019. Pareto Optimal Multigene Genetic Programming

for Prediction of Longitudinal Dispersion Coefficient.

In Water Resour. Manag., 33, 905–921.

Koza, J., R., Bennett III, F., H., Lohn, j., Dunlap, F., Keane,

M., A., Andre, D., 1997. Automated synthesis of

computational circuits using genetic programming. In

Proceedings of the IEEE Conference on Evolutionary

Computation. IEEE.

ICSOFT 2021 - 16th International Conference on Software Technologies

588