Investing Data with Untrusted Parties using HE

Mark Dockendorf, Ram Dantu, Kirill Morozov and Sanjukta Bhowmick

Department of Computer Science, University of North Texas, Denton, U.S.A.

Keywords:

Homomorphic, Encryption, Graphs, Privacy.

Abstract:

Data such as an individual’s income, favorite sports team, typical commute route, vehicle maintenance history,

medical records, etc. are typically not useful for making large-scale decisions such as where to build a new

hospital, identifying which roads are in need of upkeep, and the like. However, aggregates of of these data

across hundreds of individuals are useful to governments and to companies. Data cooperatives/unions offer a

place for individuals to store their data and a service of data aggregation and interpretation to governments,

non-proﬁt organizations, and businesses while maintaining individuals’ anonymity. We propose the use of

anonymization techniques coupled with graph algorithms over homomorphically encrypted (HE) graphs as

a basis of analysis for this accumulated data. We believe this approach ensures individuals’ privacy and

anonymity while preserving the usefulness of the plaintext data.

1 INTRODUCTION AND

MOTIVATION

Data has become one of the world’s most prized com-

modities. Its value lies in its potential to provide in-

sight, be it to corporations, interest groups, or gov-

ernments (World Economic Forum, 2011). Large

amounts of data are harvested by these various enti-

ties for any number of economic, social, or cultural

purposes. Purchase history, browsing history, medi-

cal records, ﬁnancial information—there is no limit

to the value of large datasets, and some organization

somewhere will have a use for them.

But who is in control of the world’s data? As of

now, data is largely the property of a few inﬂuential

companies (Walsh, 2019). This raises several con-

cerns. Firstly, individuals are not in control of their

data. They do not know who has access to their data

and how they are using it. Secondly, there is no guar-

antee that the data is secure and properly anonymized.

Identiﬁable information may be in plain view to those

who do not need to see it.

The formation of data cooperatives addresses both

concerns. A data cooperative is a legal construct

wherein members voluntarily pool data for the beneﬁt

of the group (Geuns et al., 2020). Through a data co-

operative, individuals are given the choice to control

their data. They can choose to share their data, who

can use it, and how it is used. Furthermore, co-ops

have a vested interest in keeping their members safe

against data theft and advocating for their members’

rights (Ligett et al., 2019). This construct supports the

privacy and security of the individual’s information.

Despite being a somewhat novel concept, numer-

ous data cooperatives have already formed success-

fully. For example, there exists a Swiss co-op, Health-

bank, that aggregates personal health data for the pur-

pose of research and medical advancement. Another

project called Driver’s Seat is a co-op comprised of

on-demand drivers (e.g., Uber or Lyft drivers) who

choose to share data related to their travels. This

allows the members of the co-op to optimize their

workﬂow using insights from the data pool. More re-

cently, there is interest in creating a data cooperative

that collects information about contact tracing such

that super-spreaders of COVID-19 can be identiﬁed

(Dockendorf et al., 2021). Authors have also used

data cooperatives to mine and chain fake data. This

work was selected as one of the hard problems in the

science of security and we will be presenting at the

Hot Topics in Science of Security conference (Salau

et al., 2021; Salau et al., 2021). These applications

demonstrate the wide variety of functions that a data

cooperative can serve.

Data cooperatives are useful, but how can a co-

op ensure that their data is secure? A key concern is

that information from a cooperative can be misused to

obtain conﬁdential data about individuals. Pieces of

information that aren’t anonymized properly can be

cross-referenced to obtain an individual’s entire pro-

Dockendorf, M., Dantu, R., Morozov, K. and Bhowmick, S.

Investing Data with Untrusted Parties using HE.

DOI: 10.5220/0010606908450853

In Proceedings of the 18th International Conference on Security and Cryptography (SECRYPT 2021), pages 845-853

ISBN: 978-989-758-524-1

845

ﬁle, including emails, addresses, and social security

information. This personally identiﬁable information

can be used for identity theft, blackmail, or surveil-

lance.

These security concerns can be mitigated through

graph anonymization and homomorphic encryption.

All data, particularly that from computer logs, net-

work logs, and ﬁnancial logs, can be represented by

graphs. These graphs can be anonymized by modify-

ing their structure using k-core decomposition. This

method involves edge swapping at lower cores such

that the structure of the higher cores is retained, pre-

serving the network’s structure while obscuring iden-

tiﬁable information. These graphs can be secured fur-

ther using homomorphic encryption, a cornerstone of

modern cryptographic protocol design. To securely

analyze this encrypted data, graph operations are lay-

ered over the homomorphic encryption. By using

these two methods, a multi-modal security framework

is built that allows users of the data cooperative to see

data insights without accessing the data itself.

2 BACKGROUND

Network Analysis. Complex systems of interact-

ing entities such as social networks, computer net-

works, and ﬁnancial systems are naturally represented

as graphs. In this context, network analysis algo-

rithms form a basis for secure data analytics in the

areas such as electronic commerce and computational

epidemiology. Network analysis is an active area of

research, where graph algorithms are used to explore

properties of complex interactive systems. Of partic-

ular importance are centrality metrics that are used

for measuring the importance of entities represented

as vertices. For example, in a contact graph, vertices

with high centrality point at potential superspread-

ers. Some of the popular metrics are degree centrality

(vertex degree), closeness centrality (mean distance

of the vertex from other vertices), betweenness cen-

trality (fraction of shortest paths passing through the

vertex), and eigenvector centrality and its variations

such as PageRank (the number of important neigh-

bors of the vertex) (Newman, 2010).

Homomorphic Encryption (HE). Such encryption

schemes support computation on encrypted data,

without access to a private key. Of particular inter-

est in this context are the so called fully homomor-

phic encryption (FHE) schemes, which support com-

putation of arbitrary functions—see (Halevi, 2017)

for a comprehensive survey. These cryptosystems

ideally ﬁt the scenario of data cooperatives since the

former provide conﬁdentiality of members’ personal

data while enabling computations on them. Multi-key

FHE schemes introduced by Lopez-Alt et al. (L

opez-

Alt et al., 2012) will be particularly useful in this set-

ting, as they allow computation on data encrypted us-

ing different keys. FHE schemes are known to be de-

manding in terms of computational resources. There-

fore, the main challenge for their deployment in the

practical scenario is to ensure that a wide range of al-

gorithms can be run on large amounts of encrypted

data.

3 PROPOSED ARCHITECTURE

Figure 1 shows a high-level block diagram of of how

a data union/cooperative that employs HE graphs for

data analysis might be structured. Importantly, this

diagram is for a data union that does not utilize cloud

services.

Individuals or apps (on behalf of individuals) sub-

mit data to the data union through the Personal Data

API. These individuals own their respective data.

Multiparty encryption is used on all data submitted,

and all data owners are assumed to be opt-out of all

data analysis unless they grant consent to either a cat-

egory of usage or consent to participate in a speciﬁc

data study. This API validates the data to ensure it

meets a standard of input and enables the multiparty

encryption for permanent storage. The data owner

may retrieve this information from the data union by

validating their credentials (ie. with username and

password). However, the data returned will only be

decrypted by the data union, so the data owner must

still possess their own key to fully unlock it. When a

data owner grants new usage permission on their data,

the Personal Data API will send their data to them

(with both data union and data owner encryption in-

place). The data owner will unlock the data using his

or her key, and transmit back to the data union. Im-

portantly, not all data need be transmitted every time,

only the relevant data will be transmitted for decryp-

tion.

Encrypted Storage keeps a copy of all input data

in encrypted form using multiparty encryption. The

individual will keep a copy of their key, which could

be a physical USB keyring or similar, and the data

union/cooperative keeps the other key. If the data

union/cooperative wants to use a set of personal infor-

mation to generate aggregates, consent (and the key)

of the individual is required. The storage used should

be resilient without presence of electricity (ie. optical

storage). This portion of the data union/cooperative

is modeled after a traditional bank’s safety deposit

boxes where (i) identity veriﬁcation, (ii) the owner’s

SECRYPT 2021 - 18th International Conference on Security and Cryptography

846

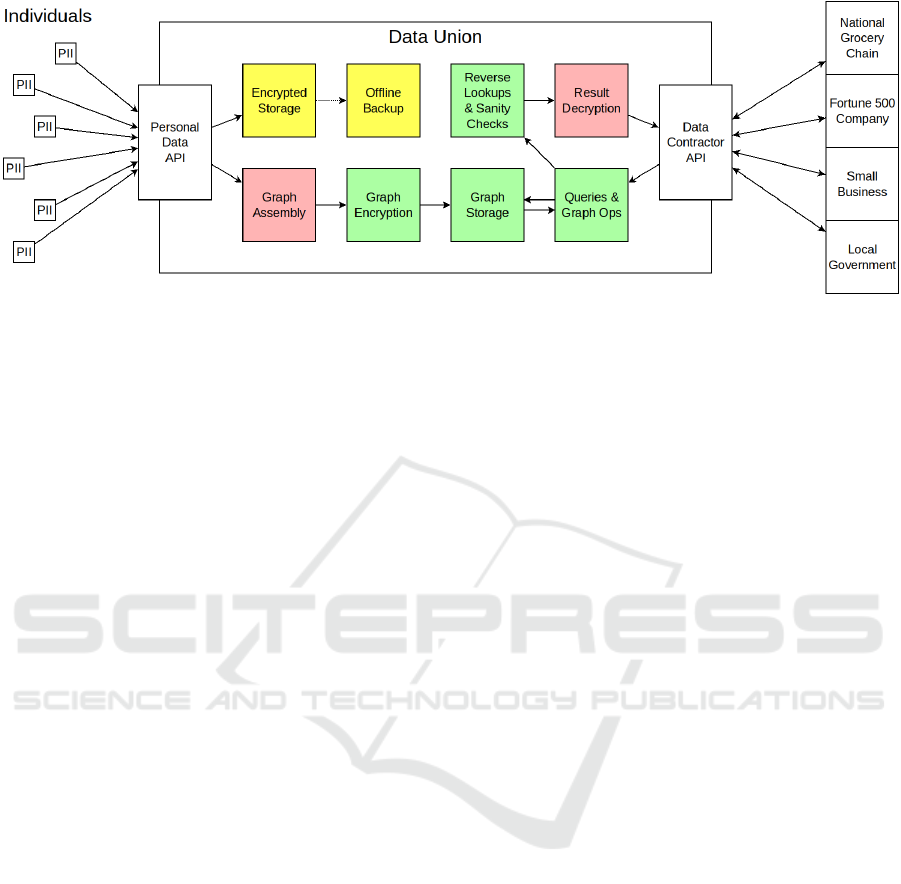
Figure 1: High-level diagram for a data union. Architecture modules that are red handle sensitive data and either (i) handle

plaintext sensitive data or (ii) may possess the key to the sensitive data they handle. Modules in green handle exclusively

HE graph data and public graph data. The yellow blocks, use traditional multiparty encryption, so the data stored is not

computable.

key, and (iii) the bank’s key are all required for ac-

cess. The data union should also maintain an ofﬂine

backup of this encrypted storage that is updated peri-

odically (ie. daily, weekly, etc).

Graph Assembly takes data (currently not en-

crypted or with the infrastructure processing it know-

ing the key) and assembles graphs based on desired

relations. Each individual’s data can be encrypted in-

dependent of one-another: this allows the data union

to access the data with the owner’s consent, transform

the data into the appropriate form, and immediately

forward the organized data to Graph Encryption and

forget the plaintext values. Each data point can be

used in the creation of multiple graphs and matrices

that transform data, mapping from one type of graph

to another (ie. people to roads used in their com-

mutes), will also be created. This subsystem shreds

plaintext data (overwrites with random data) once the

values have been encrypted.

Graph Encryption takes values created by Graph

Assembly and converts them to HE Graphs; notably,

individual columns/rows can be encrypted without all

others being present. This allows the plaintext val-

ues to be removed from system memory. For each

attribute vector, there is an associated set of encryp-

tion schemes to encrypt the data under. A graph or

attribute vector may be encrypted in many forms (ie

binary, ﬁxed-point, integer). This subsystem is re-

sponsible for updating HE graphs in Graph Storage as

their values change. This subsystem shreds plaintext

data once it is no longer needed and forgets ciphertext

data once it is stored in Graph Storage.

Graph Storage keeps HE Graphs and answers

queries. Functionally, this subsystem is a database.

This subsystem will deny read access to ciphertext

graphs for all subsystems other than Graph Opera-

tions.

Graph Operations performs operations re-

quested by the Data Contractor API after basic val-

idation. Speciﬁcally, this subsystem (1) parses aggre-

gate algebra into operations (a series of parallel op-

erations) and (2) executes the requested matrix math.

This subsystem has read access to graph storage and

is responsible for performing HE Graph operations

(centralities, BFSs, etc) and data transformations.

Reverse Lookups & Sanity Checking ensures no

one’s personal information will be exposed because

of the query (ie. enough participants to be sufﬁciently

anonymous). This subsystem is also responsible for

performing lookups that transform indices back into

the appropriate names (ie. road segment index 51253

to “5500-6000 block of Main St.”). Naturally, this

module does not have a lookup table for data like peo-

ple’s names: this would violate their privacy.

Result Decryption decrypts the aggregated re-

sults, which should not be able to identify any indi-

vidual. Companies, governments, and non-proﬁt or-

ganizations submit queries to the Data Contractor API

and receive their results when this module ﬁnishes.

The Data Contractor API accepts, validates, and

answers requests for aggregates by companies, gov-

ernments, etc. This API will return an error when a

referenced value is not in a lookup table or when the

starting value for an aggregate is not part of a public

data set. These error might happen when an aggregate

references something that is not public data, such as

a person’s name, or the aggregate starts with a crafted

vector on vertices that represents data that is not pub-

lic.

Architecture Enabling Multi-modal Privacy. Ta-

ble 1 shows a comparison of the two methods ensur-

ing data privacy: anonymization and HE. In order to

Investing Data with Untrusted Parties using HE

847

capitalize on both of these methods, we propose that

encrypted graphs be placed on the cloud, which we

conditionally call “public”—it will be accessible by

entities in the data co-op who need access to speciﬁc

information on the user data. The anonymized data

will be placed on the cloud, which we will call “pri-

vate”. This cloud will provide anonymized graphs to

those in the co-op who need to see the entire network

structure (e.g., for statistical analysis), but who do not

need speciﬁc user identities.

4 APPLICATIONS FOR THE

PROPOSED METHODS

Table 1: Comparison of graph anonymization and graph en-

cryption approaches.

Graph Anonymization Graph Encryption

Function Obscuring: (i) links be-

tween vertices and in-

dividuals (identity), (ii)

links between pairs of

individuals, and (iii)

inference of attributes

among individuals.

Data conﬁden-

tiality, and hence

protection against

data leakage, e.g.,

due to unautho-

rized access.

Security Data are available but

distorted to obscure

sensitive information.

Data are sealed

and hence their

privacy is pre-

served.

Inter-

operability

GDPR: Cross-border

data transfers (between

countries) mandate

anonymization

Encryption not al-

lowed for cross-

border data trans-

fers.

Ensuring Privacy Through Anonymization and

Homomorphic Encryption. The two main meth-

ods of protecting privacy and security of data are (i)

Anonymization and (ii) Encryption. As per their dif-

ferent features, as listed in Table 1, we posit that data

analysts who need to explore new algorithms work

with the anonymized graph, and co-op members who

need data insights use the encrypted graph. Hence,

our framework includes homomorphic encryption for

processing queries on the encrypted networks, and

anonymization based on core-periphery structure of

the graph for analyzing structural properties of the

networks.

Graph Anonymization Using K-core Decomposi-

tion. The primary issue of graph anonymization is

that the anonymized graph should retain the important

structural properties of the network, while obscuring

information that can identify an individual to a node

in the network. We posit that anonymizing graphs

based on their k-core property is particularly suited

for our application because of the following proper-

ties:

1. Utility. It has been demonstrated (Meyer et al.,

2014; Laishram et al., 2018) that high centrality

vertices have higher core numbers. Moreover, k-

core is used as a submodule to compute clusters

and fast dissemination algorithms which are based

on super-spreaders.

2. Accuracy. All anonymization techniques change

the structure of the network, which can affect ac-

curacy of the analysis. We have shown (Sakar et

al., 2018) that changes are more disruptive within

the inner cores of the network, than in the periph-

eral cores. Therefore, retaining structure of the

inner cores will reduce the effect of noise.

3. Efﬁciency. Compared to most other anonymiza-

tion methods, computing k-core of graphs is much

faster with complexity of only O(d

max

|V | + |E|).

We aim to develop anonymization algorithms of

comparable complexity.

Most graph anonymization algorithms try to mini-

mize the number of changes. Our studies in (Uﬁmtsev

et al., 2016; Cheon et al., 2018) have shown that the

changes to the higher cores disrupt the centrality val-

ues more than changes to the periphery.

We therefore propose to develop an anonymiza-

tion scheme that disrupts the periphery but retains the

structure at the higher cores. We achieve this using the

two steps: (i) edge swapping for vertices with lower

cores; and (ii) adding nodes and edges to preserve k-

(core, property) anonymity at higher cores.

Edge Swapping at Lower Cores. Swapping edges

between nodes of low core numbers, i.e., nodes at the

periphery, retain the overall degree distribution of the

graph, but changes the degrees of the individual nodes

whose edges were swapped. This leads to a restruc-

turing of the periphery of the graph (see Figure 2(b)).

Rationale. This step helps in reducing active at-

tacks to de-anonymize the network. Active attacks

(Narayanan et al., 2009) are done by planting new

entities (nodes) to the original network before it gets

anonymized and linking these entities to some impor-

tant nodes. Once the network is anonymized, the at-

tacker knows the structure of the nodes that he planted

and can identify them in the anonymized graph. He

can then use links in these nodes to identify important

nodes.

Since the planted entities rarely occupy an impor-

tant position in the graph, they are likely to have lower

core numbers. Edge swapping is likely to distort the

structure of the planted nodes (and other peripheral

nodes), making it difﬁcult for the attacker to identify

them after anonymization. For example, let the at-

tacker create a planted subgraph of a chain of degree-

SECRYPT 2021 - 18th International Conference on Security and Cryptography

848

Figure 2: K-core decomposition-based graph anonymiza-

tion. (a) Original graph. (b) Graph after edge swapping.

The periphery structure (cores 1, 2) is disrupted. (c) Graph

after k-(core, degree) anonymity. Vertices in the higher core

(3), all have the same degree and core number.

1 core-1 node connected to a degree-3 core-2 node

(P-L in Figure 2(a)), which is connected to high core

nodes. After edge swapping disrupts the periphery,

the attacker cannot ﬁnd his planted subgraph.

Preserving k-(core, property) Anonymity at

Higher Cores. The k-(core, property) anonymity

asserts that for a given vertex property, there would

be at least k vertices with high core numbers that

have the same core number and the same value of the

property. For example, if the property is degree, then

there should be at least k-1 vertices with the same

core number and the same degree (see Figure 2(c)).

We aim to modify the graph by adding nodes to the

lower cores and connecting them with higher cores,

as that will reduce the disruption of the network.

Rationale. Consider that the attacker knows some

vertices with a unique property. The anonymization

process aims to create k vertices with that property,

such that the attacker can guess the vertices correctly

with probability of only 1/k.

Similar schemes have been proposed to obtain a

set of vertices of the same property, such as k-degree

anonymity (Chen et al., 2020) (degree), (k,d)-core

anonymity (Assam et al., 2014) (core number) and k-

isomorphism (Cheng et al., 2010) (subgraphs). Our

approach of anonymizing based on pairs rather than

only one element provides more ﬂexibility of group-

ing the nodes and modifying the structure of the net-

work. For example, in Figure 2(c) after adding a new

vertex U and connecting C to K, all the vertices in

core 3 have the same core number and the same de-

gree.

Novelty of Our Approach. The novelty of our ap-

proach is that we partition the network into smaller

subgraphs that contain or primarily contribute to data

analysis (the higher cores), and the larger subgraphs

that do not have as much effect on the analysis (the

lower cores). Since there are fewer nodes with high

core numbers, we apply aggressive anonymization

techniques, such as k-(core, property) anonymization.

For the lower cores, with larger number of vertices,

there is “safety in numbers” and we can apply less

stringent and thus less expensive techniques.

Homomorphic Encryption Enabling Graph Anal-

ysis. We will develop a framework for computing

graph algorithms on encrypted data. We will focus

on algorithms related to centrality and clustering.

Secure Matrix Multiplication Mechanism. This

mechanism will be at the core of our framework. We

will depart from the encrypted matrix multiplication

algorithm by Jiang et al. (Jiang et al., 2018).

As bootstrapping time typically dominates the

cost of computation over encrypted data, it is impor-

tant to minimize the multiplicative depth of the circuit

to be computed. Jiang et al. deploy the fully homo-

morphic encryption scheme HEAAN by Cheon et al.

(Cheon et al., 2017; Cheon et al., 2018) and an in-

tricate combination of ciphertext packing, rotations,

and SIMD-like parallelization to run the multiplica-

tion of d × d dense matrices using O(d) homomor-

phic operations with multiplicative depth one. When

analyzing data from the data co-op pool, we wish to

make considerations for sparse matrices. Therefore,

we will develop our own secure matrix computation

mechanism, leveraging parallelization used, e.g., in

the sparse matrix multiplication algorithm of Buluc et

al. (Bulu¸c et al., 2009). We will also use the HEAAN

scheme, as we will need matrix computation over the

reals, which this scheme is designed to support. Fig-

ure 3 presents a high-level overview of matrix opera-

tions to be covered by our approach. We next sketch

two examples of how this framework will support net-

work analysis.

Secure Computation of Label Propagation. To ex-

emplify our methodology, let us consider our pro-

posed secure computation of clustering in detail.

Speciﬁcally, we will implement the label propagation

algorithm of (Zhu et al., 2003). Typically, label propa-

gation is computed by applying matrix multiplication

iteratively. However, this may result in prohibitively

high multiplication depth, and hence computational

cost. Zhu and Ghahramani (Zhu et al., 2003) pre-

sented the following ﬁxed-point solution to the label

propagation, which will allow us to avoid iterations

(Mallawaarachchi, 2020; Zhukov, 2015).

Let A denote the adjacency matrix of a graph. Let

D be a degree matrix, which is a diagonal matrix

whose diagonal elements are computed as d

= Σ

i j

where a

i j

are the elements of A. For simplicity of

this presentation, we will assume that the probability

of transitioning from a node its neighbors is the same

Investing Data with Untrusted Parties using HE

849

Figure 3: The proposed framework for graph network anal-

ysis on encrypted data. The listed graph operations will

be implemented to support the data cooperative graph al-

gorithms. We plan to contribute the corresponding libraries

to the software projects such as PALISADE. The blue ar-

row highlights the operations underlying the clustering al-

gorithm.

for each neighbor. In the label propagation algorithm,

given an adjacency matrix and labels for the labeled

nodes-which we will represent using the matrix Y

we will compute a vector of labels for the unlabeled

nodes. Again, for simplicity, we will assume that the

following two steps will be done by the data enabler

as preprocessing:

1. Compute the transition probability matrix T =

−1

A. As a result of this computation, this matrix will

have the following form: T =



I 0



, where I is the

identity matrix, and T

and T

are the submatrices of

the probability transition matrix, which are responsi-

ble for probability to get from unlabeled nodes to un-

labeled nodes, and that to get from unlabeled nodes to

labeled nodes, respectively.

2. Compute the matrix T

= (I − T

)

−1

· T

which represented the ﬁxed-point solution.

For simplicity, we assume that the data enabler

will send to the cloud a homomorphic encryption of

(denoted by Enc(T

)) instead of encryption of the

adjacency matrix A. Implementation of the above

computation steps over an encrypted adjacency ma-

trix is left as a future work. Now, as evidenced in

(Zhu et al., 2003; Mallawaarachchi, 2020), computa-

tion of the label propagation reduces to (i) a matrix

multiplication of T by the label matrix Y

, and then

(ii) computations of the maximums over the rows of

the resulting matrix. Let n be the number of unlabeled

nodes, and let Y

denote their label vector (which is to

be computed).

5 EXPERIMENTS

We successfully implemented breadth-ﬁrst search,

degree centrality, farness centrality (the reciprocal of

closeness centrality), and page rank on HE graphs

with greater than 99.999% accuracy for all algorithms

when compared to a cleartext calculation. Most of

these results are not optimized and are preliminary in

nature. Heuristically choosing optimized conﬁgura-

tions for the HE schemes that encrypt graphs is part

of our active research. These results prove that it is

possible to run well-established graph operations on

HE graphs with high accuracy.

Algorithm Sketch 1: HE Degree Centrality.

(1 and 2 may be done ofﬂine)

Input: G, an adjacency matrix.

Output: v

1. Trusted machine selects prime modulus, p, such

that p > V (G), and initializes BFVrns scheme.

2. Trusted machine encrypts G, into column-packed

ciphertexts, forming cG, which is stored for later use.

3. When degree centrality is invoked, cloud ma-

chine(s) sum all columns of cG, return cipher vector,

cv, to trusted machine.

4. Trusted machine decrypts cv into v and returns v to

client.

Degree centrality is the fastest of all algorithms

currently as it utilizes packed ciphertexts (each col-

umn of G is encrypted into a single ciphertext), which

allows for vectorization to improve performance. No-

tably, degree calculation is faster than encryption

now: calculation was optimized, encryption is not yet

optimized.

Figure 4: Degree centrality calculation is near-linear time

due to packed ciphertexts.

Among other algorithms, we implemented a pre-

liminary binary BFS (binBFS). Unlike degree cen-

trality, which uses somewhat-homomorphic encryp-

tion (SHE), this algorithm uses fully-homomorphic

encryption (FHE). As a result, this algorithm is slower

but can be called any number of times. The core

SECRYPT 2021 - 18th International Conference on Security and Cryptography

850

of binBFS is a naive binary matrix multiply. This

algorithm repeatedly calls b = B

b, where B

BinFHE(G). This work is preliminary and has not

been optimized.

Figure 5: A single ring of expansion on a breadth-ﬁrst

search requires O(n

) time as a result of the current naive

binary matrix-vector multiply.

Farness centrality is another fast algorithm due to

packed ciphertexts. The calculation of the ciphertext

distance matrix, D

, is currently not optimized and

very slow. However, calculating D

can be started

once G

is received and is not applicable to trans-

formation matrices (discussed later).

Figure 6: Unlike the calculation of the distance matrix, the

time to calculate farness centrality is approximately O(n).

6 RELATED WORK

Our work is on HE operations for graphs with the op-

tion for use on any generic distributed system with-

out compromising data privacy. This work runs

parallel to similar efforts for data analysis such as

machine learning over homomorphically encrypted

data and MIT’s Enigma, which offers data integrity

over a distributed system. These analysis could be

completed on untrusted distributed systems, such as

MIT Enigma(Zyskind et al., 2015), without compro-

mising data privacy. In addition to inter-personal

graph constructs, personal data can be assembled into

attribute vectors, encrypted, and used for machine

learning(Aslett et al., 2015), which, in turn can be

part of a federated learning technique. Even when

these other schemes are used, our approach offers the

ability to reﬁne training datasets based on graph oper-

ations, thus offering more accurate training for neural

networks.

7 CONCLUSION

In this paper, we discussed problems that arise from

“big data” and acknowledge the partial solution that

data cooperatives provide. Next, we introduced a high

level architecture for data cooperatives/unions that

use anonymization and/or encryption to secure par-

ticipants’ data. We believe this new architecture we

are developing will serve to complete the data coop-

erative model by adding privacy-protecting measures.

We outlined our approach to anonymization: edge

swapping for vertices with lower cores and adding

nodes/edges to preserve k-(core, property) at higher

cores. Although our anonymization is in active devel-

opment, we have no results to share at this time.

We used homomorphic encryption to ensure pri-

vacy where anonymization may degrade the accuracy

of some metrics or where anonymization alone may

not be sufﬁcient to preserve the privacy of partici-

pants. Finally, we present results from our experi-

ments showing the time complexity of several com-

mon graph operations on HE graphs: degree central-

ity, BFS, and farness centrality. These results show

that use of homomorphic encryption is feasible for

preserving privacy in data cooperatives.

The major limitation of our current work is that

there is no efﬁcient way to transform a ciphertext of

one encryption scheme (HEAAN, BFV, etc.) into a

ciphertext of a different encryption scheme other than

decryption and re-encryption. While this is not a

problem now, it will signiﬁcantly impact our future

work.

8 FUTURE WORK

While we have previously applied graph operations

over HE graphs to locate super-spreaders, all of the

graphs used were contact graphs. That is, each graph

mapped vertices of a given type to vertices of that

same type: people to people or location to location.

Bridging different graphs would involve the use of

transformation matrices (composed of attribute vec-

tors) to map one graph’s vertex set to another graph’s

vertex set. This is how we would accomplish linking

graphs that contain different types of data. Consider

the following example:

Investing Data with Untrusted Parties using HE

851

Let E be a transformation matrix mapping peo-

ple (columns) to their current employers (rows). This

matrix contains personal information and needs to be

encrypted.

Let R be a graph of road segments in a city with

outbound edges to every road segment that can be

reached from a given road segment. This graph is

public data and does not need to be encrypted.

Let T be the transformation matrix that maps peo-

ple (columns) to the segments of road they use com-

muting to and from work. This information is per-

sonal and also needs to be encrypted.

Given a ciphertext vector of people, p, which can

be obtained by selecting an employer in vector e

(single-member set), and performing p = E

, we

can calculate r, the degree to which their commutes

are centered on each segment of roadway r = T p.

Likewise, an alternative query might be to take a road

segment that is excessively congested during rush

hour, and perform p = BinMult(T

, r), which would

result in p, the people who use that segment of road

during their commute. From there, p could be multi-

plied by E to get e

, the degree centrality of each em-

ployer relative to that congested road segment. With

this result, a city could ask the most central employers

in e to stagger the start of their business day, reducing

pollution caused by commuters sitting in trafﬁc and

the strain on the city’s infrastructure.

With the mix of graphs and transformation matri-

ces, a large number of meaningful aggregates can be

composed through matrix operations. These transfor-

mation matrices have the added bonus of being mean-

ingful attribute vectors. This means they can poten-

tially be used to effectively train machine learning al-

gorithms beyond their use in computing.

If we are to standardize these HE graph operations

for analysis, there must be a well-deﬁned algebra for

transforming one type of graph data into another. We

are working on adapting our HE graph algorithms to

optimize for a hybrid approach where some data is

public (plaintext) and other data, personal informa-

tion, is encrypted. Our goal is to reduce all meaning-

ful metrics to matrix operations.

ACKNOWLEDGMENTS

The authors would like to thank Noelle Mansilla for

her help in organizing this paper.

REFERENCES

World Economic Forum, (2011, January). “Personal

Data: The Emergence of a New Asset Class.” [On-

line]. Available: http://www3.weforum.org/docs/

WEF ITTC PersonalDataNewAsset Report 2011.

pdf

D. Walsh, “How Credit Unions Could Help People

Make the Most of Personal Data.” 2019. [Online].

Available: https://mitsloan.mit.edu/ideas-made-to-

matter/how-credit-unions-could-help-people-make-

most-personal-data

J. Geuns and A. Brandusescu, “Shifting Power

Through Data Governance.” [Online]. Available:

https://foundation.mozilla.org/en/data-futures-

lab/data-for-empowerment/shifting-power-through-

data-governance/

K. Ligett and K. Nissim, “Changes in Data Ownership

and Usage.” [Online]. Available: https://simons.

berkeley.edu/sites/default/ﬁles/docs/11268/dataco-

opspresentationlongjanuary2019pptx.pdf

M. Dockendorf, R. Dantu, K. Morozov, and S. Bhowmick,

“Locating Super-Spreaders with Homomorphically

Encrypted Graphs,” 2021.

J. Golbeck and J.L. Klavans, “Introduction to Social Media

Investigation,” Waltham, MA: Syngress, 2015.

K. Liu and E. Terzi, “Towards identity anonymization on

graphs,” in Proceedings of the 2008 ACM SIGMOD

International Conference on Management of Data.

ACM, 2008.

P. Meyer, H. Siy, and S. Bhowmick, “Identifying Impor-

tant Classes Of Large Software Systems Through K-

Core Decomposition,” Advances in Complex Systems

(ACS), vol. 17, 2014.

R. Laishram, A. E. Sariy¨uce, T. Eliassi-Rad, A. Pinar,

and S. Soundarajan, “Measuring and improving the

core resilience of networks,” in Proc. of WWW 2018,

2018, pp. 609–618.

S. Sarkar, S. Bhowmick, and A. Mukherjee, “On rich

clubs of path-based centralities in networks,” in

Proceedings of the 27th ACM International Con-

ference on Information and Knowledge Manage-

ment, ser. CIKM ’18. New York, NY, USA: ACM,

2018, pp. 567–576. [Online]. https://dl.acm.org/doi/

10.1145/3269206.3271763.

V. Uﬁmtsev, S. Sarkar, A. Mukherjee, and S. Bhowmick,

“Understanding stability of noisy networks through

centrality measures and local connections,” CIKM

2016, 2016. [Online]. Available: arXiv:1609.05402

J. H. Cheon, K. Han, A. Kim, M. Kim, and Y. Song, “Boot-

strapping for approximate homomorphic encryption,”

in EUROCRYPT 2018, ser. LNCS, vol. 10820, 2018,

pp. 360–384.

A. Narayanan and V. Shmatikov, “De-anonymizing social

networks,” in 2009 30th IEEE Symposium on Security

and Privacy, 2009, pp. 173–187.

H. Chen, I. Iliashenko and K. Laine, “When HEAAN meets

FV: a new somewhat homomorphic encryption with

reduced memory overhead,” IACR ePrint Arch., vol.

2020/121, 2020.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

852

R. Assam, M. Hassani, M. Brysch, and T. Seidl, “(k, d)-core

anonymity: Structural anonymization of massive net-

works,” in Proceedings of the 26th International Con-

ference on Scientiﬁc and Statistical Database Manage-

ment, ser. SSDBM 2014.

J. Cheng, A. W. Fu, and J. Liu, “K-isomorphism: Privacy

preserving network publication against structural at-

tacks,” 2010.

J. H. Cheon, A. Kim, M. Kim, and Y. S. Song, “Homomor-

phic encryption for arithmetic of approximate num-

bers,” in ASIACRYPT 2017, ser. LNCS, vol. 10624,

2017, pp. 409–437.

A. Bulu¸c, J. T. Fineman, M. Frigo, J. R. Gilbert, and

C. E. Leiserson, “Parallel sparse matrixvector and

matrix-transpose-vector multiplication using com-

pressed sparse blocks,” in Proc. SPAA 2009. ACM,

2009, pp. 233–244.

X. Jiang, M. Kim, K. E. Lauter, and Y. Song, “Secure out-

sourced matrix computation and application to neural

networks,” in Proc. ACM CCS 2018. ACM, 2018, pp.

1209–1222.

X. Zhu and Z. Ghahramani, “Learning from labeled

and unlabeled data with label propagation,” 2003.

[Online]. Available: http://mlg.eng.cam.ac.uk/zoubin/

papers/CMU-CALD-02-107.pdf

V. Mallawaarachchi, “Label propagation demystiﬁed.”

2020. [Online]. Available: https://towardsdatascience.

com/label-propagation-demystiﬁed-cd5390f27472

L. Zhukov, “Structural analysis and visualization of

networks course, hse.” 2015. [Online]. Available:

http://www.leonidzhukov.net/hse/2015/networks/

lectures/lecture17.pdf

S. B. Seidman, “Network structure and minimum degree,”

Social networks, vol. 5, no. 3, pp.269–287, 1983.

P. Holme, “Core-periphery organization of complex net-

works,” Physical Review E, vol. 72, no. 4, p. 046111,

2005.

M. P. Rombach, M. A. Porter, J. H. Fowler, and P. J. Mucha,

“Core-periphery structure in networks,” SIAM Jour-

nal on Applied mathematics, vol. 74, no. 1, pp.

167–190, 2014.

V. Batagelj and M. Zaversnik, “An o(m) algorithm

for cores decomposition of networks,” CoRR, vol.

cs.DS/0310049, 2003.

J. Cheng, Y. Ke, S. Chu, and M. T. Ozsu, “Efﬁcient core

decomposition in massive networks,” in Proc. IEEE

ICDE 2011. IEEE, 2011, pp. 51–62.

W. Khaouid, M. Barsky, V. Srinivasan, and A. Thomo, “K-

core decomposition of large networks on a single pc,”

Proceedings of the VLDB Endowment, vol. 9, no. 1,

pp. 13–23, 2015.

A. Sala, X. Zhao, C. Wilson, H. Zheng, and B. Y. Zhao,

“Sharing graphs using differentially private graph

models,” 2011.

S. Ji, P. Mittal, and R. Beyah, “Graph data anonymization,

de-anonymization attacks, and de-anonymizability

quantiﬁcation: A survey,” IEEE Communications Sur-

veys Tutorials, 2017.

S. Ji, W. Li, P. Mittal, X. Hu, and R. Beyah, “Secgraph: A

uniform and open-source evaluation system for graph

data anonymization and de-anonymization.” USENIX

Association, 2015.

M. Chase and S. Kamara, “Structured encryption and con-

trolled disclosure,” in Proc. ASIACRYPT 2010, ser.

LNCS, vol. 6477. Springer, 2010, pp. 577–594.

X. Meng, S. Kamara, K. Nissim, and G. Kollios, “GRECS:

graph encryption for approximate shortest distance

queries,” in Proc. 22nd ACM CCS Conference. ACM,

2015, pp. 504–517.

Q. Wang, K. Ren, M. Du, Q. Li, and A. Mohaisen, “Secgdb:

Graph encryption for exact shortest distance queries

with efﬁcient updates,” in Financial Cryptography and

Data Security - 21st International Conference, FC

2017, ser. LNCS, vol. 10322. Springer, 2017, pp.

79–97.

C. Zhang, L. Zhu, C. Xu, K. Sharif, C. Zhang, and X. Liu,

“Pgas: Privacy-preserving graph encryption for accu-

rate constrained shortest distance queries,” Informa-

tion Sciences, vol. 506, pp. 325 – 345, 2020

S. Halevi, “Homomorphic encryption,” in Tutorials on the

Foundations of Cryptography. Springer International

Publishing, 2017, pp. 219–276.

G. Zyskind, O. Nathan, A. Pentland, “Enigma: Decen-

tralized Computation Platform with Guaranteed Pri-

vacy,” 2015, [Online] Available: https://www.enigma.

co/enigma full.pdf.

L. Aslett, P. Esperanca, C. Holmes “A review of homomor-

phic encryption and software tools for encrypted sta-

tistical machine learning,” 2015. [Online] Available:

https://arxiv.org/pdf/1508.06574.pdf.

M. Newman, “Networks: An Introduction,” USA: Oxford

University Press, 2010.

A. L

opez-Alt, E. Tromer, V. Vaikuntanathan. On-the-ﬂy

multiparty computation on the cloud via multikey

fully homomorphic encryption. In Proceedings of the

44thannual ACM symposium on Theory of comput-

ing, pages 1219–1234. ACM, 2012.

A. Salau, R. Dantu, and K. Upadhyay ”Mining and Chain-

ing Fakeness, ” 8th Annual Hot Topics in the Science

of Security, Virtual Conference, Hosted by National

Security Agency, April 13-15, 2021.

A. Salau, R. Dantu, “Data Cooperatives for Neighbor-

hood Watch,” IEEE International Conference on

Blockchain and Cryptocurrency, Pages 1-8, Virtual

Conference, May 3-6, 2021

Investing Data with Untrusted Parties using HE

853