
Data Sharing and Assimilation in Multi-robot Systems for
Environment Mapping
Abdul Wahab Ziaullah Yousaf and Gianni A. Di Caro
a
Carnegie Mellon University in Qatar, Doha, Qatar
Keywords:
Multi-robot Mapping, Optimized Data Sharing, Data Assimilation, Distributed Gaussian Processes.
Abstract:
We consider scenarios where a mobile multi-robot system is used for mapping a spatial field. Gaussian pro-
cesses are a widely employed regression model for this type of tasks. For the sake of generality, scalability, and
robustness, we assume that planning and control are fully distributed and that robots can only communicate
via range-limited channels. In such scenarios, one core challenge is how to let the robots efficiently coordinate
in order to maintain a shared view of the mapping process, and, accordingly, make plans minimizing over-
laps and optimizing joint information gain from obtained measurements. A simple approach of sharing and
utilizing all the sampled data would not scale to large teams, neither for computation nor for communication
(assuming a general ad hoc robot network). Building on previous work where robots adaptively plan where
to sample data by selecting convex containment regions, we propose a data sharing and assimilation strategy
which aims to minimize the impact on communication and computation while minimizing the loss on accuracy
in map estimation. The strategy exploits convexity of the regions to create compact meta-data that are locally
shared. Submodularity of information processes and properties of GPs are used by the robots to create highly
informative summaries of the sampled regions, that are shared on-demand based on the meta-data. In turn, a
received summary is assimilated by a robot into its local GP only if/when needed. We perform a number of
studies in simulation using real data from bathymetric maps to show the efficacy of the strategy for supporting
scalability of computations and communications while guaranteeing learning accurate maps.
1 INTRODUCTION
The availability of spatial maps describing the state
of an environment with respect to values of interest
is essential for the timely modeling monitoring of its
physical, chemical, and biological properties. For in-
stance, in aquatic environments
1
there’s a clear inter-
est in having accurate maps describing values such
as depth, salinity, pH, pollution, temperature, pres-
ence of flora and fauna, etc. Typically, these quanti-
ties of interest have a continuous distribution over the
spatial field, which can extend over several kilome-
ters. Given the extension of the regions of interest, the
use of autonomous mobile robots, and in particular of
mobile multi-robot systems (MRSs), is strongly en-
visaged to effectively tackle the tasks of exploring an
a
https://orcid.org/0000-0002-2125-0557
1
In this work we are precisely motivated by perform-
ing automatic monitoring and surveying in marine environ-
ments. Therefore, we mostly refer to this type of scenarios.
However the methods presented in the rest of the paper are
general and are not restricted to mapping tasks in aquatic
environments.
environment and/or constructing data maps (Stach-
niss, 2009). In a given time budget, a well-designed
MRS can perform measures in multiple sites in par-
allel, potentially providing a large speed-up in map
construction and boosting map accuracy. In this work,
we precisely start from the use of MRSs for environ-
ment mapping missions: in a limited time budget, an
accurate map of the given region and attributes of in-
terest must be constructed by exploiting robot mobil-
ity and robots sensors providing localized measures
(i.e., the range of the sensor is very narrow, funda-
mentally point-like, which is typical, for instance, for
measuring things such as salinity, pH, concentration
of chemicals). Moreover, for the sake of generality,
we assume the use of an ad hoc network for robot
communications.
In such scenarios, measures of interest are de-
fined over a continuous field, while robots can only
take samples at discrete points, asking for building
regression models. Moreover, accounting for sensor
noise and errors, as well as for the limited time bud-
get available to cover a vast region, the number of
514
Yousaf, A. and A. Di Caro, G.
Data Sharing and Assimilation in Multi-Robot Systems for Environment Mapping.
DOI: 10.5220/0010607505140522
In Proceedings of the 18th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2021), pages 514-522
ISBN: 978-989-758-522-7
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

sampling points is necessarily limited. Therefore, a
main challenge is to plan in the MRS where to sample
and how to combine the discrete and noisy measures
into a regression model providing a reliable, contin-
uous map estimator at the end of mission. Planning
is expected to be adaptive, to account for incremen-
tally gathered evidence measures. Moreover, local-
ized sensors and submodular properties of informa-
tion environments (Krause and Guestrin, 2011) par-
tially rule out the use of approaches of intelligent
partitioning of the environment (e.g., (Cortes et al.,
2004)), asking, in general, for complex and dynamic
schemes for planning.
In the described scenario, robots need to coordi-
nate to issue plans that can jointly perform an op-
timized sampling process. Ruling out, for the sake
of generality and scalability, the use of a centralized
controller, the realization of an optimized and dis-
tributed scheme requires exchanging sampled data in
order to maintain a shared map and plan accordingly
(e.g., to direct sampling to unexplored regions, or to
those regions where estimation uncertainty is higher,
or, equivalently, where predicted information gain is
higher (Ma et al., 2018)). What data to share and how
to use (i.e., assimilate) the shared data in a distributed
MRS for planning purposes is the main focus of this
work: we will introduce a novel strategy for the selec-
tion of data to share and for data assimilation in dis-
tributed MRSs. Note that data sharing and assimila-
tion must ensure scalability of communications (i.e.,
make a parsimonious use of available bandwidth) and
of on-board computations (i.e., allow near real-time
computations), while guaranteeing high accuracy in
final map estimation. In general, use and control of
data sharing is a central issue in MRSs, being involved
in virtually any task of interest (e.g. (Roumeliotis and
Bekey, 2002; Jager and Nebel, 2001)).
Since the importance of each piece of data that
can be shared depends in turn on how data is used
to build a regression model, we consider here Gaus-
sian Processes (GPs) (Rasmussen, 2003) as the ref-
erence model to learn the target mapping. This is
a specific yet general choice since GPs are widely
employed in the relevant robotics literature for envi-
ronmental data mapping (Ma et al., 2018; Li et al.,
2020; Popovi
´
c et al., 2020; Ghassemi and Chowd-
hury, 2019). While providing a number of advantages
(e.g., in terms of capturing the statistical properties
of spatial correlations), a main drawback when us-
ing GPs is related to the O(n
3
) complexity for each
model updating, with n being the size of the available
data measures. This makes it computationally expen-
sive to run in real-time on embedded platforms such
as mobile robots, as the data size grows. Moreover,
being non-parametric models, GPs put a major bur-
den on data sharing, given that the model cannot be
necessarily compacted in a few parameters.
In this work, using GPs as a target model, we pro-
vide a strategy to perform an intelligent selection and
assimilation of the sharing data in an MRS. The goal
is to limit the exposure of communicated and pro-
cessed information for the sake of scalability, while
still allowing the robots to effectively plan their sam-
pling actions. In order to frame the data sharing and
assimilation strategy in a concrete scheme for GP-
based planning, we build on our previous work (Di
Caro and Yousaf, 2021b), where robots adaptively
and iteratively identify convex containment regions
where to sample at selected locations.
The proposed strategy makes the robots exploit-
ing the convexity of the regions to create compact
meta-data descriptions, that are locally shared con-
suming little bandwidth. Submodularity in contigu-
ous regions and statistical properties of GPs are ex-
ploited to let each robot independently create com-
pact and informative data summaries of sampled re-
gions, that are shared with other robots on-demand
based on meta-data and estimated utility. In turn, a
received data summary is assimilated by a robot into
its local GP only if/when needed. Overall, the use of
compact descriptions and data summaries, as well as
the use of opportunistic communications and compu-
tations fully support scalability of the processes and
ensure a minimal, strategically tunable, loss in final
map accuracy. We show these properties through a
number of simulation studies.
2 RELATED WORK
A central aim of our work is to define a strategy to
let the robots select and share a ’minimal enough’
amount of information, in the form of GP data, to en-
able informed and coordinated planning in the MRS
while ensuring scalability. In the following we review
a few works that similarly aim to mitigate the burden
of data either in single robot or multi-robot systems.
(Ma et al., 2018) utilizes the concept of Sparse
Online Gaussian Process (SOGP), to limit the size
of the training data for GP. Their approach is well
suited for single robotic exploration case where each
data point is tested online to determine if GP could
still be modelled with existing data point i.e. without
increasing the size of variance-covariance matrix but
with re-normalized kernel parameters induced by new
data point. This is a cheaper alternative as it limits the
growth of GP, it is however not suited in the case of
multi-robots as there is no notion of ’localized sum-
Data Sharing and Assimilation in Multi-Robot Systems for Environment Mapping
515

maries’ that enable other robots to form decisions to
either consider the batch of data or reject it based on
their current budgets and location of the summaries.
In (Choudhury et al., 2002) the burden of data is
mitigated by forming multiple clusters to model mul-
tiple GP’s. Different sets of hyperparameters are used
to model the compactly supported covariance struc-
tures of different clusters. The clustering mechanism
is based on maximizing the log likelihood for each
cluster, and using a predetermined partitioning of size
m. Although the approach is well suited for address-
ing data’s computational load, the data size still re-
mains constant within each cluster, and the cluster-
ing process is done after the data collection process,
hence not suitable for online exploration.
(Chen et al., 2013) defines the pPIC algorithm
where each machine (e.g., individual robot) compute
a local summary and provide it to master, while mas-
ter computes the global summary and distribute over
the machines. The machine makes use of local data,
local summary and global summary to produce pre-
dictions over unobserved locations. They test their
algorithm for computation, time and communication
complexity (Ghassemi and Chowdhury, 2019) pro-
vides a method of decentralized data sharing where
observations of individual robot is downsampled to
fixed 400 observation if the size of data grows more
then 400 observations by each robot. Although this
can be assumed as naive approach, the exact down-
sampling technique isn’t clear.
The approaches mentioned above aim to either de-
centralize the GP such that it that can be distributed
and run over several machines in parallel or down-
sample the data to mitigate the burden of GP com-
putation, or both. Our aim is different, as we seek
to summarize data not specifically for highly accurate
predictions, but only to sufficiently produce accurate
predictions that can enable robots to plan to sample
in informative regions: summaries are only accurate
enough to ”mimic” similar behavior among the robots
as if all the data would be shared among them.
3 REGION-BASED PLANNING
As mentioned in the Introduction, we build on our
previous work (Di Caro and Yousaf, 2021b) where we
have introduced an adaptive sampling approach for
environmental mapping tasks using MRSs and GPs.
The methodology is based on an iterated multi-stage
process: (i) each robot, or group of robots, uses Monte
Carlo to perform Bayesian inference on the currently
estimated GP model with the goal of identifying the
best region where to sample new data in the next time
slice, where best here means the region maximizing
the expected information gain for GP learning; (ii) in-
side the region, Bayesian optimization is employed to
select a set of candidate locations where to go sam-
pling; (iii) an orienteering model is used to select a
subset of the locations such that the overall expected
utility is maximized and a path that satisfies given
time constraints is computed through them; (iv) each
robot then follows the computed plan: it goes to its se-
lected region and performs sampling over the selected
path. Process (i-iv) is iterated and fully distributed.
For computational reasons, as well as to support
safe and reliable robot navigation, the sampling re-
gions are chosen to be convex, elliptical more pre-
cisely (in 2D). Note that an ellipse can effectively
stretch along any desired orientation and width and
is compactly represented by a vector of only 5 param-
eters, c = (c
x
,c
y
,a
l
,a
w
,θ), defining respectively the
coordinate of the center, lengths of major and minor
axes, and rotation angle in a given reference frame. In
the following, describing our strategy for data sharing
and assimilation, we refer to sampled regions as clus-
ters (of sampled locations), to convey the fact that we
are not necessarily bounded to use elliptical regions:
our strategy can be applied to any planning scheme
producing a ’cluster’ of points, as long as it can be
compactly described by a vector of parameters such
as c defining a convenient embedding region.
In the process described above, robots can adopt
different schemes of local communication in the ad
hoc robot network, ranging from no communication,
to full, sustained communication (an ideal configura-
tion). This implements a full spectrum of coordina-
tion for maintaining a shared data map and letting the
individual robots planning being mutually aware of
others’ plans and status of the map learning process.
Hereafter, the two extreme cases are referred to as No
Data Sharing (NDS) and Full Data Sharing (FDS).
While data sharing might be essential to achieve a
coordinate and optimized planning in the distributed
MRS, this comes with a cost, both in terms of com-
munications and computations, that could negatively
impact scalability of performance. We therefore seek
for a good balance, that can let the robots share only
the truly useful data, to ensure scalability while only
minimally affecting final map accuracy.
4 DATA SHARING AND
ASSIMILATION
Our approach for data sharing and assimilating is
hinged to the submodularity property of informa-
tion gathering processes (Krause and Guestrin, 2011),
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
516

which is addressed by tracking the expected changes
in the GP model with the addition or deletion of
measurement points. The intuitive understanding of
submodularity is that if we obtain more measure-
ments in the region where there is already significant
data recorded, any additional measurements will only
marginally increase our information of the location
and will not ’influence’ our environment model sig-
nificantly. Leveraging submodularity, we can filter
the data inside the region (cluster) by forming a sum-
mary. The objective of the summary is to subsample
the data already sampled in the region, by selecting a
subset of data which is much smaller than the origi-
nal set but informative enough to minimize informa-
tion loss with respect to the GP. This subset makes
a cluster summary which can used for data sharing.
Note that, by exploiting the the fact that a cluster’s
embedding region is represented by a vector of pa-
rameters such as c for the case of ellipses, both the
data summary and coordinates and geometric descrip-
tion of the cluster (which we call its meta-data), are
expressed in compact forms suitable to be effectively
shared in the ad hoc network.
Moreover, in our strategy, we account for robots’
time budget for traveling, such that a robot, on-
demand, only requests and assimilates (i.e., data sum-
maries) that are expected to be used and that can carry
a relevant information gain for its GP. E.g., data sum-
maries of regions that are far away and beyond the
current traveling budget will not be considered.
4.1 Summaries of Cluster Data
As mentioned before, we consider the scenario where
robots sample in 2D elliptical regions that define a
data cluster. Based on the described iterative adap-
tive planning process, at a time t, a robot can have
sampled in m ≥ 1 different cluster regions, with the
measured data for locations and values being assimi-
lated in robot’s GP and stored in internal data struc-
tures, where the k-th cluster is represented by its pa-
rameters c
k
= (c
x
,c
y
,a
l
,a
w
,θ), which make the meta-
data of the cluster. At the same time, in the inter-
nal data structures, these parameters uniquely identify
the set of data points inside the cluster: c
k
→ D
k
=
[x
1
,y
1
],..,[x
i
,y
i
], where the location of a specific data
point is given by a position vector x and its value y is
the measured attribute of interest to map.
In a GP, a data point contributes to its ’local’
outcome and extends its influence to its local neigh-
bourhood based upon optimized GP’s kernel hyper-
parameters. Based on this, here we define the no-
tion of influence points: subset s of points of the full
data set in the cluster, s ⊂ D, whose presence inside
GP’s structure affects GP’s prediction outcomes the
most. Influence points form the cluster summary. A
data point that is not an influence point can be re-
moved, such that other data points assimilated inside
the GP could accurately predict the outcome value of
the removed data point by predicting its correspond-
ing mean value conditioned on the summary.
We can assess the quality of a summary set s by
measuring the prediction error that it induces on data
points x
k
that are not part of the summary set com-
pared to the prediction that the full GP would give:
error(x
k
|s) = GP(µ
x
k
|s) − y
k
(1)
Here the error is computed as the difference between
GP’s prediction outcome GP (µ
x
k
|s) for point x
k
con-
ditioned on the summary set s, and the value y
k
, which
is the prediction from the the GP including all the data
from the cluster, not only the the summary set. In the
notation GP(µ
x
k
|s), µ
x
k
indicates the mean value of
GP’s prediction at the location of that data point x
k
.
Computing the prediction error in this way, we
are making the naive assumption that to predict the
output value at certain location inside the cluster we
don’t need the GP being conditioned on data outside
the cluster, hence, the summary is localized to a single
cluster. This naive assumption forms the basis for our
summarization process and the result of which will be
tested in our computation experiments.
For each sampled cluster c
j
comprising of a set D
j
of n
j
data points, in order to define the best subset of
influence points (i.e., the summary), a robot needs to
select the subset s
j
⊂ D
j
that can provide a minimal
expected error over all points in the cluster. At this
aim, we define a combinatorial optimization problem
to find the subset s
j
⊂ D
j
such that if the GP is purely
conditioned on s
j
, its cumulative prediction error for
all the data points in the cluster is minimized (indeed,
only the points in the set D
j
\ s
j
give a contribution):
min
s
j
∈P (D
j
)
n
j
∑
k=1
y
k
− GP(µ
x
k
|s
j
)
w
2
j
(2)
where P (D
j
) is the power set of the data points D
j
inside the cluster c
j
and w
j
is equal to the cardinal-
ity of the subset s
j
. The role of w
j
is to avoid that the
whole set D
j
is selected, and, more in general, balanc-
ing prediction accuracy and size of the summary set,
acting as a penalty for large sets. It should be noticed
that the minimization problem (2) is not limited to re-
gression algorithms such as GP, but it can be utilized
to form summaries using any regression algorithm.
The optimization problem is NP-hard, hence we
tackle it with a custom heuristic to ease its solution in
online scenarios. We form adjacency matrix using the
euclidean distance between the data points. For each
Data Sharing and Assimilation in Multi-Robot Systems for Environment Mapping
517

data point in the adjacency matrix we compute its av-
erage distance to all the other data points as well as
determine its closest neighbour. We then compare its
closest neighbour to check if both the data points are
a mutually closest pair, i.e no other points are closest
to either of the pair. If this condition is satisfied, we
select the point from the pair that has greater average
distance to all the other data points. The rationale is
that spatially distant points are more informative com-
pared to neighbouring data points, due to their rela-
tively high uncertainty. The process is repeated until
all pairs are accounted for and an initial summary is
formed by the points that are selected.
We then form a GP based on this summary and test
if the prediction of the GP is accurate enough by ran-
domly comparing GP’s prediction on the un-selected
data points output value. More specifically, the k-th
data point is added to the summary and assimilated
into the GP if the following condition on the relative
prediction error is satisfied:
|GP (µ
x
k
|s
j
k−1
) − y
k
|
|y
k
|
> ε
(3)
where s
j
k−1
is the current summary set (i.e., before
checking the k-th point). ε is a strategically-defined
error bound, that was set to 0.3 in the experiments.
The choice has been motivated by the observation
that the aim of summarizing is to balance accuracy
vs. size, with the goal of preparing a summary set for
sharing that can make a receiving robot sufficiently
informed for efficient future planning. Thus, an error
bound of 30% seemed sufficient for the purpose.
The process of adding data points to the summary
set is terminated when the moving average of the last
m consecutive data points goes below the error bound
ε. In the experiment m was heuristically chosen equal
to 5. The points that the new GP had assimilated after
the termination form the summary of the given cluster.
4.2 Sharing Summary Data
Robots do not locally broadcast their summaries di-
rectly, but broadcast first their way more compact
meta-data. This is to let the nearby robots know about
the regions that are available for summaries. A robot
R hearing a meta-data message of another robot S
checks if the listed regions are already in its memory.
If this is the case, R doesn’t need the summary data
from S, preventing from obtaining duplicate data.
If the meta-data message indicated the presence of
new regions, the data of which is not in R’s memory,
the summary associated with those regions could be
useful for R’s future planning. However, before re-
questing the summaries, R uses the meta-data of each
cluster c
k
available from S to verify that the cluster is
reachable in the future, based on its currently avail-
able discounted travel budget. We discount the robots
current travel budget to account for the fact that the
robot may travel to that region sometime in future. In
practice, if a cluster c
k
is too far, it would be of no use
to get its summary, since R will never go to or traverse
that region during the rest of the mission. Therefore,
only the clusters that are reachable and correspond to
unexplored regions are explicitly requested from S.
Once received, summaries and associated meta-data
are stored in memory, but are not assimilated yet in
R’s GP model, which is explained in the next section.
4.3 Data Assimilation
The assimilation of received data summary into the
local GP is a two fold process. First, the robot de-
termines the next location / region where to sample
based on the inputs given by its local planner. Let
c
next
be the cluster region to visit. Its parameters are
compared with the meta-data of all the clusters stored
in the robot’s memory, that have been received from
other robots. If the distance of any cluster c
k
in mem-
ory falls in some close proximity of c
next
, then the
robot assimilates the summary s
k
associated to cluster
s
k
into its current GP, thereby augmenting its knowl-
edge without actually visiting the locations.
The process then repeats, where the robot identi-
fies the new cluster to visit with the augmented knowl-
edge and compares the parameters of the new region
from the planner, with all the other meta-data of clus-
ters stored in its memory. For the sake of optimiza-
tion, a robot assigns flags to clusters in its memory
whose summary has already been assimilated, and re-
moves them from future computation for assimilation.
This sequential process ensures that size of GP is
kept minimum for fast computation and sufficiently
rich for informed planning and survey. Note that the
described process is general, and not really bounded
to any specific planning strategy.
5 COMPUTATIONAL
EXPERIMENTS
We have empirically validated the proposed approach
for controlled data sharing and assimilation in a se-
ries of simulation experiments conducted in a custom
environment developed in Python. In particular, we
have addressed accuracy in learning the ground-truth
and scalability of performance and computation with
increasing number of robots in the team. We have
compared the proposed strategy with the two ’extreme
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
518

cases’ NDS and FDS mentioned in Section 3 where,
respectively, no data sharing and full data sharing hap-
pen among the robots. The NDS and FDS cases repre-
sent upper and lower bounds in terms of performance
for efficient sampling. In the NDS case each robot
is on its own such that the iterative planning for the
next region where to sample data is only based on lo-
cal G data. In the FDS case, at each instant all robots
have global knowledge of mission status (i.e., of the
estimated GP map) such that individual planning de-
cisions get implicitly coordinated.
In the following, we refer to the data sharing and
assimilation approach proposed in this paper as SDS,
standing for Selective Data Sharing.
We are motivated by surveying marine environ-
ments, so the test scenarios utilize actual bathymetry
maps from the GEBCO database (www.gebco.net).
Robot’s mission is to collectively learn these maps
by forming a global GP at the end of the experi-
ment (i.e., at the end of the mission, all individual
GP maps are merged to create one single, suitably
aggregated map). To ensure that computational ex-
periments are close to realistic physical experiments,
we have considered a time budget of T
max
= 4h for
the mission, with the robots moving at a constant ve-
locity v = 1 m/s (modeled after the LutraProp robot
bots, senseplatypus.com/lutra-prop), and a large area
to map. To equalize the experiments, we scaled all
bathymetry data to match 6000 × 6000 m
2
area and
discretized the data into a grid of 10000 × 10000 pos-
sible sampling points. Robots’ depth sensor returns
the ground-truth value corrupted by a Gaussian noise
equal to 5% of the expected value. Communication
range is set to 90m, after typical ranges in ad hoc wi-fi
networks.
2
To initialize the robot’s GP, a prior sparse
random sampling of the area is conducted on the given
dataset, with a total of 10 data points, (e.g., similar to
(Li et al., 2020; Mishra et al., 2018)).
5.1 Baseline Algorithm, Metrics for
Accuracy and Scalability
As we have pointed out, our goal with the SDS strat-
egy is to strike an effective and efficient balance
between accuracy in map reconstruction and over-
all scalability. Therefore, we need first to have a
baseline for assessing goodness in map reconstruc-
tion accuracy. At this aim, we compare the accu-
racy performance of the three considered approaches,
SDS, FDS, and NDS, against a random-waypoint
(RWP) (Bettstetter et al., 2003) model for robot mo-
bility. In RWP a robot iteratively identify the next
2
Experiments were conducted in Intel(R) Xeon(R)
CPUX5690 @ 3.47GHz hardware with 16GB RAM.
location where to sample according to a random se-
lection of direction and distance for traveling (in the
experiments we have selected angle ranges that make
a robot to have a tendency to move forward, and dis-
tances that are relatively long to attenuate the sub-
modularity effect). In practice, RWP is a random and
uninformed strategy for planning. The use of random
coverage approaches as baseline is common practice
in the literature (Popovi
´
c et al., 2020; Li et al., 2020).
In the experiments, we use the Root Mean Square
Error (RMSE) of GP’s predictions vs. bathymetry
ground truth computed over all the sampling points
in the map. Based on the RMSE, we report the per-
centage of improvement of each approach vs. RWP
according to the following formula:
RMSE (S, Ground Truth)
RMSE (RW P, Ground Truth)
× 100 (4)
where RMSE(S, Ground Truth) is the root mean
square error between the predictions given by the final
GP constructed by algorithm S and the ground truth
values. S is a substitute for SDS, FDS, NDS.
5.2 Performance in Mapping Accuracy
The results from the experiments addressing map ac-
curacy are reported in Table 1 for a team size of = 5
robots. We have considered seven different marine
rectangular areas from different parts of the world,
latitude and longitude coordinates of the corners are
shown. Each area has a different bathymetric profile,
which can be more or less rugged. E.g., in a pro-
file featuring smooth and highly correlated changes,
a fully informed approach such as FDS is expected
to strongly outperform less informed approaches. In-
stead, if the profile is rugged, showing rapid and sud-
den changes, the advantage of FDS might be compar-
atively less. Also in a mostly flat profile with a few
abrupt changes the use of an informed strategy might
not necessarily bring an advantage even over RWP,
since it’s mostly a matter of luck to hit the right spot.
Results show that FDS outperforms NDS as well
as SDS in all the instances, as expected. However, the
relative advantage differs from area to area precisely
based on the discussion above. Unfortunately, as it
will be shown in the next section, there’s a price to
pay for keeping all robots fully informed: FDS isn’t
really scalable. Moreover, in remote locations where
there is not a global communication infrastructure, it
might simply be unfeasible to assume global commu-
nications. The performance of SDS is, rightfully, be-
tween that of FDS and NDS. This shows that the con-
trolled data sharing and assimilation does well its job
by providing a mapping accuracy which is closer to
FSD than NDS indeed, but with a significant saving in
Data Sharing and Assimilation in Multi-Robot Systems for Environment Mapping
519

Table 1: Mapping accuracy of the different approaches on various bathymetry datasets. Reported percentages for FDS, NDS,
SDS are improvements over RWP according to (4).
Dataset lon0 lon1 lat0 lat1 FDS% NDS% SDS%
Oman Coast 58.389 23.66 58.914 24.197 41.56 2.34 28.93
North Pacific Ocean A 168.347 172.856 39.831 43.647 60.49 14.60 39.77
North Pacific Ocean B 145.814 152.731 31.177 35.993 9.67 5.83 12.82
North Pacific Ocean C 165.352 170.806 22.956 26.514 35.43 24.02 29.76
South Pacific Ocean 168.03 173.65 -28.15 -22.63 9.74 14.31 8.38
Philippine Sea 129.681 134.743 17.289 22.218 8.88 1.41 8.67
Genoa 8.306 9.314 43.085 44.022 69.73 64.28 50.32
Average 36.26 18.99 26.81
Standard Deviation 20.93 21.11 15.42
Parameters: n = 5, Time budget = 4hr, Max replanning period = 1h, v = 1 m/s, ε = 0.3.
computation and communications, as it will be shown
in the next section. Moreover, being inherently based
on local, range-limited communications, SDS is al-
ways a feasible approach in real scenarios.
Note that all the approaches systematically per-
form better than the RWP baseline. In SDS, data
shared in opportunistic communications enables little
less than 30% improvement in performance compared
to no communication (RWP and NDS).
Interestingly, f the cases of Genoa, South Pacific
Ocean and Philippines Sea datasets, SDS performed
nearly as good as optimistic FDS approach, without
the burden of computation that the FDS approach suf-
fers from. An interesting observation from the tested
data sets is that the standard deviation of all three
approaches are more or less the same and it is at-
tributed to exactly the same experiment environment
and survey strategy that is provided to test all three
approaches. The standard deviation in the reported
improvements is the result of how survey strategy per-
forms at particular dataset. If the dataset is more or
less flat, then informed strategies generally perform
as good as uninformed strategies and hence, the im-
provement on such datasets is usually lower.
5.3 Scalability of Computations
In order to perform a scalability analysis we study
how computations for local GP updating and commu-
nications for data sharing grow with team sizes for the
different algorithms. In particular, we measure the av-
erage data size which is assimilated into robot’s GPs
at the end of the experiment. The size M of a GP
(in terms of number of used data points) directly im-
pacts on the time for each GP updating, which goes as
O(M
3
). The more the robots engage in data sharing,
the more the GP inside robots grows, and the more
computation time is required for individual updates,
and the more communication bandwidth is used.
In the case of NDS, since there’s no data sharing,
GP’s data size is fairly independent of team size, it
thus serves as a lower bound. Instead, FDS serves as
upper bound, given that robots engage in global com-
munications. We will therefore refer the measures to
the FDS baseline, measuring the improvement (i.e.,
the reduction in size) with respect to FDS.
We consider teams of size 5, 10 and 15 robots, and
for each algorithm we measure: average GP data size
at the end of the experiment; standard deviation of the
data size; % of decrease of data size with respect the
data size in FDS; accuracy loss with respect FDS. Re-
sults are reported in Table 2 and refer to the scenario
North Pacific Ocean A of Table 1.
It can be noted from the results that the average
size of the GP data assimilated by robots in FDS
grows significantly compared to the average sizes in
SDS and NDS, which shows the poor scalability of
the FDS strategy for large team sizes. The average
data size for NDS remains more or less the same, as
expected, while the average data size in SDS seems to
increase only marginally compared to FDS. The rela-
tively large standard deviation of the data size in SDS
is the result to the stochastic nature of whole planning,
sampling, data sharing and assimilation process. On
the account for accuracy, we observe that even though
both SDS and NDS suffer from some accuracy losses,
SDS’ loss in accuracy in SDS is minimal compared to
FDS. Also we can notice a general decreasing trend
in the magnitude of loss with the increase of team
size, both for SDS and NDS. It is plausible that as the
region gets saturated with more robots for mapping,
the effects of full data sharing and utilization for effi-
cient planning of sampling actions tends to diminish.
Overall, these results well support the scalability of
the strategies with reduced or even no data sharing.
Moreover, since the computation time for obtain-
ing a new plan is proportional to the size of the GP
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
520
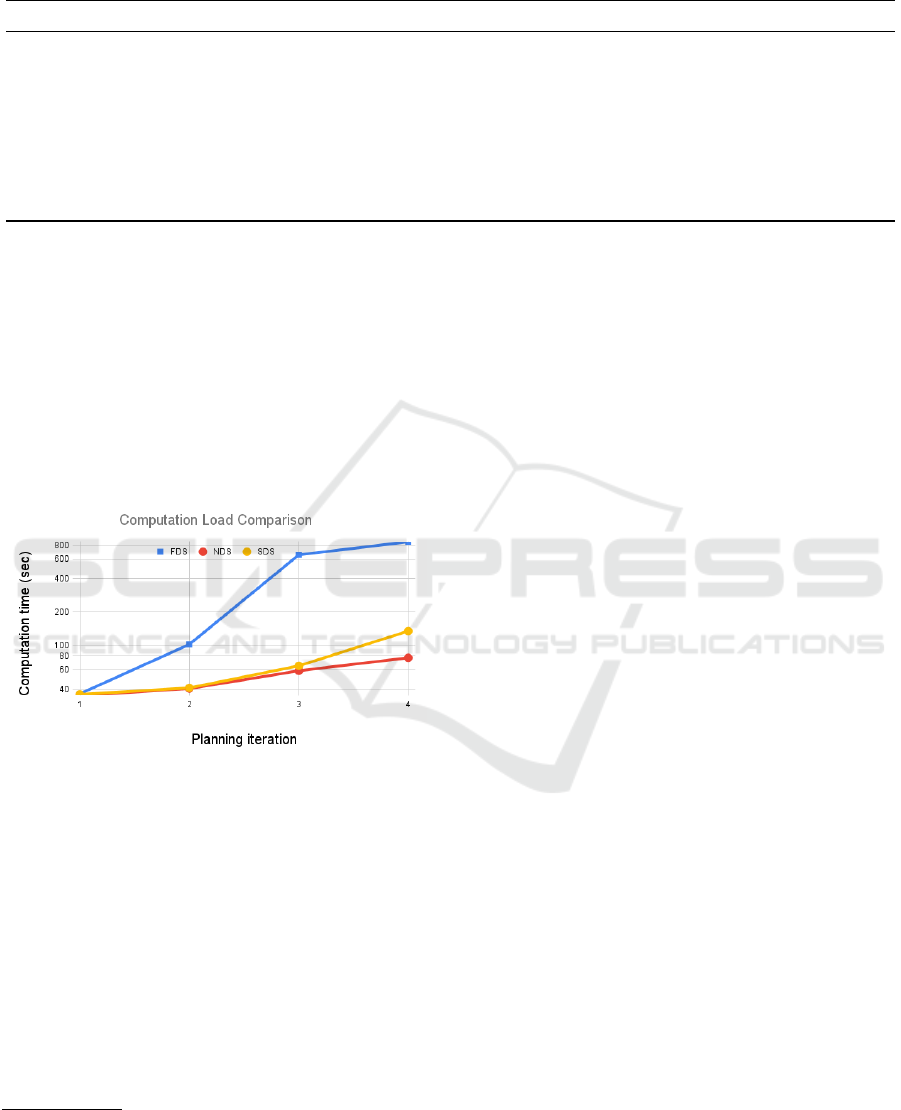
Table 2: Scalability in GP data size and mapping accuracy for various team sizes and data sharing strategies. All percentage
decreases are referred to the baseline FDS strategy. Accordingly, FDS’ percentages are reported.
# Robots Strategy Average GP size Standar dev. % Decrease of avg. GP size % Decrease in accuracy
5 FDS 318.5 - - -
5 NDS 67.4 7.1 79.8 40.0
5 SDS 197.2 10.2 38.1 14.8
10 FDS 870 - - -
10 NDS 90.5 13.9 89.5 26.5
10 SDS 259.8 39.2 70.1 7.1
15 FDS 1021 - - -
15 NDS 90.7 33.4 91.1 10.2
15 SDS 242.1 336.2 76.2 5.4
data
3
, we also analyze how planning computation
time is affected by GP’s data size. This is a central
metric to assess the capability of the robot team to
effectively operate in a real-world scenario. In fact,
if even a single planning operation would consume
a relevant fraction of the available time budget, the
robot team will not really be used to perform exten-
sive data sampling, as needed. In other words, the pre-
vious scalability of GP size needs to be accompanied
by equivalently good scalability results for computing
a plan in order to truly assess strategy scalability.
Figure 1: Computation time for planning over the iterations.
In our model, a new plan is issued at more or less
regular time intervals. Therefore, we study how com-
putation time varies across planning iterations. Note
that since GP’s size grows over time as a result of
sampling actions and data sharing, the planning com-
putation time for a robot is expected to grow accord-
ingly. Results are shown in Figure 1, which refers to
a 10-robot team for North Pacific A scenario of Table
1. Note that the y-axis in in logarithmic scale. We
can observe that the computation times for FDS are
by far the highest and raise up rapidly, showing the
non-scalability of the strategy. SDS and NDS have
similar in performance to in the first three planning it-
3
As described in (Di Caro and Yousaf, 2021b), for com-
puting a plan (i.e., a region and a path where to sample) a
robot makes use of a utility function based on a measure of
expected information gain for GP learning.
erations. This is due to the fact that robots only share
the data if they are in close proximity and only assimi-
late the data if needed in upcoming planning iteration,
so initially SDS behaves similar to NDS as far as plan
computation time is concerned. After the third itera-
tion, SDS shows an increase in computation times, but
still stays well below FDS. The same trend is shown
for larger teams (not shown). However in these cases,
SDS’ times become of order of minutes, such that a
strategic adjustment of parameter ε of Eq. (3) would
be required for efficient online execution.
From the results reported in Figure 1 and Table 1,
we can conclude that in the proposed SDS, the uti-
lization of data summaries, sharing them with other
robots on demand, and assimilating them at the right
time enable significant a retention of the accuracy
compared to the ideal FDS strategy, while keeping
computational load relatively low and therefore sup-
porting the good scalability of the SDS approach.
6 CONCLUSIONS
We have considered scenarios where a mobile and
distributed multi-robot system is used for mapping a
spatial field in a given limited time budget. Building
on our previous work (Di Caro and Yousaf, 2021b; Di
Caro and Yousaf, 2021a) we have focused on the case
where mapping is modeled as a regression task and
tackled using a GP model. Robots collectively learn
the GP by taking measures at discrete locations. In
turn, robots use the GP to iteratively and adaptively
compute plans aimed at identifying the most informa-
tive regions where to go and take measures. While the
use of multiple robots can bring clear benefits, at the
same time a number of challenges arise regarding co-
ordination and joint action planning. Central to these
challenges is the use of communications to share data
and therefore maintain a shared view of the GP map
to let the robots coordinate their planning actions.
In this paper we have precisely addressed the is-
Data Sharing and Assimilation in Multi-Robot Systems for Environment Mapping
521

sue of selectively filtering and compacting the data
that each robot could share, and define efficient strate-
gies to let nearby robots only exchange data that are
expected to be informative for a robot conditioned to
its local GP and available time budget. In addition,
we have defined a strategy for the selective assimila-
tion of the data in a robot’s GP only if and when truly
needed. All these strategies are aimed at endowing a
multi-robot system with data sharing and assimilation
mechanisms that would guarantee effective mapping
accuracy while ensuring overall scalability in compu-
tations and communications.
More specifically, we have described an orches-
trated approach (termed SDS in the text) where robots
form summaries of the regions they sample, orga-
nize the summaries into clusters with meta-data, share
their summaries with nearby robots on-demand, as-
similate the summaries into their local GP at the right
time. We tested the approach in simulation using ac-
tual bathymetry datasets and showed how the pro-
posed summarization, sharing, and assimilation strat-
egy compares against strategies where either all data
is shared and assimilated by all the robots or no data
is shared among the robots for planning. Results have
shown that the proposed strategy can balance very
well accuracy and scalability, automatically provid-
ing highly accurate maps without incurring in exces-
sive computational and communication load, overall
showing a very promising scalability.
ACKNOWLEDGEMENTS
This work was made possible by NPRP Grant 10-
0213- 170458 from the Qatar National Research Fund
(a member of Qatar Foundation). The findings herein
are solely the responsibility of the authors.
REFERENCES
Bettstetter, C., Resta, G., and Santi, P. (2003). The node
distribution of the random waypoint mobility model
for wireless ad hoc networks. IEEE Trans. on mobile
computing, 2(3):257–269.
Chen, J., Cao, N., Low, K. H., Ouyang, R., Tan, C. K.-Y.,
and Jaillet, P. (2013). Parallel gaussian process regres-
sion with low-rank covariance matrix approximations.
In 29th Conf. on Uncertainty in Artificial Intelligence
(UAI), page 152–161.
Choudhury, A., Nair, P. B., and Keane, A. J. (2002). A
data parallel approach for large-scale gaussian process
modeling. In Proc. of SIAM International Conf. on
Data Mining, pages 95–111.
Cortes, J., Martinez, S., Karatas, T., and Bullo, F. (2004).
Coverage control for mobile sensing networks. IEEE
Transactions on Robotics and Automation, 20(2):243–
255.
Di Caro, G. and Yousaf, A. W. Z. (2021a). Multi-robot
informative path planning using a leader-follower ar-
chitecture. In IEEE International Conference on
Robotics and Automation (ICRA).
Di Caro, G. A. and Yousaf, A. W. Z. (2021b). Map learn-
ing via adaptive region-based sampling in multi-robot
systems. In 15th Int. Symposium on Distributed Au-
tonomous Robotic Systems (DARS).
Ghassemi, P. and Chowdhury, S. (2019). Informative
path planning with local penalization for decentral-
ized and asynchronous swarm robotic search. In IEEE
Int. Symp. on Multi-Robot and Multi-Agent Systems
(MRS), pages 188–194.
Jager, M. and Nebel, B. (2001). Decentralized collision
avoidance, deadlock detection, and deadlock reso-
lution for multiple mobile robots. In Proceedings
of IEEE/RSJ International Conference on Intelligent
Robots and Systems (IROS), volume 3, pages 1213–
1219.
Krause, A. and Guestrin, C. (2011). Submodularity and its
applications in optimized information gathering. ACM
Transactions on Intelligent Systems and Technology
(TIST), 2(4):1–20.
Li, A. Q., Penumarthi, P. K., Banfi, J., Basilico, N., O’Kane,
J. M., Rekleitis, I., Nelakuditi, S., and Amigoni, F.
(2020). Multi-robot online sensing strategies for the
construction of communication maps. Autonomous
Robots, 44(3):299–319.
Ma, K.-C., Liu, L., Heidarsson, H. K., and Sukhatme,
G. S. (2018). Data-driven learning and planning for
environmental sampling. Journal of Field Robotics,
35(5):643–661.
Mishra, R., Chitre, M., and Swarup, S. (2018). Online infor-
mative path planning using sparse gaussian processes.
In MTS/IEEE OCEANS, pages 1–5.
Popovi
´
c, M., Vidal-Calleja, T., Hitz, G., Chung, J. J., Sa,
I., Siegwart, R., and Nieto, J. (2020). An informative
path planning framework for UAV-based terrain mon-
itoring. Autonomous Robots, pages 1–23.
Rasmussen, C. E. (2003). Gaussian processes in machine
learning. In Summer school on machine learning,
pages 63–71. Springer.
Roumeliotis, S. I. and Bekey, G. A. (2002). Distributed
multirobot localization. IEEE Trans. on Robotics and
Automation, 18(5):781–795.
Stachniss, C. (2009). Robotic mapping and exploration,
volume 55. Springer.
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
522
