Modelling Social Protests in the Republic of Belarus in 2020 based on

Diffusion Equations

Alexandr Y. Petukhov

and Dmitry I. Kaminchenko

Keldysh Institute of Applied Mathematics Russian Academy of Science, Miusskaya sq., 4, Moscow, 125047, Russia

RL “Modeling of Social and Political Processes” Nizhniy Novgorod Lobachevski State University,

603950, Gagarin ave. 23, Nizhniy Novgorod, Russia

Keywords: Protests, Belarus, Society, Diffusion Equations, Langevin Equation, Communicative Field, Social Activity,

Networks.

Abstract: In this article, we propose a model of social activity based on diffusion equations and a comparison of the

modeling results with real data of protest activity (based on data in social networks) in Belarus in 2020. A

model uses the diffusion Langevin equation. The model is based on the idea that individuals interact in society

through a communicative field - h. Besides, the control is introduced into the system through the dissipation

function. Protest data indicators were collected using the authors' content analysis of the main hashtags

associated with Belarusian protests. Then the results of modeling were compared with the obtained data and

analyzed. Based on the modeling we have revealed a general similarity in dynamics and characteristic patterns

as well as have made a forecast for the development of the situation in 2021.

1 INTRODUCTION

Social conflict can be defined as a peak stage in the

development of contradictions between individuals,

groups of individuals, and society as a whole, is

characterized by the existence of conflicting interests,

goals, and views of the subjects of interaction.

Conflicts may be hidden or explicit, but they are

always based on the absence of compromise, and

sometimes even arise from a dialog between two or

more parties (Dollard et al. 1993). The development

of general conflictology at the present stage was

significantly influenced by the works of international

scientists, who had laid the theoretical foundation for

solving specific problems of complex

interdisciplinary science. These are the classic works

of L. Coser, R. Dahrendorf, J. Habermas, H. Becker,

A. S. Akhiezer as well as other studies on social

conflicts (Dahrendorf, 1965; Gurr and Harff, 1994;

Galtung, 1969; Gurr, 1993; Greenfeld, 1992; Isajiw,

1974; Boulding, К, 1969; Krisberg, 1998), modeling

of social processes (Castellano, Fortunato, and

Loreto, 2009; Smith, 2003; Traud, 2011).

https://orcid.org/0000-0002-7412-5397

https://orcid.org/0000-0002-3193-3423

Mathematical modeling based on nonlinear

dynamics is widely used in natural science, but it is

still applied quite rarely in sociological research. In

recent years, significant progress has been made in

the development of models of social and political

processes (Plotnitskiy, 2001).

As a rule, the modeling of the dynamics of the

linear system in classical models is based on the use

of multidimensional equations, difference equations,

the mathematical apparatus of cellular automata, the

mathematical apparatus of catastrophe theory, the

mathematical apparatus of self-organized criticality

theory, the stochastic differential Langevin equations

and Itô-Stratonovich, the analysis of systems with

chaos and reconstruction of stable states (attractors)

by time series (Malkov, 2009; Romanovsky

Stepanova and Chernavsky, 1984; Haken, 1985,

Malinetskiy and Potapov, 2000).

A certain class of works was devoted to ethnic

diversity and its impact on economic and

sociocultural development, as well as other social

processes associated with it (Shabrov, 1996;

Ottaviano and Peri, 2005; Weber, Davydov and

Dower, 2015). These are the interdisciplinary

Petukhov, A. and Kaminchenko, D.

Modelling Social Protests in the Republic of Belarus in 2020 based on Diffusion Equations.

DOI: 10.5220/0010612104450452

In Proceedings of the 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2021), pages 445-452

ISBN: 978-989-758-528-9

445

researches dealing with social problems and their

correlation with the economy taking into account

ethno-cultural factors, as well as their joint influence

on potential and existing conflicts.

Forecasting and description of socio-political

processes are carried out by many other methods

(Mikhailov and Gorbatikov, 2012; Smith, 2003;

Traud, 2011).

In fact, given the significant impact of such

phenomena on the society and the processes

associated with it, the methods and ways for

describing and predicting ethno-social conflicts are

extremely important.

In recent years, significant progress has been

made in the development of models of social and

political processes (Abzalilov, 2012). Mathematical

modeling based on nonlinear dynamics is widely used

in natural science, but it is still applied quite rarely in

sociological research.

2 FUNDAMENTALS OF THE

MODEL

Socio-political processes are subject to constant

changes and deformations, therefore from the point

of view of mathematical modeling they cannot be set

with a high degree of precision. Here we can trace

the analogy with the Brownian particle, i.e. a

particle that seemingly moves along a rather defined

trajectory, but under close examination, this

trajectory turns out to be strongly tortuous, with

many small fractures (Holyst, Kasperski and

Schweitger, 2000; Petukhov et al. 2018; Gutz and

Коrobitsyn, 2000). These small changes

(fluctuations) are explained by the chaotic motion of

other molecules. In social processes, fluctuations

can be interpreted as manifestations of the free will

of its participants, as well as other random

manifestations of the external environment (Gutz

and Коrobitsyn, 2000).

In physics, these processes are, as a rule,

described by the Langevin equation of the stochastic

diffusion, which has been relatively approved for

modeling of some social processes as well. For

example, the model of public opinion, developed by

Holyst J.A., Kacperski K., Schweiter F. (Holyst,

Kasperski and Schweitger, 2000), is based on the use

of this equation.

This approach has several advantages:

1. As it has already been mentioned, the

approach allows taking into account the

manifestations of the free will of its individual

participants, as well as other random

manifestations of the external environment for

the social system.

2. The behavior of a social system can be

calculated, both for its entirety and separate

individuals.

3. This approach allows identifying some

distinctive stable modes of functioning of

social systems, depending on various initial

conditions.

4. Diffusion equations, as a mathematical

apparatus, have been sufficiently validated

and studied from the point of view of

numerical simulation.

The model is based on the assumption that

individuals interact in society through a

communicative field - h (a similar concept was

introduced in (Holyst, Kasperski and Schweitger,

2000), but with another parametrization and another

type of initial equations).

The need to introduce this concept was caused by

a number of factors:

1. Any alive cognitive system (including both

society and a person) carries out the activity

and functioning on the basis of the exchange

of information in one form or another. It can

be either information from electrical impulses

in the brain or the cerebellum opioid system,

or information flows on the Internet.

2. Therefore, modeling of individuals’ behavior

in society will be directly related to modeling

their information exchange.

3. Accordingly, it is reasonable to introduce a

function as the basis of the model that will

simulate the information exchange between

individuals.

This is the reason why the function h, in fact, the

function of information exchange between

individuals, was developed. Physically, it is a field

created by every person in society, simulating

information interaction. Besides, from the point of

view of physical and mathematical description of this

field, we should keep in mind that here we are talking

about a society, which is difficult to refer to an object

in classical physical spatial topology. Objectively,

from the point of view of information transfer from

an individual to an individual, space in society

combines both classical spatial coordinates and

additional specific parameters and features. This is

associated with the fact that in the modern

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

446

information world there is no need to be close to the

object of influence to transmit information to it.

Thus, the society is a multidimensional, social-

physical space that reflects the ability of one

individual to "reach" another individual with his

communicative field, that is, to influence it, its

parameters, and the ability to move in a given space.

Accordingly, the position of the individual relative to

other individuals in such a space, among other things,

models the level of relationships between them and

involvement in the information exchange. The

proximity of individuals to each other in this model

suggests that there is a regular exchange of

information between them and a social connection

has arisen. The conflict in such a statement of the

problem should be regarded as a variant of the

interaction of individuals, or groups of individuals, as

a result of which the distance (i.e., social distance xi -

xj, where xi and xj are the coordinates in social and

physical space, i, j = (1, N), where N is the number of

individuals or consolidated groups of individuals)

between them is growing rapidly.

Conflict management or various options for

conflict mediation (Dahrendorf, 1965; Gurr and

Harff, 1994; Isajiw, 1974; Boulding, К, 1969), from

the point of view of modeling, are an additional

function that depends at least on the coordinates and

affects the overall stability and structure of the social

system. There are several physical analogies that

similarly influence physical systems; for example, a

dissipative function that can have different forms in

different physical conditions (Holyst, Kasperski and

Schweitger, 2000).

2.1 Mathematical Representation of

the System

The communicative field, as in (Petukhov et al.

2018), is represented by a diffusion equation with a

divergent type of diffusion:

𝜕

𝜕𝑡

ℎ

(

𝑥



,𝑡

)

=𝑓𝑥



,𝑥



𝜗𝑥



,𝑥



𝛿

(











),(











)





+𝐷ℎ

(

𝑥



,𝑡

)

−ℎ

(

𝑥



,𝑡



)

,

(1)

where f(x_i,x_j ) is a function that describes the

interaction between individuals, which is modeled by

the classical Gaussian distribution:

This interaction is an information exchange

between individuals, which is carried out through any

communicative physical means.

𝜗(𝑥



,𝑥







√



𝑒

(







)







Function 𝜗𝑥



,𝑥



 is introduced instead of the

delta-function to simplify the process of computer

modeling;

𝛿

(











),(











)

– is the inverse Kronecker symbol;

𝐷 – is the diffusion coefficient describing the

spread of the communicative field.

The movement of an individual in space is

described by the Langevin equation:

𝑑𝑥



𝑑𝑡

=𝑢(𝑥



)+𝑘





𝑘







𝜕

𝜕𝑥



ℎ𝑥



,𝑡



,



√

2𝐷𝜉



(

𝑡

)

(2)

𝑢

(

𝑥

)

– is the control function, which we set as:

𝑢

(

𝑥

)

=−

𝑥



𝜏

where 𝜏− is the time of relaxation in the society,

𝑘



– coefficient of social activity of the i

individual or a group of individuals,

𝑘





– coefficient of the scientific and technological

progress of the i

individual or a group of individuals,

𝜉



(

𝑡

)

− stochastic force.

We believe that the distinctive parameters of the

system can take on values:

0<𝑘



,𝑘



,𝐷<1.

In the general case, the following are chosen as

the initial conditions for equations (1) and (2):

𝑥





=𝑥



ℎ

(

𝑥



,𝑡=0

)

=ℎ



The field ℎ



(𝑥,𝑡) affects an individual I in the

following way. Being at the point x

, the individual

falls under the influence of the communication field

of another individual (or several). Depending on the

difference between its coefficients and the

coefficients affecting individuals, it can react in the

following ways:

1. Changes the value of its coefficients under the

influence of other individuals

2. Moves in the direction of the area where the

difference of the coefficients is relatively

minimal at the moment

Modelling Social Protests in the Republic of Belarus in 2020 based on Diffusion Equations

447

Let us consider 𝑝



(𝑘



,𝑘



,𝑡,𝑥



,𝑥



) as the

probability of the impact of the communication field

of an individual (or a cluster of individuals) j on the

communication field of an individual i in a way to

change its coefficients K

and K

(separately or

together) at time t. In this case, the probability of

movement of an individual i in the direction of the

area where the difference of the coefficients is

relatively minimal at present -1−𝑝



(𝑘



,𝑘



,𝑡,𝑥



,𝑥



The change in probability then:

𝑑

𝑑𝑡

𝑝



(𝑘



,𝑘



,𝑡,𝑥



,𝑥



)

=𝜐(𝑘



𝑘



′

)



′



𝑝



(𝑘

′



,𝑘

′



,𝑡,𝑥



,𝑥



)𝜗(𝛥𝑥



𝛥𝑘



)−

−𝑝



(𝑘



,𝑘



,𝑡,𝑥



,𝑥



)

∑

𝜐(𝑘

′



𝑘



)





′

𝜗(𝛥𝑥



,𝛥𝑘



′

(3)

𝜗(𝛥𝑥



𝛥𝑘



) – a parameter characterizing the

induction effect of the communication field.

𝜐(𝑘



𝑘



′

) – abstract probabilities of changing the

coefficients per unit of time:

𝜐(𝑘



′

𝑘





𝑘



≠𝑘



′

→𝜂𝑒𝑥𝑝ℎ





′

(𝑥



,𝑡)−ℎ





(𝑥



,𝑡)/𝑄

𝑘



=𝑘



′

→0

(4)

где Q – a parameter of social freedom

characterizing the degree of freedom of movement of

individuals in a given social system.

The next stage of the study must be focused on the

data of protests in Belarus, for the reason that the

results of the modeling are of special interest for us in

this study, and then compare them with real data.

3 SOCIAL MEDIA AS A

SUBSYSTEM OF THE MODERN

POLITICAL AND

COMMUNICATIVE SPACE

If we consider the general field of modern political

communication as a separate system, so the political

and communicative space of social media is its

subsystem. Such features of communicative

interactions as dynamism, interactivity, and

connectivity have a special manifestation in this

subsystem. This subsystem is closely connected with

the other subsystems of political communication

which often play the role of an external environment

to it, sending its impulses that cause a certain reaction

within this subsystem. The example of a similar

reaction in the political and communicative space of

social media can be noticed in the course of the

protest events in the Republic of Belarus.

The choice of this social conflict is caused by its

relevance, sufficiency of informational

representation, and active presentation on social

media. The experience of previous social conflicts

with high integration of social media demonstrates

that the activity of participants in the process on the

internet can serve as a marker for determining their

level of involvement (Erz, Marder and Osadchaya,

2018; Lidgren, 2019; Bonilla and Rosa, 2015).

To conduct our research, we carried out a

quantitative content analysis of the subject of posts

published by residents of the Republic of Belarus in

the support system of modern social networks

Facebook, dedicated to protesting actions that began

immediately after summing up the results of the

presidential elections in Belarus on 9 Aug. 2020. We

have chosen a message (Facebook users’ notes) as a

unit of analysis and a word as a unit of calculating

(keyword, hashtag).

When writing texts of messages on social media,

several specific hashtags are often used (“a keyword

or phrase indicated by a hash sign that turns this

word/phrase into a hyperlink” and reflects the subject

and content of the message (Erz, Marder and

Osadchaya, 2018, p. 50). During the reflection of the

protest events in Belarus in the Facebook information

field, a number of certain hashtags became integral

elements of the symbolic semantic core of the

communication activity of the republic's residents on

Facebook. Among the designated hashtags are the

following: “#Belarus2020”, “#Беларусь2020”,

“#ЖывеБеларусь” (“#Long live Belarus”),

“#ВерымМожамПераможам” (“#believecanwin”).

As it is known, hashtags are not just words or

expressions corresponding to the used sign, but,

“tools of activating certain interpretive frames”,

according to S. Lindgren (Lidgren, 2019, p. 421).

They play a semiotic role pointing out the intended

meaning of the utterance, allowing users to state in

the message that semantic meaning, which,

otherwise, might not be so obvious (Bonilla, Y., and

J. Rosa, 2015, p.5). Thus, in some cases, hashtags

mark the corresponding user posts with a certain

value, fixing a meaningful message to the audience in

the post itself, or with a certain meaning, stating a

meaningful message to the audience in the post.

The time interval for content analysis is from 11

Aug. to 2 Oct. During the indicated period, 604

messages were selected including the hashtags

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

448

mentioned above as a component element. It is

necessary to emphasize that we have analyzed only

messages published by residents of the Republic of

Belarus based on open data on Facebook.

3.1 Results of Content Analysis

The dynamics of changes in the frequency of posting

messages with the indicated hashtags in general by

days is presented in Figure 1.

The dynamics of changes in the frequency of

posting messages with the indicated hashtags

separately by days is presented in Figure 2.

Figure 1.

In messages dedicated to protest activity in

Belarus, it was more often used (in comparison with

others) «#ВерымМожамПераможам» (213

messages) and «#Belarus2020» (202 messages) by

residents of the Republic. The hashtag

«#ЖывеБеларусь» was used in 164 in posts and

«#Беларусь2020 – 25 in messages.

Figure 2.

4 RESULTS OF THE MODELING

The modeling was carried out in the MatLab 2013b

environment. Two variants with different initial

conditions were served as a basis for research.

The first variant (Figure 3) represents the

modeling of social indignation without any external

influence (without the control function), in order to

Along axes: axis y – change in social activity Δkc, axis x –

timing t.

Figure 3.

11 August

15 August

19 August

23 August

27 August

31 August

4 September

8 September

12 September

16 September

20 September

24 September

28 September

2 October

Number of messages

Number of messages with hashtags

#Belarus2020, #ЖывеБеларусь,

#Беларусь2020,

#ВерымМожамПераможам в

Facebook

11 August

17 August

23 August

29 August

4 September

10 September

16 September

22 September

28 September

Number of messages

Number of messages with hashtags

#Belarus2020, #ЖывеБеларусь,

#Беларусь2020,

#ВерымМожамПераможам в

Facebook

#Belarus20

#ЖывеБел

арусь

#Беларусь

2020

#ВерымМо

жамПерам

ожам

Modelling Social Protests in the Republic of Belarus in 2020 based on Diffusion Equations

449

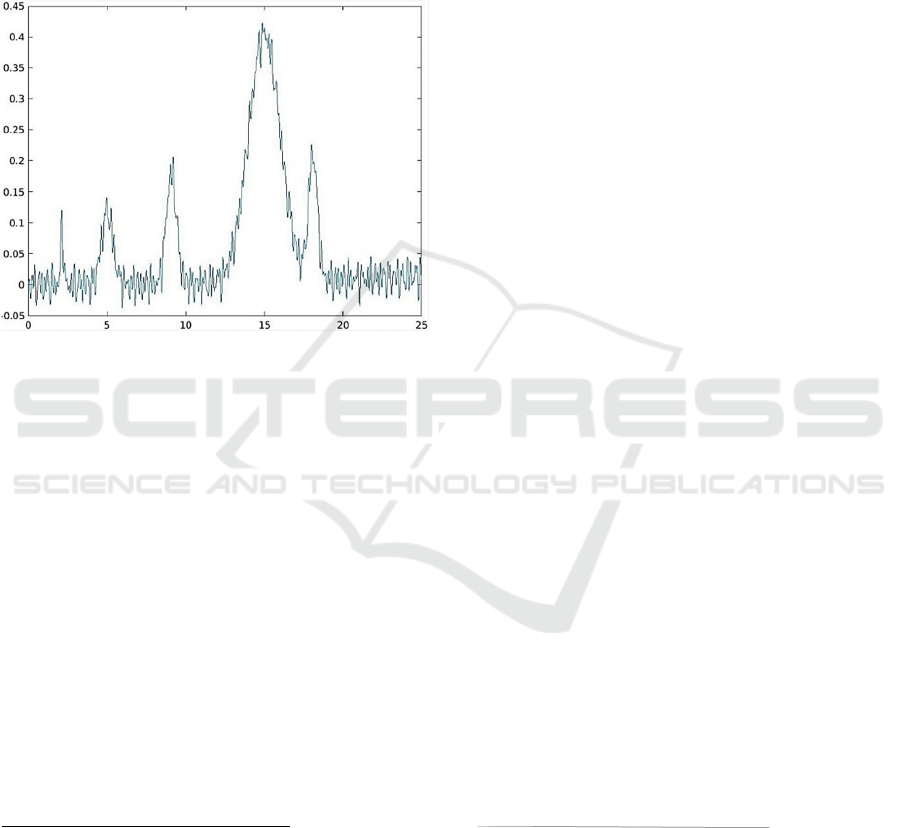
analyze the variant of a closed system and to make a

conclusion on how the internal social conflict should

proceed in this case. The modeling results are similar

to earlier works on the dynamics of social activity in

conflict conditions (Petukhov 2020).

The second situation refers to a variant of social

disturbance with external influence/control creating a

sequential series of “disturbances” in the

communication field of the social system (Figure 4).

Along axes: axis y – change in social activity Δkc, axis x –

timing t.

Figure 4.

4.1 Data Analysis and Comparison

We have analyzed the intensity of use of the

designated hashtags on Facebook (for the period from

11 Aug. to 2 Oct.) and identified a number of days

when some of these hashtags were used especially

intensively: 9, 20, 21, 23, and 27 September. Only 20

and 27 Sept. were days off, which is important to

emphasize because the main rally activity took place

in Belarus exactly on weekends. Therefore, the active

use of the hashtags mentioned above could become a

reaction to events that happened in the external

environment (towards the political and

communicative field of Belarus).

The reason for the active use of thematic hashtags

on 9 Sept. could become a speech of one of the leaders

Nikolaev P. Sanctions against the authorities:

Tsikhanouskaya spoke at the PACE // Internet edition

Gazeta.ru. URL: https://www.gazeta.ru/politics/2020/09/

08_a_13241324.shtml

Krayushkins M United Nations Human Rights Council

condemned what is happening in Belarus // Internet

edition Gazeta.ru. URL: https://www.gazeta.ru/social/

news/2020/09/18/n_14958775.shtml

Kazantseva К. The US does not officially recognize

Lukashenko as the legitimate president of the Republic of

of the Belarusian opposition Svetlana

Tsikhanouskaya at the Parliamentary Assembly of the

Council of Europe (PACE) on 8 Sept. During her

speech, Svetlana Tsikhanouskaya made an appeal to

PACE for imposing sanctions against the leadership

of Belarus

An important external factor that contributed to

the increase in communication activity on Facebook

(using the considered hashtags) in the period from 20

to 23 Sept. could be the resolution of the United

Nations Human Rights Council, adopted at the

meeting held on 18 Sept. The resolution condemns

violations of human rights in Belarus, calling on the

country's authorities to take measures to resolve the

situation

. A statement by a representative of the US

State Department was released directly on 23 Sept.

According to this statement, the US did not officially

recognize A.G. Lukashenko as the legitimate

president of the Republic of Belarus

. On the same

day the official representative of the German

government S. Seibert, the head of the Czech

Ministry of Foreign Affairs T. Petršicek, and the head

of the Danish Foreign Ministry J. Kofod also declared

that their states did not recognize the legality of A.G.

Lukashenko for the presidency of the Republic of

Belarus

On 27 Sept. French President E. Macron declared

in an interview with a weekly Journal du Dimanche

that, in his opinion, the Belarusian leader A.G.

Lukashenka must resign

. It provoked a response

from the leadership of Belarus and can also be viewed

as an informational influence of the external

environment on the political and communicative

space of Belarus.

When comparing curve trajectory in Figure 1 and

Figure 2 with Figure 3 and Figure 4, it is necessary to

emphasize the repeated cyclicity in Figure 1, Figure 2

and cyclicity of the same nature in Fig. which, as

noted, demonstrates the reaction of the

communicative field (subsystem) to external

information impulses. They cause an increase in the

intensity of social activity and contribute to the

activation of communicative actions of social media

users with the use of certain content-semantic

Belarus // Internet edition Gazeta.ru. URL: https://www.

gazeta.ru/politics/news/2020/09/23/n_14981911.shtml

Fakhrutdinov P. "What a farce": Europe condemned

Lukashenka's inauguration // Интернет- Internet edition

Gazeta.ru. URL: https://www.gazeta.ru/politics/2020/09/

23_a_13263973.shtml

Ermolov A. "Lukashenko must leave": Macron accused

Minsk of authoritarianism // Internet edition Gazeta.ru.

URL: https://www.gazeta.ru/politics/2020/09/27_a_132

70117.shtml

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

450

(thematic) verbal tools (hashtags).

Also, a comparison of the results and general

characteristic patterns indicates the similarity of real

data (from the point of view of repetition of growing

peaks of activity) with the simulation results in Figure

4, which from a perspective of the presented concept

of the approach implies an increasing cyclical

external interference in the social conflict in Belarus.

Based on the results of modeling, we should

predict (at the time of the survey in Nov. 2020) that

the main peak of social disturbance is likely still

ahead. Of course, various additional factors, such as

the coronavirus epidemic, can interfere in the process.

However, from the point of view of the model, the

process has not yet reached the main maximum and

its appearance can be assumed at the beginning of

2021 if external influence and main internal trends

persist.

5 CONCLUSIONS

This article proposed a model based on diffusion

equations (Langevin equations, in particular) that

models information and communication interactions

of individuals in society in various conditions. One of

the main parameters of the model is the coefficient of

social activity, and the change of this parameter can

be indicative in the context of ongoing social conflicts

from the point of view of analyzing the state of

society.

In order to test the model, we have chosen a

specific real situation - public protests in Belarus in

2020.

It also should be pointed out that informational

influences from the external environment can make

an impact on the political and communicative field of

the political system, causing a response from the

communication participant. In particular, one of the

consequences of such an impact is an increase of user

activity in the context of modern social media support

platforms, which use special symbolic elements,

certain hashtags, in the process of text

communication acts. According to the conducted

analysis of the communicative actions of the

inhabitants of Belarus on Facebook certain events (of

a certain nature and political orientation) that took

place in the information field of foreign states and

international organizations, often preceded (and/or

accompanied) the active use of the appropriate

hashtags.

The results of the conducted content analysis

partially correspond to the results of modeling,

especially the general pattern in Figure 4, which

makes it possible to assume that there is an external

influence/interference in conflict processes in the

Republic of Belarus.

We have also made a forecast for the development

of the situation and the possibility of a larger

disturbance in the social system when/while

maintaining the current trends and the level of

external influence.

REFERENCES

Abzalilov D.F. (2012) Mathematical modeling in

sociology: Educational-methodical manual for

sociologists. Kazan. CFU.

Bonilla, Y., and J. Rosa. (2015) #Ferguson: Digital Protest,

Hashtag Ethnography, and the Racial Politicsof Social

Media in the United States: #Ferguson. American

Ethnologist. 2015. 42 (1) 4–17. https://doi.org/10.1111/

amet.12112

Boulding, К. (1969) General Theory of Systems – The

Skeleton of Science Studies on the general theory of

systems. М. Nauka, p. 171-182.

Castellano, C., Fortunato, S. & Loreto, V. (2009) Statistical

physics of social dynamics. Reviews of Modern

Physics, 81, 591–646.

Dahrendorf R. (1965) Elemente einer Theorie des sozialen

Konflikts. Dahrendorf R. Gesellschaft und Freiheit.

Miinchen.

Dollard J., Doob L. W., Miller N. E., Mowrer О. H., Sears

R. R. (1993) Frustration and Aggression. New Haven

and London.

Erz A., Marder B., Osadchaya E. (2018) Hashtags:

Motivational drivers, their users, and differences

between influencers and followers. Computer in human

behaviour. 89. 48–60.

Galtung J. (1969) Violence, peace and peace research.

Journal of Peace Research. 6(3);

Greenfeld L. Nationalism: Five Roads to Modernity.

Cambridge (Mass.): Harvard University Press, 1992.

Gurr T. R. (1993) Minorities at Risk. A Global View of

Ethnopolitical Conflicts. Washington,

Gurr Т., Harff B. (1994) Ethnic Conflict in World Politics.

Boulder, San Francisco, Oxford,

Gutz А.К., Коrobitsyn V.V. (2000) Mathematical Models

of Social Systems Textbook. Omsk: Omsk State

University.

Haken G. Synergetics. (1985) Hierarchy of instabilities in

self-organizing systems and devices. M. Mir.

Holyst J.A., Kasperski K., Schweitger F. (2000) Phase

transitions in social impact models of opinion

formation. Physica. A285. p. 199-210.

Isajiw W.W. (1974) Definitions of Ethnicity. Ethnicity, 1(2)

Krisberg L. (1998) Constructive Conflicts: From

Escalation to Resolution. Lanham Boulder, New York,

Oxford.

Lidgren S. (2019) Movement Mobilization in the Age of

Hashtag Activism: Examining the Challenge of Noise,

Modelling Social Protests in the Republic of Belarus in 2020 based on Diffusion Equations

451

Hate, and Disengagement in the #MeToo Campaign.

Policy & Internet. 11(4). P. 418-438. doi:

10.1002/poi3.212

Malinetskiy G.G., Potapov A.B. (2000) Modern problems

of nonlinear dynamics. M. Editorial URSS.

Malkov V.P. (2009). Mathematical modeling of historical

dynamics: approaches and models. M.

Mikhailov, A. P. Gorbatikov E. A., (2012) The basic model

of the duumvirate in the system of power-society,

Matem. modeling, 24(1), 33–45

Ottaviano G.I.P. and Peri G. (2005) Cities and Cultures.

Journal of Urban Economics, 58(2), p. 304-337.

Petukhov A.Y., Malkhanov A.O., Sandalov V.M.,

Petukhov Y.V. (2020) Mathematical modeling ethno-

social conflicts with the introduction of the control

function. Simulation. 96(3) 337–346, DOI:

10.1177/0037549719884629

Petukhov A.Y., Malkhanov A.O., Sandalov V.M.,

Petukhov Y.V. (2018) Modeling conflict in a social

system using diffusion equations. Simulation. April 16,

2018. 94(12), 1–9. DOI: 10.1177/0037549718761573

Plotnitskiy Yu. М. (2001) Models of Social Processes:

Textbook for Higher Education Institutions. М. Logos.

Shabrov О.F. (1996) A system approach and computer

modeling in political science research. Social sciences

and contemporaneity. 2, 100-110.

Smith, L. M., Lerman, K., Garcia-Cardona, C., Percus, A.

G. & Ghosh, R. (2003) Spectral clustering with

epidemic diffusion. Physical Review E, 88, 042813.

Traud, A. L., Kelsic, E. D., Mucha, P. J. & Porter, M. A.

(2011) Comparing community structure to

characteristics in online collegiate social networks.

SIAM Review, 53, 526–543.

Romanovsky Yu.M., Stepanova N.V., Chernavsky D.S.

(1984) Mathematical Biophysics. M. Science.

Weber S., Davydov D.V., Dower P.A. (2015) Transfers and

Conflict Prevention: Pros and Cons. Economics and

Mathematical Methods. 51(2), pp. 60-69.

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

452