Attribute Relation Modeling for Pulmonary Nodule Malignancy
Reasoning
Stanley T. Yu
1
and Gangming Zhao
2,∗
1
Stanford Online High School, Redwood City, CA 94063, U.S.A.
2
The University of Hong Kong, Pokfulam, Hong Kong
Keywords:
Graph Convolutional Networks, Bayesian Networks, Benign-Malignant Classification.
Abstract:
Predicting the malignancy of pulmonary nodules found in chest CT images have become much more accu-
rate due to powerful deep convolutional neural networks. However, attributes, such as lobulation, spiculation,
and texture, as well as the correlations and dependencies among such attributes have rarely been exploited
in deep learning-based algorithms albeit they are frequently used by human experts during nodule assess-
ment. In this paper, we propose a hybrid machine learning framework consisting of two relation modeling
modules: Attribute Graph Network and Bayesian Network, which effectively take advantage of attributes and
the correlations and dependencies among them to improve the classification performance of pulmonary nod-
ules. According to experiments on the LIDC−IDRI benchmark dataset, our method achieves an accuracy of
93.59%, which gains a 4.57% improvement over the 3D Dense-FPN baseline.
1 INTRODUCTION
Lung cancer gives rise to the most cancer-related
deaths all around the world (Bray et al., 2018).
Early diagnosis and treatment are of great impor-
tance to long-term survival of lung cancer patients.
In addition, chest computed tomography (CT) has
been widely used for the diagnosis of lung cancer.
Therefore, the benign-malignant classification of pul-
monary nodules found in CT images is critical for the
early screening of lung cancer. Nevertheless, it still
remains a major challenge to accurately differentiate
between benign and malignant nodules because of the
diversity of nodules. With the success of deep learn-
ing, deep convolutional neural networks (CNNs) have
become an important method for lung nodule classifi-
cation. Early deep learning based methods primarily
focused on network architectures and data augmen-
tation schemes. They all aimed to extract deep dis-
criminative features from CT images but overlook im-
portant phenotypical evidences. For example, Shen
et al. (Shen et al., 2015) proposed a multi-scale 2D
CNN, which integrates a multi-crop pooling strategy
for nodule malignancy classification. Dey et al. (Dey
et al., 2018) designed a 3D multi-output DenseNet for
the task of end-to-end lung nodule diagnosis.
In fact, attributes, such as lobulation, spiculation,
and texture, have been commonly used to describe the
∗
characteristics of lung nodules in CT images for as-
sisting nodule assessment (Wang et al., 2019). There-
fore, it is essential to take advantage of such at-
tributes for improving the nodule classification accu-
racy. Early researchers primarily utilized the multi-
task learning (MTL) strategy to jointly learn the at-
tribute regression and nodule classification tasks. For
instance, Liu et al. (Liu et al., 2018) used a multi-
task framework to conduct lung nodule classification
and attribute score regression, which resulted in per-
formance gain in both tasks. Shen et al. (Shen et al.,
2019) also provided a hierarchical design that utilized
both vision features and semantic features to predict
the malignancy of nodules. Nonetheless, there have
been few methods to exploit the connections between
malignancy and attributes as well as potential corre-
lations and dependencies among such attributes for
distinguishing benign and malignant nodules. There-
fore, how to exploit and model the hidden relations
among these attributes for boosting the accuracy of
nodule malignancy prediction still remains an open
and important question. To our best knowledge, few
papers have focused on this perspective. Our pa-
per is the first piece of work that proposes a hybrid
machine learning framework to explicitly exploit at-
tributes as well as the correlations and dependencies
among such attributes. In addition, the success of
deep learning models greatly relies on a large num-
ber of carefully annotated data. However, datasets
in the radiology domain are typically not as large as
Yu, S. and Zhao, G.
Attribute Relation Modeling for Pulmonary Nodule Malignancy Reasoning.
DOI: 10.5220/0010616000590066
In Proceedings of the 2nd International Conference on Deep Learning Theory and Applications (DeLTA 2021), pages 59-66
ISBN: 978-989-758-526-5
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
59

those in the natural image domain. Furthermore, it is
more time consuming and expensive to annotate med-
ical images than natural images. These factors pre-
vent researchers in the radiology domain from obtain-
ing sufficiently large annotated datasets for training
deep learning models, which is one of the most seri-
ous obstacles to improve the generalization capability
of deep learning based nodule classification models.
To address the aforementioned issues, we pro-
pose a hybrid machine learning framework for lung
nodule malignancy reasoning based on attribute re-
lation modeling, which takes full advantage of both
graph convolutional networks (GCN) and Bayesian
networks (BN) to boost the performance of nodule
classification. Specifically, on the basis of a back-
bone network for deep feature representation, we pro-
pose to utilize a graph convolutional network and a
Bayesian network simultaneously to model hidden re-
lations across various attributes of a lung nodule. The
motivation is stated as follows. Since a Bayesian net-
work does not require a large training dataset and is
capable of modeling conditional dependencies, i.e.,
the causation between malignancy and attributes, it
can serve as a regularization module in a deep learn-
ing framework. Meanwhile, a graph convolutional
network is a powerful deep network for modeling re-
lations and is capable of performing high-level rea-
soning across various attributes. When there is suf-
ficient training data, the GCN could significantly im-
prove the baseline classification performance. A hy-
brid model integrating these two types of networks
can achieve a strong generalization capability. Specif-
ically, residual learning is introduced to fuse the re-
sults from the GCN and BN for final malignancy pre-
diction.
The contributions of this paper are summarized as
follows.
• We propose a unified machine learning frame-
work for lung nodule malignancy reasoning. It
aims to model hidden relations across various di-
agnostic attributes via the fusion of a graph con-
volutional network and a Bayesian network.
• We demonstrate the effectiveness of the proposed
framework, which achieves state-of-the-art per-
formance on the LIDC−DRI benchmark dataset.
• We conduct a systematic ablation study to verify
that the proposed hybrid model performs better
than GCN alone.
2 RELATED WORK
2.1 Attribute Learning
Attributes, such as texture, color, and shape, are of
great importance to describe objects. Attribute learn-
ing has been studied in computer vision for many
years (Ferrari and Zisserman, 2008; Kumar et al.,
2009; Akata et al., 2013; Lampert et al., 2013; Liang
et al., 2017; Liang et al., 2018; Min et al., 2019).
Ferrari et al. (Ferrari and Zisserman, 2008) proposed
to use low-level semantic features for attribute repre-
sentation and they presented a probabilistic genera-
tive model for visual attributes, together with an im-
age likelihood learning algorithm. Human faces have
many attributes, and remain a challenge for attribute
learning. Kumar et al. (Kumar et al., 2009) trained bi-
nary classifiers to recognize the presence or absence
of describable aspects of facial visual appearance us-
ing traditional hand-crafted features. Liu et al. (Liu
et al., 2015) proposed a CNN framework for face lo-
calization and attribute prediction, respectively. At-
tributes have also been exploited in tasks such as zero-
shot learning (Lampert et al., 2013; Jiang et al., 2017).
Effectively modeling the hidden relations among at-
tributes is useful for learning a clear reasoning model
and better causal association. Nonetheless, most of
the early works in attribute learning did not model re-
lations among attributes and explore such relations for
attribute reasoning. The development of graph neu-
ral networks (GNN) (Kipf and Welling, 2016) made
it possible to learn relations among attributes. For
example, Meng et al. (Meng et al., 2018) used mes-
sage passing to perform end-to-end learning of image
representations, their relations as well as the interplay
among different attributes. They observed that rela-
tive attribute learning naturally benefits from exploit-
ing the graph of dependencies among different image
attributes. In this paper, we not only utilize a graph
neural network to model the correlations among at-
tributes, but also embed a Bayesian network into the
framework to better model causality.
2.2 Bayesian Networks
Bayesian networks (BN), introduced by Judea
Pearl (Pearl, 1998), represent a natural approach to
model causality and perform logical reasoning. The
learning of Bayesian networks includes two phases:
structure learning and parameter learning. The most
intuitive method for structure learning is that of
‘search and score,’ where one searches the space of
directed acyclic graphs (DAGs) using dynamic pro-
gramming and identifies the one that minimizes the
DeLTA 2021 - 2nd International Conference on Deep Learning Theory and Applications
60

objective function (Wit et al., 2012). For param-
eter learning, the most frequently used method is
maximum likelihood estimation (MLE) (Pearl, 1998).
However, when given a dataset, BN cannot learn a
feature representation, which limits its further devel-
opment. Recently, researchers have started to focus
on the integration between BN and deep learning. For
example, Rohekar et al. (Rohekar et al., 2018) pro-
posed to utilize BN models for learning better deep
neural networks. Meanwhile, a few improved ver-
sions of BN have been proposed for new applications
in computer vision. For example, Barik (Barik and
Honorio, 2019) improved BN using low-rank condi-
tional probability tables. Elidan et al. (Elidan, 2010)
used the Copula Bayesian Network model for rep-
resenting multivariate continuous distributions. The
method in this paper differs from the above work in
that it exploits the representation power of deep neu-
ral networks and the causality modeling capability of
BN by embedding them into a unified framework.
3 METHODOLOGY
3.1 Overview
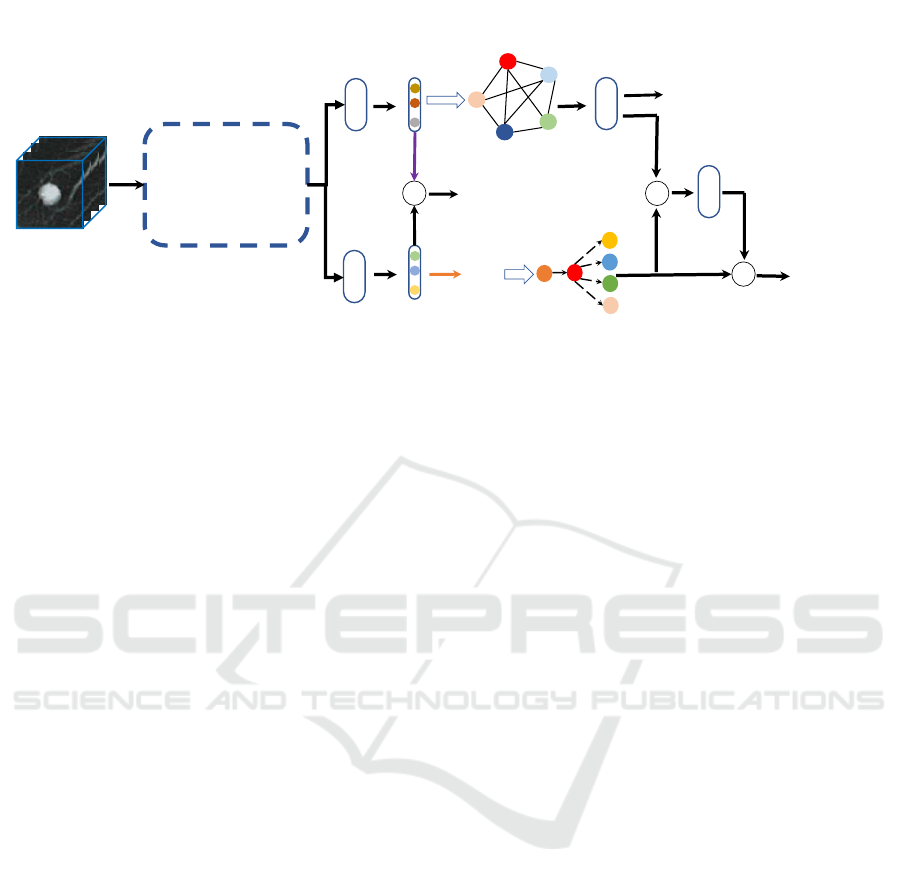
The proposed deep learning framework takes a 3D CT
patch I enclosing a nodule as input and outputs the
probability of malignancy P
m
(Fig. 1). Our frame-
work primarily consists of three modules: a feature
extraction module, a hybrid attribute relation model-
ing module, and a residual fusion module. The feature
extraction module, which is based on a 3D Dense-
FPN (Fig. 2), extracts features representing multi-
ple semantic attributes. The attribute relation model-
ing module has two parallel components, an attribute
graph network and a Bayesian network. Those ex-
tracted features are fed into two separate branches,
one for each of these two components. In both
branches, the extracted features are first transformed
by a distinct fully connected layer. In the first branch,
the transformed features are called attribute relation
features (ARF), which are fed into the attribute graph
network (AGN), which enhances feature representa-
tion and improves their discriminative power between
benign and malignant nodules. Meanwhile, in the
second branch, the transformed features are called at-
tribute knowledge features (AKF), which are further
converted into attribute scores (AS) via an argmax op-
eration. Afterwards, the AS are fed into the Bayesian
network (BN), through which the causation between
malignancy and other attributes are determined to
help explain how the deep learning model interprets
CT image patches from an expert-interpretable man-
ner. Finally, a residual fusion module, which views
the BN branch as the baseline and the AGN branch as
the residual, is introduced to fuse the outputs of AGN
and BN to obtain the ultimate probability of malig-
nancy.
3.2 Attribute Graph Network
The Attribute Graph Network in this study is based
on GCN, which utilized deep graph convolution to
learn high-level knowledge representation from at-
tribute features to facilitate the benign−alignant nod-
ule classification. Specifically, the AGN can be repre-
sented as an undirected graph G =< V,E,A >, where
V and E are set of nodes and edges respectively, and
A is the adjacency matrix which represents the con-
nections among nodes of G. Here, each node is the
deep feature of a kind of attribute (e.g., subtlety, lob-
ulation). We consider a graph neural network φ
G
to
model the relation among various nodes with a layer-
wise propagation rule as follows:
H
i+1
= σ

D
−1/2
(A
0
)D
−1/2
[H
i
W
i
+ σ(H
i
W
0
i
)]

, (1)
where i ∈ {0,1,2},
A
0
= ω
0
A + ω
1
I, (2)
D
kk
=
∑
j
A
k j
. (3)
In the above equations, A
0
is a weighted sum of the
adjacency matrix A and the identity matrix I, D is the
degree matrix of G, W and W
0
denote two trainable
weight matrices, σ is a non-linear activation function
(e.g., ReLU) and H is the matrix of activations. Dif-
ferent from the original propagation rule for graph
neural networks, our modified propagation rule has an
extra non-linear term σ(H
i
W
0
i
). Results from our ab-
lation study (Section 4.2) will verify the effectiveness
of the added non-linear term.
More specifically, the modeling process of AGN
is as follows. First, the input of AGN, H
0
, is the
matrix of attribute relation features (ARF, shown in
Fig. 1) with a size of M × C, where M is the num-
ber of attributes and C is the feature dimensionality
of each attribute. Then a graph neural network φ
G
,
which has three layers {φ
0
g
,φ
1
g
,φ
2
g
}, is built according
to (Kipf and Welling, 2016). The number of output
channels of the three layers are 128, 64, and 32, re-
spectively. The AGN can be trained in an end-to-
end manner when cascaded with the feature extraction
backbone. The result of knowledge reasoning per-
formed with the AGN is sent into the residual fusion
module, which produces the final malignancy predic-
tion.
Attribute Relation Modeling for Pulmonary Nodule Malignancy Reasoning
61

3D CT patch
Attribute Graph
Network
Bayesian Network
F
C
C
F
C
+


  
3D Dense-FPN
F
C
F
C
AKF
  


ARF
  


  


+


C  




 2
AS
  
ArgMax
Figure 1: Our proposed framework consists of three stages: 1) Deep feature extraction using the 3D Dense-FPN backbone; 2)
hybrid attribute relation modeling via an attribute graph network and a Bayesian network; 3) fusion of AGN and BN reasoning
results for final malignancy prediction.
3.3 Bayesian Network Integration
A Bayesian network is incorporated to model prob-
abilistic dependencies among various attributes of
a nodule for malignancy reasoning. Specifically, a
Bayesian network, B =< V ,E, Θ >, is a directed
acyclic graph (DAG) < V ,E > with a conditional
probability table (CPT) for each node, and Θ repre-
sents all parameters (CPTs), which encodes the joint
probability distribution of the BN. Each node v
i
∈ V
stands for a random variable, and a directed edge
e ∈ E between two nodes (v
i
,v
j
) indicates v
i
proba-
bilistically depends on v
j
. The training of a Bayesian
network undergoes two phases, structure learning and
parameter learning (Pearl, 1998; Pearl, 2014; Eaton
and Murphy, 2012). We adopt dynamic programming
with the Bayesian information criterion (BIC) (Wit
et al., 2012) for structure learning to determine the
topology of the DAG and maximum likelihood esti-
mation for parameter learning to determine Θ. Our
BN module first learns its structure and then updates
all parameters, i.e. the conditional probability tables
at all nodes in the network.
In this study, each node in the BN holds the score
of a certain semantic attribute (e.g., lobulation, spic-
ulation) of a pulmonary nodule. Note that the malig-
nancy of the nodule is also a node in the BN. Fig. 3
shows the BN structure learned from the LIDC−IDRI
dataset. The learned BN structure indicates that the
node for malignancy has one parent node (i.e., spicu-
lation) and four children nodes (i.e., subtlety, calcifi-
cation, margin and lobulation). The remaining three
attributes (i.e., internal structure, sphericity and tex-
ture) do not have any probabilistic dependencies with
either malignancy or the other five attributes in Fig. 3.
Once the BN has been trained, it is cascaded with
the 3D Dense-FPN backbone, whose output becomes
the input evidences in the Bayesian network. We per-
form inference in the Bayesian network using the con-
ditional probability tables as well as the input evi-
dences, and obtain marginal posterior distributions at
all nodes, including the node for disease diagnosis, as
the output of the Bayesian network. Let the nodes in
the Bayesian network be v
i
,i ∈ {0,1,...,n}. Accord-
ing to (Pearl, 1998), the marginal posterior distribu-
tion p
m
of malignancy is formulated as
p
m
=
Z
...
Z
V
P(v
0
,v
1
,...,v
n
)dv
1
...dv
n
, (4)
where
P(v
0
,v
1
,...,v
n
) = Π
n
i=0
P(v
i
|Parents(v
i
)), (5)
where v
0
represents the node for malignancy, and
Parents(v
i
) is NULL if v
i
does not have any parent
nodes. The equation in (5) is derived using the local
Markov property of Bayesian networks. In practice,
to evaluate (4), we use the belief propagation algo-
rithm in (Pearl, 1982). Consequently, the input evi-
dence at a node in the Bayesian network is modeled
as an incoming message from an auxiliary child node.
3.4 Residual Fusion and Training
Scheme
Once attribute relation modeling and malignancy rea-
soning have been carried out within both the AGN and
BN, malignancy reasoning results from these two net-
works need to be fused to further improve the predic-
tion accuracy because the fused result could provide
more complete information to distinguish the subtle
DeLTA 2021 - 2nd International Conference on Deep Learning Theory and Applications
62

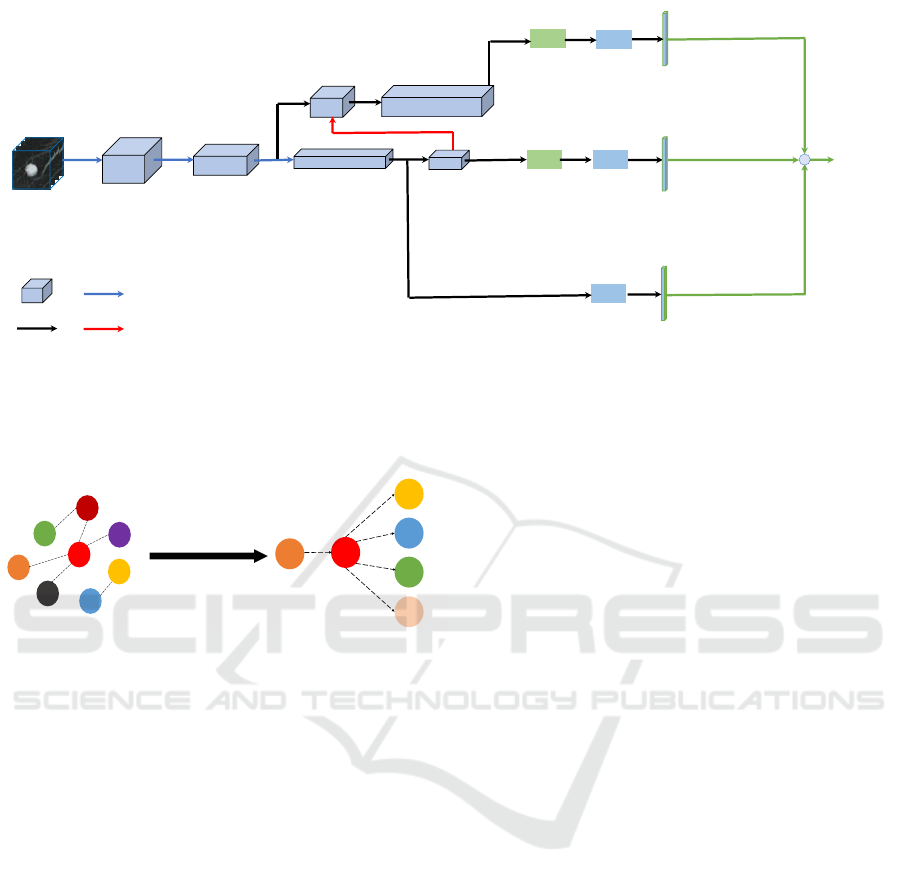
2D-Pool, S:2
Down-sampling
Up-sampling
3D Dense-Feature
Channel
3D CT patch 3D Dense-Feature 80 3D Dense-Feature 136 3D Dense-Feature 260
3D Dense-Feature 136+30
Forward
GMP
GMP
3D Dense-Feature 262
Feature
+
FC
FC
FC
Figure 2: Overview of 3D Dense-FPN. It consists of a triple-stream structure, which aims to learn global and multi-scale local
features. The top feature map has a small receptive field, which can extract small-scale features with the help of Global Mean
Pooling (GMP); the middle feature map has a large receptive field, and thus can extract large-scale features; the bottom stream
uses a FC layer, leading to the global image information. Then the sum of these three extracted features (three green lines)
is fed into our hybrid attribute relation model. The module is supervised by the Cross-Entropy Loss. ‘3D Dense-Feature 80’
means the feature map from a Dense-Block with 80 output channels.
SPI
MAL
SUB
CAL
MAR
LOB
DP Learning
Initial State
Learned State
Figure 3: The Bayesian network structure learned from the
LIDC-IDRI dataset. Notations are defined as follows. SPI:
spiculation; MAL: malignancy; SUB: subtlety; CAL: calci-
fication; MAR: margin; LOB: lobulation.
differences between benign and malignant nodules.
One straightforward fusion scheme is concatenation,
however, it does not distinguish the role of each origi-
nal result. In this study, residual learning is adopted as
the fusion strategy to fuse the output of the AGN and
BN, which proves to be a more effective approach,
as verified by our ablation study (Section 4.2). As
shown in Fig. 1, the BN is set up to produce the base-
line result while the AGN produces the residual on
top of the baseline result. The reason for the BN be-
ing the baseline is that Bayesian networks could pro-
vide more reliable predictions when there is a short-
age of training data, which is a common situation in
radiology. Meanwhile, with the AGN being the resid-
ual branch, it can be taken as a feature enhancement
module that provides high-level knowledge represen-
tations in a more discriminative embedding space,
where the classification performance could be further
improved when there is abundant training data. Our
residual fusion scheme can be expressed as follows,
p
m
= W
1
C(σ(W
0
(H
out
)), p
m
) + p
m
, (6)
where W
0
and W
1
are two fully connected layers, C is
the concatenation operator.
The training procedure of the proposed hybrid
model consists of three phases. First, the feature ex-
traction backbone (i.e., the 3D Dense-FPN) is trained
using the attribute classification loss in (7). Next,
the trained backbone is cascaded with the AGN,
and the cascaded network is trained using the bi-
nary benign−malignant nodule classification loss in
(8). Meanwhile, dynamic programming and maxi-
mum likelihood estimation are used for the structure
and parameter learning of the BN, respectively. Fi-
nally, the feature extraction backbone, AGN and BN
are all connected, and the residual learning loss func-
tion in (9) is used to train the whole network from end
to end. However, the BN is fixed after stand alone
training, and no gradient would be generated for BN
during the end-to-end training.
Loss
att
=
∑
i
∑
j
−y
i j
a
log(p
i j
a
), (7)
where i ∈ {0,1,...,M − 1}, j ∈ {0,1,...,N
c
− 1}.
Loss
bm
=
∑
i
−y
i
m
log(p
i
m
),i ∈ {0,1}, (8)
Loss = Loss
att
+ Loss
bm
. (9)
In the above equations, p
a
with a size of M × N
c
(at-
tribute category number) is the prediction result of the
attributes, which is obtained by performing the soft-
max operation over the sum of φ
FC
(ARF) and AKF,
as shown in Fig. 1. And y
a
and y
m
are the ground-truth
attribute labels and malignancy labels, respectively.
Attribute Relation Modeling for Pulmonary Nodule Malignancy Reasoning
63

Table 1: Comparison with Existing Benign−Malignant
Nodule Classification Models.
Methods Accuracy %
TumorNet (Hussein et al., 2017) 82.47
TumorNet-attribute (Hussein et al., 2017) 92.31
SHC-DCNN (Buty et al., 2016) 82.4
MCNN (Shen et al., 2015) 86.84
CNN-MTL (Hussein et al., 2017) 91.26
MK-SSAC (Xie et al., 2019) 92.53
MSCS-DeepLN (Xu et al., 2020) 92.64
3D-DENSE-FPN 89.02
3D-DENSE-FPN + AGN 92.04
3D-DENSE-FPN + BN 90.2
Proposed 93.59
4 EXPERIMENTS
4.1 Datasets and Settings
Dataset. The evaluation is performed on the
LIDC−IDRI dataset (Armato III et al., 2011) from
Lung Image Database Consortium. It includes 1010
patients (1018 scans) and 2660 nodules with slice
thickness varying from 0.45 mm to 5.0 mm. There
are nine labeled attributes for each nodule, i.e.,
subtlety, internal structure, calcification, sphericity,
margin, lobulation, spiculation, radiographic solidity,
and malignancy. 1404 nodules are considered in
our experiments, 898 benign and 506 malignant.
The CT volume is normalized to 0.6 mm along
each dimension (pixel spacing and slice thickness).
A 48 × 48 × 48 image patch is extracted for each
nodule. 64% patches are sampled to form the training
set, 10% form the validation set and the remaining
ones belong to the testing set.
Experimental Settings. The proposed model is
trained from scratch using PyTorch (Paszke et al.,
2019) while Adam (Kingma and Ba, 2014) being the
optimizer with a learning rate of 1e-3. In addition,
to verify the generalization capability of our method
under limited training data, we reduce the number of
training samples to 1/4 and 1/8 of the original number
of samples in the training set. We use simpler net-
works for AGN to achieve optimal performance on
reduced training data, as shown in Table 2.
4.2 Experimental Results
Comparison with State-of-the-Art Methods. Table
1 shows the performance of our proposed framework
and existing state-of-the-art classification models
on the LIDC-IDRI dataset. It indicates that our
proposed model achieves the highest accuracy of
93.59%, which is 4.57% higher than the performance
of the 3D Dense-FPN baseline. The inclusion of
either AGN or BN improves the performance, which
verifies the effectiveness of our method. In addition,
the residual fusion of AGN and BN further boosts the
classification accuracy.
Ablation Study. We conduct a systematic ablation
study to verify the effectiveness of individual modules
in our framework. According to Table 2, we make
the following conclusions. 1) Both AGN and BN can
improve the performance of the baseline. AGN im-
proves the accuracy from 89.02% to 92.04% while
BN also achieves a 1.18% performance gain. 2) AGN
performs better than the original GCN because of the
additional non-linear term. 3) We compare the perfor-
mance of different fusion strategies, and find out that
the proposed residual fusion outperforms the concate-
nation of AGN and BN outputs.
5 CONCLUSIONS
We have presented a hybrid machine learning frame-
work for lung nodule malignancy reasoning through
attribute relation modeling. A residual fusion strategy
is utilized in our framework to integrate two networks,
an attribute graph network and a Bayesian network.
Comprehensive experimental results on the LIDC-
IDRI benchmark dataset demonstrate that the whole
hybrid model can achieve a state-of-the-art classifi-
cation performance on the LIDC-IDRI dataset and
a strong generalization capability regardless of the
amount of training data.
REFERENCES
Akata, Z., Perronnin, F., Harchaoui, Z., and Schmid, C.
(2013). Label-embedding for attribute-based classi-
fication. In Proceedings of the IEEE Conference on
Computer Vision and Pattern Recognition, pages 819–
826.
Armato III, S. G., McLennan, G., Bidaut, L., McNitt-Gray,
M. F., Meyer, C. R., Reeves, A. P., Zhao, B., Aberle,
D. R., Henschke, C. I., Hoffman, E. A., et al. (2011).
The lung image database consortium (lidc) and image
database resource initiative (idri): a completed refer-
ence database of lung nodules on ct scans. Medical
physics, 38(2):915–931.
Barik, A. and Honorio, J. (2019). Learning bayesian net-
works with low rank conditional probability tables. In
Advances in Neural Information Processing Systems,
pages 8964–8973.
Bray, F., Ferlay, J., Soerjomataram, I., Siegel, R. L., Torre,
DeLTA 2021 - 2nd International Conference on Deep Learning Theory and Applications
64

Table 2: Ablation Study.
Training Nums Method Accuracy % Improvement % GCN-Channels
All-Training Samples
Base 89.02 - -
Base+GCN 91.03 2.01 128-64-32
Base+AGN 92.04 3.02 128-64-32
Base+BN 90.20 1.18 -
Ours-concat 92.12 3.10 128-64-32
Ours-residual 93.59 4.57 128-64-32
L. A., and Jemal, A. (2018). Global cancer statistics
2018: Globocan estimates of incidence and mortality
worldwide for 36 cancers in 185 countries. CA: a can-
cer journal for clinicians, 68(6):394–424.
Buty, M., Xu, Z., Gao, M., Bagci, U., Wu, A., and Mollura,
D. J. (2016). Characterization of lung nodule malig-
nancy using hybrid shape and appearance features. In
International Conference on Medical Image Comput-
ing and Computer-Assisted Intervention, pages 662–
670. Springer.
Dey, R., Lu, Z., and Hong, Y. (2018). Diagnostic classifi-
cation of lung nodules using 3d neural networks. In
2018 IEEE 15th International Symposium on Biomed-
ical Imaging (ISBI 2018), pages 774–778. IEEE.
Eaton, D. and Murphy, K. (2012). Bayesian structure learn-
ing using dynamic programming and mcmc. arXiv
preprint arXiv:1206.5247.
Elidan, G. (2010). Copula bayesian networks. In Advances
in neural information processing systems, pages 559–
567.
Ferrari, V. and Zisserman, A. (2008). Learning visual at-
tributes. In Advances in neural information process-
ing systems, pages 433–440.
Hussein, S., Gillies, R., Cao, K., Song, Q., and Bagci,
U. (2017). Tumornet: Lung nodule characteriza-
tion using multi-view convolutional neural network
with gaussian process. In 2017 IEEE 14th Inter-
national Symposium on Biomedical Imaging (ISBI
2017), pages 1007–1010. IEEE.
Jiang, H., Wang, R., Shan, S., Yang, Y., and Chen, X.
(2017). Learning discriminative latent attributes for
zero-shot classification. In Proceedings of the IEEE
International Conference on Computer Vision, pages
4223–4232.
Kingma, D. P. and Ba, J. (2014). Adam: A
method for stochastic optimization. arXiv preprint
arXiv:1412.6980.
Kipf, T. N. and Welling, M. (2016). Semi-supervised clas-
sification with graph convolutional networks. arXiv
preprint arXiv:1609.02907.
Kumar, N., Berg, A. C., Belhumeur, P. N., and Nayar, S. K.
(2009). Attribute and simile classifiers for face veri-
fication. In 2009 IEEE 12th international conference
on computer vision, pages 365–372. IEEE.
Lampert, C. H., Nickisch, H., and Harmeling, S. (2013).
Attribute-based classification for zero-shot visual ob-
ject categorization. IEEE transactions on pattern
analysis and machine intelligence, 36(3):453–465.
Liang, K., Chang, H., Ma, B., Shan, S., and Chen, X.
(2018). Unifying visual attribute learning with ob-
ject recognition in a multiplicative framework. IEEE
transactions on pattern analysis and machine intelli-
gence, 41(7):1747–1760.
Liang, K., Guo, Y., Chang, H., and Chen, X. (2017). In-
complete attribute learning with auxiliary labels. In
IJCAI, pages 2252–2258.
Liu, L., Dou, Q., Chen, H., Olatunji, I. E., Qin, J., and Heng,
P.-A. (2018). Mtmr-net: Multi-task deep learning with
margin ranking loss for lung nodule analysis. In Deep
Learning in Medical Image Analysis and Multimodal
Learning for Clinical Decision Support, pages 74–82.
Springer.
Liu, Z., Luo, P., Wang, X., and Tang, X. (2015). Deep
learning face attributes in the wild. In Proceedings
of the IEEE international conference on computer vi-
sion, pages 3730–3738.
Meng, Z., Adluru, N., Kim, H. J., Fung, G., and Singh,
V. (2018). Efficient relative attribute learning using
graph neural networks. In Proceedings of the Euro-
pean conference on computer vision (ECCV), pages
552–567.
Min, W., Mei, S., Liu, L., Wang, Y., and Jiang, S. (2019).
Multi-task deep relative attribute learning for visual
urban perception. IEEE Transactions on Image Pro-
cessing, 29:657–669.
Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J.,
Chanan, G., Killeen, T., Lin, Z., Gimelshein, N.,
Antiga, L., et al. (2019). Pytorch: An imperative
style, high-performance deep learning library. In
Advances in Neural Information Processing Systems,
pages 8024–8035.
Pearl, J. (1982). Reverend bayes on inference engines:
a distributed hierarchical approach. In Proceedings
of the Second AAAI Conference on Artificial Intelli-
gence, pages 133–136.
Pearl, J. (1998). Bayesian networks. In The handbook
of brain theory and neural networks, pages 149–153.
MIT Press.
Pearl, J. (2014). Probabilistic reasoning in intelligent sys-
tems: networks of plausible inference. Elsevier.
Rohekar, R. Y., Nisimov, S., Gurwicz, Y., Koren, G., and
Novik, G. (2018). Constructing deep neural net-
works by bayesian network structure learning. In
Advances in Neural Information Processing Systems,
pages 3047–3058.
Shen, S., Han, S. X., Aberle, D. R., Bui, A. A., and Hsu, W.
(2019). An interpretable deep hierarchical semantic
convolutional neural network for lung nodule malig-
nancy classification. Expert systems with applications,
128:84–95.
Attribute Relation Modeling for Pulmonary Nodule Malignancy Reasoning
65

Shen, W., Zhou, M., Yang, F., Yang, C., and Tian, J.
(2015). Multi-scale convolutional neural networks for
lung nodule classification. In International Confer-
ence on Information Processing in Medical Imaging,
pages 588–599. Springer.
Wang, Q., Huang, J., Liu, Z., Cheng, J.-Z., and Zhou, Y.
(2019). Higher-order transfer learning for pulmonary
nodule attribute prediction in chest ct images. In 2019
IEEE International Conference on Bioinformatics and
Biomedicine (BIBM 2019), pages 741–745.
Wit, E., Heuvel, E. v. d., and Romeijn, J.-W. (2012). ‘all
models are wrong...’: an introduction to model uncer-
tainty. Statistica Neerlandica, 66(3):217–236.
Xie, Y., Zhang, J., and Xia, Y. (2019). Semi-supervised
adversarial model for benign–malignant lung nodule
classification on chest ct. Medical image analysis,
57:237–248.
Xu, X., Wang, C., Guo, J., Gan, Y., Wang, J., Bai, H.,
Zhang, L., Li, W., and Yi, Z. (2020). Mscs-deepln:
Evaluating lung nodule malignancy using multi-scale
cost-sensitive neural networks. Medical Image Analy-
sis, page 101772.
DeLTA 2021 - 2nd International Conference on Deep Learning Theory and Applications
66