Synthesizing Fundus Photographies for Training Segmentation Networks

Jannes S. Magnusson

1,∗ a

, Ahmed J. Aﬁﬁ

2 b

, Shengjia Zhang

3 c

, Andreas Ley

and Olaf Hellwich

Institute of Computer-assisted Cardiovascular Medicine, Charit

e–Universit

atsmedizin Berlin,

Augustenburger Platz 1, 13353 Berlin, Germany

Computer Vision and Remote Sensing, Technische Universit

at Berlin, Marchstr. 23, 10587 Berlin, Germany

Shanghai Key Laboratory of Digital Media Processing and Transmission, Shanghai Jiao Tong University,

800 Dongchuan Rd., Minhang District, Shanghai, China

Keywords:

Fundus Image Synthezis, Retina Vessel Segmentation, Convolutional Neural Networks, ResNet, U-Net.

Abstract:

Automated semantic segmentation of medical imagery is a vital application using modern Deep Learning

methods as they can support clinicians in their decision-making processes. However, training these models

requires a large amount of training data which can be especially hard to obtain in the medical ﬁeld due to

ethical and data protection regulations. In this paper, we present a novel method to synthesize realistic retinal

fundus images. The process mainly includes the vessel tree generation and synthesis of non-vascular regions

(retinal background, fovea, and optic disc). We show that combining the (virtually) unlimited synthetic data

with the limited real data during training boosts segmentation performance beyond what can be achieved

with real data alone. We test the performance of the proposed method on the DRIVE and STARE databases.

The results highlight that the proposed data augmentation technique achieves state-of-the-art performance and

accuracy.

1 INTRODUCTION

Fundus photography is used for important medical

examinations of the retina to notice different dis-

eases early, such as age-related macular degenera-

tion, diabetic retinopathy, glaucoma, and many oth-

ers (Abr

amoff et al., 2010). A large number of algo-

rithms for optic disc (OD) detection, vessel segmenta-

tion, and width measurements were developed in or-

der to help clinicians with the diagnosis of diseases

(Patton et al., 2006). Among those methods, vessel

segmentation is a tough task due to varying vessel

sizes, low contrast images, and differences in the ap-

pearance of diseases like microaneurysms and hemor-

rhages (Liskowski and Krawiec, 2016a). Overcoming

these challenges may improve the diagnosis process

of different diseases.

To solve the retinal vessel segmentation (RVS)

task, deep learning plays a signiﬁcant role in recent

approaches. Different neural network architectures

were proposed to solve this problem (see Section 2.2).

https://orcid.org/0000-0002-3913-735X

https://orcid.org/0000-0001-6782-6753

https://orcid.org/0000-0001-7664-6500

∗

Corresponding author

Figure 1: The pipeline of the proposed method. In three

almost independent tasks, the image is generated piece by

piece, merged, and applied to general adjustments of illu-

mination, intensity, etc.

The main issue that was tackled is the issue of seg-

menting tiny vessels correctly ((Soomro et al., 2017),

(Feng et al., 2020)). Many methods introduced a large

and complex preprocessing pipeline to improve the

input image characteristics like contrast and illumina-

tion combined with data augmentation. This under-

Magnusson, J., Aﬁﬁ, A., Zhang, S., Ley, A. and Hellwich, O.

Synthesizing Fundus Photographies for Training Segmentation Networks.

DOI: 10.5220/0010618100670078

In Proceedings of the 2nd International Conference on Deep Learning Theory and Applications (DeLTA 2021), pages 67-78

ISBN: 978-989-758-526-5

lines the actual problem. There are databases avail-

able to use for training. They are mostly limited to

very few images (20 for STARE (Hoover et al., 2000),

40 for DRIVE (Staal et al., 2004)). Each image had

to be labeled by hand. Labeling one image needs

to be done by an expert for several hours (Hoover

et al., 2000) which makes gathering data very expen-

sive. Additionally, medical data is always linked to

patient privacy (Guibas et al., 2017). This limited

amount of images cannot fulﬁll the requirement of

sufﬁcient training data of an accurate segmentation

network based on deep learning. Synthesizing fun-

dus images can overcome this problem and provide a

ﬂexible environment to generate more data for train-

ing and validation.

In the past, some approaches were developed to

generate synthetic data. (Fiorini et al., 2014) and

(Zhao et al., 2018) only focus on generating synthetic

backgrounds by using real vessel trees. (Costa et al.,

2017b) provides a generation method for vessel trees

which produces unrealistic vessel trees with recoiling

branches and a little number of tiny vessels. Tiny ves-

sels are the main challenge in retinal vessel segmen-

tation. Synthetic data must therefore provide a de-

cent amount of tiny vessels to be sufﬁcient for well-

performing segmentation approaches.

The main contribution of the presented work is a

complete pipeline to synthesize realistic retinal fun-

dus images based on observations to the DRIVE

database. Figure 1 shows the pipeline of the proposed

synthesizing method. It mainly includes three parts:

• the generation of the vessel tree by a novel ap-

proach which overcomes the limitation of statisti-

cal models based on limited available data

• synthesizing non-vascular regions (optic disc,

background, and fovea)

• merging all components and adding ﬁnal tone

mapping

The advantage of this method is the focus on tiny

vessels to improve their segmentation. Lastly, it is

shown that data augmentation based on the synthetic

images achieves state-of-the-art performance in RVS

for DRIVE and STARE databases. The algorithm

and ﬁnal trained networks are publically available on

github

2 STATE-OF-THE-ART

Starting with state-of-the-art methods on retinal im-

age synthesis gives an overview of problems that are

https://github.com/jannessm/RetinaSynthesis

tackled by the presented method. To evaluate our

method, the impact in retinal image segmentation

must be discussed. Therefore, current progress in reti-

nal vessel segmentation is stated in the following.

2.1 Retinal Image Synthesis

The conventional approach of image synthesis tries

to ﬁnd mathematical models to describe image for-

mation and its characteristics. These can either be

based on anatomical knowledge or on statistical dis-

tributions and deviations.

The retinal image consists of three main elements:

the optic disc, the fovea, and the vascular network. A

complete process must synthesize all of them plus the

orange-red retinal tissue in the background. For the

generation of the background and the fovea, Fiorini

et al. (Fiorini et al., 2014) proposed a patch-based

approach, in which a color intensity distribution map

and its corresponding clustering map are constructed

from real images to build a dictionary of tiles for syn-

thesizing images. Additionally, Fiorini et al. (Fiorini

et al., 2014) developed a parametric intensity model

for the optic disc generation. The parameters were

estimated over 30 images from the High-Resolution

Fundus (HRF) Image Database (Budai et al., 2013).

Bonaldi et al. (Bonaldi et al., 2016) used an Ac-

tive Shape Model to extract the skeleton. A statistical

representation of landmarks on the image was devel-

oped. A spatial density distribution map of these land-

marks was used to generate bifurcation points. Mur-

ray’s Law is used to determine the angle and diameter

of branches.

Zhao et al. developed another GAN approach to

generate synthetic images according to a given ves-

sel tree (Zhao et al., 2018) similarly as (Costa et al.,

2017a).

A purely data-driven method has been proposed to

generate synthetic retinal images by deep learning ap-

proach (Costa et al., 2017b). An adversarial autoen-

coder is implemented to generate vessel networks fol-

lowed by a generative adversarial network (GAN) to

generate background, fovea, and optical disc accord-

ing to the vessel tree.

This brief overview stresses the lack of complete

pipelines of generating synthetic images including

synthetic vessel trees. The main issue of the usage of

deep learning-based approaches for vessel tree gener-

ation is that the density of vessels sometimes is too

high, some branches recoil, and the amount of tiny

vessels is less than for real images. Therefore, a

model is presented in the following to generate im-

ages with tiny vessels and an accurate representation

of these in the ground truth.

DeLTA 2021 - 2nd International Conference on Deep Learning Theory and Applications

2.2 Segmentation

Medical image analysis aims to develop auxiliary

tools e.g. algorithm-based computer software to help

clinicians to make better diagnoses and therapy plans.

Many approaches have been proposed to solve the

problem of retinal vessel segmentation (RVS). The

ﬁrst publication in 1989 uses Gaussian-shaped distri-

butions to approximate the gray-level proﬁle and by

ﬁlter matching, vessel segments are detected (Chaud-

huri et al., 1989). By then many publications ad-

dressed RVS in different ways. Some approaches

used hand-crafted features like pixels’ maximal gra-

dient and curvature in scale-space (Mart

ınez-P

erez

et al., 1999), or an active contour model which was

grown along vessels for detection (Al-Diri et al.,

2009).

With the growth of successes in deep learning, the

segmentation problem was addressed by neural net-

works (Soomro et al., 2019b). In 2015, Zhang et al.

(Zhang et al., 2015) trained a two-layer competitive

neural network (Kohonen’s self-organizing map) but

still, the average accuracy was only almost as good

as the human observer (see Table 2). In the same

year, another approach used a simple convolutional

network with 5 convolutional layers. It outperforms

the previous method but still performs worse than the

human observer used as the gold standard (Melin

cak

et al., 2015). In 2016, a very similar architecture was

used (4 convolutional layers with less max-pooling

than the previous work) and introduced a large pre-

processing pipeline including contrast normalization

and whitening. For data augmentation, not only sub-

sampling was used but also different transformations

like rotation and scaling (Liskowski and Krawiec,

2016b). These steps improved speciﬁcity and accu-

racy beyond the human observer. Far less successful

was the attempt to use a two-stage binarization by Yao

et al. (Yao et al., 2016). The enhanced green channel

of the input sample and a prediction of a CNN with 3

convolutions were combined into a ﬁnal segmentation

result.

Ngo and Han presented a multi-level CNN archi-

tecture in 2017 that used two scales of the image as

an input (Ngo and Han, 2017). Therefore, the high

detail in the large input could be combined with the

overall context from the large image. Soomro et al.

(Soomro et al., 2017) focused on both, using more ad-

vanced CNN architectures and improving the prepro-

cessing pipeline to enhance the feature quality that is

passed to the CNN. They used an encoder-decoder ar-

chitecture inspired by the success of the SegNet. For

preprocessing the image, morphological methods and

color-to-grey conversions based on PCA were used.

Later on, they showed that a modiﬁed version of the

U-Net in combination with the dice-loss further im-

proved the results (Soomro et al., 2019a). The ad-

vantage of the dice-loss is the consideration of unbal-

anced classes, like in this case. Vessels only appear

in 10% of all pixels (Soomro et al., 2017). (Hu et al.,

2018), (Wang et al., 2019), (Feng et al., 2020), and

(Zou et al., 2020) followed the approach of using pre-

vious features and combining these with deeper ones

in the neural network architecture. These achieved

state-of-the-art results. Since this paper focuses on

the generation of synthetic images, the success of U-

Net like architectures is used to prove the applicability

of the presented method.

However, the most prominent issue is missing out

on tiny vessels in the retinal images, which are hard

to detect. Often humans do not agree on the presence

of the tiniest vessels in the image. This and the limit

of available data is crucial for segmenting tiny vessels

based on deep learning. To improve the training pro-

cedure in segmentation, image synthesis is a good and

practical way to augment databases.

3 SYNTHESIS

The process of image synthesis involves two parts.

Firstly, the background with the fovea, optic disc,

and vessel trees are generated separately. Afterward,

those are combined into one image and a mask from

the DRIVE database is used to create the circular

crop. The combination is done by the Porter Duff

Composition (Porter, 1984). Examples of the ﬁnal

images can be seen in Figure 2. It is obvious to the hu-

man eye that these images are artiﬁcial but the results

show that the most important aspects to improve seg-

mentation are included. In contrast to the deep learn-

ing methods of (Zhao et al., 2018) and (Costa et al.,

2017b) additional variance of vessel trees and back-

grounds are added that are not included in the limited

amount of real data.

3.1 Background and Fovea

To generate realistic backgrounds for retinal images,

Perlin noise is used with ﬁve different octaves for pro-

ducing a non-uniform texture of the background. For

the fovea part, a simple circle will be colored by a

dark gradient. This results in smooth transitions be-

tween the fovea and the texture produced by the Perlin

noise. The color ranges are chosen on the basis of the

DRIVE database.

Synthesizing Fundus Photographies for Training Segmentation Networks

Figure 2: Examples of the generated synthetic images

created by the proposed method with their corresponding

ground-truths. In this overview, the different random pa-

rameters like mirroring or color ranges of the image are

clearly visible.

3.1.1 Texture

Perlin noise (Perlin, 2002) is used to generate the

background texture. It is a powerful method that is

often used in procedural content generation. Here, the

two-dimensional Perlin noise is implemented follow-

ing (Perlin, 2002). A pseudo-random gradient vector

is generated and interpolated by the quintic function

− 15t

+ 10t

. This is proposed to overcome arti-

facts. Furthermore, a mixture of ﬁve octaves P( f req)

with different amplitudes are used depending on the

size of s of the image which improves the result:

Texture = 0.1P(

) + 0.1P(

)

+ 0.2P(

) + 0.3P(

128

)

(1)

3.1.2 Fovea

It can be seen in Figure 1 that the fovea appears as

a darker spot in the center of the image. Hence, it

is sufﬁcient to use a gradient in that area that alters

the intensity of the texture generated before. This is

achieved by the following formulas.

dist(x,y,x

,r) =

min



(x − x

)

+ (y − y

)



(2)

f (x,y,x

,r) = 0.5 +

3dist − 2dist

(3)

Figure 3: The RGB value distributions of the optic disc of

a sample from the DRIVE database (from top to bottom:

R, G, B; from left to right: original image, mathematical

model). The discontinuity in the left images is the result of

removing vessels in the optic disc area as shown in Figure

Equation 2 calculates the distance to the center of

the fovea (x

) which is chosen randomly. r denotes

the radius of the fovea which is picked according to

the anatomical characteristics. Equation 3 uses this

distance to create an intensity factor in the range of

[0.58,1]. This factor is applied to each color channel.

3.2 Optic Disc

The optic disc has a yellow circular shape. More pre-

cisely, it is made up of an inner circle and an outer

circle. Both of them are brighter than other structures

in the image and the inner circle is brighter than the

outer circle.

To analyze the most signiﬁcant aspects of the op-

tic disc, the color distribution of the retinal image in

three color channels is plotted in Figure 3. It stresses

that red values form a mountain with a ﬂat hilltop.

The surface of green values and blue values have a

cone-shaped structure on the top of a shape that is

similar to the previous red value surface. To synthe-

size the optic disc, the method from (Fiorini et al.,

2014) is adopted to calculate color values (Equation

4 and Equation 7). Because the distribution of green

values and blue values are almost the same, they share

the same mathematical model.

R(x,y, p

) = z

+ exp[l − m]

(4)

where l and m are deﬁned as

DeLTA 2021 - 2nd International Conference on Deep Learning Theory and Applications

Figure 4: From left to right: real retinal image, segmented

optic disc (after removing vessels), randomly synthesized

optic disc 1, and the randomly synthesized optic disc 2.

l = −(

x − x

+ cos(wφ)

)

(5)

m = (

y − y

+ cos(wφ)

)

(6)

GB(x,y,p

) = R(x,y, p

)

− kexp



−(

x − x

)

− (

y − y

)



(7)

In these equations, p

= [z

,σ

], p

,σ

], and q

= [k,x

,σ

] are the cor-

responding parameter sets. z denotes the base color

value. a denotes how large the plain area on the hill-

top is. (x

) describes the center of the inner circle

and the outer circle of the optic disc. σ denotes the

degree of spread or scatter. k denotes the height of the

cone-shaped structure and φ = arctan(y − y

,x − x

They are all estimated by ﬁtting the model to real im-

ages using a non-linear least squares regression. To

eliminate the inﬂuence of the vessels over the optic

disc whose colors are darker, the optic disc is ex-

tracted. Then the model is ﬁtted to this extracted

area as shown in Figure 4. The position of the op-

tic disc is determined by the fovea’s position and the

distance between them according to medical knowl-

edge (Patzelt, 2009). By adding small and reasonable

random offsets to each parameter, many different op-

tic disc images can be generated.

3.3 Vessels

The vessel tree is generated in three steps. Firstly,

a starting and target point for each vessel has to be

determined. Then the path between those points has

to be generated to display each pixel. Finally, the path

is drawn on an image. In the following, the horizontal

image size is denoted as h. In contrast to the method

of Castro et al. (Castro et al., 2020), various levels of

vessels are distinguished to enhance the control over

each level.

3.3.1 Select Target Points

For selecting a target point, three levels of branches

are differentiated. Each level follows a different

heuristic. The ﬁrst level vessels are the main branches

starting from the center of the optic disc. There are

four vessels for arteries and four for veins. Each ves-

sel leads to one edge of the image. To randomize

the resulting branches, for each vessel a random point

from a speciﬁc area in each corner of the image is se-

lected. These regions are either left to the fovea or

right to the optic disc, assuming that the optic disc

is always right to the fovea. The regions left to the

fovea are therefore determined by the location of the

fovea. The regions right to the optic disc are selected

according to the position of the optic disc and the im-

age dimensions. All values are selected empirically

with the assumption that the main vessels have to go

beyond the boundaries of the image.

For the second level (the subbranches of the main

vessels), the position on the starting point on the main

vessel is analyzed and a new target point is selected.

The calculation of this new target point differs be-

tween points on the left of the optic disc and on the

right of the optic disc.

If the starting point is left to the optic disc, either

the new vessel grows to the fovea or away from it.

But for both opportunities, the new x coordinate is

to the left of the starting point. Therefore, the main

direction of the new vessel differs less than 90

◦

to the

main direction from the parent. This is important to

ensure realistic blood ﬂow. The y direction is either

almost at the fovea (with a probability of 0.5) or the

y position of the starting point added with a random

number j ∈ [40,0.3h]. As a reminder, h denotes the

image width.

For the second case for the second level of

branches (the starting point lies right to the optic

disc), the direction vector from the starting point to

the target point of the parent vessel is normalized

to a length of 1, then rotated by α ∈ [30

◦

,70

◦

], and

stretched to the length l ∈ [40,0.3h].

The last heuristic covers all levels higher than

level 2. In this method, a window w with a size s

of the binary image of the tree is analyzed around the

starting point p

. All regions between vessels in w

are segmented and labeled uniquely. If a region con-

tains more than 1% of the image size and is directly

located next to the parent vessel of p

, the center c

of this region is considered as a candidate for a new

target point. Additionally, only candidates are consid-

ered, where the path from p

to c does not cross any

other vessel. If candidates were found, the center of

the largest region is selected as a ﬁnal candidate. To

prevent parallel vessels, the angle between p

to the

parent’s target point, and from p

to the ﬁnal candi-

date needs to be higher than 20

◦

To get a center of a large area, the size of the

Synthesizing Fundus Photographies for Training Segmentation Networks

Figure 5: In the left setup, the vessel needs to move around the fovea. Starting at the current point x. ~r is rotated by θ to x

With respect to the baseline from x to x

, x

is again rotated by a random angle ∈ [−30

◦

,30

◦

]. This results in a next point i

which is added to the current vessel. In the right setup, the baseline can be set straightforward to the target point. Resulting in

point i after the same rotations θ and by an random angle as in the left setup.

window s is increased until the maximum of 2h/3 is

reached or a candidate moved more than 3 px in an

increasing step. The movement indicates that two re-

gions have merged because of the increased width of

the window.

3.3.2 Determine the Vessel Path

To imitate realistic retinal vessels, a curly vessel path

is required. Additionally, the vessels need to curve

around the fovea at ﬁrst and then head to the target

point.

The positions of the fovea, the target point y, and

the current point x are used to determine a new and

next point i which is at a random distance of l. The

vector from the fovea to x is called~r, the vector from

the fovea to y is called ~r

and ~r

is the vector from the

fovea to i. Two situations are discriminated, either the

angle between ~r and ~r

is larger than 90

◦

or smaller

than 90

◦

. Both situations are visualized in Figure 5.

In the ﬁrst situation, x is near the starting point.

An angle θ is calculated based on l and |~r| in Equa-

tion 8. Parameter ε is introduced to add randomness.

Then~r is rotated by θ towards y. The endpoint is de-

noted as x

so that the vector from x to x

is denoted as

. Afterwards,

is rotated in a range of [−30

◦

,30

◦

]

to get the ﬁnal direction to i so that the vessel path

appears curly. At last, i is determined with a distance

l from x (see left sketch of Figure 5).

θ =

|~r| + ε

,ε ∈ [−20,10] (8)

In the second situation as shown on the right in

Figure 5, the baseline is directly set from x to y and

the location of i is determined within an angle range

of [−30

◦

,30

◦

] and distance of l from x.

The method is repeated until the distance between

x and y is smaller than a threshold of 0.03h or x is out

of the image.

3.3.3 Drawing Vessels

To create colored images from the points generated

along a vessel, all points are interpolated by a cubic

spline. Next, colors are selected and widths are de-

termined along the path. From the target point to the

starting point the width is increased by Equation 9.

This function increases the width for every i-th point

on the path by α, starting from a diameter of d pt.

Each level of vessels has its own α and d which en-

sures realistic diameters.

f (x) =

α · i

+ d

565

(9)

For the colors, different values for arteries and

veins are chosen empirically by comparing the result

with real images. Arteries are colored with a RBGA

value of (150, 30, 10, t) and veins have a color of (110,

10, 5, t). t determines the transparency of the vessel

so that the ends of vessels will disappear slowly as can

be noticed in real fundus photographies.

3.4 CNN Architecture and Training

Details

The underlying architecture is based on a modiﬁed

encoder-decoder architecture called Res-U-Nets. A

similar architecture was used by (Ibtehaz and Rah-

man, 2020) which has shown great performance on

medical segmentation tasks. One difference to our

network is that residual blocks are used within the en-

coder and decoder (Figure 6) instead of normal con-

volutions. Furthermore, (Ibtehaz and Rahman, 2020)

adds other residual convolutions in the connection

from the encoder to the decoder where the used net-

work does not further process the data on these con-

nections. The last difference is the inclusion of two

downsampling and upsampling blocks in the encoder

DeLTA 2021 - 2nd International Conference on Deep Learning Theory and Applications

Figure 6: The architecture used to evaluate the generated synthetic images on the left. The purple and blue blocks represent

residual blocks for encoder and decoder respectively from the right of this ﬁgure. At the top, one can see the encoder, whereas

the bottom describes a decoder block.

and decoder. The whole network can be seen in Fig-

ure 6 which outlines the U-Net shape and refers to the

special residual network blocks in different colors.

The resulting network is trained on patches of size

128 × 128 pixels with basic data augmentation pre-

processing including random brightness, contrast, and

noise to gain robustness in the predictions. Through

the limitation of real images, the main goal of the

training process is to retrieve all important statistics

from these images which are learned by the ﬁrst lay-

ers. For all deeper layers, it is important to learn the

overall structure of retinal images. This is covered

well by the generated, synthetic images. Therefore,

the proposed training process uses mini-batches of 32

items including 16 synthetic and 16 realistic patches

of the DRIVE dataset.

To check the usefulness of the synthesized fun-

dus images by the proposed method, four experiments

are conducted and evaluated quantitatively and quali-

tatively. The four experiments only differ in the input

data and size of the Res-U-Net that was used.

The ﬁrst experiment consists of a small Res-U-Net

with residual blocks trained only on the training im-

ages of the DRIVE database. To increase the amount

of data and avoid overﬁtting, basic data augmentation

is applied. In the second experiment, a deeper Res-

U-Net is trained using the same data as before. By

the ﬁrst two experiments, the impact of enlarging the

network can be seen.

To evaluate different data setups with synthetic

images, the next two experiments are using the same

network as before with synthetic data only. The fourth

model is trained using combined training images from

the DRIVE database and the synthetic images.

In all experiments, the trained models are tested

on the testing images of the DRIVE database. The

ﬁrst three experiments perform as the base setups and

the fourth trained model is the main model which is

compared against other state-of-the-art methods. Fol-

lowing, some details about the network architecture

are stated.

4 EVALUATION

4.1 Databases

To evaluate the proposed method and its usefulness

for RVS, we use two publicly available databases

named DRIVE and STARE. These two databases are

widely used to evaluate the performance of retinal

vessel segmentation methods.

The DRIVE database (Staal et al., 2004) contains

40 images along with their segmented vessel images.

The images have a resolution of 768 ×584 pixels. The

images are divided into two sets, 20 images are in the

training set and 20 images are in the testing set.

STARE database (Hoover et al., 2000) contains 20

images. This database is challenging because 10 im-

ages contain pathologies. The images have a resolu-

tion of 605 × 700 pixels.

The performance of the proposed method is mea-

sured through the following four parameters:

Sensitivity(Se) =

T P

T P + FN

(10)

Speci f icity(Sp) =

T N

T N + FP

(11)

Accuracy(Acc) =

T P + T N

T P + FP + FN + T N

(12)

TP is true positive, TN is true negative, FP is false

positive, and FN is false negative.

Synthesizing Fundus Photographies for Training Segmentation Networks

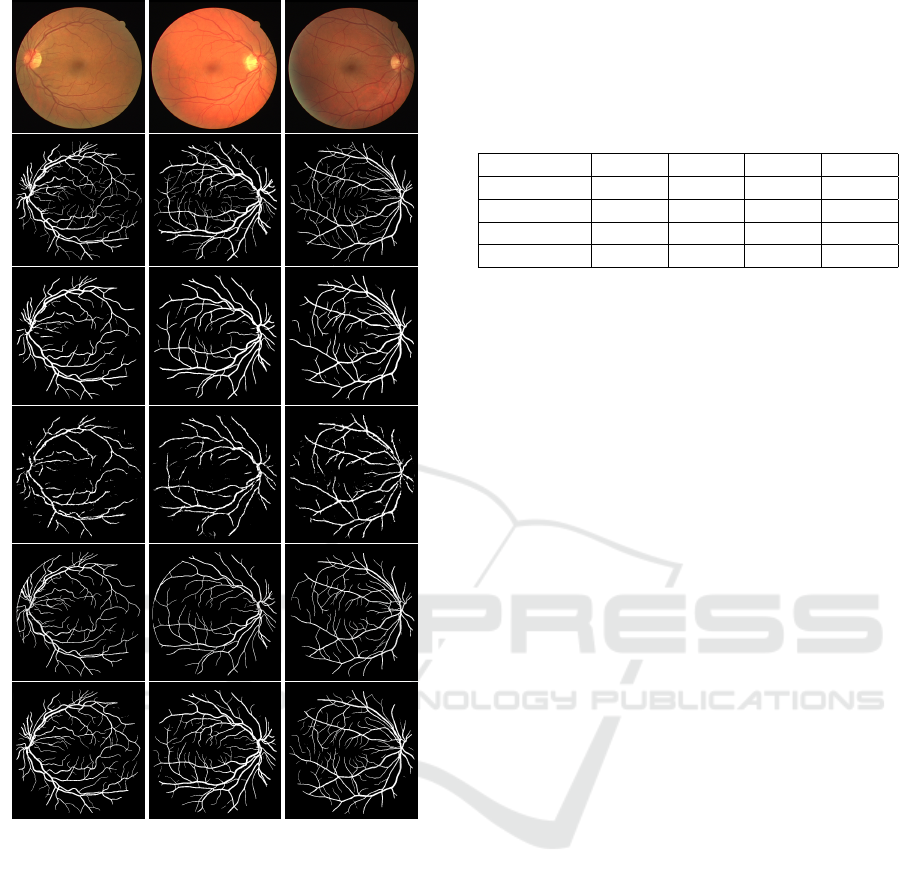
Figure 7: The segmented images from different experi-

ments. From top to bottom: input image, ground-truth,

segmented images from the small model trained using

DRIVE database, the segmented images from the large

model trained using DRIVE database, the segmented im-

ages from the large model trained using synthetic images,

and the segmented images from the large model trained us-

ing a mix of real and synthetic images.

4.2 Results

Table 1 reports the quantitative results of each experi-

ment. Experiment 1 (DRIVE 1) demonstrates that the

small network can be trained to generate segmented

vessel images using a small number of images after

applying data augmentation. The sensitivity and ac-

curacy of this model reached 0.7448 and 0.9493, re-

spectively. Figure 7 (third row) presents the gener-

ated segmented images where some tiny vessels are

Table 1: Quantitative results of different experiments using

different conﬁgurations with respect to the training images

and the model. DRIVE 1 refers to a small network trained

only on DRIVE images whereas DRIVE 2 is a larger net-

work with the same training data. Synthetic and combined

represent experiments on the large network with only syn-

thetic data or DRIVE and synthetic data, respectively.

Experiment Se Sp Acc AUC

DRIVE 1 0.7448 0.9796 0.9493 0.9609

DRIVE 2 0.56 0.977 0.9237 0.7865

synthetic 0.667 0.9858 0.9449 0.9541

combined 0.8334 0.9715 0.9554 0.9784

missing but the general results are plausible. When

training a large network without synthetic images, the

accuracy and sensitivity drop as reported in Table 1

(DRIVE 2). Through the number of model parame-

ters, it is hard to optimize a large model with a small

number of training images. Figure 7 (fourth row)

shows the output of this model and it is clear that the

accuracy is lower than in the other experiments and

the model drops out many vessels. This setup has a

problem with indicating the main structure of the ves-

sels as the model is large and the number of training

samples is small.

In the third experiment, the network learns the

general structure of the vessel tree from synthetic data

which improves memorizing the different shapes of

tiny and thick vessels. The accuracy of this model

improves compared to the same model trained only on

DRIVE images. However, because the model didn’t

train on real images, the accuracy is lower than the

accuracy of the small model (ﬁrst experiment). The

generated images are shown in Figure 7 (ﬁfth row).

They show that the model can extract more vessels

and can ﬁnd the tiny ones. The vessel trees of the

synthetic images contain many tiny vessels. Conse-

quently, the network is able to learn how to extract

them. This underlines that the proposed method pro-

duces images that are realistic enough to be used for

training models.

In the last experiment, the model performs best

among the other experiments as the model uses data

from real and synthetic images. The model learns dif-

ferent structures and generalizes the statistics by com-

bining real and synthetic images during training. This

can be clearly seen in Figure 7 (sixth row) as the gen-

erated images contain thick and tiny vessels and are

comparable to the ground-truth images. Additionally,

this model obtains an accuracy of 0.9554 and a sen-

sitivity of 0.8334. Figure 8 shows the AUC result of

the best-trained model in experiment 4.

Furthermore, we validate the proposed method on

the STARE database qualitatively. Figure 9 shows

output segmented images of selected input images

DeLTA 2021 - 2nd International Conference on Deep Learning Theory and Applications

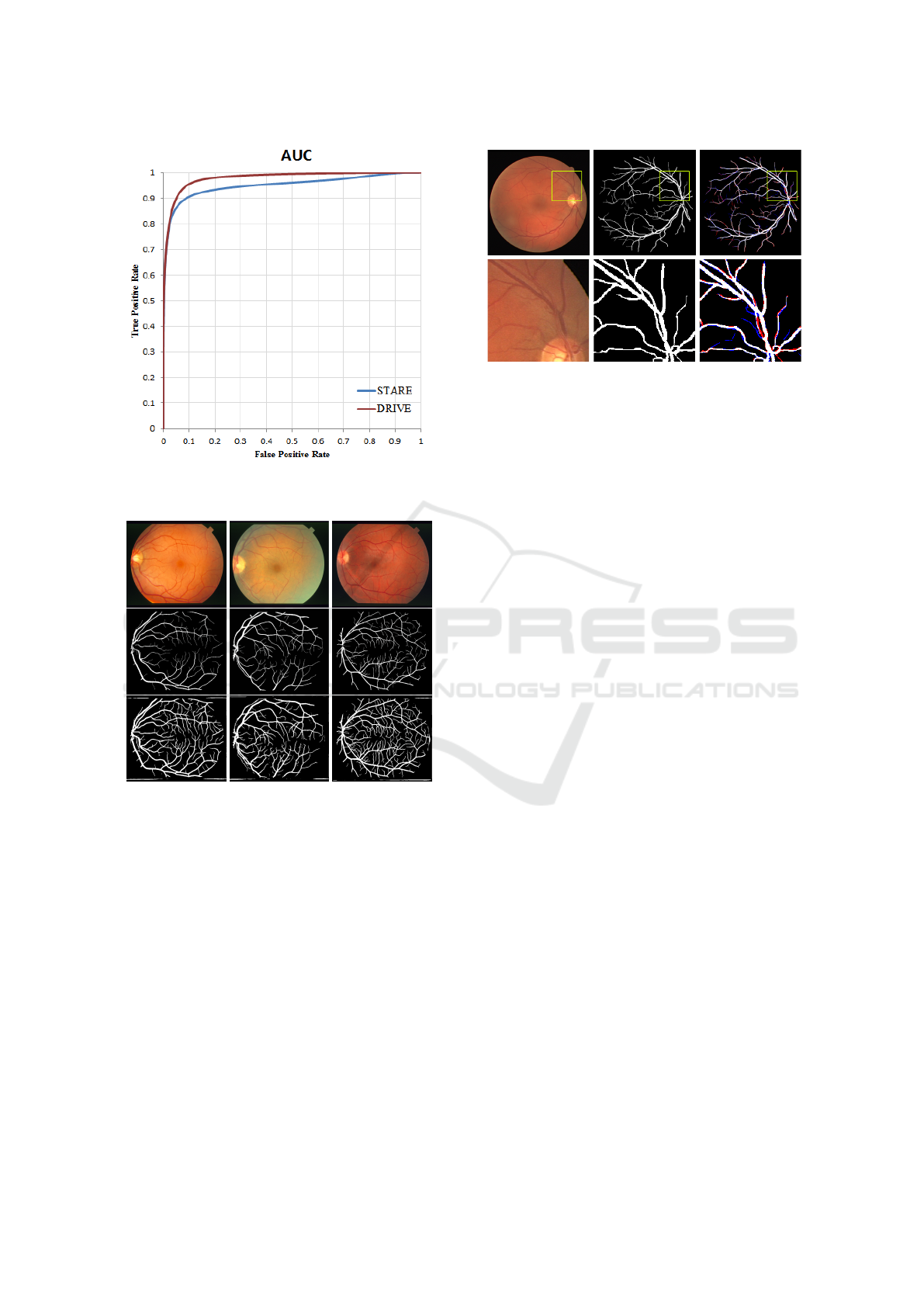
Figure 8: Area Under Curve plots of the DRIVE and

STARE databases.

Figure 9: Segmented images from experiment 4 on the

STARE database. From top to bottom: input image,

ground-truth, segmented images from the large model

trained using a mix of real and synthetic images. It is no-

table that much more small vessels were recognized which

were not segmented by the human expert.

from the STARE results. It is clearly shown that the

proposed method managed to segment the vessels ac-

curately. Figure 8 shows the AUC plot of the pro-

posed method on the STARE database. It is noted

that the proposed model was only trained on DRIVE

data and therefore shows that the applied method

also translates well from DRIVE to the more difﬁcult

STARE data.

Figure 10: An example of the important observation of the

predictions from experiment 4 is shown. From left to right

an image from the DRIVE database, the respective ground-

truth, and the prediction of the combined method are pre-

sented. In the right image, red marks false positive predic-

tions and blue marks true negative predictions.

4.3 Further Observations

An interesting observation of the generated images

is that in some generated images the model extracts

vessels that are not found in the ground-truth images.

Figure 10 shows an example of a segmented image

that contains vessels that are not recognized by the

expert but by the presented network. In Figure 10, the

red color denotes vessels that are in the ground-truth

but the model didn’t detect them as vessels. The blue

color denotes vessels that are extracted by the model

but they are not in the ground-truth.

4.4 Comparison to State-of-the-Art

Methods

To prove the feasibility of using synthetic images for

training, our proposed method is compared against

other deep learning-based methods for retinal blood

vessel segmentation on the DRIVE and STARE

databases. As reported in Table 2 and Table 3, our

method scores the highest sensitivity and AUC com-

paring to the other reported methods.

AUC can be argued to be more relevant since sen-

sitivity, speciﬁcity, and accuracy depend on a ﬁxed

threshold. Whereas AUC indicates the accuracy over

all possible thresholds. This indicates that the method

trained on real and synthetic images has the capabil-

ity to detect and segment more vessels than previous

methods. Correspondingly, it also extracts vessel-like

shapes that are not in the ground-truth images. This is

a result of using the synthetic images during training

where the synthetic images cover large different cases

of the vessels tree. From Table 2, it is clearly shown

that the setup of a model with the mixed training data

Synthesizing Fundus Photographies for Training Segmentation Networks

Table 2: Comparison of the proposed method trained using mixed images with other CNN-based learning methods on the

DRIVE database.

Method Se Sp Acc AUC

Human observer 0.7598 0.9725 0.9473 -

Zhang et al. (Zhang et al., 2015) - - 0.940 -

Melinscak et al. (Melin

cak et al., 2015) - - 0.9466 0.9749

Liskowski and Krawiec (Liskowski and Krawiec, 2016b) 0.7520 0.9806 0.9515 0.9710

Yao et al. (Yao et al., 2016) 0.7731 0.9603 0.9360 -

Ngo and Han (Ngo and Han, 2017) 0.7464 0.9836 0.9533 0.9752

Soomro et al. (Soomro et al., 2017) 0.746 0.917 0.947 0.8310

Soomro et al. (Soomro et al., 2018) 0.739 0.956 0.948 0.8440

Hu et al. (Hu et al., 2018) 0.7772 0.9793 0.9533 0.9759

Wang et al. (Wang et al., 2019) 0.7986 0.9736 0.9511 0.9740

Feng et al. (Feng et al., 2020) 0.7625 0.9809 0.9528 0.9678

Zou et al. (Zou et al., 2020) 0.7761 0.9792 0.9519 -

Joshua et al. (Joshua et al., 2020) 0.8309 0.9742 0.9615 -

Pedro Costa et al. (Costa et al., 2017b) - - - 0.887 ± 0.004

Our method 0.8334 0.9715 0.9554 0.9784

Table 3: Comparison of the proposed method trained using mixed images with other CNN-based learning methods on the

STARE database.

Method Se Sp Acc AUC

Liskowski and Krawiec (Liskowski and Krawiec, 2016b) 0.8145 0.9866 0.9696 0.988

Soomro et al. (Soomro et al., 2017) 0.748 0.922 0.947 0.853

Soomro et al. (Soomro et al., 2018) 0.748 0.962 0.947 0.855

Hu et al. (Hu et al., 2018) 0.7543 0.9814 0.9632 0.9751

Wang et al. (Wang et al., 2019) 0.7914 0.9722 0.9538 0.9704

Feng et al. (Feng et al., 2020) 0.7709 0.9848 0.9633 0.97

Zou et al. (Zou et al., 2020) 0.7107 0.9754 0.9477 -

Joshua et al. (Joshua et al., 2020) 0.7506 0.9824 0.9658 -

Our method 0.818 0.9705 0.9589 0.9421

Table 4: Quantitative comparison between the proposed

method and approaches for fundus synthesis of Z. (Zhao

et al., 2018) and C. (Costa et al., 2017b). It highlights the

advantage of our method when synthetic images are com-

bined with the data of the DRIVE database.

Data Se Sp AUC

real (ours) 0.7448 0.9796 0.9609

real (Z.) 0.8033 0.9785 -

real (C.) - - 0.887

synthetic (ours) 0.667 0.9858 0.9541

synthetic (Z.) 0.6857 0.9779 -

synthetic (C.) - - 0.841

combined (ours) 0.8334 0.9715 0.9784

combined (Z.) 0.8038 0.9815 -

improves the model performance and outperforms the

usual training techniques on the DRIVE database. Ta-

ble 3 shows the performance of the proposed method

against other methods on the STARE database.

Since the main contribution is the synthesis

pipeline, the proposed method is compared to the

state-of-the-art methods in generating synthetic fun-

dus images by GANs (Costa et al., 2017b), (Zhao

et al., 2018). The results are summarized in Table

4. It can be seen that our approach achieved compa-

rable results with the beneﬁt of a complete adjustable

pipeline for adding characteristics of speciﬁc diseases

(see Table 4). The pipeline presented in this work

generates vessel trees which Zhao et al. does not

(Zhao et al., 2018). Additionally, it creates more re-

alistic vessel trees than the GAN approach of Costa

et al. which has recoiling branches and less tiny ves-

sels (Costa et al., 2017b). The recently published ves-

sel tree synthesis approach of Castro et al. was not

evaluated on the task of vessel segmentation and can

therefore not be compared (Castro et al., 2020).

DeLTA 2021 - 2nd International Conference on Deep Learning Theory and Applications

5 CONCLUSION

This paper presented a completely new approach to

synthesize retinal fundus photographs and using the

synthetic images for CNN training. In comparison to

other state-of-the-art approaches like the method pre-

sented in (Costa et al., 2017b), the proposed synthe-

sizing method generates a very realistic vessels tree

without unconnected vessels. The ﬁnal synthesized

image is a realistic image that achieves state-of-the-art

performance in segmentation networks without com-

plex preprocessing and can, therefore, be used to en-

large training sets and solve the problem of lacking

training data. The proposed approach improved the

performance of vessel segmentation as shown quanti-

tatively and qualitatively from the conducted experi-

ments and the comparison against state-of-the-art reti-

nal vessel segmentation.

As future work, we will consider different

databases that are used in retinal vessel segmentation

such as HRF or CHASE DB1 to be synthesized which

includes various disease patterns. The synthesizing

process will be adjustable to generate more realistic

images with different resolutions and generalize the

statistical shapes of different real databases.

Finally, it is stressed that due to the highly ad-

justable pipeline, the generated images are easily use-

able for optic disc segmentation and fovea localiza-

tion tasks.

REFERENCES

Abr

amoff, M. D., Garvin, M. K., and Sonka, M. (2010).

Retinal imaging and image analysis. IEEE reviews in

biomedical engineering, 3:169–208.

Al-Diri, B., Hunter, A., and Steel, D. (2009). An ac-

tive contour model for segmenting and measuring reti-

nal vessels. IEEE Transactions on Medical imaging,

28(9):1488–1497.

Bonaldi, L., Menti, E., Ballerini, L., Ruggeri, A., and

Trucco, E. (2016). Automatic generation of synthetic

retinal fundus images: Vascular network. In MIUA,

pages 54–60.

Budai, A., Bock, R., Maier, A., Hornegger, J., and Michel-

son, G. (2013). Robust vessel segmentation in fundus

images. International journal of biomedical imaging,

2013.

Castro, D. L., Valenti, C., and Tegolo, D. (2020). Retinal

image synthesis through the least action principle. In

2020 5th International Conf. on Intelligent Informat-

ics and Biomedical Sciences (ICIIBMS), pages 111–

116. IEEE.

Chaudhuri, S., Chatterjee, S., Katz, N., Nelson, M., and

Goldbaum, M. (1989). Detection of blood vessels in

retinal images using two-dimensional matched ﬁlters.

IEEE Transactions on medical imaging, 8(3):263–

269.

Costa, P., Galdran, A., Meyer, M. I., Mendonc¸a, A. M., and

Campilho, A. (2017a). Adversarial synthesis of reti-

nal images from vessel trees. In International Confer-

ence Image Analysis and Recognition, pages 516–523.

Springer.

Costa, P., Galdran, A., Meyer, M. I., Niemeijer, M.,

Abr

amoff, M., Mendonc¸a, A. M., and Campilho,

A. (2017b). End-to-end adversarial retinal image

synthesis. IEEE transactions on medical imaging,

37(3):781–791.

Feng, S., Zhuo, Z., Pan, D., and Tian, Q. (2020). Ccnet: A

cross-connected convolutional network for segment-

ing retinal vessels using multi-scale features. Neuro-

computing, 392:268–276.

Fiorini, S., Ballerini, L., Trucco, E., and Ruggeri, A. (2014).

Automatic generation of synthetic retinal fundus im-

ages. In Eurographics Italian Chapter Conference,

pages 41–44.

Guibas, J. T., Virdi, T. S., and Li, P. S. (2017). Synthetic

medical images from dual generative adversarial net-

works. arXiv preprint arXiv:1709.01872.

Hoover, A., Kouznetsova, V., and Goldbaum, M. (2000).

Locating blood vessels in retinal images by piecewise

threshold probing of a matched ﬁlter response. IEEE

Transactions on Medical imaging, 19(3):203–210.

Hu, K., Zhang, Z., Niu, X., Zhang, Y., Cao, C., Xiao, F.,

and Gao, X. (2018). Retinal vessel segmentation of

color fundus images using multiscale convolutional

neural network with an improved cross-entropy loss

function. Neurocomputing, 309:179–191.

Ibtehaz, N. and Rahman, M. S. (2020). Multiresunet:

Rethinking the u-net architecture for multimodal

biomedical image segmentation. Neural Networks,

121:74 – 87.

Joshua, A. O., Nelwamondo, F. V., and Mabuza-Hocquet,

G. (2020). Blood vessel segmentation from fundus

images using modiﬁed u-net convolutional neural net-

work. Journal of Image and Graphics, 8(1).

Liskowski, P. and Krawiec, K. (2016a). Segmenting reti-

nal blood vessels with deep neural networks. IEEE

transactions on medical imaging, 35(11):2369–2380.

Liskowski, P. and Krawiec, K. (2016b). Segmenting reti-

nal blood vessels with deep neural networks. IEEE

transactions on medical imaging, 35(11):2369–2380.

Mart

ınez-P

erez, M. E., Hughes, A. D., Stanton, A. V.,

Thom, S. A., Bharath, A. A., and Parker, K. H.

(1999). Retinal blood vessel segmentation by means

of scale-space analysis and region growing. In In-

ternational Conference on Medical Image Comput-

ing and Computer-Assisted Intervention, pages 90–

97. Springer.

Melin

cak, M., Prenta

c, P., and Lon

cari

c, S. (2015). Reti-

nal vessel segmentation using deep neural networks.

In 10th International Conference on Computer Vision

Theory and Applications (VISAPP 2015).

Ngo, L. and Han, J.-H. (2017). Multi-level deep neural

network for efﬁcient segmentation of blood vessels

Synthesizing Fundus Photographies for Training Segmentation Networks

in fundus images. Electronics Letters, 53(16):1096–

1098.

Patton, N., Aslam, T. M., MacGillivray, T., Deary, I. J.,

Dhillon, B., Eikelboom, R. H., Yogesan, K., and Con-

stable, I. J. (2006). Retinal image analysis: concepts,

applications and potential. Progress in retinal and eye

research, 25(1):99–127.

Patzelt, J. (2009). Basics Augenheilkunde. Elsevier, Ur-

ban&FischerVerlag.

Perlin, K. (2002). Improving noise. In Proceedings of the

29th annual conference on Computer graphics and in-

teractive techniques, pages 681–682.

Porter, T. (1984). Compositing digital images. Computer

Graphics Volume18, Number3 July 1984, pages 253–

259.

Soomro, T. A., Aﬁﬁ, A. J., Gao, J., Hellwich, O., Khan,

M. A., Paul, M., and Zheng, L. (2017). Boosting sen-

sitivity of a retinal vessel segmentation algorithm with

convolutional neural network. In 2017 International

Conference on Digital Image Computing: Techniques

and Applications (DICTA), pages 1–8. IEEE.

Soomro, T. A., Aﬁﬁ, A. J., Gao, J., Hellwich, O., Paul, M.,

and Zheng, L. (2018). Strided u-net model: Retinal

vessels segmentation using dice loss. In 2018 Dig-

ital Image Computing: Techniques and Applications

(DICTA), pages 1–8. IEEE.

Soomro, T. A., Aﬁﬁ, A. J., Gao, J., Hellwich, O., Zheng,

L., and Paul, M. (2019a). Strided fully convolutional

neural network for boosting the sensitivity of retinal

blood vessels segmentation. Expert Systems with Ap-

plications, 134:36–52.

Soomro, T. A., Aﬁﬁ, A. J., Zheng, L., Soomro, S., Gao,

J., Hellwich, O., and Paul, M. (2019b). Deep learn-

ing models for retinal blood vessels segmentation: A

review. IEEE Access, 7:71696–71717.

Staal, J., Abr

amoff, M. D., Niemeijer, M., Viergever, M. A.,

and Van Ginneken, B. (2004). Ridge-based vessel seg-

mentation in color images of the retina. IEEE trans-

actions on medical imaging, 23(4):501–509.

Wang, C., Zhao, Z., Ren, Q., Xu, Y., and Yu, Y. (2019).

Dense u-net based on patch-based learning for retinal

vessel segmentation. Entropy, 21(2):168.

Yao, Z., Zhang, Z., and Xu, L.-Q. (2016). Convolu-

tional neural network for retinal blood vessel segmen-

tation. In 2016 9th international symposium on Com-

putational intelligence and design (ISCID), volume 1,

pages 406–409. IEEE.

Zhang, J., Cui, Y., Jiang, W., and Wang, L. (2015). Blood

vessel segmentation of retinal images based on neural

network. In International Conference on Image and

Graphics, pages 11–17. Springer.

Zhao, H., Li, H., Maurer-Stroh, S., and Cheng, L. (2018).

Synthesizing retinal and neuronal images with gener-

ative adversarial nets. Medical image analysis, 49:14–

26.

Zou, B., Dai, Y., He, Q., Zhu, C., Liu, G., Su, Y., and

Tang, R. (2020). Multi-label classiﬁcation scheme

based on local regression for retinal vessel segmenta-

tion. IEEE/ACM Transactions on Computational Bi-

ology and Bioinformatics.

DeLTA 2021 - 2nd International Conference on Deep Learning Theory and Applications