
Control System Design via Constraint Satisfaction using
Convolutional Neural Networks and Black Hole Optimization
Saber Yaghoobi
a
and M. Sami Fadali
b
Department of Electrical and Biomedical Engineering, University of Nevada, Reno, U.S.A.
Keywords: Bouc-Wen Hysteresis Model, Constraint Satisfaction Problem, Control System Design, MBH Optimization
Algorithm, Deep Learning, PID Controller.
Abstract: This paper proposes a new approach to control system design through solving a Constraint Satisfaction
Problem (CSP) using artificial intelligence, first using a genetic algorithm then using a Convolutional Neural
Network (CNN). The genetic algorithm determines the feasible controller parameters by minimizing a cost
function subject to inequality design constraints. The CNN-finds the parameters by designing a deep neural
network. It is shown that the evolutionary optimization algorithm converges almost surely to the optimal
solution. To demonstrate the methodologies, they are applied to the design of PID controllers for linear and
nonlinear systems. Two examples are presented, an armature-controlled DC motor and Bouc-Wen nonlinear
hysteresis model. Simulations results show that the proposed methods yield solutions that satisfy design
specifications.
1 INTRODUCTION
Many problems in science and engineering can be
posed as a constraint satisfaction problem with
constraints that guarantee a desirable solution (Tsang,
2014). The solution, or set of solutions, is a set of
values that satisfy all the constraints and the region of
acceptable solutions is known as the feasible region.
Because of complex nature of CSPs, the solution
requires a mixture of combinatorial and heuristics
search. One of the fields that focuses on dealing with
CSPs is constraint programming (CP) (Lecoutre,
2009). Other fields of research that present solutions
as CSPs are Mixed Integer Programming (Alfa et al.,
2016), Satisfiability Modulo Theories (Barret and
Tinelli, 2018), Answer Set Programming (Lifschitz,
2019), and Boolean Satisfiability Problem
(Ohrimenko, 2007).
CSP algorithms can be divided into three different
classes: backtracking search (Wu & Van Beek, 2007);
constraint propagation (Bessiere, 2007); and
structure-driven algorithms (Dechter & Rossi, 2006).
Algorithms that utilize different versions of
backtracking search construct a solution by extending
a partial instantiation, step by step. While applying
a
https://orcid.org/ 0000-0002-4859-5707
b
https://orcid.org/ 0000-0002-3865-2499
intelligent backtracking strategies these algorithms
rely on different heuristics in order to avoid getting
trapped in dead ends. Constraint propagation
algorithms eliminate non-solution elements from the
search space to reduce the solution space. This
strategy can be used as a pre-process for the problem
before using a search algorithm, or used within the
search algorithm to boost its performance. Structure-
driven algorithms use the structure of the primal or
dual graph of the problem at hand. Structure-based
methods can also be coupled with other types of
algorithms to solve CSPs (Ruttkay, 1998).
Several decades ago, Zakian and Al-naib
proposed a new approach to control system design by
numerical solution of a set of inequalities (Zakian &
Al-Naib, 1973; Zakian, 1979; Zakian, 1996; Zakian,
2005). The inequalities provided constraints on
standard performance criteria, such as percentage
overshoot and settling time, and the solution of the
CSP yielded good controller designs. As part of his
methodology, Zakian introduced the principle of
matching so as to select the design constraints that
guarantee that the system will match its environment
(Zakian, 1996; Zakian, 2005; Zakian 1991). Zakian’s
approach, known as the method of inequalities or
232
Yaghoobi, S. and Fadali, M.
Control System Design via Constraint Satisfaction using Convolutional Neural Networks and Black Hole Optimization.
DOI: 10.5220/0010618902320239
In Proceedings of the 18th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2021), pages 232-239
ISBN: 978-989-758-522-7
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Zakian’s framework (Bada, 1985), gained popularity
because it provided good solutions to complex control
problems. Khaisongkram et al. (Khaisongkram et al.,
2004) used Zakian’s framework to design a controller
for a binary distillation column under disturbances.
Hirapongsananurak et al. used it to design a controller
for doubly-fed induction generator DFIG-based wind
power generation (Chirapongsananurak et al., 2010).
Interval constraint satisfaction was also used to
design a robust fractional-order multivariable
controller (Patil et al., 2017). Researchers extended
Zakian’s approach to controller design with fuzzy
constraints. Tuan et al. (Tyan et al., 1996) proposed a
methodology of fuzzy constraint-based controller
design via constraint-network processing. Guan et al.
(Guan & Friedrich, 1993) used a fuzzy CSP in
structural design.
The reliance on numerical solutions of
inequalities limited the applicability of the method of
inequalities. The applicability of the approach can be
extended by the use of new and powerful artificial
intelligence methodologies. To our knowledge, there
has been little work on the use of artificial intelligence
to solve a CSP for control system design with crisp
constraints. The solution of these problems for
complex systems is quite difficult and warrants the
use of intelligent methodologies such as deep learning
and evolutionary algorithms. Deep learning
algorithms provide an excellent tool for precisely
tuning controllers due to their flexible representation
of decision variables and performance evaluation, as
well as their robustness to difficult search
environments (Ding-gang et al., 2020). Applications
of evolutionary algorithms include parameter and
structure optimization for controller design and
model identification (Haralampidis et al., 2005), fault
detection (Omer et al., 2016), robustness analysis
(Fleming & Purshouse, 2002). This paper proposes
the use of Modified Black Hole algorithm (MBH) and
Convolutional Neural Networks to design controllers
solving a CSP. The constraints are selected to provide
values for control design criteria that guarantee good
controller performance.
To demonstrate the CSP control design
methodologies, two design examples are presented.
The first is the design of a PID controller for an
armature controlled DC motor. This simple example,
while solvable by traditional approaches, serves to
clearly explain the controller design steps. The
second example is the well-known Bouc-Wen
hysteresis model. Hysteretic behaviour occurs in a
vast range of physical systems such as magnetism,
piezo-electric materials, and mechanical vibration
(Din et al., 2016). However, conventional controller
design is difficult for the Bouc-Wen model because it
is highly nonlinear and includes a large number of
parameters, making its model identification a
challenging problem (Charalampakis & Koumousis,
2008). The second example includes comparison to
two well known algorithms, particle swarm
optimization (PSO) (Kennedy et al., 1995) and the
firefly algorithm (Xin-She, 2008).
The paper is organized as follows. Section 2
reviews the constraint satisfaction problem and,
Section 3 presents the penalty function method.
Section 4 discusses the use of convolutional neural
network to solve CSPs. Section 5 presents two
examples and their simulation results. Section 6 is the
conclusion.
2 CONSTRAINT SATISFACTION
PROBLEM (CSP)
A CSP is defined in terms of a tuple (𝑋,𝐷,𝐶), where
𝑋={𝑥
,…,𝑥
} is a finite set of variables with
domains
{
𝐷
,…,𝐷
}
, respectively, and 𝐶 is a ranked
finite set of constraints. Each constraint in 𝐶 restricts
the values that one can simultaneously assign to a
subset of the variables. A constraint is defined as 𝑛-
ary if it contains 𝑛 variables. A binary constraint CSP
is a CSP with unary and binary constraints only. The
main goal of the CSP is to assign at least one value to
each variable, while satisfying all the constraints in 𝐶.
The following is a formal definition of the
CSP(Popescu, 1997).
Definition 1: Constraint Satisfaction Problem.
Given a set of 𝑛 variables {𝑥
,…,𝑥
} with domains
{
𝐷
,…,𝐷
}
, respectively and a set of constraints
{
𝐶
,… ,𝐶
}
find at least one set of values {𝑣
,...,𝑣
}
that satisfy all the constraints.
Example: Consider the CSP with
(i) the set of variables:
𝑋 = {𝑥
,𝑥
,𝑥
,𝑥
},
(ii) the domains:
𝐷
= {0,1,2,3} ; 𝐷
= {1,3}; 𝐷
= {1,3,4,5};
and (iii) the constraints:
𝐶={𝑥
<𝑥
;𝑥
+𝑥
<𝑥
;𝑥
+𝑥
>3;𝑥
+
𝑥
>𝑥
},
an admissible instantiation is 𝑥
=0,𝑥
=3,𝑥
=1.
Control System Design via Constraint Satisfaction using Convolutional Neural Networks and Black Hole Optimization
233
3 MBH SOLUTION USING A
PENALTY FUNCTION
A constrained optimization problem can be converted
into an unconstrained problem and solved using an
evolutionary algorithm. The solution is obtained
using penalty methods by adding (or multiplying) a
violation term to the cost function that introduces a
high cost for constraint violation. Consider the
constrained optimization problem:
𝑀𝑖𝑛𝑖𝑚𝑖𝑧𝑒
{
𝑓
(
𝑥
)
:𝑥 ∈𝐶
}
(1)
where 𝑓 is function on ℛ
𝑛
and 𝐶 is a constraint set in
ℛ
𝑛
, or
𝑀𝑖𝑛𝑖𝑚𝑖𝑧𝑒
{
𝑓
(
𝑥
)
}
, 𝑠.𝑡. 𝑔(𝑥)≥𝑔
(2)
The penalty function method replaces problem (2)
with an unconstrained approximation of the form:
𝑀𝑖𝑛𝑖𝑚𝑖𝑧𝑒
𝑓
(
𝑥
)
+ 𝑤
𝑉
(3)
where 𝑤
𝑔𝑖
is the 𝑖
𝑡ℎ
weight and 𝑉
𝑔𝑖
is a penalty
function on ℛ
𝑛
.Alternatively, the penalty function is
implemented as follows:
𝑀𝑖𝑛𝑖𝑚𝑖𝑧𝑒 {
𝑓
(
𝑥
)
1+ 𝑤
𝑉
}
(4)
The penalty function 𝑉 is defined as:
𝑉
{
𝑔
(
𝑥
)
≥𝑔
}
=
0, 𝑔(𝑥)≥𝑔
1−
𝑔
(
𝑥
)
𝑔
,𝑔(𝑥)<𝑔
(5)
or
𝑉
{
𝑔
(
𝑥
)
≤𝑔
}
=
0, 𝑔
(
𝑥
)
≤𝑔
𝑔
(
𝑥
)
𝑔
−1, 𝑔
(
𝑥
)
>𝑔
(6)
The modified black hole algorithm, which is
discussed in the next section, is used to minimize the
penalty value (5).
3.1 Modified Black Hole Algorithm
The Black Hole (BH) algorithm is an optimization
technique inspired by the engulfing behavior of black
holes(Gan & Zhang, 2019). The method was shown
to improve the convergence rate and efficiency of the
particle swarm optimization (PSO) algorithm (Gan &
Zhang, 2019). A modified version of the black hole
algorithm (MBH) overcomes drawbacks of the BH
algorithm, such as getting trapped in local minima,
and can solve both high and low dimensional
problems (Yaghoobi & Mojallali, 2016).
Like other population-based evolutionary
algorithms, the MBH generates a random population
and calculates the cost function values for all the
particles. The particle with the lowest cost is
designated as the black hole and all other particles are
designated as stars. At this step, stars begin to
gravitate towards the black hole and their movement
can be formulated as:
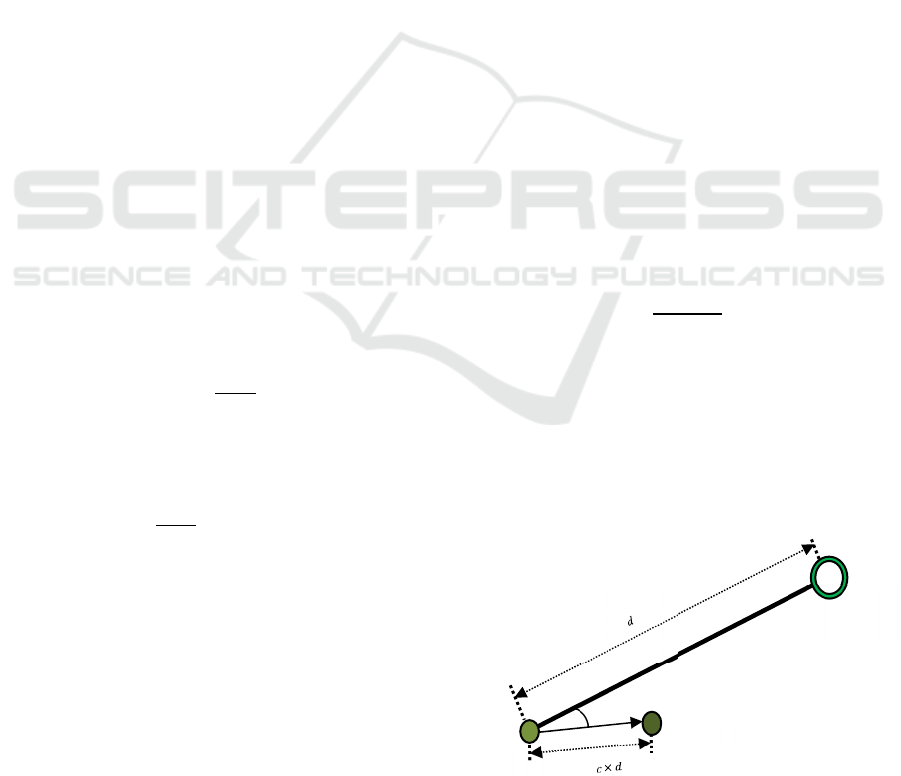
𝑥
𝑠𝑡𝑎𝑟
𝑖+1
=𝑥
𝑠𝑡𝑎𝑟
𝑖
+𝐶×𝑑
(7)
where 𝑥
𝑠𝑡𝑎𝑟
𝑖+1
and 𝑥
𝑠𝑡𝑎𝑟
𝑖
are the star locations in their
respective generations. 𝐶 is a matrix whose elements
are uniformly distributed random numbers, ranging
between 0 and 2, and 𝑑 is the vector of connectivity
between each particle and the black hole. Fig. 1 shows
how a star moves towards the black hole.
After each iteration, each star becomes closer to
the black hole and its cost is recalculated. If the cost
of a particle becomes lower than that of the black
hole, they exchange locations, as shown in Fig. 2. If a
particle approaches the minimum distance from the
black hole while providing a higher cost, it is
removed and a new particle is generated randomly in
the search space. The distance is defined as:
𝑟=
𝑓
∑
𝑓
(8)
where 𝑓
𝑐
stands for the cost of black hole, 𝑁
𝑝𝑜𝑝
is the
number of members in each iteration, and 𝑓
𝑛
is the
𝑛
𝑡ℎ
particle cost. At the end of every generation, the
black hole will always occupy the location that
provides the lowest cost and the stars are propelled
towards the best search space.
Figure 1: Moving particles (stars) towards the black hole.
Star’s position
S
tar’s new
p
osition
Black Hole
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
234

Figure 2: Exchanging position of a star and black hole.
3.2 Convergence Analysis of MBH
A critical issue with metaheuristic algorithms is their
convergence to an optimal, or at least satisfactory,
solution. Powerful hybrids that combine
metaheuristic techniques with well-established
methods from mathematical programming give the
convergence issue a new relevance (Gutjahr, 2009).
Every evolutionary optimization algorithm such as
MBH includes the following steps:
1. Find 𝑥
∈𝑆 and set 𝑡=0.
2. Generate a vector 𝑉
∈ℛ
using a probability
measure 𝜇
.
3. Set 𝑥
=𝐷(𝑥
,𝑉
), choose 𝜇
, set 𝑡=𝑡+1
and return to Step 2.
where D is a mapping that combines the new velocity
vector, V
t
, with the current solution, x
t
.
Any metaheuristic optimization algorithm will at
least converge to a local minimum if the algorithm
satisfies the algorithm condition and the convergence
condition (Van den Berg & Engelbrecht, 2010). The
two conditions are:
Condition I (Algorithm Condition): The mapping
𝐷:𝑆×ℛ
→𝑆 must satisfy 𝑓
(
𝐷(𝑥
,𝑉
)
)
≤𝑓
(
𝑥
)
.
This condition simply says that the solution generated
by mapping 𝐷 in iteration 𝑡+1 is no worse than the
solution in iteration 𝑡.
Condition II (Convergence Condition): For any
subset 𝐴 ⊆ 𝑆 with 𝑐
(
𝐴
)
>0, we have that:
1−𝜇
𝑡
(
𝐴
)
=0
∞
𝑡=0
(9)
Condition II means that for any measurable 𝐴⊆𝑆
with non-negative measure 𝑐, the probability of
repeatedly missing the set 𝐴, must be zero.
Conditions I and II lead to the following theorem.
Theorem 1 (Solis & Wets, 1981): Suppose that 𝑓 is
a measurable function, 𝑆 is a measurable subset of
ℛ
and Condition I and Condition II are satisfied. Let
{𝑥
}
be a sequence generated by a random search
algorithm. Then 𝑥
converges almost surely to the
optimality region 𝑅
lim
→
𝑃[𝑥
∈𝑅
]=1
(10)
where 𝑃[𝑥
∈𝑅
] is the probability that the point 𝑥
generated by the algorithm at time 𝑡 is in 𝑅
.
Proof: Considering Condition I, if 𝑥
∈𝑅
then 𝑥
∈
𝑅
for all 𝑡
≥𝑡+1. Thus, the probabilities satisfy
𝑃
[
𝑥
∈𝑅
]
=1−𝑃
[
𝑥
∈𝑆\𝑅
]
≥1−
[
1−𝜇
(
𝑅
)
]
(11)
Combining (11) and Condition II gives
1≥lim
→
𝑃
[
𝑥
∈𝑅
]
≥1−lim
→
[
1−𝜇
(
𝑅
)]
=1
(12)
Corollary I: The MBH converges almost surely to
the optimality region 𝑅
.
Proof: It was shown in (Yaghoobi & Mojallali, 2016)
that the position of the black hole does not change
until a better solution is found. Hence, the MBH
satisfies Condition I. Since MBH omits the stars that
reach the minimum distance defined by equation (11)
and new stars are generated randomly in the search
space, the sample space from which any new star is
drawn has the support 𝑀
=𝑆. This implies that
𝑐[𝑀
]=𝑐[𝑆], which implies that Condition II is
satisfied. It follows from Theorem 1 that the MBH
converges almost surely to the optimality region.
Corollary I establishes that the MBH is a global
search algorithm.
4 CONVOLUTIONAL NEURAL
NETWORK FOR SOLVING CSP
With the expansion of interest in artificial
intelligence (AI) applications, their usage in solving
mathematical problems has grown exponentially.
There have been many attempts to apply these AI
techniques to constraint satisfaction problems. Here a
constraint logic program (CLP) is treated as a
network of constraints to solve the constraint
satisfaction problem. Each computation in a CLP can
be shown as a sequence of linear steps, since the
check satisfiability of the system of constraints is
applied at each resolution step, which is linear in the
size of the current constraint problem. The constraint
propagation information is performed at each step
during any CLP derivation. To our knowledge, none
Control System Design via Constraint Satisfaction using Convolutional Neural Networks and Black Hole Optimization
235

of the recent advances in deep learning have been
exploited to solve this important problem. We can
represent a CSP with an artificial neural network
where the variables of the problem are represented by
a finite number of neurons divided into multiple
layers. The ANN model of a CSP is shown in Fig. 3,
where the ANN is a mapping of a set of input patterns
𝐼
to a corresponding set of output patterns 𝑂
,
.
The training data is a set of ordered pairs 𝐻
=
𝐼
,𝑂
,
that is used to train the network. The
training process consists in the computation of the set
of values {𝑣
,...,𝑣
} that satisfies the constraints
{
𝐶
,… ,𝐶
}
.
Figure 3: The ANN model of a CSP.
5 DESIGN EXAMPLES
We apply the design methodologies to two systems,
an armature-controlled DC motor and a nonlinear
Bouc-Wen system. The first example is intended to
show the steps of the design methodologies while the
second demonstrates the ability of the methodologies
to handle difficult controller design problems. We
design PID controller for each of the two systems.
The controller generates a control signal using the
error signal, its integral and its derivative:
𝑢
(
𝑡
)
= 𝐾
𝑒
(
𝑡
)
+ 𝐾
𝑒
(
𝜏
)
𝑑𝜏
+𝐾
𝑑
𝑑𝑡
𝑒(𝑡)
(13)
where 𝑢
(
𝑡
)
is the control signal, 𝑒
(
𝑡
)
is the error
signal defined as 𝑒
(
𝑡
)
= 𝑅
(
𝑡
)
–𝑦
(
𝑡
)
, the difference
between the reference signal 𝑅(𝑡) and the output
signal 𝑦(𝑡). The controller parameter, 𝐾
𝑝
,𝐾
𝑖
, and 𝐾
𝑑
,
denote the proportional gain, the integral gain, and the
derivative gain, respectively.
Figure 4: Unit Step response comparison between MBH
and CNN.
Example 1. Linear System (DC Motor).
Consider an armature-controlled DC motor whose
transfer function with armature voltage as input and
angular position as output is:
𝐺
(
𝑠
)
=
1
𝑆
+9𝑆
+ 22𝑠+ 15
(14)
The controller is designed to satisfy the following
design constraints:
Table 1: Step response evaluation criteria for the DC motor.
Violation Cost
Settling
Time
Peak
Value
Final
Value
Max.
0.0138 1.8555 1.8549 1.0638 1.0013
Min.
0 0.9996 0.9996 1.0135 0.9999
Mean
6.9416×10
-4
1.2041 1.1967 1.0231 1.00006
Std.
0.0031 0.2503 0.2539 0.0124 3.1102×10
-4
0.9 <𝑀𝑎𝑥𝑖𝑚𝑢𝑚 𝑂𝑣𝑒𝑟𝑠ℎ𝑜𝑜𝑡<1.1
(15)
𝑆𝑡𝑒𝑎𝑑𝑦 − 𝑠𝑡𝑎𝑡𝑒𝐸𝑟𝑟𝑜𝑟<5%
(16)
The cost function for MBH algorithm is the integral
of the error over time. Twenty runs of MBH
algorithm and deep neural network with a weight
vector 𝑤
𝑔
=
[
1 1000 100
]
, yield controllers
that provide step responses that satisfy the design
constraints, as shown in Fig. 2. The best run provided
the controller parameter values 𝐾
𝑝
=38. 2401, 𝐾
𝑖
=
28.52 and 𝐾
=10 for the CNN method and 𝐾
𝑝
=
37. 9147, 𝐾
𝑖
=28.7847 and 𝐾
𝑑
=10 for the MBH
method. Table 1 shows the values of the design
criteria for the selected parameter values. The
simulation results clearly show that the proposed
approach provides a good design for the DC motor
with a fast response, small overshoot and negligible
steady-state error. Fig. 4 shows the step response
comparison between two different proposed methods.
As it is clear from the figure, The MBH-Based
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
236

method has a faster response with a small and almost
negligible overshoot.
Example 2. Nonlinear Bouc-Wen System.
The Bouc–Wen model was originally applied for
nonlinear vibrational mechanics (Xin-She, 2008).
The model represents hysteresis as the superposition
of a linear component 𝑋(𝑡) and a hysteretic
component ℎ(𝑡). The classical hysteretic Bouc–Wen
model is described as follows:
𝑦
(
𝑡
)
=𝑋
(
𝑡
)
+ℎ
(
𝑡
)
=𝑘.𝑢
(
𝑡
)
+ℎ
(
𝑡
)
(17)
ℎ
(
𝑡
)
= 𝛼𝑢
(
𝑡
)
−𝛽𝑢
(
𝑡
)|
ℎ
(
𝑡
)|
−𝛾
|
𝑢
(
𝑡
)||
ℎ
(
𝑡
)|
ℎ(𝑡)
(18)
where 𝑢(𝑡) is the input, 𝑦(𝑡) is the output, and
𝑘,𝛼,𝛽,𝛾 and 𝑛 are the model parameters that
determine the shape of the hysteresis curves. The
parameter 𝑛 is often equal to unity to simplify the
model and the hysteresis component then becomes:
ℎ
(
𝑡
)
= 𝛼𝑢
(
𝑡
)
−𝛽𝑢
(
𝑡
)|
ℎ
(
𝑡
)|
−𝛾
|
𝑢
(
𝑡
)|
ℎ(𝑡)
(19)
We consider a Bouc-Wen model with parameter
values 𝑘 =0.2181,𝛼= −0.1453, 𝛽= 2.8847
and 𝛾=3.4124 (Gan & Zhang, 2019), with the input
signal 𝑢
(
𝑡
)
= 5sin(2𝜋× 40𝑡) + 5. The model is
used to generate the data using by the deep neural
network to select the controller parameters. Fig. 5
shows the Simulink implementation of the Bouc-Wen
model.
The controller must satisfy the following design
constraints:
I. Error Constraint: 𝐸𝑟𝑟𝑜𝑟<10
(20)
Table 2: Response characteristics for the Bouc-Wen
system.
Error Slope
MBH 9.4035 0.9993
CNN 9.6452 0.9975
PSO 27.6085 0.8694
FA 32.6452 0.9108
II. Input-output Constraint:
0.95 ≤ 𝑠𝑙𝑜𝑝𝑒 𝑜𝑓 𝑖𝑛𝑝𝑢𝑡−𝑜𝑢𝑡𝑝𝑢𝑡 𝑑𝑖𝑎𝑔𝑟𝑎𝑚≤1.05
(21)
where 𝐸𝑟𝑟𝑜𝑟 is defined as the integral square error:
𝐸𝑟𝑟𝑜𝑟= (𝑦
(
𝑡
)
− 𝑢(𝑡))
𝑑𝑡
(22)
The proposed CNN approach selected the PID
controller parameter values 𝐾
𝑝
=92.8537, 𝐾
𝑖
=
49.3467, and 𝐾
𝑑
=7.1 , with an integral square error
of 9.2457. The MBH penalty-based method selected
the values 𝐾
𝑝
=99.4486,𝐾
𝑖
=61.1953, and 𝐾
𝑑
=
11.1. The integral square error for this design is
9.4035. Both methods provide a feasible integral
square error that is lower than the upper bound of 10.
The input-output plot of Fig. 5 shows that the
controlled system follows the output in both the
controlled and uncontrolled scenarios. The input-
output plot is linear with slope 0.993, which satisfies
the desired criteria. The tracking performance
improves with the MBH and CNN-tuned PID
controllers. Table 2 is a comparison between our two
controllers, PSO (Kennedy et al., 1995), and the Firefly
Algorithm (Xin-She, 2008). Fig. 6 demonstrates the
error evolution over time for the four approaches. The
figure shows that the error of the proposed design is
always significantly smaller than the other approaches.
The error for proposed design drops much faster than
other approaches then remains within a much smaller
bounded range. The results show that the MBH and
CNN-based approaches provide more accurate
tracking than PSO and FA.
(a)
(b)
Figure 5: Input-Output plot of (a) controlled and (b)
uncontrolled systems with the input 𝑢
(
𝑡
)
=5sin(2𝜋∗
40𝑡)+ 5.
y(t)
Control System Design via Constraint Satisfaction using Convolutional Neural Networks and Black Hole Optimization
237
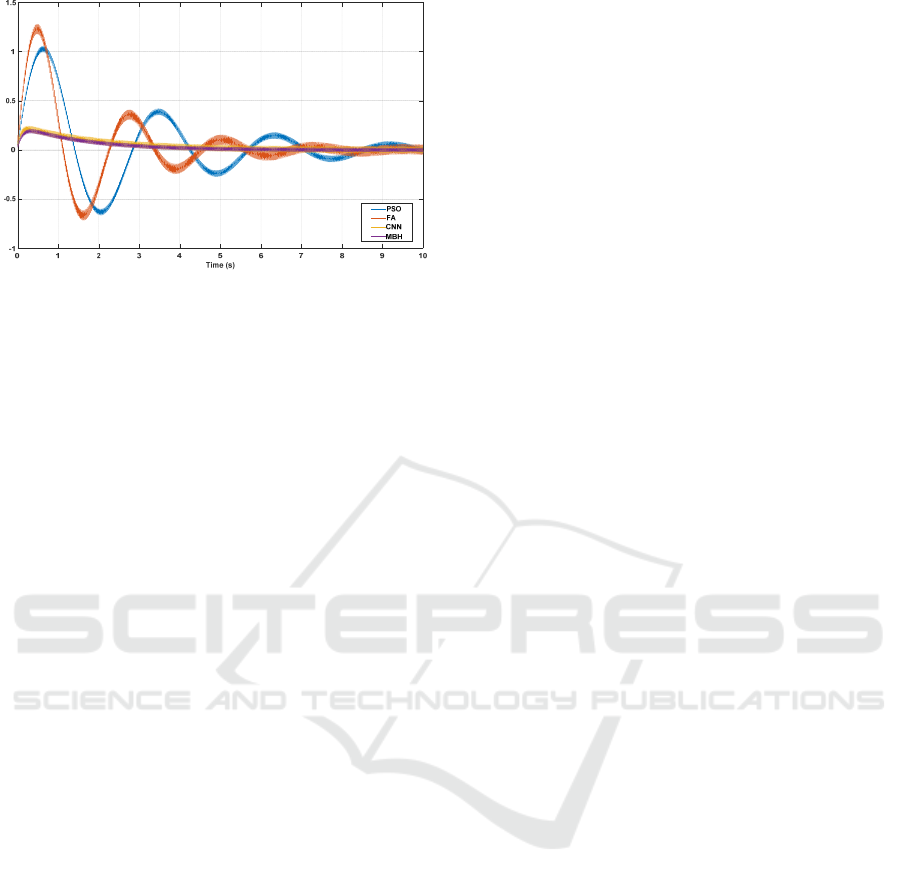
Figure 6: Error of four different studied designs over time.
6 CONCLUSION
This paper proposes intelligent control system design
by solving a constraint satisfaction problem. The
problem is solved using MBH optimization and using
a deep neural network. To demonstrate the design
methodology, two design and simulation examples
are presented. The first example is PID control for an
armature controlled DC motor and it demonstrates the
simplicity of the design methodology. The second is
PID control of Bouc-Wen hysteresis and it
demonstrates the applicability of the methodology to
challenging nonlinear systems. The performance of
the Bouc-Wen controller obtained using the proposed
method is compared to the results obtained using
particle swarm optimization and the firefly algorithm.
Simulation results show that the MBH and CNN
solution provide better controller performance with
faster and more accurate tracking that compares
favorably with the particle swarm algorithm and the
firefly algorithm. Future work will apply the
methodology to nonlinear multivariable systems
using input-output data without the benefit of a
mathematical model.
REFERENCES
Tsang, E. (2014). Foundations of constraint satisfaction:
the classic text. BoD–Books on Demand.
Lecoutre, C., Saïs, L., Tabary, S., & Vidal, V. (2009).
Reasoning from last conflict (s) in constraint
programming. Artificial Intelligence, 173(18), 1592-
1614.
Alfa, A. S., Maharaj, B. T., Lall, S., & Pal, S. (2016).
Mixed-integer programming based techniques for
resource allocation in underlay cognitive radio
networks: A survey. Journal of Communications and
Networks, 18(5), 744-761.
Barrett, C., & Tinelli, C. (2018). Satisfiability modulo
theories. In Handbook of Model Checking (pp. 305-
343). Springer, Cham.
Lifschitz, V. (2019). Answer set programming (pp. 1-147).
Berlin: Springer.
Ohrimenko, O., Stuckey, P. J., & Codish, M. (2007,
September). Propagation= lazy clause generation. In
International Conference on Principles and Practice of
Constraint Programming (pp. 544-558). Springer,
Berlin, Heidelberg.
Wu, H., & Van Beek, P. (2007, September). On universal
restart strategies for backtracking search. In
International Conference on Principles and Practice of
Constraint Programming (pp. 681-695). Springer,
Berlin, Heidelberg.
Bessiere, C. (2006). Constraint propagation. In Foundations
of Artificial Intelligence (Vol. 2, pp. 29-83). Elsevier.
Dechter, R., & Rossi, F. (2006). Constraint satisfaction.
Encyclopedia of Cognitive Science.
Ruttkay, Z. (1998). Constraint satisfaction-a survey. CWI
Quarterly, 11(2&3), 123-162.
Zakian, V., & Al-Naib, U. (1973, November). Design of
dynamical and control systems by the method of
inequalities. In Proceedings of the Institution of
Electrical Engineers (Vol. 120, No. 11, pp. 1421-1427).
IET Digital Library.
Zakian, V. (1979, June). New formulation for the method of
inequalities. In Proceedings of the Institution of
Electrical Engineers (Vol. 126, No. 6, pp. 579-584). IET.
Zakian, V. (1996). Perspectives on the principle of
matching and the method of inequalities. International
Journal of Control, 65(1), 147-175.
Zakian, V. (2005). Control systems design. Springer-Verlag
London Limited.
Zakian, V. (1991). Well matched systems. IMA Journal of
Mathematical Control and Information, 8(1), 29-38.
Bada, A. T. (1985, November). Design of delayed control
systems using Zakian's framework. In IEE Proceedings
D-Control Theory and Applications (Vol. 132, No. 6,
pp. 251-256). IET.
Khaisongkram, W., Banjerdpongchai, D., &
Arunsawatwong, S. (2004, July). Controller design for
a binary distillation column under disturbances with
bounds on magnitudes and derivatives using Zakian's
framework. In 2004 5th Asian Control Conference
(IEEE Cat. No. 04EX904) (Vol. 3, pp. 1676-1684).
IEEE.
Chirapongsananurak, P., Hoonchareon, N., &
Arunsawatwong, S. (2010, November). Controller
design for DFIG-based wind power generation using
Zakian's framework. In TENCON 2010-2010 IEEE
Region 10 Conference (pp. 1284-1289). IEEE.
Patil, M. D., Nataraj, P. S. V., & Vyawahare, V. A. (2017).
Design of robust fractional-order controllers and
prefilters for multivariable system using interval
constraint satisfaction technique. International Journal
of Dynamics and Control, 5(1), 145-158.
Tyan, C. Y., Wang, P. P., Bahler, D. R., & Rangaswamy, S.
P. (1996). A new methodology of fuzzy constraint-
based controller design via constraint-network
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
238

processing. IEEE transactions on fuzzy systems, 4(2),
166-178.
Guan, Q., & Friedrich, G. (1993, March). Fuzzy control
over constraint satisfaction problem solving in
structural design. In [Proceedings 1993] Second IEEE
International Conference on Fuzzy Systems (pp. 1316-
1320). IEEE.
Gao, D. G., Sun, Y. G., Luo, S. H., Lin, G. B., & Tong, L.
S. (2020). Deep learning controller design of embedded
control system for maglev train via deep belief network
algorithm. Design Automation for Embedded Systems,
24(3), 161-181.
Haralampidis, Y., Papadimitriou, C., & Pavlidou, M.
(2005). Multi‐objective framework for structural model
identification. Earthquake engineering & structural
dynamics, 34(6), 665-685.
Omer, Z. M., Fardoun, A. A., & Hussain, A. (2016, July).
Large scale photovoltaic array fault diagnosis for
optimized solar cell parameters extracted by heuristic
evolutionary algorithm. In 2016 Ieee Power And
Energy Society General Meeting (pesgm) (pp. 1-5).
IEEE.
Fleming, P. J., & Purshouse, R. C. (2002). Evolutionary
algorithms in control systems engineering: a survey.
Control engineering practice, 10(11), 1223-1241.
Ding, B., Li, Y., Xiao, X., & Tang, Y. (2016, December).
Optimized PID tracking control for piezoelectric
actuators based on the Bouc-Wen model. In 2016 IEEE
International Conference on Robotics and Biomimetics
(ROBIO) (pp. 1576-1581). IEEE.
Charalampakis, A. E., & Koumousis, V. K. (2008).
Identification of Bouc–Wen hysteretic systems by a
hybrid evolutionary algorithm. Journal of Sound and
Vibration, 314(3-5), 571-585.
Kennedy, J., & Eberhart, R. (1995, November). Particle
swarm optimization. In Proceedings of ICNN'95-
international conference on neural networks (Vol. 4, pp.
1942-1948). IEEE.
Yang, X. S. (2009, October). Firefly algorithms for
multimodal optimization. In International symposium
on stochastic algorithms (pp. 169-178). Springer,
Berlin, Heidelberg.
Gan, J., & Zhang, X. (2019). Nonlinear hysteresis modeling
of piezoelectric actuators using a generalized Bouc–
Wen model. Micromachines, 10(3), 183.
Yaghoobi, S., & Mojallali, H. (2016). Modified black hole
algorithm with genetic operators. International Journal
of Computational Intelligence Systems, 9(4), 652-665.
Gutjahr, W. J. (2009). Convergence analysis of
metaheuristics. In Matheuristics (pp. 159-187).
Springer, Boston, MA.
Van den Bergh, F., & Engelbrecht, A. P. (2010). A
convergence proof for the particle swarm optimiser.
Fundamenta Informaticae, 105(4), 341-374.
Solis, F. J., & Wets, R. J. B. (1981). Minimization by
random search techniques. Mathematics of operations
research, 6(1), 19-30.
Popescu, I. (1997). Using artificial neural networks for
constraint satisfaction problem. Nonlinear Analysis:
Theory, Methods & Applications, 30(5), 2937-2944.
Control System Design via Constraint Satisfaction using Convolutional Neural Networks and Black Hole Optimization
239
