Generating Synthetic Training Data for

Deep Learning-based UAV Trajectory Prediction

Stefan Becker

1 a

, Ronny Hug

1 b

, Wolfgang Huebner

1 c

Michael Arens

1 d

and Brendan T. Morris

2 e

Fraunhofer Center for Machine Learning, Fraunhofer IOSB, Ettlingen, Germany

University of Nevada, Las Vegas, U.S.A.

Keywords:

Unmanned-Aerial-Vehicle (UAV), Synthetic Data Generation, Trajectory Prediction, Deep-learning,

Recurrent Neural Networks (RNNs), Training Data, Quadrotors.

Abstract:

Deep learning-based models, such as recurrent neural networks (RNNs), have been applied to various se-

quence learning tasks with great success. Following this, these models are increasingly replacing classic

approaches in object tracking applications for motion prediction. On the one hand, these models can cap-

ture complex object dynamics with less modeling required, but on the other hand, they depend on a large

amount of training data for parameter tuning. Towards this end, we present an approach for generating syn-

thetic trajectory data of unmanned-aerial-vehicles (UAVs) in image space. Since UAVs, or rather quadrotors

are dynamical systems, they can not follow arbitrary trajectories. With the prerequisite that UAV trajectories

fulﬁll a smoothness criterion corresponding to a minimal change of higher-order motion, methods for plan-

ning aggressive quadrotors ﬂights can be utilized to generate optimal trajectories through a sequence of 3D

waypoints. By projecting these maneuver trajectories, which are suitable for controlling quadrotors, to image

space, a versatile trajectory data set is realized. To demonstrate the applicability of the synthetic trajectory

data, we show that an RNN-based prediction model solely trained on the generated data can outperform clas-

sic reference models on a real-world UAV tracking dataset. The evaluation is done on the publicly available

ANTI-UAV dataset.

1 INTRODUCTION

The rise of unmanned-aerial-vehicles (UAVs), such

as quadrotors, in the consumer market has led to con-

cerns about associated potential risks for security or

privacy. The potential intended or unintended mis-

uses pertain to various areas of public life, includ-

ing locations, such as airports, mass events, or public

demonstrations (Laurenzis et al., 2020). Thus, auto-

mated UAV detection and tracking have become in-

creasingly important for security services for antici-

pating UAV behavior. Video-based solutions offer the

beneﬁt of covering large areas and are cost-effective

to acquire (Sommer et al., 2017). The basic compo-

nents of such a video-based approach are the appear-

ance model and the prediction model which is tradi-

https://orcid.org/0000-0001-7367-2519

https://orcid.org/0000-0001-6104-710X

https://orcid.org/0000-0001-5634-6324

https://orcid.org/0000-0002-7857-0332

https://orcid.org/0000-0002-8592-8806

tionally realized with Bayesian ﬁlter. The prediction

model tasks within detection and tracking pipelines,

among others, are the prediction of the object be-

havior and bridging detection failures. Following the

success of deep learning-based models in various se-

quence processing tasks, these models become the

standard choice for object motion prediction. A sig-

niﬁcant drawback of deep learning models is the re-

quirement of a large amount of training data.

In order to overcome the problem of limited train-

ing data in the context of UAV tracking in image se-

quences, this paper proposes to utilize methods from

planning aggressive UAV ﬂights to generate suitable

and versatile trajectories. The synthetically generated

3D trajectories are mapped into image space before

they serve as training data for deep learning predic-

tion models.

Despite the increasing number of trajectory

datasets for object classes like pedestrians (e.g., Tra-

jNet++ dataset (Kothari et al., 2021)) or vehicles

(e.g., InD dataset (Bock et al., 2020)), datasets with

Becker, S., Hug, R., Huebner, W., Arens, M. and Morris, B.

Generating Synthetic Training Data for Deep Learning-based UAV Trajectory Prediction.

DOI: 10.5220/0010621400003061

In Proceedings of the 2nd International Conference on Robotics, Computer Vision and Intelligent Systems (ROBOVIS 2021), pages 13-21

ISBN: 978-989-758-537-1

UAV trajectories and UAV in general are very lim-

ited. For the aforementioned object classes of pedes-

trians and vehicles, mostly RNN-based deep learning

models are successfully applied for trajectory predic-

tion (Alahi et al., 2016). Independent of the existing

deep learning variants for trajectory prediction relying

on generative adversarial networks (GANs) (Amirian

et al., 2019; Gupta et al., 2018), temporal convolu-

tion networks (TCNs) (Becker et al., 2018; Nikhil and

Morris, 2018), and transformers (Giuliari et al., 2021;

Saleh, 2020), an RNN-based prediction model is cho-

sen as reference. The reader is referred to these sur-

veys (Rasouli, 2020; Rudenko et al., 2020; Kothari

et al., 2021) for a comprehensive overview of current

deep learning-based approaches for trajectory predic-

tion.

Although the focus is on motion prediction and

not on appearance modeling for UAV detection and

tracking, we throw a brief glance at some of the

current approaches that rely on images or use other

modalities. Besides image-based methods, common

modalities for UAV detections are RADAR, acous-

tics, radio-frequencies, and LIDAR. Comparisons of

key characteristics of different deep learning-based

approaches on single or fused modality information

are presented in Samaras et al. (2019); Taha and

Shoufan (2019); Unlu et al. (2019). A review with the

focus on radar-based UAV detection methods is given

by Christnacher et al. (2016). Approaches for acous-

tic sensors are, for example, presented in the work of

Kartashov et al. (2020) and Jeon et al. (2017). An ex-

ample to detect and identify UAVs based on their ra-

dio frequency signature is the approach of Xiao and

Zhang (2019). For LIDAR, there exist, for exam-

ple, the approaches of Hammer et al. (2019, 2018).

Image-based approaches can be divided into using

electro-optical sensors or infrared sensors. Their ap-

pearance modeling, however, is very similar. A fur-

ther division can be made into one-stage strategies

or two-stage strategies. In one-stage strategies, a di-

rect classiﬁcation and localization is applied. In two-

stage strategies, a general (moving) object detection

is followed by a classiﬁcation step. For ﬁxed cam-

eras, the latter strategy is preferred. Different image-

based approaches are, for example, presented in Schu-

mann et al. (2018); Schumann et al. (2017), Sommer

et al. (2017), M

uller and Erdn

uß (2019), and Rozant-

sev et al. (2017).

The paper is structured as follows. Section 2

presents the proposed methods for generating realis-

tic UAV trajectory data in image sequences. Section

3 brieﬂy introduces the used RNN-based UAV trajec-

tory prediction model. In addition to an analysis of

the diversity of the synthetically generated data, sec-

tion 4 includes an evaluation on the real-world ANTI-

UAV dataset (Jiang et al., 2021). Finally, a conclusion

is given in section 5.

2 SYNTHETIC DATA

GENERATION

In this section the proposed approach for generating

realistic, synthetic trajectory data is presented.

Minimum Snap Trajectories (MST): UAVs can not

ﬂy arbitrary trajectories due to the fact that they are

dynamical systems with strict constraints on achiev-

able velocities, accelerations and inputs. These con-

straints determine optimal trajectories with a series

of waypoints in a set of positions and orientations

in conjunction with control inputs (Mellinger, 2012).

Thus, the goal of trajectory generation in control-

ling UAVs is to generate inputs to the motion con-

trol system, which ensures that the planned trajec-

tory can be executed. Here, we apply an explicit

optimization method that enables autonomous, ag-

gressive, high-speed quadrotor ﬂight through com-

plex environments. In the remainder of this paper, the

terms quadrotor and UAV are used interchangeably,

although there exist various other UAV concepts. The

principle procedure can be adapted to all other de-

signs. Since we are only interested in the trajectory

data, the actual control design can, to some extent, be

neglected as long as the planned target trajectory is

suitable for control.

Minimum snap trajectories (MST) have proven

very effective as quadrotor trajectories since the mo-

tor commands and attitude accelerations of the UAV

are proportional to the snap, or the fourth derivative,

of the path (Richter et al., 2016). Of course, the

difference between the target trajectory and the exe-

cuted trajectory depends on the actual controller and

physical limitations (e.g., maximum speed) of a UAV.

Firstly, physical constraints can be considered in plan-

ning. Secondly, in most cases, a well-designed con-

troller can closely follow the target trajectory. For

our purpose, the trajectory of the actual ﬂight can, in

a way, be seen as only a slight variation of the tar-

get trajectory. However, quadrotor dynamics relying

on four control inputs (i

,··· ,i

) for nested feedback

control (inner attitude control loop and outer position

control loop, see for example Michael et al. (2010))

are differential ﬂat (Mellinger and Kumar, 2011). In

other words, the states and the inputs can be written as

functions of four selected ﬂat outputs and their deriva-

tives. This facilitates the automated generation of tra-

jectories since any smooth trajectory (with reasonably

bounded derivatives) in the space of ﬂat outputs can

ROBOVIS 2021 - 2nd International Conference on Robotics, Computer Vision and Intelligent Systems

zoomed-in detail

Figure 1: Visualization of a generated MST (target trajectory) along waypoints in the viewing frustum of a camera. The MST

is highlighted in purple. The sampled waypoints in the viewing frustum of the camera are shown in yellow. The corresponding

UAV ﬂights with a PD controller as proposed from Michael et al. (2010) are shown in red.

be followed by the quadrotor. Following Mellinger et

al., the ﬂat outputs are given by p = [r

,ψ]

, where

r = [x,y, z]

are the coordinates of the center of mass

in the world coordinate system and ψ is the yaw an-

gle. The ﬂat outputs at a given time t are given by

p(t), which deﬁnes a smooth curve. A waypoint de-

notes a position in space along a yaw angle. Tra-

jectory planning speciﬁes navigating through m way-

points at speciﬁed times by staying in a safe corridor.

Trivial trajectories such as straight lines lead to dis-

continuities in higher-order motion. Thus, such tra-

jectories are undesirable because they include inﬁnite

curvatures at waypoints, which require the quadro-

tor to stop at each waypoint. The differentiability of

polynomial trajectories makes them a natural choice

for use in a differentially ﬂat representation of the

quadrotor dynamics. Thus, for following a speciﬁc

trajectory p

(t) = [r

,ψ

(t)]

(with controller for a

UAV), the smooth trajectory p

(t) is deﬁned as piece-

wise polynomial functions of order n over m time in-

tervals:

(t) =











∑

i=0

) t

6 t 6 t

∑

i=0

) t

6 t 6 t

∑

i=0

) t

m−1

6 t 6 t

(1)

The goal is to ﬁnd trajectories that minimize func-

tionals which can be written using these basis func-

tions. These kinds of problems can be solved with

tools from the calculus of variations and are standard

problems in robotics (Craig, 1989). Hence, in order to

ﬁnd the smooth target trajectory p

(t)

tar

, the integral

of the k

derivative of position squared and the k

derivative of yaw angle squared is minimized:

(t)

tar

= arg min

(t)



+ c

(2)

Here, c

and c

are constants to make the inte-

grand non-dimensional. Continuity of the k

deriva-

tives of r

and k

derivatives of ψ

is enforced as a

criterion for smoothness. In other words, the conti-

nuity of the derivatives determines the boundary con-

ditions at the waypoints. As mentioned above, some

UAV control input depends on the fourth derivative

of the positions and the second derivative of the yaw.

Accordingly, p

(t)

tar

is calculated by minimizing the

integral of the square of the norm of the snap (k

= 4),

and for the yaw angle, k

= 2 holds.

The above problem can be formulated as a

quadratic problem QP (Bertsekas, 1999). Thereby,

i j

= [x

i j

,ψ

i j

]

are written as a 4nm × 1

vector~c with decision variables {x

i j

,ψ

i j

min ~c

Q~c +

subject to A~c ≤

b. (3)

Here, the objective function incorporates the mini-

mization of the functional while the constraints can

be used to satisfy constraints on the ﬂat outputs and

their derivatives and thus constraints on the states and

the inputs. The initial conditions, ﬁnal condition, or

intermediate condition on any derivative of the trajec-

tory are speciﬁed as equality constraint in 3. For a

more detailed explanation on generating MSTs, how

to incorporate corridor constraints, and how to calcu-

Generating Synthetic Training Data for Deep Learning-based UAV Trajectory Prediction

late the angular velocities, angular accelerations, to-

tal thrust, and moments required over the entire tra-

jectory for the controller, the reader is referred to the

work of Mellinger and Kumar (2011). Richter et al.

(2016) presented an extended version of MST gener-

ation, where the solution of the quadratic problem is

numerically more stable.

Training Data Generation: With the described

method, we can generate MSTs suitable to aggressive

maneuver ﬂights for UAV control in a 3D environ-

ment. In order to generate versatile trajectory data

in image space, further steps are required. The over-

all generation pipeline is explained in the following.

Firstly, a desired camera model with known intrin-

sic parameters is selected. The selection depends on

the targeted sensor set-up of the detection and track-

ing system. In our case, we choose a pinhole cam-

era model without distortion effects loosely orientated

on the ANTI-UAV dataset (Jiang et al., 2021) with re-

gard to an intermediate image resolution (in pixels)

(1176 × 640) between the infrared (640 × 512) and

electro-optical camera (1920 × 1080) resolutions of

the ANTI-UAV dataset. In case all camera parame-

ters are known, the corresponding distortion coefﬁ-

cient should be considered. In the experiments the

focal length (in pixels) is set to 1240, the princi-

ple point coordinates (in pixels) are set to p

= 579,

= 212. For setting up the external parameters, the

camera is placed close to the ground plane sampled

from an uniform distribution Uni(1m,2m) to set the

height above ground. The inclination angle is sam-

pled from Uni(10°, 20°). Given the ﬁxed camera pa-

rameters, the viewing frustum is calculated for a cho-

sen near distance to the camera center (d

near

= 10m)

and a far distance to the camera center (d

f ar

= 30m).

For generating a single MST, a set of waypoints in-

side the viewing frustum is sampled. The number

of waypoints is randomly varied between 3 and 7.

The travel time for each segment is approximated

by using the Euclidean distance between two way-

points and a sampled constant speed for the UAV

Uni(1m/s,8m/s). The resulting straight-line trajec-

tory serves as an initial solution of the MST calcu-

lation. The frame rate of the camera is sampled from

Uni(10 f ps,20 f ps) for every run. In our experiments,

we assumed a completely free space in the viewing

frustum. As mentioned, corridor constraints, which

can be used for simulating an object to ﬂy through,

can be integrated with the method of Mellinger and

Kumar (2011). For the synthetic training dataset,

1000 MSTs are generated. The main steps for the

synthetic data generation pipeline of a single run are

as follows:

• Selection of a desired camera model with known

intrinsic parameters.

• Extrinsic parameters are sampled from the height

and inclination angle distribution.

• Calculation of the corresponding viewing frustum

with d

near

and d

f ar

• Sampling of waypoints inside viewing frustum.

• Estimation of the initial solution with ﬁxed, sam-

pled UAV speed.

• MST trajectory generation using the method of

Mellinger and Kumar (2011).

• Projection of the 3D center of mass positions of

the MST to image space using the camera parame-

ters at ﬁxed time intervals (reciprocal of the drawn

frame rate of a single run).

This procedure is repeated until the desired num-

ber of samples are generated. Note that sanity checks

and abort criteria for the trajectory are applied at the

end and during every run. For example, requirements

on the minimum and maximum length of consecu-

tive image points. In Figure 1, generated MSTs along

sampled waypoints in a 3D-environment are visual-

ized. The viewing frustum for a ﬁxed inclination an-

gle of 15° is shown as a dotted gray line. The actual

ﬂight trajectory of a UAV is realized with a propor-

tional–derivative (PD) controller as is proposed by

Michael et al. (2010). Although the controller de-

sign is relatively simple, the UAV can closely follow

the target trajectory. Thus, directly using the planned

MST seems to be a legitimate design choice.

Figure 2: Visualization of generated UAV trajectories as ob-

served from the camera.

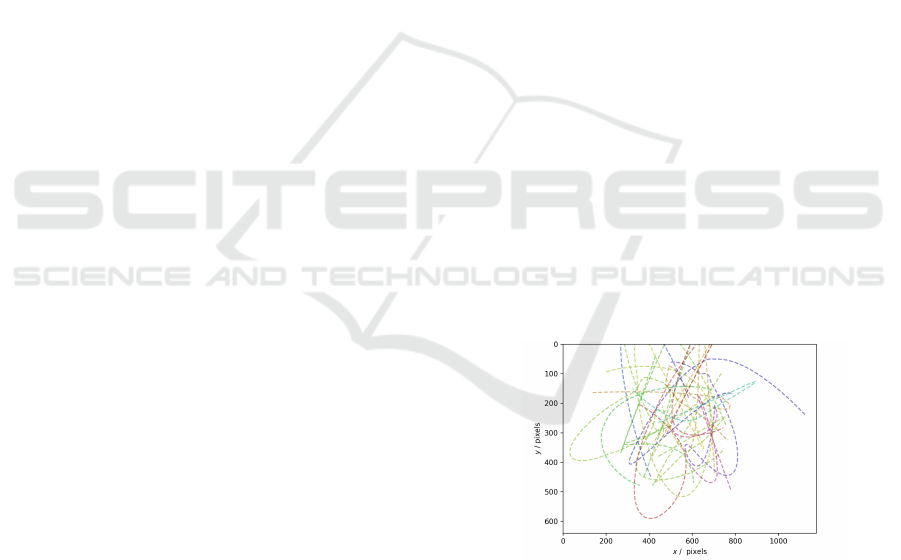
In Figure 2, exemplary generated training samples

are depicted. The ﬁgure illustrates the diversity in

the generated trajectory data reﬂecting several motion

prototypes present in trajectory data. A more detailed

analysis of the diversity and suitability of the gener-

ated synthetic data is given in section 4. Before that,

we will brieﬂy introduce the deep learning-based ref-

erence prediction model.

ROBOVIS 2021 - 2nd International Conference on Robotics, Computer Vision and Intelligent Systems

2D image space

zoomed-in detail

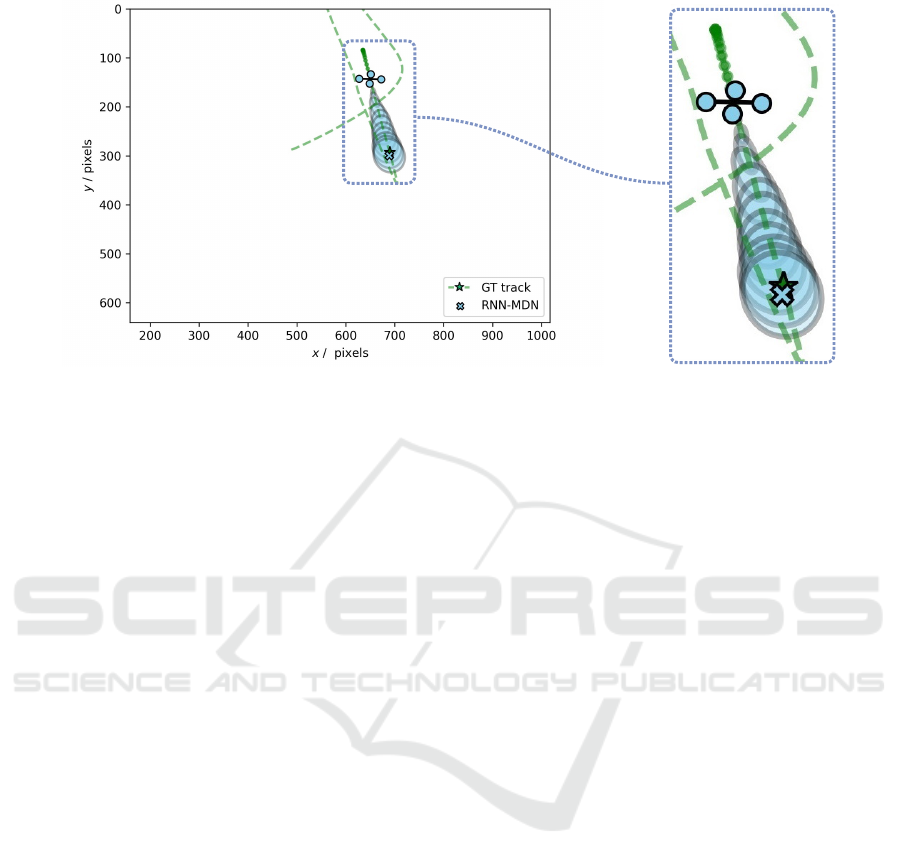
Figure 3: Visualization of the predicted distribution of an RNN-MDN on a synthetic UAV trajectory in image space for 12

steps into the future (on the left). A corresponding zoomed-in detail is shown on the right. The corresponding position of the

ground truth (GT) track is highlighted with a green star.

3 PREDICTION MODEL

For trajectory prediction, an RNN-based model is

considered, which predicts a distribution over the next

N image positions and is conditioned on the previ-

ous observations ~u

0:t

. ~u

0:t

are the image coordinates

from time 0 up to t. As mentioned above, RNN-based

models are a common choice from the variants of

deep learning-based models for trajectory prediction.

For generating the distribution over the next positions,

the model outputs the parameter of a mixture den-

sity network (MDN). Such RNN-MDNs are applied

to capture the motion of different object types. Orig-

inated from a model introduced by Graves (2014),

modiﬁed versions have been successfully utilized to

predict pedestrian (Alahi et al., 2016), vehicle (Deo

and Trivedi, 2018) or cyclist (Pool et al., 2021) mo-

tions. Although these modiﬁed versions also incor-

porate some contextual cues (e.g., interactions from

other objects), single objects motion is encoded with

such an RNN-MDN variant.

Given an input sequence U of consecutive observed

image positions ~u

= (u

) at time step t along a tra-

jectory, the model generates a probability distribution

over future positions {~u

t+1

,...,~u

t+N

}. The model is

realized as an RNN encoder. With an embedding of

the inputs and using a single Gaussian component, the

model can be deﬁned as follows:

= EMB(~u

;

= RNN(

t−1

,~e

;

RNN

{

~µ

t+n

}

n=1

= MLP(

;

MLP

) (4)

Here, RNN(·) is the recurrent network,

h the hid-

den state of the RNN, MLP(·) the multilayer percep-

tron, and EMB(·) an embedding layer.

Θ represents

the weights and biases of the MLP, EMB, or respec-

tively of the RNN. The model is trained by maximiz-

ing the likelihood of the data given the output Gaus-

sian distribution. This results in the following loss

function:

L(U) = −

∑

n=1

−logN (~u

t+n

~µ

t+n

). (5)

Implementation Details: The RNN-MDN is imple-

mented using Tensorﬂow (Abadi et al., 2015) and is

trained for 2000 epochs using an ADAM optimizer

(Kingma and Ba, 2015) with a decreasing learning

rate, starting from 0.01 with a learning rate decay of

0.95 and a decay factor of

/10. The RNN hidden state

and embedding dimension is 64. For the experiments,

the long short-term memory (LSTM) (Hochreiter and

Schmidhuber, 1997) RNN variant is utilized.

An example prediction of the RNN-MDN on a syn-

thetically generated UAV trajectory in image space is

depicted in Figure 3. On the left, the predicted dis-

tribution for 12 steps into the future is shown in blue.

The corresponding ground truth position is marked as

a green star. On the right, the corresponding 3D UAV

trajectory is shown in green.

Generating Synthetic Training Data for Deep Learning-based UAV Trajectory Prediction

Data Aligned Data Constant Curve (l) Curve (r) Acceleration Deceleration

Prototypes

Figure 4: Data, aligned data and learned prototypes for the synthetic UAV trajectories projected to image space. The pro-

totypes represent different motion patterns (from left to right): Constant velocity, curvilinear motion (left and right curve),

acceleration and deceleration.

Table 1: Results for a comparison between the an RNN-MDN prediction model trained on the synthetic generated data, a

Kalman ﬁlter with CV motion model, and using linear interpolation. The prediction is done for 8, 10, and 16 frames into the

future.

EO (1920 × 1080)

8/8 8/10 8/12

Approach FDE/pixels σ

FDE

/pixels FDE/pixels σ

FDE

/pixels FDE/pixels σ

FDE

/pixels

RNN-MDN 60.304 35.202 82.780 46.124 121.453 55.489

Kalman ﬁlter (CV) 81.061 60.333 110.041 84.530 179.459 104.408

Linear interpolation 86.998 67.113 119.106 89.067 183.558 108.522

IR (640 × 512)

8/8 8/10 8/12

Approach FDE/pixels σ

FDE

/pixels FDE/pixels σ

FDE

/pixels FDE/pixels σ

FDE

/pixels

RNN-MDN 20.849 18.604 41.378 21.100 61.459 24.490

Kalman ﬁlter (CV) 22.340 24.630 43.172 32.522 68.012 37.047

Linear interpolation 24.235 26.517 45.434 35.837 69.665 37.714

4 EVALUATION & ANALYSIS

This section analyzes the diversity of the generated

synthetic data and the suitability for training deep-

learning prediction models.

Diversity Analysis: For analyzing the diversity of the

synthetically generated data, we use the approach of

Hug et al. (2021). The approach learns a representa-

tion of the provided trajectory data by ﬁrst employing

a spatial sequence alignment, which enables a subse-

quent learning vector quantization (LVQ) stage. Each

trajectory dataset can be reduced to a small number

of prototypical sub-sequences specifying distinct mo-

tion patterns, where each sample can be assumed to

be a variation of these prototypes (Hug et al., 2020).

Thus, the resulting quantized representation of the

trajectory data, the prototypes, reﬂect basic motion

patterns, such as constant or curvilinear motion,

while variations occur primarily in position, orienta-

tion, curvature and scale. For further details on the

dataset analysis methods, the reader is referred to the

work of Hug et al. (2021). The resulting prototypes

of the generated training data are depicted in Figure 4.

The learned prototypes show that the generated

synthetic data includes several different motion pat-

terns. Besides, the diversity of the learned prototypes

is visible. The dataset consists of, for example,

distinguishable motion patterns reﬂecting constant

velocity motion, curvilinear motion, acceleration,

and deceleration.

Suitability Analysis: In order to analyze the suitabil-

ity of the generated trajectory data, the RNN-MDN

is trained as an exemplary deep learning-based pre-

diction model according to section 3. For evaluation,

the real-world ANTI-UAV dataset (Jiang et al., 2021)

is used. The dataset consists of 100 high-quality,

full HD video sequences (both electro-optical (EO)

and infrared (IR)), spanning multiple occurrences of

multi-scale UAVs, annotated with bounding boxes.

As inputs for the prediction models, the center po-

sitions of the provided annotations are used. As clas-

sical reference models, a Kalman ﬁlter with a con-

stant velocity (CV) motion model and linear interpo-

lation are utilized. For the Kalman ﬁlter, the obser-

vation noise is assumed to be a white Gaussian noise

process ~w

∼ N (0,(1.5pixels)

). Thereby, the uncer-

ROBOVIS 2021 - 2nd International Conference on Robotics, Computer Vision and Intelligent Systems

IR Sequence: 20190925 183946 1 6 IR Sequence: 20190925 152412 1 1

EO Sequence: 20190925 131530 1 5 EO Sequence: 20190925 133630 1 7

Figure 5: Example predictions for the Anti-UAV dataset Jiang et al. (2021). The top images show two samples from the IR

sequences. The bottom images depict two samples from the EO sequences.

tainty in the annotation is considered. The process

noise is modeled as the acceleration increment during

a sampling interval (white noise acceleration model

Bar-Shalom et al. (2002)) with σ

= 0.5

pixels

/f rame

For dealing with the minor annotation uncertainty, a

small white Gaussian noise is added to the generated

trajectory positions corresponding to the assumed ob-

servation noise. Since RNN are able to generalize

from noisy inputs up to an extent (see for example

(Becker et al., 2018)), the noisy trajectories are used

for conditioning during training of the RNN-MDN.

The performance is compared with the ﬁnal displace-

ment error (FDE) for three different time-horizons, in

particular, 8 frames, 10 frames, and 12 frames into

the future. The FDE is calculated as the average Eu-

clidean distance between the predicted ﬁnal positions

and the ground truth positions.

The results for the EO and the IR video sequences

are summarized in table 1. Although the RNN-MDN

is solely trained on the synthetically generated UAV

data, the model could outperform the traditional ref-

erence models on the EO and the IR sequences of the

ANTI-UAV dataset. It should be noted that no cam-

era motion compensation is applied. Thus, the re-

sults of all considered prediction models can be fur-

ther improved. For longer prediction horizons, all er-

rors are relatively high due to the maneuvering be-

havior of the UAVs. However, in case the predic-

tion model is utilized to bridge detection failures for

supporting the appearance model of the detection and

tracking pipeline, the number of subsequent failures

should be lower than the shown 12 frames time hori-

zon. Since the RNN-MDN relying on synthetic data

achieved better performance than the reference mod-

els, it is better suited to anticipate the short-term UAV

behavior. In Figure 5, the predicted distributions of

future positions are visualized for the EO sequences

or respectively IR sequences. The ground truth future

positions are highlighted as green stars. The covari-

ance ellipses around the predicted position are shown

in blue. The ﬁnal predicted positions are marked as a

blue cross.

5 CONCLUSION

This paper presents an approach for generating syn-

thetic trajectory data of UAVs in image space. By

utilizing methods for planning maneuvering UAV

ﬂights, minimum snap trajectories along a sequence

Generating Synthetic Training Data for Deep Learning-based UAV Trajectory Prediction

of 3D waypoints are generated. By selecting the de-

sired camera model with known camera parameters,

the trajectories can be projected to the observer’s per-

spective. To demonstrate the applicability of the syn-

thetic trajectory data, we show that an RNN-MDN

prediction model solely trained on the synthetically

generated data is able to outperform classic reference

models on a real-world UAV tracking dataset.

REFERENCES

Abadi, M. et al. (2015). TensorFlow: Large-scale machine

learning on heterogeneous systems. Software avail-

able from tensorﬂow.org. 5

Alahi, A., Goel, K., Ramanathan, V., Robicquet, A., Fei-

Fei, L., and Savarese, S. (2016). Social LSTM: Hu-

man Trajectory Prediction in Crowded Spaces. In

Conference on Computer Vision and Pattern Recog-

nition (CVPR), pages 961–971. 2, 5

Amirian, J., Hayet, J.-B., and Pettre, J. (2019). Social

Ways: Learning Multi-Modal Distributions of Pedes-

trian Trajectories With GANs. In Conference on

Computer Vision and Pattern Recognition Workshops

(CVPRW), pages 2964–2972. 2

Bar-Shalom, Y., Kirubarajan, T., and Li, X.-R. (2002). Esti-

mation with Applications to Tracking and Navigation.

John Wiley & Sons, Inc., New York, NY, USA. 7

Becker, S., Hug, R., H

ubner, W., and Arens, M. (2018).

RED: A simple but effective Baseline Predictor for

the TrajNet Benchmark. In The European Confer-

ence on Computer Vision Workshops (ECCVW), vol-

ume 11131 of Lecture Notes in Computer Science,

pages 138–153. Springer. 2, 7

Bertsekas, D. (1999). Nonlinear Programming. Athena Sci-

entiﬁc. 3

Bock, J., Krajewski, R., Moers, T., Runde, S., Vater, L., and

Eckstein, L. (2020). The ind dataset: A drone dataset

of naturalistic road user trajectories at german inter-

sections. 2020 IEEE Intelligent Vehicles Symposium

(IV), pages 1929–1934. 1

Christnacher, F., Hengy, S., Laurenzis, M., Matwyschuk,

A., Naz, P., Schertzer, S., and Schmitt, G. (2016). Op-

tical and acoustical UAV detection. In Kamerman,

G. and Steinvall, O., editors, Electro-Optical Remote

Sensing X, volume 9988, pages 83 – 95. International

Society for Optics and Photonics, SPIE. 2

Craig, J. (1989). Introduction to Robotics: Mechanics and

Control. Addison-Wesley Longman Publishing Co.,

Inc., USA, 2nd edition. 3

Deo, N. and Trivedi, M. M. (2018). Multi-modal trajec-

tory prediction of surrounding vehicles with maneuver

based lstms. In 2018 IEEE Intelligent Vehicles Sym-

posium (IV), pages 1179–1184. 5

Giuliari, F., Hasan, I., Cristani, M., and Galasso, F. (2021).

Transformer Networks for Trajectory Forecasting.

In International Conference on Pattern Recognition

(ICPR), pages 10335–10342. 2

Graves, A. (2014). Generating sequences with recurrent

neural networks. 5

Gupta, A., Johnson, J., Fei-Fei, L., Savarese, S., and Alahi,

A. (2018). Social GAN: Socially Acceptable Trajec-

tories with Generative Adversarial Networks. In Con-

ference on Computer Vision and Pattern Recognition

(CVPR), pages 2255–2264. 2

Hammer, M., Borgmann, B., Hebel, M., and Arens, M.

(2019). UAV detection, tracking, and classiﬁcation by

sensor fusion of a 360° lidar system and an alignable

classiﬁcation sensor. In Turner, M. D. and Kamerman,

G. W., editors, Laser Radar Technology and Applica-

tions XXIV, volume 11005, pages 99 – 108. Interna-

tional Society for Optics and Photonics, SPIE. 2

Hammer, M., Hebel, M., Laurenzis, M., and Arens, M.

(2018). Lidar-based detection and tracking of small

UAVs. In Buller, G. S., Hollins, R. C., Lamb, R. A.,

and Mueller, M., editors, Emerging Imaging and Sens-

ing Technologies for Security and Defence III; and

Unmanned Sensors, Systems, and Countermeasures,

volume 10799, pages 177 – 185. International Society

for Optics and Photonics, SPIE. 2

Hochreiter, S. and Schmidhuber, J. (1997). Long Short-

Term Memory. Neural Computation, 9(8):1735–

1780. 5

Hug, R., Becker, S., H

ubner, W., and Arens, M. (2021).

Quantifying the complexity of standard benchmark-

ing datasets for long-term human trajectory predic-

tion. IEEE Access, 9:77693–77704. 6

Hug, R., Becker, S., H

ubner, W., and Arens, M. (2020).

A short note on analyzing sequence complexity in tra-

jectory prediction benchmarks. In Workshop on Long-

term Human Motion Prediction (LHMP). 6

Jeon, S., Shin, J., Lee, Y., Kim, W., Kwon, Y., and Yang,

H. (2017). Empirical study of drone sound detection

in real-life environment with deep neural networks. In

European Signal Processing Conference (EUSIPCO),

pages 1858–1862. 2

Jiang, N., Wang, K., Peng, X., Yu, X., Wang, Q., Xing, J.,

Li, G., Zhao, J., Guo, G., and Han, Z. (2021). Anti-

uav: A large multi-modal benchmark for uav tracking.

2, 4, 6, 7

Kartashov, V., Oleynikov, V., Koryttsev, I., Sheiko, S.,

Zubkov, O., Babkin, S., and Selieznov, I. (2020). Use

of acoustic signature for detection, recognition and

direction ﬁnding of small unmanned aerial vehicles.

In 2020 IEEE 15th International Conference on Ad-

vanced Trends in Radioelectronics, Telecommunica-

tions and Computer Engineering (TCSET), pages 1–4.

Kingma, D. and Ba, J. (2015). Adam: A method for

stochastic optimization. In International Conference

on Learning Representations (ICLR). 5

Kothari, P., Kreiss, S., and Alahi, A. (2021). Human trajec-

tory forecasting in crowds: A deep learning perspec-

tive. IEEE Transactions on Intelligent Transportation

Systems, pages 1–15. 1, 2

Laurenzis, M., Rebert, M., Schertzer, S., Bacher, E., and

Christnacher, F. (2020). Prediction of MUAV ﬂight

behavior from active and passive imaging in complex

ROBOVIS 2021 - 2nd International Conference on Robotics, Computer Vision and Intelligent Systems

environment. In Laser Radar Technology and Ap-

plications, volume 11410, pages 10–17. International

Society for Optics and Photonics, SPIE. 1

Mellinger, D. (2012). Trajectory Generation and Control

for Quadrotors. PhD thesis, University of Pennsylva-

nia. 2

Mellinger, D. and Kumar, V. (2011). Minimum snap tra-

jectory generation and control for quadrotors. In In-

ternational Conference on Robotics and Automation

(ICRA), pages 2520–2525. 2, 4

Michael, N., Mellinger, D., Lindsey, Q., and Kumar, V.

(2010). The grasp multiple micro-uav testbed. IEEE

Robotics Automation Magazine, 17(3):56–65. 2, 3, 4

uller, T. and Erdn

uß, B. (2019). Robust drone detection

with static VIS and SWIR cameras for day and night

counter-UAV. In Counterterrorism, Crime Fight-

ing, Forensics, and Surveillance Technologies, vol-

ume 11166, pages 58–72. International Society for

Optics and Photonics, SPIE. 2

Nikhil, N. and Morris, B. T. (2018). Convolutional Neu-

ral Network for Trajectory Prediction. In The Euro-

pean Conference on Computer Vision Workshops (EC-

CVW), volume 11131 of Lecture Notes in Computer

Science, pages 186–196. Springer. 2

Pool, E., Kooij, J. F. P., and Gavrila, D. M. (2021). Crafted

vs. learned representations in predictive models - a

case study on cyclist path prediction. IEEE Transac-

tions on Intelligent Vehicles, pages 1–1. 5

Rasouli, A. (2020). Deep Learning for Vision-based Pre-

diction: A Survey. arXiv preprint arXiv:2007.00095.

Richter, C., Bry, A., and Roy, N. (2016). Polyno-

mial Trajectory Planning for Aggressive Quadrotor

Flight in Dense Indoor Environments, pages 649–666.

Springer, Cham. 2, 4

Rozantsev, A., Lepetit, V., and Fua, P. (2017). Detecting

ﬂying objects using a single moving camera. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, 39(5):879–892. 2

Rudenko, A., Palmieri, L., Herman, M., Kitani, K. M.,

Gavrila, D. M., and Arras, K. O. (2020). Human Mo-

tion Trajectory Prediction: A Survey. The Interna-

tional Journal of Robotics Research, 39:895 – 935. 2

Saleh, K. (2020). Pedestrian Trajectory Prediction using

Context-Augmented Transformer Networks. arXiv

preprint arXiv:2012.01757. 2

Samaras, S., Diamantidou, E., Ataloglou, D., Sakellariou,

N., Vafeiadis, A., Magoulianitis, V., Lalas, A., Dimou,

A., Zarpalas, D., Votis, K., Daras, P., and Tzovaras,

D. (2019). Deep learning on multi sensor data for

counter uav applications—a systematic review. Sen-

sors, 19(22). 2

Schumann, A., Sommer, L., Klatte, J., Schuchert, T., and

Beyerer, J. (2017). Deep cross-domain ﬂying ob-

ject classiﬁcation for robust uav detection. In Inter-

national Conference on Advanced Video and Signal

Based Surveillance (AVSS), pages 1–6. 2

Schumann, A., Sommer, L., M

uller, T., and Voth, S. (2018).

An image processing pipeline for long range UAV de-

tection. In Emerging Imaging and Sensing Technolo-

gies for Security and Defence III; and Unmanned Sen-

sors, Systems, and Countermeasures, volume 10799,

pages 186–194. International Society for Optics and

Photonics, SPIE. 2

Sommer, L., Schumann, A., M

uller, T., Schuchert, T., and

Beyerer, J. (2017). Flying object detection for auto-

matic uav recognition. In International Conference

on Advanced Video and Signal Based Surveillance

(AVSS), pages 1–6. 1, 2

Taha, B. and Shoufan, A. (2019). Machine learning-based

drone detection and classiﬁcation: State-of-the-art in

research. IEEE Access, 7:138669–138682. 2

Unlu, E., Zenou, E., Riviere, N., and Dupouy, P.-E. (2019).

Deep learning-based strategies for the detection and

tracking of drones using several cameras. IPSJ

Transactions on Computer Vision and Applications,

11(1):7. 2

Xiao, Y. and Zhang, X. (2019). Micro-uav detection and

identiﬁcation based on radio frequency signature. In

International Conference on Systems and Informatics

(ICSAI), pages 1056–1062. 2

Generating Synthetic Training Data for Deep Learning-based UAV Trajectory Prediction