Fast and Efﬁcient Union of Sparse Orthonormal Transform for Image

Compression

Gihwan Lee

and Yoonsik Choe

Department of Electrical and Electronic Engineering, Yonsei University, Seoul, South Korea

Keywords:

Sparse Coding, Dictionary Learning, Orthogonal Sparse Coding, Image Compression, Image Transform,

Sparse Transform, Union of Orthonormal Bases.

Abstract:

Sparse coding has been widely used in image processing. Overcomplete-based sparse coding is powerful

to represent data as a small number of bases, but with time-consuming optimization methods. Orthogonal

sparse coding is relatively fast and well-suitable in image compression like analytic transforms with better

performance than the existing analytic transforms. Thus, there have been many attempts to design image

transform based on orthogonal sparse coding. In this paper, we introduce an extension of sparse orthonormal

transform (SOT) based on unions of orthonormal bases (UONB) for image compression. Different from

UONB, we allocate image patches to one orthonormal dictionary according to their direction. To accelerate

the method, we factorize our dictionaries into the discrete cosine transform matrix and another orthonormal

matrix. In addition, for more effective implementation, calculation of direction is also conducted in DCT

domain. As expected, our framework fulﬁlls the goal of improving compression performance of SOT with

fast implementation. Through experiments, we verify that proposed method produces similar performance to

overcomplete dictionary outperforms SOT in compression with rather faster speed. The proposed methods are

from twice to four times faster than the SOT and hundreds of times faster than UONB.

1 INTRODUCTION

For the past decades, sparse coding, which express

the input image with a small amount of information

minimizing the loss of original information as much

as possible, has been an important tool and is widely

used in many signal and image processing applica-

tions (Zhang et al., 2015). In compression, they have

not yet been applied in standards, but many works to

design transform for compression or transform coding

scheme to be used for compression standards (Sezer

et al., 2015) have been proposed. Because sparse cod-

ing can increase coding efﬁciency by rate-distortion

optimization and quantization as in (Kalluri et al.,

2019), a set of sparse coding transforms can replace

conventional transforms, such as DCT.

Sparse coding techniques are generally based on

an overcomplete dictionary (Aharon et al., 2006),

(Elad and Aharon, 2006), indicating a dictionary with

larger number of columns than the number of rows.

Therefore, its atoms are generally nonorthogonal with

redundant properties and can make better representa-

https://orcid.org/0000-0001-5458-752X

https://orcid.org/0000-0002-4856-8741

tive dictionary to input signal. Owing to this charac-

teristic, it has been a powerful tool in ﬁelds. Mathe-

matically, given a dataset X ∈ R

n×N

, it is formulated

as:

min

D,A

X −DA

+ λ

, (1)

where D ∈ R

n×m

is an overcomplete dictionary (m >

n) and A ∈ R

m×N

is a sparse coefﬁcient.

However, for sparse coding based on an over-

complete dictionary, ﬁnding an appropriate dictionary

is generally a nondeterministic polynomial time-hard

problem. This requires iterative optimization such

as the method of optimal directions (MOD), the al-

ternating direction method of multipliers (ADMM)

and augmented Lagrange multipliers (ALM), with

greedy algorithms, such as basis pursuit and orthog-

onal matching pursuit to estimate the approximate

value (Zhang et al., 2015). They are sufﬁciently

good methods to solve the sparse approximation prob-

lem, but they inevitably require considerable time and

memory resources for learning. Therefore, it is one of

main open problems in the ﬁeld to design fast and ef-

ﬁcient dictionary learning algorithms.

Lee, G. and Choe, Y.

Fast and Efﬁcient Union of Sparse Orthonormal Transform for Image Compression.

DOI: 10.5220/0010647200950102

In Proceedings of the 18th International Conference on Signal Processing and Multimedia Applications (SIGMAP 2021), pages 95-102

ISBN: 978-989-758-525-8

To overcome this problem, (Lesage et al., 2005)

proposed a sparse coding method. When a dictio-

nary is square and orthogonal, the dictionary learning

scheme becomes the orthogonal Procrustes problem.

Therefore, this is solved by relatively simple and ef-

ﬁcient singular value decomposition (SVD). (Lesage

et al., 2005) and (Rusu and Dumitrescu, 2013) pro-

posed methods implementing an overcomplete dic-

tionary using unions of orthonormal bases (UONB).

The basic formulation, which was proposed ﬁrst by

(Lesage et al., 2005), is formulated as:

min

D,A

X −[D

|...|D

+ λ

s.t. D

= D

= I

(2)

where D

∈ R

n×n

is an orthogonal sub-dictionary and

i = 1, ...,L.

On the other hands (Sch

utze et al., 2016), (Sezer

et al., 2008) and (Sezer et al., 2015) proposed efﬁcient

dictionary learning methods based on an orthogonal

dictionary. Orthogonal sparse coding techniques are

mathematically simple and fast because they also re-

quire iterative optimization, but there are closed-form

solutions of dictionary and coefﬁcient matrix for each

iteration. They cannot only compute the orthogonal

dictionary via singular value decomposition, but the

coefﬁcients are also easily computed by inner prod-

ucts and thresholding.

In addition, this ﬁts well in image compression.

Many image compression methods depend on ana-

lytic transforms. Transform is similar in purpose to

sparse coding in that it represents the input signal with

minimal basis. Because of this reason, there have

been many attempts to substitute analytic transform

with sparse coding-based ones. However, the over-

complete dictionary is not a square matrix and does

not have to be orthogonal. Then, it does not contain

the same bases as the transform and has no inverse

transform. Because of these problems, these meth-

ods cannot replace the existing analytic transforms re-

gardless of its capabilities. Unlike this, the existing

orthogonal transforms such as discrete cosine trans-

form (DCT) and Karhunen-Loeve transform (KLT)

have been widely used in image compression ﬁeld and

the orthogonal dictionaries, since orthogonal sparse

coding have similar properties with the transforms,

such as it is invertible and satisﬁes Parseval’s theorem.

Sparse orthonormal transform exploited the orthogo-

nal sparse coding scheme and proposed an orthogo-

nal transform for image compression. This is theo-

retically reduced to the KLT in Gaussian process and

superior in non-Gaussian processes with higher com-

putation speed than that of overcomplete dictionary-

based methods.

In this paper, we expand the SOT to outperform

the performance of orthonormal dictionary learning

based on the union of orthonormal bases. However,

different from (Lesage et al., 2005), which use block

coordinate relaxation or greedy orthogonal matching

pursuit in coefﬁcient update, we adapt hard threshold

method of inner product, used in orthogonal sparse

coding. To this end, we classify input data and allo-

cate each orthogonal dictionary and its coefﬁcients to

each classiﬁed input data. When the number of or-

thogonal dictionaries increases, the compression per-

formance also increases, but the computational time

is also proportional to the number. To prevent this,

we use a double-sparsity structure proposed in (Ru-

binstein et al., 2010). We use a DCT matrix as a

ﬁxed base dictionary of double-sparsity structure. In

this way, we design a transform which outperform the

performance of the SOT, but this algorithm is rather

faster.

2 SPARSE ORTHONORMAL

TRANSFORM

For the past few decades, there have been many at-

tempts to make data-driven transforms using sparse

coding to achieve better performance than analytic

transforms (Sezer et al., 2015), (Ravishankar and

Bresler, 2013). Especially the orthogonal dictionary-

based sparse coding does not only give more com-

pact representations of input data than existing an-

alytic transforms, but also decorrelates the data like

analytic transforms. Also, the orthonormal dictionary

can not be only applied as a dictionary form, but also

as a transform. It is because the inverse matrix of or-

thonormal dictionary is its transpose,

X −GA



X −G



X −A



. The ﬁrst is a dic-

tionary form and the last is equal to transform, which

makes data sparse by product. In this section, we in-

troduce a recent work based on an orthogonal sparse

coding called sparse orthonormal transform (SOT).

In (Sezer et al., 2008) and (Sezer et al., 2015), the

basic idea of SOT is simple. It was designed based on

an orthogonal sparse coding methodology. Sezer et

al. formulated a transform with an orthonormal ma-

trix and an L

norm constraint to the transform coef-

ﬁcients:

min

G,A

X −GA

+ λ

s.t. G

G = GG

= I

(3)

where A is the sparse transform coefﬁcient, G is the

SOT matrix, and I

is n ×n. They use an iterative op-

timization methods to ﬁnd two variables, a dictionary

SIGMAP 2021 - 18th International Conference on Signal Processing and Multimedia Applications

and a coefﬁcient matrix. This problem is solved by

following algorithm:

Given the dataset X = {x

,...,x

} ∈ R

n×N

λ > 0 and initial orthonormal matrix G

Initialization:

G = G

Iterations:

Iterate until the stopping criterion is met:

1. Update the coefﬁcients:

A = T (G

X, λ

1/2

) .

2. Find the optimal dictionary:

(a) Compute the singular value decomposition:

= UΣV

(b) Update new dictionary:

G = UV

T (·, α) is a hard-threshold operator, which zeror-

izes when the absolute value is smaller than α. U

and V are left and right singular vector matrix respec-

tively. They verify that SOT is the principled exten-

sions of KLT because this transform is theoretically

reduced to KLT in Gaussian processes. It is well-

known that the KLT is optimal in Gaussian process

and it shows that the optimal dictionary in Equation

(3) has same structure with KLT in Gaussian process.

In other words, the SOT is also optimal in Gaussian

process, and is superior to KLT in non-Gaussian pro-

cess. They experimentally show the transform is su-

perior to DCT and KLT in image compression.

3 PROPOSED METHOD

3.1 Motivation

(Sezer et al., 2015) proposed the SOT, which im-

proves the existing analytic transforms in image com-

pression and has the same properties of analytic trans-

forms. In addition, it is relatively efﬁcient than over-

complete dictionary-based methods because it elim-

inates time-consuming greedy algorithms by orthog-

onal sparse coding schemes. However, the orthog-

onal dictionary is well ﬁt to compress images, but

restricts its performance because of its size. To the

best of our knowledge, there are some attempts to

achieve close performance to an overcomplete dic-

tionary with orthogonal dictionary, but an orthogo-

nal dictionary generally has poorer performance than

the one of overcomplete dictionary. Dictionaries with

larger size generally have more redundant represen-

tation, so they produces sparser representation of the

input data.

In this paper, we propose an extension of SOT.

To overcome the limitation of orthogonal dictionary,

we construct the dictionary as several orthogonal dic-

tionaries such as UONB in (2). However, because

large number of dictionaries require more computa-

tions and time, we propose another technique to miti-

gate the problem.

3.2 Algorithm Explanation

We used the method in (Lesage et al., 2005) to con-

struct overall dictionary and modiﬁed this for fast im-

plementation. (Lesage et al., 2005) exploits a greedy

algorithm to update coefﬁcients A in Equation (2).

Different from UONB, coefﬁcients update scheme of

orthogonal sparse coding exploits simple hard thresh-

old method (Sch

utze et al., 2016). To extend the or-

thogonal sparse coding algorithm in Section 2 to our

algorithm, we assign each input data to an orthogonal

dictionary. In other words, we classify input data to

generate more optimal orthogonal dictionary for each

group. We discern input image patches by their direc-

tions. We assume that when the patches with similar

direction are gathered, the more optimal dictionary is

generated. The assumption comes from DCT, which

gives optimal performance for horizontal or vertical

directional patches in image compression, but poor

performance for arbitrary directional patches (Pavez

et al., 2015).

Figure 1: The basis of two-dimensional discrete cosine

transform. Each basis include horizontal or vertical direc-

tional information.

In this paper, we exploit the DCT matrix because

of its characteristics for improving performance and

reducing time spent for the SOT. As the DCT is pop-

Fast and Efﬁcient Union of Sparse Orthonormal Transform for Image Compression

ular in image compression ﬁelds, it has been impor-

tant to analyze and extract information of images in

the compressed domain for fast implementation. In

particular, (Shen and Sethi, 1996) designed an edge

model in the DCT domain, based on the characteris-

tics of the DCT. As mentioned earlier, the DCT gives

optimal performance for horizontal and vertical direc-

tional data. It is because the bases of the DCT repre-

sent the horizontal and vertical directions or the di-

agonal directions made by their combinations. The

two directional bases have the same edge complex-

ity, according to their order. This is well illustrated

in the bases in Figure 1. The bases in the red box

show the same complex edge information in differ-

ent directions. (Shen and Sethi, 1996) directly ex-

tracted low-level features, such as edge orientation,

edge offset, and edge strength, from DCT compressed

images. (Shen and Sethi, 1996) suggested four met-

rics for edge orientation, with coefﬁcients based on

the 8x8 block DCT, and we use and introduce one of

the metrics.

For simple and efﬁcient implementation, the pro-

posed method exploit DCT matrix in two ways. First,

we discern the patches in DCT domain with a formu-

lation below:

θ =







tan

−1

(



), , where C

≥ 0

◦

−tan

−1

(



), where C

< 0,

(4)

where C

and C

are DCT coefﬁcients in (0, 1) and

(1, 0), which are corresponding to the bases in the red

box in Figure1. We restrict the range of direction from

◦

to 90

◦

Then, we quantize the θ in L levels. L is the num-

ber of orthogonal dictionaries used in the proposed

method. As in (Lesage et al., 2005), we construct the

dictionary as a set of several orthonormal dictionar-

ies, i.e. D = [D

|...|D

], where D

s are orthogonal

square matrix. Then, we classify input data into L

groups and assign each to an orthogonal dictionary.

When the value of L increases, it is generally natural

that the performance of compression also improves.

We verify this via experiments in Section 4.

However, with the performance improvement, the

number of orthogonal dictionaries is also increased.

Because this leads to increasing computation time, it

signiﬁcantly impairs the strength of orthogonal sparse

coding. To prevent this, the DCT matrix is used again.

We exploit the so-called double sparsity method pro-

posed in (Rubinstein et al., 2010). (Rubinstein et al.,

2010) proposed the method to bridge the gap between

analytic approach and learning-based approach. They

factorize a dictionary as two matrices, which are a

prespeciﬁed base dictionary and an atom representa-

tion matrix.

We construct our dictionary by the product two-

dimensional DCT matrix as a ﬁxed base dictionary

and another dictionary, which is only computed via

optimization procedure.

In a mathematical formulation:

D = T H, (5)

where T is a DCT matrix in R

n×n

and H is an or-

thonormal matrix in R

n×n

As mentioned above, the object of using DCT

matrix as base dictionary is to reduce the convergence

time of algorithm. Because it is well-known that the

DCT matrix produces quite good sparsity in advance,

it accelerates the algorithm with fewer iterations

than the case, which constructs dictionary with only

a dictionary. Based on equations (4) and (5), our

proposed method can be formulated in detail:

For an input data X = [X

|...|X

] ∈ R

n×N

where the X

is the patch of which direction is be-

tween (90

◦

/L)(i −1) and (90

◦

/L)i, the dictionary is

D = T [H

|...|H

] ∈ R

n×Ln

and the sparse coefﬁ-

cient matrix is A = [A

|...|A

]

∈ R

Ln×N

min

∑

l=1

−T H

+ λ

s.t. H

= H

= I

(6)

where i = 1, ..., L.

For efﬁcient implementation, all data is processed

in DCT domain during all procedure. First, input im-

age patches are transformed in DCT domain by prod-

uct with two-dimensional DCT matrix. Second, the

patches are classiﬁed through Equation (4). Since

a DCT matrix is orthonormal matrix, the Frobenius

norm of the DCT matrix,

, is 1. Then the Equa-

tion (6) is transformed as follows:

min

∑

l=1



−H



+ λ

s.t. H

= H

= I

(7)

where

= T

, the transformed data in DCT do-

main.

Then, our overall proposed algorithm is indicated

below:

Given the input

√

n ×

√

n image patches, the dataset

X = {x

,...,x

} ∈ R

n×N

, λ > 0 and the number of

dictionaries, L,

Initialization:

1. The input data X

s are transformed into DCT

domain.

SIGMAP 2021 - 18th International Conference on Signal Processing and Multimedia Applications

2. Classify the transformed data

s into L groups

via Equation(4).

Iterations:

Iterate until the stopping criterion is met:

1. Update the coefﬁcients: for each coefﬁcient

matrix l = 1,...,L,

= T (H

,λ

1/2

2. Find the optimal dictionary: For each orthogo-

nal dictionary l = 1,...,L,

(a) Compute the singular value decomposition:

= U

(b) Update dictionary by the inner product:

= U

4 EXPERIMENTS

4.1 Experimental Environment

We experimented with our methods using images in

Figure 2. To create equivalent environments for com-

parison, we resized the image to 256×256 pixels and

segmented it to 256 ×256 or 8 ×8 patches before ap-

plying the algorithm. To measure the performances

of different algorithm, we focused on image compres-

sion, comparing PSNR (dB) with the number of used

coefﬁcients. Sparse coding-based algorithms are de-

pendent on the value of λ in their formulation, Equa-

tions (3) and (6), and this decides the best sparsity.

In the compression sense, the optimal value is varied

from the number of coefﬁcients or bases used in com-

pression scheme. In this paper, we heuristically try to

ﬁnd the value for each level of sparsity before these

experiments for each method. Then, in experiments,

we only use the optimal values of λ as prior informa-

tion and do not consider the computation time to ﬁnd

it.

All the algorithms used in these experiments are

conducted with the same stopping condition. We set

the stopping condition to the difference of objective

functions between present and 10 iterations past.

For equivalent comparisons, each algorithm and

all experiments were implemented using MATLAB

R2021a in Windows 10 Education on a same com-

puter, equipped with an Intel i7-9700 CPU and 32-GB

RAM.

4.2 Experimental Results

In this subsection, we ﬁrst compare the SOT and the

proposed method with different number of dictionar-

ies for energy compaction. The SOT is achieved by

(a) Lena.

(b) peppers.

Figure 2: The test image. We experiment and verify pro-

posed method with Lena and peppers image.

(a) Lena.

(b) peppers.

Figure 3: The object quality comparison: PSNR (dB) versus

the number of retained coefﬁcient for 4 x 4 patches between

SOT and our methods.

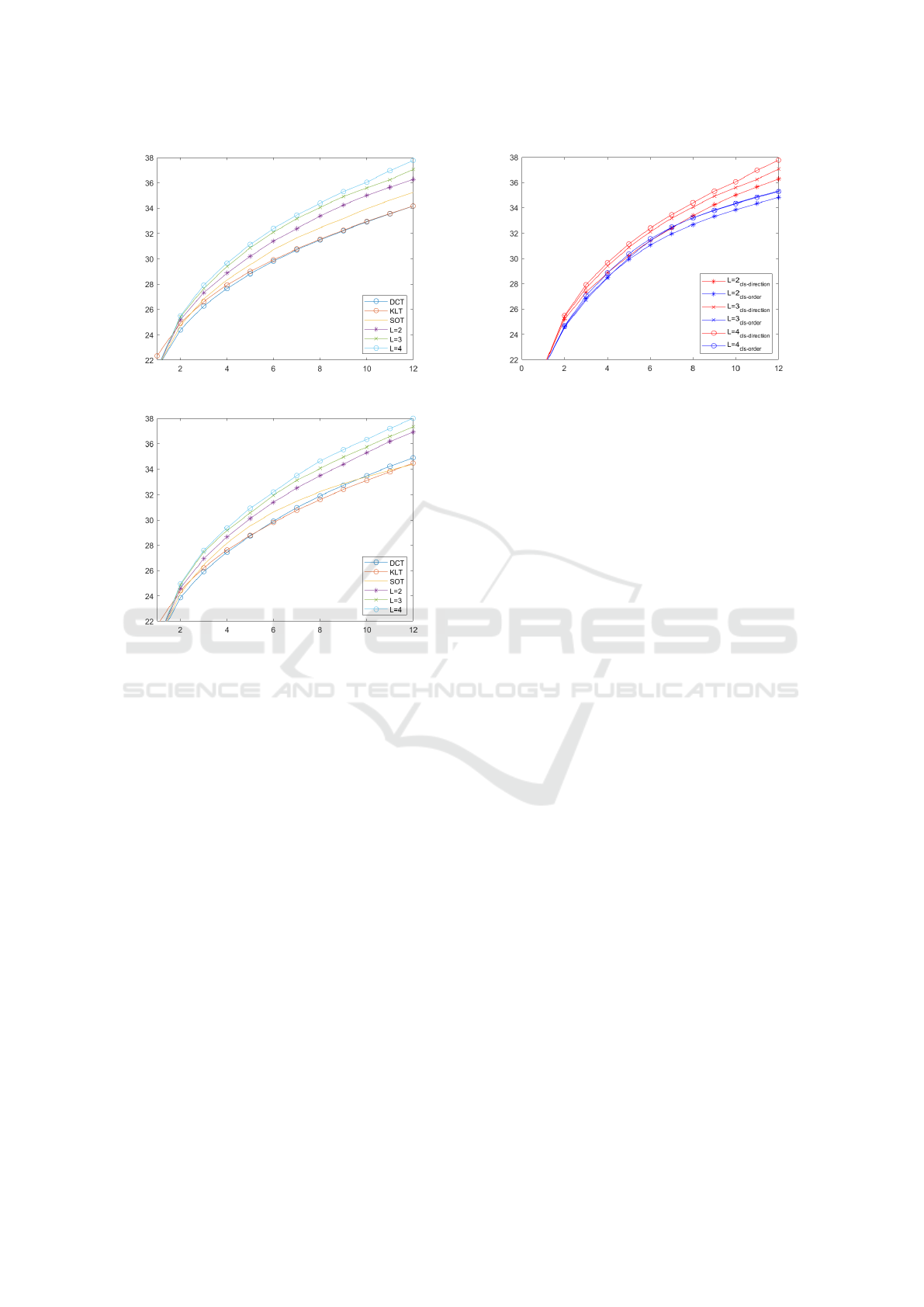
the algorithm in Section 2. Figures 3 and 4 show

the comparison of the objective qualities, in PSNR

(dB), for each number of retained bases. All proposed

methods with different number of dictionaries outper-

form the SOT method in PSNR (dB). As shown in

Figures 3 and 4, our method has improvement from

SOT, which is constructed by one orthonormal dictio-

nary, in performance. We analyze the result rise from

Fast and Efﬁcient Union of Sparse Orthonormal Transform for Image Compression

(a) Lena.

(b) peppers.

Figure 4: The object quality comparison: PSNR (dB) versus

the number of retained coefﬁcient for 8 x 8 patches between

SOT and our methods.

two conditions: (a) sparse coding algorithms work

better based on the input data classiﬁed according to

their structure than whole unstructured input data, and

(b) the dictionary from small dataset is more adaptive

and well representative than from large dataset. In

addition, it is interesting that the difference of recon-

struction error between proposed method and SOT in

Figure 4 is less than the difference in Figure 3. Small

patches have more simple and dominant directional

information than large patches. Large patches usu-

ally have more complex and have diverse orientations.

This makes the difference.

Figure 5 explains the assertion (a) is reasonable.

We verify our proposed classiﬁcation method for in-

put data by Equation (4) works well. Figure 5

plots the difference between two different classiﬁca-

tion methods. We compare our classiﬁcation method

based on Equation (4) with simply grouping the data

evenly in order. In Figure 5, ‘cls-direction’ indicates

our classiﬁcation method using direction and ‘cls-

order’ indicates a sequentially grouping way. In all

cases, our methods produce better performance. It

Figure 5: The object quality comparison: PSNR (dB) versus

the number of retained coefﬁcient for 8 x 8 patches between

classiﬁcation methods with different number of orthogonal

dictionaries.

indicates that the dictionary made of data including

similar structure is better at expressing than the dic-

tionary made of irregular and unstructured data.

To compare with the overcomplete dictionary-

based algorithm, we use UONB with optimization in

(Lesage et al., 2005) and block coordinate relaxation

algorithm, which is faster than the orthogonal match-

ing pursuit. Experiment is conducted by the differ-

ent numbers of dictionaries of proposed method and

UONB from 2 to 5. Figure 6 shows the experimen-

tal result. We observe that the difference between our

method and UONB in Figure 6. In Figure 6, proposed

method is more powerful for small patches. In Figure

6-(b), performance graphs of UONB have the cross-

ing point of performance at about 4 retained coefﬁ-

cients. At the two and three in X-axis, the UONB with

two dictionaries gives better performance than oth-

ers, but at more than four coefﬁcients, large number

of dictionaries make better performance. Different

from UONB, our method results in an improved per-

formance with the increasing number of dictionaries.

Comparing the two methods, our method outperforms

UONB when the number of coefﬁcients is small. As

the number of bases increases, the performance dif-

ference of UONB is greater, and when a large number

of coefﬁcients are used, UONB shows better perfor-

mance. We infer that this result comes from differ-

ence between overcomplete and orthogonal dictionar-

ies. Despite the number of dictionaries, our method

is based on square orthogonal dictionaries. This leads

to the difference of expressiveness when the number

of basis are increased.

4.3 Processing Time

One of our main contributions is to reduce computa-

tion and time with improved performance. To reduce

SIGMAP 2021 - 18th International Conference on Signal Processing and Multimedia Applications

100

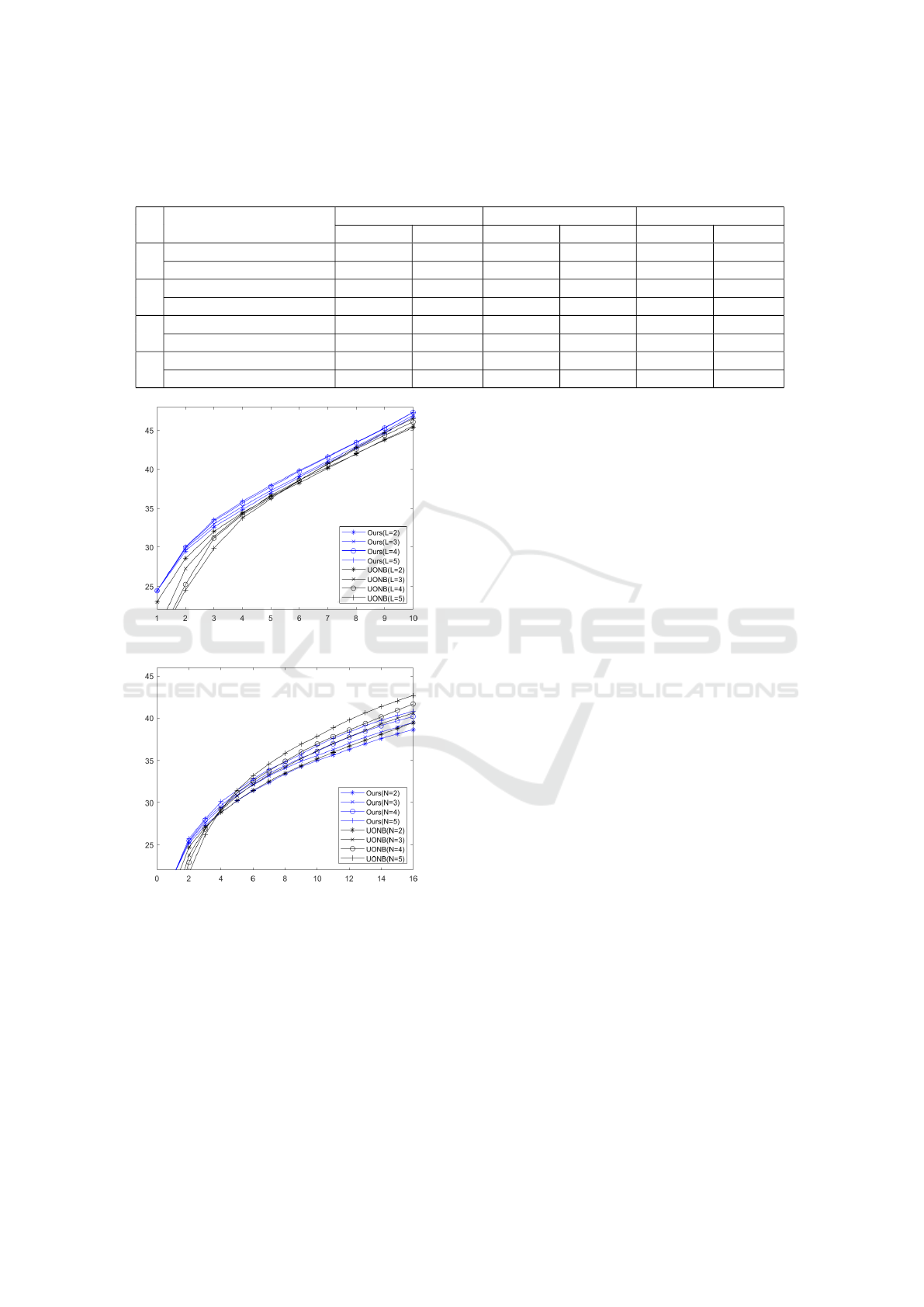
Table 1: The processing time and number of iterations for each method. L indicates the number of orthogonal dictionaries. We

compare each algorithm with λ optimal for two different number of retained coefﬁcients. The bold texts indicate minimum

results.

L # of retained coefﬁcients

SOT UONB Proposed

Iterations Time (s) Iterations Time (s) Iterations Time (s)

3 2095 1.4553 - - - -

5 2741 1.9480 - - - -

3 - - 622 49.7882 72 0.0498

5 - - 536 82.9780 107 0.0650

3 - - 628 343.3251 183 0.1174

5 - - 505 97.5815 157 0.0872

3 - - 482 57.8052 195 0.0920

5 - - 754 101.3284 192 0.1007

(a) 4 ×4 patches.

(b) 8 ×8 patches.

Figure 6: The object quality comparison: PSNR (dB) ver-

sus the number of retained coefﬁcient for different patch

sizes of Lena image between UONB and our methods with

different number of orthogonal dictionaries.

time, we tried to make the best use of DCT matrix.

In Table 1, we compared SOT, UONB, and proposed

method for the number of iterations and spent time

in seconds until convergence. In this section, we ex-

periment UONB and proposed method for three dic-

tionary sizes, L = 2, 3, 4. Because SOT use only an

orthogonal dictionary, it is only marked in L = 1. For

designing equivalent experimental setting, we set λs

optimal to two level of sparsity, 3 and 5. In this sec-

tion, the time to search λ is not considered.

From the Table 1, we observe that our proposed

method works the best at all cases. SOT works better

than UONB in time. Although the number of itera-

tions required in convergence for SOT is much larger

than one required for UONB, SOT is much faster than

UONB, because it does not use greedy algorithms.

Comparing our method and UONB, the number of

iteration for our proposed method is several times

smaller than UONB. The degree of reduction is differ-

ent, about twice to four times, but in all cases our al-

gorithm requires less iterations. Comparing the com-

putation time, the differences become larger than iter-

ations. Because our method requires smaller number

of iterations as mentioned and computation time for

each iteration is much less than UONB like SOT, our

method is hundreds times faster than UONB on aver-

age.

One of the interesting points of this section is the

comparison between SOT and proposed method. Al-

though proposed method tries to ﬁnd more dictionar-

ies and coefﬁcients than SOT, we achieve reduction

in the number of iterations by factorizing a dictionary

into DCT matrix and an orthonormal matrix, and it

leads to prevent from increase in time.

5 CONCLUSIONS

In this paper, we proposed a novel sparse coding-

based image transform framework for efﬁcient imple-

mentation as the form of extension of SOT. Overcom-

plete dictionary-based methods produce good sparse

representation, but require a long time and many re-

sources because of their iterative or greedy optimiza-

tions. Also, it does not ﬁt to image compression

as analytic transforms, which are invertible and sat-

isfy Parseval’s theorem. Orthogonal sparse coding is

Fast and Efﬁcient Union of Sparse Orthonormal Transform for Image Compression

101

proposed to overcome the time-consuming algorithm

of overcomplete dictionary-based algorithm. The or-

thogonal sparse coding also has a lot in common with

analytic transforms such as DCT and KLT. Because

the dictionary is square and orthonormal, this is in-

vertible and conserves the energy of data. Thus, or-

thogonal sparse coding-based transforms for image

compression have been proposed for past decades.

One of these transforms is SOT. SOT is theoreti-

cally proved to outdo KLT (Sezer et al., 2015). We

extend the SOT based on unions of several orthonor-

mal dictionaries such as UONB. Although the num-

ber of variables to be computed increases, we pre-

vent from increasing computational time by making

the best use of DCT matrix for classiﬁcation of input

data and factorization of dictionaries. As the result

of these efforts, the proposed method outperforms the

SOT with reduction of computation time. The section

4 veriﬁes that our method satisﬁes the object of this

paper through PSNR graphs and a table of processing

time.

In this paper, we only proposed sparse coding-

based transform scheme for image compression. In

the future works, we attempt to design the overall

transform coding scheme for better image compres-

sion as in (Sezer et al., 2015).

ACKNOWLEDGEMENTS

This work was supported by Institute of Informa-

tion & communications Technology Planning & Eval-

uation (IITP) grant funded by the Korea govern-

ment(MSIT) (No.2021-0-00022, AI model optimiza-

tion and lightweight technology development for edge

computing environment).

REFERENCES

Aharon, M., Elad, M., and Bruckstein, A. (2006). K-svd:

An algorithm for designing overcomplete dictionaries

for sparse representation. IEEE Transactions on Sig-

nal Processing, 54(11):4311–4322.

Elad, M. and Aharon, M. (2006). Image denoising via

sparse and redundant representations over learned dic-

tionaries. IEEE Transactions on Image Processing,

15(12):3736–3745.

Kalluri, M., Jiang, M., Ling, N., Zheng, J., and Zhang, P.

(2019). Adaptive rd optimal sparse coding with quan-

tization for image compression. IEEE Transactions on

Multimedia, 21(1):39–50.

Lesage, S., Gribonval, R., Bimbot, F., and Benaroya, L.

(2005). Learning unions of orthonormal bases with

thresholded singular value decomposition. In Pro-

ceedings. (ICASSP ’05). IEEE International Confer-

ence on Acoustics, Speech, and Signal Processing,

2005., volume 5, pages v/293–v/296 Vol. 5.

Pavez, E., Egilmez, H. E., Wang, Y., and Ortega, A. (2015).

Gtt: Graph template transforms with applications to

image coding. In 2015 Picture Coding Symposium

(PCS), pages 199–203.

Ravishankar, S. and Bresler, Y. (2013). Learning sparsify-

ing transforms. IEEE Transactions on Signal Process-

ing, 61(5):1072–1086.

Rubinstein, R., Zibulevsky, M., and Elad, M. (2010). Dou-

ble sparsity: Learning sparse dictionaries for sparse

signal approximation. IEEE Transactions on Signal

Processing, 58(3):1553–1564.

Rusu, C. and Dumitrescu, B. (2013). Block orthonor-

mal overcomplete dictionary learning. In 21st Eu-

ropean Signal Processing Conference (EUSIPCO

2013), pages 1–5.

Sch

utze, H., Barth, E., and Martinetz, T. (2016). Learning

efﬁcient data representations with orthogonal sparse

coding. IEEE Transactions on Computational Imag-

ing, 2(3):177–189.

Sezer, O. G., Guleryuz, O. G., and Altunbasak, Y.

(2015). Approximation and compression with sparse

orthonormal transforms. IEEE Transactions on Image

Processing, 24(8):2328–2343.

Sezer, O. G., Harmanci, O., and Guleryuz, O. G. (2008).

Sparse orthonormal transforms for image compres-

sion. In 2008 15th IEEE International Conference on

Image Processing, pages 149–152.

Shen, B. and Sethi, I. K. (1996). Direct feature extraction

from compressed images. In Sethi, I. K. and Jain,

R. C., editors, Storage and Retrieval for Still Image

and Video Databases IV, volume 2670, pages 404 –

414. International Society for Optics and Photonics,

SPIE.

Zhang, Z., Xu, Y., Yang, J., Li, X., and Zhang, D. (2015).

A survey of sparse representation: Algorithms and ap-

plications. IEEE Access, 3:490–530.

SIGMAP 2021 - 18th International Conference on Signal Processing and Multimedia Applications

102