A Two-stage Genetic Algorithm for a Novel FJSP with Working Centers

in a Real-world Industrial Application

David Govi

, Alessandro Rizzuto

, Federico Schipani

and Alessandro Lazzeri

Deepclever S.r.l., Via Bure Vecchia Nord n.c. 115, 51100, Pistoia (PT), Italy

Keywords:

Two-stage Genetic Algorithm, Working Centers, Flexible Job Shop Scheduling, Chromosome Representation,

Local Search, Population Initialization.

Abstract:

Inspired by industrial issues and demands, we deﬁne a novel version of the Flexible Job Shop Scheduling

Problem with Working Center. A working center is agroup of machines performing the same type of operation.

The job operations of different types follow a strict sequence across the working centers, while any order

is allowed among operations of the same type. This paper illustrates a genetic algorithm with a two-stage

chromosome representation, adapted genetic operators, local search, and social disaster technique to deal

with a real-world industrial application. The algorithm has been tested on a classical benchmark to assess its

adaptability and compare its performance with state-of-the-art techniques; then, we tested different variations

of the proposed algorithm on a real-case test instance showing a consistent improvement when compared with

the heuristic in use at the industrial company.

1 INTRODUCTION

Production scheduling is one of the most critical tasks

in manufacturing systems and it has been extensively

studied by the scientiﬁc community. The problem

is of more than academic interest. The effective

scheduling of operations processed by the shop ﬂoor

reduces the working-process inventory and increases

the throughput with a positive impact on the perfor-

mances. The scheduling problem is concerned with

allocating available production resources to tasks and

determining the sequence of operations that can op-

timize business metrics. In literature, the job shop

scheduling problem (JSP), which is NP-hard, is the

standard formulation of the production scheduling

problem. In the JSP, an operation can be performedby

only one machine and a machine can perform a single

operation at a time. However, to cope with a more

complex real case scenarios, the JSP has been ex-

tended by allowing an operation executable on more

than one machine (Flexible JSP), on all the machines

(Total Flexible JSP), or on a subset of the machines

(Partial Flexible JSP) (Xie et al., 2019).

https://orcid.org/0000-0001-6283-3225

https://orcid.org/0000-0002-1074-1035

https://orcid.org/0000-0002-6119-7033

https://orcid.org/0000-0003-3112-9010

A peculiar and practice-oriented speciﬁcation of

the FJSP is the one described by Behnke and Geiger.

In their work, they illustrate a context where similar

machines are pooled to working centers. In this set-

ting, if an operation is assignable to a machine it is

also assignable to any other machines belonging to

the same working center. Another interesting prop-

erty of the context is that the sequence of operations

is ﬁxed and the ﬁrst and the last operations of each job

must be processed by machines from the ﬁrst and last

working center (Behnke and Geiger, 2012).

The latter scenario comes close to that encoun-

tered during our research work, conducted with an

Italian company. Here working centers aggregate ma-

chines performing a certain type of operation. More-

over, while the sequence of the operations from one

working center to the next is ﬁxed, the operations of

the same working center can be performed in any pos-

sible order. The company had shown difﬁculties in

ﬁnding an optimized scheduling strategy that would

allow to comply with such constraints, not commonly

studied in the FJSP ﬁeld, and better distribute the

working load. In order to answer this necessity, in this

paper we introduce an extended variation of the FJSP

with Working Center proposed by Behnke and Geiger

and illustrate an adapted genetic algorithm with a two-

stage chromosome representation, local search and

social disaster technique.

Govi, D., Rizzuto, A., Schipani, F. and Lazzeri, A.

A Two-stage Genetic Algorithm for a Novel FJSP with Working Centers in a Real-world Industrial Application.

DOI: 10.5220/0010654900003062

In Proceedings of the 2nd International Conference on Innovative Intelligent Industrial Production and Logistics (IN4PL 2021), pages 75-83

ISBN: 978-989-758-535-7

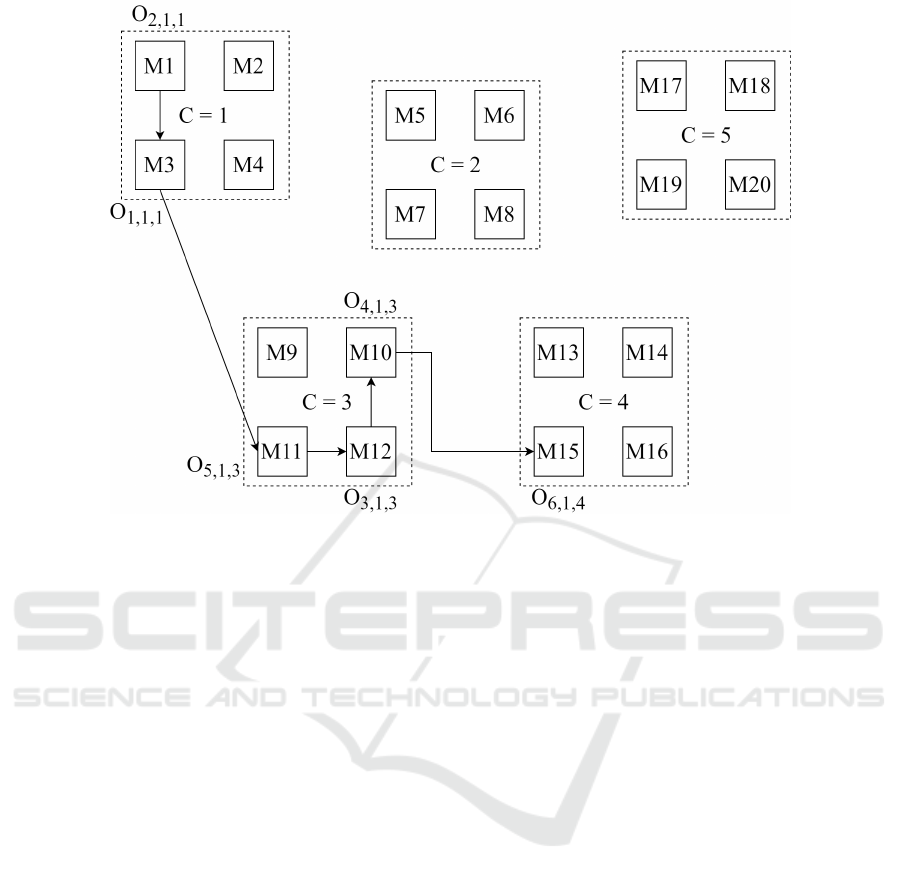
Figure 1: Possible operation sequence through working centers for a job j = {o

1,1,1

2,1,1

3,1,3

4,1,3

5,1,3

6,1,4

Our contribution consists of:

• the formalization of an industrial problem as a

variation of the FJSP;

• the implementation of an adapted encod-

ing/decoding system that makes a GA able to

handle solutions complying with the presented

constraints without performing corrections;

• the development of a scheduling strategy that im-

proves human performances in an industrial con-

text.

Population-based meta-heuristics have been in-

deed widely applied for solving the FJSP, with the ge-

netic algorithm (GA) being the most popular among

them. The algorithm integrates different strategies for

generating the initial population, selecting the indi-

viduals for reproduction and reproducing new solu-

tions (Xie et al., 2019). Genetic algorithms encode

problems for which they aim at optimizing a cost

function in chromosomes: the individuals of the pop-

ulation are vectors whose elements are called genes.

When dealing with the FJSP and its relative sub-

classes, it is common practice to represent the prob-

lem using a two-sides chromosome. A chromosome

can indeed be split in two parts that behave differ-

ently and encode different information: one encodes

the machine assignment, while the other encodes the

operation sequencing (Gao et al., 2008) (Yang et al.,

2009) (Zhang et al., 2011) (Rahmati and Zandieh,

2012) (Defersha and Rooyani, 2020). In this work,

we extend the typical pipeline of the genetic algorithm

with local search and social disaster technique. Lo-

cal search can help avoid local minima by exploring

the local space around a particular solution, possibly

improving it. It can be used at different stages of the

global search (Yun et al., 2013) or directly at the end

of the global search process (Nouri et al., 2018). The

second technique we use is called social disaster tech-

nique. The general idea is to diagnose the situation of

loss of genetic diversity of the population, and in such

case to apply a catastrophic operator to it. These op-

erators have the purpose to return the population to an

acceptable degree of genetic diversity, by replacing

a number of selected individuals with others gener-

ated at random (Rocha and Neves, 1999). Both tech-

niques are designed to help the model provide bet-

ter solutions avoiding premature convergence to lo-

cal optima, avoiding the waste of computational time

around fruitless areas of the search space.

The structure of the paper is as follows: After de-

tailing each constraint and assumption of our prob-

lem in Section 2, we illustrate chromosome repre-

sentation, gantt building, the entire pipeline and each

feature in Section 3. In Section 4 we discuss perfor-

mances sustained on a test instance for the FJSP and

on a test instance retrieved in our use case. Finally, in

Section 5 we discuss obtained results, possible addi-

tional features and further improvements.

IN4PL 2021 - 2nd International Conference on Innovative Intelligent Industrial Production and Logistics

2 PROBLEM DEFINITION

Our problem can be described as a set of n jobs

J = {1,2,..., n} where each job j consists of a num-

ber of operations P

= {1,2,..., p}. Every operation

is traceable to a class of operations called type k ∈ K

with K = {1,2, ...,l}. Thus, we deﬁne the p-th oper-

ation of job j of type k as o

p, j,k

∈ O, where O is the

set containing the operations of all jobs. The opera-

tions O are to be processed on a set of machines M,

divided into subsets of machines called Working Cen-

ters c ∈ C = {1, 2,..., w} , where w = l. All machines

grouped in a working center have the property to pro-

cess only one type of operations k, making it possi-

ble to draw a one-to-one correspondence between the

type of operations K and working centersC. Finally, a

machine m

belongs to one and only one working cen-

ter c of the shop ﬂoor M. A machine m

is described

by a set of features that identify the capability of the

machine to perform certain operations. Hence, there

is no guarantee that a machine m

can perform all op-

erations of type k. The mapping between an opera-

tion and the subset of machines that are able to pro-

cess it is deﬁned by our real-world casuistry, where

operations of the same type can widely differ from

each other over several parameters and is not the ob-

ject of this work. The sequence of operations for each

job is not predetermined. The only constraint is im-

posed by the operation type. In fact, for each job,

all the operations of type k have to be performed be-

fore any operation of type k + 1. Also, jobs are not

necessarily characterized by the presence of opera-

tions belonging to all K types (i.e., in Figure 1 there

is no operation on machines where c = 2), while the

aforementioned sequence constraint is always valid.

Figure 1 shows the assignment of the operations of

job j = {o

1,1,1

2,1,1

3,1,3

4,1,3

5,1,3

6,1,4

} to the

working centers.

We aim at giving an ordered set of couplingsas so-

lution, e.g., h(o

2,1,1

,m1

),(o

1,1,1

,m3

),(o

5,1,3

,m11

3,1,3

,m12

),(o

4,1,3

,m10

),(o

6,1,4

,m15

)i, that as-

sociates each operation of each job to one of the avail-

able machines. A coupling (o

p, j,k

) has a cost in

terms of time t, which is the processing time of the

operation on the machine. Different machines offer

different performances for the same operations, thus

resulting in different processing times. Newer ma-

chines, indeed, are expected to outperform older and

consumed machines. Once retrieved where and when

an operation is going to be processed, and having a

forecast of the cost of the operation itself, we can

build a gantt chart, as we shall detail in Section 3.1,

to better visualize the solution and to eventually cal-

culate the total cost of the solution itself.

Finally, we adopt makespan as the indicator to op-

timize while constructing suitable solutions for the

described problem. Makespan is commonly deﬁned

as C

max

: the completion time of the last operation of

the last job in the system (T¨urkyılmaz et al., 2020).

To sum up, our problem can be summarized by the

following constraints and assumptions:

• All jobs are available at release dates;

• Not all machines are necessarily available at time

zero;

• Each operation can only be processed on one ma-

chine at a time;

• Each machine can only perform one operation at

a time.

• Each operation cannot be interrupted during the

processing process;

• Machines are grouped in Working Centers;

• Machines of each Working Center can only per-

form operations of the corresponding type k;

• Not all machines belonging to a Working Center

can perform all operations of the corresponding

type k;

• Operations can require a different processing time

on different machines;

• There is no precedence constraint among jobs;

• For each job, the sequence of operations is con-

strained by operation types;

• There is no precedence constraint among opera-

tions of the same type.

3 PROPOSED APPROACH

In order to return suitable solutions in a real indus-

trial context, according to constraints outlined in Sec-

tion 2, we implement a dual-stage genetic algorithm

with an adapted encoding-decodingchromosome rep-

resentation and pipeline, local search and social dis-

asters technique.

3.1 Chromosome Representation

The problem presented can be divided into two sub-

problems: the machine assignment and the operation

sequencing. For this reason, we utilize a two-sides

chromosome to represent a possible solution to the

problem: the left segment encodes the machine as-

signment while the right segment encodes the opera-

tion sequence (Figure 2).

A Two-stage Genetic Algorithm for a Novel FJSP with Working Centers in a Real-world Industrial Application

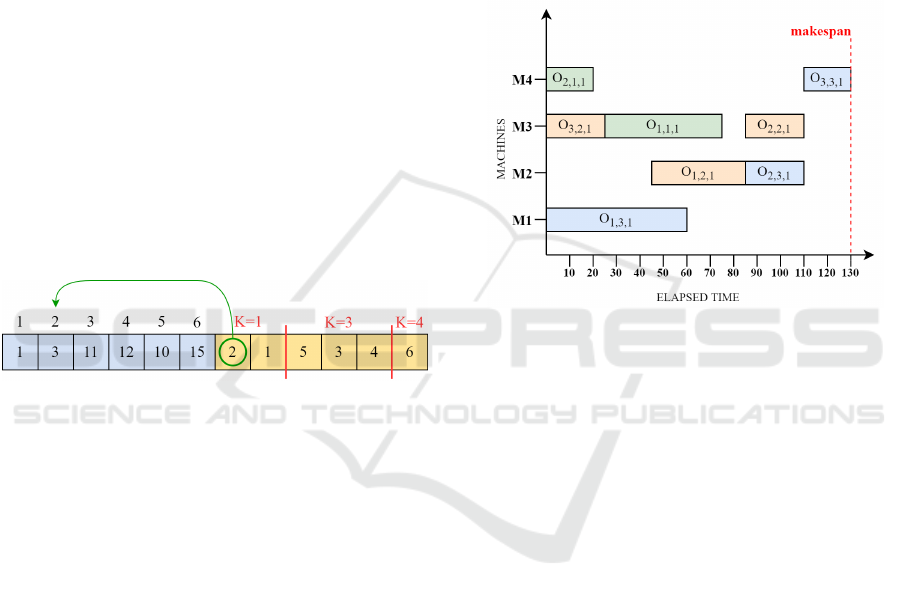
For the sake of clarity, we start by detailing the

right portion of the chromosome which represents

the operation permutation. The right segment has n

genes, each one representing one element of the op-

eration sequence to schedule. The index i identiﬁes a

gene, while the value of the gene identiﬁes an opera-

tion p. The operations are sorted by their respective

type of operation, thus each operation of type k has

an index i smaller than each operation of type k + 1.

For instance, in Figure 2, operations with K = 1 are

given ids in the range [1,2]. This way the grouping

for operation types also determines s sub-portions of

the chromosome, where s 6 l, where operations have

no predeﬁned sequence and guarantee the respect of

sequence constraints. In Figure 2, for example, we

have three operations of type K = 3; these opera-

tions are assigned ids [3,4,5], hence are identiﬁed in

the chromosome as the genes with values 3, 4 and

5. Moreover, these operations can occupy positions

in the right vector at indexes 3, 4 and 5. It is to be

noted how Figure 1 and Figure 2 only refer to a single

job for convenience, while generally a chromosome

represents a complete solution composed of multiple

jobs.

Figure 2: The chromosome representation of the solution

described in Figure 1.

The left segment of the chromosome has n genes,

each one indexed by operation p. The value of the

p-th gene is the machine m

assigned to perform the

operation o

p, j,k

. To sum up, the left segment of the

chromosome provides the couplings (o

p, j,k

), i.e.,

the assignment of the operation to a machine, while

the right segment encodes the order of the coupling in

the solution.

We have seen how each id used as the value for

genes of the right segment is eventually traceable to

an operation o

p, j,k

. In the left segment of the chro-

mosome, each gene represents the id of the machine

to which we assign the corresponding operation. This

correspondence is mapped by the vector index of the

gene, physiologically ordered from 1 to n. They in-

deed correspond to the ids we assigned to the opera-

tions in the right segment. Figure 2 shows graphically

how a gene in the right segment of the chromosome

identiﬁes an operation for which the corresponding

gene in the left segment of the chromosome reports

the assigned machine. As for the example, the opera-

tion with id 2 is assigned to machine 8.

3.2 Gantt Building

To evaluate each generated solution we need to be

able to decode and organize them under the form of

a gantt chart. By iterating over the right segment of

the chromosome we extract information about which

operations must be inserted ﬁrst into the gantt and

on which machine, using the correspondences seen

in Section 3.1. Then, for each operation, we set the

earliest possible starting time just after the ﬁnish time

of the latest operation of the same job already put in

production.

Figure 3: Example of a gantt chart utilized to evaluate the

makespan.

In fact, for each operation we need to check when

the last operation belonging to the same job termi-

nated its processing and then check on the queue of

the assigned machine; here we look for the earli-

est point where we can insert the operation without

generating overlappingswith other operations already

placed on the machine (Demir and

Is¸leyen, 2014).

The procedure seen as a pseudo-code is:

FOR op in chromosome

op_start = 0

op_finish = 0

prev_op = eventual latest operation

of the same job

IF prev_op not empty:

op_start = prev_op_finish

op_finish = op_start + op_exec_time

FOR i scheduled on op_machine:

IF op_start >= i_finish:

move forward in loop

IF op_finish > i_start:

op_start = i_finish

op_finish = op_start +

op_exec_time

IN4PL 2021 - 2nd International Conference on Innovative Intelligent Industrial Production and Logistics

Once the gantt chart is built we can use it to calcu-

late C

max

. In Figure 3 processing time is represented

on the X-axis and is expressed in minutes; for three

hypothetical jobs, we can see the positioning of their

operations over time and space (machine assignment)

and identify C

max

of the schedule as 130 minutes.

3.3 Genetic Operators

Our two-stage representation of the problem deviates

from the classical pipeline of the genetic algorithm to

respect the dual nature of our chromosome represen-

tation and to introduce some variations.

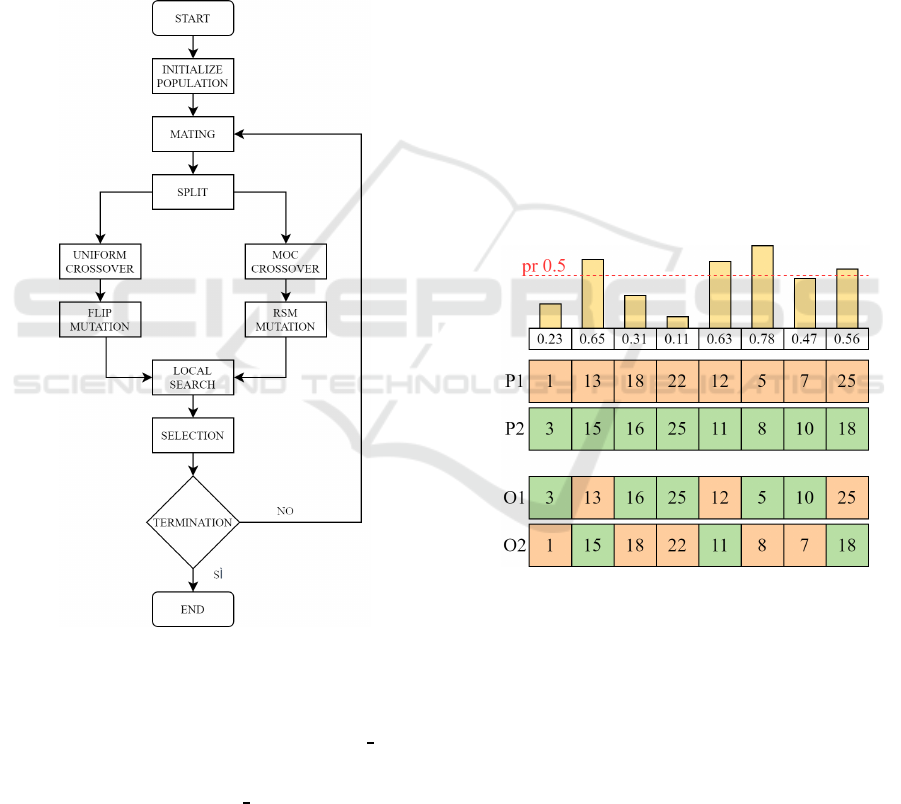
Figure 4: Our adjusted pipeline for the genetic algorithm.

We initialize the population by sampling N ran-

dom suitable chromosomes, with N being a product

of the length of the chromosome and a pop factor

parameter:

N = 2 · L· pop factor (1)

To emphasize the distance between starting individu-

als and cover wider portions of the search space with-

out exploding the population size, we force the sam-

pling process to generate distant chromosomes. To do

so we introduce a dissimilarity distance Dist that can

measure the difference between two chromosomes. In

the machine assignment segment, we verify whether

the two chromosomesdiffer gene by gene. When they

do, Dist is incremented by the number of alternative

machines available to process the operation identiﬁed

by the gene in question. In the operation sequenc-

ing segment, we increase Dist by 1 for each gene in

which the two chromosomes differ. Distmax is the

maximum distance retrievable as deﬁned by Nouri et

al (Nouri et al., 2018). When sampling each chromo-

some we check its distance with all other individuals

in the population. If Dist > Distmax· 0.5 we add the

chromosome to the initial population. This procedure

ensures a good level of variability before starting the

global search. We evaluate and sort each generated

chromosome by C

max

. Then we enter the crossover

procedure by checking how many chromosomes are

going to be mated, according to the Crossover Rate,

and randomly select and mate chromosomes. At this

point, our pipeline deviates and we split each chromo-

some into two segments, as seen in Section 3.1. Both

segments of the chromosomes need to be treated sep-

arately and undergo different crossover and mutation

procedures.

Figure 5: Uniform Crossover.

For the left segment of the chromosomes, par-

ents undergo the crossover procedure with a Uniform

Crossover. In Uniform Crossover two offspring are

generated by combining genes of the two parents, fol-

lowing the direction impressed by a probability pr.

Iterating in parallel over each gene of both parents,

if pr > 0.5 offspring 1 takes the gene from parent 1

while offspring 2 takes the gene from parent 2 and

vice versa when pr < 0.5 (Magalhaes-Mendes, 2013),

as shown in Figure 5. Uniform Crossover always gen-

erates suitable chromosomes according to our con-

straints. The same can be said for the Flip Mutation,

the chosen mutation operator. Offspring are mutated

with a probability indicated as Mutation Rate, while

A Two-stage Genetic Algorithm for a Novel FJSP with Working Centers in a Real-world Industrial Application

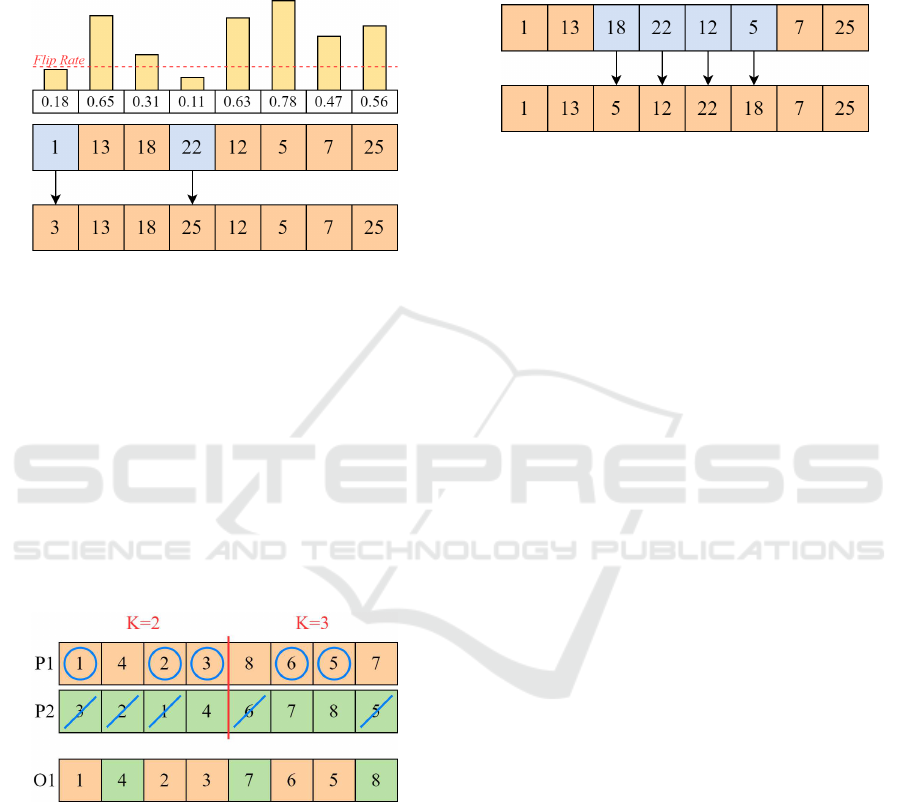
another parameter Flip Rate expresses the percentage

of genes to ﬂip. The ﬂipping of each gene happens to

respect the domain of the alternative machines avail-

able to process the operation identiﬁed by the gene in

question, trying to adopt, when possible, a different

value from the original one (Kala, 2016). For the right

Figure 6: Flip Mutation.

portion of the chromosomes, parents undergo the

crossover procedure with a Modiﬁed Order Crossover

(MOC) operator. MOC Crossover constructs an off-

spring by choosing a number of genes from one parent

and preserving the relativeorder of the elements of the

other parent and a second offspring by repeating the

procedure with reverted roles between the two parents

(Umbarkar and Sheth, 2015). MOC Rate determines

the number of genes to preserve as a percentage of

the chromosome length. Given the nature of the chro-

mosomes at hand, this crossover operation is to be

performed separately for each of the s sub-portions of

the chromosome deﬁned in Section 3.1. Offspring are

Figure 7: MOC Crossover.

mutated with the same probability determined by the

Mutation Rate by a Reverse Sequence Mutation op-

erator. This mutation operator reverses the order of

a sub-vector of random length from the chromosome

at hand (Abdoun et al., 2012). As for the crossover

operation, this mutation operation is performed sep-

arately for each of the s sub-portions of the chromo-

some. Both the strategies adopted for the two respec-

tive segments are chosen to comply with the machine

assignment and operation permutation constraints, in

order to avoid the necessity to operate corrections on

generated offspring as well as overcoming and im-

proving some solutions seen in literature (Moon et al.,

2002) (Yun et al., 2013). Moreover, new solutions in-

serted into the population are always checked not to

be already present in the population to avoid damag-

ing repetitions.

Figure 8: Reverse Sequence Mutation.

After crossovers and mutations are performed, the

two segments of the offspring are recombined to-

gether. At this point, all offspring are evaluated and

added to the initial population. Before moving for-

ward to the following generation, the extended popu-

lation is cut back to its original size by selecting the

N best individuals, granting them a presence into the

next generation (Chudasama et al., 2011).

3.4 Additional Features

In our model, we incorporate two additional features

that are not part of the typical pipeline of the genetic

algorithm: local search and social disaster technique.

For the former, we utilize a Hill-climbing algorithm

as seen in (Ceylan, 2006). At each generation we run

the local search on two solutions: the best offspring

and a randomly picked chromosome (Wan and Birch,

2013). The algorithm explores the local space around

the interested solution by changing it one bit at a time.

At each step, the local search algorithm changes the

machine assignment segment by ﬂipping a randomly

picked gene and the operation permutation segment

by swapping two randomly picked genes. If the pro-

duced solution improves the starting solution, the al-

gorithm stops and the starting solution is updated into

the population; otherwise, the algorithm performs an-

other step until the maximum number of available

steps max step is reached. For the latter, we use a pa-

rameter named counter, which is initialized at 1, and

we introduce a hyper-parameter patience. We check

after each generation whether we have improved the

best solution. If it has not improved we increase the

counter by 1. If it does improve we reset the counter

to 0. If counter == patience we remove the worst

N/2 individuals from the population, randomly re-

initialize an equivalentnumber of new individuals and

reset the counter.

IN4PL 2021 - 2nd International Conference on Innovative Intelligent Industrial Production and Logistics

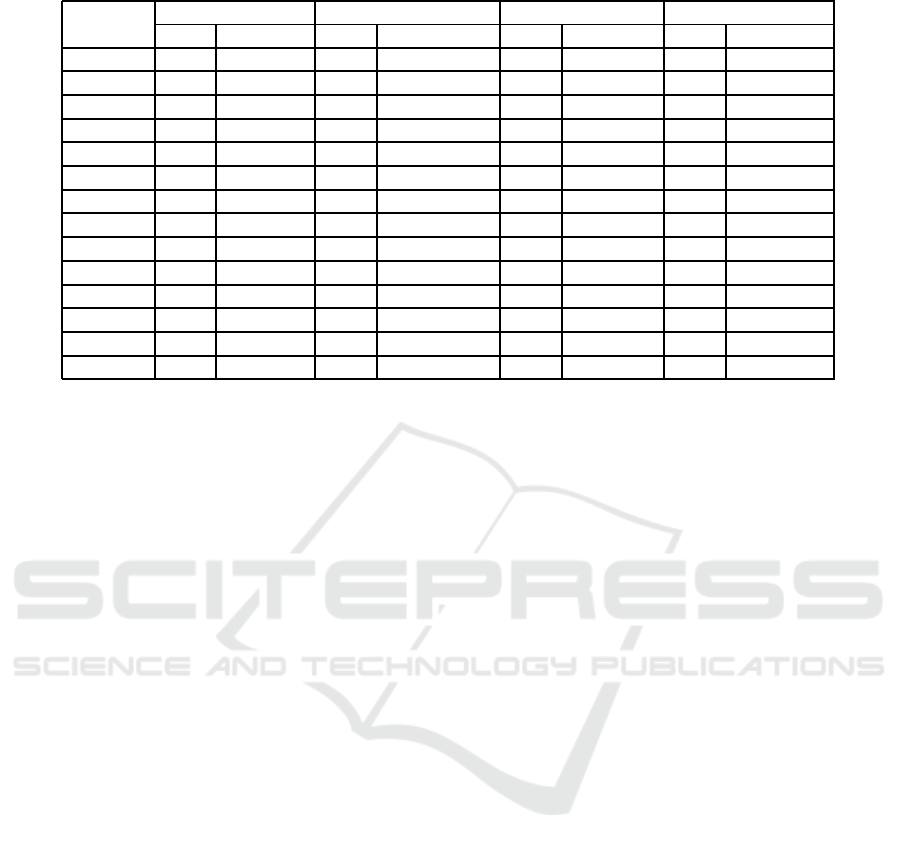
Table 1: Comparison of results on BCdata.

Instance

proposed GA Rahmati et al., 2012 Nouri et al., 2018 Best

max

Avg C

max

Avg C

max

Avg C

max

Difference

mt10c1 930 942,4 946 947 927 930 927 0,32%

mt10cc 915 920 946 946 917 918.6 910 0,55%

mt10x 934 943,6 961 961 923 931.4 918 1,74%

mt10xx 940 945,2 945 945 918 924.4 918 2,40%

mt10xxx 934 941,4 954 954 918 921 918 1,74%

mt10xy 916 922,4 951 951 908 910 905 1,22%

mt10xyz 855 873,8 858 858 868 871.8 847 0,94%

setb4c9 970 983,8 959 959 927 936.6 914 6,13%

setb4cc 969 972 944 950 938 946.8 909 6,60%

setb4x 971 989,8 942 951 944 956.2 925 4,97%

setb4xx 967 984,8 967 967 942 953.6 925 4,54%

setb4xxx 987 992,4 991 991 949 958.6 925 6,70%

setb4xy 961 978,4 978 982 931 941.8 916 4,91%

setb4xyz 960 964,4 930 930.5 926 929.8 905 6,08%

4 EXPERIMENTAL RESULTS

AND DISCUSSION

We evaluated the proposed algorithm on two datasets:

the benchmark dataset of (Chambers and Barnes,

1996) and a real-world scheduling dataset from an in-

dustrial company. The former dataset is well known

and we compared our performances with other state-

of-the-art approaches. For the latter dataset, we com-

pared our approach with the scheduling heuristic cur-

rently in use at the company we collaborated with;

ﬁnally, we also studied different combinations of ge-

netic operators of the proposed algorithm.

Barnes and Chambers constructed a set of data

(BCdata) from three of the most challenging classi-

cal job shop scheduling problems by replicating ma-

chines. The processing times for operations on repli-

cated machines are assumed to be identical to the

original (Chambers and Barnes, 1996). We tested the

algorithm over 14 test instances by Barnes and Cham-

bers, choosing the hyper-parameters experimentally

as follows:

• Pop factor: 10;

• Crossover Probability: 0.6;

• MOC Rate = 0.7;

• Mutation Rate = 0.3;

• Flip rate = 0.4;

Due to the non-deterministic nature of the genetic

algorithm, we ran our model 5 times on each in-

stance over 200 generations. For each instance, we

recorded the minimum and the average C

max

found

over the 5 runs. Table 1 compares our GA with

BBO algorithm of Rahmati and Zandieh (Rahmati

and Zandieh, 2012), the hybrid metaheuristics-based

multiagent model of Nouri (Nouri et al., 2018) and

the best results obtained in literature also listing the

percentage difference from our results.

Our algorithm can compete with the two proposed

approaches to the point of obtaining better results on

instances mt10cc and mt10xyz. However, it is to be

noted that our algorithm does not converge toward

the known global optimum, achieving better results

for the mt10 series, with margin ranging from 0.32%

to 2.40%, than the setb4 series, with margin ranging

from 4.54% to 6.70%. This difference in the perfor-

mances may be due to the unique setting of hyper-

parameter which may require ﬁne-tuning for each in-

stance of the BCdata dataset.

For the second experimental setting, we are pro-

vided with a test instance composed of a total of 309

operations divided into 16 jobs with a mean of 19,3

operations each. The instance is anonymized so that

jobs, operations and operation types are identiﬁed by

numerical progressive ids. The operations are dis-

tributed among operation types as follows:

• type 1: 55 operations

• type 2: 29 operations

• type 3: 27 operations

The number of machines available to each operation

is variable and ranges from 1 to 5. Machine fea-

tures are not discussed in this work and information

on alternative available machines for each operation

is given in the test instance.

On this instance, we ran our algorithm 10 times

over 500 generations. We varied our algorithm in four

A Two-stage Genetic Algorithm for a Novel FJSP with Working Centers in a Real-world Industrial Application

different combinations in order to justify the choice

made in terms of genetical operators and to use an

additional feature such as the local search:

1. The proposed approach;

2. The proposed approach without the local search;

3. The proposed algorithm with a different set of ge-

netic operators, namely:

• K-point Crossover instead of Uniform

Crossover (Umbarkar and Sheth, 2015);

• OX Crossover instead of MOC Crossover

(Magalhaes-Mendes, 2013);

• Twors Mutation instead of Reverse Sequence

Mutation (Abdoun et al., 2012);

4. The setting number 3 without the local search.

Hyperparameters are held the same for each ap-

proach and are chosen experimentally as follows:

• Pop factor: 1;

• Crossover Probability: 0.8;

• MOC Rate = 0.6;

• Mutation Rate = 1.;

• Flip rate = 0.2;

To resemble the schedule that would be sent to

production in the original industrial environment,

we used as a baseline a solution obtained with the

scheduling heuristic used by the production manager,

which is not different from the min-min heuristic as

know in literature (Durasevi´c and Jakobovi´c, 2018).

The heuristic can produce different solutions, so we

ran it 1000 times to better represent the variability of

human behavior. We then sorted the obtained results

per C

max

, selected the ﬁrst and the ﬁfth-best to show a

range of possible results obtained by a human expert,

and used them both as a baseline.

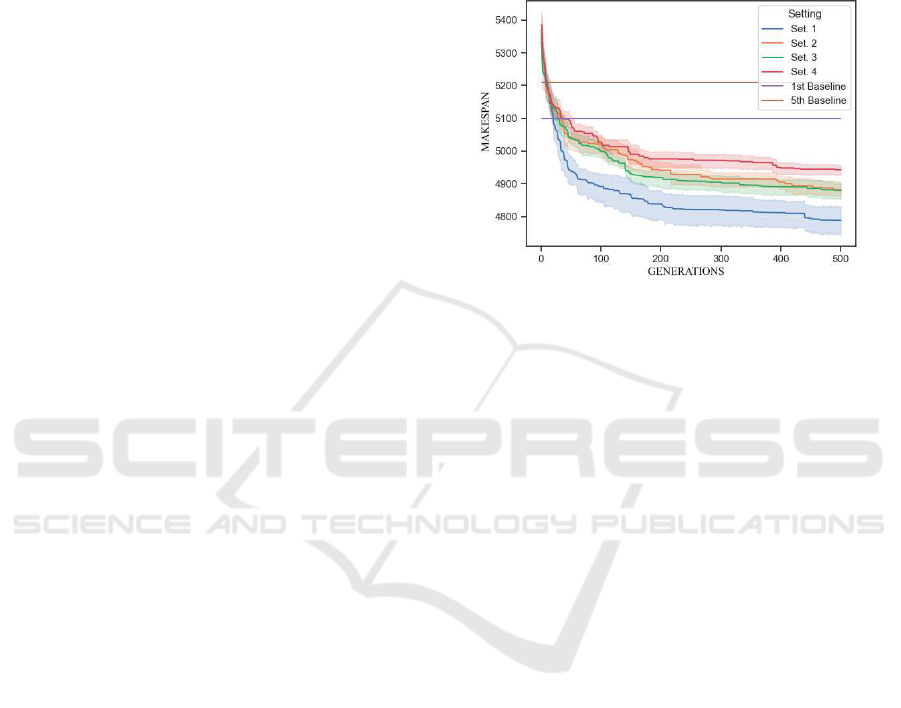
Figure 9 shows the obtained results in a line chart.

The area around each line gives an idea of the vari-

ability of the results obtained, as it is delimited by

the minimum and the maximum C

max

value seen at a

certain generation during the 10 runs. Both approach

1 and approach 3 perform better than the respective

versions without the use of local search, namely ap-

proach 2 and 4, showing how important the effec-

tive use of a local search algorithm combined with

the global search algorithm can be. The proposed ap-

proach performs better than the alternativeone both in

the short and in the long term: it is quicker in terms of

generations to reach the ﬁtness level obtained by the

production manager’s heuristic; it is better at the 100

generations mark, being able to efﬁciently explore lo-

cal portions of the search pace and improve rapidly; it

is better after 500 generations, still being able to im-

prove, managing to escape local minima with the use

of social disaster technique. When compared with the

ﬁfth baseline, the algorithm is able to obtain an im-

provement of 8.68% at the 100 generations mark and

of 10% after 500 generations. When compared with

the ﬁfth baseline, the algorithm is able to obtain an

improvement of 6.73% at the 100 generations mark

and of 8% after 500 generations.

Figure 9: Comparison of results for the second experimental

setting.

Eventually, our approach improves the baseline

scheduling saving up to 412 minutes of working time

when compared with the ﬁrst baseline.

5 CONCLUSIONS

In this work, we presented a novel version of the

Flexible Job Shop Scheduling Problem with Working

Center, in which the operations have strict sequence

constraints. In order to handle such constraints in

an industrial environment, we developed a genetic

algorithm with a two-stage chromosome representa-

tion with its encoding/decoding system, adapted ge-

netic operators, local search and social disaster tech-

nique. To evaluate the proposed algorithm we ﬁrst

compared it with other approaches on a benchmark

dataset obtaining good results. Finally, we tested our

algorithm on a test instance provided by the com-

pany which inspired such formulation of the problem.

We compared the results with the heuristic adopted

by the production manager and with different set-

tings of the proposed approach. We showed how in

both analyzed settings the use of local search im-

proves the performances and allows for quick con-

vergence to good solutions. Also, we were able to

show signiﬁcant improvements against both baselines

produced by a human heuristic by a margin of 8%

to 10%. Further development of this work will be

to dynamically handle the arrival of new operations

during the scheduling process, considering attach-

IN4PL 2021 - 2nd International Conference on Innovative Intelligent Industrial Production and Logistics

ment/detachment setup time too, while accounting for

computational performances, especially in compari-

son with other research works and with commercial

products.

ACKNOWLEDGMENTS

We thank the anonymousreviewers for their construc-

tive feedback and Simone Giovannetti for proofread-

ing the article. We wish to thank Polaris Engineering

S.r.l. for ﬁnancially supporting this research as well

as providing invaluable technical knowledge.

REFERENCES

Abdoun, O., Abouchabaka, J., and Tajani, C. (2012). An-

alyzing the performance of mutation operators to

solve the travelling salesman problem. arXiv preprint

arXiv:1203.3099.

Behnke, D. and Geiger, M. J. (2012). Test instances for

the ﬂexible job shop scheduling problem with work

centers.

Ceylan, H. (2006). Developing combined genetic

algorithm—hill-climbing optimization method for

area trafﬁc control. Journal of Transportation Engi-

neering, 132(8):663–671.

Chambers, J. B. and Barnes, J. W. (1996). Tabu search

for the ﬂexible-routing job shop problem. Graduate

program in Operations Research and Industrial Engi-

neering, The University of Texas at Austin, Technical

Report Series, ORP96-10.

Chudasama, C., Shah, S., and Panchal, M. (2011). Com-

parison of parents selection methods of genetic algo-

rithm for tsp. In International Conference on Com-

puter Communication and Networks CSI-COMNET-

2011, Proceedings, pages 85–87.

Defersha, F. M. and Rooyani, D. (2020). An efﬁ-

cient two-stage genetic algorithm for a ﬂexible job-

shop scheduling problem with sequence dependent

attached/detached setup, machine release date and

lag-time. Computers & Industrial Engineering,

147:106605.

Demir, Y. and

Is¸leyen, S. K. (2014). An effective genetic

algorithm for ﬂexible job-shop scheduling with over-

lapping in operations. International Journal of Pro-

duction Research, 52(13):3905–3921.

Durasevi´c, M. and Jakobovi´c, D. (2018). A survey

of dispatching rules for the dynamic unrelated ma-

chines environment. Expert Systems with Applica-

tions, 113:555–569.

Gao, J., Sun, L., and Gen, M. (2008). A hybrid genetic and

variable neighborhood descent algorithm for ﬂexible

job shop scheduling problems. Computers & Opera-

tions Research, 35(9):2892–2907.

Kala, R. (2016). 6 - optimization-based planning. In Kala,

R., editor, On-Road Intelligent Vehicles, pages 109–

150. Butterworth-Heinemann.

Magalhaes-Mendes, J. (2013). A comparative study of

crossover operators for genetic algorithms to solve the

job shop scheduling problem. WSEAS transactions on

computers, 12(4):164–173.

Moon, C., Kim, J., Choi, G., and Seo, Y. (2002). An ef-

ﬁcient genetic algorithm for the traveling salesman

problem with precedence constraints. European Jour-

nal of Operational Research, 140(3):606–617.

Nouri, H. E., Driss, O. B., and Gh´edira, K. (2018).

Solving the ﬂexible job shop problem by hybrid

metaheuristics-based multiagent model. Journal of In-

dustrial Engineering International, 14(1):1–14.

Rahmati, S. H. A. and Zandieh, M. (2012). A new

biogeography-based optimization (bbo) algorithm for

the ﬂexible job shop scheduling problem. The Interna-

tional Journal of Advanced Manufacturing Technol-

ogy, 58(9):1115–1129.

Rocha, M. and Neves, J. (1999). Preventing premature con-

vergence to local optima in genetic algorithms via ran-

dom offspring generation. In International Confer-

ence on Industrial, Engineering and Other Applica-

tions of Applied Intelligent Systems, pages 127–136.

Springer.

T¨urkyılmaz, A., S¸envar,

O.,

Unal,

I., and Bulkan, S. (2020).

A research survey: heuristic approaches for solving

multi objective ﬂexible job shop problems. Journal of

Intelligent Manufacturing, pages 1–35.

Umbarkar, A. J. and Sheth, P. D. (2015). Crossover opera-

tors in genetic algorithms: a review. ICTACT journal

on soft computing, 6(1).

Wan, W. and Birch, J. B. (2013). An improved hybrid

genetic algorithm with a new local search procedure.

Journal of Applied Mathematics, 2013.

Xie, J., Gao, L., Peng, K., Li, X., and Li, H. (2019). Review

on ﬂexible job shop scheduling. IET Collaborative

Intelligent Manufacturing, 1(3):67–77.

Yang, X., Zeng, J., and Liang, J. (2009). Apply mga to

multi-objective ﬂexible job shop scheduling problem.

In 2009 International conference on information man-

agement, innovation management and industrial engi-

neering, volume 3, pages 436–439. IEEE.

Yun, Y., Chung, H., and Moon, C. (2013). Hybrid ge-

netic algorithm approach for precedence-constrained

sequencing problem. Computers & Industrial Engi-

neering, 65(1):137–147.

Zhang, G., Gao, L., and Shi, Y. (2011). An effective genetic

algorithm for the ﬂexible job-shop scheduling prob-

lem. Expert Systems with Applications, 38(4):3563–

3573.

A Two-stage Genetic Algorithm for a Novel FJSP with Working Centers in a Real-world Industrial Application