Data-driven Support of Coaches in Professional Cycling using Race

Performance Prediction

∗

Aleksei Karetnikov

1 a

, Wim Nuijten

2,3

and Marwan Hassani

2 b

Software Competence Center Hagenberg GmbH (SCCH), Hagenberg, Austria

Process Analytics Group, TU Eindhoven, Eindhoven, The Netherlands

Jheronimus Academy of Data Science, ’s-Hertogenbosch, The Netherlands

Keywords:

Sports Analytics, Cyclist Performance, Data-driven Performance Prediction, Maximum Mean Power.

Abstract:

In individual sports, the judgment of which training activity will lead to the best performance is mostly based

on the expert knowledge of the coach. Recent advances in data collection and data science have opened up

new possibilities for performing a data-driven analysis to support the coach in improving the training programs

of the athletes. In this paper, we investigate several methods to do such analysis for professional cyclists.

We provide the coach with a framework to predict the Maximum Mean Powers (MMPs) of a cyclist in an

upcoming race based on the recently performed training sessions. This way the coach can experiment with

several planned alternatives to ﬁgure out the best way for preparing the athlete for a race. We conduct multiple

prediction models through an extensive analysis of a real dataset collected recently about the performance of

professional riders with varying physiologies and temporal performance peaks. We show that the application

of the hybrid model using XGBoost and CatBoost has clear advantages. Additionally, we show that the

accuracy of our general model can be further increased by ﬁltering according to the mountain stages. We

have additionally validated the proposed framework using an openly available real dataset and the results

were consistent with those of the collected data. We offer an open source implementation of our proposed

framework.

1 INTRODUCTION

The prediction of the competitive performance of an

athlete based on the performed training sessions of

that athlete is at the heart of preparing athletes to

perform well in competitions (Jobson et al., 2009).

At present day, the judgement of what training activ-

ity will lead to the best sports performance is mostly

based on the expert knowledge of the coach of the ath-

lete. Recent developments in data collection and data

science have opened up the possibilities for doing a

data-driven analysis to support the coach in improv-

ing the training programs for optimizing the perfor-

mance of the athlete (Castronovo et al., 2013). In this

paper we investigate ways to do such analysis for pro-

https://orcid.org/0000-0002-2672-8548

https://orcid.org/0000-0002-4027-4351

∗

Most of the core project activities were done at TU

Eindhoven.

The research reported in this paper has been partly

funded by BMK, BMDW, and the State of Upper Austria

in the frame of the COMET Programme managed by FFG.

fessional cyclists, where we aim to provide the coach

with a method to predict the performance of the ath-

lete in an upcoming race based on recently performed

training sessions and planned training sessions in the

near future (Figure 1).

Currently, there are a few studies which are show-

ing surprisingly high accuracy (up to 95%) of the

instant parameter prediction (Hilmkil et al., 2018;

Kataoka and Gray, 2019). In a different study, an

analysis of the training sessions was performed in

400-metres hurdles races (Przednowek et al., 2014),

but its application in cycling should be examined.

Thus, to the best of our knowledge, there is no com-

plete framework that could be applied for the predic-

tion of an athlete’s performance for a long-term time

in cycling.

In this paper, we are using aggregated training ses-

sions and race data for building a prediction model

that could be used for a comparative analysis of dif-

ferent training sessions options. We found that the

application of the general hybrid model that is based

on XGBoost (Chen and Guestrin, 2016) and CatBoost

Karetnikov, A., Nuijten, W. and Hassani, M.

Data-driven Support of Coaches in Professional Cycling using Race Performance Prediction.

DOI: 10.5220/0010656300003059

In Proceedings of the 9th International Conference on Sport Sciences Research and Technology Support (icSPORTS 2021), pages 43-53

ISBN: 978-989-758-539-5; ISSN: 2184-3201

 2021 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved

(Yandex, 2019) has undoubtedly advantages when

compared to the individual model. We found addi-

tionally that ﬁltering the mountain stages gives an

additional growth of the prediction quality whereas

omitting of the time-trials is not positively affecting

the accuracy. By ﬁltering the mountain stages, we

have reached an RMAE (Relative mean absolute er-

ror (Gepsoft, 2019)) of less than 4% in 88% of the

cases, the rest 12% can be predicted with an RMAE

of less than 6%.

The remainder of this paper is organized as fol-

lows. Section 2 proposes an overview of previous

studies in data analysis in sport and the related areas

with similar background and their shortcomings from

our perspective in the particular case. Section 3 de-

scribes the problem, general knowledge about perfor-

mance in cycling and an idea that combines the best

approaches of the previous studies and proposes new

opportunities for better prediction quality. Then, in

Section 4 an extensive evaluation of various predic-

tion techniques is described. These results were also

validated by application of the same approach on the

open cyclicng data 5. Finally, Section 6 presents a

conclusion and a discussion.

Figure 1: A visual representation of the application sce-

nario.

2 PREVIOUS STUDIES ON

PERFORMANCE PREDICTION

Currently, several studies targeting the performance

analysis using different prediction methods in sports

competitions exist. In (Rastegari, 2013) an overview

of different prediction methods in sport is given. In

general, it was found that some disciplines are bet-

ter predicted by the regression models whereas other

could be better described by neural networks and tree

models. For instance, the Lasso regression model has

the best performance in hurdles races (Przednowek

et al., 2014) whereas swimming (Maszczyk et al.,

2012) is better predicted by a neural network. Then,

in (Przednowek and Wiktorowicz, 2013) the authors

demonstrate that Linear models seem to be relatively

better for walking activities. Furthermore, in several

cases, the prediction quality can be improved by in-

cluding additional contextual parameters like air tem-

perature, meteo-conditions, additional metrics (Has-

sani and Seidl, 2011). In (Kataoka and Gray, 2019)

the authors are focused on the prediction of current

power measurements. Some of the parameters were

retrieved from public GPS data. This approach de-

pends on the real-time data availability and the guar-

anteed access to this data. Additionally, its accuracy is

relatively low (the lowest MAE is 60.13 Watts for re-

gression model and 63.97 Watts for XGBoost which

was chosen as the “best” model). The article does

not have any explanation about this value but accord-

ing to evaluation on the available dataset, it is be-

tween 12% and 20% of the average power. This re-

sult was tested only on one race. Additionally, in (Le-

ung and W. Joseph, 2014; Przednowek et al., 2014)

the authors demonstrate results of non-linear models

(indeed a decision tree) which have shown the best

performance among the classical models, but some of

the used variables are not applicable in cycling be-

cause they are applicable only for animals or using

well identiﬁed different types of exercises (walking or

running). Moreover, this paper is describing predic-

tion of repetitive ﬁxed-length sprints, where cycling

distances are always different. Finally, the authors

of (Leung and W. Joseph, 2014) introduce a signiﬁ-

cantly more precise model which was developed for

their special case. The prediction of the statistical re-

sults is a common problem for almost all the inter-

ested stakeholders. The professional cycling teams

are also interested in special performance measure-

ments such as heart rate, power, speed and other pa-

rameters that could be tracked by various sensors of

bike computers. These parameters can be predicted

with reasonable precision. For example, in (Hilmkil

et al., 2018) an LSTM model was used to predict the

heart-rate of another professional cycling team. The

results are given only in absolute units but its rough

estimation tells that prediction quality is about 90%.

Moreover, in (Cecchini et al., 2014) a Feed Forward

Neural Network was used to predict the muscle force

of a rider. The authors have reached an RMSE less

than 1%.

As such, all the available studies are showing ac-

ceptable prediction quality in the particular questions

and sport disciplines, but there is no available study

aiming at a more complex analysis of cycling compe-

titions as a whole. Probably, prediction models from

other sport disciplines could be re-used, but it was

not tested yet either. Furthermore, there are only a

few studies that were working particularly with pro-

fessional cycling. Recently, the vast majority of such

studies are oriented on the analysis of LLTH (Live

icSPORTS 2021 - 9th International Conference on Sport Sciences Research and Technology Support

Low Train High) approach and the comparison with

LHTL (Live High Train Low) (Burtscher et al., 2006;

Hamlin, 2013; Fulco et al., 2000; Garvican-Lewis

et al., 2015). It requires careful analysis of the avail-

able prediction techniques which could be used for

this kind of “what-if” analysis, the identiﬁcation of

the main predictors and the veriﬁcation of the model

on the real dataset.

We propose a general framework that can use dif-

ferent kind of prediction models (Yandex, 2019; Chen

and Guestrin, 2016) and we are able to test differ-

ent combinations of those and achieve an accuracy of

more than 90% by RMAE. Additionally, all the pos-

sible deviations in the input data and the prediction

model are detected because it was validated not only

by the theoretical knowledge, but also by the practical

experience of the professional team.

3 OVERVIEW OF THE

PROPOSED FRAMEWORK

3.1 Preliminaries

This paper is focused on the prediction of race perfor-

mance based on the measurements from the training

sessions. Some of the race parameters are known in

advance (like length and elevation) and could be used

in the ﬁnal model. In general, this model is based on

historical data from previous combinations of races

and training sessions. Additionally, our research if

focused on use of the high altitude training (LLTH

approach). The main idea of this training method is

the reduced air density with altitude that has a posi-

tive inﬂuence on the air-resistance of the rider, but it

signiﬁcantly reduces efﬁciency of the aerobic energy

system. This effect is useful not only as a real devel-

opment of muscles but also as a placebo (Burtscher

et al., 2006). We are using the Maximum Mean Pow-

ers (MMPs) as the performance metric. This way the

coach can test several planned alternatives to ﬁgure

out the best way to prepare the athlete for a compe-

tition. According to the requirements of the profes-

sional team, we are mostly focusing on the mountain

stages of the multi-days races of the Grand Tour. The

duration of the cycling season is almost 1 year and as

such it includes different periods of the performance

levels for each cyclist (Cintia et al., 2013). We focus

on predicting peak performances in crucial stages as

scheduled in one of the Grand tours. These are the

main seasonal targets of overall standings riders.

The most important variables that describe race

performance in this particular case are the measure-

Figure 2: A visual representation of TOP 3 MMP selection.

We calculate the moving average during the given time pe-

riod with temporal padding between the MMPs to avoid an

overlap. The highest MMP1 is shown in the middle. The

two other values MMP2 and MMP3 should have a mini-

mum distance between each other.

ments of Mean Maximal Power (MMP) of the athletes

for various time periods (5, 6, 15, 30 and 45 minutes).

These variables are the highest average power during

the given period according to (Xert, 2019). In other

words, it is a maximal moving average of the data

sample. Additionally, the N-largest MMP could be

also calculated. In that case, all the MMPs should be

carefully checked, so that they do not have any over-

lapping power measurements. This principle is repre-

sented in Figure 2. Where there are 3 equal intervals

that have a predeﬁned minimal interval between each

other. The color intensity of this image shows the or-

der of the measurements sorted by its value. The chart

on the background is shown for better visual percep-

tion and it does not represent any real data. In this

paper, we are mostly focused on the prediction of the

ﬁrst MMP, but the predictors are also based on the

ﬁrst and the second MMP values from the training

sessions.

Since one of our focuses is the mountain stages,

we assume that the riders have competitive advan-

tages on these stages and thus, the maximum per-

formance. According to the domain expert, the ﬂat

stages are mostly depending on the race situation

that is not predictable because of the unknown rivals’

strategy. Moreover, it can be inﬂuenced by the tacti-

cal decision of the coach. Thus, we need to predict the

mean possible values of the MMPs for these stages.

Another assumption of our research is that each

training camp day has its own effect (estimated by

its weight which is calculated as a linear distance be-

tween the connected days) on each of the race days

(see Figure 3). To make these weights more applica-

ble, they could be normalized. As a result, each of M

race days is predicted using N training camp days and

Data-driven Support of Coaches in Professional Cycling using Race Performance Prediction

according to the assumption, the closest days have the

highest effect on the result. Note that the sum of these

weights (normalized delays between the training ses-

sions and the race days) is equal to 1. It is impor-

tant that one training session can be related to multi-

ple races but each race has only one related training

session. In some special cases, the whole race could

be considered as a training session if it was a high

altitude race (Figure 3).

3.2 Model Description

The proposed model is based on performance data

from 3 pro-riders for all the years of their profes-

sional activity in the team. They were collected by

various sensors on bikes and then combined by a cy-

cling computer. In this setting Garmin hardware was

used. The input dataset includes 32 raw (from the

sensors) variables and 108 contextual and aggregated

attributes. Then, those were reduced to 48 variables

(Table 1). A more detailed explanation of the process

will be given in the next section. Our feature selec-

tion strategy was applied in a continuous consultation

with the domain experts, thus some of the training at-

tributes were manually ignored due to the conceptual

importance of race parameters for the planning of the

training sessions. The the model was trained again

and tested by different training camp settings. If the

model was not responsive to change of these parame-

ters, the selection of the predictors was repeated. Fi-

nally, we have identiﬁed a subset of 48 variables that

provides both reasonable prediction quality and the

required functionality.

Out research focuses on use of the aggregated race

data obtained from the cycling computers and its sen-

sors.

The overall pipeline of the developed framework

is shown in Figure 4. It includes extraction and pre-

processing of the raw data from the sensors. The lat-

ter stage performs aggregations of the cycling ses-

sions and a combination of the training-race pairs

that are used by the Machine Learning model. The

aggregation principle is shown in Figure 3. The

model uses 48 attributes that are automatically re-

trieved from the dataset to predict 5 depended vari-

ables: mmp5m (Mean Maximal Power over 5 min-

utes), mmp6m, mmp15m, mmp30m and mmp45m.

The selection of these depended variables was based

on the necessities of the professional team. The ex-

amined dataset is taken from one of the Grand Tour

events. Additional contextual data (year as a pro-

fessional, weight and other) are also available. We

are unable to reveal those or further details about the

dataset as we have signed a non-disclosure agreement

with the owner company. After a series of tests, a

race proﬁle hypothesis was proposed. In detail, it was

suggested that different race types have a signiﬁcant

effect on the scale of power measurements. Quick

time trials and races in mountains require higher en-

ergy consumption and, as a result, higher power out-

put. The races were divided into 4 groups: all the

races, only mountain stages, only time-trials and only

time-trials in mountains. The mountain stages were

deﬁned as the races which have max altitude higher

than 1500 m and the time-trials were ﬁltered by the

race name. Additionally, since these measurements

are available only for limited time periods, the whole

dataset is relatively small for such a prediction. Thus,

the second hypothesis states that the lack of data could

be compensated by an assumption of almost identical

parameters of professional riders. A similar assump-

tion was proven useful in swimming (Maszczyk et al.,

2012). To prove this idea in cycling, the model was

separately tested on the data from only one (individual

sample) and all the available (general sample) riders.

As a result, 8 different models were examined.

Moreover, the accuracy could be increased by ﬁl-

tering the input dataset wrt the rider and/or the race

proﬁle. Thus, in this work we are testing an individ-

ual model and additionally a general one. The general

model is trained on data from all the comparably sim-

ilar riders. Additionally, special models were tested

with the data ﬁltered by mountains stages and time-

trials in various combinations.

It is clear that prediction of the power measure-

ments is principally a non-trivial task because it de-

pends not only on the previous performance of the

rider but also on all of his/her competitors because

of psychological factors. Since all the performance

measurements are always conﬁdential for the teams,

it is impossible to retrieve their data. An indirect

data collection from open sources and various image-

capturing algorithms which use online translation of

the event would of course be possible.

3.3 Prediction Models

This paper estimates the most performative models

from previous studies: Linear Regression + model

with interactions, Lasso Regression (Przednowek

et al., 2014), LSTM (Hilmkil et al., 2018), Deci-

sion Tree (Rastegari, 2013), Random Forest Regres-

sion (Kataoka and Gray, 2019), XGBoost (Przed-

nowek et al., 2014). These models were examined

to ﬁnd the best performing settings. So, the Linear,

non-linear and Lasso regressions were tested in En-

try, Stepwise and Forward modes (selection of the in-

dependent variables) (Efroymson, 1960). The vari-

icSPORTS 2021 - 9th International Conference on Sport Sciences Research and Technology Support

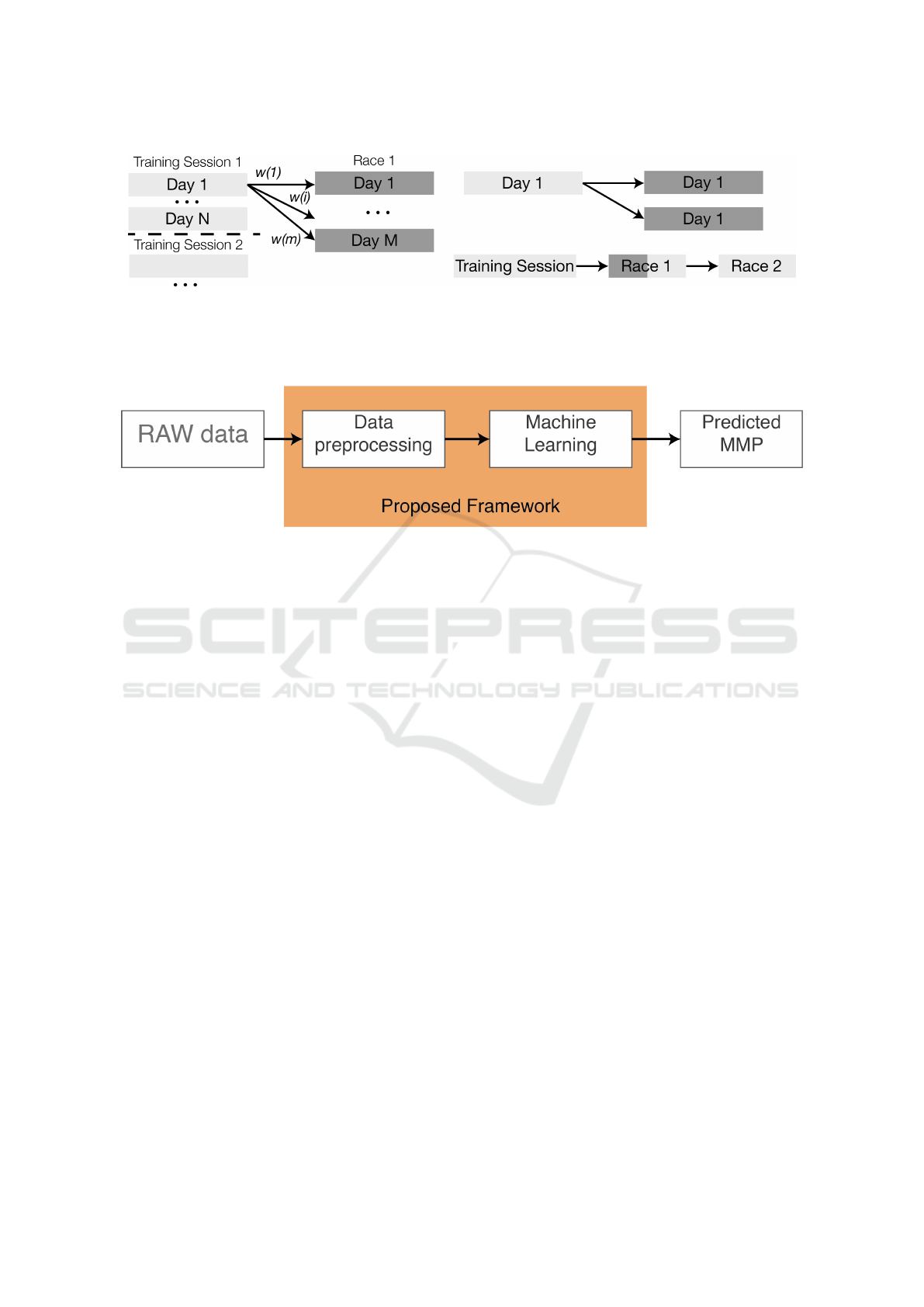
Figure 3: Visual representation of the training-race combinations (left) and possible sequences of training sessions and races

(right). Each day of the training session has a contribution to each day of the race. At the same time, if there is more than one

race after the training session in a predeﬁned period, that race could be considered as a training session. In the ﬁgure, each of

the days 1 to N has an inﬂuence on each of the M race days with a particular weight. If there is more than one race the training

session inﬂuences on more race days and the races in the middle could be considered as an additional training session.

Figure 4: Pipeline of the proposed framework.

ables were estimated by SPSS (IBM, 2019) and then

fed manually to the model as Scikit-learn (Pedregosa

et al., 2011) does not support these models. Further-

more, semi-log and log models (Kenneth, 2011) were

examined. In the case of an LSTM model, various ar-

chitectures of layers and neurons were tested. Since

it is a time-consuming procedure, these settings were

taken from previous studies (Eckhardt, 2018; Hilmkil

et al., 2018; Przednowek et al., 2014) and then 2

times smaller and 2 times larger number of layers

were also checked. The initial seed for the weights

was randomized according to (Brownlee, 2017). The

tree models were also evaluated. In the majority of

previous studies (Przednowek et al., 2014; Kataoka

and Gray, 2019) the settings of these models were

not clearly presented. Probably, only default param-

eters were checked. To avoid any possible bias, we

checked them with different seeds and depth settings.

Finally, according to the preliminary data overview

and knowledge, the races were additionally classiﬁed

by 2 categories: time trial and mountain stages (max-

imal elevation is higher than 1500 m). All the models

were tested with normalized datasets except for the

gradient boosting that does not require that. This step

is important because these special races have princi-

pally different strategies of the riders and the scale of

the obtained measurements could be signiﬁcantly dif-

ferent. For instance, a higher energy consumption is

expected during the mountain stages. To avoid prob-

lems with the interpretation of the results, this paper

reports the Relative MAE (RMAE) which could be

easily estimated (Gepsoft, 2019).

4 EXPERIMENTAL EVALUATION

The full source code of the framework with a link to

the open-source dataset is available in (Karetnikov,

2021).

4.1 Experimental Settings

The previously described models were trained on the

specially divided dataset of the multiday races. This

dataset includes 41 races and 23 training sessions

from 3 professional riders. These training and race

sessions are combined is such a way that every race is

always connected to a training session. The mapping

is performed according to the temporal dimension of

the data considering a fact that effect of a training

can be vanished after a particular time. In this study

we use a threshold of 30 days. We predict data only

for the TOP-2 riders and use data from an additional

athlete with comparably equal performance to enrich

the input dataset. We perform these experiments with

2 main models: general (training on the common

dataset) and individual (training only on the personal

dataset). Then, we are using one of the latest multi-

day races of the Grand Tour where both riders were

participating to perform an optimization of the models

Data-driven Support of Coaches in Professional Cycling using Race Performance Prediction

Table 1: Input attributes of the model.

Attribute (Group) Description

Distance on High Altitude Total Distance on the altitude higher than 1500 m (race)

Altitude Max altitude, total elevation (race)

Time-Trial ﬂag True of False

Delay

(training session-race) Normalized delay (0;1]

Distance Total distance

Speed Average speed during the training session

Power Total work, mean power, 1st, 2nd MMP 5, 6, 10, 12, 15, 20, 30, 40, 45 min

Special effort special effort (AVG Power > FTP, t >= 20 min), tempo effort

(AVG Power > 90%*FTP, t >= 8 min), bursts (AVG Power > FTP, t > 4 s)

Altitude Avg, Max altitude, Total elevation

Time, s Total time, time on the altitude higher than 1500 m

Grade slope grade during the MMPs

hyperparameters. When we have identiﬁed the most

performative models, they were also cross-validated

according to the k-folds algorithm. The folds were

split according to the race id as it is shown in Figure

5. It leads to different sizes of the train and test sub-

sets but it helps to produce a more robust evaluation.

For the cross-validation of the models, we ﬁlter only

the races that are longer than 4 days.

Figure 5: The dataset train-test splitting method. The

framework uses a modiﬁed k-folds split algorithm that splits

the dataset according to the race id rather than the ﬁxed size

of the subsets.

4.2 Results

Regarding the model’s performance, some practically

useful results were discovered. Figures 6 and 7 show

an average RMAE (Gepsoft, 2019) of the predicted

results for the 2 examined riders. It is based on one

of the Grand Tour races where all the riders were

present. Additionally, these results are shown for

the already tuned models. First, the examination of

the models on the full general and individual dataset

has shown that normally an average RMAE of all the

prediction techniques is 1-2% higher for the individ-

ual model (Figure 6). In general, the min RMAE of

the main model is 10.74%. Then, one can ﬁnd that

the mountain model is comparatively more performa-

tive (it can have a mean RMAE of 3.42% and a min

RMAE of a single race day smaller of 0.03%) than

the main one (Figure 7). The hypothesis that the time-

trials have different prediction opportunities was not

conﬁrmed. The prediction quality is even less than

the of the ﬁrst model (Figure 8). It can be explained

by an extremely small subset of time-trials (normally,

no more than 10% of the race). So, we should be fo-

cused only on the two general models (Figure 6 and

7). In details, the best performing model in the both

cases is the stepwise regression. Normally, its RMAE

is 1-2% lower than that of the other models. Some-

times, the LASSO model helps to improve this error

by mere 0.1%. Then, the Random Forest Regression

and the CatBoost models have almost the similar per-

formance. The next roughly similar group of the mod-

els consists of the XGBoost model and the Decision

Tree. The latter technique is more accurate in most of

the situations. The full multiple-linear regression is

signiﬁcantly less accurate than the previous methods.

Finally, the LSTM model cannot be considered as a

possible prediction method due to its enormous error

that is higher than 20% despite varying the number of

layers and neurons as discussed in Section 3.2.

The examination of the linear regression models

has shown that a stepwise model (Efroymson, 1960)

performs insigniﬁcantly better than the full one. Ac-

cording to the mean R

of all the predicted variables,

43.1% of the MMP values could be explained by the

full set of predictors. The stepwise model, which is

based on 9 out of the 140 variables, increases this

metrics by an insigniﬁcant 0.28% but, in practice, this

was conﬁrmed for all the models except the individ-

ual ones (Figures 6 - 8). The linear regression models

show completely similar performance, as can be seen

in Figure 8, but they have a very limited practical ap-

plication due to the observed overﬁtting of the model

and the incorrect selection of the prediction features

by the Stepwise algorithm. That does not help to an-

swer the question about settings of the training ses-

sions. The same conclusion can be drawn for the

icSPORTS 2021 - 9th International Conference on Sport Sciences Research and Technology Support

Figure 6: A comparison of prediction methods for the gen-

eral and the individual model with 2 riders by average

RMAE. Y-axis represents RMAE (lower is better), X-axis

represents different MMPs. The models are encoded by the

color of the bars and given in the same order as in the leg-

end.

Lasso regression.

The same observation was obtained after various

tests on trees’ depth. We found that the best models

are: the Decision Tree, Random Forest Tree (RFR),

XGBoost, and CatBoost. Accordingly, the following

experiments are related only to these models. To con-

ﬁrm the repeatability of the prediction and lack of de-

pendency on a random factor, a series of the differ-

ent seed tests with the RFR, XGBoost, and CatBoost

were performed. These results demonstrated an ex-

tremely small variation of the mean RMAE that con-

ﬁrms the repeatability of the experiment. The results

of the RFR model are shown in Table 3. All the val-

ues are given in % and one can ﬁnd that the highest

deviation is equal to 0.07%. The other model did not

show a variation higher than 0.02%.

Then, it is clear that an LSTM model cannot be

used in this situation because it has shown signiﬁ-

cantly higher RMAE than all other methods. At the

same time, the ﬁndings about the best performative

prediction technique from (Kataoka and Gray, 2019)

and (Przednowek et al., 2014) were conﬁrmed. It

was realised that the most accurate prediction mod-

els is XGBoost, CatBoost and Random Forest Tree

Figure 7: Comparison of prediction methods for the gen-

eral and the individual model with (mountain stages) with 2

riders by average RMAE.

Figure 8: Comparison of prediction methods for the general

and the individual model (without time-trials) with 2 riders

by average RMAE.

Data-driven Support of Coaches in Professional Cycling using Race Performance Prediction

(the more detailed analysis has shown that accuracy

can dramatically drop in the case of Rider 2). Since

the CatBoost model is generally more accurate than

XGBoost (Pallapothu, 2019), we are focusing on

this model. One of the ﬁndings is that the exten-

sion of the ﬁrst dataset with only two riders by an-

other athlete has signiﬁcantly improved the predic-

tion quality of the CatBoost model. Previously, the

XGBoost method was over-performing this relatively

new model. In some cases, the Random Forest Tree

model is slightly more accurate (for instance, the pre-

diction of the MMPs for more than 30 minutes) but

this fact should be considered as an outlier because

it happened only for one rider. Moreover, this differ-

ence is less than 1%.

Since the two models (XGBoost and CatBoost)

have relatively similar accuracy, they were addition-

ally cross-validated by all the multi-days races (the

races that have more than 4 days). The dataset of

this experiment includes 23 races. From Table 2, that

represents the experiment’s results, we can conclude

that the mountain stages can be better predicted by an

XGBoost model (0.23% more performative than Cat-

Boost) whereas prediction of all the other stages can

be done better by a CatBoost model (1.82% more per-

formative than XGBoost).

4.3 Discussion of the Results

To conclude this section, the main hypothesis about

the application of the general model was success-

fully conﬁrmed. Another hypothesis about applica-

tion of the special models for the special races was

only partly conﬁrmed. The separation of the moun-

tain stages has provided a signiﬁcantly higher perfor-

mance of the model whereas a model that is aimed

only on the time-trials did not demonstrate any out-

standing performance. As such, the prediction of the

mountain stages can be done with an average RMAE

of less than 6.65%. All other stages can be pre-

dicted by the general model, which shows an error

of no higher than 13.13% (Table 2). The smallest

RMAE for a single race that was obtained during the

cross-validation experiment is 0.03% for the moun-

tain stages and 0.05% for all the other race stages.

5 EXPERIMENTING ON OPEN

SOURCE DATA

Since the original model is based on the dataset

owned by our leading industrial partner, the frame-

work was additionally validated with the use of the

open cycling data(Jr. et al., 2017) to encourage re-

searchers and practitioners to repeat our results. This

dataset includes data from 5 cyclists with a race his-

tory of more than 8 years. After data pre-processing,

we discovered that only 319 days from the whole

dataset could be used. This happened because the

dataset was ﬁltered by the presence of the power mea-

surements and the minimum length of the cycling ses-

sion should be more than 30 minutes. Then, the raw

dataset was converted into a table to make the further

operations more interactive. Additionally, this bench-

mark was aimed to prove the performance of the gen-

eral model. So, it is possible that we could meet dupli-

cates of the days. In these cases, only the ﬁrst met row

was kept. Since the data is well anonymized, it is im-

possible to map the available days with the real train-

ing and race sessions. To overcome this limitation, we

have decided to create training-race clusters consider-

ing a fact that the effect of the training is neglected in

more than 30 days. After these clusters were created,

only those with 4 or more days were used for further

consideration. This is important because only under

these constraints we could guarantee to have at least

3 training days before a single-day race. The thresh-

old of about 60% of the training days was identiﬁed

by the analysis of the collected professional dataset

and we decided to keep its settings. After that step,

it was possible to apply the training-race combination

algorithm that was described earlier to obtain the ﬁ-

nal dataset for the evaluation that consists of 819 rows

and 26 race clusters. Then, we have performed a sub-

experiment to identify the size of the training subset

for the cross-validation step. We found that the most

optimal size is 10 race clusters out of 26 that is about

40% of the whole dataset. More detailed results are

shown in Figure 9.

Figure 9: Experimental setting of the most optimal train

subset size corresponding to the lowest RMAE average.

icSPORTS 2021 - 9th International Conference on Sport Sciences Research and Technology Support

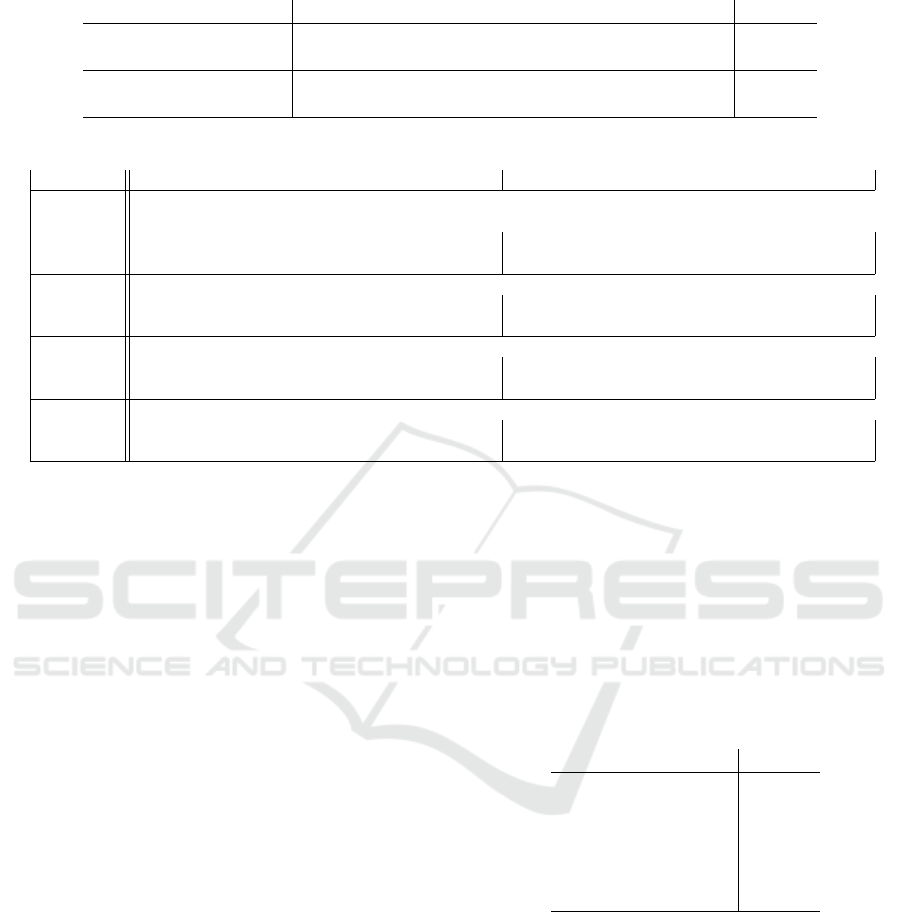
Table 2: Cross-validation of the models of 23 races each of multiple days.

Model Dataset MMP5 MMP10 MMP15 MMP30 MMP45 MEAN

XGBoost

Flat 13.54 13.79 13.56 14.19 13.79 13.77

Mountains 6.62 6.49 5.98 6.64 6.5 6.65

CatBoost

Flat 12.7 13.28 13.02 13.15 13.52 13.13

Mountains 6.68 6.62 5.8 6.59 8.28 6.79

Table 3: RMAE means and its variation for different random seeds (from 0 to 1000 with a step of 1) of the RFR model in %.

Parameter MMP5m MMP15m MMP30m MMP45m MMP5m MMP15m MMP30m MMP45m

Rider 1 Rider 2

General model

Mean 17.07 17.02 22.74 25.75 2.82 8.8 8.99 11.96

Variance 0.11 0.06 0.06 0.06 0.02 0.02 0.03 0.02

General model with only mountain stages

Mean 3.27 2.79 5.6 3.11 3.78 2.94 2.18 3.3

Variance 0.02 0.02 0.04 0.02 0.03 0 0.01 0

Individual model

Mean 6.61 3.6 5.78 8.61 3.19 3.82 2.28 5.44

Variance 0.02 0.03 0.07 0.05 0.02 0.01 0 0.01

Individual model with only mountain stages

Mean 6.61 3.6 5.78 8.61 3.19 3.82 2.28 5.44

Variance 0.02 0.03 0.07 0.05 0.02 0.01 0 0.01

Consequently, a full cross-validation of the previ-

ously described model was performed. For the par-

ticular dataset, we performed 16 iterations. Finally,

the obtained results were compared to the previously

obtained ones. This comparison is shown in Fig-

ure 10. Overall, the highest difference was found

in the performance of the Decision Tree model that

demonstrates a worse performance of more than 7

percentage points growth of MAE. In the collected

professional dataset, we have already identiﬁed that

the most performative model in our framework was

CatBoost that has shown more reasonable behavior.

The aggregated average results are shown in Table 4.

Although the Linear Regression model was more per-

formative in some of the cases, we could identify its

overﬁtting behavior in the original experiment. Ad-

ditionally, the relative difference between CatBoost

and Random Forest Tree is not recognizable to reject

the previous decision about CatBoost that has shown

an average MAE difference of 1.81%. Despite the

fact that on average all the models have shown a rela-

tively lower performance, which could be explained

by limitations of the available dataset, all of them

have demonstrated an improved performance to pre-

dict MMP 45 minutes.

Finally, the main target of the benchmark was met.

It was possible to evaluate the framework with the use

of the open dataset with a mixed proﬁle of the ath-

letes. Considering the mainly used CatBoost model,

an average MAE difference is acceptable to conﬁrm

the robustness of the approach and repeatability of the

experiment. It means that the model does not have

a high prediction quality variation and it is not lim-

ited only by the original subset of the athletes with

the strong mountain races proﬁle. On the contrary,

it is possible to signiﬁcantly improve its performance

by use of the special settings that correspond to the

rider’s proﬁle. The full source code of the framework

with a link to the open-source dataset is available in

(Karetnikov, 2021).

Table 4: Mean RMAE difference between the base model

based on the proprietary dataset and the model trained with

an open-source dataset in percentage points.

Model RMAE

Linear Regression 0.8

Random Forest Tree 1.74

CatBoost 1.81

LASSO Regression 2.79

XGBoost 4.21

Decision Tree 4.78

6 CONCLUSION AND OUTLOOK

The validity of the proposed framework that predicts

the performance (in this paper it is MMP) of a pro-

fessional rider with a general model was conﬁrmed.

The general model, that was trained on the data from

several riders with comparably similar skills, is better

performative in prediction of a single rider’s perfor-

mance than the model that is based only on the data

of this individual rider. It can be explained by ex-

tending the training dataset. The same method was

Data-driven Support of Coaches in Professional Cycling using Race Performance Prediction

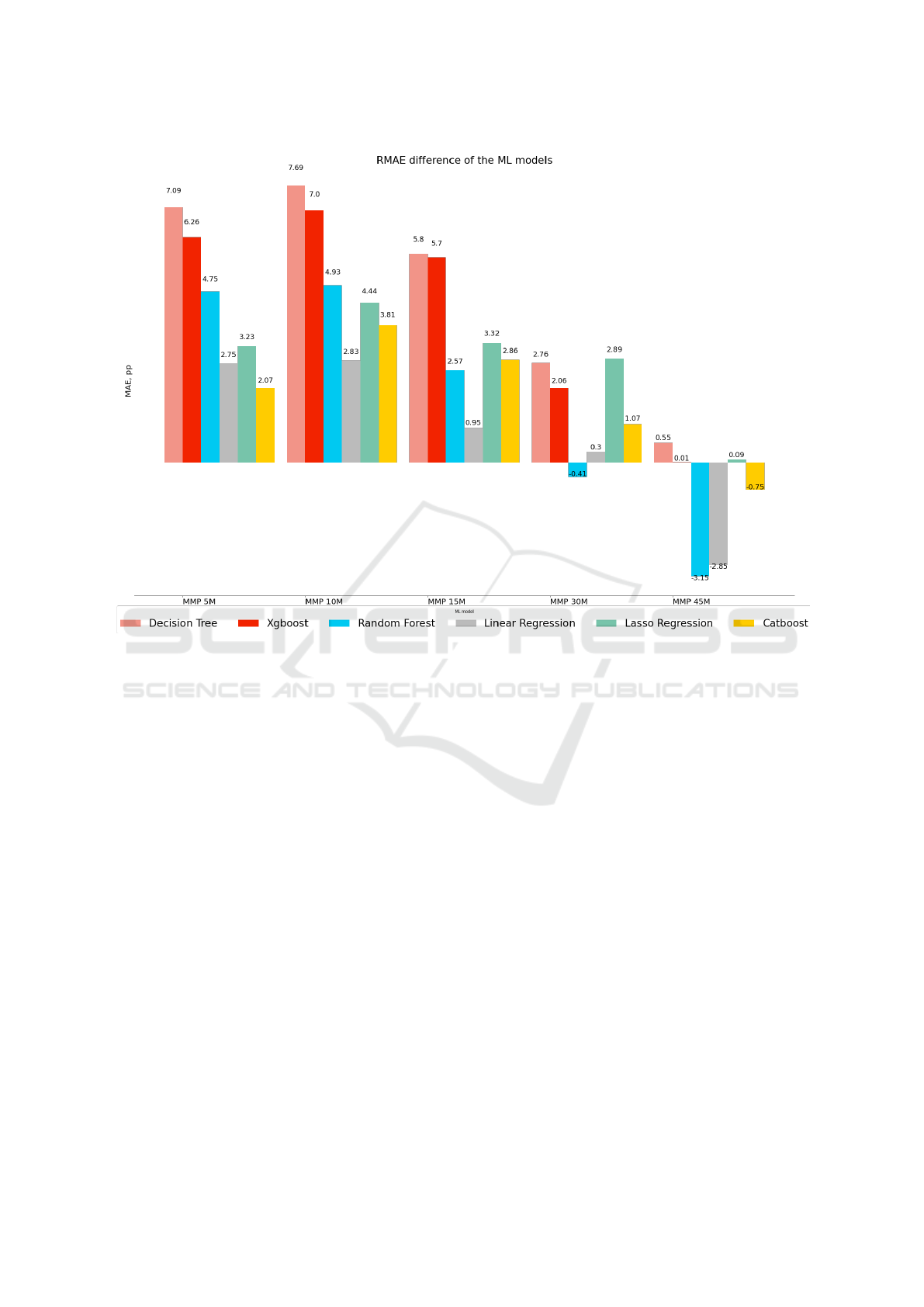
Figure 10: The performance difference between the original collected dataset and the open dataset in %. The y-axis represents

an absolute difference in percentage points in comparison with the model trained with a proprietary dataset. The x-axis shows

different predicted MMPs. The models are encoded by color in the same order as in the legend.

applied in (Maszczyk et al., 2012) and we have con-

ﬁrmed that it is also relevant in professional cycling.

This has been conﬁrmed by the experiment that in-

cluded various tests on 8 tuned prediction techniques.

Finally, we have discovered that the best results can be

obtained with application of a hybrid solution that in-

cludes XGBoost (only mountain stages) and CatBoost

(the ﬂat stages) models. We found that the moun-

tain model performs signiﬁcantly better than the main

model. This happens because it uses only the ﬁltered

subset that includes only the relevant races. Addition-

ally, it can be explained by tactics of the team when

the rider artiﬁcially reduces his/her performance dur-

ing the ﬂat stages. These additional contextual at-

tributes of the race stages can be considered in the

future work. Moreover, the extension of the dataset

by the time-frame and number of the considered rid-

ers can be helpful to obtain even more accurate results

since the method has some principal limitations which

are related to data availability but its potential oppor-

tunities could be already identiﬁed. This research has

also identiﬁed some interesting characteristics about

the predictors of the tested models. For instance, the

stepwise linear models are mostly depended on the

race proﬁle (in terms of the route which is known in

advance) than on the previous training session. How-

ever, other models have obtained a lot of beneﬁts with

the application of additional context parameters such

as the weight of the rider, the analytical aggregation of

the data from sensors (MMP and other) and the nor-

malized effect of the training sessions which helps to

estimate the inﬂuence of the training days on the race

more carefully. Additionally, the approach was vali-

dated with an open-source dataset that has conﬁrmed

the robustness of the proposed framework. In conclu-

sion, this paper has shown that the niche of sport data

in cycling has a lot of opportunities in professional

sport.

In the future, we would like to check the possibil-

ity of applying a real-time prediction (Hassani et al.,

2019; Lu et al., 2017; Hassani, 2015) to track the

changes of performance during the training sessions

by using several input streams of parameters.

icSPORTS 2021 - 9th International Conference on Sport Sciences Research and Technology Support

REFERENCES

Brownlee, J. (2017). Machine learning mastery.how to get

reproducible results with keras. Last accessed 17 June

2019.

Burtscher, M., Faulhaber, M., Flatz, M., Likar, R., and

Nachbauer, W. (2006). Effects of short-term acclima-

tization to altitude (3200 m) on aerobic and anaerobic

exercise performance. International journal of sports

medicine, 27:629–35.

Castronovo, M., Conforto, S., Schmid, M., Bibbo, D., and

D’Alessio, T. (2013). How to assess performance in

cycling: the multivariate nature of inﬂuencing factors

and related indicators. Frontiers in physiology, 4:116.

Cecchini, G., Maria Lozito, G., Schmid, M., Conforto, S.,

Riganti Fulginei, F., and Bibbo, D. (2014). Neural

networks for muscle forces prediction in cycling. Al-

gorithms, 7:621–634.

Chen, T. and Guestrin, C. (2016). XGBoost: A scalable

tree boosting system. In Proceedings of the 22nd

ACM SIGKDD International Conference on Knowl-

edge Discovery and Data Mining, KDD ’16, pages

785–794, New York, NY, USA. ACM.

Cintia, P., Pappalardo, L., and Pedreschi, D. (2013). “En-

gine Matters”: A ﬁrst large scale data driven study

on cyclists’ performance. In 2013 IEEE 13th Interna-

tional Conference on Data Mining Workshops, pages

147–153.

Eckhardt, K. (2018). Towards machine learning.choosing

the right hyperparameters for a simple lstm using

keras. Last accessed 19 June 2019.

Efroymson, M. (1960). Multiple regression analysis. Math-

ematical Methods for Digital Computers.

Fulco, C., Rock, P., and Cymerman, A. (2000). Improving

athletic performance: Is altitude residence or altitude

training helpful? Aviation, space, and environmental

medicine, 71:162–71.

Garvican-Lewis, L., Clark, B., Martin, D., Olaf Schu-

macher, Y., McDonald, W., Stephens, B., Ma, F.,

Thompson, K., J Gore, C., and Menaspà, P. (2015).

Impact of altitude on power output during cycling

stage racing. PloS one, 10:e0143028.

Gepsoft (2019). Choosing the ﬁtness function. Last ac-

cessed 20 June 2019.

Gepsoft (2019). Mean absolute error. Last accessed 1 July

2019.

Hamlin, M. (2013). Live low-train high in elite athletes: A

case study of a responder and non-responder. Journal

of Athletic Enhancement, 4.

Hassani, M. (2015). Efﬁcient clustering of big data streams.

PhD thesis, RWTH Aachen University, Germany.

Hassani, M. and Seidl, T. (2011). Towards a mobile health

context prediction: Sequential pattern mining in mul-

tiple streams. In 12th IEEE International Conference

on Mobile Data Management, MDM Volume 2, pages

55–57.

Hassani, M., Töws, D., Cuzzocrea, A., and Seidl, T. (2019).

BFSPMiner: an effective and efﬁcient batch-free algo-

rithm for mining sequential patterns over data streams.

Int. J. Data Sci. Anal., 8(3):223–239.

Hilmkil, A., Ivarsson, O., Johansson, M., Kuylenstierna, D.,

and Erp, T. (2018). Towards machine learning on data

from professional cyclists. Proceedings of the World

Congress of Performance Analysis of Sport XII.

IBM (2019). Ibm knowledge center. Last accessed 20 June

2019.

Jobson, S., Passﬁeld, L., Atkinson, G., Barton, G., and

Scarf, P. (2009). The analysis and utilization of cy-

cling training data. Sports medicine (Auckland, N.Z.),

39:833–44.

Jr., I. F., Rauter, S., Fister, D., and Fister, I. (2017). A col-

lection of sport activity datasets with an emphasis on

powermeter data. Technical report, 2017.

Karetnikov, A. (2021). Cycling framework openlapp. https:

//github.com/alexey-ka/OpenLapp. Last accessed 14

May 2021.

Kataoka, Y. and Gray, P. (2019). Real-time power perfor-

mance prediction in tour de france. Machine Learning

and Data Mining for Sports Analytics. MLSA 2018.

Lecture Notes in Computer Science, 11330:121–130.

Kenneth, B. (2011). Linear regression models with loga-

rithmic transformations. Last accessed 4 July 2019.

Leung, C. and W. Joseph, K. (2014). Sports data mining:

Predicting results for the college football games. Pro-

cedia Computer Science, 35.

Lu, Y., Hassani, M., and Seidl, T. (2017). Incremen-

tal temporal pattern mining using efﬁcient batch-free

stream clustering. In Proceedings of the 29th In-

ternational Conference on Scientiﬁc and Statistical

Database Management, Chicago, IL, USA, June 27-

29, 2017, pages 7:1–7:12.

Maszczyk, A., Roczniok, R., Wa

skiewicz, Z., Czuba, M.,

Mikolajec, K., Zajac, A., and Stanula, A. (2012). Ap-

plication of regression and neural models to predict

competitive swimming performance. Perceptual and

motor skills, 114:610–26.

Pallapothu, H. S. R. (2019). What’s so special about cat-

boost? Last accessed 4 July 2019.

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,

Thirion, B., Grisel, O., Blondel, M., Prettenhofer,

P., Weiss, R., Dubourg, V., Vanderplas, J., Passos,

A., Cournapeau, D., Brucher, M., Perrot, M., and

Duchesnay, E. (2011). Scikit-learn: Machine learning

in Python. Journal of Machine Learning Research,

12:2825–2830.

Przednowek, K., Iskra, J., and Przednowek, K. H. (2014).

Predictive modeling in 400-metres hurdles races. ic-

SPORTS 2014 - Proceedings of the 2nd International

Congress on Sports Sciences Research and Technol-

ogy Support.

Przednowek, K. and Wiktorowicz, K. (2013). Prediction of

the result in race walking using regularized regression

models. Journal of Theoretical and Applied Computer

Science, 7:45–58.

Rastegari, H. (2013). A review of data mining techniques

for result prediction in sports. Advances in Computer

Science, 2.

Xert (2019). Xert – discover. improve. perform. – smart

power-based training software. Last accessed 15 June

2019.

Yandex (2019). Overview of CatBoost. Last accessed 31

June 2019.

Data-driven Support of Coaches in Professional Cycling using Race Performance Prediction