Online Metric Facility Service Leasing with Duration-Speciﬁc Dormant

Fees

Christine Markarian

and Peter Khallouf

Department of Engineering and Information Technology, University of Dubai, U.A.E.

Data Science - Data and IT, International University of Applied Sciences, Germany

Keywords:

Facility Location, Service Leasing, Duration-Speciﬁc Dormant Fees, Online Algorithms, Optimization

Problems, Competitive Analysis.

Abstract:

Inspired by the COVID-19 pandemic, a new online facility model, known as the Online Facility Service Leas-

ing problem (OFSL), has been recently introduced. In OFSL, services at different (health) facility locations

are leased for different durations and costs. Each service at each facility is associated with a dormant fee

that needs to be paid for each day on which the service is not leased at the facility. Clients arrive over time,

each requesting a number of services, and need to be served by connecting them to multiple facilities jointly

offering the requested services. The aim is to decide which services to lease, when, and for how long, in order

to serve all clients as soon as they appear with minimum costs of leasing, connecting, and dormant fees. In

this paper, we study a generalization of OFSL in which we are additionally given a parameter d, such that,

should the service be not leased for more than d consecutive days, a dormant fee is to be paid (d = 0 in the

case of OFSL). We call this variant the Online Facility Service Leasing with Duration-Speciﬁc Dormant Fees

(d-OFSL). We particularly focus on the metric version of the problem in which facilities and clients reside in

the metric space. We refer to it as metric d-OFSL and design the ﬁrst online algorithm for the problem. The

latter is a deterministic algorithm based on a primal-dual approach. We measure its performance by compar-

ing it to the optimal ofﬂine solution for all instances of the problem. This performance analysis is known as

competitive analysis and is the standard to evaluate online algorithms.

1 INTRODUCTION

The COVID-19 pandemic has been a wake-up call

to most communities around the world. Many have

been striving to provide adequate timely health-care

services to their patients as they ran out of resources.

As a result, new temporary strategies were adopted,

including leasing facility services at different loca-

tions to satisfy the needs of patients as fast as pos-

sible. Challenging decisions had to be made in re-

gards to leasing contracts, budgeting, and distribut-

ing patients to health centers. Consequently, a signiﬁ-

cant number of works addressing such decisions from

various perspectives appeared in the literature (Choi,

2021; Queiroz et al., 2020; Ivanov, 2020; Howard,

2021; Nikolopoulos et al., 2021). Recently, a new

online facility model, known as the Online Facil-

ity Service Leasing problem (OFSL), has been intro-

duced (Markarian and Khallouf, 2021). The latter

was motivated by the following optimization prob-

lem. Imagine a company that has made contracts to

lease resources at a number of facility locations, each

offering some services. These services are reserved

for the company for as long as the corresponding con-

tract states. The company is given a number of lease

types for leasing the services. Each type is character-

ized by a duration and cost. Lease prices respect the

economy of scale such that a longer lease type costs

more but cheaper per unit time. Each day a service is

not leased at a facility, a dormant fee needs to be paid.

This fee is the cost the company pays for reserving

the service. Clients arrive over time. The company

does not know in advance how many will come and

when will they come. Each would request a number

of services, such as testing, treatment, and vaccina-

tion. The goal is to decide when to lease which ser-

vices at which facility locations such that each client

is served by connecting it to multiple facilities jointly

offering the requested services, at minimum possible

costs of leasing, connecting, and dormant fees.

In this paper, we study a generalization of OFSL

in which we are additionally given a parameter d,

Markarian, C. and Khallouf, P.

Online Metric Facility Service Leasing with Duration-Speciﬁc Dormant Fees.

DOI: 10.5220/0010668600003062

In Proceedings of the 2nd International Conference on Innovative Intelligent Industrial Production and Logistics (IN4PL 2021), pages 25-31

ISBN: 978-989-758-535-7

such that, should the service be not leased for more

than d consecutive days, a dormant fee is to be paid

(d = 0 in the case of OFSL). We call this variant

the Online Facility Service Leasing with Duration-

Speciﬁc Dormant Fees problem (d-OFSL). We partic-

ularly focus on the metric version of the problem in

which facilities and clients reside in the metric space

and respect the triangle inequality. We refer to it as

metric d-OFSL and design the ﬁrst online algorithm

for the problem. The latter is a deterministic algo-

rithm based on a primal-dual approach. We mea-

sure its performance by comparing its output to the

optimal ofﬂine solution for all instances of the prob-

lem. This performance analysis is a worst-case analy-

sis known as competitive analysis and is the standard

to evaluate online algorithms (Borodin and El-Yaniv,

2005). An online algorithm is said to have a compet-

itive ratio r where r is the worst-case ratio of the cost

of the online algorithm to that of the optimal ofﬂine

solution, for all instances of the problem. The latter

is refered to as r-competitive online algorithm. The

challenge is to design online algorithms that can be

proven to have a small r.

We develop the ﬁrst online algorithm for metric

d-OFSL, with an O((L +

min

) · log l

max

)-competitive

ratio, where:

– L is the number of lease types available

– d is the maximum number of days after which a

dormant fee needs to be paid

– l

min

is the shortest lease duration

– l

max

is the longest lease duration

In addition to generalizing OFSL, metric d-OFSL

generalizes two well-known online optimization

problems, the Parking Permit problem (PP) (Meyer-

son, 2005) and the Metric Online Facility Location

problem (metric OFL) (Meyerson, 2001). There is a

lower bound of Ω(L) on the competitive ratio of any

deterministic algorithm for PP, where L is the num-

ber of lease types available. Moreover, there is a

lower bound of Ω(

logn

loglog n

) on the competitive ratio of

any randomized algorithm for metric OFL (Fotakis,

2003), where n is the number of clients. These imply

a lower bound of Ω(L+

logn

loglog n

) on the competitive ra-

tio of any deterministic algorithm for metric d-OFSL,

where n is the number of clients.

We note here that the algorithm for OFSL

in (Markarian and Khallouf, 2021) can’t be extended

to our problem, since the latter is for the non-metric

variant. In general, results for the metric variants,

including the one in this paper, exploit the metric

properties of the problem to achieve better bounds

on the competitive ratio in comparison to the non-

metric variants. Moreover, similar techniques as those

in (Markarian and Khallouf, 2021) could have been

used to achieve a non-trivial competitive ratio for the

non-metric variant of d-OFSL, and hence our moti-

vation in this paper to target the metric version rather

than the non-metric version of the problem.

Outline. The rest of the paper is structured as fol-

lows. In Section 2, we present a summary of works

related to metric d-OFSL. In Section 3, we give a for-

mal description of metric d-OFSL. In Section 4, we

give a graph formulation of metric d-OFSL. Follow-

ing this graph formulation, we give, in Section 5, a

primal-dual program for metric d-OFSL. In Section

6, we present our online algorithm and prove its com-

petitive ratio in Section 7. We conclude in Section 8

with some remarks and future work.

2 RELATED WORK

Meyerson (Meyerson, 2005) introduced the ﬁrst on-

line leasing framework, with a simple problem known

as the Parking Permit problem (PP), for which he

gave upper and lower competitive bounds. He pre-

sented an O(L)-competitive deterministic algorithm

and an O(log L)-competitive randomized algorithm

along with matching lower bounds.

Many network optimization problems were

formed based on this framework (Anthony and

Gupta, 2007; Markarian and Kassar, 2020; Nagarajan

and Williamson, 2013; Abshoff et al., 2016). Later,

a number of extensions to the original framework

were introduced, including lease prices changing

over time, clients with deadlines, and lease types with

dimensions (Feldkord et al., 2017; Li et al., 2018;

Markarian, 2018; De Lima et al., 2017b; De Lima

et al., 2020).

Online Facility Location problems have been

intensively studied in the metric setting. Mey-

erson (Meyerson, 2001) proposed a randomized

O(logn)-competitive algorithm for the Online Facil-

ity Location problem (OFL), where n is the num-

ber of clients. Later Fotakis (Fotakis, 2003) gave an

O(logn/log log n)-competitive algorithm and showed

that this bound is optimal. Many other results that

include other online variations were also known (Fo-

takis, 2007; Fotakis, 2011; San Felice et al., 2015).

A number of leasing variants of OFL were

also studied (Abshoff et al., 2016; Nagarajan and

Williamson, 2013; Markarian and Meyer auf der

Heide, 2019; Li et al., 2018; De Lima et al., 2017a).

Unlike in these variants, in d-OFSL and OFSL, ser-

vices rather than facilities are leased. Moreover, un-

like the case in d-OFSL and OFSL, all clients in these

IN4PL 2021 - 2nd International Conference on Innovative Intelligent Industrial Production and Logistics

variants can be served by all facilities. d-OFSL and

OFSL generalize these variants by having one service

offered by all facilities and setting all dormant fees

to 0. Despite the differences, many of the techniques

used in these variants do seem helpful in solving d-

OFSL and OFSL, as we will see in the coming sec-

tions.

3 PROBLEM DESCRIPTION

In this section, we give a formal description of met-

ric Online Facility Service Leasing with Duration-

Speciﬁc Dormant Fees (metric d-OFSL).

Deﬁnition 1. (metric d-OFSL) Given m facility loca-

tions and k services. Each facility location offers a

subset of the k services. These services can be leased

with L different types, each differing by a duration and

price. Given a positive integer d ≥ 2. For each service

at each facility location, there is a dormant fee that

needs to be paid whenever the service is not leased for

d consecutive days. There are at most n clients which

arrive over time. Each day, a subset of the clients ar-

rives, each requesting a subset of the k services. The

algorithm serves a client by connecting it to a number

of facility locations jointly offering the requested ser-

vices, such that these services are leased at the time

of the client’s arrival. Connecting a client to a facility

location incurs a connecting cost which is equal to the

distance between the client and the facility location.

To each day, the algorithm reacts by deciding which

services to lease at which facility locations with which

lease type in order to serve all arriving clients. The

goal is to minimize the total leasing costs, connecting

costs, and dormant fees.

Next, we describe the Dormant-Fee-Interval

model and the Lease-Interval model. These will be

assumed for the dormant fees and the lease structures,

respectively.

Dormant-Fee-Interval Model. The algorithm pays

a dormant fee, if needed, only on days x where x

mod d ≡ 1, without affecting the competitive ratio.

Proof. Consider an instance I of the original problem.

Let Opt be an optimal solution for I. In the Dormant-

Fee Interval model, we are only allowed to pay a dor-

mant fee on days x : x mod d ≡ 1. Let i be an in-

terval of d days at the end of which Opt has paid a

dormant fee. Starting from day 0, we will divide the

timeline into intervals of length d. Interval i crosses at

most two of these intervals. We can create a feasible

solution for the Dormant-Fee Interval model by pay-

ing the dormant fee associated with the ﬁrst interval

crossed by i. This would not affect the feasibility of

the solution constructed. Doing this for all the inter-

vals associated with dormant fees paid by Opt would

complete the proof.

Lease-Interval Model. Meyerson (Meyerson,

2005) showed that the following can be assumed by

losing only a constant factor in the competitive ratio.

– Leases of the same duration do not overlap.

– All lease durations are power of two.

This model has also been assumed in (Markarian

and Khallouf, 2021) and many leasing optimization

problems studied thus far (Nagarajan and Williamson,

2013; Abshoff et al., 2016; Li et al., 2018; Markarian,

2015).

4 GRAPH FORMULATION

In this section, we formulate d-OFSL as a graph-

theoretic problem.

– For each client which arrives, we create a node,

called actual client node at the location of the

client. This client needs to be served as soon as it

arrives. For each service it is requesting, it needs

to be connected to at least one facility location of-

fering the service.

– For each service at each facility, we create a node,

called actual service node at the location of the

facility. This actual service node can be leased

for L different durations.

– For each service at each facility, we create a node,

called virtual service node at the location of the

facility. This virtual service node can be leased

only for a duration of a single day and has cost

equal to the dormant fee associated with the ser-

vice. Moreover, it can be leased only on days x : x

mod d ≡ 0. Figure 2 shows an example of d = 5.

– For each service at each facility, we create a node,

called virtual client node at the location of the fa-

cility. This client appears on days x : x mod d ≡ 1

and requests to be connected either to the virtual

service node or to the actual service node associ-

ated with it. Moreover, it can be served on any

day starting from the day y it appears until day

y + d − 1. Figure 2 shows an example of d = 5.

– We add an edge from an actual client node to an

actual service node if the client corresponding to

the client node has requested the service corre-

sponding to the service node. The weight of this

edge would be equal to the connecting cost be-

tween the client and the facility location.

Online Metric Facility Service Leasing with Duration-Speciﬁc Dormant Fees

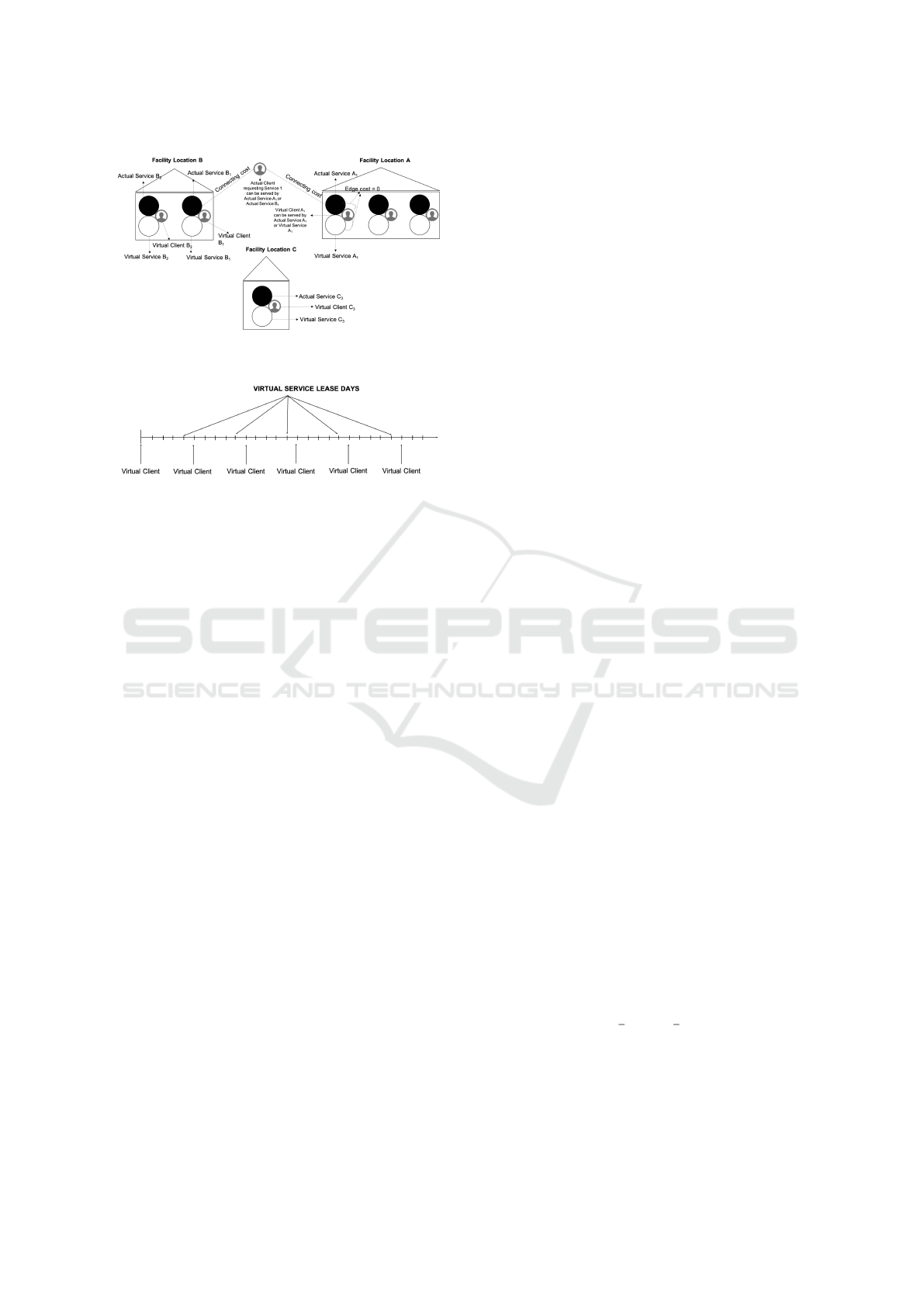
Figure 1: Three facility locations and a client requesting

one service.

Figure 2: Virtual client, virtual service lease days for d = 5.

– From each virtual client node, we add two edges,

of weight 0, one to its corresponding actual ser-

vice node and another to its corresponding virtual

service node.

Figure 1 shows an example of three facility loca-

tions, each offering one, two, and three services, re-

spectively, and one client requesting one service.

Initially, the algorithm knows all about the facil-

ity locations, the services, and the lease prices. The

client locations and their requests are revealed over

time when clients show up. Each day, the online al-

gorithm reacts to the client nodes created by purchas-

ing from the available leases. Edges correpond to the

connecting costs that will be paid upon connecting a

client to a facility location. Notice that, a virtual client

in our formulation is associated with a deadline that

represents whether or not a dormant fee will be paid.

Each service at each facility is associated with such a

client that appears every d days to ensure that every

d days, the algorithm checks whether it is required to

pay a dormant fee for the service or not. Figure 1 il-

lustrates the days on which virtual client nodes appear

and virtual service nodes are leased.

5 PRIMAL-DUAL

FORMULATION

In this section, we present an integer linear program

and the corresponding relaxed dual program for the

graph-theoretic problem described above. Fig. 3 il-

lustrates this formulation.

min

∑

(i,k,t)∈S

ikt

∑

( js,t,d)∈R

∑

i∈S

i js

i, jstd

∑

i∈S

i, jstd

≥ 1 ( js,t,d) ∈ R

∑

ikt

− y

i, jstd

≥ 0 (i,k,t

) ∈ S

( js,t,d) ∈ R

i, jstd

∈ {0,1} i ∈ S

( js,t,d) ∈ R

ikt

∈ {0,1} (i, k,t) ∈ S

max

∑

( js,t,d)∈R

jstd

− β

i, jstd

≤ c

i js

i ∈ S

( js,t,d) ∈ R

∑

( js,t

,d)∈R

i, jst

≤ c

(i,k,t) ∈ S

i, jstd

≥ 0 i ∈ S

( js,t,d) ∈ R

jstd

≥ 0 ( js,t,d) ∈ R

Figure 3: Linear Programming Formulation of.

The objective function has two parts. The ﬁrst part

represents the costs incurred by leasing services. We

denote each service at each facility as a triplet (i,k,t),

where i is the service type, k is the lease type, and t is

the starting day of the lease. A variable x

ikt

is assigned

to each (i, k,t) indicating whether it is bought or not.

is the cost of leasing service i with type k.

A request is characterized by a client-service pair,

such that for each service requested by a client, we

generate a request ( js,t, d) refering to client j re-

questing service s, arriving at time t, and having dead-

line t +d. c

i js

is the cost of connecting j to i.

The second part of the objective function repre-

sents the costs incurred by connecting each request to

a service, such that variable y

i, jstd

indicates whether

request ( js,t, d) is connected to service i. Recall that

all requests associated with actual client nodes have

deadline 0.

The ﬁrst primal constraint guarantees that each re-

quest is connected to at least one service. The second

constraint makes sure that each request is only con-

nected to a service that is leased within the arrival

time and the deadline of the request. We denote by

S the collection of all service triplets and by R the

collection of all request triplets. We denote by S

the

collection of service triplets that can serve request js.

We call these triplets nominees. Let H

be the nth

harmonic number 1 +

+ ... +

IN4PL 2021 - 2nd International Conference on Innovative Intelligent Industrial Production and Logistics

6 ONLINE PRIMAL-DUAL

ALGORITHM

In this section, we present an online deterministic

primal-dual algorithm for metric d-OFSL.

The main idea of the algorithm is that whenever

a client arrives and a request is formed, as long as (i)

the dual constraints associated with it are not violated

and (ii) the request’s dual variable is not equal to the

distance to a purchased nominee, the algorithm keeps

increasing its dual variables. Algorithm 1 illustrates

the steps that react to each request formed.

Algorithm 1: Online Primal-Dual Algorithm for metric d-

OFSL.

When a request ( js,t,d) is generated, we increase

its variable α

jstd

and the variables β

i, jstd

corre-

sponding to its nominees while maintaining α

jstd

−

i, jstd

≥ 0, until:

(i) either the dual constraint of some nominee

(i,k,t

) ∈ S

becomes tight:

∑

i, jstd

= c

: ( js,t, d) ∈ R

So, we buy (i,k,t

) (i.e., we set its primal

variable x

ikt

to 1).

(ii) or α

jstd

= c

i js

for some bought nominee

(i,k,t

) ∈ S

We connect ( js,t, d) to the closest bought nomi-

nee.

7 COMPETITIVE ANALYSIS

In this section, we give a competitive analysis of our

algorithm, based on dual ﬁtting arguments (Freund

and Rawitz, 2003; Jain et al., 2003; Jain and Vazirani,

2001).

The proof ideas are based on our previous result

in (Li et al., 2018). We partition the timeline into

rounds τ

:= { (i − 1)l

max

,... ,il

max

− 1 } of length l

max

and conduct the analysis on the ﬁrst l

max

time steps

only. This has been proven to be sufﬁcient to con-

clude the competitive ratio of the algorithm (Abshoff

et al., 2016).

Note that according to the primal-dual formula-

tion, the dormant fees are embedded in the primal-

dual program as leasing costs. Hence, they will not

appear in the analysis.

Notice that our algorithm outputs a feasible pri-

mal solution and an infeasible dual solution. Conse-

quently, the proof will be composed of two parts. In

the ﬁrst part (Lemma 1), the cost of the primal so-

lution will be bounded by O(L +

min

) times the cost

of the dual solution. In the second part (Lemma 2),

the infeasible dual solution constructed will be scaled

down by O(H

max

) to make it feasible. Using Weak

Duality Theorem, we will imply the competitive ratio

of the algorithm.

Lemma 1. The cost of the primal solution con-

structed by the algorithm is at most (L +

min

) ·

∑

( js,t,d)∈R

jstd

Proof. We ﬁrst show that the sum of the connection

costs is at most

∑

( js,t,d)∈R

jstd

and then show that

the sum of the leasing costs is at most (L +

min

) ·

∑

( js,t,d)∈R

jstd

A request ( js,t, d) is either assigned to an already

leased service or it leads to leasing a new service. If

it is the ﬁrst case, then the request has increased only

the variable α

jstd

until α

jstd

= c

i js

. If it is the sec-

ond case, then the request has increased both α

jstd

and β

i, jstd

as long as α

jstd

−β

i, jstd

≤ c

i js

, while main-

taining α

jstd

− β

i, jstd

≥ 0. Thus α

jstd

≥ c

i js

. We can

sum up over all requests and get a total connection

cost of O(

∑

( js,t,d)∈R

jstd

As for the leasing costs, we say a request con-

tributes to the leasing cost of a service of type k if

it has caused such a service lease to be purchased.

The total contribution of request ( js,t,d) to service

leases of type k can be upper bounded by α

jstd

This is because the number of nominees of type k does

not exceed

(the maximum is for the virtual clients

case). Summing up over all L lease types yields:

∑

j=1

≤ L + d



1−(1/2)

1−1/2

i

L + d



1 − (1/2)



Since L ≥ 1, we have:

L + d



1 − (1/2)



≤ L +

min

The sum of all clients’ contributions implies the total

leasing costs:

∑

( js,t,d)∈R

jstd



L +

min



The following Lemma has been proven in (Ab-

shoff et al., 2016; Li et al., 2018; Nagarajan and

Williamson, 2013). It shows that it is sufﬁcient to

divide the infeasible dual solution by 2(H

max

+ 1) to

yield a feasible dual solution. Its proof is based on re-

peatedly exploiting the triangle inequality. Moreover,

the bound is not based on the number of clients but

Online Metric Facility Service Leasing with Duration-Speciﬁc Dormant Fees

rather on the number of time steps. That is why the

additional number of clients resulting from the virtual

client nodes does not appear in the analysis.

Lemma 2. For any service (i,k,t) ∈ S

and µ =

2(H

max

+1)

, it holds that:

∑

( js,t

,d)∈R

µ · α

jst

− β

i, jst

≤ c

i js

Notice that both bounds do not depend on the

number of services and that is why the additional

number of clients resulting from the virtual service

nodes does not appear in the analysis too.

By combining the two lemmata, we obtain the fol-

lowing theorem.

Theorem 1. There is an online deterministic O((L +

min

) · log l

max

)-competitive algorithm for metric d-

OFSL, where L is the number of lease types available,

d is the maximum number of days after which a dor-

mant fee needs to be paid, l

min

is the shortest lease

duration, and l

max

is the longest lease duration.

8 CONCLUDING REMARKS

In this paper, we have introduced a natural general-

ization of the well-known facility location problem in

the online setting. The latter appears as a sub-problem

in many real-world optimization scenarios involving

serving clients, as they appear over time, by leased

resources.

The ﬁrst research direction would be to close the

gap between the upper and lower bounds for metric d-

OFSL. This can be done by either designing another

algorithm, or by improving the analysis of the cur-

rent one. Proving a better lower bound would also be

worth trying.

Furthermore, we have considered in this paper a

ﬁxed parameter d for all our facility services. It is

important to note here that our algorithm does extend

to the case where this parameter differs between one

service and the other. Yet, it is not clear whether the

same can be said if we consider other variations of the

parameter. That is, it could be that we have to pay a

small fee the ﬁrst time we leave a service unleased and

then a higher fee in the next times. It would be inter-

esting to investigate about these variations, by observ-

ing their connection to actual real-world examples.

This brings us to the next research direction,

which would be to actually implement the proposed

algorithm and evaluate it under real-world or simu-

lated instances of the optimization problem.

REFERENCES

Abshoff, S., Kling, P., Markarian, C., Meyer auf der Heide,

F., and Pietrzyk, P. (2016). Towards the price of leas-

ing online. Journal of Combinatorial Optimization,

32(4):1197–1216.

Anthony, B. M. and Gupta, A. (2007). Infrastructure leas-

ing problems. In International Conference on Integer

Programming and Combinatorial Optimization, pages

424–438. Springer.

Borodin, A. and El-Yaniv, R. (2005). Online computation

and competitive analysis. cambridge university press.

Choi, T.-M. (2021). Fighting against covid-19: what op-

erations research can help and the sense-and-respond

framework. Annals of Operations Research, pages 1–

17.

De Lima, M. S., San Felice, M. C., and Lee, O. (2017a).

Connected facility leasing problems. In ICTCS/CILC,

pages 162–173.

De Lima, M. S., San Felice, M. C., and Lee, O. (2017b). On

generalizations of the parking permit problem and net-

work leasing problems. Electronic Notes in Discrete

Mathematics, 62:225–230.

De Lima, M. S., San Felice, M. C., and Lee, O. (2020).

Group parking permit problems. Discrete Applied

Mathematics, 281:172–194.

Feldkord, B., Markarian, C., and Meyer auf der Heide, F.

(2017). Price ﬂuctuation in online leasing. In Inter-

national Conference on Combinatorial Optimization

and Applications, pages 17–31. Springer.

Fotakis, D. (2003). On the competitive ratio for online fa-

cility location. In Baeten, J. C. M., Lenstra, J. K.,

Parrow, J., and Woeginger, G. J., editors, Automata,

Languages and Programming, pages 637–652, Berlin,

Heidelberg. Springer Berlin Heidelberg.

Fotakis, D. (2007). A primal-dual algorithm for online non-

uniform facility location. Journal of Discrete Algo-

rithms, 5(1):141–148.

Fotakis, D. (2011). Online and incremental algorithms for

facility location. ACM SIGACT News, 42(1):97–131.

Freund, A. and Rawitz, D. (2003). Combinatorial interpre-

tations of dual ﬁtting and primal ﬁtting. In Approxima-

tion and Online Algorithms, First International Work-

shop, WAOA 2003, Budapest, Hungary, September 16-

18, 2003, Revised Papers, pages 137–150.

Howard, M. C. (2021). Who wants to reopen the econ-

omy during the covid-19 pandemic? the daring and

uncaring. Personality and Individual Differences,

168:110335.

Ivanov, D. (2020). Viable supply chain model: inte-

grating agility, resilience and sustainability perspec-

tives—lessons from and thinking beyond the covid-19

pandemic. Annals of Operations Research, pages 1–

21.

Jain, K., Mahdian, M., Markakis, E., Saberi, A., and Vazi-

rani, V. V. (2003). Greedy facility location algorithms

analyzed using dual ﬁtting with factor-revealing lp. J.

ACM, 50(6):795–824.

IN4PL 2021 - 2nd International Conference on Innovative Intelligent Industrial Production and Logistics

Jain, K. and Vazirani, V. V. (2001). Approximation algo-

rithms for metric facility location and k-median prob-

lems using the primal-dual schema and lagrangian re-

laxation. J. ACM, 48(2):274–296.

Li, S., Markarian, C., and Meyer Auf Der Heide, F. (2018).

Towards ﬂexible demands in online leasing problems.

Algorithmica, 80(5):1556–1574.

Markarian, C. (2015). Online resource leasing. PhD thesis,

University of Paderborn, Germany.

Markarian, C. (2018). Leasing with uncertainty. In Op-

erations Research Proceedings 2017, pages 429–434.

Springer.

Markarian, C. and Kassar, A.-N. (2020). Online deter-

ministic algorithms for connected dominating set &

set cover leasing problems. In International Confer-

ence on Operations Research and Enterprise Systems

(ICORES), pages 121–128.

Markarian, C. and Khallouf, P. (2021). Online facility ser-

vice leasing inspired by the covid-19 pandemic. In

18th International Conference of Informatics In Con-

trol Automation And Robotics (ICINCO’21), page To

appear.

Markarian, C. and Meyer auf der Heide, F. (2019). On-

line algorithms for leasing vertex cover and leasing

non-metric facility location. In International Confer-

ence on Operations Research and Enterprise Systems

(ICORES), pages 315–321.

Meyerson, A. (2001). Online facility location. In Proceed-

ings 42nd IEEE Symposium on Foundations of Com-

puter Science, pages 426–431.

Meyerson, A. (2005). The parking permit problem. In 46th

Annual IEEE Symposium on Foundations of Computer

Science (FOCS’05), pages 274–282. IEEE.

Nagarajan, C. and Williamson, D. P. (2013). Ofﬂine

and online facility leasing. Discrete Optimization,

10(4):361–370.

Nikolopoulos, K., Punia, S., Sch

afers, A., Tsinopoulos, C.,

and Vasilakis, C. (2021). Forecasting and planning

during a pandemic: Covid-19 growth rates, supply

chain disruptions, and governmental decisions. Eu-

ropean Journal of Operational Research, 290(1):99–

115.

Queiroz, M. M., Ivanov, D., Dolgui, A., and Wamba, S. F.

(2020). Impacts of epidemic outbreaks on supply

chains: mapping a research agenda amid the covid-19

pandemic through a structured literature review. An-

nals of operations research, pages 1–38.

San Felice, M. C., Cheung, S.-S., Lee, O., and Williamson,

D. P. (2015). The online prize-collecting facility loca-

tion problem. Electronic Notes in Discrete Mathemat-

ics, 50:151–156.

Online Metric Facility Service Leasing with Duration-Speciﬁc Dormant Fees