A Ridesharing Recommendation Framework

with Hard and Soft Constraints

Mow Fei Kim and Hamidah Ibrahim

Department of Computer Science, Faculty of Computer Science and Information Technology,

Universiti Putra Malaysia, Malaysia

Keywords: Ridesharing, Hard Constraints, Soft Constraints, Recommendation System.

Abstract: Ridesharing, the act or practice of sharing automobile trips, has now becoming very popular due to many

benefits it provides not only to the society, economic but also the environment. There are several ridesharing

frameworks and applications being proposed, however in identifying a ridesharing group consisting of a driver

and passengers (also known as riders), most of these solutions rely on the hard constraints which include

timeslot (departure and arrival), location (departure and arrival), and capacity of the vehicle. Since these

people will be sharing a ride together and they are strangers to each other, it is important to consider their

preferences in identifying an ideal group. These preferences, called soft constraints in this paper, include

among others race, age group, gender, non-smoking, etc. This is for assuring a pleasant, cosy, and most

importantly a safe journey. Hence, this paper proposes a ridesharing recommendation framework that aims at

identifying an ideal group by considering both the hard and the soft constraints. The framework is then

embedded into a mobile application prototype, named SAGE, which aims to provide a safe, available, green,

and economical ridesharing service.

1 INTRODUCTION

In this modern era, the rapid growth of technologies

has brought significant changes to the society in

various aspects of economy including sharing

economy. Sharing economy also known as

collaborative consumption economy, is a new

economic phenomenon, in which the sharing and

reusing of the redundant products or services by

individuals or organisations are through online

platforms (Juho et al., 2015; Georgina, 2018; Steven

and Matthias, 2019). The popularity of the mobile

phones, especially smart phones which are mainly

used for communicating and accessing information

on the Internet has facilitates the emergence of

sharing economy. One of the focuses in sharing

economy in transportation sector is ridesharing

service.

Ridesharing, also known as carpooling, is now

getting popular worldwide. It can be defined as the

sharing of a ride by individuals in a personal vehicle

https://orcid.org/0000-0002-9900-0531

with the same journey and schedules (Mitja et al.,

2015; Hajra et al., 2018). Different from ride-hailing

which creates new capacity issues, ridesharing which

can fully utilise the capacity of the vehicle, brings

many benefits, not only to society, but also

environment (Biying et al., 2017; Xuan et al., 2017;

Wang et al., 2018). To the society, it reduces the

expenses of the transportation per individual such as

toll fee, parking fee, and fuel fee as the individuals

share those expenses. It also enhances the travel

convenience as the effective utilisation of capacity

can result in fewer trips, less travel time although

spent the same amount of expenses in one trip (Ziru

et al., 2016; Conner-Simons, 2017; Xuan et al., 2017;

Hajra et al., 2018).

Since ridesharing service is a new and growing

phenomenon in Malaysia (Indra and Ibrahim, 2017;

Muhamad et al., 2019), only limited ridesharing

services exist in Malaysia. Most of the ridesharing

applications in the worldwide market aim at matching

a driver to riders that are having the same journey and

schedules. Hence, they only consider hard

Kim, M. and Ibrahim, H.

A Ridesharing Recommendation Framework with Hard and Soft Constraints.

DOI: 10.5220/0010705900003058

In Proceedings of the 17th International Conference on Web Information Systems and Technologies (WEBIST 2021), pages 371-379

ISBN: 978-989-758-536-4; ISSN: 2184-3252

371

constraints that include timeslot (departure and

arrival), location (departure and arrival), and number

of empty seats in forming the group. Soft constraints

such as demographic (age group, gender, race, etc.)

and environmental preferences (non-smoking, peace

and quiet, music on, etc.) that reflect the users’

preferences are also important and should be taken

into consideration in forming an ideal group. This is

for assuring a pleasant, cosy and most importantly a

safe journey (Benish et al., 2018; Diep et al., 2021)

as these people will be sharing a ride together and

they are strangers to each other. For instance, a female

passenger will feel safer if she shares a ride with the

other female passengers and driver. Hence, it is

important to consider not only the hard constraints,

but also the soft constraints in forming an ideal group.

In this paper, we propose a ridesharing

recommendation framework, that provides a platform

for the public to share rides with others who own the

same journey and travel time. The framework

attempts to identify an ideal group which consists of

a driver and passengers (also known as riders) by

considering both (i) the hard constraints which

include the timeslot (departure and arrival), location

(departure and arrival), and number of empty seats;

and (ii) the soft constraints which include

demographic (age, race, gender, etc.) and

environmental preferences of the users (non-

smoking, peace and quiet, music on, etc.). The

proposed framework is then embedded into a mobile

application prototype, named SAGE. In general the

main contributions of this work are briefly described

as follows:

• we have devised a matching mechanism to

automatically identify an ideal group which

consists of a driver and passengers by

considering both the hard constraints and soft

constraints,

• we have designed a flexible filtering function

for users to express their preferences with

regards to both the hard and soft constraints,

and

• we have developed a mobile application

prototype, SAGE, that incorporates the

conceptual design of the proposed framework.

This paper is organized as follows: Section 2

presents the existing ridesharing solutions. In Section

3, the definitions and notations that are used in the

rest of the paper are set out. Our proposed framework

and its implementation are elaborated in Section 4

and Section 5, respectively. Conclusion and future

works are presented in the final section of this paper,

Section 6.

2 RELATED WORK

This section presents the reviews that have been

conducted on several existing ridesharing solutions

with emphasise given on the criteria they used in

identifying a ridesharing group. We categorized these

works into two main categories, namely: ridesharing

frameworks and ridesharing applications.

Ridesharing frameworks: several ridesharing

frameworks have been proposed, each having a

unique aim. An early work by Douglas and Eduardo

(2013) aims at maximizing the number of shared trips

by proposing a framework and heuristic-based

models. In the case of taxis, people going to close

locations can share the costs of the trip, whereas in

the case of rides, the driver and passengers can share

costs as well. Later, Nusrat et al. (2016) propose a

framework for dynamic vehicle pooling and a

ridesharing system that are not limited to any

particular type of vehicle. Hence, vehicle such as car,

bus or even lorry can be pooled using the proposed

system. Meanwhile, Na et al. (2017) propose a new

ridesharing model, with a requirement that if a driver

shares a ride with a rider, the shared route percentage

must exceeds an expectation rate of the driver. Hajra

et al. (2018) on the other hand introduce the highest

aggregated score vehicular recommendation

(HASVR) framework that recommends a vehicle

with the highest aggregated score to the requesting

passenger. They consider five parameters, namely:

average time delay, vehicle’s capacity, fare reduction,

driving distance, and profit increment in calculating the

score. A real-time ride-sharing framework is proposed

by Yuhan et al. (2021) with a dynamic timeframe and

anticipation-based migration to handle the density

variation of commuters in different time periods.

Ridesharing applications: There are several

ridesharing applications available in the market

which include Uber, Grab, Lyft, WeRide, and Ryde.

Uber is a ride-hailing and ridesharing application in

over 785 metropolitan areas worldwide. It is available

for up to two people per party and provides up to two

additional stops when requesting a ride, as well as

allowing the users to choose their preferred driver

based on their experiences with the driver. Whereas,

Grab is a ride-hailing and ridesharing application

which dominates the taxi market in Southeast Asia.

GrabShare enables passengers to share a ride with

another party who have the same destination, and

passenger is only allowed to bring along a friend.

GrabHitch enables the passenger to schedule ride in

advance and get a shared lift at half of the usual price.

Lyft is one of the largest ridesharing applications and

it offers transport in over 600 U.S. cities including

WEBIST 2021 - 17th International Conference on Web Information Systems and Technologies

372

New York City, Los Angeles, and San Francisco, as

well as 12 cities in Canada. Lyft allows the

passengers to share a ride with another party and

share fare with up to 60% discount rate. Meanwhile,

WeRide is a new ridesharing application that provides

carpooling service in Malaysia and Singapore.

WeRide operates under the “You Decide Your Ride”

concept in which users decide their ride preferences

and cost sharing’s details. Another ridesharing

application is Ryde, a Singapore-based transport-

booking application. Similar to the other ridesharing

applications, Ryde provides carpooling service that

intends to help the car owners in offsetting petrol and

parking costs, as well as to make travelling eco-

friendly by reducing carbon emissions. Besides, Ryde

provides the feature of setting preferred driver or

passenger and sending them private requests.

From the above, most of the ridesharing solutions

consider the hard constraints which include timeslot

(arrival and departure), location (arrival and

departure), and number of empty seats during the

matching process as these are the core criteria that

must be satisfied. Whereas, none of them take into

account the preferences of the driver and passengers

in identifying an ideal ridesharing group.

3 PRELIMINARIES

In this section, we present the necessary definitions

and introduce the notations and symbols that are used

throughout this paper. These symbols and notations

are summarized in Table 2.

Definition 1. Properties of a Driver: a driver, 𝐷



, is

associated with two main elements denoted by 𝐷



(𝑃





, 𝑅





) where 𝑃





is the profile of the driver, 𝐷



which include race, age, gender, etc.; whereas 𝑅





the driver’s request.

Definition 2. Properties of a Driver’s Request: each

request, 𝑅





, submitted by a driver, 𝐷



, is associated

with four elements (SA-𝐷



, TA-𝐷



, PA-𝐷



, 𝐶) where

SA-𝐷



, Spatial Attributes, represent the departure

(

𝑆𝐴



)

and arrival

(

𝑆𝐴



)

locations of the trip

specified by the driver, 𝐷



; TA-𝐷



, Temporal

Attributes, represent the departure

(

𝑇𝐴



)

and arrival

(

𝑇𝐴



)

time/date of the trip specified by the driver, 𝐷



;

PA-𝐷



, Preference Attributes, represent the

preferences of the driver, 𝐷



, like race, age group,

gender, etc. of the passenger(s); whereas C is the

capacity of the vehicle. SA-𝐷



, TA-𝐷



, and 𝐶 are the

hard constraints whereas PA-𝐷



is the soft constraint.

Hard constraints are conditions that must be satisfied.

Definition 3. Properties of a Passenger: a passenger,

𝑃



, is associated with two main elements denoted by

𝑃



= (𝑃





, 𝑅





) where 𝑃





is the profile of the

passenger, 𝑃



, which include race, age, gender, etc.;

whereas 𝑅





is the passenger’s request.

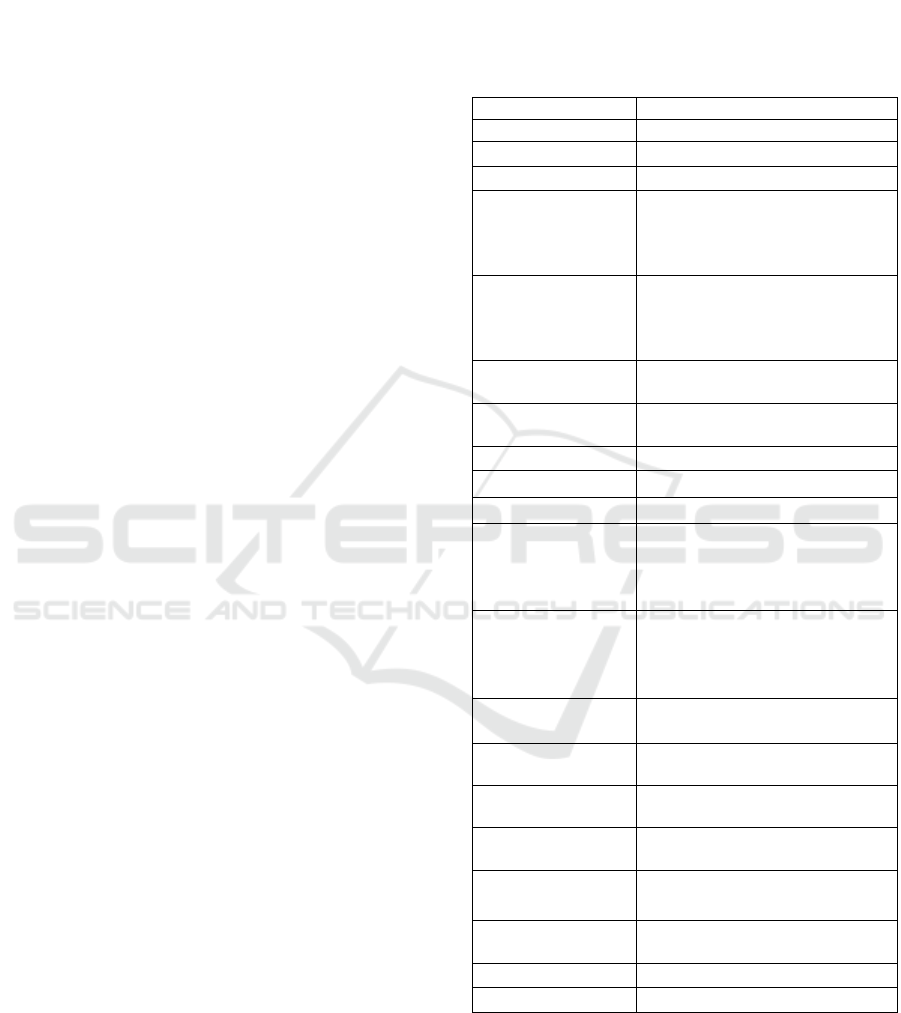
Table 1: List of symbols/notations.

mbols/Notations Descri

tions

𝐷



The 𝑖th drive

𝑃





The profile of driver 𝐷



𝑅





The request submitted by 𝐷



SA-𝐷



= (𝑆𝐴



, 𝑆𝐴



)

Spatial attributes associated to

𝐷



consisting of a departure

location, 𝑆𝐴



, and an arrival

location, 𝑆𝐴



TA-𝐷



= (𝑇𝐴



, 𝑇𝐴



)

Temporal attributes associated to

𝐷



consisting of a departure

time/date, 𝑇𝐴



, and an arrival

time/date, 𝑇𝐴



PA-𝐷



Preference attributes, i.e. the

references of 𝐷



𝐶

Capacity of the vehicle owns by

the driver, 𝐷



𝑃



The 𝑗th passenger

𝑃





The profile of passenger 𝑃



𝑅





The request submitted by 𝑃



SA-𝑃



= (𝑆𝐴



, 𝑆𝐴



)

Spatial attributes associated to

𝑃



consisting of a departure

location, 𝑆𝐴



, and an arrival

location, 𝑆𝐴



TA-𝑃



= (𝑇𝐴



, 𝑇𝐴



)

Temporal attributes associated to

𝑃



consisting of a departure

time/date, 𝑇𝐴



, and an arrival

time/date, 𝑇𝐴



PA-𝑃



Preference attributes, i.e. the

preferences of 𝑃



ℎ

The number of hard

constraints/attributes

𝑠

The number of soft

constraints/attributes

𝑛=ℎ+𝑠

The number of criteria considered

in the matching process

𝑊













The weight value between 𝑅





and 𝑅





𝑇𝑊-𝑃





-𝑞 The total weight value of the 𝑞th

group

𝑃





-𝑜

The ideal group

𝑐



The 𝑢th criterion

Definition 4. Properties of a Passenger’s Request:

each request, 𝑅





, submitted by a passenger, 𝑃



, is

associated with three elements (SA-𝑃



, TA-𝑃



, PA-𝑃



)

where SA-𝑃



, Spatial Attributes, represent the

departure

(

𝑆𝐴



)

and arrival

(

𝑆𝐴



)

locations of the

A Ridesharing Recommendation Framework with Hard and Soft Constraints

373

trip specified by the passenger, 𝑃



; TA-𝑃



, Temporal

Attributes, represent the departure

(

𝑇𝐴



)

and arrival

(

𝑇𝐴



)

time/date of the trip specified by the passenger,

𝑃



; PA-𝑃



, Preference Attributes, represent the

preferences of the passenger, 𝑃



, like race, age group,

gender, etc. of the group members. Both SA-𝑃



and

TA-𝑃



are the hard constraints, whereas PA-𝑃



is the

soft constraint.

Definition 5. Totally Match between 𝑅





and 𝑅





: the

request of a driver, 𝑅





, is said to totally match with

the request of a passenger, 𝑅





, iff both the hard and

soft constraints specified by the driver, 𝐷



, are the

same as the hard and soft constraints specified by the

passenger, 𝑃



, i.e. SA-𝐷



= SA-𝑃



∧ TA-𝐷



= TA-𝑃



∧

PA-𝐷



= PA-𝑃



Definition 6. Not Match between 𝑅





and 𝑅





: the

request of a driver, 𝑅





, is said to not match with the

request of a passenger, 𝑅





, iff at least one of the hard

constraints specified by the driver, 𝐷



, does not match

with the hard constraints specified by the passenger,

𝑃



, i.e. SA-𝐷



≠ SA-𝑃



∨ TA-𝐷



≠ TA-𝑃



Definition 7. Partially Match between 𝑅





and 𝑅





the request of a driver, 𝑅





, is said to partially match

with the request of a passenger, 𝑅





, iff the hard

constraints specified by the driver, 𝐷



, and the

passenger, 𝑃



, are the same, i.e. SA-𝐷



= SA-𝑃



∧ TA-

𝐷



= TA-𝑃



; whereas there is at least one preferences

specified by 𝐷



that does not match with the soft

constraints specified by the passenger, 𝑃



For the following definitions, we use the

following variables to represent the number of criteria

considered in the matching process:

Hard constraints: ℎ criteria

Soft constraints: 𝑠 criteria

Total criteria, 𝑛=ℎ +𝑠

Also, every single criterion that is matched is given a

value 1 whereas not matched is given a value 0.

Definition 8. Weight for Totally Match between 𝑅





and 𝑅





: for a given 𝑛 criteria the weight for totally

match between 𝑅





and 𝑅





, denoted by 𝑊







 





is 𝑛.

Definition 9. Weight for Not Match between 𝑅





and 𝑅





: for a given 𝑛 criteria the weight, 𝑊







 





for not match between 𝑅





and 𝑅





is 0≤

𝑊







 





≤

(

ℎ−1

)

+𝑠.

Definition 10. Weight for Partially Match between

𝑅





and 𝑅





: for a given 𝑛 criteria the weight,

𝑊







 





, for partially match between 𝑅





and 𝑅





is ℎ≤𝑊







 





≤ℎ+(𝑠−1).

Definition 11. Possible Group of a 𝑅





: given the

profile of a driver 𝐷



, 𝑃





, the driver’s request, 𝑅





and a set of passengers, 𝑃=

{

𝑃



,𝑃



,…,𝑃



}

, a possible

group is defined as 𝑃





-𝑞={𝑃



,𝑃



,…,𝑃



}, where

𝑚 ≤ 𝐶; ∀𝑃



∈𝑃





-𝑞, 𝑅





and 𝑅





are either totally

match or partially match, and 𝑞 is the 𝑞th possible

group derived for 𝐷



. If there are 𝑘 passengers that

meet the above conditions, then the number of

possible groups that can be derived is

!

!()!

. Hence,

given a possible group, 𝑃





-𝑞, the total weight for the

group, 𝑇𝑊-𝑃





-𝑞 is given by the formula, 𝑇𝑊-𝑃





𝑞=

∑

𝑊







 









The problem tackled by this paper is formulated

as follows:

given the profile of a driver 𝐷



, 𝑃





, the

driver’s request 𝑅





, a set of passengers 𝑃=

{

𝑃



,𝑃



,…,𝑃



}

, find an ideal group 𝑃





-𝑜=

{𝑃



,𝑃



,…,𝑃



} where 𝑚 ≤ 𝐶; ∀𝑃



∈𝑃





-𝑜, 𝑅





and 𝑅





are either totally match or partially match;

and the total weight, 𝑇𝑊-𝑃





-𝑜=

∑

𝑊







 









max(𝑇𝑊-𝑃





-1, 𝑇𝑊-𝑃





-2, …, 𝑇𝑊-𝑃





-𝑟) where 𝑟

is the number of possible groups derived based on

𝑅





Throughout this paper, the samples given in Table

1 are used to clarify the phases of the proposed

framework. Table 1(a) and Table 1(b) present

samples of drivers’ requests and passengers’ requests,

respectively. Here, we assume the following: list of

departure locations, 𝑆𝐴



= {𝐴, 𝐵, 𝐶, 𝐷, 𝐸}, list of

arrival locations, 𝑆𝐴



= {𝐴, 𝐵, 𝐶, 𝐷, 𝐸}, the requests

are on the same date, and the time is given in range,

for instance, 𝑇𝐴



= [12:13] which means the departure

time is between 12 to 13 noon. This can be easily

modified to suit other possible ranges of time slots.

For example [12:12] means exactly at 12 noon.

Similar notation is used for arrival time, 𝑇𝐴



Meanwhile, for the preferences, we assume there are

𝑠 preferences, labelled as 𝑝𝑟



, 𝑝𝑟



, …, 𝑝𝑟



. Examples

of possible preferences are race, age group, gender,

etc. Since indicating the preferences is optional,

hence the symbol ‘−‘ is used to indicate that the

preference is not important to the driver/passenger.

WEBIST 2021 - 17th International Conference on Web Information Systems and Technologies

374

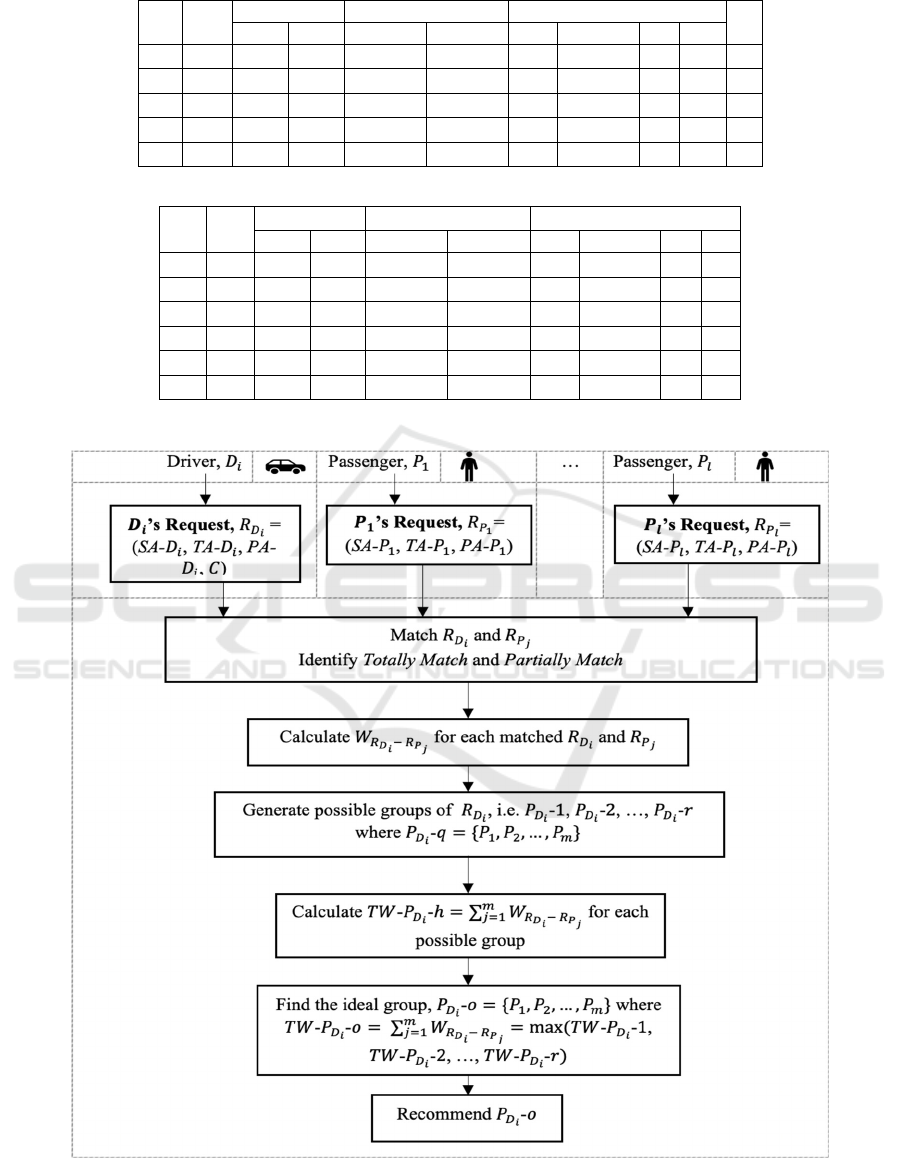
Table 2: Sample of Requests.

𝐷



𝑃





SA-𝐷



TA-𝐷



PA-𝐷



𝐶

𝑆𝐴



𝑆𝐴



𝑇𝐴



𝑇𝐴



𝑝𝑟



𝑝𝑟



…

𝑝𝑟



𝐷



𝑃





𝐴 𝐵

[12:13] [14:15]

𝑚

[20:30] …

𝑚

𝐷



𝑃





𝐷 𝐸

[9:10] [12:13]

𝑚

[20:30] …

−

𝐷



𝑃





𝐴 𝐶

[7:8] [10:11]

𝑖

[20:30] …

𝑓

𝐷



𝑃





𝐸 𝐷

[16:17] [19:20]

𝑐

[20:30] …

−

𝐷



𝑃





𝐵 𝐸

[9:10] [12:13]

𝑚

[20:30] …

𝑚

(a) Drivers’ Requests

𝑃



𝑃





SA-𝑃



TA-𝑃



PA-𝑃



𝑆𝐴



𝑆𝐴



𝑇𝐴



𝑇𝐴



𝑝𝑟



𝑝𝑟



…

𝑝𝑟



𝑃



𝑃





𝐴 𝐵

[12:13] [14:15]

𝑚

[20:30] …

𝑚

𝑃



𝑃





𝐷 𝐸

[9:10] [12:13]

𝑐

[20:30] …

𝑚

𝑃



𝑃





𝐴 𝐵

[12:13] [14:15]

𝑚

[30:40] …

𝑓

𝑃



𝑃





𝐴 𝐶

[16:17] [19:20]

𝑚

[20:30] …

𝑓

𝑃



𝑃





𝐴 𝐵

[12:13] [14:15]

𝑖

[40:50] …

𝑚

𝑃



𝑃





𝐴 𝐶

[7:8] [10:11]

𝑚

[20:30] …

𝑓

(b) Passengers’ Requests

Figure 1: The Proposed Ridesharing Recommendation Framework.

A Ridesharing Recommendation Framework with Hard and Soft Constraints

375

4 THE PROPOSED

FRAMEWORK

This section presents our proposed framework which

aims at identifying an ideal group, 𝑃





-𝑜, given a

driver, 𝐷



, with request, 𝑅





, and a set of passengers,

𝑃=

{

𝑃



,𝑃



,…,𝑃



}

with each passenger having their

own request denoted by 𝑅





. The proposed

framework consists of five main phases as shown in

Figure 1 before an ideal group, 𝑃





-𝑜, is identified and

recommended. These phases are: (i) match 𝑅





and 𝑅





, (ii) calculate 𝑊







 





for each matched 𝑅





and 𝑅





, (iii) generate possible groups of 𝑅





, i.e.

𝑃





-1, 𝑃





-2, …, 𝑃





-𝑟, (iv) calculate 𝑇𝑊-𝑃





-𝑞=

∑

𝑊







 









for each possible group, and (v) find

the ideal group, 𝑃





-𝑜={𝑃



,𝑃



,…,𝑃



} where 𝑇𝑊-

𝑃





-𝑜=

∑

𝑊







 









=max(𝑇𝑊-𝑃





-1, 𝑇𝑊-

𝑃





-2, …, 𝑇𝑊-𝑃





-𝑟). These phases are further

elaborated in the following paragraphs.

Phase 1 Match 𝑅





and 𝑅





– This phase aims at

identifying the passengers that match with a given

driver’s request, 𝑅





. Hence, at this stage the 𝑅





and 𝑅





of each passenger are compared based on the

hard constraints. Those pairs of 𝑅





and 𝑅





that do

not match as defined by Definition 6 are filtered out.

Hence, only those pairs of 𝑅





and 𝑅





that meet the

Definition 5 and Definition 7 are considered in the

next phases. These pairs are said to satisfy the

conditions SA-𝐷



= SA-𝑃



and TA-𝐷



= TA-𝑃



where

SA-𝐷



(SA-𝑃



) represents the departure

(

𝑆𝐴



)

and

arrival

(

𝑆𝐴



)

locations of the trip specified by the

driver 𝐷



(passenger 𝑃



, respectively) and TA-𝐷



(TA-

𝑃



) represents the departure

(

𝑇𝐴



)

and arrival

(

𝑇𝐴



)

time/date of the trip specified by the driver 𝐷



(passenger 𝑃



, respectively). The following algorithm

gives the detail steps of this phase.

Input: 𝑅





, 𝑃=

{

𝑃



,𝑃



,…,𝑃



}

, 𝑅





Output: 𝐹𝑃 = 𝑃



,𝑃



,…,𝑃





Step 1: 𝐹𝑃 = {}

Step 2: For each 𝑃



∈𝑃 do

Step 3: If 𝑆𝐴



of 𝐷



= 𝑆𝐴



of 𝑃



AND

𝑆𝐴



of 𝐷



= 𝑆𝐴



of 𝑃



AND

𝑇𝐴



of 𝐷



= 𝑇𝐴



of 𝑃



AND

𝑇𝐴



of 𝐷



= 𝑇𝐴



of 𝑃



Then

𝐹𝑃 = 𝐹𝑃 ∪ 𝑃



Step 4: Return 𝐹𝑃

Example: Based on Table 1, given the hard

constraints of 𝑅





= < 𝑆𝐴



,𝑆𝐴



,𝑇𝐴



,𝑇𝐴



> = <

𝐴,𝐵,

[

12:13

]

[

14:15

]

>, then 𝐹𝑃 =

{

𝑃



,𝑃



,𝑃



}

Meanwhile, 𝐹𝑃 =

{

𝑃



}

for the request 𝑅





= <

𝐷,𝐸,[9:10],[12:13] >.

Phase 2 Calculate 𝑊







 





for each matched 𝑅





and 𝑅





– Once, the set of passengers that satisfied

the hard constraints has been identified, i.e. 𝐹𝑃, then

the weight 𝑊







 





for each matched pair 𝑅





and 𝑅





is calculated. The weight value indicates the

degree of similarities between 𝑅





and 𝑅





. Here, the

Definition 8 and Definition 10 are applied. If every

criterion, 𝑐



, that is matched is given a value 1

whereas not matched is given a value 0, and assuming

that there are ℎ criteria for hard constraints and 𝑠

criteria for soft constraints with 𝑛=ℎ +𝑠, then if

𝑅





and 𝑅





are totally matched (100% similar), the

weight 𝑊







 





∑

𝑤(𝑐



)





=𝑛 where 𝑤

(

𝑐



)

the weight value given based on the criterion, 𝑐



However, if 𝑅





and 𝑅





are partially matched (100%

similar based on ℎ criteria whereas not 100% similar

based on 𝑠 criteria), the weight 𝑊







 





=ℎ≤

∑

𝑤(𝑐



)





≤ℎ+(𝑠−1). Here, we assume every

criterion is equally important. This is as given below:

𝑤

(

𝑐



)

=

1, 𝑐



of 𝐷



= 𝑐



of 𝑃



0, 𝑐



of 𝐷



≠ 𝑐



of 𝑃



Example: Given the 𝐹𝑃 =

{

𝑃



,𝑃



,𝑃



}

derived in

the previous phase, the weight 𝑊







 





for each

matched pair 𝑅





and 𝑅





is as follows: 𝑊







 





7, 𝑊







 





= 6, and 𝑊







 





= 5. Here, we assume

ℎ = 4 (𝑆𝐴



, 𝑆𝐴



, 𝑇𝐴



, 𝑇𝐴



) and 𝑠 = 3 (𝑝𝑟



, 𝑝𝑟



, 𝑝𝑟



This can be easily extended to cater other preferences.

Based on the weight and the number of criteria

considered, the requests 𝑅





and 𝑅





reflect totally

matched and Definition 8 is applied. Meanwhile, the

pairs 𝑅





and 𝑅





and 𝑅





and 𝑅





reflect partially

matched whereby Definition 10 is applied.

Meanwhile, the 𝑊







 





= 5.

Phase 3 Generate possible groups of 𝑅





, i.e. 𝑃





-1,

𝑃





-2, …, 𝑃





-𝑟 – Given the capacity, 𝐶, defined by

the driver, 𝐷



, and based on the 𝐹𝑃 identified in the

first phase, this phase generates all possible groups by

simply performing permutation on the elements of

𝐹𝑃. The number of possible groups as defined by

Definition 11 is

!

!()!

where 𝑘 is the number of

WEBIST 2021 - 17th International Conference on Web Information Systems and Technologies

376

elements (passengers) in 𝐹𝑃. The number of possible

groups reflects the number of ways the 𝑘 passengers

can be grouped based on the capacity, 𝐶. For instance,

if 𝐶 = 2 and 𝑘=4, then there are

!

!()!

= 6 different

ways to group the 4 passengers where each group has

two passengers to accommodate the capacity, 𝐶=2.

If these four passengers are labelled as 𝑃



,𝑃



, 𝑃



,𝑃



then the 6 different ways are {𝑃



,𝑃



}, {𝑃



,𝑃



{𝑃



,𝑃



}, {𝑃



,𝑃



}, {𝑃



,𝑃



}, and {𝑃



,𝑃



}. Although to

select 2 passengers from these 4 potential passengers

that are having the closest preferences to 𝐷



can be

easily done by picking 2 passengers with the highest

𝑊







 





values, it is natural to recommend several

solutions in a recommendation system. In other

words, these 6 different ways should be

recommended in certain ranking order whereas the

final decision is to be made by the user. It also caters

the possibilities of passengers cancelling their trip.

Example: Given the 𝐹𝑃 =

{

𝑃



,𝑃



,𝑃



}

derived in

the previous phase, the number of possible groups is

!

!()!

= 3. These groups are as follows: 𝑃





-1 =

{

𝑃



,𝑃



}

, 𝑃





-2 =

{

𝑃



,𝑃



}

, 𝑃





-3 =

{

𝑃



,𝑃



}

. Since,

there is only one passenger that matched the request

of 𝐷



, 𝑃





-1 =

{

𝑃



}

Phase 4 Calculate 𝑇𝑊-𝑃





-ℎ=

∑

𝑊







 









for

each possible group – Once all possible groups have

been generated, before any of them is recommended,

it is important to determine among all these possible

groups which one is the ideal group as highlighted in

the problem formulation. Literally, the group with the

highest total weight is the ideal group. Hence, this

phase calculates the total weight, 𝑇𝑊-𝑃





-𝑞=

∑

𝑊







 









, for each possible group.

Example: Based on the possible groups derived in

the previous phase, 𝑃





-1 =

{

𝑃



,𝑃



}

, 𝑃





-2 =

{

𝑃



,𝑃



}

𝑃





-3 =

{

𝑃



,𝑃



}

, the total weight, 𝑇𝑊-𝑃





-𝑞 for each

group is as follows: 𝑇𝑊-𝑃





-1 = 𝑊







 





𝑊







 





= 13, 𝑇𝑊-𝑃





-2 = 𝑊







 





𝑊







 





= 12, and 𝑇𝑊-𝑃





-3 = 𝑊







 





𝑊







 





= 11.

Phase 5 Find the ideal group, 𝑃





-𝑜={𝑃



,𝑃



,…,𝑃



}

where 𝑇𝑊-𝑃





-𝑜=

∑

𝑊







 









=𝑚𝑎𝑥(𝑇𝑊-

𝑃





-1, 𝑇𝑊-𝑃





-2, …, 𝑇𝑊-𝑃





-𝑟) – This phase

determines the ideal group of a given 𝑅





denoted by

𝑃





-𝑜 by analysing the following optimal function:

𝑇𝑊-𝑃





-𝑜=

∑

𝑊







 









=max(𝑇𝑊-𝑃





-1,

𝑇𝑊-𝑃





-2, …, 𝑇𝑊-𝑃





-𝑟). In other words, the

possible group with the maximum total weight value

is the ideal group for the given 𝑅





. It reflects the

similarities of the group members. If 𝑛 is the total

number of criteria considered and 𝑘 is the number of

selected passengers, then 𝑛×𝑘 is the maximum total

weight which implies all members of the group have

the same exact preferences. For instance, if we

assume ℎ = 4 (𝑆𝐴



, 𝑆𝐴



, 𝑇𝐴



, 𝑇𝐴



) and 𝑠 = 3 (𝑝𝑟



𝑝𝑟



, 𝑝𝑟



) as given in Table 1, if the maximum total

weight achieved is 7×2=14, this implies that the 2

passengers and the driver have the same preferences

with 100% similarities.

Example: Applying the above optimal function to

the total weights derived in the previous phase, 𝑇𝑊-

𝑃





-𝑜=

∑

𝑊







 









=max(𝑇𝑊-𝑃





-1, 𝑇𝑊-

𝑃





-2, 𝑇𝑊-𝑃





-3) = max(13, 12, 11) = 13. This

means the ideal group is 𝑃





-1 =

{

𝑃



,𝑃



}

5 FRAMEWORK

IMPLEMENTATION

This section presents the results of implementing the

proposed framework on a ridesharing mobile

application prototype, named SAGE. It provides a

platform for the public to share rides with others who

own the same journey and travel time. SAGE aims to

provide a safe, available, green and economical

ridesharing as defined below: (i) safe – among the

criteria used by SAGE in identifying an ideal group is

the demographic of the group members. This is to

ensure that members of the group will have a

pleasant, cosy and most importantly a safe journey;

(ii) available – SAGE is available from anywhere and

anytime of the day, i.e. it is available 24 hours 7 days

a week; (iii) green – SAGE focuses on ridesharing

service that aims to utilise the capacity of a vehicle to

reduce the emission of air pollutant from vehicle

exhaust, hence keeping a green environment; and (iv)

economical – it reduces the expenses of the

transportation per individual, as these expenses are

borne among the members.

SAGE is developed using Android platform. A

smartphone, Huawei Mate 20, as well as two virtual

devices created from Android Studio are used as the

emulators to test SAGE. The minimum SDK version

for SAGE is set to API level 24 which is compatible

to run on approximately 73.7% of the devices that are

active on the Google Play Store. Java programming

language is used as the primary programming

language in developing SAGE.

Figure 2 presents samples of SAGE interfaces

when a driver, 𝐷



, registered into the system. The

A Ridesharing Recommendation Framework with Hard and Soft Constraints

377

profile of the driver 𝐷



is captured at this stage which

among others include name, email address, phone

number, gender, race, date of birth, etc. It also

captured the details of the vehicle owns by the driver,

𝐷



. Similar interfaces are also designed to capture the

details of a passenger, 𝑃



, as shown in Figure 3.

Figure 2: Interfaces for registration of a 𝐷



Figure 3: Interfaces for registration of a 𝑃



Figure 4 presents the interfaces for users to

schedule a trip. Here, users either 𝐷



or 𝑃



are required

to fill in the fields related to hard constraints which

include From (𝑆𝐴



), To (𝑆𝐴



), Date (𝑇𝐴



,𝑇𝐴



Time Range (𝑇𝐴



), and Seater (𝐶, only applicable for

a driver). As for the soft constraints, we have included

the following: race, gender, age group, language, and

preferred environment. In specifying the preferences,

users may select a particular value or choose All

which implies that the field is not important to the

users. Meanwhile, Figure 5 shows a sample of

interfaces during a trip.

Once a request has been submitted by a driver, 𝐷



all requests submitted by passengers that are saved in

the system are filtered and only those requests that

matched with the hard constraints as specified by the

driver, 𝐷



, are listed. This list represents the 𝐹𝑃 list

described in Section 4. The driver can further filter

the list to narrow down the searching.

Figure 4: Interfaces for scheduling a trip.

Figure 5: Example of a trip.

We have tested SAGE with several cases and the

initial results show that SAGE is functioning well

according to the conceptual framework described in

Section 4. However, more testing needs to be

conducted before SAGE can be fully utilised.

6 CONCLUSION AND FUTURE

WORK

Ridesharing is now becoming one of the popular

sharing economy due to the benefits it provides. This

paper proposes a ridesharing recommendation

framework that aims at identifying an ideal group

consisting of a driver and passengers by considering

both the hard and soft constraints. There are five

phases, namely: (i) match 𝑅





and 𝑅





, (ii) calculate

WEBIST 2021 - 17th International Conference on Web Information Systems and Technologies

378

the weight, 𝑊







 





, for each matched 𝑅





and 𝑅





(iii) generate possible groups of 𝑅





, (iv) calculate the

total weight, 𝑇𝑊-𝑃





-𝑞, for each possible group, and

(v) find the ideal group, 𝑃





-𝑜={𝑃



,𝑃



,…,𝑃



}. The

framework is embedded into a mobile application

prototype, named SAGE. SAGE has been tested in a

small-scale environment. Hence, testing SAGE in a

large-scale environment will be the next step to be

conducted. Moreover, we attempt to further analyse

the performance of the proposed framework/SAGE

with regard to processing time and accuracy.

REFERENCES

Benish, C., Ansar-Ul-Haque, Y., Samar, E-A., and Elhadi,

S. (2018). Passenger Safety in Ride-Sharing Services.

Proceedings of the 8

International Symposium on

Frontiers in Ambient and Mobile Systems (FAMS-

2018), pp. 1044–1050.

Biying, Y., Ye, M., Mei-Mei, X., Baojun, T., Bin, W., and

Jinyue, Y. (2017). Environmental Benefits from

Ridesharing: A Case of Beijing. Journal of Applied

Energy, 191: 141– 152.

Conner-Simons, A. (2017). How Ride-sharing can Improve

Traffic, Save Money, and Help the Environment.

Massachusetts Institute of Technology (MIT) News on

Campus and Around the World.

Diep, N. S., Duy, Q. N-P., and Lester, W. J. (2021). Effects

of Perceived Safety, Involvement and Perceived

Service Quality on Loyalty Intention among Ride-

Sourcing Passengers. Transportation. 48: 369–393.

Douglas, O. S. and Eduardo, C. X. (2013). Dynamic Taxi

and Ridesharing: A Framework and Heuristics for the

Optimization Problem. Proceedings of the Twenty-

Third International Joint Conference on Artificial

Intelligence, pp. 2885 – 2891.

Georgina, G. (2018). The Definitions of Sharing Economy:

A Systematic Literature Review. Journal of

Management, 13(2): 175–189.

Hajra, Q., Osman, K., Muhammad, U. S. K., Atta, U. R. K.,

and Raheel, N. (2018).

An Optimal Ride Sharing

Recommendation Framework for Carpooling Services.

IEEE Access, Vol. 6(1): 62296–62313.

Indra, B. and Ibrahim, H. (2017). The Influence of

Customer Satisfaction on Ride-Sharing Services in

Malaysia. International Journal of Accounting &

Business Management, 5(2): 184–196.

Juho, H., Mimmi, S., and Antti U. (2015). The Sharing

Economy: Why People Participate in Collaborative

Consumption. Journal of the Association for

Information Science and Technology, 67(9), pp. 2047–

2059.

Mitja, S., Niels, A., Martin, S., and Mirko, G. (2015). The

Benefits of Meeting Points in Ride-sharing Systems.

Transportation Research Part B: Methodological, 82:

36–53.

Muhamad, K. O., Azimah, D., Zaimy, J. J., and Ainie, H.

A. (2019). Developing a Psychometric Model for E-

Hailing Jobs to Boost Malaysian B40 Income.

International Journal of Academic Research in

Business and Social Sciences, 9(3): 1461–1471.

Na, T., Guoliang, L., Tianyu, Z., Jianhua, F., Hanchao, M.,

and Zhiguo, G. (2017), An Efficient Ride-Sharing

Framework for Maximizing Shared Route. IEEE

Transactions on Knowledge and Data Engineering,

30(2): 219–233.

Nusrat, J. F., Md., N. A. A. R., Sifat, M., Mohammad, S.

U., and Nafees, M. (2016). A Framework for Dynamic

Vehicle Pooling and Ride-Sharing System.

Proceedings of the International Workshop on

Computational Intelligence (IWCI), pp. 204–208.

Steven, K. C. and Matthias, L. (2019). Defining the Sharing

Economy for Sustainability. Journal of Sustainability,

11(567): 1–25.

Wang, Y. et al. (2018). An Empirical Study of Consumers’

Intention to Use Ride-Sharing Services: Using an

Extended Technology Acceptance Model.

Transportation, 47: 397–415.

Xuan, W., Hassan, M. A., and Helmut, S. (2017). Does Ride

Sharing have Social Benefits? Proceedings of the

Twenty-third Americas Conference on Information

Systems, pp. 1 – 8.

Yuhan, G., Yu, Z., and Youssef, B. (2021). Real-time Ride-

sharing Framework with Dynamic Timeframe and

Anticipation-based Migration, European Journal of

Operational Research, 288(3): 810–828.

Ziru, L., Yili, H., and Zhongju, Z. (2016). An Empirical

Analysis of On-Demand Ride-Sharing and Traffic

Congestion. Proceedings of the International

Conference on Information Systems, pp. 1–24.

https://www.grab.com/my/driver/transport/share/

https://www.lyft.com

https://www.rydesharing.com

https://www.uber.com

https://weride.my

A Ridesharing Recommendation Framework with Hard and Soft Constraints

379