Impact of Tailored Network Splitting and Community Features’ Change

Rates on Prediction Accuracy in Dynamic Social Networks

Narimene Dakiche

, Karima Benatchba

, Fatima Benbouzid-Si Tayeb

and Yahya Slimani

Laboratoire des M

ethodes de Conception de Syst

emes (LMCS), Ecole Nationale Sup

erieure d’Informatique (ESI),

BP 68M - 16270 Oued Smar, Alger, Algeria

Computer Science Department, ISAMM Institute of Manouba, 2010 Manouba, Tunisia

Keywords:

Dynamic Social Networks, Community Behavioral Events, Evolution Prediction.

Abstract:

With its various real-life applications, predicting community evolution is a challenging task in the ﬁeld of

social network analysis. In this paper, we analyze communities’ evolution prediction accuracy in dynamic

social networks. The proposed approach combines two key concepts of the process, aiming to enrich the

prediction model by additional information that could improve the results: (1) a tailored network splitting

that results in snapshots of different periods rather than a static one, and (2) the change rates of communities’

features that characterize them over time instead of absolute values of features. Our experiments on four real-

world social networks conﬁrm that community evolution prediction can be achieved with a very high accuracy

by using both tailored network splitting as a ﬁrst step of prediction process and change rates of features.

1 INTRODUCTION

Nowadays, social networks have become widespread

and increasingly popular. For numerous useful pur-

poses, Social Network Analysis (SNA) exploits graph

theories to study the social relationships between in-

teracting actors. Indeed, graphs are commonly used

to represent social networks in which nodes are of-

ten individuals or social entities and edges describe

their social interactions (Tabassum et al., 2018). The

dynamic network is a further abstraction of the net-

work concept that evolve over time. Several changes

happen as new nodes join the network, existing nodes

leave it, and existing pairs of nodes develop new rela-

tionships or end old ones. Social networks are known

to have a community structure, i.e., groups of nodes

closer to each other in comparison to other nodes of

the network. These communities may undergo differ-

ent behavioral events and transitions over time such as

growth, split, merge and survive (Br

odka et al., 2013).

The prediction of community evolutionary events

is the heart of social network analysis’ phenomenal

rise. The main issues in the related literature are how

to identify communities’ behavioral events that may

have taken place, and how to forecast their future.

Previous works on predicting community evolution

(Dakiche et al., 2021; Rajita et al., 2020; Saganowski

et al., 2019; Pavlopoulou et al., 2017;

Ilhan and

u, 2016; Diakidis et al., 2015; Takaffoli et al.,

2014; Br

odka et al., 2013) are typically addressed

through the same main steps. First, the dynamic net-

work is divided into a time-series of snapshots. Then,

for each snapshot, an algorithm of community detec-

tion is used to identify its communities. Subsequently,

a set of relevant features is computed, for each com-

munity, to describe its state. Then, similar communi-

ties of successive snapshots are matched to label the

transformation with an appropriate possible behav-

ioral event. As a results, evolution sequences describ-

ing the states of each pair of matched communities are

created. Finally, the classiﬁcation step consists in de-

riving information from the evolution sequences and

predicting the upcoming behavioral events of commu-

nities.

This process faces two main issues. The ﬁrst one

concerns the dynamic social network splitting into a

sequence of consecutive snapshots, each one contains

a set of interactions aggregated over discrete time pe-

riods. However, the challenge related to network’s

splitting is the resolution level at which the interac-

tions are aggregated to build the snapshots. Indeed,

the detected community structures, their behavioral

events, and the prediction are all inﬂuenced by the

periods selected to split the network. In order to deal

with this issue, Dakiche et al. (2018) have investigated

the problem of choosing the appropriate scale for net-

Dakiche, N., Benatchba, K., Benbouzid-Si Tayeb, F. and Slimani, Y.

Impact of Tailored Network Splitting and Community Features’ Change Rates on Prediction Accuracy in Dynamic Social Networks.

DOI: 10.5220/0010709300003058

In Proceedings of the 17th International Conference on Web Information Systems and Technologies (WEBIST 2021), pages 95-102

ISBN: 978-989-758-536-4; ISSN: 2184-3252

work splitting which would improve the prediction.

Later, they proposed a new framework that provides a

tailored network splitting by examining activity dis-

tribution of users over time to produce more accu-

rate community evolution prediction (Dakiche et al.,

2021).

The second issue is related to community features’

computation and the selection of a suitable set of

features to describe communities and how those fea-

tures are used in the prediction task. Indeed, there

is an abundance of community structural and tem-

poral features that could be considered by comput-

ing their absolutes values (

Ilhan and

u, 2016;

Pavlopoulou et al., 2017; Saganowski et al., 2019;

Rajita et al., 2020). In this sens, Dakiche et al.

(2019) have investigated community evolution pre-

diction based on change rates of features that describe

a community throughout its evolution life-cycle rather

than absolute values of features.

In this paper, we investigate community evolution

prediction accuracy by, simultaneously, using a tai-

lored network splitting rather than a static one and

the change rates of features that represent the com-

munities instead of absolute values of features. Our

challenge is to achieve very high community evolu-

tion prediction accuracy. The rest of the paper is orga-

nized as follows. Section 2 introduces the community

evolution prediction approach. Section 3 presents the

experimental study and the obtained results. Finally,

Section 4 summarizes the work and outlines future

developments.

2 COMMUNITY EVOLUTION

PREDICTION

Community evolution prediction is typically ad-

dressed as a supervised learning task where commu-

nities history is exploited to forecast their behavioral

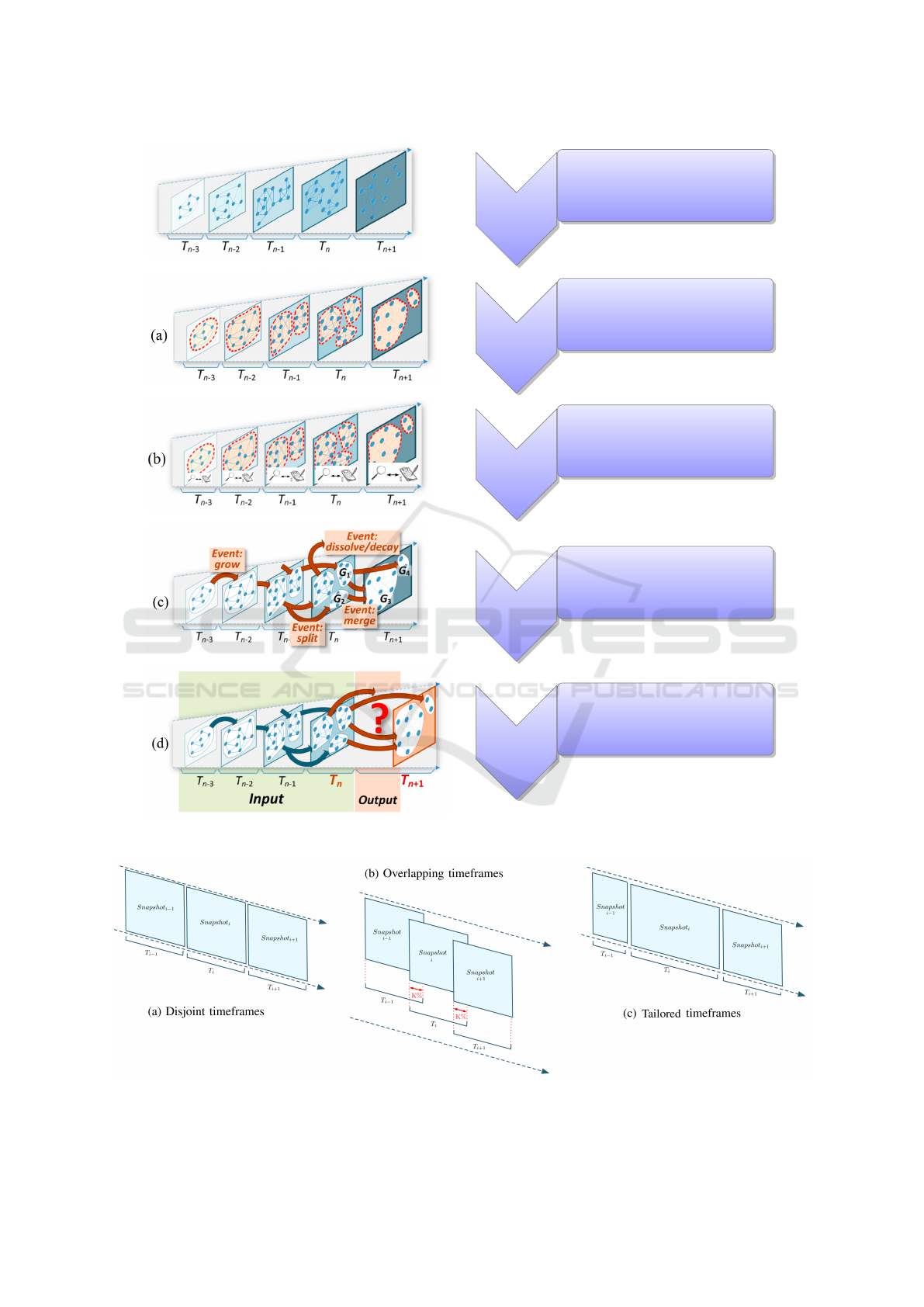
transformations. As shown in Fig. 1, it consists of the

following essential steps: (1) The dynamic social net-

work data is separated into a number of snapshots; (2)

Then, for each snapshot, a community detection algo-

rithm is applied to determine its communities; (3) For

each community, a set of mostly structural features

such as cohesion, size, and density, is computed to

describe its state; (4) Following that, identical com-

munities from successive snapshots are matched us-

ing a community evolution tracker, and the change is

tagged with a suitable event among the potential be-

havioral events. (4) Finally, to forecast future occur-

ring events in communities’ life-cycle, a predictive

model is built. In next subsections, through the dif-

ferent phases of community evolution prediction pro-

cess, we will present the new features incorporated.

2.1 Network Splitting

A dynamic social network G = (V, E

) is deﬁned by

a set of nodes V and a set of time-stamped edges.

Each edge e ∈ E

represents an interaction between

two nodes u, v ∈ V at time t (Holme and Saram

aki,

2012). It is usually split into τ consecutive snapshots

G = (G

, ..., G

)., where G

= (V

, E

) corresponds to

a graph with only the set of nodes and edges that ap-

pears in the interval (t

i+1

Usually, existing works on community evolution

prediction use snapshots of an arbitrary ﬁxed-length

aggregation period, with or without overlap. The

snapshots’ durations are frequently based on conve-

nience or intuition, or selected according to the col-

lecting data technology (hourly, daily, monthly, and

yearly) (Pavlopoulou et al., 2017;

Ilhan and

2016; Diakidis et al., 2015). Very recently, Dakiche

et al. (2021) introduced the concept of network tai-

lored splitting. It consists in analyzing the network

data distribution over time and grouping periods that

have low activity interactions in one snapshot, while

times with high activity interactions are broken up

into many snapshots. Their approach depends on a

parameter γ that outputs the data amount required per

snapshot. Thus, the snapshots’ periods may differ.

Fig. 2 illustrates the three types of snapshots.

2.2 Community Detection

Community detection consists in ﬁnding groups of

nodes closer to each other in comparison to other

nodes of the network. While G

represents the

graph of the i

snapshot in a dynamic network,

the k detected communities are denoted by C

, ...,C

) where community C

∈ C

, 1 ≤ p ≤ k,

is also a graph denoted by (V

, E

In the literature, several methods have been

proposed (El Moussaoui et al., 2019), each of

which draws communities with distinct characteris-

tics. Some of these result in disjointed communi-

ties, while others result in communities that over-

lap. It is often hard to compare the inﬂuence of two

types of community detection algorithms on classiﬁ-

cation accuracy because each approach produces dif-

ferent communities, which result in different behav-

ioral events.

We adopt Clique Percolation Method (CPM

)

(Palla et al., 2005) rather than modularity maximiza-

tion (Clauset et al., 2004) in this study. Indeed, CPM

http://www.cﬁnder.org/

WEBIST 2021 - 17th International Conference on Web Information Systems and Technologies

Network

splitting

Split the dynamic social network

into a sequence of consecutive

snapshots G = (G

, , G

Community

detection

Detect community structures

of each graph G

in the se-

quence: C

= (C

, C

, , C

) .

Feature

extraction

Comupte a set of features

= (f

, f

, , f

) for

each community c

in C

Event

detection

Apply a community event

tracker to identify the behav-

ioral events of communities.

Classiﬁcation

(Prediction)

Apply the classiﬁers on com-

munity evolution sequences to

produce the prediction results.

Figure 1: Community evolution prediction process (Dakiche et al., 2021).

Figure 2: Different snapshot types (Dakiche et al., 2018).

Impact of Tailored Network Splitting and Community Features’ Change Rates on Prediction Accuracy in Dynamic Social Networks

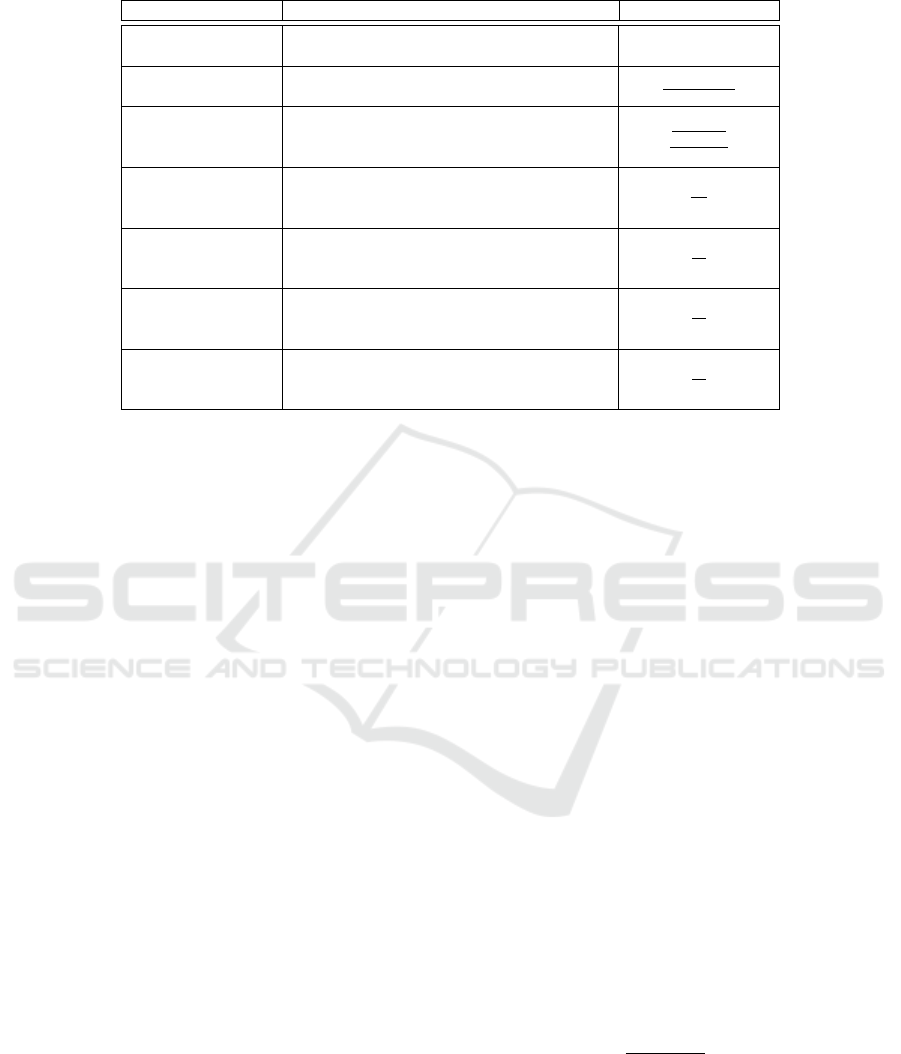
Table 1: A set of community structural features.

Feature Deﬁnition Formula

Size Ratio

Total of nodes inside the community i at

time t

Density

Ratio of edges to the maximum possible

edges.

2|E

|(|V

|−1)

Cohesion

Strength of connections inside the commu-

nity in relation to the connections outside of

it.

2|E

|(|V

|−1)

‘

Average Cluster-

ing Coefﬁcient

Ratio of the sum of clustering coefﬁcient

of the community nodes cc

to the total of

nodes in the community.

Average Degree

Centrality

Ratio of the sum of degrees of the nodes in

the community D

to the total of nodes in

the community

Average Closeness

Centrality

Ratio of the total node closeness in the com-

munity C

to the total of nodes in the com-

munity.

Average Eigen-

Vector Centrality

Ratio of the total node EigenVector in the

community E

to the total of nodes in the

community.

discovers more realistic overlapping communities. In

the next stage, the detected communities are used to

compute relevant features that describe their statuses.

2.3 Feature Extraction

A variety of metrics can be used to characterize a

community at a given snapshot. Researchers have

put in a lot of work to propose such metrics, and as

a result, there are a lot of them. The selection of the

proper collection of measures to include for the pre-

diction is a critical problem that has been discussed in

the literature (Saganowski et al., 2019).

We use two kinds of features to build information

about communities that describe their several prop-

erties: structural community features and community

inﬂuential members features. Indeed, these features

have been shown to be useful for prediction results

(Shahriari et al., 2016). The following sections go

through the features that were taken into considera-

tion.

2.3.1 Structural Features of Communities

Community structures gather nodes which are more

closely linked to one another than to the rest of the

network. We may use all of the information gained

from communities’ topological study. To achieve this,

we select features from Table 1 that we believe are

sufﬁcient to capture various community properties.

2.3.2 Inﬂuential Members Features

We normally include all members and their proper-

ties while assessing the network dynamics. How-

ever, communities are frequently headed by individ-

uals with signiﬁcant inﬂuence over the others and

who shape their community’s evolution. In this sens,

we evaluate the characteristics of the most prominent

nodes, referred to as leaders. In general, nodes with

the greatest 20% eigenvector centrality values are re-

garded as leaders (Takaffoli et al., 2014). We look at

the following characteristics for the detected leaders:

• LeaderDegCen: leaders average degree.

• LeaderClosenessCentrality: leaders average

closeness.

• LeaderEigenCentrality: leaders average eigen-

vector.

Usually, absolute values of communities’ features are

employed to represent them. Yet, Dakiche et al.

(2019) proposed to use the rates at which community

features change. The objective is to leverage these

change rates to generate new data to be exploited in

the prediction step. Formally, the change rates of

community C

characteristics f

are computed de-

pending on its prior instance’s existing properties, i.e.

t−1

. The following formula is used to calculate the

rate of change of the j

feature of community i at

time t:

i,t

− f

i,t−1

∗ 100 (1)

with f

, 1 ≤ j ≤ 10 are the features introduced above

that represent community structure and its inﬂuential

members.

WEBIST 2021 - 17th International Conference on Web Information Systems and Technologies

2.4 Event Detection

This phase’s most important purpose is to detect com-

munity behavioral events between snapshots. It en-

tails locating a number of comparable communities in

various time points which are ordered by time snap-

shots. Thus, a dynamic community is formalized as

DC = {C

, ...,C

}, where t

< t

< ... < t

and C

represents the community instance at time ti. Further-

more, the evolution of a community is represented by

the events that occur from one snapshot to the next,

such as splitting, growing, merging, dissolving, and

so on. This complicates the task of locating a speciﬁc

community at time t

among those of time t

i+1

In the literature, there are numerous taxonomies

that deﬁne the transitions that are expected to oc-

cur for a community. Thus, community evolution

can then be described as a time-ordered succession

of communities, beginning with the ﬁrst appearance

and ending with the last appearance. In this study,

we apply the GED method (Group Evolution Detec-

tion (Br

odka et al., 2013)), which was chosen as the

one that gives the most satisfying results in the recent

evaluation of existing evolution trackers (He et al.,

2017). To match similar communities, GED uses an

inclusion measure. It computes the extent to which

one community is integrated into another by comput-

ing the amount and quality of community members as

follows:

I(C

t+1

) =

∩C

t+1

∑

u∈C

∩C

t+1

NI(C

(u))

∑

u∈C

NI(C

(u))

(2)

The ﬁrst half of the equation reﬂects the quantity,

which represents the proportion of nodes from C

who

also belong to C

. The second portion of the equation

expresses the quality, which represents the contribu-

tion of important nodes from C

in C

. As a result, the

inclusion measure produces a balance between com-

munities with a large number of less important nodes

and communities with a small number of signiﬁcant

nodes. NI(C

(u)) is usually a statistical metric that

evaluates the relevance of a node within its commu-

nity.

2.5 Prediction

The predictive step consists in using previously com-

puted features and identiﬁed behavioral events as

community evolution sequences to train and test the

classiﬁers. A community evolution sequence is made

up of a community and its multiple preceding in-

stances from earlier frames. It consists of the present

community C

, the p

community of snapshot t

, and

its previous instances C

i−1

, C

i−2

, ..., C

i−n

. Each com-

munity instance is described by its structural features

and its identiﬁed evolution event. For example, Fig.

3 depicts an evolution sequence that includes two in-

stances of a community Ci at snapshot t −1 and snap-

shot t , as well as its evolution event. Thus, the aim is

to forecast the community C

’s next behavioral event

between snapshots t and t + 1.

Figure 3: An evolution sequence of two states (Dakiche

et al., 2021).

To perform the prediction, we adopt a multi-class

classiﬁcation method. The result is one of the be-

havioral events except the forming one. Indeed, the

forming event cannot be regarded as a response vari-

able because it refers to the formation of a commu-

nity. Otherwise, each of the remaining behavioral

events is treated as a class of the prediction model. To

assign relevant event labels, we use Logistic, Naive-

Bays, J48, and Support Vector Machines (SMO) clas-

siﬁers

3 EXPERIMENTAL STUDY

In this section, we analyze the investigate of dynamic

networks’ tailored splitting on the predictive model

based on community features’ change rates. To do so,

we use four different networks (see Table 2):

1. CollegeMsg Network: it is a students’ network in

which they exchange private messages on an on-

line social network at the University of California,

Irvine (Panzarasa et al., 2009). It contains data

over 193 days between 15

April and 26

Octo-

ber 2004.

2. Facebook Wall-posting Network: it is a directed

network of posts to other users’ wall on Face-

book New Orleans network. Each directed edge

is one post that links a person who publishes a

post to a user whose wall the post is published on

(Viswanath et al., 2009). It contains data over 4

years between 14

September 2004 and 22

Jan-

uary 2009.

WEKA Data Mining implementation of the classiﬁers

(Hall et al., 2009)

Impact of Tailored Network Splitting and Community Features’ Change Rates on Prediction Accuracy in Dynamic Social Networks

Table 2: Networks’ information.

Network Nodes Interactions Period

CollegeMsg 1 899 59 835 15

April - 26

October 2004

Facebook 46 952 87 993 14

September 2004 - 22

January 2009

ML King 2013 327 707 421 083 25

August - 02

September 2013

Moscow Athletics 2013 88 804 303 330 5

August - 19

August 2013

3. ML King 2013 Network: it is a social relation-

ships network between Twitter’s users during the

exceptional event of the 50

anniversary of Mar-

tin Luther King’s speech “I have a dream ...” in

2013 (Omodei et al., 2015). It contains data over

7 days between 25

August and 02

September,

2013.

4. Moscow Athletics 2013 network: it is a so-

cial relationships network between Twitter’s users

during the exceptional event of World Champi-

onships in Athletics in 2013 (Omodei et al., 2015).

It contains data over 14 days between 5

August

and 19

August, 2013.

For each network, we considered both static and

tailored splitting of the network. Then, for each

splitting, we considered the predictive model with

and without communities descriptive features’ change

rates. This resulted in four scenarios for each network

as follows:

• using static network splitting with absolute values

of community features,

• using static network splitting with change rates of

community features,

• using tailored network splitting with absolute val-

ues of community features,

• using tailored network splitting with change rates

of community features.

In order to obtain the tailored splitting of each net-

work, we have conducted several tests which revealed

that the best tailored splitting for both Facebook and

CollegeMsg networks was obtained with α = 2, 5%,

while the best tailored splitting for ML King 2013

and Moscow Athletics 2013 networks was obtained

with α = 5%. Consequently, we have considered for

each network its corresponding tailored splitting with

a static splitting that produces the same number of

snapshots. This results in static splitting of 40 snap-

shots for Facebook (40 days per snapshot) and Col-

legeMsg (5 days per snapshot) networks and 20 snap-

shots for Moscow Athletics 2013 (12 hours per snap-

shot) and ML King 2013 (6 hours per snapshot) net-

works.

Table 3 presents the prediction results of all net-

works which are expressed as the F-measure val-

ues obtained with the best performing classiﬁers un-

der different evolutionary sequence lengths. The F-

measure is the harmonic mean of precision and recall,

which reaches its highest level at 1 and its lowest level

at 0 (Sasaki, 2007). We used this F-measure to present

the classiﬁcation performance of each particular event

(class). Nonetheless, we use the average F-measure of

all events to represent overall classiﬁcation quality in

this paper. Indeed, we select the average F-measure

because it considers each class to be equally impor-

tant. Thus, the results of minority classes are not lost.

By analyzing the results of all networks, we can

notice that using a static network splitting with abso-

lute values of communities’ features gives the low-

est prediction accuracy. Yet, when considering the

change rates of communities’ features, the predictive

model achieved better results. Those good results are

also obtained when using a tailored splitting of the

network even with absolute values of features. The

last scenario which combines tailored network split-

ting with change rates of communities’ features im-

proves signiﬁcantly the prediction results compared

to other scenarios and achieves the highest prediction

accuracy for all networks. Consequently, the results

have shown that using the change rates of descriptive

community features improves the prediction. How-

ever, these results can still be improved by using the

tailored splitting of the network which allows a better

follow-up of the communities.

4 CONCLUSION

Community evolution prediction process involves

several steps and choices made in each step can affect

the prediction accuracy. For instance, a static network

splitting may result in a large number of snapshots

that are difﬁcult to exploit or snapshots that are mean-

ingless for tracking evolution. Moreover, there is an

abundance of features that could be considered to de-

scribe communities and the selection of a suitable set

is a challenging task.

In this work, we investigated the impact of using

tailored network splitting and change rates of features

on community evolution prediction accuracy. The ex-

periments have shown that using the change rates of

descriptive community features improves prediction

compared to using absolute values of features. In ad-

WEBIST 2021 - 17th International Conference on Web Information Systems and Technologies

100

Table 3: F-measure values, of all networks, using (1) a static network splitting and (2) a tailored network splitting, both with

(a) features’ absolute values and (b) features’ change rates.

CollegeMsg network

(1) Static network splitting with : (2) Tailored network splitting with :

P Classiﬁer (a) features’ absolute values (b) features’ change rates (a) features’ absolute values (b) features’ change rates

Logistic 0,733 0,845 0,787 0,884

NaiveBayes 0,736 0,886 0,820 0,884

J48 0,719 0,780 0,786 0,901

SMO 0,767 0,804 0,829 0,906

Logistic 0,774 0,800 0,809 0,875

NaiveBayes 0,722 0,782 0,855 0,898

J48 0,746 0,820 0,792 0,902

SMO 0,785 0,813 0,776 0,908

Logistic 0,746 0,788 0,789 0,897

NaiveBayes 0,741 0,822 0,828 0,892

J48 0,705 0,821 0,873 0,860

SMO 0,772 0,785 0,877 0,904

Facebook wall posting network

(1) Static network splitting with : (2) Tailored network splitting with :

P Classiﬁer (a) features’ absolute values (b) features’ change rates (a) features’ absolute values (b) features’ change rates

Logistic 0,726 0,700 0.786 0,917

NaiveBayes 0,664 0,696 0.887 0,884

J48 0,779 0,768 0.892 0,912

SMO 0,758 0,752 0.885 0,907

Logistic 0,728 0,736 0.897 0,901

NaiveBayes 0,622 0,728 0.901 0,926

J48 0,737 0,746 0.896 0,893

SMO 0,684 0,732 0.894 0,908

Logistic 0,689 0,749 0.776 0,923

NaiveBayes 0,637 0,729 0.824 0,933

J48 0,742 0,768 0.865 0,888

SMO 0,728 0,734 0.865 0,908

Moscow Athletics 2013 network

(1) Static network splitting with : (2) Tailored network splitting with :

P Classiﬁer (a) features’ absolute values (b) features’ change rates (a) features’ absolute values (b) features’ change rates

Logistic 0,698 0,794 0,842 0,867

NaiveBayes 0,720 0,798 0,828 0,883

J48 0,696 0,815 0,790 0,893

SMO 0,723 0,819 0,791 0,890

Logistic 0,757 0,808 0,833 0,876

NaiveBayes 0,763 0,830 0,816 0,875

J48 0,703 0,811 0,831 0,891

SMO 0,684 0,796 0,813 0,860

Logistic 0,705 0,798 0,832 0,898

NaiveBayes 0,703 0,829 0,815 0,893

J48 0,728 0,805 0,814 0,885

SMO 0,759 0,827 0,818 0,870

ML king 2013 network

(1) Static network splitting with : (2) Tailored network splitting with :

P Classiﬁer (a) features’ absolute values (b) features’ change rates (a) features’ absolute values (b) features’ change rates

Logistic 0,750 0,794 0,870 0,910

NaiveBayes 0,724 0,864 0,876 0,918

J48 0,847 0,886 0,877 0,860

SMO 0,757 0,848 0,853 0,909

Logistic 0,846 0,854 0,875 0,906

NaiveBayes 0,819 0,795 0,851 0,899

J48 0,874 0,809 0,843 0,899

SMO 0,834 0,849 0,873 0,920

Logistic 0,871 0,839 0,842 0,915

NaiveBayes 0,715 0,828 0,888 0,881

J48 0,791 0,818 0,881 0,912

SMO 0,766 0,832 0,851 0,910

Impact of Tailored Network Splitting and Community Features’ Change Rates on Prediction Accuracy in Dynamic Social Networks

101

dition, these results have been further improved by

using a tailored splitting of the network. Indeed, the

latter allows a better follow-up of community struc-

tures.

REFERENCES

odka, P., Saganowski, S., and Kazienko, P. (2013).

Ged: the method for group evolution discovery in so-

cial networks. Social Network Analysis and Mining,

3(1):1–14.

Clauset, A., Newman, M. E., and Moore, C. (2004). Finding

community structure in very large networks. Physical

review E, 70(6):066111.

Dakiche, N., Benbouzid-Si Tayeb, F., Benatchba, K., and

Slimani, Y. (2021). Tailored network splitting for

community evolution prediction in dynamic social

networks. New Generation Computing, pages 1–38.

Dakiche, N., Benbouzid-Si Tayeb, F., Slimani, Y., and Be-

natchba, K. (2018). Sensitive analysis of timeframe

type and size impact on community evolution predic-

tion. In 2018 IEEE International Conference on Fuzzy

Systems (FUZZ-IEEE). IEEE.

Dakiche, N., Benbouzid-Si Tayeb, F., Slimani, Y., and

Benatchba, K. (2019). Community evolution pre-

diction in dynamic social networks using commu-

nity features’ change rates. In Proceedings of the

34th ACM/SIGAPP Symposium on Applied Comput-

ing, pages 2078–2085.

Diakidis, G., Karna, D., Fasarakis-Hilliard, D., Vogiatzis,

D., and Paliouras, G. (2015). Predicting the evolution

of communities in social networks. In Proceedings of

the 5th International Conference on Web Intelligence,

Mining and Semantics, pages 1–6. ACM.

El Moussaoui, M., Agouti, T., Tikniouine, A., and El Ad-

nani, M. (2019). A comprehensive literature review on

community detection: Approaches and applications.

Procedia Computer Science, 151:295–302.

Hall, M., Frank, E., Holmes, G., Pfahringer, B., Reutemann,

P., and Witten, I. H. (2009). The weka data min-

ing software: An update. SIGKDD Explor. Newsl.,

11(1):10–18.

He, Z., Tajeuna, E. G., Wang, S., and Bouguessa, M. (2017).

A comparative study of different approaches for track-

ing communities in evolving social networks. In 2017

IEEE International Conference on Data Science and

Advanced Analytics (DSAA), pages 89–98. IEEE.

Holme, P. and Saram

aki, J. (2012). Temporal networks.

Physics reports, 519(3):97–125.

Ilhan, N. and

u, S¸. G. (2016). Feature identiﬁcation

for predicting community evolution in dynamic social

networks. Engineering Applications of Artiﬁcial In-

telligence, 55:202–218.

Omodei, E., De Domenico, M., and Arenas, A. (2015).

Characterizing interactions in online social networks

during exceptional events. Frontiers in Physics, 3:59.

Palla, G., Der

enyi, I., Farkas, I., and Vicsek, T. (2005).

Uncovering the overlapping community structure of

complex networks in nature and society. Nature,

435(7043):814–818.

Panzarasa, P., Opsahl, T., and Carley, K. M. (2009). Pat-

terns and dynamics of users’ behavior and interaction:

Network analysis of an online community. Journal

of the American Society for Information Science and

Technology, 60(5):911–932.

Pavlopoulou, M. E. G., Tzortzis, G., Vogiatzis, D., and

Paliouras, G. (2017). Predicting the evolution of com-

munities in social networks using structural and tem-

poral features. In 2017 12th International Workshop

on Semantic and Social Media Adaptation and Per-

sonalization (SMAP), pages 40–45. IEEE.

Rajita, B., Ranjan, Y., Umesh, C. T., and Panda, S. (2020).

Spark-based parallel method for prediction of events.

Arabian Journal for Science and Engineering, pages

1–17.

Saganowski, S., Br

odka, P., Koziarski, M., and Kazienko,

P. (2019). Analysis of group evolution prediction in

complex networks. PloS one, 14(10):e0224194.

Sasaki, Y. (2007). The truth of the f-measure. Teach Tutor

Mater, 1(5):1–5.

Shahriari, M., Gunashekar, S., Domarus, M. v., and

Klamma, R. (2016). Predictive analysis of temporal

and overlapping community structures in social me-

dia. In Proceedings of the 25th International Confer-

ence Companion on World Wide Web, pages 855–860.

International World Wide Web Conferences Steering

Committee.

Tabassum, S., Pereira, F. S., Fernandes, S., and Gama, J.

(2018). Social network analysis: An overview. Wiley

Interdisciplinary Reviews: Data Mining and Knowl-

edge Discovery, 8(5):e1256.

Takaffoli, M., Rabbany, R., and Za

ıane, O. R. (2014). Com-

munity evolution prediction in dynamic social net-

works. In 2014 IEEE/ACM International Conference

on Advances in Social Networks Analysis and Mining

(ASONAM), pages 9–16. IEEE.

Viswanath, B., Mislove, A., Cha, M., and Gummadi, K. P.

(2009). On the evolution of user interaction in face-

book. In Proceedings of the 2nd ACM SIGCOMM

Workshop on Social Networks (WOSN’09).

WEBIST 2021 - 17th International Conference on Web Information Systems and Technologies

102