Reconfigurable Scheduling as a Discrete-Event Process:

Monte Carlo Tree Search in Industrial Manufacturing

T. J. Helliwell

, B. Morgan

, A. Vincent

, G. Forgeoux

and M. Mahfouf

Automatic Control & Systems Engineering Department, University of Sheffield, Sheffield, U.K.

Advanced Manufacturing Research Center (AMRC), University of Sheffield, Sheffield, U.K.

Safran Landing Systems, Gloucester, U.K.

Keywords: Reconfigurable Scheduling, Autonomous Planning, Discrete-Event Systems, Evolutionary Computing,

Generative Models, Manufacturing Systems.

Abstract: In this paper we introduce a theoretical basis for reconfigurable makespan scheduling that is computationally-

efficient and general purpose in manufacturing. A full-scale scale case study for batch production in the

aerospace industry is shown. A knowledge-based Discrete-Event System, based on a Timed Petri Net, is

injected with the initial - current - state and simulated to generate trajectories that represent valid possible

schedules or policies analogous to the Monte-Carlo Tree Search (MCTS) planning algorithm. A new, concise,

evolutionary metaheuristic is proposed called Elitist Trajectory Mutation (ETM) in order to exploit high

performing schedules in localising search and optimisation. The advantage of this approach is

reconfigurability, extensibility and ability to be parallelised to enable satisficing performance for real-time

applications such as intelligent industrial cyber-physical systems scheduling, autonomous control of

distributed systems and active industrial informatics.

INTRODUCTION

Autonomous systems require abilities to discover and

execute rapid planning in or near real-time to exhibit

continuously intelligent control and behavior. Highly

valuable autonomous systems are of a distributed,

discrete-event nature and are characterized

dynamically complex, holonic, chaotic, non-linear

and emergent properties. Markov Decision Processes

(MDP) may be modelled efficiently using Discrete-

Event Systems (DES) [or Discrete-Event Dynamical

Systems (DEDS)] and controlled using event-graphs

or schedules; a powerful, high-level contextual

abstraction.

This paper discusses a Monte-Carlo Tree Search

(MCTS) approach in which autonomous supervisory

agent is embodied with a compositional, knowledge-

based DES model. This is used as a computationally

efficient Markovian representation for discovering

what possible actions are available to a state. The

process is recursive; by inferring what actions

(controlled events) are logically possible (or feasible)

from a given state, and selecting an action, a new state

is generated, time is incremented and this loop is

repeated, generating useful data in a rapid planning

process. This replicates the lookahead process in

Artificial Intelligence (AI) to generate, bifurcate, and

traverse state space trees. However, in this case, time

is modelled explicitly, allowing significant depth –

i.e. planning or scheduling horizons, to be traversed

for search, optimisation and presentation of

controlled system performance, regardless of inherent

combinatorial state explosion.

We show how DES can be used as a ‘scheduling

machine’, modelled using prior knowledge of

deterministic processing time intervals and

dependencies to define a short reconfigurable

scheduling program written in MATLAB

. By seeing

a task as a composition of sub-tasks, and using

knowledge of their respective durations and

dependencies, makespan scheduling may be cast as a

stepwise planning problem.

In 1.1 we discuss previous work and claims; 1.2

define contributions and remark on previous claims.

In 2, we show a Timed Petri Net model for a full-scale

industrial case study from aerospace manufacturing

and the search process [i.e. simulation] to generate

trajectories; in 2.5 a new metaheuristic we call Elitist

Trajectory Mutation (ETM) that exploits high-

performing trajectories is described and 3 closes with

Helliwell, T., Morgan, B., Vincent, A., Forgeoux, G. and Mahfouf, M.

Reconﬁgurable Scheduling as a Discrete-Event Process: Monte Carlo Tree Search in Industrial Manufacturing.

DOI: 10.5220/0010711600003062

In Proceedings of the 2nd International Conference on Innovative Intelligent Industr ial Production and Logistics (IN4PL 2021), pages 151-162

ISBN: 978-989-758-535-7

151

some important observations and extensive

considerations for further work.

1.1 State-of-the-Art

It is necessitated by the subject that previous work

must be considered in discrete sections whilst

retaining a manufacturing perspective; 1) discusses

scheduling in an applied context, the raison d’etre

along with contemporary themes, 2) discusses

scheduling as a mathematical or computational

problem, including Petri Nets and useful

classifications, 3) discusses Discrete-Event System

Simulation (DESS) and finally, 4) identifies broad

fields of inspiration.

1.1.1 Scheduling in Contemporary

Manufacturing

There have been a number of observations on the

significant gap between scheduling theory and

scheduling practice (Maccarthy & Liu, 1993); (Chen

& Shukla, 1996). Scheduling is often a high-level

abstraction of a discrete control or optimization

problem, relating to Systems-of-Systems (SoS)

(Zeigler, Bernard P., Sarjoughian, 2013), Multi-Agent

Systems (MAS) (Ferber, 1999); (Wooldridge, 2009)

and Distributed Systems (DS). Issues include

deficient accuracy (poor prior predictions of task

durations, neglecting inclusion of domain

knowledge) or brittleness of schedules (exogenous

events rendering the schedule infeasible) that

discourage the use of scheduling systems.

(Cowling & Johansson, 2002) noted scheduling

models and algorithms are unable to utilise real-time

information, implying that existing offerings are

exclusively offline and manual. This is in

contravention with the advent of the Cyber-Physical

Systems (CPS) paradigm, and the broader theme of

‘Industrie 4.0’ (Oztemel & Gursev, 2020) that

provides a real-time substrate for machine perception

and environment observation via computer models

and algorithms that enable continuous large-scale

intelligent behaviour through physical control.

The development towards Cyber-Physical

Manufacturing Systems (CPMS) (Váncza &

Monostori, 2017); (Lee, Bagheri, & Kao, 2015)

followed by Autonomous Manufacturing Systems

(AMS) is an international priority since high-

productivity, sustainable (Ambrogio, Guido, Palaia,

& Filice, 2020), adaptive, self-organising, self-

optimising supply chains are in significant

commercial demand (Romero-Silva & Hernández-

López, 2020) and represent the ultimate goal of

contemporary industrial systems.

A connection to the manufacturing system

through a so-called Digital Twin (Feldt, Kourouklis,

Kontny, & Wagenitz, 2020); (Li, Wang, Zhu, & Liu,

2020) which we define as a computer or data model,

provides means to capture or observe the current

actualised state of the system and input it as an initial

state (or initial conditions) of a simulation or planning

system. (Luo, Fang, & Huang, 2015) discussed the

use of Radio Frequency Identification (RFID) with

application to real-time scheduling to enable shop

floor visibility. In regards to real time data acquisition

and ingestion, the paradigm CPMS (Cheng et al.,

2018) demands deployment of high-volume and low-

latency data ‘plumbing’, as mentioned by (Rossit,

Tohmé, & Frutos, 2019) and many others.

1.1.2 Scheduling as a Mathematical and

Computational Problem

(Charpentier & Thomas, 2005) made comments

regarding concept of ‘model reduction’ - a core idea

in Artificial Intelligence - on manufacturing system

scheduling in 2004, whilst literature suggests a sharp

distinction between ‘simulation’ and ‘mathematical

modelling’ approaches.

Automatic generation of schedules without

knowledge is compute-intensive; classically NP-Hard

problem (non-polynomial time class of

computational complexity). The Multiway Number

Partitioning Problem (MNPP) is an example of a NP-

Hard decision problem with well-established solvers

in which a multiset of integers must be partitioned

into a fixed number of subsets, where the sum of

subsets is as equal as possible. This is often cast as

contextually relevant to makespan minimization and

the multiprocessor scheduling problem.

Unfortunately the MNPP exploits what would be

hidden or unactualised information in the case of

choice, dependencies and where processors have

different speeds (also known as task durations).

Brucker & Schelie were one of the first to address

the Flexible Job Shop Scheduling (FJSSP) problem

(Brucker & Schlie, 1990). Although the FJSSP

structure relates to a specific type of manufacturing

system, if tasks are equivalent to jobs, characteristic

features arise - significant dependencies between

tasks, task transformations (or relabelling), variation

in processing duration (or speed) and complex

relations between tasks and resources.

(Chan, Bhagwat, & Chan, 2014) outlined a

methodology for the study of manufacturing system

control with respect to routing flexibility, sequencing

and dispatching rules, and argued that as a systems

flexibility increases, so does the importance of

IN4PL 2021 - 2nd International Conference on Innovative Intelligent Industrial Production and Logistics

152

optimal decision making. (Tuncel & Bayhan, 2007)

extensively reviewed the application of Petri Nets to

production scheduling. (Baruwa, Piera, & Guasch,

2016) combined Timed Coloured Petri Nets (TCPN)

and a reachability graph Heuristic Search (HS).

Semiconductor fabrication has been a popular

application of manufacturing scheduling problems

featuring re-entrant flows and close integration of

Autonomous Material Handling Systems (AMHS),

where (Ghasemi, Azzouz, Laipple, Kabak, & Heavey,

2020) conducted a recent case study in a Bosch

facility.

(Ouelhadj & Petrovic, 2009)’s work brought

particular clarity to classification of dynamic

scheduling or real-time scheduling problems into

categories of completely reactive, predictive–

reactive and pro-active scheduling.

Reactive scheduling is the dominant approach;

myopic, low-level decentralised production or

dispatching rules; decisions that are inferenced in real

time, forming ‘atomic components’ of a schedule; an

appealing online approach in dynamic scenarios

where uncertainties and disturbances are prolific.

Similarly to this work, the search process results in

the construction of schedules – may be seen as

discovering or training a knowledgebase in the form

of a lookup table, where the engine is a set of states

that are time-indexed with an associated action or

controlled event. The controller is then simply

‘looking up’ by inputting the current time to find the

output action. An immediate weakness (besides the

lack of reconfigurability, i.e. the complete

configuration space must be exhaustively covered by

the engine) is in its general lack of ‘informatics’ or

decision support – it is difficult for users to examine

or interpret the effects of control in a global,

emergent, cumulative system context over time

intervals, nor could it manage a different goal. A

visual representation of system behaviour that is

‘predictive’ or ‘forecasted’ is key deliverable for the

next generation of industrial informatics.

Predictive schedules which take place a priori

(before) or upon the episode start, and cover the bulk

of contemporary research, these constructed methods

are far more computationally demanding on account

of having to manage exploration of state space that is

subject to combinatorial explosion. Hence, they are

reconfigurable insofar as sufficient time is available

for an acceptably high-performing schedule to be

generated.

The third type, to which this work belongs,

predictive-reactive scheduling or

online/dynamic/real-time scheduling, where

classification as real-time is deeply application

specific. Here, the ability to continuously refine or

rapidly re-generate new event-driven control policies

to repair or rapidly reschedule appears; schedules are

revised in response to observed real-time events. The

difficulty is rapidly rediscovering a rule base that is

near-optimal in the ‘space of all rule bases’ when

disturbances potentially render the existing rule-base

invalid. An a recent example of this conventional,

knowledge-free approach is discussed by (Mejía &

Pereira, 2020), using a small case study (Petri Net

structure) and metaheuristic Non-Sorting Genetic

Algorithm (NSGA-II) using a

High-Performance

Computing (HPC) cluster. This again leads us directly

into concerns relating to computational complexity.

1.1.3 Discrete-Event Simulation as a

Surrogate Model for Search and Tree

Generation

(Negahban & Smith, 2014) claimed that Discrete-

Event System Simulation (DESS) is a

“computationally expensive tool”, followed by

(Shiue, Lee, & Su, 2018) regarding multi-pass

simulation as “inappropriate for shop floor control

because it requires intensive computational effort to

select the best scheduling method for each scheduling

period”. (Negahban & Smith, 2014) suggest “the use

of simulation as a basis for real-time system

controller is still a hard task due to the response time,

data collection and aggregation issues”.

An avenue for future work in achieving higher

performance is in Parallel Discrete-Event System

Simulation (PDESS) (Fujimoto, 2016) (Pellegrini &

Quaglia, 2017) research while the broader scientific

community are shifting numerical workloads such as

training Machine Learning (ML) models to an

Graphics Processing Unit (GPU).

1.1.4 Inspirational Background Work

In laying theory for optimization-and-simulation

based scheduling [see (Negahban & Smith, 2014) for

a wide review of manufacturing informatics

applications], inspiration was found in (Ramadge &

Wonham, 1989) that covers early theoretical work

behind DES control, (Sutton & Barto, 2018)’s

Reinforcement Learning (RL) (also covered by

(Bertsekas & Tsitsiklis, 1996)) especially in its use of

the Markov Decision Process (MDP) formalism

(Howard, 1960) to use policies over ‘episodes’ (see

(Dietterich & Zhang, 1995) for early work on

scheduling).

Learning Classifier Systems (LCS) (Butz, 2015)

(Bull, 2015); (Urbanowicz & Moore, 2009) for

automatically discovering interpretable

Reconﬁgurable Scheduling as a Discrete-Event Process: Monte Carlo Tree Search in Industrial Manufacturing

153

knowledgebases that achieve rule-chaining, efficient

tabular learning and credit assignment. We also note

similarities between this work and Temporal Logic or

Tense Logic; a system of rules for representing and

reasoning about propositions qualified in terms of

time, and introduces a concept of branching time

independently replicated here. A final observation is

that Petri Net structures are similar to the Recurrent

Neural Network (RNN)(Sepp & Jurgen, 1997) in that

once instantiated, models systematically allow

persistence of data, constraining dimensionality in

temporally dynamic behaviour.

1.2 Contribution & Claims

It has been observed that in many scheduling

problems that relate to real systems retain a similar

structure in that the task types and duration observed

are consistent and deterministic, only the state data

(e.g. number of tasks, resource configurations, etc)

and the definition of the objective function [a

generalised term for optimal behaviour] change over

episode instances. In order to exploit this,

reconfigurability has been a principal research

objective – the scheduling problem changes; a

reconfigurable scheduling system can react to this

change by adjusting system parameters and structure

- a framework which has the capability to solve

scheduling problems in the same universe of

discourse by serving all possible state configurations

with minor added complexity.

The most interesting prospect to commercial

industry that keep developmental and computational

requirements low are symbolic reasoning approaches

and lightweight simulation frameworks. We suggest

that simulation and optimisation frameworks need to

be built with a ‘real-time application’ mentality where

clear limitations on what is computationally tractable

for real-time use should be considered from the

outset. This requires revisiting foundational theory in

DES - graphical models, such as Petri Nets, need only

define the relations or dependencies between

variables followed by intentional programming to

minimise the number of computer operations.

Real time information is essential in order to

establish the state of the controlled system. “Industrie

4.0” applications enable this via data from the CPS

layer that enables easy injection of the initial state for

rescheduling. This will address concerns regarding

immediate response expected from real-time control

and rescheduling that adapts to these disruptions or

disturbances automatically. In the context of these

two points, we have found a fruitful analogy is

viewing the control of DES (in applications such as

real-time scheduling of manufacturing systems)

through the lens of path or trajectory planning in

Robotics.

The apparent distinction between mathematical

and computational approaches is superficial in that

strictly speaking, the representational power of both

are along the same continuum and the trade-off is

between the ease of model definition, model

verification and computational tractability for

complex manufacturing systems. Graphical models,

such as Petri Nets, are mathematical and

programmatic representation hybrids that define rules

of interactions between variables as a form of model

reduction - the logical, formal systems description

directly relates to exhibited computational efficiency.

DES Simulation (DESS) complexity is largely an

extension of Petri Nets using Finite State Automata

(FSA) or Finite State Machines (FSM) and

supporting software for data collection, visualisation

and statistics gathering capabilities.

On the one hand, all systems will experience some

form of combinatorial state explosion and many will

be sufficiently complex to make rule base discovery

intractable for long planning horizons. On the other

hand, DESS software used by manufacturing

researchers focus primarily on ease-of-use; user

interfaces, 3D representations and other such features

which do little to optimize the speed of simulation

itself - some of the very earliest programming

languages [such as Fortran, Simula67 and Simscript]

initially targeted scientific and numerical computing

followed by simulation modelling, including DESS,

through the introduction of objects, classes etc. Since

that time, we have had a monumental increase in

computational processing which has been unutilised

by prioritizing the aforementioned features used in

research, or overlooked as a software requirement by

developers and vendors. We make some observations

in regards to parallelisation of our technique and

algorithm in Section 2.4.

In addition to use of inefficient simulation models,

we observe that approaches in existing work do not

combine the simulation and optimization/search

process together into the same program, but instead

deploy a low bandwidth approach where the

optimisation algorithm (typically an evolutionary

metaheuristic) generates a complete possible solution

with combinatorial complexity of the space of actions

𝚺

𝑪

to the power of episode length 𝒆

𝒕

that is then

evaluated by the simulation for both feasibility 𝑭

(Boolean) and multi-objective (𝑶

𝟏

,𝑶

𝟐

,…,𝑶

𝒏

)

performance (or cost). (Sutton & Barto, 2018)

addressed this oversight directly; ‘Evolutionary

methods ignore much of the useful structure of the

IN4PL 2021 - 2nd International Conference on Innovative Intelligent Industrial Production and Logistics

154

reinforcement learning problem: they do not use the

fact that the policy they are searching for is a function

from states to actions; they do not notice which states

an individual passes through during its lifetime, or

which actions it selects’.

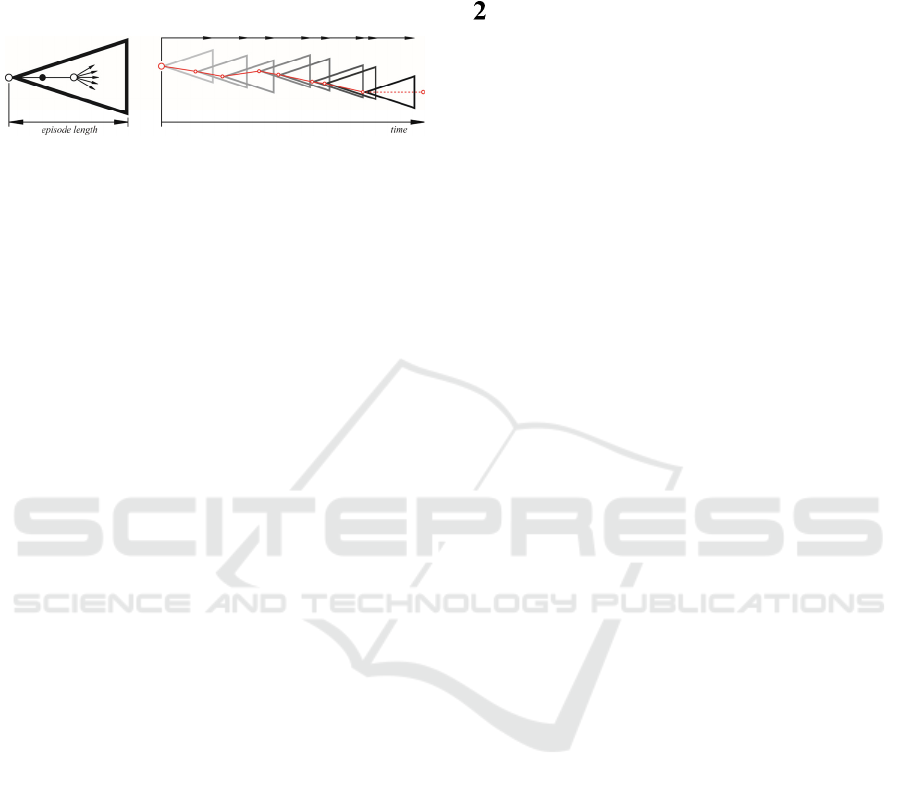
Figure 1: Rolling windows; breaking down continuous time

into episode lengths, and conducting scheduling processes

within these spaces, where the left hand node is the initial

state and the triangular shape represents the bifurcating

search in future state space.

The finite set of possible states for DES is

exceptionally large and using this model free

approach means many generated solutions are likely

to be logically impossible or unfeasible; 𝑭=𝟎

(False), thus waste valuable computational search

[removing the possibility of real-time scheduling and

forcing use of HPC] since they do not exploit the tree-

like compositional structure of DES process

trajectories (see Fig. 3), nor capture the full detail of

the system behaviour in the simulation at each time

instance, particularly in regards to dynamically

varying constraints.

Further, we advocate that the simulation need only

be at the so-called supervisory level of abstraction so

that the branching factor (choice – the number of

feasible actions) is manageable on a case-by-case

basis. This is analogous in older literature to

Hierarchical Task Decomposition (HTD) (Moore &

Flann, 1999) and Hierarchical Task Networks (HTN)

(Dvorak, Bartak, Bit-Monnot, Ingrand, & Ghallab,

2014) (Cao & Sanderson, 1994) and more recently the

idea of general idea of attention (Wang, Hao, & Cao,

2020) - an intelligent system can only consider so

many possibilities at once in order to be tractable. Our

approach is that secondary effects of sub-actions or

sub-tasks, (for instance, the use of transportation or

logistics systems, setting-up of resources), are

procedurally generated after the higher-level decision

to assign a task to a resource has been made. The

ramifications of these tasks are therefore experiential

and observed only in the resulting, constructed

schedule and respective statistical data but are not

considered a priori as part of the decision itself.

METHODOLOGY

The approach discussed here exploits the Timed Petri

Net as an explicit model to represent a state transition

function. This allows construction of each solution by

first defining this model (in 2.1), taking an

observation or percept as input (in 2.2), recording this

input as an initial state marking, which is a basic form

of object permanence, querying the DES model

(which is conceptually our knowledge representation)

to find only the logically feasible components of the

solution at each time step (in 2:3), followed by a

policy for selection over the space of feasible actions

(a Monte-Carlo selection used, resulting in Monte

Carlo Tree Search (MCTS)). This casts it as a

planning problem - analogous to a fully observable,

non-stationary MDP formalism as a stepwise

stochastic decision process, which is the source of its

reconfigurability whilst avoiding the need to ‘solve’

the MDP using sample-inefficient and potentially

unstable methods seen in RL. This results in a fast,

elegant and efficient depth-first search and

deliberation process that belongs to the class of

anytime optimal algorithms which run continuously

and give the optimal-so-far when queried.

2.1 Modelling Scheduling Processes

through DES

In the context of Industrie 4.0, scheduling problems

are applicable to some physical environment or

system under control that are continuously evolving

in real-time. This ‘infinite’ time horizon (i.e. the

continuous physical reality) may be divided into in a

rolling window of sequential episodes using a

receding horizon. Fig. 1 illustrates this concept

graphically. Our definition of a schedule is an event-

driven control policy over some time interval that is

optimized towards a mixture of emergent or

cumulative properties and the occurrence of specific

events. Systems that are scheduled orient around

sequencing tasks in concurrent systems and use

categorical, symbolic relations between tasks (or

Reconﬁgurable Scheduling as a Discrete-Event Process: Monte Carlo Tree Search in Industrial Manufacturing

155

Figure 2: The Timed Petri-Net Structure of the Discrete-Event System; we have 7 part (task) types, each passing through as

many as 32 sequential sub-tasks completed on 36 workcenters (resources). 200 controlled events, the links, represent actions

- routing rules - that indicate the assignment of a sub-task to a resource. Conceptually, tokens represent the presence of a part,

and will move around this diagram as the process is simulated.

jobs) and resources (or processors) that are executed

dynamically in serial or in parallel.

The ‘Petri Net’ is a form of DES model and was

conceptualised by Carl Adam Petri in 1962 in his PhD

thesis “Communication with Automata” and are

particularly suitable for the modelling of systems

characterised by concurrency, parallelism, conflicts,

causal dependency, synchronisation and crucially,

choice. Stochastic Petri Nets (SPNs) and Generalised

Stochastic Petri Nets (GSPNs) are extensions which

aim to model unpredictable behaviour, whilst Timed

Petri Nets (TPNs) extend PN to include time

representations such as time delays or durations to be

associated with transitions, places and arcs. This

enables TPN to become applicable in scheduling

problems; temporally dynamic behaviour [a DES

‘trajectory’] is driven entirely by sequentially indexed

asynchronous events. Two terms, selected on account

of their semantic generality, define the fundamental

components of scheduling problems; tasks and

resources. A ‘task’ represents some contextual

process abstraction from some lower-level system. In

computer programs; instantiation and deployment of

specific controller or an on-line discriminatory

statistical model, in hierarchical multi-agent robotic

swarms; task decomposition for an individual robot,

a manufacturing system; a machine, in a computer

system; a processing unit. Meanwhile, a ‘resource’

represents some finite affordance; utilization of a sub-

system.

Petri Nets are a directed bipartite graph, where

mathematical topological structures model the

pairwise relations between objects; these relations

represent ‘domain knowledge’ within the system.

Task type queues and resources are the nodes or

vertices and the links or edges are the relations. There

are two types of nodes; places and transitions.

Transitions are durationless events representing

decisions to dynamically map tasks to resources.

Tasks are represented by tokens that are unit

variables; they provide logical information in that

their presence indicates a true condition and

additionally represent queues by using real-valued

integers for volumes. The Petri Net structure may be

defined as a mathematical incidence matrix that

relates tasks to resources. Provided these

relationships are represented, it is not important how

this is implemented in a computer program –

emphasis should be placed on high performance; e.g.

sparse arrays or hash maps.

This system belongs to Safran Landing Systems

(SLS), Gloucester, and produces large titanium and

steel structural components for landing gear for the

next generation of civil aircraft. There are parallel

machines, multi-part machines, re-entrant flows and

significant scope for assignment conflicts. Taking one

part as an example, there are 1440 unique possible

paths through the system and any number of possible

parts in the system (provided maximum number of

tokens is not exceeded) at any one time (i.e. a given

state). Tokens represent tasks or in this case, parts.

Tokens belong to places. Petri Net ‘places’ are of two

forms; task type queues (the rectangular elements in

‘Part Distributions’ on the top of Fig. 2) or the

resources or processors (which are the circular

elements on the bottom of Fig. 2 that are denoted as

‘Workcenters’). Events 𝚺

𝒊

are encoded with unique

integer keys and are executed as single asynchronous

or multiple synchronous state transitions (central in

Fig. 2 as ‘Routing Rules’ which are controlled events

𝚺

𝑪

exclusively; rules which we want the agent to

discover by searching through different firing

sequences). The complex relation between resources

and the tasks are indicated by the edges - defining a

holistic, irreducible system of rules. In this work, we

introduce a concept known as task transformation –

when a task or part leaves a process or resource via a

uncontrolled event 𝚺

𝑼

it is transformed or ‘re-

labelled’ by going into the subsequent task queue.

The set of 𝚺

𝑼

is not shown in the diagram Fig. 2.,

IN4PL 2021 - 2nd International Conference on Innovative Intelligent Industrial Production and Logistics

156

Figure 3: Trajectory Mutation; all represent state space in the vertical and time in the horizontal. On the left we show a purely

exploratory process, each trajectory is recorded, the highest relative performance (the elite trajectory) is shown by a red trace.

In the centre, we show the unexplored controlled events associated with the elite trajectory. By selecting, at random, elements

from this set of unexplored controlled events, we ‘branch off’ from the elite trajectory. On the right, we show these new

trajectories from their branching points in blue. The process is repeated iteratively.

since they are a mirror of the controlled events, with

this small variation only. In this way, a task persists

through as many intermediate states or sub-tasks as

required by the application, even where these

intermediary states have different processing

requirements. This inventive step was driven by the

complex modelling requirements inherent to the

highly flexible case study, and this contribution

exploits the procedural processes inherent to

hierarchical task decomposition.

2.2 Percepts & Inputs in DES

When the agent takes an observation of the real

system under control, tokens are initialised and

distributed into their respective places and any

anticipated uncontrolled events are added to the event

list to isomorphically represent the state. The concept

of future events being associated to the present state

is a further important contribution. A similar concept

is employed in continuous-time domain control as

systems of differential equations, since these too

allow the controller to delineate inputs by providing

data a predictive property.

2.3 Inferring Logically Feasible

Controlled Events

We use a process of deduction that exploits the

persistence of data (tokens) discussed in 2.2 so that

the compositionality of the process is retained.

Constructing only feasible trajectories from the initial

state exploits the explicit mapping between state and

possible events. Once the Petri Net is marked – i.e.

injected with state, the subset 𝚺





⊆ 𝚺



must

be discovered by applying propositions first,

followed by executing singular or combinations of

controlled events in a trial and error method. The

propositions are;

Proposition 1: No element in instances of the state or

marking vector, (i.e. the Petri Net values) can be less

than 0.

Proposition 2: The value of an integer in a resource

place cannot exceed the maximum task-capacity of

the respective resource.

Once discovered, elements in 𝚺





are

selected until the set 𝚺





becomes empty. This

means that over a given number of assignments, in-

process tasks are blocking the processing of out-of-

process tasks, or that the resources available cannot

process waiting tasks. In which case the system is in

an Invariant Behaviour (IB) state, in which

unmodelled, lower-level processes are observed.

The maximum branching factor of sequential

decisions is far smaller – one controlled event per

time step 𝚺





=1, in combination, the upper bound is

𝚺





𝚺

𝑪

−1. Although the blocking mechanism

will reduce this value significantly. The process of

discovering neighboring states through controlled

events is recursively repeated until the pre-defined

episode length is reached or the goal is completed –

i.e. tokens or processes have reached an acceptable

intermediate or finished state. The states which the

model passes through define the Behaviour

Permutation (𝑩𝑷) and respective Controlled Event

Permutation ( 𝑪𝑬𝑷 ) as a dimensional map or

permutation of selected controlled events. Together,

these define feasible trajectory over an episode of

time. This could also be called a policy, a plan, or

simply a schedule. This is because at each time

instance 𝒕, the system is fully defined - there is an

expected state 𝑩𝑷

𝒕

and control decision 𝑪𝑬𝑷

𝒕

. In

addition to these maps, we include a truth table or

bitmap 𝑪𝑬𝑷

𝑼

that records unexplored CEP

elements, shown centrally in Fig. 3. This is used in

the new algorithm discussed in 2.5. A number of

trajectories conceptually creates a complex tree

structure of branching time, where the initial state is

the root node, the trajectory a branch the final state is

the leaf node, shown at the left of Fig. 3.

Reconﬁgurable Scheduling as a Discrete-Event Process: Monte Carlo Tree Search in Industrial Manufacturing

157

Figure 4: Results; on the far left, we have the mean of individuals for each simulation step, where the CTRL is pure MCTS

shown in black. The other colours are various types of MCTS-ETL, with a 5, 10, 25 and 50 individual population types with

a two-term power curve fitting. Although MCTS has some optimisation capability as a result of sampling the space, MCTS-

ETL search outperformed MCTS in both discovery of the minimum makespan and the population average makespan. On the

right is the underlying data for the MCTS-ETL-POP:10 for each processor core.

2.4 Real-time Robust Control

There are many ways in which disruptive events

change the initial state input to the system – new

orders, order deletion, re-routings, changes in due

dates or random resource unavailability/breakdown,

errors in gathering state data and changes to futures

events [e.g. a resource is scheduled for maintenance

which is recorded as an anticipated event].

Any Disturbances or Are Reflected in the

Updating of the Initial State and/or an Adjustment to

the Event List Respectively. This Essentially Defines

a New Problem and Triggers an Entirely New Search

Process, but Because Trajectories Are Generated

Rapidly, the Claim for Real-Time System Control

Remains Intact. Further, Because Multiple Instances

of the DES Are Independent, and the Initial

Population Is Purely Exploratory, the Search May Be

Conducted using Parallel Processing, Increasing the

Speed of Rescheduling Dramatically.

2.5 Elitist Trajectory Mutation

A final contribution is the presentation of a simple

tabular metaheuristic inspired by ideas from

evolutionary computing called Elitist Trajectory

Mutation (ETM). Because each trajectory has an

inherent branch-like structure, any direct exploitation

of its information content must be maintained in order

to localise search and converge to near-optimal

makespan performance. This makes many highly

popular exploitation approaches, such as crossover in

Genetic Algorithms, non-sensical. Instead, the

mutation operator here is restricted to feasible, pre-

discovered mutations. The emphasis on a tabular or

memory-based approach is reflective of an overall

attempt to keep computational requirements low.

As shown in in Fig. 3 (left), the search process

hitherto described generates an initial population that

is purely exploratory by sampling the state space

generated by the TPN – a Monte-Carlo Tree Search

(MCTS). The highest performing trajectory (the elite

individual) is used as the phenotype. The sum of

unexplored controlled events of this individual is used

as the upper limit on a pseudo-random real-valued

integer, where the lower limit is 1. The integer

generated selects an element in 𝑪𝑬𝑷

𝑼

from this

individual’s map, selects the respective controlled

event (the mutation) and constructs a new trajectory

from that point, using MCTS as normal. This means

that every mutation is verified as feasible and

guarantees feasible trajectories are generated.

IN4PL 2021 - 2nd International Conference on Innovative Intelligent Industrial Production and Logistics

158

Figure 5: Industrial Informatics; in the top plot we have the schedule itself, 672 parts (tasks) comprised of 19200 processes

(sub-tasks) that are distributed over a period of 5x10

minutes; approximately 347 days on the 36 workcenters (resources).

Workcenter ‘WC:06’ shows exceptional utilization. Note that a continuous colour block indicates continuous processing.

Factory utilization varies significantly over the time period. Using a maximum partially processed sub-task volume limit of

30, there is a largely linear production rate shown in the lower two plots.

This process may be repeated using generation-based

populations or hill-climbing. Convergence to local

minima is avoided by selection of elements in 𝑪𝑬𝑷

𝑼

that are ‘early’ in the trajectory (thereby are in effect,

more exploratory), whilst ‘late’ elements mutations

are more exploitative. As shown in Fig. 4, in addition

to being attractively simple and computationally

cheap, we found this metaheuristic to converge

quickly and effectively in industrial test cases, far

exceeding the performance of purely exploratory

search alone.

ANALYSIS & DISCUSSIONS

The main difficulty is that DES model development,

verification and validation from knowledge is

exceptionally time-consuming. A software approach

to take a description to a working DES model would,

at a minimum, reduce development time and could

help avoid human modelling errors. Initial efforts

have been discussed in (Helliwell, Morgan, &

Mahfouf, 2021). It may be possible to reduce the

model’s computational complexity further by using

adjusting the number of significant figures used in

variables. In complex scheduling problems,

exploiting this imprecision could be a useful pre-

processing step. In a small set of cases where

‘scheduling problem’ or ‘scheduling machine’ is

defined as a DES, we believe some areas of state

space are unexplored by the naïve trajectory-

generation process used - we intend on covering these

cases in a short paper in future.

The makespan minimization approach is a single

objective; further detail could include adding more

costs or objectives, for instance, resource context

switching: apply a reward or punishment to the

complete system upon a change in state for a

resource. Complex or mixed utility functions as

programs or collections of terms, assigning credit to

occurrence of certain events at certain times,

cumulative rewards, rather than a closed-form single

or multiple scalar objectives (i.e. multi-objective)

seen in typical optimisation or reaching ‘goal states’

in planning.

Interval scheduling of industrial systems that have

choice, hidden information and high number of

dependencies lack a standard problem that could

facilitate benchmarking different approaches in

Reconﬁgurable Scheduling as a Discrete-Event Process: Monte Carlo Tree Search in Industrial Manufacturing

159

methodology, software architecture (including

memory structures and processes), programming

language choice, implementation into hardware

(including considering the trends in heterogeneous

and parallel computing) and algorithm design.

We see the next step in real-time manufacturing

operations control is the final type discussed by

(Ouelhadj & Petrovic, 2009); robust pro-active

scheduling, which attempt to integrate risk into

predictive models, essentially pre-empting the effects

of uncertainty and disruptions to minimise the effects

on performance measure – indeed, there are

significant possibilities in combining Uncertainty

Quantification (UQ) with global optimization of

industrial systems. Precalculation of schedules is

using the simulation models to consider unactualised

initial states, possible configurations that have not

been expressed by the system under control –

generating hypothetical scenarios in the form of

experiments to utilise unused computational

resources. For instance, the initial state could be

gathered from the CPS layer, followed by a random

generation of resource unavailability, variations in

delivery requirements, and variations of constraints.

The difficulty here is transferring the learning from

these cases into a flexible knowledge representation

that can help inform future searches rather than a

brittle tabulation or memoisation approach. We are

seeing similar ideas manifest in ML as self-supervised

learning and self-play.

Two aspects relate to the frameworks overall

computational intelligence; brute computation and

better algorithmic processes. It is challenging to

establish a clear relationship between the proposed

approach and ML approaches. Pre-trained black-box

metamodels have been recently explored in the

context of Deep Reinforcement Learning (DRL) by

(L. Hu et al., 2020), (Xia et al., 2020) and (H. Hu, Jia,

He, Fu, & Liu, 2020). The challenge is establishing

objectively just how reconfigurable these approaches

are and whether they can ensure a significant

generalisation capability, and if required, the training

or optimisation process is sufficiently

computationally demanding to conflict with real time

applications.

A further weakness in an ML approach is that the

model cannot be easily updated. In many industrial

applications, it is inevitable that the structure of the

controlled system is subject to variation (e.g. new part

or resource) and the configuration space defined is

therefore new. This would need a complete re-

training in the case of an ML approach. In the

proposed method, this would only require updating

the explicit Petri Net structure, whilst the scheduling

mechanism itself remains intact. Independence

between trajectories indicates this could be an

example of an Embarrassingly Parallel (EP)

[Processing] problem, in which case framework

deployment in multi-core CPU or Graphical

Processing Unit (GPU) would allow multiple DES

evolutions occurring in parallel, rapidly exploring

state space. In this research, we have successfully

used a multi-core approach, but believe that GPU will

be more performant.

In future work, we envisage probabilistic

approaches that integrates ML as a supportive ‘black-

box’ sub-system. The existing method operates as a

first operation that creates self-supervised, synthetic

data (of near-optimal trajectories) that can be used to

train a generalised function such as Artificial Neural

Network (ANN). The output of such a function would

weight the space of feasible actions (a policy) as a

secondary operation. This would enable faster-still

real-time control of those systems with high

branching factors (e.g. large DES models that express

high flexibility and high feasibility). Candidates that

have inspired such an approach include high-

performing online graph-based metaheuristics, such

as Ant Colony Optimisation (ACO).

4 CONCLUSIONS

In this paper we show how an extended TPN can be

used to define a computationally efficient MCTS

scheme for makespan minimisation of full-scale

industrial batch-scheduling problems. We show how

this can be extended into the ETM algorithm specific

to DES to localise search and optimisation.

ACKNOWLEDGEMENTS

The authors would like to acknowledge staff at Safran

Landing Systems, Gloucester and University of

Sheffield, Advanced Manufacturing Research Center

(AMRC), Sheffield in their support of this work and

the EPSRC Grant Number EP/L016257/1.

REFERENCES

Ambrogio, G., Guido, R., Palaia, D., & Filice, L. (2020).

Job shop scheduling model for a sustainable

manufacturing. Procedia Manufacturing, 42, 538–541.

https://doi.org/10.1016/j.promfg.2020.02.034

Baruwa, O. T., Piera, M. A., & Guasch, A. (2016).

TIMSPAT – Reachability graph search-based

IN4PL 2021 - 2nd International Conference on Innovative Intelligent Industrial Production and Logistics

160

optimization tool for colored Petri net-based

scheduling. Computers and Industrial Engineering,

101, 372–390.

https://doi.org/10.1016/j.cie.2016.07.031

Bertsekas, D. P., & Tsitsiklis, J. (1996). Neuro-Dynamic

Programming.

Brucker, P., & Schlie, R. (1990). Job-shop scheduling with

multi-purpose machines. Computing, 45(4), 369–375.

https://doi.org/10.1007/BF02238804

Bull, L. (2015). A brief history of learning classifier

systems: from CS-1 to XCS and its variants.

Evolutionary Intelligence, 8(2–3), 55–70.

https://doi.org/10.1007/s12065-015-0125-y

Butz, M. V. (2015). Learning classifier systems. Springer

Handbook of Computational Intelligence, (June), 961–

981. https://doi.org/10.1007/978-3-662-43505-2_47

Cao, T., & Sanderson, A. C. (1994). Task Decomposition

and Analysis of Robotic Assembly Task Plans Using

Petri Nets. IEEE Transactions on Industrial

Electronics, 41(6), 620–630.

https://doi.org/10.1109/41.334579

Chan, F. T. S., Bhagwat, R., & Chan, H. K. (2014). The

effect of responsiveness of the control-decision system

to the performance of FMS. Computers and Industrial

Engineering, 72(1), 32–42.

https://doi.org/10.1016/j.cie.2014.03.003

Charpentier, P., & Thomas, A. (2005). Reducing simulation

models for scheduling manufacturing facilities. 161,

111–125. https://doi.org/10.1016/j.ejor.2003.08.042

Chen, F. ., & Shukla, C. S. (1996). The state of the art in

intelligent real-time FMS control : a comprehensive

survey. Journal of Intelligent Manufacturing, 7, 441–

455.

Cheng, Y., Zhang, Y., Ji, P., Xu, W., Zhou, Z., & Tao, F.

(2018). Cyber-physical integration for moving digital

factories forward towards smart manufacturing: a

survey. International Journal of Advanced

Manufacturing Technology, 97(1–4), 1209–1221.

https://doi.org/10.1007/s00170-018-2001-2

Cowling, P., & Johansson, M. (2002). Using real time

information for effective dynamic scheduling. 139,

230–244.

Dietterich, T. G., & Zhang, W. (1995). A Reinforcement

Learning Approach to Job-shop Scheduling. Ijcai,

1114–1120. Retrieved from

http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.

1.1.8.3850&rep=rep1&type=pdf

Dvorak, F., Bartak, R., Bit-Monnot, A., Ingrand, F., &

Ghallab, M. (2014). Planning and Acting with

Temporal and Hierarchical Decomposition Models.

Proceedings - International Conference on Tools with

Artificial Intelligence, ICTAI, 2014-

Decem, 115–121.

https://doi.org/10.1109/ICTAI.2014.27

Feldt, J., Kourouklis, T., Kontny, H., & Wagenitz, A.

(2020). Digital twin: Revealing potentials of real-time

autonomous decisions at a manufacturing company.

Procedia CIRP, 88, 185–190.

https://doi.org/10.1016/j.procir.2020.05.033

Ferber, J. (1999). Multi-Agent System: An Introduction to

Distributed Artificial Intelligence.

Fujimoto, R. M. (2016). Research challenges in parallel and

distributed simulation. ACM Transactions on Modeling

and Computer Simulation, 26(4), 1–29.

https://doi.org/10.1145/2866577

Ghasemi, A., Azzouz, R., Laipple, G., Kabak, K. E., &

Heavey, C. (2020). Optimizing capacity allocation in

semiconductor manufacturing photolithography area –

Case study: Robert Bosch. Journal of Manufacturing

Systems, 54(November 2019), 123–137.

https://doi.org/10.1016/j.jmsy.2019.11.012

Helliwell, T. J., Morgan, B., & Mahfouf, M. (2021).

Searching & Generating Discrete-Event Systems.

Proceedings of the 18th International Conference on

Informatics in Control, Automation and Robotics,

ICINCO 2021, 203–210.

https://doi.org/10.5220/0010584302030210

Howard, R. A. (1960). Dynamic Programming and Markov

Processes.

Hu, H., Jia, X., He, Q., Fu, S., & Liu, K. (2020). Deep

reinforcement learning based AGVs real-time

scheduling with mixed rule for flexible shop floor in

industry 4.0. Computers and Industrial Engineering,

149(January), 106749.

https://doi.org/10.1016/j.cie.2020.106749

Hu, L., Liu, Z., Hu, W., Wang, Y., Tan, J., & Wu, F. (2020).

Petri-net-based dynamic scheduling of flexible

manufacturing system via deep reinforcement learning

with graph convolutional network. Journal of

Manufacturing Systems, 55(December 2019), 1–14.

https://doi.org/10.1016/j.jmsy.2020.02.004

Lee, J., Bagheri, B., & Kao, H. A. (2015). A Cyber-Physical

Systems architecture for Industry 4.0-based

manufacturing systems. Manufacturing Letters, 3, 18–

23. https://doi.org/10.1016/j.mfglet.2014.12.001

Li, X., Wang, L., Zhu, C., & Liu, Z. (2020). Framework for

manufacturing-tasks semantic modelling and

manufacturing-resource recommendation for digital

twin shop-floor. Journal of Manufacturing Systems,

(August), 0–1.

https://doi.org/10.1016/j.jmsy.2020.08.003

Luo, H., Fang, J., & Huang, G. Q. (2015). Real-time

scheduling for hybrid flowshop in ubiquitous

manufacturing environment. Computers and Industrial

Engineering, 84, 12–23.

https://doi.org/10.1016/j.cie.2014.09.019

Maccarthy, B. L., & Liu, J. (1993). Addressing the gap in

scheduling research: a review of optimization and

heuristic methods in production scheduling.

International Journal of Production Research, 31(2),

299–309. https://doi.org/10.1080/00207549308956726

Mejía, G., & Pereira, J. (2020). Multiobjective scheduling

algorithm for flexible manufacturing systems with Petri

nets. Journal of Manufacturing Systems, 54(January),

272–284. https://doi.org/10.1016/j.jmsy.2020.01.003

Moore, K. L., & Flann, N. S. (1999). Hierarchical task

decomposition approach to path planning and control

for an omni-directional autonomous mobile robot.

IEEE International Symposium on Intelligent Control -

Proceedings, 302–307.

https://doi.org/10.1109/isic.1999.796672

Reconﬁgurable Scheduling as a Discrete-Event Process: Monte Carlo Tree Search in Industrial Manufacturing

161

Negahban, A., & Smith, J. S. (2014). Simulation for

manufacturing system design and operation: Literature

review and analysis. Journal of Manufacturing

Systems, 33(2), 241–261.

https://doi.org/10.1016/j.jmsy.2013.12.007

Ouelhadj, D., & Petrovic, S. (2009). A survey of dynamic

scheduling in manufacturing systems. (October 2008),

417–431. https://doi.org/10.1007/s10951-008-0090-8

Oztemel, E., & Gursev, S. (2020). Literature review of

Industry 4.0 and related technologies. Journal of

Intelligent Manufacturing, 31(1), 127–182.

https://doi.org/10.1007/s10845-018-1433-8

Pellegrini, A., & Quaglia, F. (2017). A fine-grain time-

sharing Time Warp system. ACM Transactions on

Modeling and Computer Simulation, 27(2).

https://doi.org/10.1145/3013528

Ramadge, P. J. G., & Wonham, W. M. (1989). The control

of discrete event systems. Proceedings of the IEEE,

Vol. 77, pp. 81–98. https://doi.org/10.1109/5.21072

Romero-Silva, R., & Hernández-López, G. (2020). Shop-

floor scheduling as a competitive advantage: A study on

the relevance of cyber-physical systems in different

manufacturing contexts. International Journal of

Production Economics, 224(February 2018).

https://doi.org/10.1016/j.ijpe.2019.107555

Rossit, D. A., Tohmé, F., & Frutos, M. (2019). Industry 4.0:

Smart Scheduling. International Journal of Production

Research, 57(12), 3802–3813.

https://doi.org/10.1080/00207543.2018.1504248

Sepp, H., & Jurgen, S. (1997). Long Short-Term Memory.

Neural Computation, 9(8), 1–32.

Shiue, Y. R., Lee, K. C., & Su, C. T. (2018). Real-time

scheduling for a smart factory using a reinforcement

learning approach. Computers and Industrial

Engineering, (101), 0–1.

https://doi.org/10.1016/j.cie.2018.03.039

Sutton, R. . S., & Barto, A. G. (2018). Reinforcement

Learning: An Introduction (2nd Ed.). In MIT Press.

https://doi.org/10.1109/TNN.1998.712192

Tuncel, G., & Bayhan, G. M. (2007). Applications of Petri

nets in production scheduling : a review. 762–773.

https://doi.org/10.1007/s00170-006-0640-1

Urbanowicz, R. J., & Moore, J. H. (2009). Learning

Classifier Systems: A Complete Introduction, Review,

and Roadmap. Journal of Artificial Evolution and

Applications, 2009, 1–25.

https://doi.org/10.1155/2009/736398

Váncza, J., & Monostori, L. (2017). Cyber-physical

Manufacturing in the Light of Professor Kanji Ueda’s

Legacy. Procedia CIRP, 63, 631–638.

https://doi.org/10.1016/j.procir.2017.04.059

Wang, Q., Hao, Y., & Cao, J. (2020). ADRL: An attention-

based deep reinforcement learning framework for

knowledge graph reasoning. Knowledge-Based

Systems, 197, 105910.

https://doi.org/10.1016/j.knosys.2020.105910

Wooldridge, M. (2009). An Introduction to MultiAgent

Systems: Second Edition.

Xia, K., Sacco, C., Kirkpatrick, M., Saidy, C., Nguyen, L.,

Kircaliali, A., & Harik, R. (2020). A digital twin to train

deep reinforcement learning agent for smart

manufacturing plants: Environment, interfaces and

intelligence. Journal of Manufacturing Systems, (June),

1–21. https://doi.org/10.1016/j.jmsy.2020.06.012

Zeigler, Bernard P., Sarjoughian, H. S. (2013). Guide to

Modeling and Simulation of Systems of Systems.

IN4PL 2021 - 2nd International Conference on Innovative Intelligent Industrial Production and Logistics

162