A Method for Calculating the Flow and Sediment Distributions in the

Interactive Regions between the Channels and Plains of Compound

Channels

Zuwen Ji

and Yanxiang

Hou

State Key Laboratory of Simulation and Regulation of River Basin Water Cycle, China Institute of Water Resources and

Hydropower Research, Beijing, China, 100048

Keywords: Compound channels, Flow velocities, Sediment concentrations, Main channels, Flood plains

Abstract: In the present study, on the basis of the generalized experimental data of compound channels, and the regional

characteristics of flow and sediment movements, four regions were proposed according to the compound

sections of channels and plains. These included the undisturbed regions in the main channels; interactive

regions between the channels and the plains; undisturbed regions in the floodplains; and the boundary regions.

The interactive regions between the channels and plains, which were characterized by the most complicated

water flow regimes, were further divided into logarithmic flow velocity zones (inner zones) and non-

logarithmic flow velocity zones (outer zones). Then, by introducing an S-shaped curve, a method for

determining the boundary between the inner zones and outer zones was proposed. The water-sediment

exchange intensity in the interactive region is higher than that in other areas, so it is a key point in the study

of compound channel.

1 INTRODUCTION

Compound channels, which have obvious flood

plains and main channels in their sectional

morphology, are the most common pattern of

manifestation of alluvial rivers. In China, the lower

reaches of the Yellow River have the characteristics

of a typical compound channel. The main stream is

approximately 880 km in length and begins in

Mengjin County. The channel is mainly composed of

flood plains and a main channel. The flood plain area

is approximately 3,500 km

and accounts for 84% of

the total channel area (Hu et al., 2012). Under natural

conditions, due to the alluvial characteristics of the

channel, it has been observed that although the

compound channel maintains the pattern of channel

and plains areas in the section morphology, the

location of its main channel often moves. These

movements are often shown as swings of the channel

onto the plains. This type of swinging action not only

directly threatens the safety of the channel’s

regulation works, such as flood control dykes, but

also brings adverse effects to such industrial and

agricultural production processes as intake and

drainage utilities, flood plain utilization processes,

and so on (Zhang, 2017).

It has been accepted that the determination of the

laws of flow and sediment movements in compound

channels are very important problems in current

engineering practices. Also, the results of such studies

would be of great value in the theoretical

development of river dynamics. The theoretical

studies of flood plain flow structures can potentially

promote the development of river dynamics and lay

foundations for the study of the laws of flow and

sediment movements in compound channels. At the

present time, there are abundant research results

available regarding the characteristics of clear water

flow in channel-plain compound channels. These

studies have mainly included the flow capacities of

compound channels and the resistance characteristics

of channels and plains (Hang, 2016; Rhodes & Knight,

1994), as well as the flow structures and turbulence

intensities of channels and plains (Shiono & Knight,

1991; Tominaga & Nezu, 1991), flow velocities,

distribution characteristics of flood plains (Tominaga

& Nezu, 1991; Hu et al., 2010), and so on. Previously,

many research achievements were made in the study

of muddy water flow, which have mainly included the

134

Ji, Z. and Hou, Y.

A Method for Calculating the Flow and Sediment Distributions in the Interactive Regions between the Channels and Plains of Compound Channels.

In Proceedings of the 7th International Conference on Water Resource and Environment (WRE 2021), pages 134-139

ISBN: 978-989-758-560-9; ISSN: 1755-1315

sediment concentrations and distribution

characteristics of channels and plains (Hu et al., 2010;

Edmonds et al., 2017; Armugha et al., 2018), and the

sediment accumulations and distributions in channels

and plains of natural channels (Liu et al., 2016; Chen

et al., 1996; Ji et al., 2019). However, it was found

that in the existing study results, there have been only

a few studies conducted regarding the regional

characteristics of the sediment and water distributions

in the channels and plains of compound channels.

Therefore, based on the experimental data and

existing research results (Walling et al., 2015; Min et

al., 2017), this study focused on the interactive

regions of channels and plains, and proposed a

method of determining the boundaries between the

inner and outer zones, which would provide technical

support and theoretical guidance for the planning and

management of the plain areas of compound

channels.

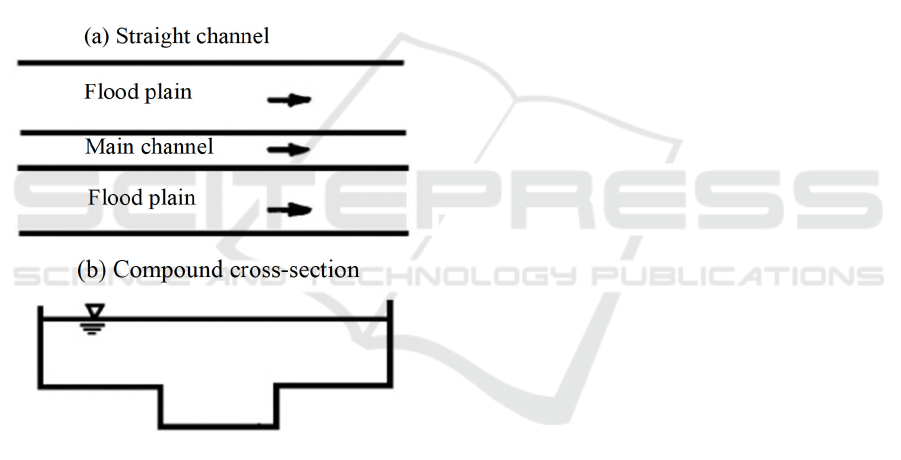
Figure 1: Structural form of the compound channel.

2 BASIC SITUATION OF THE

EXPERIMENTAL AREA

In a previous related study, the author performed a

large number of experiments regarding the

distributions of flow and sediment in the channel and

plain areas within a 30 m long self-circulating

channel (Hu et al., 2010; Ji et al., 2019). The self-

circulating plain consisted of a straight channel and

wide-narrow alternating channels, and its sections

were mainly rectangular sections. The beds of the

channel and plain areas had a height difference of

0.06, and the bed and side wall of the channel were

cement surfaces. The channel structure is shown in

Figure 1. In the experiment, sections were compound

rectangular sections, with the same widths as the main

channel and height differences from the channel and

plain areas.

During the experiment, the experimental water

depths had ranged between 0.03 and 0.13 m, and the

sediment concentrations had ranged from 4 to 83

kg/m

. Fly ash was used in the experiment as the

experimental model sand. The median particle sizes

of the experimental model sand ranged between 0.014

and 0.056 mm; the specific gravity was 2,100 kg/m

;

and the non-uniformity coefficient was between 1.73

and 2.12.

3 REGIONAL HARACTERISTICS

OF COMPOUND CHANNEL

Due to the height differences in the beds of the

different channels and plains of the compound

channel, the momentum transfers among the channel

and plain flows tended to be obvious. The flow

energy losses at the boundary areas of the channels

and plains were found to be larger, and the flow

capacities of compound channels had become

obviously smaller than those of single rectangular

channels of the same scale. According to the existing

research results, the distributions of the flow and

sediment in channels and plains had the following

characteristics:

(1) From the average flow velocities of the

channel and plain sections, it could be seen that the

average velocities of the main channels and the entire

sections of the compound channels first increased,

then decreased, and then increased once again with

the increases in the water depths. Meanwhile, the

average velocities of the plain areas tended to

increase monotonously with the increases in the water

depths. The average sediment concentrations of the

plain areas were less than the average sediment

concentrations of the main channels. The ratios of the

average sediment concentrations of the channel and

plain areas had increased with the increases in the

relative water depths of the channels and plains (Hu

et al., 2010).

(2) It could be seen from the average velocities in

the vertical direction that the lateral variations of the

velocity gradients near the boundaries between the

channels and the plains in compound channels tended

to be large. Also, water flow exchanges characterized

by strong momentum were observed between the

main channels and the plains. The peak values of the

A Method for Calculating the Flow and Sediment Distributions in the Interactive Regions between the Channels and Plains of Compound

Channels

135

momentum exchanges between the channels and the

plains had generally appeared near the boundaries

between the channels and the plains, and then had

gradually decreased toward both sides (Shiono et al.,

1991). It was found that when the channel and plain

areas were sufficiently wide, areas had existed where

the lateral velocity gradients tended to remain

constant in both the main channels and the plains. In

those areas, the flow had basically not been affected

by the momentum exchanges between the channels

and the plains. Moreover, interactive zones of the

channel and plain areas were evident between the two

regions, in which the lateral gradients of the flow

velocities had changed greatly, and the flow

movements had strong three-dimensional

characteristics. Correspondingly, the vertical mean

gradients of the sediment concentrations had tended

to gradually increase from the vicinities of the

boundaries between the channels and plains to both

sides of the channels and plains. The vertical

heterogeneity of the sediment concentrations in the

plain areas was found to be much greater than that of

the main channels, which had been observed to reach

minimal values near the boundaries of the channels

and plains, and then gradually increase toward both

sides of the channels and plains (Hu et al., 2010; Chen

et al., 1996).

(3) From the perspective of the vertical

distributions, the vertical velocity distributions of the

water flow far away from the boundaries of the

channels and plains and the boundary wall areas were

less deformed. However, in the areas near the

boundaries of the channels and plains, the vertical

velocity distributions tended to be more deformed.

The maximum velocities of the vertical velocity

distributions on one side of the main channel were

observed to be no longer at the surface of the water,

but at certain depth levels below the water surface. On

one side of the plain, the water velocities had

gradually increased from the bottom to the surface,

with the maximum velocities still observed on the

water surface. In addition, the vertical velocities at

certain depths from the bed surfaces had still obeyed

the logarithmic distributions. However, outside of

those ranges, the vertical velocities had tended to

deviate from the logarithmic distributions, and the

measured values on one side of main channel was

consistently smaller than the calculated value of

logarithmic formula. Also, the measured values on

the plain side was consistently larger than the

calculated value of formula. However, in the

transverse direction, the differences between the

measured values and calculated values of the flow

velocities had reached the maximums at the

boundaries of the channels and plains, and those

differences had then gradually decreased toward one

side of the main channel or plain. In the vertical

direction, the difference between the measured values

and the calculated values was zero at a certain water

depth from the bed surface and had gradually

increased in an upward direction to reach the

maximum near the water surface (Hu et al., 2010).

Therefore, from the aforementioned research

results regarding the flow and sediment movements

in a compound channel, it could be ascertained that

obvious regional characteristics had existed in the

sectional distributions.

4 DETERMINATIONS OF THE

INTERACTIVE ZONES IN

COMPOUND CHANNEL

4.1 Zoning of the Compound Sections

in Compound Channel

In the current study, in accordance with the

movement characteristics of the flow in the channels

and plains of a compound channel, a cross-section of

the flow of the compound channel was divided into

four regions as follows: 1. An undisturbed region of

the main channel (Region I); interactive region

between the channels and plains (Region II);

undisturbed region in the floodplains (Region III);

and a boundary region (Region IV), as detailed in

Figure 2. Moreover, the formula (Hu et al., 2010)

which was used for calculating the width of each

region is also presented in Figure 2. In the formula, h

represents the bed height differences of the channels

and plains; b

is the width at one side of main

channel in the interactive zone of the channels and

plains; b

is the width at one side of plain in the

interactive zone of the channels and plains; Z

I-II

indicates the transverse coordinates of the boundary

of the undisturbed region in the main channel and the

interactive region between the channels and plains;

II-III

is the transverse coordinates of the boundary of

the interactive region between the channel and plain

areas and the undisturbed region in the flood plain;

and Z

III-IV

indicates the transverse coordinates at the

boundary between the undisturbed region in the flood

plain and the boundary region.

In view of the regional characteristics of the flow

and sediment distributions in compound channels,

especially in the most critical interactive zones

between the channels and plains (Walling et al.,

2015), the interactive zone between the channels and

WRE 2021 - The International Conference on Water Resource and Environment

136

plains was further divided into a logarithmic velocity

zone (inner zone) and a non-logarithmic velocity zone

(outer zone). The boundary of those zones is indicated

by αH in Figure 3.

Figure 2: Schematic diagram for the sectional zoning of a

compound channel.

Figure 3: Schematic diagram for the velocity zoning in the

interactive zone between the channels and the plains of a

compound channel.

4.2 Determination of the Boundary

between the Inner and Outer Zones

in the Interactive Regions

In the present study, from the characteristics of the

vertical velocity distributions of the water flow, it

could be seen that the boundary between the inner and

outer zones of the channel-plain interaction zone was

basically an "S" type distribution (Walling et al.,

2015) in the main channel and plain areas. For that

reason, an S-type curve was introduced for the

purpose of demonstrating the boundary between the

inner and outer zones of the channel-plain interaction

zone (Hu et al., 2010; Liu et al., 2016; Chen et al.,

1996; Ji et al., 2019). The formula (Wang & Guo,

1979) was as follows:

M/(1+Nexp(-Cz))y =

)

Where M, N, and C are the undetermined

coefficients larger than 0, when z = 0 and y =

M/(1+N); and when it tends to be ∞, y = M. In order

to facilitate the analysis process, the coordinate

system was required to be appropriately transformed.

The origin of the coordinate system was shifted from

the middle position O of the main channel bed (Figure

2) to the peak O’ of the boundary of the channel and

plain areas (Figure 3). The coordinate variables were

then accordingly transformed from y and z to y' and

z'. After the coordinate system transformation was

completed, the curve fitting was carried out according

to the measured data of the main channel and plains,

respectively. Then, for any three observational values

(z1, y1), (z2, y2), and (z3, y3), the simultaneous

equations were obtained by substituting Formula (1),

respectively, and the following formula was obtained

by setting z2 = (z1+z3)/2:

()()

21 3 123 2 13

()

yy y yyy y yy=+− −2

)

After the estimated value of M was obtained,

Formula (1) was transposed and the following

formula was obtained after taking the natural

logarithm:

()

ln( ) ln

yy NCz−=−

)

Then, if was set, Formula (3) could be

transformed to a linear formula as follows:

lnyNCz=−

)

Therefore, the conformity of y and z to the

logistical equation (Zwillinger, 1997) can be obtained

by the correlation coefficient of and z:

yz yz y

SP SS SS

=⋅

)

The regression statistics N and C can then be

calculated using the following formula:

CSPSS−=

exp( )NyCx=+

)

Then, according to the above-mentioned linear

processing method, the data at the turning point of

one side of main channel at the boundary of Z

I-II

and

O', as well as at the boundary between the inner zone

and outer zone; or the data at the turning point at one

side of plain at the boundary O' and Z

II-III

, as well as

the boundary between the inner zone and outer zone,

respectively, which could be substituted into

(IV) (II I)

(II) (I)

ZI- I I

ZII-III

ZIII-IV

II I

bmc

bfp

A Method for Calculating the Flow and Sediment Distributions in the Interactive Regions between the Channels and Plains of Compound

Channels

137

Formulas (2) and (6), for the purpose of fitting and

calculating the M, N and C values. Therefore, the

formula for the calculation of the boundary between

the inner and outer zones of the interactive region of

the channel and plain areas could be successfully

obtained as follows:

For the main channel:

()

' 1.0046 1 99.4571exp 9.9877 '

fp mo

yH zb=+

bz−≤≤

)

For the plain areas:

()

' 1.0104 1 100.04171exp 9.1699 '

fp fo

yH zb=+ −

zb≤≤

(8)

Where b

and bmo represent the widths at one

side of main channel and plain in the interactive zone

of the channels and plains, respectively; H

is the

water depths of the plain areas; and y' and z' are the

vertical and lateral coordinates with the boundary

between the channels and plains as the center of the

circle. The fitting results of boundary of the

interactive zone between the main channels and

plains in the interactive zone of the channel and plain

areas are shown in Figure 4.

In combination with the results detailed in Figures

2 and 3, it could be seen that αH represented the

distance from the boundary between the inner and

outer zones of the channel and plain areas interactive

zone to the bed surface of the channel. As detailed in

the figures, one side of the main channel was

represented by αH = h

+y', and so on. The sizes of the

boundary values of the inner and outer zones could

then be expressed using the following formula:

()

mc d mc

yh H

bz−≤≤

)

Where H

indicates the water depth in the main

channel and is y' in the calculation results of Formula

(7). For the plain areas, the sizes of the values of

boundary between the inner and outer zones could be

calculated using the following formula:

fp fp

zb≤≤

(10)

Where y' is calculated according to Formula (8).

Figure 4: Comparisons between the calculated and

measured values of the boundary between the inner and

outer zones of the interactive zone of the channel and plain

areas.

5 CONCLUSIONS

The flow and sediment movements of the channels

and plains in the examined compound channel had

displayed obvious regional characteristics. Therefore,

in accordance with those observed characteristics, the

compound sections of the channels and plains could

be divided into the following: An undisturbed region

in the main channel; interactive region of the channels

and plains; undisturbed region in the flood plain; and

the boundary wall region. The interactive region of

the channels and plains which had best reflected the

flow and sediment distribution characteristics of the

channels and plains included the logarithmic velocity

zone (inner zone) and the non-logarithmic velocity

zone (outer zone). It was found that the vertical

distributions of the water flow in the inner zone had

followed the logarithmic velocity formula. Also, the

velocity of water flow on the side of the main channel

in the outer zone was observed to be lower than the

WRE 2021 - The International Conference on Water Resource and Environment

138

calculation results of the logarithmic formula, while

that on the side of the plain area was found to be larger

than the calculation results of the logarithmic

formula. Therefore, based on these findings, the

boundary between the inner zone and the outer zone

had been successfully determined in this study. Then,

by introducing an S-shaped curve, the calculation

formula of the boundary was deduced, which

provided a clear basis for the control and management

of the channel and plain areas.

This study’s analysis results of the different zones

indicated that the interactive zone of the channels and

plains should be considered as the key point for the

regulation and management of a compound channel.

ACKNOWLEDGEMENTS

It was supported by the National natural science

foundation of China(grant No. 51879282) and the

National Key Research and Development Program of

China (grant No.2017YFC0405501) and Technology

Project of Power China (grant No. DJ-PTZX-2019-

05) and the Open Research Fund of State Key

Laboratory of Simulation and Regulation of Water

Cycle in River Basin, China Institute of Water

Resources and Hydropower Research(grant No.

SKL2018ZY07).

REFERENCES

Armugha, K., Liaqat, A. K. R., Ali, P. Y., & Himanshu, G.

(2018). Characterization of channel planform features

and sinuosity indices in parts of Yamuna River flood

plain using remote sensing and GIS techniques.

Arabian Journal of Geosciences, 11(17), 1-11.

Chen, L. Zheng, Y. Z., & Zhou, Y. L. (1996). Commutative

form and function between water and sediment of silt

laden flow in compound channel. Journal of Sediment

Research, 1996(2), 45-49.

Edmonds, D. A., Moron, S., & Amos, K. (2017). The role

of floodplain width and alluvial bar growth as a

precursor for the formation of anabranching rivers.

Geomorphology, 278(1), 78-90.

Hu, C. H., Chen, J. G., and Guo, Q. C. (2012). Shaping and

maintaining a medium-sized main channel in the Lower

Yellow River. International Journal of Sediment

Research, 27(3), 259–270.

Hang, Y. F. (2016). Impact on composite roughness by

cross-section morphology of compound channel. Port

and Waterway Engineering, 2016(8), 94-98.

Hu, C. H., & Ji Z. W., & Guo, Q. C. (2010). Flow

movement and sediment transport in compound

channels. Journal of Hydraulic Research, 48(1), 23-32.

Ji, Z. W., Hu, C. H., & Zhao, X. (2019). Characteristics of

water and sediment distribution in the lotus-root-shape

compound channels. Proceedings of the 38TH IAHR

World Congress-IAHR (Panama), 307-314.

Liu, C., Shan, Y. Q., Liu, X. N.,Yang, K. J., & Liao, H. S.

(2016). The effect of floodplain grass on the flow

characteristics of meandering compound channels.

Journal of Hydrology, 542, 1-17.

Min, Z., He, Q. H., Carling, P. A., & Zhang, M. W. (2017).

Sedimentation of overbank floods in the confined

complex channel–floodplain system of the Lower

Yellow River. Hydrological Processes, 31(20), 3472–

3488.

Rhodes, D. G., & Knight, D. W. (1994). Velocity and

boundary shear in a wide compound duct. Journal of

Hydraulic Research, 1994(5), 743-764.

Shiono, K., & Knight, D. W. (1991). Turbulent open-

channel flows with variable depth across the channel.

Journal of Fluid Mechanics, 222(1), 617-646.

Tominaga, A., & Nezu, L. (1991). Turbulent structure in

compound open-channel flow. Journal of Hydraulic

Engineering, 117(1), 21-41.

Walling, D. E., Owens, P. N., & Leeks, G. J. L. (2015).

Rates of contemporary overbank sedimentation and

sediment storage on the floodplains of the main channel

systems of the Yorkshire Ouse and River. Tweed

Hydrological Processes, 13(7), 993-1009.

Wang, Z. X., & Guo, D. R. (1979).

Introduction to Special

Functions. Beijing: Science Press.

Zwillinger, D. (1997). Handbook of Differential Equations.

New York: Acdemic Press.

Zhang, J. L. (2017). Reconstruction and Ecological

Management of the Lower Yellow River. Floodplain

Yellow River, 39(6), 24-27.

A Method for Calculating the Flow and Sediment Distributions in the Interactive Regions between the Channels and Plains of Compound

Channels

139