
Optimization of Hydropower Reservoir System Operations based on
Improved CSO-PSO
Jun Hou
1*
, Heng Zhou
1
and Guangdong Wu
2
1
Upper Changjiang river Bureau of Hydrological and Water Resources Survery, Chongqing,400020, China
2
Changjiang River Scientific Research Institute of Changjiang Water Resources Commission, Wuhan, Hubei 430010, China
Keywords: The chicken swarm algorithm, Particle swarm optimization, Improved chicken swarm optimization with
particle swarm optimization, Optimization of hydropower reservoir system operations, Convergence speed
Abstract: The chicken swarm optimization is a fresh swarm intelligence algorithm that simulates the hierarchical system
and foraging behavior in the chick group. Compared with the traditional intelligent algorithm, it has better
convergence performance. In the process of operation, it is found that the convergence speed of traditional
algorithm is very slow and readily falls into the local optimal solution,,and it is extremly difficult to obtain
the global optimal solution, which makes the calculation process more prone to blindness. Based on the
blindness in the optimization process of the chicken swarm algorithm, a particle swarm optimization and
improved chicken swarm optimization (ICSO-PSO) algorithm is proposed in this paper. The particle swarm
optimization (PSO) algorithm is introduced in the update process of the rooster position. Based on the optimal
operation model of Hydropower Reservoir System, the ICSO-PSO algorithm is used to optimize the
hydropower reservoir system operation problem. Analyze different optimization algorithms through case
studies, the applicability of the optimization of hydropower reservoir system operations based on improved
CSO-PSO is demonstrated to be effective.
1 INTRODUCTION
Reservoir operation is the process of adjusting the
water balance relationship and redistributing the
inflow runoff under the system considering the
scheduling objectives of flood control, irrigation,
power generation, water supply and related
constraints (
Duan, 2014), to guarantee the safety of the
dam of reservoirs and auxiliary facilities. Optimal
dispatch is superior to conventional dispatch in
dealing with difficult problems in reservoir
dispatching (
Zhang, 2005). Reservoir optimal
dispatching is to establish single-objective or multi-
objective dispatching rules for reservoir operation,
optimize the boundary conditions of reservoir
operation, and maximize the benefit of reservoir
dispatching operation objectives.
With the continuous advancement of science and
technology, a variety of optimization models have
been formed, which have gradually been used in
reservoir dispatching. The main optimization
algorithms include linear programming, dynamic
programming, and bionic population intelligence
algorithms (
Wang et al., 2009). Among them, the
biomimetic population intelligent algorithm is a new
type of intelligent optimization algorithm that
simulates the living habits and natural survival rules
of biological groups. In 2014, Meng Xianbing et al
(2014) proposed a population intelligence
optimization algorithm, CSO algorithm, which
achieved good optimization results by grouping and
updating the population based on the foraging
behavior of chicken swarm, and it has been applied in
some fields. Banerjee and Chattopadhyay
(2015) used
the CSO algorithm to improve the serial concatenated
convolutional Turbo code. Kong and Wu
(2015)
studied the chicken position update formula by
quoting the learning factor in the Chicken swarm
optimization, thus it has been demonstrated that this
algorithm is superior to other optimization algorithms
in solving high-dimensional optimization problems.
Hafez et al.
(2016) took the CSO algorithm as part of
the evaluation function and proposed a feature
selection system and applied it to the data set. In 2016,
Chen and Mao
(2016) applied the CSO algorithm to
the wireless sensor network node localization
algorithm and achieved good location accuracy. Mu
et al.
(Mu et al., 2016) applied the CSO algorithm to
optimizing the robot's movement trajectory in 2016.
Hou, J., Zhou, H. and Wu, G.
Optimization of Hydropower Reser voir System Operations based on Improved CSO-PSO.
In Proceedings of the 7th International Conference on Water Resource and Environment (WRE 2021), pages 189-195
ISBN: 978-989-758-560-9; ISSN: 1755-1315
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
189

In actual optimization problems, the solution
update method of the CSO algorithm is relatively
simple, which sometimes causes the solution process
to fall into a local optimum, which affects the solution
accuracy and convergence speed. Therefore, while
continuously improving the CSO algorithm, it has
become the focus of research to enable it to have
better optimization capabilities. Wu et al.
(2018)
introduced the crossover operator to the improvement
of the CSO algorithm when applying the CSO
algorithm to the optimization of reentry trajectory,
thereby solving the problem that the algorithm easily
plunges into local optimality. Wei and Chi
(2017) cited
the dissipative structure in the CSO algorithm, and the
global optimization capability and convergence speed
of the original chicken swarm algorithm have been
significantly improved
Therefore, an algorithm called ICSO-PSO has
been proposed, which combines the advantages of the
Chicken Swarm Optimization and Particle Swarm
Optimization (PSO) algorithm
(Li, 2009). The
improvement of cock’s update method in the previous
CSO algorithm leads to improving the solution
accuracy and convergence speed of the algorithm.
This paper applied the ICSO-PSO algorithm to the
reservoir operation optimization, the feasibility and
effectiveness of the ICSO-PSO algorithm is further
demonstrated.
2 PROBLEM FORMULATION
2.1 Basic Principles of Chicken Swarm
Optimization Algorithm
The CSO algorithm is presented based on the research
on chicken swarm hierarchy and foraging behavior
(
Zhang & Zhang. 2018). When solving the problem, the
chicken swarm is compartmentalized into several
groups according to the fitness of each chicken in the
swarm, and each group is comprised hens, roosters
and chicks. With the three different groups of chicks,
the dominance relationship in the chicken group is
updated every G generation. Everyone in the
algorithm is represented as a feasible solution to the
problem. The three groups of hens, roosters and
chicks are searched in the solution space in their own
way. By comprehensively comparing the fitness
values of these groups of hens, roosters and chicks,
the global optimal individual and global optimal
value can be found. Among them, the foraging
method of the chicks is following the hen, and the
foraging method of the hen is to follow the rooster, so
the rooster plays a leading role in the foraging of the
entire chicken swarm. Correspondingly, the
advantage of the rooster is greatest in the foraging
competition, followed by the hen, and the most
disadvantaged is the chick, so the hen protects its own
chicks who live together. The fitness value of the
object function to its location represents the superior
performance of each chicken in the swarm.
At the same time, the entire chicken swarm is
classified by the fitness value of the function, and the
problem optimal solution to be optimized is
represented by the spatial position of the best
individual in the chicken swarm. Suppose the
foraging range is D-dimensions, the chicken swarm is
G groups (randomly divided), and each group
contains N chickens. Among them, the rooster
number is R, the hen number is H, and the chick
number is M (
Hafez et al., 2016). The mathematical
expression is as follows:
(1) Rooster's foraging behavior
For roosters, those with higher fitness values have
a larger food search space than those with lower
fitness values. The position update equation of the
rooster i in dimension j at time t is as follows:
x
,
x
,
1N
0,σ
(1)
σ
1, if f
f
exp
,otherwise
k∈
1,N
,ki
(2)
Where N
0,σ
is a Normal distribution with
mean 0 and standard deviation σ
. k i s a r o o s t e r ’ s
index, which is randomly selected from the rooters
group (k≠i). f is the objective function value. ε is the
constant smallest in the computer, and its function is
to avoid the denominator in the formula being 0.
Equations (1) and (2) simulate the rooster's
random moving foraging behavior and the
competition behavior between different groups of
roosters, respectively.
(2) Foraging behavior of hens
For hens, they usually follow their spouse's
rooster to forage, but the other side of the shield, they
also randomly steal food from other chickens. This
process is in competition with other chickens. In
addition, stronger hens have an advantage over
weaker hens in grabbing food. The position update
equation of the hen i in dimension j at time t is as
follows:
x
,
x
,
S
Rndx
,
x
,
S
Rnd
x
,
x
,
(3)
WRE 2021 - The International Conference on Water Resource and Environment
190

S
expf
f
abs
f
ε
⁄
(4)
S
expf
f
(5)
where Rnd is a random number over [0,1], r
is a
rooster index, which is the i-th hen’s group-mate, at
the same time, r
is a chicken index (rooster or hen),
which is randomly selected from the swarm, and the
foraging ability of r
is stronger than that of hen i.
r
r
. Therefore, S
<1<S
, when S
=0, hen i
can only steal food from other chicks, and when S
=0,
hen i will forage within its own territory.
(3) Foraging behavior of chicks
For chicks, they will hunt around their mothers for
food. The position update equation of the chick i in
dimension j at time t is as follows:
x
,
x
,
Fx
,
x
,
(6)
where m is the hen followed by the i-th chick, F (F ∈
0,2
) is a parameter, which means that the chick
would follow its mother to forage for food.
2.2 The ICSO-PSO
In the operation of the algorithm, it is founded that the
traditional chicken swarm algorithm converges
slowly, and it readily caught in a local solution, and it
is difficult to gain the overall optimal solution.
Therefore, in order to obtain the overall optimal
solution, the PSO algorithm is introduced (
Shi, 2018)
The ICSO-PSO algorithm uses the PSO algorithm
to optimize and improve the rooster position update
formula in the CSO algorithm. Roosters are the
dominant group within the groups, and they are closer
to the position of the optimal solution. However, in
the standard CSO algorithm, the rooster adopts the
position update method based on the normal
distribution, so that the position update of the rooster
only changes in the same direction, and it is difficult
to fluctuate left and right. Therefore, the method of
updating the position based on the normal distribution
has certain advantages. The blindness of the
algorithm reduces the convergence speed of the
algorithm. To solve this problem, this paper proposes
the location update method of PSO algorithm to
improve the search breadth of rooster in CSO
algorithm. The improved position update formula of
the rooster is as follows:
x
,
x
,
v
,
(7)
v
,
wv
,
r
Rndp
x
,
r
Rndg
x
,
(8)
where v
,
is the velocity of hen i in dimension j at
time t.; p
and g
respectively denotes the
personal best position and the global best position in
the iterative process of the algorithm; r
and r
are
the learning factors. w is the inertia weight.
3 RESERVOIR OPTIMAL
DISPATCH BASED ON
IMPROVED CHICKEN SWARM
OPTIMIZATION
During the flood season, the dispatch of hydropower
stations essentially involves two aspects, namely
flood control and power generation. The flood
characteristics, regional composition and actual flood
control requirements and reservoir engineering
storage and discharge control capabilities should be
comprehensively considered, and the conflicts
between flood control and power generation, flood
control safety and economic benefits should be
properly handled. When the flood is small and
ensuring safety, the focus of reservoir operation
should be to maximize the power generation. When
floods are large and a large amount of flood discharge
and water discards are inevitable, flood control
dispatching is the main focus, followed by power
generation.
When there is large flood, the optimal dispatching
of hydropower stations focuses on improving the
utilization rate of water, thereby increasing the power
generation of the reservoir and reducing the amount
of water discarded by the reservoir. That is, in the case
of satisfying all constraint conditions, maximize the
target benefit of the reservoir operation.
3.1 Objective Function
Reservoir scheduling involves solving the unit
commitment problems. The problem is more
complicated, and supplementary conditions are
needed. The corresponding optimization problem can
be delivered as:
OBJ : Emax
∑
kQ
H
∆t
(9)
where
E
is the maximum power generation,
k
is
the comprehensive output coefficient of the
hydropower station,Q
is the generation flow of the
Optimization of Hydropower Reservoir System Operations based on Improved CSO-PSO
191

period
t
, t is the calculation period,
T
i s t h e
total hours of the calculation period.
3.2 Constraints
(1) Water Balance Equation
V
∆
V
Q
Q
Q
Q
∆t (10)
where V
∆
a n d V
respectively represent the
storage capacity of the reservoir at time t+∆t and t,
Q
represents the inflow flow of the reservoir during
the period ∆t , Q
represents the diversion flow
between the reservoirs, Q
shows the power
generation flow of the reservoir. Q
represents the
abandoned reservoir water flow.
(2) Flow Constraint
Q
Q
Q
(11)
where Q
shows the outflow of the reservoir in the
period ∆t, ; Q
and Q
respectively represent
the minimum discharge flow and the maximum
discharge flow.
(3) Water Level Constraint
Z
Z
Z
(12)
where Z
is water level of the reservoir at the end of
time t, Z
and Z
respectively represent the
lowest and highest water levels that the reservoir is
allowed to reach at time t after considering the benefit
and safety needs.
(4) Output Constraint
N
N
N
(13)
where N
is the average output of the hydropower
station in the period t, N
is the minimum
allowable output of the hydropower station, N
is
the maximum allowable output of the hydropower
station.
3.3 Optimization Model Solving Steps
The method of referencing the ICSO-PSO algorithm
to solve the problem in the optimal operation of the
reservoir is:
(1) Population Initialization
Set the reservoir water level Z
z
,z
,⋯,z
corresponding to the reservoir at the end of each
period as the position of each chicken in the T-
dimensional foraging space x
x
,x
,⋯,x
.
T i s t h e D in the text. Combining with the water
level constraint conditions, select the corresponding
value for the initial position of each chicken
according to formula (14), and assign the number of
iteration t to 0. which is
x
,
x
Rndx
x
(14)
where x
,
is the initial position of the i-th
chicken in dimension j, x
an d x
are the
upper and lower bounds of the j-th dimension of the
foraging space, namely the water level Z
a n d
Z
values of the power station.
(2) Classification Of Chicken Swarm
Randomly divide the chicken swarm obtained by
initialization in step (1) into G group, and calculate
the fitness value f
x
according to the position
of each chicken in each group, and classify each
group of chickens based on it. Among them, the
chickens with the best fitness value are classified as
roosters, the relatively weakest chickens are classified
as chicks, and the others are classified as hens.
(3) Chicken Swarm Foraging
In the swarm, each rooster forages according to
formula (1) and formula (7), each hen forages
according to formula (3), and each chick forages
according to formula (6), so that the position is
updated.
(4) Swarm Update
According to the updated position of each chicken
in the swarm, the fitness value f
x
corresponding to this position is calculated, use it as
a basis to classify each group of chickens again the
same as step (2) division method. Remember the
number of iterations as t=t+1
(5) Termination of Judgment
If it is satisfied that the iterations number t
reaches the maximum maxgen, or the fitness value
absf
f
ε corresponding to the best
chicken in the swarm, then terminate the iteration and
go to (6) ; otherwise, go to (3) and loop iteratively.
(6) Output Result
Output the location of the optimal chicken and the
corresponding fitness value, which is the reservoir
water level value Z
z
,z
,⋯,z
and the
corresponding maximum power generation at the end
of each period of the reservoir.
4 OPTIMIZED SCHEDULING
INSTANCE CALCULATION
4.1 Basic Information of Reservoir
Operation
In this paper, a comprehensive annual regulating
WRE 2021 - The International Conference on Water Resource and Environment
192

reservoir is selected as the research object, and the
inflow process line of the reservoir, the water level
storage capacity and the downstream water level and
flow relationship of the reservoir are all known. The
normal storage level of the reservoir is 160.00m, the
minimum is 136.00m, and the limit is 155.00m; the
installed capacity is 320,000 kW, the designed
guaranteed power output is 125,000 kW, and the
comprehensive power output coefficient is 8.5.
Optimize the water level of the reservoir at the end of
each month to optimize the power generation during
the operation period. Operating environment:
Microsoft Visual Basic 6.0.
4.2 Analysis of Optimization Results
In order to reasonably verify the effectiveness and
feasibility of the ICSO-PSO algorithm, a relatively
common dynamic programming algorithm (DP) (
Li,
2016)
was selected to optimize the operation of the
reservoir, and the optimization effects of the two were
compared. The algorithm parameters are set as
follows: Discrete the feasible region of DP water level
by 1000 points; In ICSO-PSO, 10 groups of chickens
are selected, the number of chickens in each group N
is 1000, the rooster number is 0.3N, the hen number
is 0.6N, and the chick number is 0.1N, and F is a
random number in the interval [0, 2]. In addition, the
learning factor r
= r
=1.49445; w
.
;
when the scheduling goal and related constraints are
the same, the maximum number of iterations
(maxgen) is assigned 100 times, and then repeatedly
test 10 times independently. The result of ICSO-PSO
optimization algorithm is randomly selected once for
detailed analysis, showing in Table 1~3 and Figure
1~2.
Table 1: Comparison of discharge flow and downstream irrigation and shipping water between two optimization algorithms
time
downstream
irrigation and
shipping water
/
(
m³/s
)
ICSO-PSO DP
discharge
flow/(m³/s)
difference
/(m³/s)
discharge flow
/(m³/s)
difference
/(m³/s)
novembe
r
204.82 200.09 0.09 200 4.82
decembe
r
201.69 204.96 4.96 200 1.69
januar
y
205.3 201.09 1.09 200 5.3
februar
y
204.74 203.83 3.83 200 4.74
march
202.95 202.37 2.37 200 2.95
a
p
ril
322.06 322.33 2.33 320 2.06
ma
y
442.43 440.13 0.13 440 2.43
j
une
360.38 360.35 0.35 360 0.38
jul
y
302.34 306.56 6.56 300 2.34
au
g
ust
346.59 344.69 84.69 260 86.59
septembe
r
393.7 400.6 160.6 240 153.7
octobe
r
350 350 150 200 150
It can be seen from Table 1 that this optimization
algorithm can meet the water demand of downstream
irrigation and shipping, and for the discharge, both
optimization algorithms are feasible.
Table 2: Power Generation Analysis of Two Optimization Algorithms
time
ICSO-PSO DP
ICSO-PSO is better than DP
algorithm's power ratio /(%)
power generation / (million
kWꞏh)
power generation / ( million
kWꞏh)
novembe
r
117.77 120.45 -2.22
decembe
r
117.81 115.89 1.66
j
anuar
y
111.92 114.10 -1.91
februar
y
108.72 109.00 -0.26
march 102.65 102.64 0.01
april 154.12 153.32 0.52
ma
y
206.53 206.53 0.00
june 173.82 172.84 0.57
j
ul
y
159.69 157.07 1.67
Optimization of Hydropower Reservoir System Operations based on Improved CSO-PSO
193
august 193.61 194.41 -0.41
se
p
tembe
r
232.52 228.41 1.80
octobe
r
205.48 205.48 0.00
y
ea
r
1884.64 1880.14 0.24
It can be seen from Table 2 that the power
generation dispatched by the ICSO-PSO optimization
algorithm for four months is lower than that of the DP
optimization algorithm, and six months is higher, two
months is equal, but the annual power generation
capacity dispatched by the ICSO-PSO optimization
algorithm is better than the DP optimization
algorithm, generating 0.24% more.
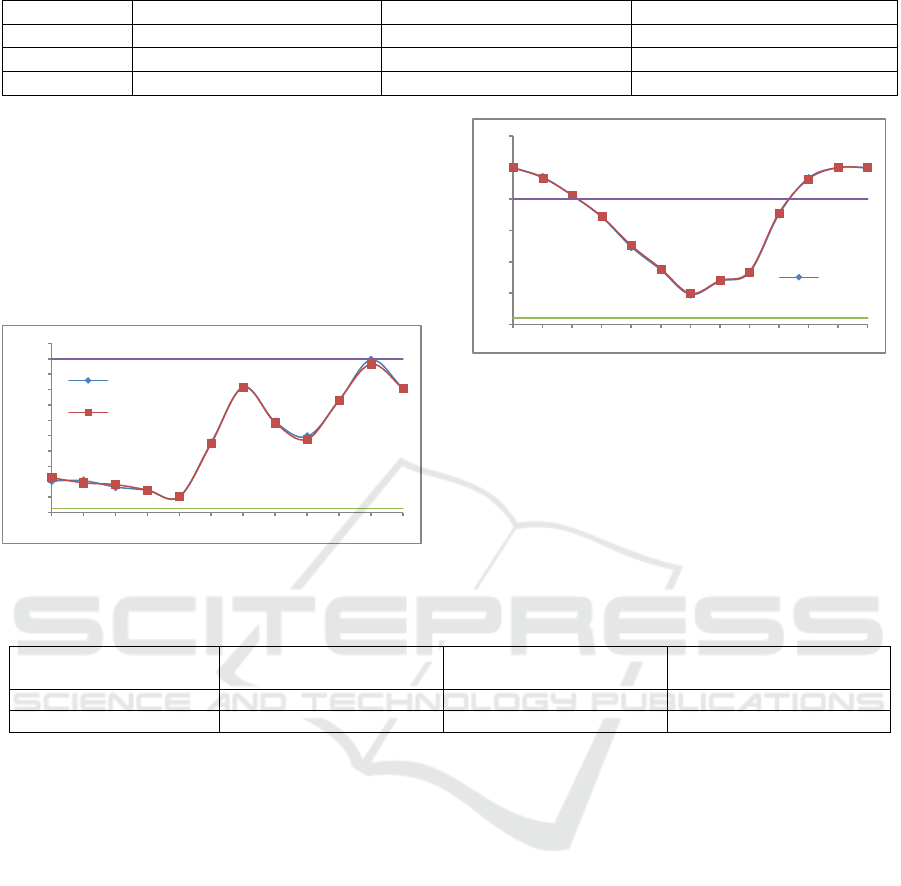
Figure 1: Comparison of the output of two optimal dispatch.
Figure 2: The dispatching process of two optimization
algorithms
Note: The scheduling sequence number starts from
November and ends in October of the following year.
It can be shown from Figure 1 that both
optimization algorithm could meet the power output
requirements of the power plant. For power output,
both optimization algorithms are feasible.
Table 3: Comparison of two optimization algorithms.
algorithm test count
maximum power
g
eneration
/
(
million kWꞏh
)
average power generation/
(
million kWꞏh
)
DP
——
1880.15
——
ICSO-PSO 10 1884.48 1882.67
It can be shown from Table 3 that the ICSO-PSO
algorithm optimized dispatching is 2.49 million kWꞏh
more than the DP. Obviously, the ICSO-PSO
algorithm is better than DP. It can be seen from Table
1~3 and Figure 1~2 that the ICSO-PSO algorithm has
better optimization results , that is, the algorithm has
good optimization performance when dealing with
the optimization operation of the reservoir, so it is
feasible to use the ICSO-PSO algorithm to solve the
optimization operation of the reservoir; and in the
simulation optimization process, it is found that the
ICSO-PSO algorithm prevents the premature
phenomenon of the original algorithm due to the
blindness of location update during the optimization
process.
5 CONCLUSION
This paper combines the original chicken swarm
algorithm with the particle swarm algorithm and
presents an improved chicken swarm algorithm
(ICSO-PSO), which introduces a corresponding PSO
optimization algorithm for the rooster position update
method. It strengthens the role of the leader in the
optimization process, improves the calculation
efficiency, solves the problem of dimension disaster
and locally optimal solution, reduces the blindness of
the optimization process, and improves the
convergence rate in the optimization process. By
comparing with the DP optimization algorithm, the
ICSO-PSO optimization results are better. Therefore,
the ICSO-PSO can be used as an effective tool for
solving optimization problems.
REFERENCES
Banerjee, S., & Chattopadhyay, S. (2015). Improved
serially concatenated convolution turbo code (SCCTC)
using chicken swarm optimization. IEEE Power
0,12
0,14
0,16
0,18
0,20
0,22
0,24
0,26
0,28
0,30
0,32
0,34
123456789101112
poweroutput/(millionkW)
theschedulingsequencenumber
ICSO‐PSO
DP
135
140
145
150
155
160
165
12345678910111213
waterlevel/m
theschedulingsequencenumber
ICSO‐PSO
WRE 2021 - The International Conference on Water Resource and Environment
194

Communication and Information Technology
Conference (PCITC), Bhubaneswar, India.
Chen, P., & Mao, Y. (2016). Wireless sensor network node
localization algorithm based on chicken swarm
optimization and multi-power mobile anchor. The 3rd
International Conference on Materials Engineering,
Manufacturing Technology and Control, Taiyuan,
China.
Duan, Y. H. (2014). Research on Scheduling Optimization
run of small cascade Hydropower Stations. Zhengzhou:
Zhengzhou University.
Hafez, A. I., Zawbaa, H.M., & Emary, E. (2016). An
innovative approach for feature selection based on
chicken swarm optimization. IEEE International
Conference on Soft Computing & Pattern Recognition,
Tokyo, Japan.
Kong, F., & Wu, D. H. (2015). An Improved Chicken
Swarm Optimization Algorithm. Journal of Jiangnan
University: Natural Science Edition, 14(6), 681-688.
Li, J. Z. (2009). Research On Particle Swarm Optimization
Algorithm. CD Technology, 6, 25+34+41.
Li, Y. Y. (2016). Study on Long-term Optimal Scheduling
and Combined Dispatching Chart of Cascade
Hydropower Stations. Wuhan: Huazhong University of
Science & Technology.
Meng, X., Liu, Y., & Gao, X. (2014). A New Bio-inspired
Algorithm:Chicken Swarm Optimization. Berlin:
Springer International Publishing.
Mu, Y., Zhang, L., & Chen, X. (2016). Optimal trajectory
planning for robotic manipulators using chicken swarm
optimization. IEEE International Conference on
Intelligent Human-machine Systems & Cybernetics,
Chengdu, China.
Shi, X. D. (2018). Research of Intelligence Algorithm Based
Particle Swarm Optimization and Swarm Optimization.
Yinchuan: Ningxia University.Zhang, J. J. (2005).
Present Situation of Study on Real-time control of
Reservior Group and Ways of Solving Related
Problems. Jilin Water Resources, 10, 34-36.
Wang, G. L., Liang, G. H., & Peng, Y. (2009). Model of
Flood Control Operation of Reservior Based on Particle
Swarm Optimization Algorithm and Its Application.
Water Resources and Power, 1, 74-76.
Wei, Y. M., & Chi, L. M. (2017). Application of Dissipation
Chicken Swarm Optimization in Reservoir Optimal
Operation. Water Power, 43(3), 111-114.
Wu, Y., Yan, B., & Qu, X. J. (2018). Proved chicken swarm
optimization method for reentry trajectory optimization.
Mathematical Problems in Engineering, 2, 1-13.
Zhang, Y. J., & Zhang, S. Q. (2018). Application of
improved constrained chicken swarm optimization
algorithm in neural networks. Computer Engineering &
Science, 12, 2252-2257.
Optimization of Hydropower Reservoir System Operations based on Improved CSO-PSO
195
