Automatic Recognition of Human Activities

Combining Model-based AI and Machine Learning

Constantin Patsch, Marsil Zakour and Rahul Chaudhari

Human Activity Understanding Group, Chair of Media Technology (LMT), Technical University Munich (TUM),

Arcisstr. 21, Munich, Germany

Keywords:

Activity and Plan Recognition, Knowledge Representation and Reasoning, Machine Learning.

Abstract:

Developing intelligent assistants for activities of daily living (ADL) is an important topic in eldercare due to

the aging society in industrialized countries. Recognizing activities and understanding the human’s intended

goal are the major challenges associated with such a system. We propose a hybrid model for composite activity

recognition in a household environment by combining Machine Learning and knowledge-based models. The

Machine Learning part, based on structural Recurrent Neural Networks (S-RNN), performs low-level activity

recognition based on video data. The knowledge-based part, based on our extended Activation Spreading

Network architecture, models and recognizes the contextual meaning of an activity within a plan structure.

This model is able to recognize activities, underlying goals and sub-goals, and is able to predict subsequent

activities. Evaluating our action S-RNN on data from the 3D activity simulator HOIsim yields a macro average

F1 score of 0.97 and an accuracy of 0.99. The hybrid model is evaluated with activation value graphs.

1 INTRODUCTION

With the increasing median age in industrialized

countries, the relative portion of elderly people within

the population is steadily increasing. For neurode-

generative diseases like Alzheimer’s, assistive sys-

tems might help affected elderly people to accomplish

tasks by providing guidance according to assessed in-

tentions. Activity understanding systems for smart

home environments based on sensory and visual data

have proven to be capable of recognizing and predict-

ing activities (Du et al., 2019) and also useful in health

monitoring applications (Yordanova et al., 2019).

In order to recognize and understand human activ-

ities, we have to understand the contextual importance

or relevance of an activity within the human’s activity

sequence towards a certain goal. Contextual impor-

tance indicates the signiﬁcance of an activity within

the plan structure as well as the logical interdepen-

dencies between activities. In this context, reason-

ing about the logic soundness of a recognized activity,

given previous activity recognitions and the informa-

tion of a plan structure, is essential. We assume that

the humans are not explicitly conveying their intent to

the system, and that the goal is not known beforehand.

The contribution of this paper is a hybrid activity

recognition model consisting of our action Structural-

RNN (S-RNN) architecture inspired by Jain et al.

(2016) and a new Activation Spreading Network for-

mulation based on the work of Saffar et al. (2015). We

present an interoperation mechanism for the S-RNN

and the ASN architectures. Our hybrid recognition

model for composite activities, depicted in Figure 1,

pursues the following objectives:

• contextual activity recognition based on logical

interdependencies in the plan structure,

• predictions of feasible future activities,

• consideration of partial observability and missing

activity recognitions,

• recognition of intended goals and subgoals, and

• consideration of interleaved activities contribut-

ing to multiple goals.

2 RELATED WORK

2.1 Model-based Artiﬁcial Intelligence

On the one hand, approaches based on an explicit

plan library compare activity sequence recognitions

to existing plans (Goldman et al., 2013; Levine and

Williams, 2014; Saffar et al., 2015). On the other

Patsch, C., Zakour, M. and Chaudhari, R.

Automatic Recognition of Human Activities Combining Model-based AI and Machine Learning.

DOI: 10.5220/0010747000003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 3, pages 15-22

ISBN: 978-989-758-547-0; ISSN: 2184-433X

method_1: drink tea from cup

make tea

move cup

to self

grab cup

place tea

bag in cup

pour

kettle to

cup

method_1: make tea

drink tea from cup

High level plan

recognition

Activity recognition:

Comparision of feasible

object-action

combinations

object: [kettle, cup]

action: grab

object: [tea bag]

...

Machine Learning

based on

visual/sensory

observations

action: pour

object: kettle

t-1t-2t-3

object: cup

tt-4

action: grab

t-5t-6

object: tea bag

object: microwave

grab

kettle

grab tea

bag

...

action: pour

method_2: make tea

...

method_2: drink tea from cup

...

Figure 1: Hybrid model, showing exemplary recognitions

and methods, within a tea drinking plan.

hand, generative approaches try to exploit ontologi-

cal and probabilistic knowledge to synthesize feasible

activity sequences given observations (Ramırez and

Geffner, 2011; Yordanova et al., 2019; Chen and Nu-

gent, 2019).

Goldman et al. (2013) propose a model for plan

recognition based on an explicit plan library, that de-

composes goals into activities by exploiting their hi-

erarchical structure. They incorporate partial ordering

by deﬁning subtasks in terms of logical and temporal

preconditions. Their model probabilistically assesses

the most likely goal from the plan library based on the

contribution of an activity observation to a plan.

Saffar et al. (2015) introduce an Activation

Spreading Network (ASN) that captures the hierarchi-

cal dependencies between several abstractions of ac-

tivities, while grouping them according to their afﬁl-

iation to their respective subgoals and goals. Hereby,

preconditions between subsequent activities intro-

duce logical order. Action-object recognitions from

the RGB-D video data enable activation value prop-

agation throughout the plan library in order to recog-

nize the most likely goal, and ensure a logically sound

activity recognition process. Our work partly relies

on the above concepts from Saffar et al. (2015), while

we introduce activity predictions, improved long-term

recognition robustness and compatibility with Ma-

chine Learning frameworks.

2.2 Machine Learning based Models

Machine Learning based models recognize activities

based on sensory and visual data as shown in (Kop-

pula et al., 2013; Jain et al., 2016; Du et al., 2019;

Shan et al., 2020; Bokhari and Kitani, 2016). Du

et al. (2019) use LSTMs and RFID data for activity

recognition. Bokhari and Kitani (2016) employ Q-

learning and a Markov Decision Process to capture

an activity sequence progression. Shan et al. (2020)

propose a framework for hand-object contact recogni-

tion and hand state estimation in order to understand

human object interaction and human object manipu-

lation based on video data.

In the context of human activity and object af-

fordance learning from RGB-D data, Koppula et al.

(2013) propose the CAD120 dataset based on spatio-

temporal features while introducing semantic object

affordances. Based on this dataset, Jain et al. (2016)

introduce Structural Recurrent Neural Networks (S-

RNNs) that use Deep Learning based on spatio-

temporal graphs for action and affordance recogni-

tion. These graphs capture the interactions between

the human and the surrounding objects within a tem-

poral segment of an action. Actions are classiﬁed

based on human-speciﬁc and shared human-object

features with the help of the corresponding RNNs,

whereas the object classiﬁcation is based on object-

speciﬁc and shared human-object features. Our work

borrows the feature preprocessing process as well as

the general framework of the S-RNN, while we di-

rectly use object-speciﬁc features for the action recog-

nition process without considering affordances.

3 HYBRID ACTIVITY MODEL

3.1 Activation Spreading Network

In this section we explain our ASN architecture, an

extension of the one presented by Saffar et al. (2015).

We developed this ASN to meet the requirement of

performing high-level contextual activity recognition

in the hybrid activity recognition model. Compared

to the work by Saffar et al. (2015), our ASN provides:

• compatibility with discrete Machine Learning

model recognitions,

• weighting based on activity distinctiveness,

• contextual recognition of longer complex activity

sequences, independent of activity duration,

• activity predictions, and

• recovery from misclassiﬁed and missing activities

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

3.1.1 Extended Activation Spreading Network

Architecture

The ASN is a directed acyclic graph consisting of

nodes n ∈ N , sum edges e ∈ E

, max edges ma ∈ E

and ordering/precondition edges o ∈ E

. N repre-

sents the set of all nodes and E the set of edges in

the ASN, where E

⊂ E and E

⊂ E . N consists of

operator nodes n

∈ N

, method nodes n

∈ N

and

compound nodes n

∈ N

, where N

⊂ N , N

⊂ N

and N

⊂ N is valid.

The operator nodes are the leaf nodes within the

network representing activities that can be recognized

by the low-level activity recognition framework. The

method nodes take the sum over the weighted activa-

tion values of the child nodes that are connected to it

with sum edges. Hereby, each sum edge connected to

a method has its own weight. The assignment of the

activities to the respective sum edges is captured in

the SumEdges dictionary according to deﬁnition 3.2.

All methods connected to the same compound node

with max edges represent different ways of achieving

that compound node. The max edges m ∈ E

only en-

able the method that has the highest activation value

between competing methods to spread its activation

value. Compound nodes can either again contribute

to their parent method, or if they are on the highest

level within the ASN, they are denoted as goal nodes.

Deﬁnition 3.1 (Activation Value Dictionary).

ActValN contains the activation value of every node

n ∈ N . The activation value ac(n) ∈ [0, 1] of each

node is calculated based on the low-level activity

recognition and activation value propagation process.

The structure is deﬁned by:

ActValN = {n

: ac(n

), n

: ac(n

), ..., n

: ac(n

)},

where k denotes the number of available operator,

method and compound nodes in the plan library and

ac(n) denotes the activation value of the node n ∈ N .

Deﬁnition 3.2 (Sum Edge Dictionary). SumEdges

contains the activities contributing to their respective

methods. Accordingly, SumEdges is formulated as:

SumEdges = {n

: [l

], n

: [l

], ..., n

: [l

]},

where j denotes the number of all available meth-

ods within the plan library and [l

] denotes an ar-

ray containing the speciﬁc activity nodes n ∈ N that

are associated with the respective method n

∈ N

Sum edges e ∈ E

are displayed with black arrows in

graphical plan structures.

Deﬁnition 3.3 (Max Edge Dictionary). n

∈ N

are

method nodes that lead to a certain compound node

∈ N

which is determined by MaxEdges as:

MaxEdges = {n

: [methodlist

], n

: [methodlist

..., n

: [methodlist

]}.

Hereby, b denotes the number of compound nodes

within the plan library and methodlist

denotes the

method nodes that are associated with the respective

compound node n

. Max edges ma ∈ E

are dis-

played with red arrows in graphical plan structures.

Deﬁnition 3.4 (Ordering/Precondition Edge Dictio-

nary). PrecondEdges has the methods n

as keys,

while containing a list of precondition lists for each

activity within the method:

PrecondEdges = {n

: [c(n

), c(n

), ..., c(n

)],

: [c(n

), c(n

), ..., c(n

)], ...,

: [c(n

), c(n

), ..., c(n

m j

)]}.

Hereby, each c(n

m j

) denotes a list of precondition ac-

tivity nodes that are associated with the activity node

m j

. The number of entries f

m j

associated with a

method j depends on the number of activities that are

assigned to the respective method in the SumEdges

dictionary. Precondition edges o ∈ E

are displayed

with green arrows in graphical plan structures.

Deﬁnition 3.5 (Activation Sum Edge Dictionary).

ActSumEdges is a dictionary that contains a list of bi-

nary values, with a separate binary value for every ac-

tivity within a method indicating whether the precon-

ditions of the activity in PrecondEdges are fulﬁlled.

Accordingly it is deﬁned as:

ActSumEdges = {n

: actsum

, n

: actsum

..., n

: actsum

where j denotes the number of methods within the

plan library and actsum

denotes the list of activation

values of the sum edges connecting the activity nodes

n ∈ N with their respective methods n

∈ N

In the following we explain our adaptations and

extensions to the original ASN framework. Saffar

et al. (2015) introduced a uniform decay of activa-

tion values, which we replace with a time independent

binary activation value deﬁnition for operator nodes,

in order to take long and complex activity sequences

into account. Thus, we prevent the decay of an ac-

tivity’s relevance throughout time which means that

activity durations do not inﬂuence the contribution to

the recognition process. This formulation also en-

ables the connection of the Machine Learning model

outputs and the ASN operators, as the ASN is able to

accept time discrete activity recognitions.

Moreover, we introduce a new weighting scheme

for the edges connecting activity nodes within the

ASN. Our weighting process relies on the frequency

Automatic Recognition of Human Activities Combining Model-based AI and Machine Learning

of an activity within competing plans, and the higher

importance of compound nodes that incorporate sev-

eral different activities. We initialize the weights of

the sum edges as

|subactivities(n

. The weighting of

the sum edge of an activity is relatively increased to

the other sum edges within the method, if the activity

is rather unique for the respective plan. The weighting

of sum edges connecting compound nodes to method

nodes is ampliﬁed relatively to simple operator nodes.

Moreover, we normalize the weights of sum edges,

which enforces a comparability between activities in-

dependent of the hierarchical level.

As another extension we introduce state effects

that represent the validity of a certain state upon com-

pleting a subgoal within the ASN. This is important

for recognizing activity sequences that are likely to

be repeated several times. A state effect is valid until

another state effect is introduced.

Furthermore, we introduce a backpropagation

procedure that enables predictions about future ac-

tivities. At ﬁrst, we determine the most likely goal

with the highest activation value and then consider the

child nodes of the method that constructs this com-

pound node. We iteratively traverse the hierarchy to-

wards the lowest levels in the plan constituting the

currently assessed goal. In case of compound nodes,

we iterate through the child nodes of their method. On

each hierarchical level, the validity of the precondi-

tions is checked as they serve as an indicator for pos-

sible next activities. When predicting future activities,

the ones that have activated sum edges due to fulﬁlled

preconditions and that are directly subsequent to pre-

viously activated activities are considered. Lastly, the

ASN recovers from misclassiﬁcations and missed ac-

tivities by setting the activation value of an activity to

1 if it has been missed or misclassiﬁed, while serv-

ing as a precondition for two subsequent successfully

recognized activities.

3.1.2 Activation Spreading Process

The activation value propagation process is initiated

by a new activity recognition. When the activation

value of a newly recognized activity is updated to 1,

we start by iterating from the lowest level methods

to the highest level ones in order to ensure a correct

activation value propagation within the hierarchy.

All preconditions of an activity have to be valid

in order for an activity to spread its activation value.

If all preconditions and state effect preconditions are

fulﬁlled the respective sum edge of the considered ac-

tivity is activated. The value of ActSumEdges is up-

dated from 0 to 1 for the relevant activity. After all

activities of a method have been considered, the acti-

vation value of the method gets updated by summing

over the weighted activation values from its activities.

Upon a method achieving the activation value 1, the

activation values of the activities involved with that

method get reset to 0 while the compound node main-

tains its activation value at 1. The compound node

itself is going to get reset if the method node it con-

tributes to achieves the activation value 1.

3.2 Structural Recurrent Neural

Network

In this section we explain the action recognition based

on the action-affordance S-RNN proposed by Jain

et al. (2016) and our action S-RNN.

3.2.1 Feature Preprocessing

In order for the S-RNN to be able to perform ac-

tion and affordance recognition we ﬁrst introduce the

feature preprocessing steps that are inspired by Kop-

pula et al. (2013). The features are computed based

on skeleton and object tracking performed on sta-

tionary video data. The object node features de-

pend on spatial object information within the seg-

ment, whereas the human node features rely on the

spatial information of the upper body joints. The

edge features are deﬁned for object-object edges and

human-object edges within one segment of the spatio-

temporal graph. The temporal object and human fea-

tures are deﬁned based on the relations between ad-

jacent temporal segments. Similar to Koppula et al.

(2013), the continuous feature values are discretized

by using cumulative binning into 10 bins yielding

a discrete distribution over feature values. The re-

sulting dimension of the feature vector thus yields

(number of features) × 10 . As a result we obtain a

histogram distribution over the feature values that is

especially useful when adding object features.

The spatio-temporal graph depicted in Figure 2

represents a concise representation of the relation be-

tween the human and the objects within and between

temporal segments. In order for the spatio-temporal

graph to model meaningful transitions, the video is

H HH

t-2 t-1 t

Figure 2: Exemplary spatio-temporal-graph with one hu-

man and two object nodes within three temporal segments.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

segmented in a way that every segment ideally only

contains one action. The segmentation of videos ac-

cording to actions is not investigated here, and we rely

on the provided ground truth segmentations. Labels

of human nodes are the action labels whereas an ob-

ject can be annotated with an affordance label. The

semantic affordance of an object depends on the ac-

tivity it is involved in. For example in the activity

‘pour from bottle to glass’ the action label is ‘pour’

and the affordance labels of the bottle and the glass

are ‘pourable’ and ‘pour-to’. Koppula et al. (2013) in-

troduced the notion of affordances in order to deﬁne

how an object is being interacted with in the scene.

3.2.2 Action-affordance S-RNN and Action

S-RNN

Firstly, we consider the original S-RNN based on the

joint action-affordance recognition. Hereby, an object

only has one affordance at a time which can vary over

time depending on its usage. Within a segment of the

spatio-temporal graph, while there is always only one

human node corresponding to one action label, there

is generally a higher number of object nodes which

varies depending on the scenario that results in a vary-

ing number of affordance labels. Thus, the overall

action-affordance model has to be separated into two

submodels, one dealing with affordance classiﬁcation

and the other dealing with action classiﬁcation.

However, compared to Jain et al. (2016), we do

not consider semantic affordances and only focus on

action classiﬁcation while relying on spatio-temporal-

graph features. The architecture of this action S-RNN

model is shown in ﬁgure 3. Hereby, the Human Input

layer receives the concatenation of the human node

and the human temporal edge features as an input. As

we consider only one human node within a tempo-

ral segment the number of features remains the same

throughout temporal segments. The Ob ject

Input

layer receives the concatenation of the object node,

the object-object edge and the object temporal edge

features as an input. However, as the number of ob-

Human_Object Object_Input Human_Input

LSTM

Concatenate

Out_Action

LSTM

LSTM LSTM

Figure 3: Our action S-RNN implementation.

jects might vary throughout temporal segments, the

length of concatenated features might vary accord-

ingly. Thus, we have to sum over the object related

features of each object in order to achieve a ﬁxed

length representation. Empirically, the aforemen-

tioned cumulative binning process for discretizing the

features is important to limit the information loss dur-

ing the feature summation. The Human Ob ject input

layer receives the human-object edge features as an

input. As the human node is connected to a poten-

tially varying number of object nodes, we sum over

the discretized human-object edge features.

The advantage of our approach is that we do not

need affordance labels as we only focus on action

classiﬁcation which simpliﬁes the dataset creation

process. Differently to the original S-RNN the in-

puts are not divided into terms that contribute to either

the affordance or the action classiﬁcation but rather

we directly use all features to perform action clas-

siﬁcation. Thus, the action classiﬁcation is not only

trained on the human and human-object edge features

but also on object and object-object edge features of

the spatio-temporal-graph representation.

3.3 Combining Machine Learning

Results with ASN

In the following we combine action and object recog-

nitions from the S-RNN into feasible action-object

combinations which are passed as an input to the

ASN model. We rely on simulated data where labels

of objects and kitchen furniture are available. Thus,

the object recognition part is not explicitly consid-

ered. The main focus of the matching process de-

picted in ﬁgure 4 is to combine probabilistic assess-

ments regarding actions with object recognitions, and

verify whether these action-object combinations re-

sult in feasible activities.

Given object recognitions, we only consider ob-

jects within imaginary spheres around the human

hand joints (t

sphere

). Feasible activities are obtained

by comparing the action-object combinations a

with

available operator activity nodes within the plan li-

brary. For each combination we deﬁne a joint detec-

tion score consisting of three parts. The ﬁrst part is

the score s

dist−inv

) that is calculated for each ob-

ject O

within an action-object combination based on

the equation

dist-inv

) =

sphere

− dist

human- joint-O

sphere

. (1)

The second one is the probability prob

of the action-

object combination. The third part enables the high-

level reasoning process to inﬂuence the low-level ac-

tivity recognition process by considering previous

Automatic Recognition of Human Activities Combining Model-based AI and Machine Learning

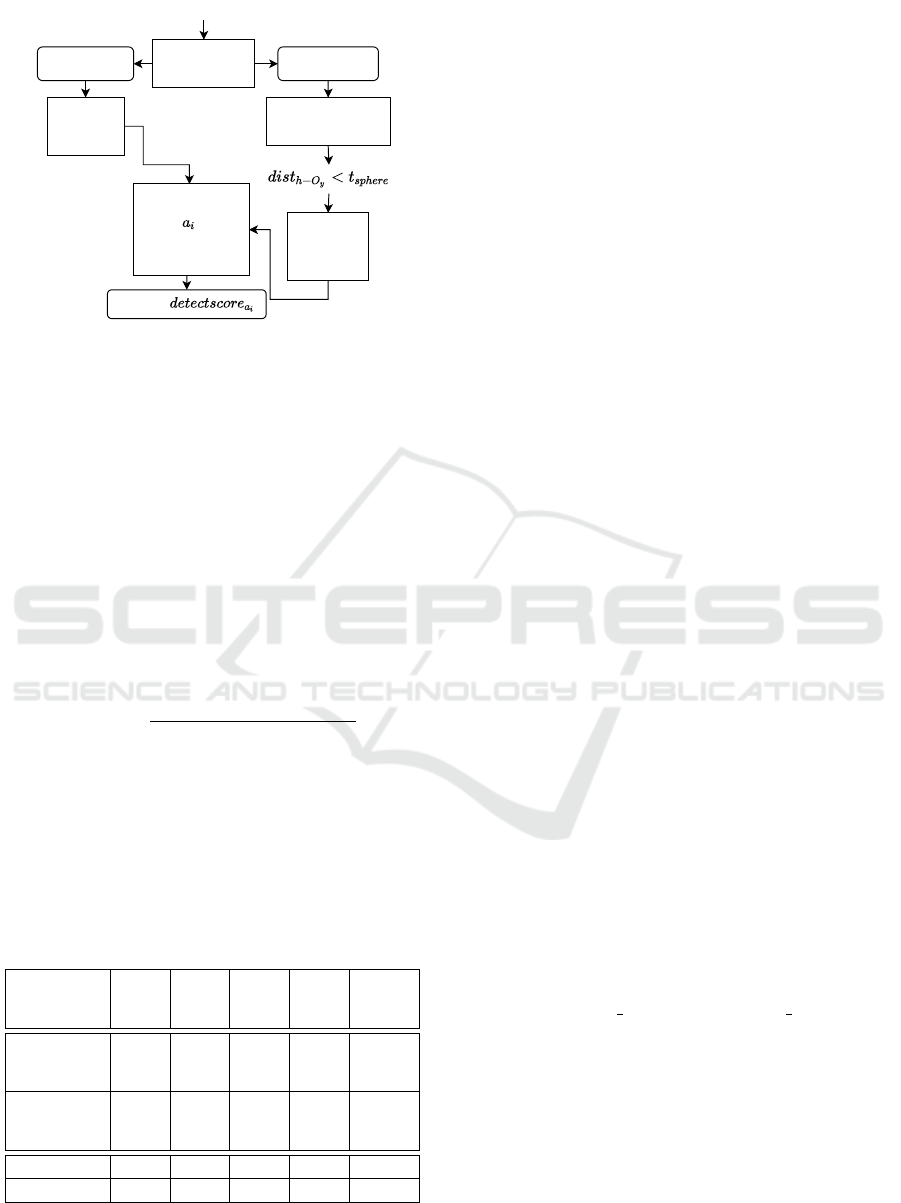
Action

recognition

pour: 0.6,

cut: 0.3,

move: 0.1

Object

recognition

bottle, faucet, glass,

cup, counter, knife,

tomato

bottle, glass,

cup, knife,

tomato

Feasible action-

object combinations

pour+bottle+cup,

pour+bottle+glass,

cut+knive+tomato

Calculate

Video + Sensory Information

Machine Learning

Models

Figure 4: Matching process between action and object

recognition and the ASN architecture.

recognitions of the ASN. If the action-object combi-

nation is contextually valid and contributes to the goal

g, which has been assessed as the most likely one, the

detection score is increased by a predeﬁned factor q.

Contextual validity is veriﬁed by comparing the pre-

dictions regarding the next activity made by the ASN

in the previous temporal segment with the currently

considered action-object combination. If an action-

object combination does not contribute to the goal g

or no goal has been determined the detection-score re-

mains unchanged. Each detection score detectscore

is deﬁned by

detectscore

∑

seg

(prob

)(s

dist-inv(O

)

seg

(q), (2)

where index i denotes the ‘i-th’ feasible action object

combination for the current segment, index y denotes

the ‘y-th’ recognized object and n

seg

equals the num-

ber of objects in the scene. The ﬁnal activity recogni-

tion is the one with the highest detectscore

Table 1: Action recognition Macro average F1 score (F1)

and accuracy (Acc) of the action-affordance S-RNN and our

action S-RNN on the test sets of the 4-fold cross-validation.

Metric

Set

Aver-

age

F1 (Act-

Aff)

0.88 0.62 0.81 0.77 0.77

Acc (Act-

Aff)

0.92 0.76 0.82 0.76 0.82

F1 (Act) 0.88 0.66 0.75 0.66 0.74

Acc (Act) 0.89 0.76 0.78 0.73 0.79

4 EVALUATION

4.1 S-RNN Results on CAD120 Dataset

In the following we compare the performance of the

action-affordance S-RNN with the action S-RNN. We

use the features provided by the CAD120 dataset

based on the multi-segmentation approach by Kop-

pula et al. (2013).

For evaluation purposes we employ 4-fold cross-

validation. We use the RMSprop optimizer provided

by Keras with a learning rate of 0.001, and categori-

cal crossentropy as a loss function. When training the

action-affordance S-RNN and our action S-RNN for

100 epochs on a batch size of 4, the results on the dif-

ferent test sets are displayed in Table 1. By summing

over all object features within a temporal segment,

compared to training on them separately, the perfor-

mance deteriorates on average by roughly 3 percent.

An important reason for that is that during the train-

ing process we have not been able to accurately dis-

tinguish the respective afﬁliation of objects to a cer-

tain temporal segment. So we summed over the aver-

age number of objects in a temporal segment within

the whole training dataset. Thus, object features of

one temporal segment might be summed with object

features of another segment. When object afﬁliation

to temporal segments is known, the performance gap

should decrease signiﬁcantly. This hypothesis is go-

ing to be investigated in section 4.2 based on simu-

lated data where the object afﬁliation is recorded.

4.2 Hybrid Model Results on Simulator

Data

In the following the hybrid model performance is

evaluated based on our action S-RNN classiﬁca-

tion performance and the activation spreading graphs

of our adapted ASN. The data originates from the

Human-Object Interaction Simulator ‘HOIsim’ of Za-

kour et al. (2021) which randomly samples activi-

ties contributing to a plan under varying kitchen en-

vironments. The simulator data consists of the plans

Break f ast, Serve Lunch and Prepare Lunch. Fur-

thermore, the plan library is extended by plans con-

tributing to the goals of drinking Tea, Co f f ee and

Juice. We compare the performance of the action-

affordance S-RNN and the action S-RNN on simu-

lator data, with the aformentioned training metrics,

and combine the resulting recognitions with the object

recognitions. During action and affordance recogni-

tion we consider 12 actions and 18 affordances.

Our action S-RNN that relies on the summed ob-

ject feature vectors yields a macro average F1 score

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

grab

spoon

place

spoon

on table

grab

bowl

place bowl

on table

grab

cereal

pour

cereal

into bowl

grab

milk

pour

milk

into

bowl

grab

spoon

eat with

spoon

m_make_cereal

make_cereal

m_eat_cereal

eat_cereal

m2_eat_cereal

grab

spoon

eat with

spoon

state-effect:

bowl : cereal

grab

spoon

m_clean_cereal

clean_cereal

state-effect:

bowl-cereal

place

spoon in

sink

grab

bowl

place

bowl in

sink

grab

cereal

place

cereal in

cupboard

grab

milk

place milk

refrigerator

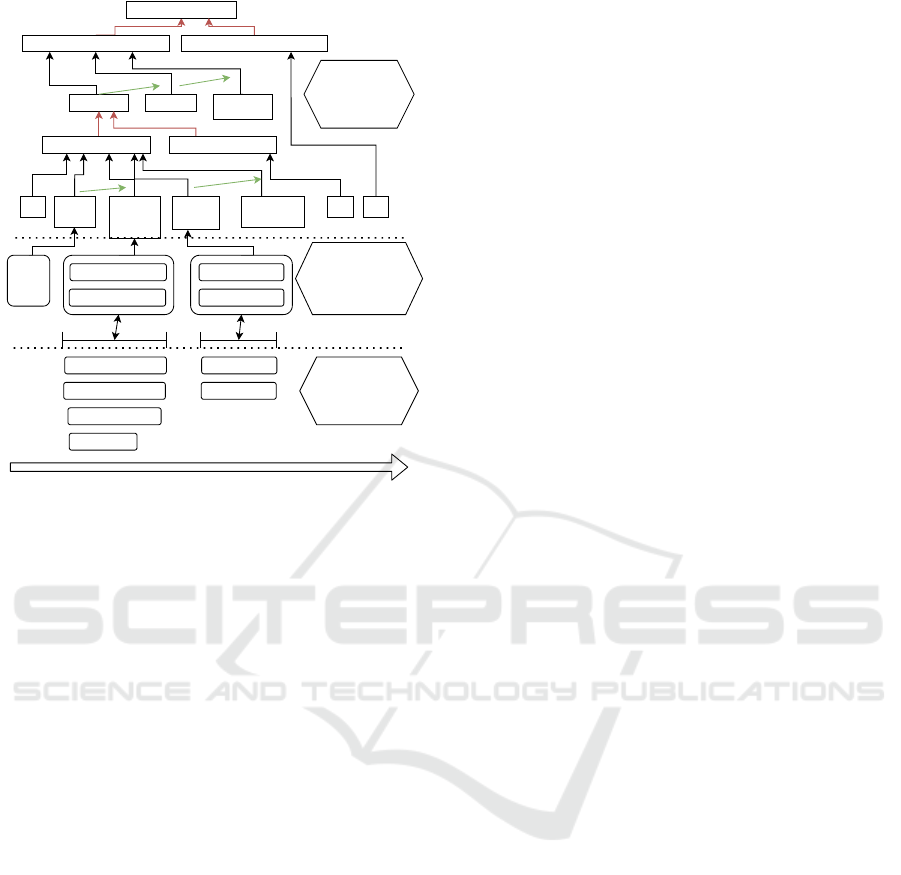
Figure 5: ASN architecture of the plan for the goals eat cereal and clean cereal.

of 0.97 and an accuracy of 0.99 on the simulator data.

The action-affordance S-RNN returns a macro aver-

age F1 score of 0.968 and an accuracy of 0.986. In

contrast to the CAD120 dataset evaluation, the per-

formance of both models is quite similar. The sim-

ilar performance metrics of the models on the simu-

lator data might further indicate that associating ob-

jects to the correct temporal segment and action label

is especially important for the action S-RNN. Given

the action recognitions of our action S-RNN we con-

sider only the three actions with the highest probabil-

ities and the ﬁrst and second closest objects based on

whether the action requires one or two objects. The

activity sequence that we consider, follows the un-

derlying intention of making breakfast and its plan

structure is depicted in ﬁgure 5. In ﬁgure 6 the ac-

tivity recognitions are displayed on the x-axis and

the activation values are displayed on the y-axis. A

change in the activation value of a method shows a

successful activity recognition contributing to the spe-

ciﬁc method of the plan library.

The ﬁrst subgoal that the human follows is

make cereal which is indicated by the highest ac-

tivation values of the yellow line. The green line

corresponds to the method of eating cereal, which

is based on the make

cereal subgoal. On the one

hand the relatively frequent activities like grab milk

or grab spoon contribute less to the recognition pro-

cess which can be concluded from the relatively low

slopes. On the other hand infrequent and more

plan speciﬁc activities like pour cereal into bowl

and pour milk into bowl lead to higher slopes of the

yellow line. Activities that do not contribute to any

method in the plan library do not inﬂuence the recog-

nition process. As soon as the method m make cereal

reaches the activation value 1, all activation values of

the activity nodes contributing to this method are re-

set to 0 to enable new recognitions. Moreover, the

method m2 eat cereal reaches the activation value 1

as the state effect precondition of the bowl containing

cereal is fulﬁlled. By considering state effects, the hy-

brid model is able to recognize the human resuming

an activity after it has been interrupted. After that the

human tidies up the objects used in the breakfast ac-

tivity which contributes to the goal clean cereal. The

activities associated with the cleaning activity are en-

abled by the state effect of the bowl containing cereal.

While the clean cereal and make cereal method

share similar activities one can see from the lower

activation value lines of the method m make cereal

compared to m clean cereal that there is no confu-

sion regarding the goal assessment as long as the ac-

tivity context is correct. Moreover, with the back-

propagation procedure one can verify which activity

recognitions serve as preconditions for subsequent ac-

tivities. Thus, we can make predictions regarding fu-

ture activities throughout the recognition sequence.

For example in case of the grab cereal recognition,

one future prediction of the hybrid model is the activ-

ity pour cereal into bowl as it is conditioned on this

activity. As there is no milk in the bowl up to that

point in time in the example the model also suggests

the activity grab

milk as it has no precondition itself

but contributes to the goal of eating cereal.

5 CONCLUSION

Machine Learning based frameworks like LSTMs are

incapable of verifying logical preconditions, captur-

ing multigoal activity execution and making long-

term activity predictions. Hence, we propose a hybrid

model consisting of a Machine Learning and a knowl-

edge based part. Compared to the action-affordance

Automatic Recognition of Human Activities Combining Model-based AI and Machine Learning

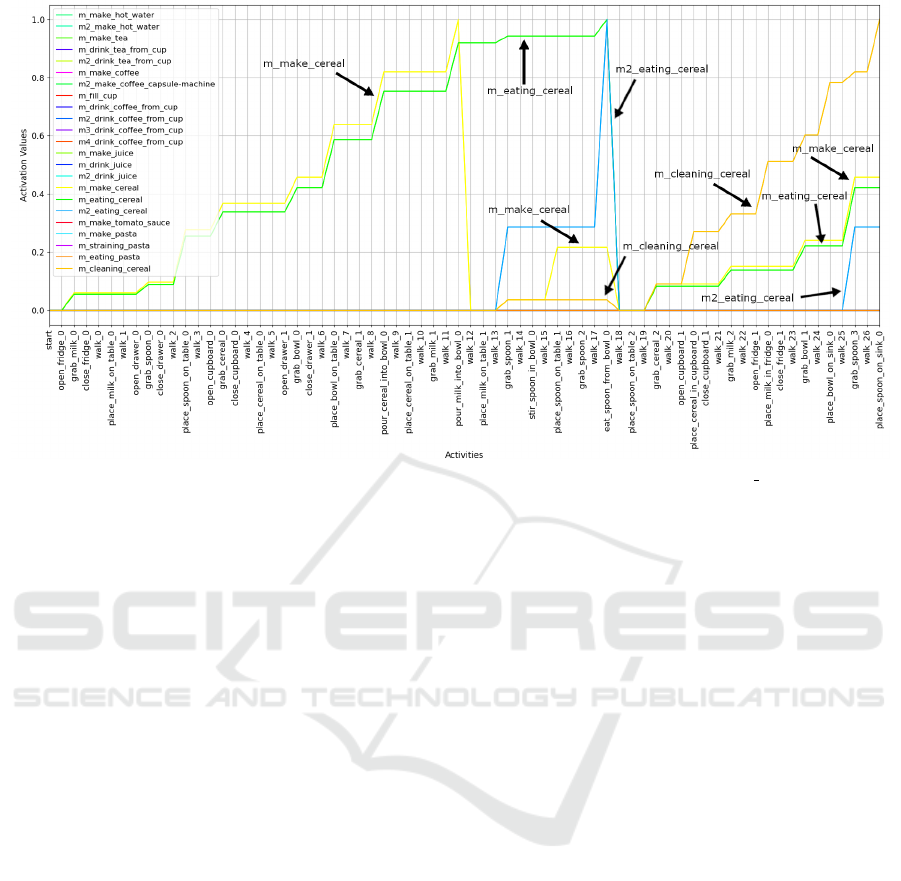
Figure 6: Activation spreading graph of a simulator test sample with the underlying goal eat cereal.

S-RNN, our action S-RNN is able to obtain similar re-

sults on simulated activity data without additional ef-

fort for affordance labeling. Our proposed ASN deals

with activity recognitions, misclassiﬁcations, missing

activities and is capable of predicting future activitiv-

ities. As the Knowledge Base is deﬁned by a human

expert, one could address the limited validity of the

plan representation by automatically extracting struc-

tured plans from sensor data. Additionally, the ap-

proach can be extended to egocentric video data. Fur-

thermore, the object classiﬁcation part has to be in-

vestigated for activity recognition on real-world data.

ACKNOWLEDGEMENT

This work has been funded by the Initiative Geriatron-

ics by StMWi Bayern (Project X, grant no. 5140951).

REFERENCES

Bokhari, S. Z. and Kitani, K. M. (2016). Long-term activity

forecasting using ﬁrst-person vision. In Asian Confer-

ence on Computer Vision, pages 346–360. Springer.

Chen, L. and Nugent, C. D. (2019). Composite activity

recognition. In Human Activity Recognition and Be-

haviour Analysis, pages 151–181. Springer.

Du, Y., Lim, Y., and Tan, Y. (2019). A novel human activ-

ity recognition and prediction in smart home based on

interaction. Sensors, 19(20):4474.

Goldman, R. P., Geib, C. W., and Miller, C. A. (2013).

A new model of plan recognition. arXiv preprint

arXiv:1301.6700.

Jain, A., Zamir, A. R., Savarese, S., and Saxena, A.

(2016). Structural-rnn: Deep learning on spatio-

temporal graphs. In Proceedings of the IEEE con-

ference on Computer Vision and Pattern Recognition,

pages 5308–5317.

Koppula, H. S., Gupta, R., and Saxena, A. (2013). Learn-

ing human activities and object affordances from rgb-

d videos. The International Journal of Robotics Re-

search, 32(8):951–970.

Levine, S. and Williams, B. (2014). Concurrent plan recog-

nition and execution for human-robot teams. In Pro-

ceedings of the International Conference on Auto-

mated Planning and Scheduling, volume 24.

Ramırez, M. and Geffner, H. (2011). Goal recognition over

POMDPs: Inferring the intention of a POMDP agent.

In IJCAI, pages 2009–2014. Citeseer.

Saffar, M. T., Nicolescu, M., Nicolescu, M., and Rekabdar,

B. (2015). Intent understanding using an activation

spreading architecture. Robotics, 4(3):284–315.

Shan, D., Geng, J., Shu, M., and Fouhey, D. F. (2020). Un-

derstanding human hands in contact at internet scale.

In Proceedings of the IEEE/CVF Conference on Com-

puter Vision and Pattern Recognition, pages 9869–

9878.

Yordanova, K., L

udtke, S., Whitehouse, S., Kr

uger, F.,

Paiement, A., Mirmehdi, M., Craddock, I., and Kirste,

T. (2019). Analysing cooking behaviour in home set-

tings: Towards health monitoring. Sensors, 19(3):646.

Zakour, M., Mellouli, A., and Chaudhari, R. (2021).

HOIsim: Synthesizing realistic 3d human-object in-

teraction data for human activity recognition. In

2021 30th IEEE International Conference on Robot

& Human Interactive Communication (RO-MAN), pp.

1124-1131.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence