
Towards a Robust, Distributed and Decentralised Smart Energy
Management of Microgrids
Sandra Garcia-Rodriguez
a
and Hassan A. Sleiman
b
Universit
´
e Paris-Saclay, CEA, List, F-91120 Palaiseau, France
Keywords:
Microgrids, Robust Decentralised Optimisation, Multi-Agent System, Evolutionary Computation.
Abstract:
Modern energy systems comprise different entities that interact to allow an intelligent production, distribution,
and consumption of energy. They need efficient and distributed demand-response management mechanisms
to find optimised configurations of parameters of the grid components. When working with time schedules,
optimisation algorithms used for this purpose usually rely on forecasts. However, forecasts bring uncertainty,
which is rarely considered in optimisation. This work presents a robust and decentralised optimisation ap-
proach that deals also with such uncertainty by searching for optimal power schedule solutions, which are
also reliable in unexpected circumstances. Based on message passing, our approach uses meta-heuristics for
performing local optimisations. The implementation and validation of our proposal was conducted by means
of a distributed multi-agent system, where the obtained results have shown the efficiency of our approach.
1 INTRODUCTION
Smart grids became one of the solutions to deal with
climate change and the continually increasing de-
mand for energy (Tuballa and Abundo, 2016). It is
an intelligent electrical grid with a distributed energy
generation, storage, integrating of customer power
supply and renewable energy. It is intended to en-
hance the effectiveness and efficiency of power deliv-
ery by using intelligent algorithms to manage the pro-
duction, distribution, and consumption of electricity.
The successful implementations of smart grids have
increased the research interest in this field.
This article focuses on a part of smart grids, called
microgrids. Microgrids are networked groups of dis-
tributed energy resources, such as solar panels or
wind turbines, located at the distribution network
side, and able to provide energy to small geographical
areas (Saad et al., 2012). It connects consumers (a.k.a
prosumers), which are small-scale co-providers of en-
ergy, and allows local electricity interchange among
them. Such interchange reduces their dependence
on the public grid, placing the generation of elec-
tricity near the end-users. Efficient demand-response
management mechanisms allows users to be energy-
efficient in the long term (Mesaric et al., 2017).
a
https://orcid.org/0000-0002-5352-2510
b
https://orcid.org/0000-0002-0018-0027
Efficient demand-response management mecha-
nisms are essential for microgrids since they pursue to
find the best configuration parameters of the compo-
nents for an optimised grid performance (Colak et al.,
2016). Such mechanisms manage the grid and try to
achieve an optimised performance for a given objec-
tive(s) such as reducing the bill, avoid power peaks
and/or energy losses, without violating the constraints
imposed by the grid definition. These decisions are
considered as optimisation problems, and are the fo-
cus of many recent studies (Gomez-Sanz et al., 2014).
In practice, the grid configuration parameters vary
from the time schedules (for a given time horizon),
to the real-time parameters (Gamarra and Guerrero,
2015). Unfortunately, the complexity arises with the
number of variables to be optimised such as the time
setups for self-controlled resources of the grid (Mo-
hamed and Koivo, 2007).
To work with scheduled configurations, optimis-
ers usually rely on forecasts instead of real-time se-
tups. Forecasts provide an estimation on what may
occur in the near future, allowing to plan the strat-
egy in advance. Currently, many types of forecasts
can be considered in a microgrid optimisation prob-
lem: some of them are related to power consump-
tion/generation such as consumption schedules, bat-
tery levels, production curve; others are related to
weather prediction, such as solar radiation and wind
speed. However, since forecasts are not 100% ac-
Garcia-Rodriguez, S. and Sleiman, H.
Towards a Robust, Distributed and Decentralised Smart Energy Management of Microgrids.
DOI: 10.5220/0010748900003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 1, pages 15-25
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
15

curate (Mahat et al., 2013), the observed parameters
may vary from the forecasted ones, which leads to
unexpected situations. In this case, the optimised
solutions (based on the non-accurate forecasts) are
more likely to lie far from the optimal ones (Garc
´
ıa
et al., 2012), which may provoke looses in money,
resources, and/or time (Liang and Zhuang, 2014).
Therefore, forecasting reliability is a key factor in op-
timisation solutions (Moreno et al., 2017).
In this paper, we present a robust and decen-
tralised optimisation algorithm implemented in a dis-
tributed manner for finding the best setup configura-
tion for the devices in a microgrid. We refer to robust-
ness as the capacity of the approach to provide stable
solutions with a performance that does not drop when
unexpected scenarios are faced. Our proposal is based
on the adaptation of the message passing algorithm
proposed by Kraning et al. (Kraning et al., 2014),
where optimisation is split in less complex problems
that are locally solved in different nodes of the grid.
The global optimisation is achieved by means of a
negotiation protocol amongst all of the grid nodes.
Local optimisations are performed using evolution-
ary computation (Zhang et al., 2011), which is con-
sidered an adequate approach for this kind of prob-
lems (Moghaddam et al., 2011; Ramaswamy and De-
coninck, 2012). For instance, metaheuristics as “Par-
ticle Swarm Optimisation” (Chen and Yu, 2005) and
SPEA2 (Zitzler et al., 2001) are adapted to our prob-
lem. Furthermore, in order to deal with the reliabil-
ity of forecasts, we consider the robustness concept
by extending the decentralised optimisation algorithm
with a robust approach, which allows handling the un-
certainty in forecasts within the optimisation process.
Our proposal was implemented by means of a
distributed multi-agent system (Al-Hinai and Alh-
elou, 2021), a technology that has been proven to be
very suitable for microgrid solutions (Farhangi, 2010;
Amin and Wollenberg, 2005). A sliding window over
different year-observations (extracted from real data
sets) was used to carry out our validation tests. Ac-
cording to the results, our algorithm provides effec-
tive solutions by considering uncertainty in its param-
eters. Comparing the optimised schedules obtained
from forecasted parameters to the equivalent real-time
ones, we can see that costs are reduced up to 60% in
some of the tested scenarios.
This paper is organized as follows: Section 2 re-
views the state of the art about distributed optimisa-
tion algorithms for microgrids; Section 3 presents the
algorithm in which the proposed solution is based;
Section 4 details our contribution, whereas Section 5
reports on the validation results. Finally Section 6
concludes our work and discusses the future lines.
2 RELATED WORK
Demand response algorithms emerged in the 1970’s,
but have experienced a renaissance by the appearance
of microgrids (Mihaylov et al., 2019). These algo-
rithms try to optimise the schedules of the control-
lable loads to satisfy the grid objectives, such as val-
ley filling and peak shaving to mention a few.
The literature reports on many optimisation al-
gorithms for microgrids, which aim at reducing the
energy imbalance and at covering the demand and
supply gap. Some of these approaches are based on
predictions only, whereas others consider the unre-
liability of predictions, aka uncertainty. One of the
main sources of uncertainty in smart grids is the in-
tegration of stochastic renewable energy sources and
the introduction of new energy intensive appliances,
which make it increasingly difficult to find an opti-
mised planning of resources in the smart grid (Decon-
inck et al., 2008; Veldman et al., 2013).
The authors in (Haring et al., 2016) developed and
compared three different schemas for optimising the
energy market, involving the customers and focusing
on the trade-off among privacy, resource exploitation
and the reward earned. The first schema provided a
centralised optimisation in which the user informa-
tion is shared with the system operator; the second
applied a centralised optimisation, based on an ag-
gregator, with whom the user partially shares cost in-
formation; and the third schema proposed a decen-
tralised schema, in which the prosumers exchanged
energy among each other without revealing their cost
information. Prediction is used in the second schema,
but without considering uncertainty.
Alternating Direction Method of Multipliers
(ADMM (Boyd et al., 2011)) was used in (Rivera
et al., 2017) and (Diekerhof et al., 2014). (Rivera
et al., 2017) proposed a scalable distributed convex
optimisation framework for electrical vehicle aggre-
gators, and covered local and global objectives and
constraints. It is intended to resolve valley filling and
minimising charging costs by providing optimised
charging plans. It focused on demonstrating the pos-
sibility of integrating electrical vehicles in the grid
and on the scalability of the framework, but it does
no tackle the uncertainty. (Diekerhof et al., 2014)
proposed a distributed optimisation system for intel-
ligently controlling electrical heat pumps at district
level, based on an ADMM, where the local objec-
tives of each participant are considered achieving the
global objectives. The authors in (Diekerhof et al.,
2016) showed the advantages and disadvantages of
distributed optimisations and proposed a particular
usage of ADMM for scheduling electro-thermal heat-
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
16

ing units. Dantzig-Wolfe decomposition (Dantzig and
Wolfe, 1960) was used by (McNamara and McLoone,
2015), who proposed a hierarchical demand-response
algorithm. The objective of this approach was to peak
minimisation and achieve both: the device and the
customer objectives. Furthermore, it tried to min-
imise the communication overheads and to improve
the quality of service by improving the response time
for the devices that need their energy as soon as pos-
sible. This work does not consider considering uncer-
tainty either.
The following proposals focused on decentralised
frameworks without including uncertainty (de Ce-
rio Mendaza et al., 2016; Meyn et al., 2015): (i)
(de Cerio Mendaza et al., 2016) proposed a hierarchi-
cal and decentralised framework that is intended for
controlling the demand-response in low voltage net-
works, where the system operator plays the aggrega-
tor role for trading energy demand flexibility and for
ensuring reliability and security. Since the framework
only focused on the demand side, just loads were con-
sidered. The authors modelled the heat pumps sys-
tems to respond to demand aggregations, which is
used in their hierarchical structure; (ii) (Meyn et al.,
2015) proposed a decentralised decision making ar-
chitecture for automated demand response that can be
used for maintaining demand-supply balance. The au-
thors provided a solution based on a randomised con-
trol strategy (using a Markovian Decision Process)
to obtain an aggregate model for a large number of
loads. Then, a so-called linear time-invariant sys-
tem approximation of the aggregate nonlinear model
is used for control design at grid level.
However, there are some proposals in the liter-
ature which do consider different kinds of uncer-
tainty in their optimisation algorithms (Moreno et al.,
2017). The authors in (Diekerhof et al., 2014) ap-
plied ADMM in a hierarchical architecture, and com-
bined it with robust optimisation and model predictive
control to handle uncertainty in heat pump schedul-
ing (Diekerhof et al., 2017). (Tajalli et al., 2021)
presented an approach for uncertainty aware manage-
ment of smart grids by using cloud based LSTM inter-
val prediction. (Chakraborty and Okabe, 2016) used
probabilistic programming approach that utilises a
Bayesian Markov Chain Monte Carlo (MCMC) sam-
pling method to create energy based balanced groups.
This allows grouping similar customers whose aggre-
gated demand has higher predictability. To face en-
ergy imbalance problem and cost reduction, the au-
thors proposed a multi-objective optimisation based
on ADMM for scheduling electrical storage units,
considering the demand uncertainty. (Zhang and Gi-
annakis, 2016) formulates a stochastic optimisation
problem based on ADMM also considering uncer-
tainty for market clearance. (Zhang et al., 2017)
contributes with a distributed robust optimiser, con-
sidering uncertainty, which uses the aggregation of
loads for service provision. Finally, (Dehghanpour
et al., 2017) also showed a hierarchical multi-agent
system framework for modelling demand response
of air conditioning loads with a day-ahead planning.
Such framework uses machine learning to model the
behaviours of agents at different levels of the frame-
work. The authors compared linear modelling and
ANN-based modelling to check the learning model
that provides more cut in the consumption cost and
maximise the benefits of the retailer.
As for the technologies used in the implementa-
tion of the algorithms that control microgrids, multi-
agent systems (MAS) technologies are considered
as potential solutions to the power industry pro-
viding flexible, extensible, and fault-tolerant solu-
tions (McArthur et al., 2007a; McArthur et al.,
2007b). They enable the implementation of large and
complex distributed applications by allowing the de-
velopment of autonomous control agents that are able
to coordinate in a cooperative and fault-tolerant en-
vironment (Al-Hinai and Alhelou, 2021). The dis-
tribution and communication characteristics of MASs
are attracting the attention in smart grids due to their
ability to unlock their potentials (Farhangi, 2010); i.e,
the autonomy of agents are adequate for the smart
devices, whereas the grid energy consumption and
production optimisation, usually performed by nego-
tiations, can be easily implemented using the agents
communication mechanisms and protocols.
Our system allows scheduling electrical units by
using the decentralised and distributed optimisation
algorithm (Kraning et al., 2014) that relies in local op-
timisations. Furthermore, it considers uncertainty in
the optimisation so that solutions become more stable
against not accurate predictions. Unlike the papers
mentioned in this section, our robust mechanism can
be adapted to any optimisation algorithm since it deals
with robustness within the cost function. Moreover
we introduce an uncertainty estimation which is only
calculated from forecasts and can be applied to any
device whose forecast values are considered for the
optimisation. This means that we do not need to cre-
ate a new robustness measure for each device model
since uncertainty is specifically computed for each de-
vice according to its historical observations and fore-
casts.
Towards a Robust, Distributed and Decentralised Smart Energy Management of Microgrids
17

3 BACKGROUND
Our proposal is based on a fully decentralised method
for dynamic network energy management that uses
message passing between entities (Kraning et al.,
2014).This work models a cooperation network com-
posed by two types of nodes, namely: the devices and
the nets. The devices (i.e. generators, fixed loads,
deferrable loads, alternate direct current transmission
lines, storage units, etc.) have their own constraints
and objectives. Devices are connected through ter-
minals to each other by means of a net (i.e. bus),
which also has its own objectives and constraints. In
the same way, nets are connected through double ter-
minal devices, such as transmission lines. A terminal
is a connection point or a link between the net and the
device.
The goal is to minimise the total network objec-
tive subject to device and net constraints over a time
horizon. For this, (Kraning et al., 2014) method re-
lies on the alternating direction method of multipliers
(ADMM), which is an algorithm that solves convex
optimisation problems by breaking them into smaller
pieces so that they will be then easier to handle (Boyd
et al., 2011).
By relaxing the equations (see (Kraning et al.,
2014) for details), the result is an iterative algorithm
that runs until the convergence criteria is satisfied.
Therefore at each iteration k the following operations
are performed in parallel:
• Every device d computes, for each termi-
nal, a new proximal power schedule p
d
=
[p
d
(1),..., p
d
(H)] ∈ R
H
that minimises a local ob-
jective function.
The problem is formulated as shown in Equa-
tion 1:
minimize
p
d
f
d
(p
d
) +
ρ
2
||p
d
− (p
k
d
− p
k
d
+ u
k
d
)||
2
2
subject to constraints
d
(1)
Formally, H is the number of time periods to
schedule (time horizon) and ρ is a scaling param-
eter. p
k
d
is the current power schedule of device
d computed in previous iteration, and p
k
d
the av-
erage of p
k
d
of each terminal (in case of just one
terminal devices p
k
d
= p
k
d
).
In the same way, u
d
= [u
d
(1),...,u
d
(H)] ∈ R
H
is
the scale price received from the net in the previ-
ous iteration. f
d
(p
d
) = c
d
(p
d
) represents the cost
function c
d
(p
d
) of applying p
d
to d. Note that
each kind of device has a specific c
d
(p
d
) formula.
However, solving the equation 1 also requires
to satisfy the constraints imposed by the device
model. Some of them are already considered
within the cost function c
d
(p
d
) of the device,
whereas local optimisers deal with the rest (see
section 5.1 for more details).
Finally, the device sends a message with p
d
to its
corresponding neighbour net(s). In case of two
terminal devices, the previous operations are re-
peated to compute p
d
for each net terminal.
• Every net n updates its scale price as u
n
= u
k
n
+ p
n
,
where p
n
is the average of all p
d
received from
their devices. Finally, u
n
is sent to all its linked
devices.
The authors showed that their approach converges
to a solution when the objectives and constraints of
the devices are convex. Such solution is decentralised
solution and needs no global coordination other than
synchronizing iterations; the problems to be solved
by each device can be locally solved efficiently and
in parallel according to the authors (Kraning et al.,
2014).
4 ROBUST DECENTRALISED
POWER SCHEDULING
OPTIMISER
This paper proposes a novel robust and decentralised
approach algorithm for solving power scheduling
problems in microgrids. Relying in the decentralised
method for dynamic network energy management
presented in section 3, we developed a robust adapta-
tion to deal with uncertainty of parameters during the
optimisation process. Our approach is implemented
within a distributed multi-agent system which allows
solving it in parallel.
In order to calculate the best power schedules
p
d
for each time period, the optimization algorithm
needs to know, in advance for these periods, the
power load curve for those devices whose regimes
cannot be controlled and the power curves estima-
tions (as maximum power generation, expected con-
sumption...) in case of self-controlled devices. Un-
fortunately, those forecasts are estimations about the
future which cannot be certain. Big deviations from
real conditions may lead to inefficient power sched-
ules that can provoke several losses as money, energy,
etc. A main contribution of this paper is the consider-
ation of such forecasts uncertainty to guide the opti-
misation process. We developed a robust mechanism
which, adapted within the cost function of those de-
vices subject to uncertainty, increases the reliability of
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
18

solutions by remaining more stable when unexpected
situations are faced.
The following Section 4.1 shows the implemen-
tation of the proposed approach whereas section 4.2
describes its robust mechanism.
4.1 Implementation
Our algorithm is implemented within a distributed
Multi-Agent System, which is based on the re-usable
architecture already introduced in (Garcia-Rodriguez
et al., 2016). Each device/net composing the micro-
grid is managed by an agent in our system which is in
charge of running a local optimisation and exchang-
ing messages with its neighbour agents. Since decen-
tralization allows distributed implementation, prob-
lem complexity is reduced by splitting computation
load in different nodes. Moreover, unlike centralised
systems which depend on a central node, our ap-
proach achieves smartness by the negotiation of all of
them. This way the probability of facing bottle neck
situations is significantly reduced.
Evolutionary computation (Zhang et al., 2011) is
selected for solving the local optimisation function of
equation 1. The use of this kind of algorithms is recur-
rent in the literature since they are proved to be good
approaches to solve microgrid problems (Sanseverino
et al., 2011). For instance, their flexibility allows to
handle most of the hard constraints in the optimisation
process (as the ones of transmission lines presented in
section 5.1). Moreover, their operators can be easily
modified to improve the algorithm performance in the
specific problem to solve. Our approach counts with
the following meta-heuristics:
• Mono-objective optimisers (problems with just
one objective function): naturally inspired algo-
rithms as particle swarm optimisation PSO (Chen
and Yu, 2005), differential evolution (Storn and
Price, 1997) or CMAES (Auger et al., 2004).
• Multi-objective optimisers (two or more objec-
tive functions): evolutionary algorithms such as
NSGA-II (Deb et al., 2002) or SPEA2 (Zitzler
et al., 2001).
Thanks to the architecture of our frame-
work (Garcia-Rodriguez et al., 2016), algorithms can
be easily added/replaced. This allowed us choosing
the best one for each local cost function.
4.2 Dealing with Uncertainty
The robust method presented here is applicable when
device forecasts (that are subject to uncertainty) are
used to optimise the microgrid power schedules.
Based on historical forecasts and observations, our
approach guides the optimisation process towards so-
lutions that shall remain stable even when forecasts
result to be very inaccurate. The main strength of this
approach lies in the use of a penalty factor, w
d
(p
d
),
used to penalise the device cost function f
d
(p
d
) of
Equation 1. The fact of placing such penalty within
the device cost function makes it easily adaptable to
any other optimisation algorithm. The penalty fac-
tor is computed for each device d according to its
proposed power schedule p
d
and its historical set of
observations-forecasts.
Therefore, for any device d whose forecasts are
used for optimising its power schedule over a time
horizon H, we can apply the robust improvement that
works as a two-phase algorithm.
4.2.1 First Phase
It is run offline and before the optimisation process
starts. Relying in the set of historical pairs forecasted-
observed parameters of the device, it computes three
values that will be used in the second phase:
• O f
d
: proportion of all observed values of d that
were greater than their forecasts in the historical
observations-forecasts set. O f
d
∈ [0, 1].
• Fo
d
: proportion of all observed values of d that
were smaller than their forecasts in the historical
observations-forecasts set. Fo
d
∈ [0, 1].
• UF
d
: performance of the forecast algorithm used
for computing the forecast parameters of the de-
vice. Its value is calculated in Equation 2 by
measuring the absolute proportional deviation be-
tween the historical real observations and their
corresponding forecasts over the time periods
[1...H] to be optimised:
UF
d
=
1
max
d
∗ H
H
∑
t=1
| f p
d
(t) − op
d
(t)| (2)
where H is the time horizon; f p
d
(t) is the fore-
casted parameter and op
d
(t) the observed param-
eter, both for time periods t ∈ [1...H]; and max
d
the maximum observed value registered in device
d.
4.2.2 Second Phase
It is called each time the optimisation algorithm eval-
uates the cost function of Equation 1. The steps fol-
lowed in this phase (see Algorithm 1) give an eval-
uation of the risk and negative impact of applying
the power schedule p
d
to device d. Such evaluation
Towards a Robust, Distributed and Decentralised Smart Energy Management of Microgrids
19

(penalty factor) is used to guide the optimisation to-
wards robust solutions.
For each time period (line 2), algorithm 1 first es-
timates the possible deviations of the proposed power
schedule p
d
(line 9). Then, considering the im-
port/export prices and constraints, it computes the
corresponding cost of those deviations from apply-
ing the proposed power schedule p
d
to a full power
control device (lines 10-17) or to a ON/OFF control
device (lines 18-26). The algorithm returns such cost
as a penalty factor w
d
(p
d
) which is then used within
the device cost function f
d
(p
d
) so that f
d
(p
d
) =
w
d
(p
d
) + c
d
(p
d
).
Algorithm 1: Robustness. Phase 2.
1: INPUTS: p
d
; f p
d
; op
d
; U F
d
; [O f
d
; Fo
d
]; H as the time
horizon;
[imp,exp] as imported/exported energy cost established
by the utility:
imp/exp > 0 microgrid pays,
imp/exp < 0 microgrid is paid,
exporting energy not allowed: exp(t) == ∞,
importing energy not allowed: imp(t) == ∞.
2: for all t ∈ H do
3: if imp(t) < 0 then
4: imp(t) = 0
5: end if
6: if exp(t) < 0 then
7: exp(t) = 0
8: end if
9: dev(t) = |p
d
(t) ∗UF
d
+ p
d
(t)|
10: if device d allows full control then
11: if dev(t) > f p
d
(t) then
12: if imp(t) = ∞ then
13: acum+ = O f
d
∗ exp(t) ∗ (dev(t) − f p
d
(t))
14: else
15: acum+ = O f
d
∗ imp(t) ∗ (dev(t) − f p
d
(t))
16: end if
17: end if
18: else
19: if exp(t) = ∞ then
20: acum+ = (Fo
d
∗ imp(t) + O f
d
∗ imp(t)) ∗
(dev(t) − f p
d
(t))
21: else if imp(t) = ∞ then
22: acum+ = (Fo
d
∗ exp(t) + O f
d
∗ exp(t)) ∗
(dev(t) − f p
d
(t))
23: else
24: acum+ = (Fo
d
∗ exp(t) + O f
d
∗ imp(t)) ∗
(dev(t) − f p
d
(t))
25: end if
26: end if
27: end for
28: w
d
(p
d
) = |acum|
29: OUTPUT: w
d
(p
d
)
Note that the value of w
d
(p
d
) varies since its de-
pends on the power schedule p
d
, the performance
of the forecaster in such device, and the export-
ing/importing energy costs and constraints.
5 SYSTEM VALIDATION
5.1 Experimental Set-up
The algorithm proposed in this paper is devel-
oped within the framework presented by (Garcia-
Rodriguez et al., 2016), which was extended in order
to implement our solution. Developed in Java, such
framework allocates all the optimisation algorithms
and implements the message passing strategy. Two
main entities that exchange messages in the system
are created, namely: devices and nets, which are rep-
resented as agents. Each kind of agent has its own
behaviours, which define the identity of the agent.
Therefore, two sets of behaviours can be assigned to
an agent: the first one is to use the agent as a device,
whereas the second one is for net agents.
Among the different integrated metaheuristics to
solve the local optimisations, three mono-objective
algorithms (CMAES(Auger et al., 2004), DE(Storn
and Price, 1997) and PSO(Chen and Yu, 2005))
were chosen for the experimental part. Their
setup is as follows: DE and CMAES with a
population size = 50 and maximum evaluations =
250000; CMAES also adds CR = F = 0.5; and PSO
with archive size = 50, maximum iterations = 5000
and mutation probability = 0.4.
Experimentation was performed over multiple
scenarios. We call “scenario” to a specific config-
uration defined by microgrid topology (devices def-
inition and constraints), buying/selling energy costs,
power limits of devices, and fix power consump-
tion/generation curves. The combination of all these
values would generate a huge number of scenarios,
however just some of them would represent feasible
real-world situations. Our approach was tested on a
nine-bus scenario that follows the “Western System
Coordinating Council” (WSCC)(Paul M. Anderson,
2003) electrical grid topology. With the aim of per-
forming a complete validation, we increased the com-
plexity of such grid to consider 9 transmission lines, 3
consumers, 3 photovoltaic generators, 5 wind genera-
tors and the connection to the external power system.
Consumers follow a fix power schedules but all gen-
erators can be controlled. True historical time series
data sets that contain pairs of forecasts-observations
were utilised for solar (National Renewable Energy
Laboratory, 2006a) and wind generation (National
Renewable Energy Laboratory, 2006b). Forecasts
were employed to run the optimisations whereas ob-
servations were used to evaluate the performance of
the solutions. Figure 1 shows the agents deployed by
our system to solve this test scenario.
In order to emulate the real world, a sliding win-
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
20
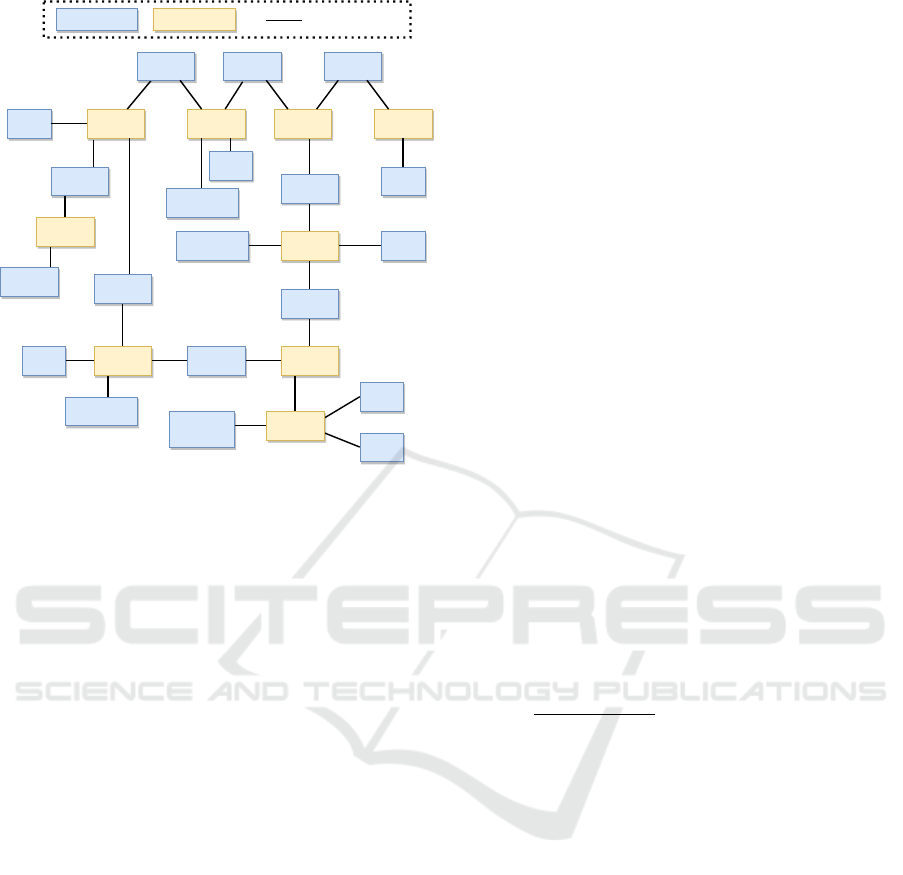
Bus 7 Bus 3
Bus 5
Bus 2
Bus 6
Bus 1
Bus 4
Bus 8 Bus 9
Wind
PV
Line 7-8 Line 8-9
Line 4-6
Line 3-9
Line 6-9
Line 2-7
Line 5-4
Consumer
Line 5-7
Consumer
PV
Wind
PV
Consumer
PV
Wind
External
Tie
PV
Device Agent Net Agent
Communication
Link
PV = Photovoltaic Generator.
Wind = Windturbine Generator.
Line X-Y = Transmission Line between Bus X to Bus Y.
Figure 1: Test Scenario: Agents deployment.
dow that contains a horizon of H = 12 periods of
hourly time-series (half a day) was moved all across
each month of real data. At each step, the window
moves one hour period and the whole set of experi-
ments is run again. We chose three months (January,
May and September) that cover the most representa-
tive climate conditions of a year for the studied re-
gions. In addition, two pairs of buying-selling energy
prices are tested. Buying price corresponds to the cost
of importing energy to the grid from the external util-
ity, and selling price is the cost when energy is ex-
ported. In order to avoid stochastic solutions, each
single experiment was repeated 10 times. Averages
and standard errors are calculated for all the results.
5.2 Device Modeling
To compute the testing scenario, our framework de-
ploys a multi-agent system composed of 18 agents
(one per device/bus of the microgrid) that run their
own local optimisation and negotiate by exchanging
messages. Following the notation of section 3, the
different kinds of devices are modelled as follows:
• Consumers (non controllable) as fixed loads. It
is a single terminal device with zero cost function
c
d
(p
d
) = 0. Considering H as the time horizon of
the optimisation, these devices must satisfy a ex-
pected consumption profile l = [l
d
(1),...,l
d
(H)] ∈
R
H
at each period, which sets the constraint:
p
d
(t) = l
d
(t), ∀t ∈ [1, ..,H].
• Photovoltaic and wind plants (controllable) as
generators. Single terminal device that generates
power over a range and imposes the constraint
P
min
d
(t) ≤ −p
d
(t) ≤ P
max
d
(t), ∀t ∈ [1, ...,H] .
The values [P
min
d
,P
max
d
] are defined by forecasts.
The cost function is c
d
(p
d
) =
∑
H
t=1
α(−p
d
(t))
where α > 0.
• Connection to the external power system as ex-
ternal tie. It counts with one terminal and consid-
ers the cost of importing energy from the source
as imp
d
= [imp
d
(1),...,imp
d
(H)] ∈ R
H
(buying),
and the cost of exporting to the source as exp
d
=
[exp
d
(1),...,exp
d
(H)] ∈ R
H
(selling).
We define its cost function as c
d
(p
d
) =
∑
H
t=1
−η
T
(t)p
d
(t) + γ
T
(t)|p
d
(t)|, where η
T
(t) =
(imp
d
(t) + exp
d
(t))/2 and γ
T
(t) = (imp
d
(t) −
exp
d
(t))/2, ∀t ∈ [1, ..,H].
• Lines that connect the elements as DC transmis-
sion lines. These devices have two terminals since
they transport power through a distance, which is
also subject to energy losses. Therefore, it has
zero cost function (c
d
(p
d
) = 0), but the power
flows are constrained: considering p
d1
as input
power and p
d2
as output power, the line has a
maximum flow capacity given by:
p
d1
(t) − p
d2
(t)
2
≥ C
max
,∀t ∈ [1, .., H]
(3)
where C
max
is a capacity constraint. It also
imposes a line loss constraint: p
d1
+ p
d2
−
`(p
d1
, p
d2
) = 0, where `(p
d1
, p
d2
): R
H
× R
H
R
H
+
is a loss function.
Following the convention used by Kraning et
al.(Kraning et al., 2014), p
d
< 0 when a device d is
giving energy to the grid and p
d
> 0 when consum-
ing.
5.3 Results Discussion
This section reports on the results of the three approx-
imations used:
• Robust Optimisation -Robust Opt-: decentralised
robust optimisation algorithm presented in this
paper (our approach).
• Standard Optimisation -Stand Opt-: decen-
tralised optimisation algorithm for energy net-
works (Kraning et al., 2014) without considering
uncertainty in parameters.
Towards a Robust, Distributed and Decentralised Smart Energy Management of Microgrids
21

• Non Optimisation -No Opt-: non-optimised ap-
proach were all generators are by default con-
nected at the maximum generation rate. It repre-
sents how a real microgrid would behave without
any smart control.
The three approaches are tested in the same sce-
narios so that their performance results are side-by-
side comparable.
When running the experimentation, we emulated
how the put in practice of the algorithms would be.
First, the optimisation is run relying in forecasted pa-
rameters (real time observations cannot be known a
priori) to get the optimal configurations (power sched-
ules) and their corresponding cost values. Then, fore-
casts are replaced by real observations and are used
to test such configurations. Finally, we compare the
deviations in terms of cost that those configurations
get from forecasted parameters (what it is expected to
find) to the observed ones (what it was faced in the
reality).
The results are shown in two tables: i) Table 2
considers exporting the energy selling as almost free,
whereas ii) Table 1 imposes to both exporting or im-
porting energy from the microgrid an associated cost.
These tables show:
• Its.: average number of iterations used by the al-
gorithm to reach the solution.
• Average Cost (C): statistics calculated over the
energy cost, measured in cost units (u). It can
be seen as the average cost across all the exper-
iments. (True currencies and electrical prices are
omitted for the validation phase).
• SEM Cost: the standard deviation of the sample-
mean’s estimate, known as “standard error of the
mean” (Barde and Barde, 2012).Both Average
Cost and SEM Cost are calculated for the same
scenarios using the theoretical situation (fore-
casted parameters) and then the real parameters
(the ones observed a posteriori).
• Cost Saving (CSv): percentage of cost saved when
running the robust optimisation over the stan-
dard optimisation (percentage over its average
cost). Its formula is defined in eq. 4 where C
i, j
is the average cost of the approach i (standard
or robust optimization) using j parameters (fore-
casts//expected or real/observed ones).
CSv =
1 −
C
real,robust
−C
f orecast,robust
C
real,stand
−C
f orecast,stand
!
∗ 100 (4)
Results in Table 1 are computed in the scenarios
where exporting and importing energy from the mi-
crogrid is penalised with 10u. The three tested months
show a similar tendency. We first compare a non-
optimised microgrid with the other two approaches to
prove that, in any case, optimisation is always nec-
essary to reduce costs (between 7000 and 42000 (u)
over the non-optimisations). The expected average
costs for standard optimisations in forecast scenarios
differ, in about 1200 (u), from the average of same
schedules but tested with real parameters. However,
robust optimisations yield much smaller deviations.
Actually, the robust optimiser reduces from 6.68% to
60.83% the average cost error over the standard opti-
miser. SEM in tables is low, which indicates few de-
viations over the average (between ±0.1 and ±1.3).
Moreover the number of iterations of both robust and
standard optimisation approaches are similar, which
makes computational effort similar too.
When analysing Table 2 (exporting energy penalty
very low), results show a similar tendency. Aver-
ages and SEMs are usually lower in non optimisa-
tion experiments, which is logical since in this case
exporting energy is almost not penalised. We also ob-
serve that the robust approach gets positive savings
in the three months, from 4.7 to 20.03% of reduc-
tion over the non robust optimisations. September
presents similar cost values as in Table 1, but May and
January are slightly different. May has a similar cost
saving but over lower average and SEM values; this
is probably because in some periods of this scenario
not all the energy produced was consumed and there-
fore it was exported out of the grid. January is the
month with less improvement. It is also the hardest
scenario to be optimised since the optimisers took re-
markably more iterations to solve it, the average costs
are closer (but still smaller) to the non-optimised case,
and SEMs are much higher as well.
Tables 3 and 4 compare the performance of the
three approaches from a different point of view. They
show the proportional cost reduction when optimised
schedules face the real scenarios or, in other words,
“how much the user would save in the real life”. In
general, and as expected, we observe that optimisa-
tions highly outperformed the standard configurations
of the microgrid. In the same line, power schedules
computed using the robust optimiser originated sig-
nificantly smaller costs than the non robust optimised
solutions and, therefore, such difference was bigger
when compared to the basic (non optimised) configu-
rations of the microgrid.
A question that raises observing the results is why
the percentage of saving cost varies up to 15% de-
pending of the months. This is due to the variation of
the weather conditions and, in consequence, the max-
imum capacity of production. Furthermore, each sce-
nario presents different flexibilities, allowing differ-
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
22
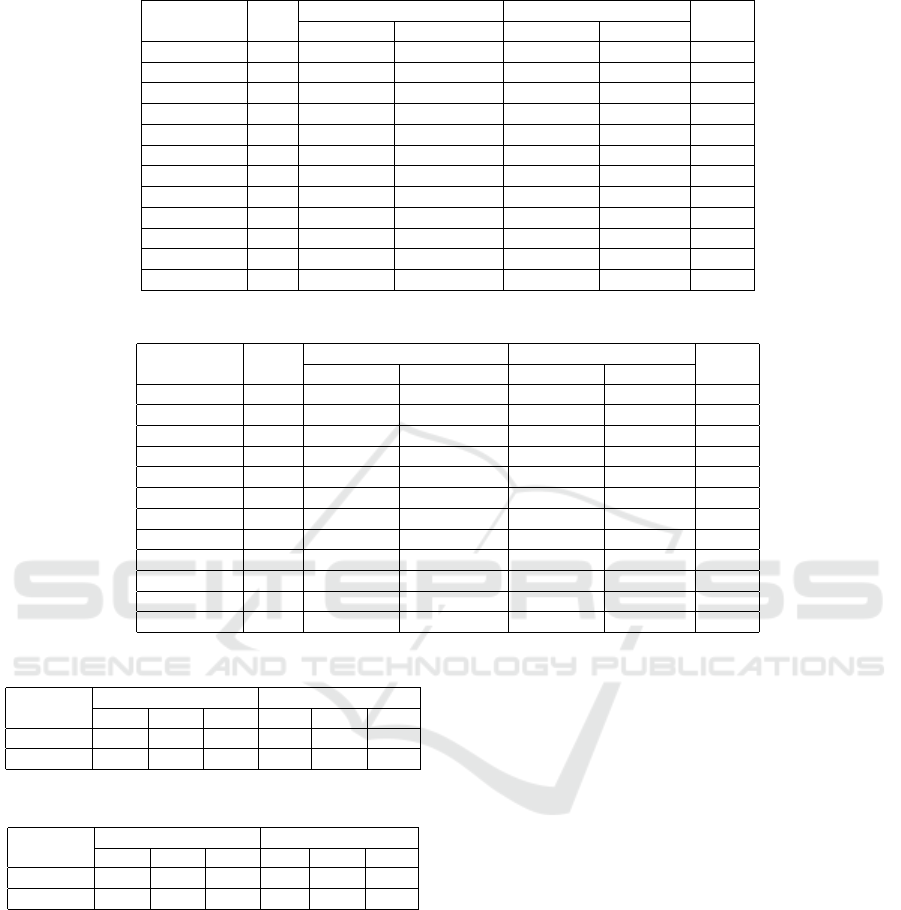
Table 1: Experimental results for energy costs: selling = 10(u/kW); buying = 10(u/kW).
Approach Its.
Average Cost (u) SEM Cost (u) CSv
(%)Forecasts Real Forecasts Real
January
No Opt – – 14337.6350 – 54.1596
Stand Opt 302 212.3893 317.4002 0.0276 0.3795
Robust Opt 302 278.6910 319.8174 0.1968 0.2539 60.83
May
No Opt – – 8935.7970 – 27.2481
Stand Opt 484 0.0000 1344.7288 0.0000 0.0408
Robust Opt 421 0.0002 1079.0624 0.0000 0.1037 19.75
September
No Opt – – 12172.7330 – 317.7966
Stand Opt 583 660.3829 2044.1316 0.5466 1.3871
Robust Opt 561 655.6976 1947.0089 0.5607 0.0193 6.68
Table 2: Experimental results for energy costs: selling = 1(u/kW); buying = 10(u/kW).
Approach Its.
Average Cost (u) SEM Cost (u) CSv
(%)Forecasts Real Forecasts Real
January
No Opt – – 2581.5314 – 182.1753
Stand Opt 1694 285.3534 2232.0703 29.3623 112.9993
Robust Opt 1607 273.1762 2128.1336 28.6996 111.1019 4.71
May
No Opt – – 6052.6184 – 374.7932
Stand Opt 421 0.0051 133.3903 0.0001 0.1081
Robust Opt 428 0.0080 106.6703 0.0002 0.0835 20.03
September
No Opt – – 10300.3550 – 465.0780
Stand Opt 1445 681.2515 2043.7722 0.9455 1.5547
Robust Opt 2158 682.8970 1955.0863 0.9505 0.1233 6.62
Table 3: Cost Saving (%) of Table 1.
10/10
No Opt Stand Opt
Jan. May Sept. Jan. May Sept.
Stand Opt 97.78 84.95 83.20 – – –
Robust Opt 97.76 87.92 84.00 -0.76 19.75 4.75
Table 4: Cost Saving (%) of Table 2.
1/10
No Opt Stand Opt
Jan. May Sept. Jan. May Sept.
Stand Opt 13.53 97.79 80.15 – – –
Robust Opt 17.56 98.23 81.01 4.65 20.03 4.33
ent degrees of optimisations. Note that the proposed
approach is more effective in more flexible scenarios
where the algorithm has more freedom to control. For
instance, in a scenario in which all devices that rely on
forecasts can be fully controlled, the robust optimisa-
tion would outperform the standard one. However,
low level of flexibility will tend to approach robust
optimisations costs to standard optimisation ones. In
conclusion: the more flexible the scenario it is, the
greater cost can be saved.
Summarising, Tables 1 to 4 showed how, for all
experiments, the robust optimisation provided micro-
grid configurations (power schedules) with the lowest
cost values. The same way, such approach performed
better when facing more flexible scenarios.
6 CONCLUSIONS AND FUTURE
LINES
In the last decades the interests and efforts for bring-
ing intelligence to conventional power grids are in-
creasing more and more. The emerge of smart grids
with distributed electrical resources keeps calling for
automatic, and distributed, control which looks for the
best decisions to make. Such search usually poses an
optimisation problem where the looking for good so-
lutions is gaining track in the research field. Many
algorithms have been proposed in the literature but
only few of them can operate in a distributed manner.
Moreover, when the solutions are schedules that shall
be used in the near future, forecasts are usually con-
sidered in the optimisation process. Unfortunately,
forecasts are never 100% accurate and, as a conse-
quence, optimisations are not usually reliable.
We propose a decentralised optimisation algo-
rithm that, implemented in a distributed manner by
Towards a Robust, Distributed and Decentralised Smart Energy Management of Microgrids
23

a multi-agent system, considers the uncertainty of the
parameters in the optimisation process. Our approach
deals with such uncertainty through a robust mecha-
nism which is added to the optimiser. Our solution
was tested and compared with the base line showing
the efficiency of this technique since the costs of the
optimized schedules computed for all tested scenarios
were significantly reduced.
Our approach can be extended in many directions
in the future: i.e., it would be interesting to explore the
optimisation from a multiobjective point of view by
considering several goals. Another interesting study
would be the collective uncertainty; i.e., to study how
forecasts of devices situated nearby by could present
the same deviations tendency. Finally, a software
analysis on how to implement and deploy the ap-
proach in a real microgrid is also a step to follow.
ACKNOWLEDGEMENTS
This work was supported by the European Commu-
nity’s Seventh Framework Programme under Grant
Agreement no. 619682 (Project MAS2TERING) and
by ITEA 2 call 8 (Project 13023 FUSE-IT).
REFERENCES
Al-Hinai, A. and Alhelou, H. H. (2021). A multi-agent
system for distribution network restoration in future
smart grids. Energy Reports.
Amin, S. and Wollenberg, B. (2005). Toward a smart grid:
Power delivery for the 21st century. IEEE Power En-
ergy Mag, 3:34 – 41.
Auger, A., Schoenauer, M., and Vanhaecke, N. (2004).
Ls-cma-es: A second-order algorithm for covariance
matrix adaptation. In Parallel Problem Solving from
Nature-PPSN VIII, pages 182–191. Springer.
Barde, M. P. and Barde, P. J. (2012). What to use to ex-
press the variability of data: Standard deviation or
standard error of mean? Perspectives in clinical re-
search, 3(3):113.
Boyd, S., Parikh, N., Chu, E., Peleato, B., and Eck-
stein, J. (2011). Distributed Optimization and Statis-
tical Learning via the Alternating Direction Method
of Multipliers. Foundations and Trends in Machine
Learning, 3(1):1–122.
Chakraborty, S. and Okabe, T. (2016). Robust energy
storage scheduling for imbalance reduction of strate-
gically formed energy balancing groups. Energy,
114:405–417.
Chen, G.-c. and Yu, J.-s. (2005). Particle swarm optimiza-
tion algorithm. INFORMATION AND CONTROL-
SHENYANG-, 34(3):318.
Colak, I., Sagiroglu, S., Fulli, G., Yesilbudak, M., and Cov-
rig, C.-F. (2016). A survey on the critical issues in
smart grid technologies. Renewable and Sustainable
Energy Reviews, 54:396 – 405.
Dantzig, G. B. and Wolfe, P. (1960). Decomposition
principle for linear programs. Operations research,
8(1):101–111.
de Cerio Mendaza, I. D., Szczesny, I. G., Pillai, J. R., and
Bak-Jensen, B. (2016). Demand response control in
low voltage grids for technical and commercial aggre-
gation services. IEEE Transactions on Smart Grid,
7(6):2771–2780.
Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002).
A fast and elitist multiobjective genetic algorithm:
NSGA-II. IEEE Transactions on Evolutionary Com-
putation, 6(2):182–197.
Deconinck, G., Vanthournout, K., Beitollahi, H., Qui, Z.,
Duan, R., Nauwelaers, B., Van Lil, E., Driesen, J., and
Belmans, R. (2008). A robust semantic overlay net-
work for microgrid control applications. In Architect-
ing Dependable Systems V, pages 101–123. Springer.
Dehghanpour, K., Nehrir, H., Sheppard, J., and Kelly, N.
(2017). Agent-based modeling of retail electrical en-
ergy markets with demand response. IEEE Transac-
tions on Smart Grid.
Diekerhof, M., Peterssen, F., and Monti, A. (2017). Hi-
erarchical distributed robust optimization for demand
response services. IEEE Transactions on Smart Grid.
Diekerhof, M., Schwarz, S., and Monti, A. (2016).
Distributed optimization for electro-thermal heating
units. In PES Innovative Smart Grid Technologies
Conference Europe (ISGT-Europe), 2016 IEEE, pages
1–6. IEEE.
Diekerhof, M., Vorkampf, S., and Monti, A. (2014).
Distributed optimization algorithm for heat pump
scheduling. In Innovative Smart Grid Technologies
Conference Europe (ISGT-Europe), 2014 IEEE PES,
pages 1–6. IEEE.
Farhangi, H. (2010). The path of the smart grid. IEEE
Power Energy Mag, 8:18 – 28.
Gamarra, C. and Guerrero, J. M. (2015). Computational op-
timization techniques applied to microgrids planning:
a review. Renewable and Sustainable Energy Reviews,
48:413–424.
Garc
´
ıa, S., Quintana, D., Galv
´
an, I. M., and Isasi, P.
(2012). Time-stamped resampling for robust evolu-
tionary portfolio optimization. Expert Systems with
Applications, 39(12):10722–10730.
Garcia-Rodriguez, S., Sleiman, H. A., and Nguyen, V.-Q.-
A. (2016). A multi-agent system architecture for mi-
crogrid management. In Trends in Practical Appli-
cations of Scalable Multi-Agent Systems, the PAAMS
Collection, pages 55–67. Springer International Pub-
lishing.
Gomez-Sanz, J. J., Garcia-Rodriguez, S., Cuartero-Soler,
N., and Hernandez-Callejo, L. (2014). Reviewing mi-
crogrids from a multi-agent systems perspective. En-
ergies, 7(5):3355–3382.
Haring, T. W., Mathieu, J. L., and Andersson, G. (2016).
Comparing centralized and decentralized contract de-
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
24

sign enabling direct load control for reserves. IEEE
Transactions on Power Systems, 31(3):2044–2054.
Kraning, M., Chu, E., Lavaei, J., and Boyd, S. (2014). Dy-
namic network energy management via proximal mes-
sage passing. Foundations and Trends in Optimiza-
tion, 1(2):73–126.
Liang, H. and Zhuang, W. (2014). Stochastic modeling
and optimization in a microgrid: A survey. Energies,
7(4):2027–2050.
Mahat, P., Escribano Jim
´
enez, J., Moldes, E. R., Haug,
S. I., Szczesny, I. G., Pollestad, K. E., and Totu, L. C.
(2013). A micro-grid battery storage management. In
2013 IEEE PES General Meeting.
McArthur, S. D., Davidson, E. M., Catterson, V. M.,
Dimeas, A. L., Hatziargyriou, N. D., Ponci, F., and
Funabashi, T. (2007a). Multi-agent systems for
power engineering applications-part i: Concepts, ap-
proaches, and technical challenges. IEEE Transac-
tions on Power systems, 22(4):1743–1752.
McArthur, S. D., Davidson, E. M., Catterson, V. M.,
Dimeas, A. L., Hatziargyriou, N. D., Ponci, F., and
Funabashi, T. (2007b). Multi-agent systems for power
engineering applications-part ii: Technologies, stan-
dards, and tools for building multi-agent systems.
IEEE Transactions on Power Systems, 22(4):1753–
1759.
McNamara, P. and McLoone, S. (2015). Hierarchical de-
mand response for peak minimization using dantzig–
wolfe decomposition. IEEE Transactions on Smart
Grid, 6(6):2807–2815.
Mesaric, P., Dukec, D., and Krajcar, S. (2017). Exploring
the potential of energy consumers in smart grid using
focus group methodology. Sustainability, 9(8):1463.
Meyn, S. P., Barooah, P., Bu
ˇ
si
´
c, A., Chen, Y., and Ehren,
J. (2015). Ancillary service to the grid using intel-
ligent deferrable loads. IEEE Transactions on Auto-
matic Control, 60(11):2847–2862.
Mihaylov, M., R
˘
adulescu, R., Razo-Zapata, I., Jurado, S.,
Arco, L., Avellana, N., and Now
´
e, A. (2019). Com-
paring stakeholder incentives across state-of-the-art
renewable support mechanisms. Renewable energy,
131:689–699.
Moghaddam, A. A., Seifi, A., Niknam, T., and Pahlavani,
M. R. A. (2011). Multi-objective operation manage-
ment of a renewable {MG} (micro-grid) with back-up
micro-turbine/fuel cell/battery hybrid power source.
Energy, 36(11):6490 – 6507.
Mohamed, F. A. and Koivo, H. N. (2007). System mod-
elling and online optimal management of microgrid
using multiobjective optimization. In Clean Electri-
cal Power, 2007. ICCEP’07. International Conference
on, pages 148–153. IEEE.
Moreno, R., Street, A., Arroyo, J. M., and Mancarella,
P. (2017). Planning low-carbon electricity systems
under uncertainty considering operational flexibility
and smart grid technologies. Phil. Trans. R. Soc. A,
375(2100):20160305.
National Renewable Energy Laboratory (2006a). So-
lar integration data sets. https://www.nrel.gov/grid/
solar-integration-data.html.
National Renewable Energy Laboratory (2006b). Wind
integration data sets. https://www.nrel.gov/grid/
wind-integration-data.html.
Paul M. Anderson, A. A. F. (2003). Power System Control
and Stability, 2nd. IEEE Press, New York.
Ramaswamy, P. and Deconinck, G. (2012). Smart grid
reconfiguration using simple genetic algorithm and
nsga-ii. In Innovative Smart Grid Technologies (ISGT
Europe), 2012 3rd IEEE PES International Confer-
ence and Exhibition on, pages 1–8.
Rivera, J., Goebel, C., and Jacobsen, H.-A. (2017). Dis-
tributed convex optimization for electric vehicle ag-
gregators. IEEE Transactions on Smart Grid.
Saad, W., Han, Z., Poor, H. V., and Basar, T. (2012). Game-
theoretic methods for the smart grid: An overview
of microgrid systems, demand-side management, and
smart grid communications. IEEE Signal Processing
Magazine, 29(5):86–105.
Sanseverino, E. R., Di Silvestre, M. L., Ippolito, M. G.,
De Paola, A., and Re, G. L. (2011). An execution,
monitoring and replanning approach for optimal en-
ergy management in microgrids. Energy, 36(5):3429–
3436.
Storn, R. and Price, K. (1997). Differential evolution–a
simple and efficient heuristic for global optimization
over continuous spaces. Journal of global optimiza-
tion, 11(4):341–359.
Tajalli, S. Z., Kavousi-Fard, A., Mardaneh, M., Khosravi,
A., and Razavi-Far, R. (2021). Uncertainty-aware
management of smart grids using cloud-based lstm-
prediction interval. IEEE Transactions on Cybernet-
ics.
Tuballa, M. L. and Abundo, M. L. (2016). A review of the
development of smart grid technologies. Renewable
and Sustainable Energy Reviews, 59:710 – 725.
Veldman, E., Gibescu, M., Slootweg, H. J., and Kling, W. L.
(2013). Scenario-based modelling of future residen-
tial electricity demands and assessing their impact on
distribution grids. Energy Policy, 56:233–247.
Zhang, J., Zhan, Z.-h., Lin, Y., Chen, N., Gong, Y.-j.,
Zhong, J.-h., Chung, H. S., Li, Y., and Shi, Y.-h.
(2011). Evolutionary computation meets machine
learning: A survey. IEEE Computational Intelligence
Magazine, 6(4):68–75.
Zhang, Y. and Giannakis, G. B. (2016). Distributed stochas-
tic market clearing with high-penetration wind power.
IEEE Transactions on Power Systems, 31(2):895–906.
Zhang, Y., Shen, S., and Mathieu, J. L. (2017). Distribu-
tionally robust chance-constrained optimal power flow
with uncertain renewables and uncertain reserves pro-
vided by loads. IEEE Transactions on Power Systems,
32(2):1378–1388.
Zitzler, E., Laumanns, M., and Thiele, L. (2001). SPEA2:
Improving the strength pareto evolutionary algorithm.
Technical Report 103, Computer Engineering and
Networks Laboratory (TIK), Swiss Federal Institute
of Technology (ETH), Zurich, Switzerland.
Towards a Robust, Distributed and Decentralised Smart Energy Management of Microgrids
25
