Time Series Augmentation based on Beta-VAE to Improve Classification
Performance
Domen Kavran, Borut
ˇ
Zalik and Niko Luka
ˇ
c
Faculty of Electrical Engineering and Computer Science, University of Maribor, Koro
ˇ
ska ulica 46, Maribor, Slovenia
Keywords:
Time Series, Augmentation, Classification, Variational Autoencoder, Beta-VAE.
Abstract:
Classification models that provide good generalization are trained with sufficiently large datasets, but these
are often not available due to restrictions and limited resources. A novel augmentation method is presented
for generating synthetic time series with Beta-VAE variational autoencoder, which has ResNet-18 inspired
architecture. The proposed augmentation method was tested on benchmark univariate time series datasets. For
each dataset, multiple variational autoencoders were used to generate different amounts of synthetic time series
samples. These were then used, along with the original train set samples, to train MiniRocket classification
models. By using the proposed augmentation method, a maximum increase of 1,22% in classification accuracy
was achieved on the tested datasets in comparison to baseline results, which were obtained by training only
with original train sets. An increase of up to 0,81% in accuracy of simple machine learning classifiers was
observed by benchmarking the proposed augmentation method with the 1-nearest neighbor algorithm.
1 INTRODUCTION
Technologically advanced industries generate
structured and unstructured big data with various
device-mounted sensors and software tools. Year by
year the rise in quantity of big data is correlated with
the expansion of Internet of Things (IoT) devices.
Their integration ranges from home appliances and
medical equipment to construction machines and
Unmanned Aerial Vehicles (UAVs). One of the most
common data types are time series. Large quantities
of time series are produced in the medical, automotive
and financial industries (Lines et al., 2017). Time
series contain measurements of observed quantities
over time, most commonly being physical quantities
(e.g. electric current, and temperature) and web
activity (e.g. media streaming). Analysis of time
series is challenging, because the acquired time series
can be high-dimensional, noisy, and may contain data
gaps (Gian Antonio et al., 2018).
Time series classification is an important part of
many advanced software applications, ranging from
identification of various anomalies and safety hazards
to recognition of medical conditions and diseases
(Lines et al., 2017). Large time series datasets are
needed to train robust state-of-the-art classification
models. Datasets are most commonly prepared
by domain experts, who hand label collected data.
That approach is time consuming, and expensive for
larger amounts of samples. Often many samples are
not available for experts to label, which harms the
generalization property of the trained models. To
solve the described problems, hand labeling can still
be performed on smaller, representative sets of time
series, although these are then used for augmentation
methods to create additional samples to be used
in the training process. Time series augmentations
are not as trivial as image augmentation techniques
(e.g. cropping, rotating, scaling), because changes
in time series can deteriorate underlying properties
of the original data (Oh et al., 2020). An alternative
approach for augmentations is generation of synthetic
data with generative models.
The proposed paper presents a novel
augmentation method for generating synthetic
time series with a residual neural network (ResNet)
based variational autoencoder, which applies
stronger constraint on the latent bottleneck, thus
making encodings disentangled. By manipulating
disentangled latent factors, individual time series
characteristics are controlled to generate new time
series samples. These are then, along with the
original train data, used for training classification
models. In the presented paper, the MiniRocket
classification algorithm was used, due to its low
computational complexity (Dempster et al., 2020).
Kavran, D., Žalik, B. and Luka
ˇ
c, N.
Time Series Augmentation based on Beta-VAE to Improve Classification Performance.
DOI: 10.5220/0010749200003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 2, pages 15-23
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
15

This paper consists of five sections. The
next section presents related work about
state-of-the-art time series classification algorithms
and augmentation methods. The third section
presents the proposed augmentation method for
generating synthetic time series samples. In the same
section, we also present the MiniRocket classification
algorithm. The effects of sythetic time series on
classification performance are presented in the fourth
section. The conclusions are given in the last section.
2 RELATED WORK
In this section, we first present current state-of-the-art
time series classification algorithms. Advanced
augmentation methods for time series data are
presented in subsection 2.2.
2.1 Time Series Classification
Many state-of-the-art classification algorithms have
been developed in recent years. Hierarchical Vote
Collective of Transformation-based Ensembles
(HIVE-COTE) is an ensemble of time series
classifiers, trained in multiple domains, including
shapelets and bag-of-words dictionaries (Lines
et al., 2017). HIVE-COTE achieved the highest
classification accuracies on benchmark datasets
compared to other state-of-the-art classifiers,
although it has very high computational complexity,
which makes it impractical to use in real-world
applications. A deep learning ensemble of five deep
Convolutional Neural Networks (CNNs), named
InceptionTime, has proven to achieve state-of-the-art
classification accuracies, while having much
lower training time complexity than HIVE-COTE
(Ismail Fawaz et al., 2020). Rocket, and its improved
version MiniRocket, are algorithms which achieve
state-of-the-art time series classification accuracies.
Both have very low computational complexity, but
MiniRocket is capable of being up to 75 times
faster than Rocket, while still achieving essentially
the same accuracy (Dempster et al., 2020). The
recently developed HIVE-COTE 2.0 introduces
improvements to the original HIVE-COTE with
additional classifiers, including Rocket, to achieve
higher classification scores (Middlehurst et al., 2021).
2.2 Time Series Augmentation Methods
Multiple advanced time series augmentations, called
AddNoise, Permutation, Scaling and Warping, have
been proposed, in order to improve time series
classification with the Fully Convolutional Neural
Network (FCN) and residual neural network (ResNet)
(Liu et al., 2020). Of all these augmentations,
at least one always improved the accuracy of the
trained model, but certain combinations of combined
augmentations have also made the classification
accuracy worse. A recently developed time
series augmentation based on interpolation has the
advantage of low computational complexity, and
has proven to benefit the models to achieve higher
classification accuracies on benchmark datasets (Oh
et al., 2020).
Augmentations can also be performed with
generative models, which are classified into two
categories - statistical models and neural network-
based models. Statistical models are often used
to enlarge training datasets to improve time series
forecasting. Time series generation models, based on
the Local and Global Trend (LGT) forecasting model,
have been shown to improve forecasting results.
GeneRAting TImeSeries (GRATIS) is a method
which uses mixture autoregressive models to simulate
time series. Neural network-based generative models
are divided into encoder-decoder networks and
generative adversarial networks (GANs). Encoder-
decoder networks for time series generation are
represented by long short-term memory (LSTM)
based autoencoders and variational autoencoders.
The underlying GAN networks are separated
into four architectures, which are either based
on fully-connected networks, residual networks,
temporal one-dimensional convolutional networks,
or two-dimensional convolutional networks, that
generate frequency spectra. Specified architectures
can be combined into various hybrid GAN networks
(Iwana and Uchida, 2021).
3 TIME SERIES GENERATION
AND CLASSIFICATION
The time series generation is performed with a
variational autoencoder (VAE), called Beta-VAE,
which discovers interpretable latent representations
from raw time series data (Higgins et al., 2017). By
sampling randomly from a Gaussian distribution, a
new latent representation is created and decoded by
the variational autoencoder. The decoded output is a
generated time series, similar to the time series which
were used for training the variational autoencoder.
Original training time series samples are used for
training Beta-VAE variational autoencoders. One
variational autoencoder has to be trained individually
for each classification class that needs additional
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
16

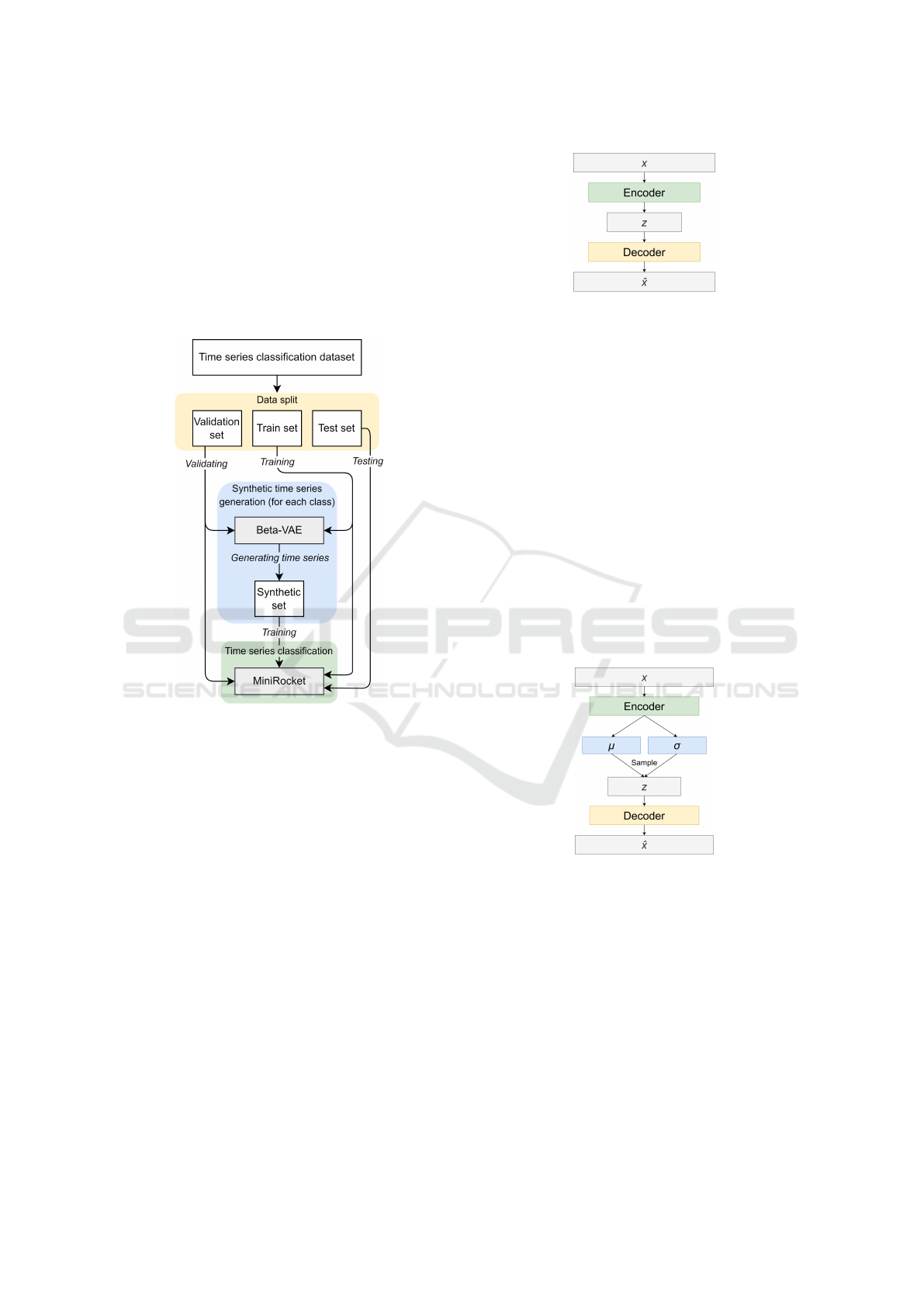
synthetic time series samples. Samples in the
validation set are used to validate variational
autoencoders and a MiniRocket classifier during their
training process. Trained Beta-VAEs are used to
generate synthetic time series samples, which are then
stored in a synthetic set. Both train and synthetic sets
are used for training the MiniRocket classifier. The
learned classification model is tested with a test set.
Figure 1 shows the described workflow, which starts
by splitting data into multiple sets.
Figure 1: Time series generation and classification
workflow for individual time series classification dataset.
The autoencoders and the proposed Beta-VAE
architecture are described in the next subsection,
while the classification algorithm MiniRocket is
presented in subsection 3.2.
3.1 Time Series Generation
3.1.1 Autoencoder
An autoencoder is a dimensionality reduction
model, that consists of two neural networks.
The encoding neural network, called encoder,
performs dimensionality reduction of the input data
x. Compressed data, also referred to as latent
representation z of size z
dim
, is reconstructed using
the decoding neural network, called decoder. The
autoencoder architecture is shown in Figure 2.
During the training of an autoencoder, a
reconstruction loss (e.g. mean squared error,
mean average error, and categorical cross-entropy)
Figure 2: Autoencoder architecture.
is used to minimize the difference between input
x and the reconstruction ˆx (Bank et al., 2020).
Latent representations capture the most significant
features of the input data, which makes autoencoders
useful for data compression and anomaly detection
applications (Bank et al., 2020).
3.1.2 Variational Autoencoder (VAE)
A variational autoencoder is a probabilistic generative
model. It has a similar architecture to an autoencoder
with additional hidden layers - mean layer µ and
Standard Deviation layer σ (Kingma and Welling,
2014). Input x conditions the latent representation
z, which is retrieved by sampling the Gaussian
distribution N , parameterized by µ and σ. The
variational autoencoder architecture is shown in
Figure 3.
Figure 3: Variational autoencoder architecture.
Latent representation sampling is written by
(1) (Sadati et al., 2019). A reparameterization
trick is performed, because sampling of the latent
representation z is stochastic. It introduces a
parameterless random variable ε, sampled from
standard Gaussian distribution. The procedure of
obtaining latent distribution z is altered - instead of
sampling the distribution, z is obtained by (2), with
 symbolizing element-wise product (Kingma and
Welling, 2014).
z ∼ N (µ, σ
2
) (1)
Time Series Augmentation based on Beta-VAE to Improve Classification Performance
17

z = µ + σ  ε, ε ∼ N (0, 1) (2)
The described process keeps µ and σ learnable during
backpropagation, and maintains the stochasticity of
the latent bottleneck z.
Loss L for the variational autoencoder consists of
two parts - reconstruction term L
r
, which measures
the error between x and ˆx, and the Kullback-Leibler
divergence term L
KL
, which measures how a
probability distribution is different from a reference
distribution. By introducing the divergence term into
the loss function, the variational autoencoder learns
a standard normal latent space distribution. The
described loss is written by (3)
L = L
r
(x, ˆx) + L
KL
(p(z|x), p(z)) (3)
where p(z|x) is the conditional distribution of the
encoder, and p(z) is N (0, 1) (Liu et al., 2019).
Generation of a new sample starts by sampling the
standard Gaussian distribution. The sampled latent
representation z is then passed into the decoder to
generate a new sample, similar to training data.
3.1.3 Beta-VAE
Latent representation z is disentangled if each unit is
sensitive to a single generative factor and invariant
to other factors. The described latent representations
are more interpretable. For example, individual
latent units in a variational autoencoder, trained on a
medical time series (e.g. ECG and EEG), can capture
abrupt changes, seasonality and short-lasting trends.
By making latent representations disentangled, latent
encodings become more efficient, which makes
generation of new data easier to control (Higgins
et al., 2017).
Beta-VAE is a variational autoencoder intended
for discovering disentangled latent factors. It has
the same basic architecture as a regular variational
autoencoder, with the only difference being the
introduction of hyperparameter β to the loss function,
written by (4) (Higgins et al., 2017).
L = L
r
(x, ˆx) + βL
KL
(p(z|x), p(z)) (4)
The weight of the Kullback-Leibler divergence term
L
KL
is adjusted with β. By increasing β above
a value of 1, a stronger constraint is applied on
latent bottleneck z, thus limiting its representation
capacity, making latent encodings more efficient,
which results in better disentanglement. Models
trained with higher β values may produce poor
quality reconstructions - excessive blurring is often
present (Higgins et al., 2017). Disentangled latent
representations have become one of the main research
areas of unsupervised deep learning.
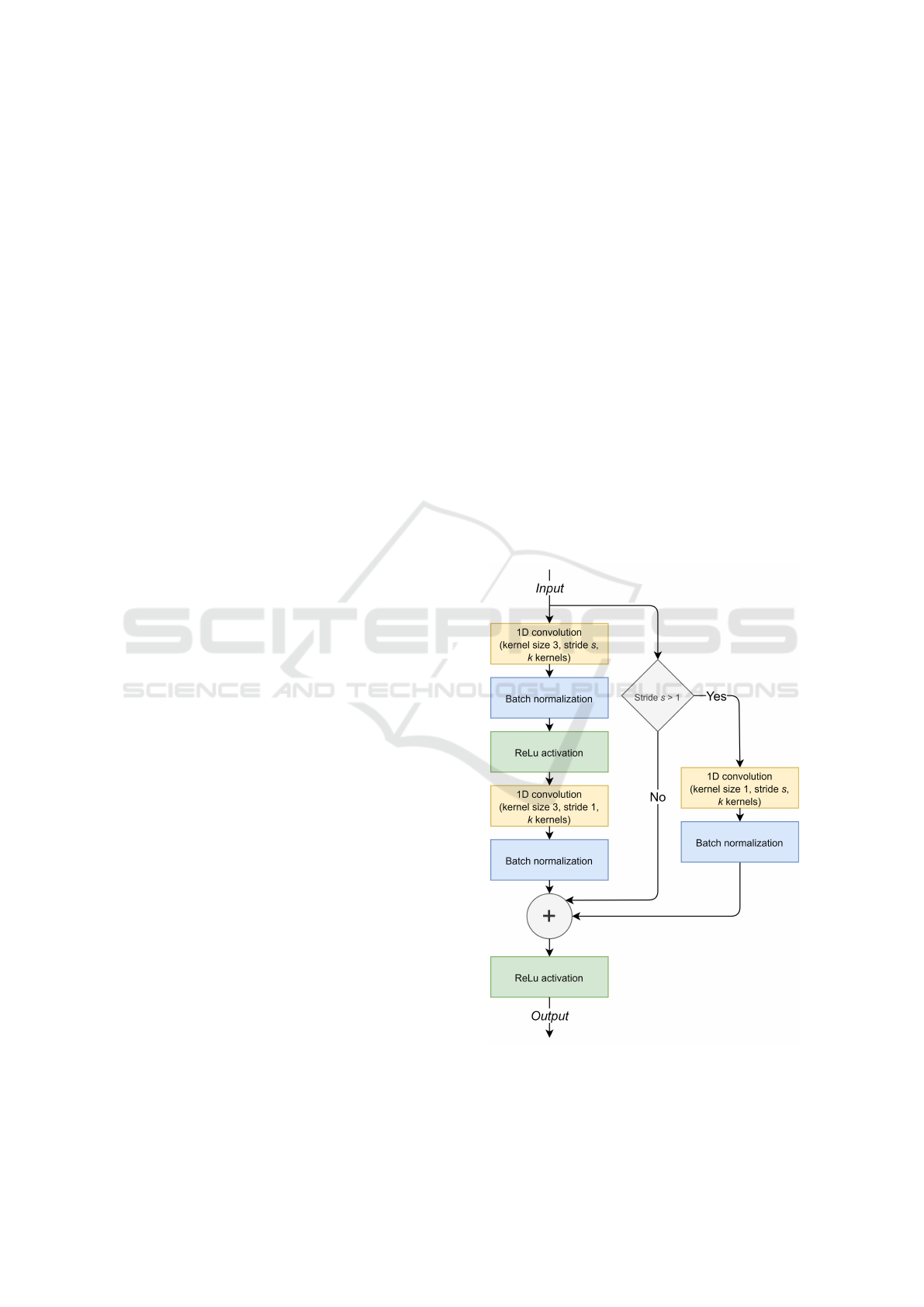
3.1.4 Proposed Beta-VAE Architecture
The encoder and decoder in the proposed Beta-VAE
architecture are 18-layer residual networks (ResNets),
adapted for time series (Wang et al., 2017). Residual
blocks are joined sequentially in a residual layer. The
size of the input x and output ˆx equals the fixed
length T of the time series. The minimal input time
series length is 8, because three residual layers in
the encoder perform convolutions with stride s = 2,
which results in the output being eight times smaller
than T . The decoder’s residual layers reverse the
downsampling effects by performing three upscale
interpolations by a factor sf = 2. If the time series
length is not divisible by 8, it should be zero padded.
ResNet-18 encoder and decoder blocks are shown
in Figures 4 and 5, where Input
channels
represents
the number of channels in the input Input to the
block. The proposed Beta-VAE architecture is shown
in Table 1.
Figure 4: ResNet-18 encoder block.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
18

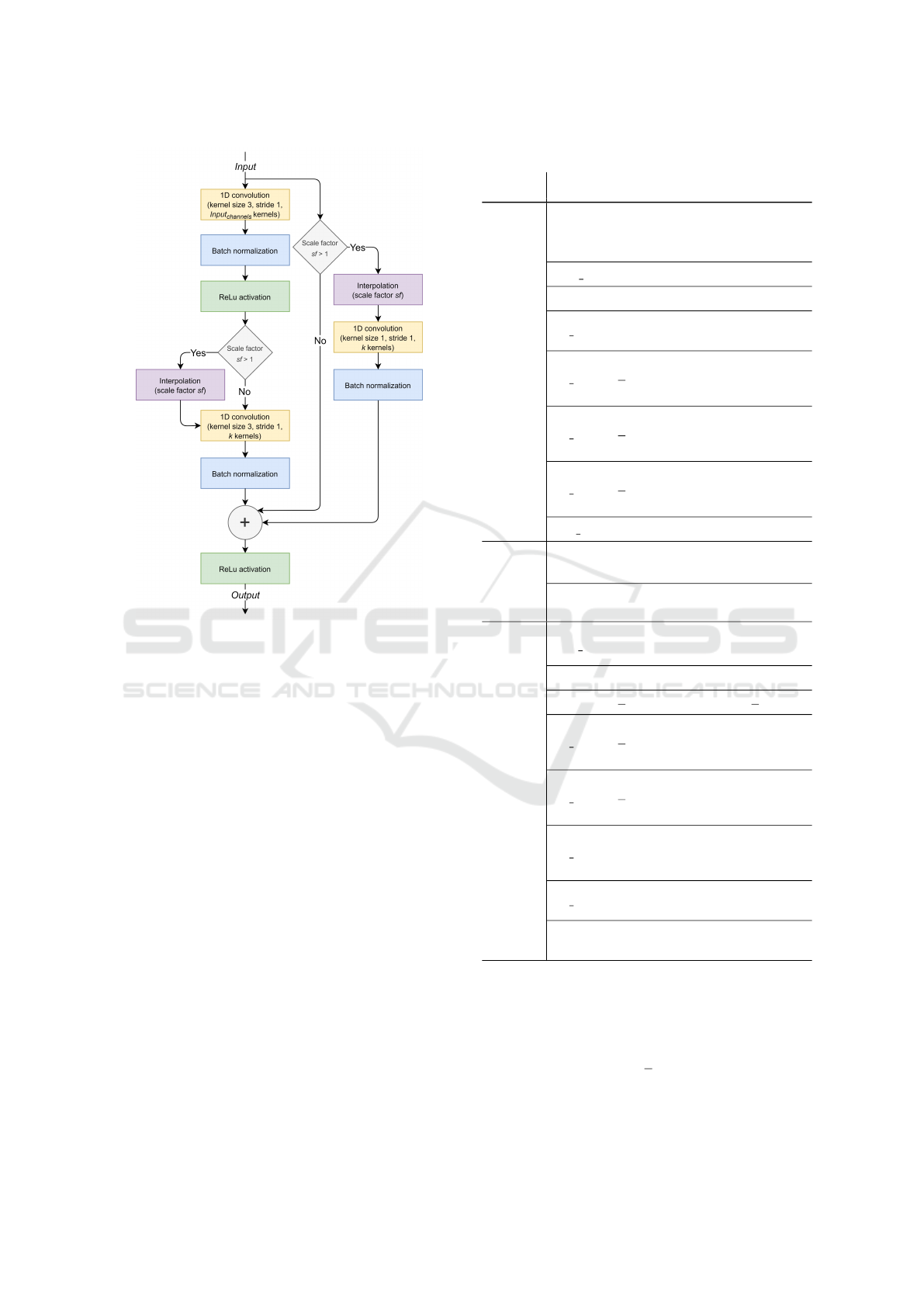
Figure 5: ResNet-18 decoder block.
3.2 Time Series Classification
Algorithm
MiniRocket (MINImally RandOm Convolutional
KErnel Transform), is a state-of-the-art time series
classification method (Dempster et al., 2020). The
advantages of the method are execution speed and
low computational expense, while still achieving high
classification accuracy scores on benchmark datasets.
The core of the MiniRocket method is feature
extraction. It starts by convolving each time series
with a fixed set of kernels of length 9. Each kernel
has weights containing values either -1 or 2. Kernels
are restricted by containing exactly 3 values of 2. The
sum of weights for each kernel is 0. 84 unique kernels
are created based on these restrictions. The only
random component of the method is the kernel bias
hyperparameter - each kernel’s bias is set by drawing
from the quantiles of the convolution output for a
randomly selected training sample. The maximum
number of dilations per kernel is 32, because larger
dilation values do not improve classification accuracy,
and make feature extraction less efficient. Half of
the kernel/dilation combinations use zero padding,
and the other half do not. The pooling method
Table 1: Proposed Beta-VAE Architecture.
Stage
Layer
name
Output
size
Description
ResNet-18
encoder
(sequential
layers)
conv1 T ×64
Convolution with kernel
size 3, stride 1, 64
kernels
batch norm T ×64 Batch normalization
relu T ×64 ReLu activation
res layer1 T ×64
Residual layer
(s=1, k=64)×2 blocks
res layer2
T
2
×128
Residual layer
(s=2, k=128)×1 block
(s=1, k=128)×1 block
res layer3
T
4
×256
Residual layer
(s=2, k=256)×1 block
(s=1, k=256)×1 block
res layer4
T
8
×512
Residual layer
(s=2, k=512)×1 block
(s=1, k=512)×1 block
avg pool 512 Average pool
Bottleneck
z
µ z
dim
512×z
dim
fully
connected layer
σ z
dim
512×z
dim
fully
connected layer
ResNet-18
decoder
(sequential
layers)
fully conn 8192
z
dim
×8192 fully
connected layer
reshape 16×512 Reshape to 16×512
interp
T
8
×512 Interpolate to
T
8
×512
res layer5
T
4
×256
Residual layer
(s f =2, k=256)×1 block
(s f =1, k=256)×1 block
res layer6
T
2
×128
Residual layer
(s f =2, k=128)×1 block
(s f =1, k=128)×1 block
res layer7 T ×64
Residual layer
(s f =2, k=64)×1 block
(s f =1, k=64)×1 block
res layer8 T ×64
Residual layer
(s f =1, k=64)×2 blocks
conv2 T
Convolution with kernel
size 3, stride 1, 1 kernel
’proportion of positive values’ (PPV) is performed
after convolution. It is defined by (5) (Dempster et al.,
2020). Feature extraction results in 10,000 features.
PPV (X ∗W − b) =
1
n
∑
[X ∗W − b > 0] (5)
The efficiency and execution speed of feature
extraction is possible by taking advantage of a small,
Time Series Augmentation based on Beta-VAE to Improve Classification Performance
19

fixed set of two-valued kernels and smart calculation
of PPV. Optimizations are performed by computing
PPV for W and −W at the same time, not using
multiplications in the convolution operations, reusing
the convolution output to compute multiple features
and for each dilation, computing all kernels (almost)
’at once’. The extracted features are used to train a
linear classifier - either a ridge regression classifier
or logistic regression, if the train set contains more
than 10,000 time series samples. In its general form,
MiniRocket feature extraction applies k kernels on
n number of time series samples of l length, which
results in linear computational complexity O(k · n · l)
(Dempster et al., 2020).
4 RESULTS
Time series classification was performed on a subset
of univariate UAE & UCR datasets (Bagnall et al.,
2021). The used datasets are presented in Table 2.
Each dataset contains time series of fixed lengths and
has a predefined train and test set. For each dataset,
synthetic time series samples for each class were
generated by Beta-VAEs with z
dim
=64 latent factors.
This number of latent factors was chosen because it
is less than the shortest time series length of 84 in the
featured datasets. Each variational autoencoder was
trained for 250 epochs with β = 2. A large number of
epochs was selected, to ensure each autoencoder was
trained until convergence. Increasing the parameter
β > 2 had a negligible effect on training losses and
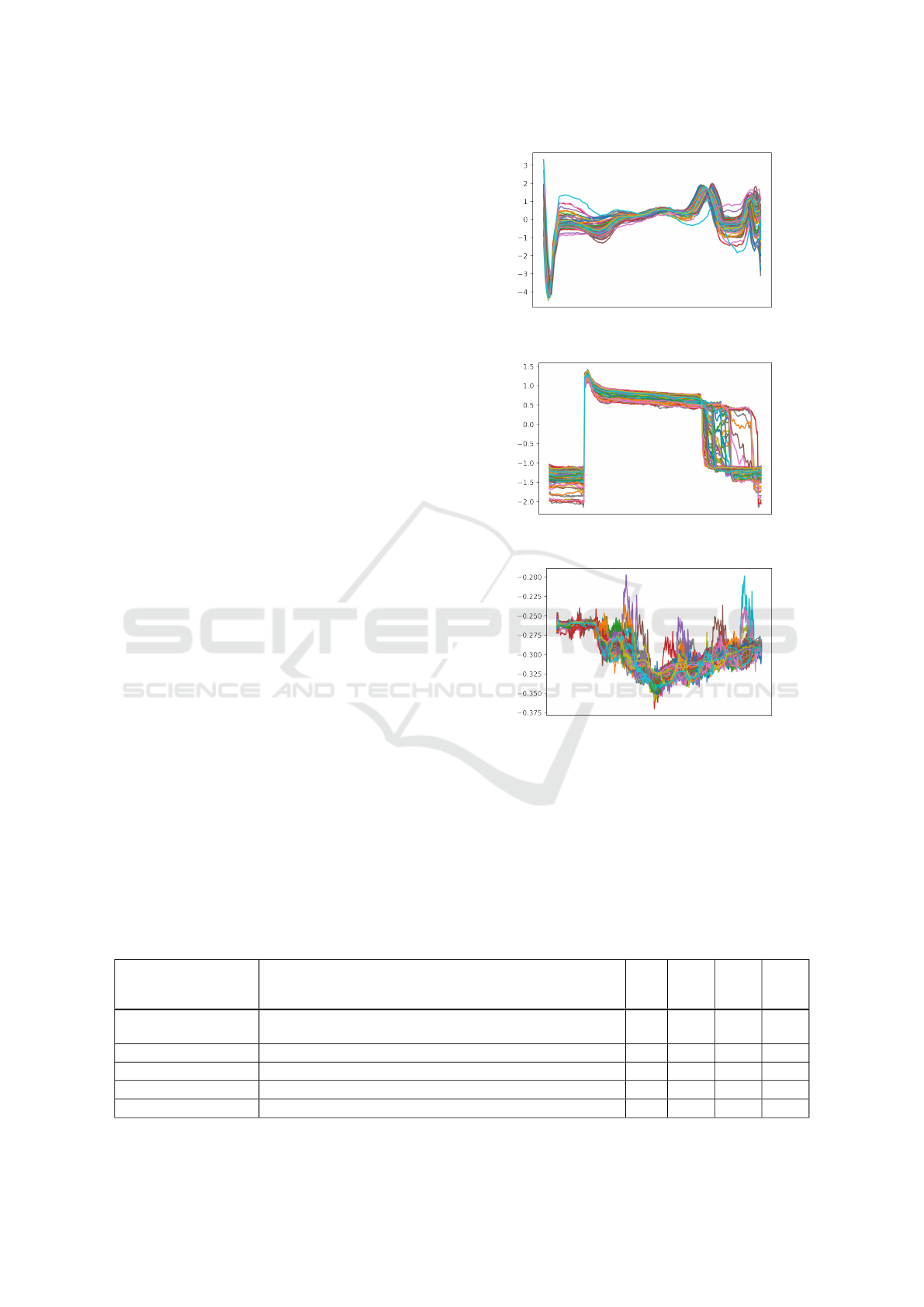
disentanglement. Examples of synthetic time series
sets for datasets ECG5000, FreezerSmallTrain and
InsectEPGSmallTrain are shown in Figures 6, 7 and
8.
The number of additional synthetic time series to
generate per class was calculated as a percentage of
the entire train set size. By doing that, class imbalance
was removed. For example, to create synthetic time
series for each class in the ECG5000 dataset for the
amount equal to 10% of the train set size (500),
Figure 6: 100 generated time series samples for the dataset
ECG5000.
Figure 7: 100 generated time series samples for the dataset
FreezerSmallTrain.
Figure 8: 100 generated time series samples for the dataset
InsectEPGSmallTrain.
variational autoencoders generate 50 synthetic time
series samples per class. For each dataset and train
data combination (either only an original train set,
or an original train set with additional various sized
synthetic sets), we initialized, trained and tested 100
MiniRocket classifier models randomly. Additionally,
1-nearest neighbor (1-NN) classifiers, which use
dynamic time warping (DTW) as a distance measure,
Table 2: Time series datasets.
Dataset name Description
Time
series
length
No. of
classes
Train
set size
Test
set size
ECG5000
ECG recordings for five categorizations of cardiovascular
diseases
140 5 500 4500
FreezerSmallTrain
Power demand of two types of freezers in 20 households 301 2 28 2850
InsectEPGSmallTrain
EPG signals of insect interaction with plants 601 3 17 249
MoteStrain
Distinguishing between humidity and temperature sensors 84 2 20 1252
SmallKitchenAppliances
Electricity consumption of three types of small kitchen appliances 720 3 375 375
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
20

were trained to observe the effects that synthetic
sets have on simple machine learning classification
algorithms. Performance analysis was done by
observing classification accuracy, written by (6),
where TP stands for True Positives, TN for True
Negatives, FP for False Positives and FN for False
Negatives in binary classification (Hossin and M.N,
2015). The highest achieved test accuracies are shown
in Tables 3 and 4. The bold text marks the highest
test classification accuracy of each dataset. The last
two columns represent the maximum positive and
negative differences between the accuracy achieved
with the original train set and the accuracies achieved
with the additional synthetic sets. Each green or
red colored maximum accuracy change represents
whether the dataset’s classification accuracies were
improved or degraded by including synthetic time
series samples in the training process. Average test
classification accuracies for each dataset, obtained
from training many MiniRocket classifiers, using both
original train sets and additional synthetic sets, are
Table 3: Highest time series test classification accuracies, obtained with 1-nearest neighbor classifiers, which used dynamic
time warping as the distance measure.
Dataset name
Train
Max.
positive
accuracy
change
Max.
negative
accuracy
change
set
Additional synthetic time series samples per class
(% of train set size)
1% 5% 10% 50% 100% 200%
ECG5000
92,44% 92,08% 91,42% 90,77% 89,11% 89,15% 88,53% / -3,91%
FreezerSmallTrain
75,89% 75,89% 75,89% 75,78% 75,64% 75,19% 76,70% +0,81% -0,70%
InsectEPGSmallTrain
100% 100% 100% 100% 100% 100% 100% / /
MoteStrain
83,46% 82,10% 83,46% 83,46% 83,94% 83,94% 82,98% +0,48% -1,36%
SmallKitchenAppliances
64,26% 64,26% 64,26% 64,26% 64,26% 64,26% 64,26% / /
Table 4: Highest time series test classification accuracies, obtained with MiniRocket classifiers.
Dataset name
Train
Max.
positive
accuracy
change
Max.
negative
accuracy
change
set
Additional synthetic time series samples per class
(% of train set size)
1% 5% 10% 50% 100% 200%
ECG5000
94,08% 94,26% 94,40% 94,17% 93,66% 93,46% 92,93% +0,32% -1,15%
FreezerSmallTrain
94,28% 94,31% 93,15% 93,64% 95,08% 95,50% 93,89% +1,22% -1,13%
InsectEPGSmallTrain
96,38% 96,38% 96,38% 96,38% 96,78% 96,38% 95,98% +0,40% -0,40%
MoteStrain
93,13% 92,33% 92,33% 92,41% 93,29% 92,41% 91,13% +0,16% -2,00%
SmallKitchenAppliances
81,33% 80,00% 78,13% 78,93% 82,13% 76,53% 82,13% +0,80% -4,80%
Figure 9: Average test classification accuracies, obtained with MiniRocket classifiers, which were trained using original train
sets and additional synthetic sets (bold error bars are Standard Deviation, with maximum and minimum accuracies being at
the top and bottom of each line; only the synthetic sets that made the maximum positive accuracy changes, as shown in Table
4, were used for calculating the statistics).
Time Series Augmentation based on Beta-VAE to Improve Classification Performance
21

shown in Figure 9.
Accuracy =
TP + TN
TP + FP + FN + TN
(6)
1-nearest neighbor classifiers achieved higher
test accuracies by using additional synthetic time
series samples for the datasets FreezerSmallTrain and
MoteStrain. Synthetic time series samples had no
effect on the classification results of the datasets
InsectEPGSmallTrain and SmallKitchenAppliances.
The classification accuracies for dataset ECG5000
degraded gradually by increasing the amount of
synthetic time series samples, resulting in a maximum
negative accuracy change of -3,91%.
The MiniRocket classification models benefited
from the synthetic time series samples for all
datasets. For the datasets InsectEPGSmallTrain,
MoteStrain and SmallKitchenAppliances, the highest
test classification accuracies were achieved with
models trained with additional synthetic sets, which,
for each class, contained an amount of samples equal
to 50% of the train set size. The test accuracies of
trained classification models for all datasets, except
SmallKitchenAppliances, decreased when they were
trained with additional synthetic sets, which, for each
class, contained an amount of samples equal to 200%
of the train set size. The test classification accuracy
for each dataset could be degraded by training with
a certain amount of synthetic time series samples.
The maximum negative accuracy change of -4,80%
occured for the dataset SmallKitchenAppliances by
training with an additional synthetic set, which, for
each class, contained an amount of samples equal to
100% of the train set size. The maximum positive
accuracy change of 1,22% occured for the dataset
FreezerSmallTrain.
1-nearest neighbor classifiers were capable of
classifying all InsectEPGSmallTrain test time series
samples correctly. For all other datasets, MiniRocket
has proven to achieve better classification accuracy
results, even up to 18,80% higher compared
to 1-nearest neighbor classifier for the dataset
FreezerSmallTrain. Figure 9 shows that use of a
synthetic set in the training process of the MiniRocket
classifier for the SmallKitchenAppliances dataset
made test accuracies more concentrated towards
the mean classification accuracy, yet still achieving
higher maximum accuracy.
5 CONCLUSIONS
A novel augmentation method for generating
synthetic time series with a residual neural network
based variational autoencoder was presented in this
paper. A variational autoencoder, called Beta-VAE,
is trained for each class in a time series classification
dataset, and later used for generating synthetic
time series samples. The train set, along with the
synthetic set, were then used for training a time
series classification model, MiniRocket. Most of
the highest classification accuracies were achieved
with models trained with additional synthetic sets,
which, for each class, contained an amount of
samples equal to 50% of the train set size. Across
the tested datasets, the proposed method achieved
a maximum increase of 1,22% in test classification
accuracy in comparison to the baseline results
obtained by training only with original train sets.
An increase of up to 0,81% in the accuracy of
simple machine learning classifiers was observed by
benchmarking the proposed augmentation method
with the 1-nearest neighbor algorithm. The amount
of synthetic time series samples should be selected
carefully by trial and error to prevent degradation of
classification accuracy. In the future, the proposed
Beta-VAE architecture will be adapted for generating
multivariate time series samples.
ACKNOWLEDGEMENTS
The authors acknowledge the financial support from
the Slovenian Research Agency (Research Core
Funding No. P2-0041, as well as Research Projects
No. L7-2633 and No. V2-2117).
REFERENCES
Bagnall, A., Lines, J., Vickers, W., and Keogh, E. (2021).
The uea and ucr time series classification repository.
Bank, D., Koenigstein, N., and Giryes, R. (2020).
Autoencoders.
Dempster, A., Schmidt, D., and Webb, G. (2020).
MINIROCKET: A Very Fast (Almost) Deterministic
Transform for Time Series Classification.
Gian Antonio, S., Angelo, C., and Matteo, T. (2018).
Chapter 9 - time-series classification methods:
Review and applications to power systems data. pages
179–220.
Higgins, I., Matthey, L., Pal, A., Burgess, C. P., Glorot,
X., Botvinick, M., Mohamed, S., and Lerchner, A.
(2017). beta-vae: Learning basic visual concepts with
a constrained variational framework. In ICLR.
Hossin, M. and M.N, S. (2015). A review on
evaluation metrics for data classification evaluations.
International Journal of Data Mining and Knowledge
Management Process, 5:01–11.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
22

Ismail Fawaz, H., Lucas, B., Forestier, G., Pelletier, C.,
Schmidt, D. F., Weber, J., Webb, G. I., Idoumghar, L.,
Muller, P.-A., and Petitjean, F. (2020). Inceptiontime:
Finding alexnet for time series classification. Data
Mining and Knowledge Discovery, 34(6):1936–1962.
Iwana, B. K. and Uchida, S. (2021). An empirical survey of
data augmentation for time series classification with
neural networks. PLOS ONE, 16(7):e0254841.
Kingma, D. and Welling, M. (2014). Auto-Encoding
Variational Bayes.
Lines, J., Taylor, S., and Bagnall, A. (2017). Hive-cote:
The hierarchical vote collective of transformation-
based ensembles for time series classification. In 2016
IEEE 16th International Conference on Data Mining
(ICDM), pages 1041–1046.
Liu, B., Zhang, Z., and Cui, R. (2020). Efficient
time series augmentation methods. In 2020
13th International Congress on Image and Signal
Processing, BioMedical Engineering and Informatics
(CISP-BMEI), pages 1004–1009.
Liu, W., Li, R., Zheng, M., Karanam, S., Wu, Z., Bhanu, B.,
Radke, R., and Camps, O. (2019). Towards Visually
Explaining Variational Autoencoders.
Middlehurst, M., Large, J., Flynn, M., Lines, J., Bostrom,
A., and Bagnall, A. (2021). HIVE-COTE 2.0: a new
meta ensemble for time series classification.
Oh, C., Han, S., and Jeong, J. (2020). Time-series
data augmentation based on interpolation. Procedia
Computer Science, 175:64–71.
Sadati, N., Zafar Nezhad, M., Chinnam, R. B., and Zhu, D.
(2019). Representation Learning with Autoencoders
for Electronic Health Records: A Comparative Study.
Wang, Z., Yan, W., and Oates, T. (2017). Time series
classification from scratch with deep neural networks:
A strong baseline.
Time Series Augmentation based on Beta-VAE to Improve Classification Performance
23