Leveraging Causal Relations to Provide Counterfactual Explanations

and Feasible Recommendations to End Users

Riccardo Crupi

, Beatriz San Miguel Gonz

alez

, Alessandro Castelnovo

and Daniele Regoli

1 a

Intesa Sanpaolo S.p.A., Turin, Italy

Fujitsu Research of Europe, Madrid, Spain

Keywords:

Explainable Artiﬁcial Intelligence, Counterfactual Explanations, Causality, Recourse.

Abstract:

Over the last years, there has been a growing debate on the ethical issues of Artiﬁcial Intelligence (AI).

Explainable Artiﬁcial Intelligence (XAI) has appeared as a key element to enhance trust of AI systems from

both technological and human-understandable perspectives. In this sense, counterfactual explanations are

becoming a de facto solution for end users to assist them in acting to achieve a desired outcome. In this paper,

we present a new method called Counterfactual Explanations as Interventions in Latent Space (CEILS) to

generate explanations focused on the production of feasible user actions. The main features of CEILS are: it

takes into account the underlying causal relations by design, and can be set on top of an arbitrary counterfactual

explanation generator. We demonstrate how CEILS succeeds through its evaluation on a real dataset of the

ﬁnancial domain.

1 INTRODUCTION

Note-worthy governmental initiatives, such as the

General Data Protection Regulation (GDPR) (The

European Union, 2016) and Ethics guidelines for

trustworthy Artiﬁcial Intelligence (AI) (High-Level

Expert Group on AI, 2019) in Europe, and the De-

fence Advanced Research Projects Agency’s Explain-

able Artiﬁcial Intelligence (XAI) program of the

United States (Gunning and Aha, 2019), endeavour

to promote the creation of trustworthy AI systems

based on human oversight, prevention of harm, trans-

parency, interpretability, accountability, etc. In this

sense, the XAI ﬁeld has appeared as a crucial set of

technologies to improve and ensure trustworthiness of

AI systems.

XAI addresses different purposes sought by the

stakeholders of AI systems (Arrieta et al., 2020). XAI

can provide reasons and justiﬁcations for the whole

logic of an AI model or a speciﬁc outcome, consid-

ering both technical and non-technical forms. For ex-

ample, AI developers can take advantage of explana-

tions to verify that AI outcomes are not erroneous,

biased or insecure; to ensure the efﬁciency and func-

tionality; and to get new insights to improve the sys-

tem. Moreover, non-technical proﬁles (i.e. regula-

https://orcid.org/0000-0003-2711-8343

tors, domain experts, executives and end users) can

receive explanations to assess and certify regulatory

compliance, gain business knowledge and get insights

to their speciﬁc situation in a human-understandable

way.

In this paper, we present CEILS

: Counterfac-

tual Explanations as Interventions in Latent Space,

a new method to generate counterfactual explana-

tions and recommendations. Counterfactual explana-

tions (Wachter et al., 2017) are a set of statements to

communicate to end users what should change in their

features in order to receive a desired result. These are

gaining large acceptance in technical, legal, and busi-

ness contexts (Barocas et al., 2020). Their advantages

include: help end users whose life is impacted by au-

tomatic decisions to interact with AI systems, do not

disclose technical details of the models, thus protect

trade secrets and commercial interests and is appro-

priate to legal frameworks.

While there are signiﬁcant efforts to generate

counterfactual explanations (Verma et al., 2020;

Stepin et al., 2021), they generally fall short of gener-

ating feasible actions that end users should carry out

in practice. CEILS, on the other hand, is designed

to leverage the underlying causal relations to generate

CEILS code is publicly available at the repository

https://github.com/FLE-ISP/CEILS

Crupi, R., San Miguel González, B., Castelnovo, A. and Regoli, D.

Leveraging Causal Relations to Provide Counterfactual Explanations and Feasible Recommendations to End Users.

DOI: 10.5220/0010761500003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 2, pages 24-32

ISBN: 978-989-758-547-0; ISSN: 2184-433X

feasible recommendations to end users on how to act

to reach a desired outcome. Moreover, CEILS does

that by building on top of an arbitrary counterfactual

generator, thus avoiding the need of dealing with an

ad hoc optimization problem.

It is important to point out that counterfactual ex-

planations and counterfactuals in the causal inference

ﬁeld are separated concepts. Generally speaking,

counterfactual explanations do not account for any

causal relationship among data, and these are not to

be confused with counterfactuals in the causal infer-

ence setting (i.e. instances answering to questions of

the form “what would have happened if. . . ”) (Pearl

et al., 2000). However, CEILS, by explicitly consider-

ing the underlying causal structure, provides a bridge

between these two otherwise unrelated concepts (see

Section 3.1.4 for more details).

The main contributions of this work are:

• to provide a novel and straightforward way to ac-

count for causality in generating counterfactual

explanations of AI models,

• to provide counterfactuals explanations along

with (causally) feasible actions to reach them.

The structure of this paper is the following. First,

Section 2 summarizes prior work for the generation

of counterfactual explanations. Then, Section 3 de-

tails the CEILS proposal and Section 4 describes its

evaluation in a real dataset of the ﬁnancial domain.

Finally, Section 5 concludes the paper and outlines

future work.

2 RELATED WORK

Most of the prior approaches for the generation of

counterfactual explanations relies on establishing an

optimization problem, usually to ﬁnd the nearest

counterfactual with respect to the input to be ex-

plained. This has been understood in different ways:

minimizing the distance among the explanation and

the original instance (proximity) (Wachter et al., 2017)

or the training data (data manifold closeness) (Joshi

et al., 2019), keeping a low number of feature changes

(sparsity) (White and Garcez, 2019), adhering to ob-

served correlations or generating a set of diverse ex-

planations (Mothilal et al., 2020).

Moreover, other works incorporate causality to

produce explanations more grounded with reality

(Mahajan et al., 2019). In general, current solu-

tions provide a common understanding of a decision.

However they fall short of assisting end users with

feasible recommendations to act and achieve a de-

sired outcome (Karimi et al., 2020). A set of pro-

posals addresses this last issue through the deﬁnition

of a recourse problem (Ustun et al., 2019; Karimi

et al., 2020). Our work is focused on the production

of counterfactual explanations with recommendations

and actions more realistic and feasible for end users.

3 PROPOSED METHOD

Figure 1 depicts a general overview of the CEILS con-

text and its main building blocks. Like other coun-

terfactual explanation methods, CEILS offers to end

user a set of statements to indicate what should be

changed in order to achieve a desired outcome. How-

ever, CEILS produces not only explanations, but also

feasible actions.

By way of example, consider a simpliﬁed scenario

of an AI model used for loan approvals that takes into

account age, income and credit score of an end user to

decide if a loan would be accepted or rejected. When

a person is denied a loan, counterfactual explanations

indicate what input data (features) should be altered

to access to the loan. For instances, the person may

receive as counterfactual explanations: “reduce your

age”, “increase your income and credit score”, “im-

prove your credit score value”, etc. As can be de-

duced from the examples, these explanations contain

unfeasible and impractical actions (i.e. for end users,

it is impossible to reduce their age, or usually they

have no control over their credit scores values). With

our proposal, feasible actions are delivered to end

users due to the fact that causal relations are taken into

account by design, e.g. credit score is in general inﬂu-

enced by age and income and age can only increase.

Therefore, using CEILS, a person could receive as a

recommended action ”increase your income”, which

would impact the credit score and guarantee the loan

approval.

The CEILS methodology consists of three main

steps:

1. creation of a model in a latent space (i.e. space of

unobserved variables) through a Structural Causal

Model – comprised by a Causal Graph and a set

of Structural Equations;

2. generation of counterfactual explanations with

an arbitrary generator using the aforementioned

model; and

3. translation of counterfactual explanations to the

original feature space.

It is important to note that our method requires as

inputs the historical data used to build the AI model

that will be explained and the causal graph that de-

scribes the causal relations among the features of the

Leveraging Causal Relations to Provide Counterfactual Explanations and Feasible Recommendations to End Users

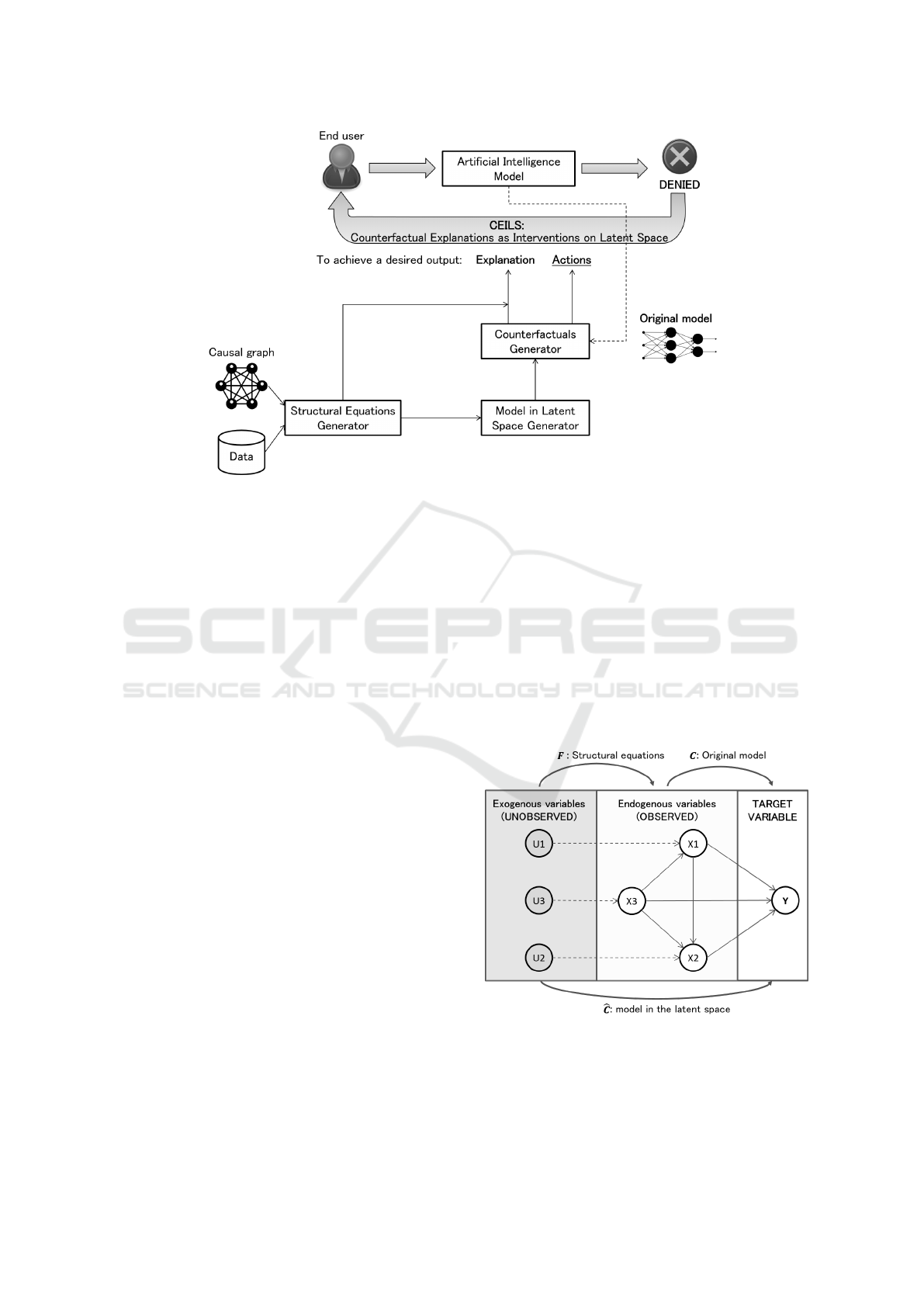
Figure 1: CEILS context and building blocks. The context in which CEILS operates is similar to other explainability methods:

a user interacting with an AI model receiving a negative outcome together with an explanation of the outcome (provided by

CEILS). Unlike other methods, CEILS provides not only explanations but also realistic actions. The main building blocks of

CEILS are shown: Data, Casual Graph, Structural Equations Generator, Model in Latent Space Generator and Counterfactuals

Generator.

dataset. Moreover, CEILS needs to have access to the

original model to generate the explanations.

On the bottom part of Figure 1 the main CEILS

building blocks are shown. Next, we detail each block

of the proposal.

3.1 CEILS: Building Blocks

3.1.1 Causal Graph

CEILS requires to access to a predeﬁned causal graph

that encodes the causal relations among the features

of the dataset. Modeling this causal knowledge is

complex and challenging since this requires under-

standing relations beyond statistical dependencies.

Different causal discovery algorithms have been pro-

posed to identify causal relationships from observa-

tional data through automatic methods (Kalainathan

et al., 2020; Kalisch et al., 2012). In general, it is

important that domain experts validate the relations

detected by the causal discovery routine, or include

new ones when deemed necessary.

Causal relationships among features are modelled

via a Directed Acyclic Graph (DAG) G = (V, E), with

the set V of vertices (or nodes) and the set E of di-

rected edges (or links). Nodes of the graph G are

composed by:

• X = (X

, . . . , X

): endogenous variables, repre-

senting the actual (observed) variables used as

predictors in the model;

• U = (U

, . . . , U

): exogenous variables, represent-

ing (unobserved) factors not accounted for by the

features X; and

• Y represents the dependent variable to be pre-

dicted by means of X.

In Figure 2 an example of a causal graph is included,

pointing out the relations among the different kind of

nodes (X, U, Y ).

Figure 2: Example of a causal graph, indicating the different

kind of nodes (U, X, and Y ), and the functions associated

with the CEILS methodology (F, C and

C ).

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

3.1.2 Structural Equations

The Structural Causal Model encodes a more detailed

description of causal relationships. This is deﬁned by

a triplet (X, U, F) where F represent a set of func-

tions called Structural Equations F : U → X , map-

ping the exogenous (unobserved) variables living in

the domain U to the endogenous (observed) ones

X ∋ X = F(U).

The ﬁrst step of the CEILS methodology is to infer

the Structural Equation from observations (X), given

the DAG. It does so by assuming an Additive Noise

Model (see, e.g., (Peters et al., 2014)):

= f

(pa(X

)) +U

, ∀ j = 1. . . d. (1)

where pa(X

) denotes the parent nodes of X

with

respect to the DAG. Thus, in the example of Fig-

ure 2 the variable X

, whose parents are the nodes

and X

, would be modeled by the equation: X

, X

) +U

A regressor model M

is trained to estimate each

function f

, predicting a variable X

from its parent

nodes. A node without parents (e.g. X

in Figure 2)

is referred to as a root node, while residuals are an

estimate of the latent variables: namely, to calculate

the value of the latent variable U given X one would

compute:

(

= X

, for all roots j,

= X

− M

(pa(X

)), for all non-roots j.

(2)

Therefore, for the example of the Figure 2, the esti-

mated value of the latent variable U

would be equal

to X

since this has no parents, while for the variable

— with parents X

and X

— the estimation of the

latent variable would be

= X

− M

, X

Structural Equations for root nodes r simply re-

duce to F

(U) = U

. Once all models M

are learned

from a training dataset, it is possible to recursively

compute the actual function F connecting U to X —

namely X = F(U) — following the causal ﬂow in the

DAG (i.e from the root nodes down to the leaves):







(U) = U

, for all roots j,

(U) = M



{

(U)

}

v∈pa(X

)



, j non-root.

(3)

Thus, starting from root nodes — for which the re-

lation is trivial — one can recursively construct the

full relation F : U 7→ X. In the example of Figure 2

equation (3) would read:

X = F(U) =





) +U

, U

) +U





. (4)

3.1.3 Model in the Latent Space

Once the relations X = F(U) are available, it is pos-

sible to build the model:

C (U) = C ◦ F(U), (5)

where C is the original model that predicts the tar-

get variable Y given X, of which we need to provide

counterfactual explanations. For example, this could

be an arbitrary machine learning classiﬁer. Therefore,

C has domain in the (latent) space of variables U and

leverages the Structural Causal Model by means of F

in order to replicate C in estimating Y .

Figure 2 shows the relations among the functions

F, C and

C in a toy example: the original model C

and the Structural Equations F, are composed to get

the model in the latent space

C .

3.1.4 Counterfactuals Generator

Given the latent-space model

C as by equation (5), an

arbitrary counterfactual explanations generator can be

employed. As we mentioned in Section 2, most ap-

proaches to generate counterfactual explanations rely

on an optimization process based on different metrics

(i.e. proximity, sparsity, etc.).

More precisely, given an instance x for which we

want to ﬁnd a counterfactual explanation, CEILS pre-

scribes the following three steps:

1. compute the latent variables u corresponding to

x by means of residuals of models





j=1

(eq. (2));

2. run a counterfactual generator for the model

C rel-

ative to the point u, thus obtaining u

= u + δ;

3. compute x

= F(u + δ).

Notice that these three points correspond precisely to

the well-known steps of counterfactual computation,

e.g. as described in chapter 4 of (Pearl et al., 2016),

namely:

1. abduction, i.e. update the unobserved variables to

account for the observed data X = x;

2. action — the crucial step — that consists in inter-

vening on variables to change the observed val-

ues;

3. prediction, i.e. use the new variables to actually

compute the counterfactual instance.

Namely, the CEILS approach — similarly to (Karimi

et al., 2020) — provides a natural bridge between the

two separate concepts of XAI counterfactual explana-

tions and causal counterfactuals in the sense of (Pearl

et al., 2016).

Leveraging Causal Relations to Provide Counterfactual Explanations and Feasible Recommendations to End Users

It is important to point out that the main advantage

of CEILS is that it provides not only the counterfac-

tual explanation x

, but also the action δ needed to

reach it. In particular, in standard counterfactual ex-

planation methods the action is seen a shift in feature

space, but this kind of actions represent, in general,

unfeasible recommendations, since they completely

neglect the fact that a change in a feature has impacts

on others. Our method, instead, recommending ac-

tions as shift in the latent space, takes into account

the underlying causal ﬂow. Incidentally, notice that

the latent space action δ is an example of soft inter-

vention (Eberhardt and Scheines, 2007) in that it is

performed on top of other changes in the variable due

to changes in its parents.

4 EVALUATION

We demonstrate the advantages of CEILS on a real

dataset of the ﬁnancial domain. The evaluation of the

results is based on a set of known metrics and new

ones that we propose to capture the particularities of

CEILS.

4.1 Dataset and Causal Graph

We use a proprietary dataset of past loan applica-

tions (Castelnovo et al., 2020). This dataset com-

prises 220,304 applications and 8 features (namely

gender, age, citizenship, monthly income, bank se-

niority, requested amount, number of installments and

rating) to determine whether the loan application is

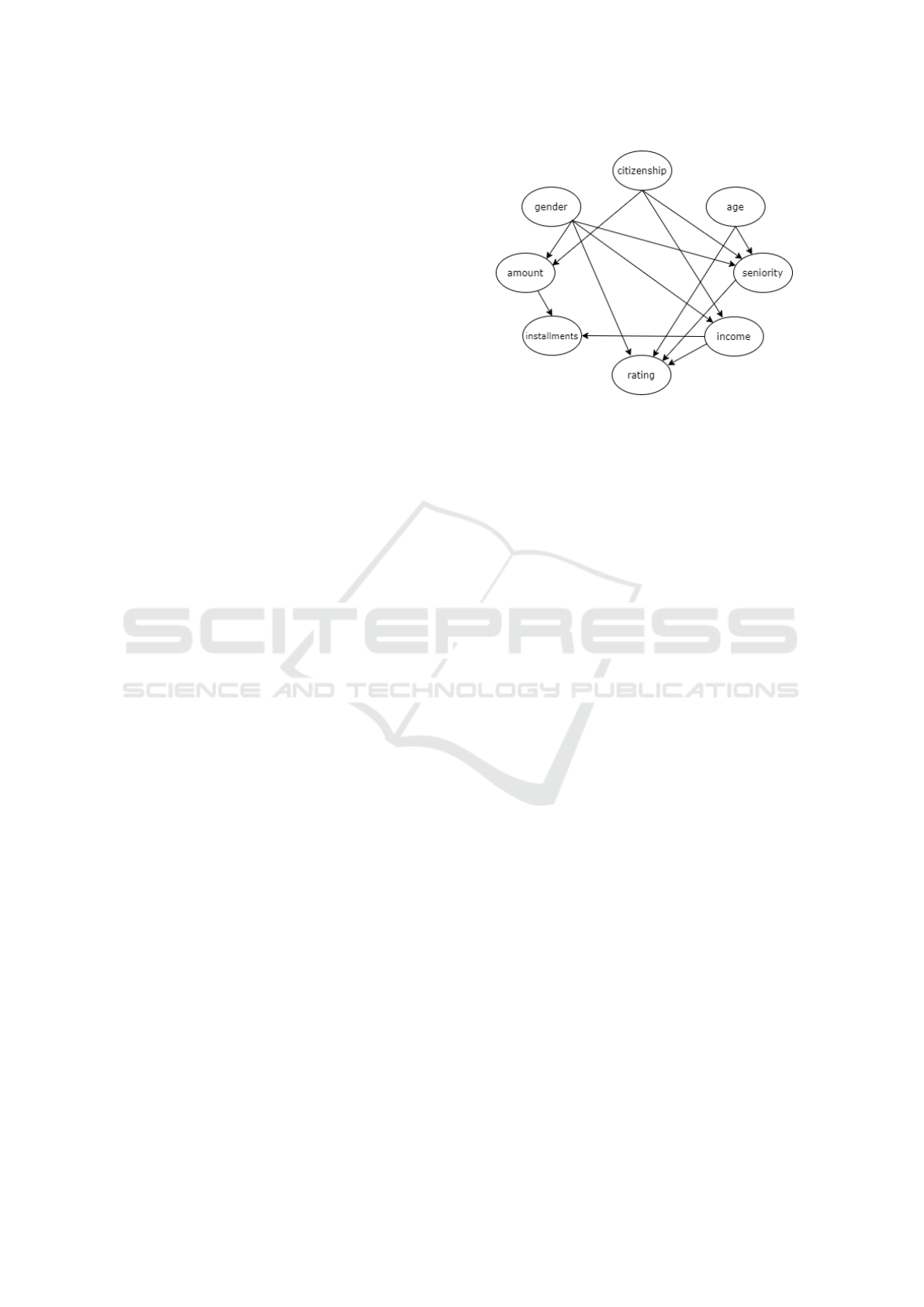
accepted or rejected. The features are related accord-

ing to the causal graph (Figure 3) that we obtain us-

ing different causal discovery algorithms. In particu-

lar, we employed the Python Causal Discovery Tool-

Box (Kalainathan and Goudet, 2019), including dif-

ferent graph modelling algorithms on observational

data (i.e. SAM, PC) and the NOTEARS algorithm

(Zheng et al., 2018) included in the Python library

CausalNex. Additionally, a manual revision has been

performed by a group of domain experts to validate

each causal relation detected or to include new ones.

Among the features, rating indicates the credit-

worthiness of an applicant, i.e. an estimation of

the probability that a customer will repay loans in a

timely manner. Usually, end users cannot directly in-

tervene on this feature, being it a complicated func-

tion of other variables. Thus, we set up our experi-

ment constraining rating in such a way that no direct

intervention is made on it. Namely, rating is consid-

ered a feature non-actionable but that can vary due to

changes in other variable. Gender and citizenship, on

Figure 3: Causal graph related to the proprietary loan appli-

cations dataset.

the other hand, are constrained to be immutable fea-

tures (they cannot change in any way), meanwhile age

and bank seniority can only increase.

4.2 Experiments Setup

First, we build the original AI model, which would be

explained, using the 8 features of the dataset to predict

the target variable that indicates if a loan application

will be accepted or rejected. This model is established

through a feed-forward neural network with 2 hidden

layers with ReLU activation functions.

On the other hand, the Structural Causal Model

relies on the DAG represented in Figure 3. Addition-

ally, Structural Equations are calculated to map un-

observed variables to the 8 observed variables using

feed-forward neural networks with 2 hidden layers.

Similarly, the model in the latent space is based on

a feed-forward neural network with 2 hidden layers

with ReLU activation functions.

The popular open source Machine Learning li-

brary, TensorFlow, is used for setting up and training

the neural networks.

We rely on counterfactual explanations guided by

prototypes proposed by (Van Looveren and Klaise,

2019) included in the open source library Al-

ibi (Klaise et al., 2019) as our baseline generator

of counterfactuals explanations. In particular, this

is used as counterfactuals generator for the CEILS

method (check Figure 1 and Section 3.1.4 for more

details) and on the other hand, to generate counter-

factuals explanations that will be compared with the

explanations generated by CEILS.

Therefore, we compute the corresponding coun-

terfactual explanations ﬁrst using the baseline ap-

proach (Van Looveren and Klaise, 2019) and then

overlaying our proposed CEILS method. 1,000 ran-

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

Table 1: Comparison results of the baseline approach and

the CEILS method based on 8 metrics.

baseline CEILS

validity 22% 82%

continuous proximity 289.57 ± 830.79 43.23 ± 109.46

categorical proximity 0.0 ± 0.0 0.09 ± 0.15

sparsity 2.86 ± 0.95 2.83 ± 1.17

sparsity action - 2.28 ± 1.04

distance 2.16 ± 1.1 1.72 ± 0.87

cost 2.51 ± 1.24 1.35 ± 0.81

feasibility 0.064 1.0

dom instances of the dataset are used as factual obser-

vations to be explained.

As mentioned above, gender and citizenship are

treated as immutable features while rating can vary

only as a consequence of changes in other variables

and cannot be directly acted upon. To implement

this, in CEILS we simply keep the corresponding la-

tent variables ﬁxed (gender and citizenship are root

nodes, thus ﬁxing their latent counterpart is equiva-

lent to constrain them to be immutable), while in the

baseline approach we directly ﬁx the variables in the

X space. This means that, for the baseline approach,

rating is effectively immutable, while in CEILS it is

non-actionable but mutable.

The two sets of explanations are evaluated based

on state-of-the-art metrics, such as validity, proxim-

ity and sparsity (refer to (Mothilal et al., 2020) for

more details). Moreover, we deﬁne three new met-

rics (i.e. distance, cost, and feasibility) to capture the

particularities of our approach. Next, we explain the

meaning of each metrics with the report of the results.

4.3 Results

Table 1 summarizes the results obtained for both

methods (baseline and CEILS) with respect to the

different metrics: validity, proximity (for continuous

and categorical features), sparsity (including the ac-

tion provided by CEILS), distance, cost and feasibil-

ity.

First, validity refers to the fraction of generated

explanations that are valid counterfactuals, i.e. that

are given a different outcome y with respect to the

factual instance. Here, we can observe the ﬁrst big

difference among the two approaches: only 22% of

instances have an associated counterfactual explana-

tion with the baseline approach, while 82% of expla-

nations are found with the CEILS method.

Intuitively the aforementioned difference in the

validity is explained by the rating feature, which is

crucial to estimate the granting of loans and we con-

ﬁgure it to be non directly actionable, since end users

cannot control it. This explains why the baseline

method falls short in providing valid counterfactual

explanations: this approach has no way of changing

the rating, thus for it is either impossible to ﬁnd actual

counterfactual explanations or they are too far to be

considered valid. On the other hand, CEILS is much

more efﬁcient in providing valid explanations, since it

can indirectly act on rating by changing variables that

causally impact it (i.e. seniority or income). More-

over, CEILS provides to end users the action to be per-

formed on these variables that are needed to change

the rating appropriately.

To clarify the differences among the methods,

consider the example included in Table 2, where

an application has been rejected and the counterfac-

tual explanation indicates how to act to have it ap-

proved (decision = 0 → decision = 1). As expected,

immutable features (i.e. gender and citizenship) do

not vary their values, while age and bank seniority

show equal or higher values with respect to the orig-

inal instance. However, the baseline method pro-

duces a counterfactual explanation with values far

away from the factual proﬁle (i.e. increase the income

to 3643.3K and almost double the amount requested

with less number of installments). On the other hand,

if we focus on the action recommended by CEILS,

this only suggests to increase the bank seniority and

the requested amount

. Increasing the bank senior-

ity (action seniority = 5.4) results in a better rating

(∆CEILS rating = -0.375), thus, ultimately, in loan

approval. Evidently, an increase in the seniority is

impossible without a corresponding increase in age:

actually, we have treated bank seniority as an action-

able feature, but it would have been more appropriate

to consider it as mutable only as a consequence of

age changes, since seniority cannot be controlled in-

dependently of age. Nevertheless, we have decided to

keep seniority actionable to focus our discussion on

rating and not to limit too much the baseline method

(for which it would have been impossible to change

seniority as well as rating).

Regarding the rest of metrics in Table 1, it is im-

portant to note that they are computed over the ex-

planations common to both methods (22% according

to the validity), i.e. on observations to which both

CEILS and the baseline were able to provide a valid

explanation. In particular, results included in the table

correspond to the mean and standard deviation of the

metrics over all valid explanations.

Both methods apparently provide the counter-intuitive

suggestion of increasing the requested amount: this is due to

the fact that the baseline method searches for explanations

as close as possible to the data distribution. In other words,

a too small requested amount is not plausible with respect

to the other suggested features.

Leveraging Causal Relations to Provide Counterfactual Explanations and Feasible Recommendations to End Users

Table 2: Example of an instance, counterfactual explana-

tions obtained by the baseline approach and CEILS method,

differences among the original instance and the counterfac-

tual explanations for both methods, and action provided by

CEILS method.

counterfactuals CEILS

variable instance baseline CEILS ∆baseline ∆CEILS action

decision 0 1 1

gender 1 1 1 0 0 0

age 30 30 30 0 0 0

citizenship 1 1 1 0 0 0

income 56.7K 3700K 56.7K 3643.3K 0 0

seniority 0 8.1 5.4 8.1 5.4 5.4

amount 210K 409K 320K 199K 110K 110K

installments 48 33.4 53.1 -14.6 5.1 0

rating 10 10 9.625 0 -0.375 0

Thus, proximity refers to the distance between

the original instance and the counterfactual explana-

tion. We distinguish among proximity for continu-

ous and categorical features. For continuous features,

we measure proximity as feature-wise L

distance re-

scaled by the Median Absolute Deviation from the

median (MAD). For categorical features, we consider

a distance of 1 if there is values mismatch. The

results show better values of proximity taking into

account continuous features for the CEILS method.

This means that the explanations obtained are closer

to the original input of the end user, which is a desir-

able propriety. Regarding the proximity for categor-

ical features, there is no major difference among the

methods.

Moreover, we measure the sparsity of the expla-

nations obtained as the number of features that need

to change with respect to the original input

. In the

feature space the difference among the methods is not

remarkable, but notice that in terms of recommended

actions (“sparsity action” in Table 1) CEILS is able to

slightly improve this metric as well.

Closely related to the proximity metric, the dis-

tance measure the L

distance between counterfac-

tual explanation and the original instance

. Again,

the CEILS method obtains better values (1.72) with

respect to the baseline method (2.16).

Finally, we propose to measure cost and feasibil-

ity: these 2 metrics are designed to compare CEILS

actions with the actions that the baseline approach

would have recommended considering the Structural

For continuous feature a tolerance threshold is consid-

ered similarly to (Mothilal et al., 2020).

Notice that for non-causal counterfactual explanations

actions actually boil down to the simple difference in feature

space, thus sparsity and sparsity action coincide. Another

way to compute actions for non-causal explanations could

be what we call ex-post actions, mentioned below in the

text.

Notice that this metric is computed over standardized

feature values.

Causal Model ex post, i.e. the actions — given the

SCM — that one should perform in order to reach the

baseline explanations.

On the one hand, cost is deﬁned as the L

norm of

the action that has to be done in order to reach a coun-

terfactual explanation

. In the evaluation, a lower

value of cost is obtained with the CEILS method

since the causal inﬂuence reduces the effort in order

to reach an explanation.

On the other hand, the feasibility metric shows

the percentage of actions that are compatible with the

feasibility constraints over features, e.g. if the vari-

able bank seniority can only increase, the action over

bank seniority must be a positive value for the corre-

sponding explanation to be feasible. We observe that

the CEILS method perfectly preserves the underlying

causality as expected (a value of 1.0), while the re-

constructed actions of the baseline spoil almost com-

pletely the actionability of the features (0.064) (e.g.

to keep the rating ﬁxed while changing income, the

baseline should actually recommend a non-null action

on rating, which is unfeasible).

5 CONCLUSIONS AND FUTURE

WORK

In this paper, we present the CEILS methodology

for generating counterfactual explanations focused on

providing feasible actions to end users who want to

achieve a desired outcome. The main novelty, which

is reached via the Structural Causal Model and by

building a model in the latent space, lies in the pos-

sibility of embedding it in any existing counterfactual

generator, effectively producing realistic recommen-

dations.

Indeed, because of variable interdependence,

static counterfactual explanations generators (in the

sense of non-causal) fail, in general, to provide feasi-

ble actions, recommending a set of interventions that

may be either impossible to perform or sub-optimal

in reaching a desired result, as outlined in Section 4

(check the example included in Table 2). On the other

hand, CEILS leverages the underlying causal relation-

ships among variables to provide recommendations

that are feasible and also to reduce the effort in terms

of actions to reach valid counterfactual proﬁles (e.g.

acting on seniority to inﬂuence rating in the example

of Table 2).

Our ﬁrst practical evaluation employs a real

dataset of the ﬁnancial domain and is based on well-

Notice that this metric is computed over standardized

feature values.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

known metrics and others that capture the particu-

larities of CEILS that conﬁrm the efﬁciency of our

method in generating feasible actions with respect to

its baseline counterfactual generator.

Despite the growing research on the ﬁeld of coun-

terfactual explanations, there are a lot of open ques-

tions and challenges yet to be tackled (Verma et al.,

2020). In particular, we are interested in relaxing

the assumption of having a complete and reliable

causal graph and work with incomplete causal rela-

tions. Moreover, as for future work, we consider to

extend our evaluation by employing other counterfac-

tual generators as baselines to analyze how it could

contribute to the overall results, and also to compare

the explanations produced by other causal methods

with the ones found with CEILS, and possibly involv-

ing end users to obtain feedback that will guide to-

wards better explanations. The preprint (Crupi et al.,

2021) includes detailed evaluations and experiments

on additional datasets.

REFERENCES

Arrieta, A. B., D

ıaz-Rodr

ıguez, N., Del Ser, J., Bennetot,

A., Tabik, S., Barbado, A., Garc

ıa, S., Gil-L

opez, S.,

Molina, D., Benjamins, R., et al. (2020). Explainable

Artiﬁcial Intelligence (XAI): Concepts, taxonomies,

opportunities and challenges toward responsible AI.

Information Fusion, 58:82–115.

Barocas, S., Selbst, A. D., and Raghavan, M. (2020). The

hidden assumptions behind counterfactual explana-

tions and principal reasons. In Proceedings of the

2020 Conference on Fairness, Accountability, and

Transparency, pages 80–89.

Castelnovo, A., Crupi, R., Del Gamba, G., Greco, G.,

Naseer, A., Regoli, D., and Gonzalez, B. S. M. (2020).

Befair: Addressing fairness in the banking sector. In

2020 IEEE International Conference on Big Data (Big

Data), pages 3652–3661. IEEE.

Crupi, R., Castelnovo, A., Regoli, D., and San

Miguel Gonz

alez, B. (2021). Counterfactual expla-

nations as interventions in latent space. arXiv preprint

arXiv:2106.07754.

Eberhardt, F. and Scheines, R. (2007). Interventions and

causal inference. Philosophy of science, 74(5):981–

995.

Gunning, D. and Aha, D. (2019). DARPA’s explainable

artiﬁcial intelligence (XAI) program. AI Magazine,

40(2):44–58.

High-Level Expert Group on AI (2019). Ethics

guidelines for trustworthy AI. https:

//ec.europa.eu/digital-single-market/en/news/

ethics-guidelines-trustworthy-ai.

Joshi, S., Koyejo, O., Vijitbenjaronk, W., Kim, B.,

and Ghosh, J. (2019). Towards realistic individ-

ual recourse and actionable explanations in black-

box decision making systems. arXiv preprint

arXiv:1907.09615.

Kalainathan, D. and Goudet, O. (2019). Causal discov-

ery toolbox: Uncover causal relationships in python.

arXiv preprint arXiv:1903.02278.

Kalainathan, D., Goudet, O., and Dutta, R. (2020). Causal

Discovery Toolbox: Uncovering causal relationships

in Python. Journal of Machine Learning Research,

21(37):1–5.

Kalisch, M., M

achler, M., Colombo, D., Maathuis, M. H.,

and B

uhlmann, P. (2012). Causal inference using

graphical models with the R package pcalg. Journal

of Statistical Software, 47:1–26.

Karimi, A.-H., Sch

olkopf, B., and Valera, I. (2020). Algo-

rithmic recourse: from counterfactual explanations to

interventions. arXiv preprint arXiv:2002.06278.

Klaise, J., Van Looveren, A., Vacanti, G., and Coca, A.

(2019). Alibi: Algorithms for monitoring and ex-

plaining machine learning models. https://github.com/

SeldonIO/alibi.

Mahajan, D., Tan, C., and Sharma, A. (2019). Pre-

serving causal constraints in counterfactual explana-

tions for machine learning classiﬁers. arXiv preprint

arXiv:1912.03277.

Mothilal, R. K., Sharma, A., and Tan, C. (2020). Explain-

ing machine learning classiﬁers through diverse coun-

terfactual explanations. In Proceedings of the 2020

Conference on Fairness, Accountability, and Trans-

parency, pages 607–617.

Pearl, J. et al. (2000). Models, reasoning and inference.

Cambridge, UK: CambridgeUniversityPress, 19.

Pearl, J., Glymour, M., and Jewell, N. P. (2016). Causal

inference in statistics: A primer. John Wiley & Sons.

Peters, J., Mooij, J. M., Janzing, D., and Sch

olkopf, B.

(2014). Causal discovery with continuous additive

noise models. Journal of Machine Learning Research,

15(58).

Stepin, I., Alonso, J. M., Catala, A., and Pereira-Fari

na, M.

(2021). A survey of contrastive and counterfactual ex-

planation generation methods for explainable artiﬁcial

intelligence. IEEE Access, 9:11974–12001.

The European Union (2016). EU General Data Protec-

tion Regulation (GDPR): Regulation (EU) 2016/679

of the European Parliament and of the Council of 27

April 2016 on the protection of natural persons with

regard to the processing of personal data and on the

free movement of such data, and repealing Directive

95/46/EC (General Data Protection Regulation). Ofﬁ-

cial Journal of the European Union. http://data.europa.

eu/eli/reg/2016/679/2016-05-04.

Ustun, B., Spangher, A., and Liu, Y. (2019). Actionable re-

course in linear classiﬁcation. In Proceedings of the

Conference on Fairness, Accountability, and Trans-

parency, pages 10–19.

Van Looveren, A. and Klaise, J. (2019). Interpretable coun-

terfactual explanations guided by prototypes. arXiv

preprint arXiv:1907.02584.

Verma, S., Dickerson, J., and Hines, K. (2020). Counter-

factual explanations for machine learning: A review.

arXiv preprint arXiv:2010.10596.

Leveraging Causal Relations to Provide Counterfactual Explanations and Feasible Recommendations to End Users

Wachter, S., Mittelstadt, B., and Russell, C. (2017). Coun-

terfactual explanations without opening the black box:

Automated decisions and the gdpr. Harv. JL & Tech.,

31:841.

White, A. and Garcez, A. d. A. (2019). Measurable coun-

terfactual local explanations for any classiﬁer. arXiv

preprint arXiv:1908.03020.

Zheng, X., Aragam, B., Ravikumar, P. K., and Xing, E. P.

(2018). Dags with no tears: Continuous optimization

for structure learning. In Advances in Neural Informa-

tion Processing Systems, pages 9472–9483.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence