On the LPSE Password Meter’s Discrepancies among Different Datasets
Agnieszka Rucka and Wojciech Wodo
Department of Fundamentals of Computer Science, Wroclaw University of Science and Technology,
Wybrzeze Wyspianskiego 27, Wroclaw, Poland
Keywords:
Password, Password Meter, Password Strength, Security, LPSE, PCFG, zxcvbn.
Abstract:
The global dataset constantly grows, along with the number of online accounts. More and more data breaches
occur, putting users’ data at risk. At the same time, users still commonly choose weak passwords. It has
been shown that password strength meters can contribute to better user choices. As the problem of password
strength estimation is nontrivial, a number of solutions have been proposed. One of them is the LPSE (Guo
and Zhang, 2018), which, according to its authors, shows very promising performance. However, we observed
a significantly worse performance of LPSE in a different dataset. In this paper we present an extensive in-
vestigation of these discrepancies. We describe our recreation of the original experiment and confront the
obtained results with the original. We analyze the data distribution in our dataset, and compare performance
of the LPSE with the widely known lightweight password meter zxcvbn. Lastly, we discuss possible reasons
for observed discrepancies (including methodological differences) and draw final conclusions.
1 INTRODUCTION
Over recent years the use of online services skyrock-
eted, bringing a significant rise in the number of ac-
counts owned by a single person. Additionally, more
often than before, these accounts contain personal or
financial information, such as e-mail and postal ad-
dresses, phone numbers, or credit card credentials.
Along with the growth of the global dataset, we ob-
serve a rising tendency in the yearly number of data
breaches, with 2019’s record in the number of leaked
data records (Risk Based Security, 2020).
Analyzes of disclosed password sets show that,
despite having contact with password-building ad-
vice on multiple occasions, users still tend to make
very weak, predictable choices. The list of the 10
most popular passwords of 2019, published by Na-
tional Cyber Security Centre (UK), is a vivid exam-
ple of that: 123456, 123456789, qwerty, password,
1111111, 12345678, abc123, 1234567, password1,
12345. The combination of sensitive data and weak
protection poses serious risk to the users.
1.1 Motivation
As Stephen Furnell and Rawan Esmael’s research
suggests, users presented with a live feedback on the
strength of their password during its creation, tend to
choose stronger phrases (Furnell and Esmael, 2017).
A reliable password meter can therefore be an im-
portant element of security framework. At the same
time, we observe that practices regarding measuring
password strength significantly differ among service
providers. There are no common standards for pass-
word policies, even among the industry leaders. Sim-
ple sets of rules are not reliable, and often accept very
weak choices. Password strength measuring is cer-
tainly a nontrival problem. Although multiple solu-
tions have been proposed so far, this field still requires
research and further development.
1.2 Contribution
The initial goal of our research was proposing a mod-
ification to a password strength measuring algorithm
LPSE (Guo and Zhang, 2018). However, during our
experiments, we observed severe discrepancies in the
performance of the unmodified original. This paper
presents a thorough analysis of this results’ mismatch.
Our contribution is providing a review for an existing
password strength measuring algorithm.
2 ANALYSIS OF THE PROBLEM
OF PASSWORD STRENGTH
This section is an introduction to the problem of pass-
words strength measuring. It aims to familiarize the
Rucka, A. and Wodo, W.
On the LPSE Password Meter’s Discrepancies among Different Datasets.
DOI: 10.5220/0010766900003120
In Proceedings of the 8th International Conference on Information Systems Security and Privacy (ICISSP 2022), pages 255-263
ISBN: 978-989-758-553-1; ISSN: 2184-4356
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
255

reader with challenges in this field, as well as com-
mon solutions. It provides an overview of exist-
ing practical approaches, along with exemplary algo-
rithms, three of which (LPSE, zxcvbn, PCFG) are rel-
evant to the later discussion.
2.1 Defining Password Strength
First, notice that the strength of a password is not an
objective value. In order to be able to measure it, we
need to establish some quantitative metric. We intu-
itively agree that a strong password should take long
to break. Therefore, time could be our first candidate.
However, running time is usually incomparable be-
tween machines, due to a number of technical issues.
Having this in mind, we propose an algorithmics-like
approach - to understand the time as the average num-
ber of operations performed. As we do not know
the algorithms used by the attacker, let us express
the strength of a password by the average number of
guesses needed to break it.
2.2 Real-world Challenges
In an ideal setting, passwords are generated randomly.
In this case, bruteforce attack is the best available
method of guessing. The average number of guesses
needed is proportional to the string’s length and space
size. However, this is a rather rare situation. More
commonly, passwords are generated pseudorandomly
(e.g. with password managers). Then, aside from
length and character set, we need to consider the qual-
ity of the PRG used. This can be achieved by cal-
culating the password’s entropy, understood in this
case as a ”measure of the source’s unpredictability”.
However, the most common setting in which pass-
word strength is measured are human-provided pass-
words. These are rarely random-looking, and are of-
ten based on existing words. As in human languages
letters have different frequencies of occurrence and
some sequences of letters are more common than oth-
ers, estimation of human-created passwords strength
is a complicated task. Basic entropy calculation is in
this case insufficient. There is no universal remedy
for this, and several approaches have been proposed.
2.3 Overview of Existing Approaches
The existing approaches can be, according to Yimin
Guo and Zhenfeng Zhang (Guo and Zhang, 2018), di-
vided into three main groups:
2.3.1 Rule-based Approach
The input passwords are checked against a set of rules
that a strong password should follow. The overall
score is calculated awarding positive choices and
penalizing negative. This approach was commonly
found in the early, rather naive password meters,
which employed some simple rules, such as use
of one capital letter, one number, etc. However,
when the rules are properly chosen, the meter might
have satisfying performance. An example of a good
rule-based meter is the zxcvbn (Wheeler, 2016).
Example - the zxcvbn algorithm
It detects weak patterns in the password, and divides
it into substrings accordingly. The weak patterns
identified are:
• repeat (e.g. 111, abcabc)
• sequence (e.g. 12345)
• reverse (e.g. drowssap)
• keyboard (e.g. qwerty, zxcvbn)
• date (e.g. 05122020)
The score of each of substrings is calculated sepa-
rately. If a dictionary entry is found, it is scored based
the word’s rank in the dictionary. The remaining parts
of the password are considered random strings and
their score is defined by their entropy. The overall
score of the password is a sum of all the substrings’
scores.
2.3.2 Similarity-evaluation Approach
The core of this method is the concept of an ideal
strong password. A model of such universally strong
password is proposed and described. The strength
meter evaluates similarity of input to the universally
strong password. The closer the input password to
the ideal one, the stronger it is. This approach is
represented by the LPSE algorithm (Guo and Zhang,
2018).
Example - the LPSE (lightweight password strength
estimation) algorithm
In this method the measured password is encoded as a
vector of the string’s characteristics. The universally
strong password, also expressed as such vector,
serves as a reference. For this pair of vectors, two
metrics are calculated: cosine-length similarity and
password distance similarity. The pair of values
is the translated to the overall score of the input.
The characteristics’ vector calculation is tweaked
by a small set of rules that detect highly predictable
sequences.
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
256

2.3.3 Probability-based Approach
This class of methods refers directly to number of
guesses needed to break a password, rather than es-
timating its entropy. Firstly, a model is prepared, bas-
ing on a list of plaintext passwords. Later, it is used
to aid a guessing algorithm in determining the input
password. The strength of the password is defined
by the number of guesses needed to figure it out cor-
rectly.
As the class is broadly defined, there are several
approaches that can be identified as its represen-
tatives. Here, the two most well-known will be
presented. As they are significantly more complex
than the previous two algorithms, their description
will be more general. For a deeper insight, please
refer to the original works.
Example - Markov chains and finite automata
method (Narayanan and Shmatikov, 2005)
This method is based upon the following assump-
tions:
• humans choose passwords to be memorable,
meaning that they either consist of existing words
of some language or resemble them. Therefore,
they tend to choose letters with probabilities close
to their frequency of occurrence in the chosen
language. These can be predicted with Markov
chains-based methods.
• the use of numbers and special characters in pass-
words usually follows a few popular patterns,
which are deployed as ”mangling rules” (like
in popular password cracker John the Ripper).
These can be generalized by finite automata.
The authors of the solution present several algorithms
for generation of a wordlist for a dictionary attack,
basing on the Markov chains, the finite automata
and, finally, a mixed approach. Their method is
reported to outperform the Oechslin’s ”rainbow”
attack (Oechslin, 2003), widely regarded as the
fastest method for large spaces exhaustion.
Example - PCFG (probabilistic context-free
grammar based meter) (Weir et al., 2009)
The method itself is not a password meter, but a
password guesser. Yet, it can be used for estimating
passwords strength as well. A list of passwords in
plaintext is used to automatically extract common
structure patterns in them and create a probabilistic
context-free grammar. From the grammar, mangling
rules for the guesser are extracted. Then, a dictionary
attack is performed, using these rules to modify
dictionary entries. This method of creating mangling
rules (as opposed to setting them manually, or relying
on a default set, as in standard password crackers)
leads to significantly better performance - in the
original paper, up to 129% more passwords were
cracked than by John the Ripper.
3 THE LPSE ALGORITHM
This section presents a description of the LPSE algo-
rithm. It summarizes Chapter 3 of the original work
(Guo and Zhang, 2018). Its goal is to provide the
Reader with understanding of the method, as it will
be analysed further in this paper.
3.1 Design Objectives
The LPSE authors’ goal was to provide a lightweight
password meter, suitable for use on the client-side,
that would show better performance than existing
leading solutions, such as zxcvbn. The algorithm was
designed to be computationally lightweight, need a
limited amount of additional data (such as lengthy
dictionaries), and be easy to implement.
3.2 Vectors of Characteristics
In this method, the passwords are represented as vec-
tors α = (x
1
, x
2
, x
3
, x
4
, x
5
), where x
i
’s represent, re-
spectively: digits, lowercase letters, uppercase letters,
special characters and password length. As uppercase
letters and special characters tend to be included in
strong passwords, their use is awarded with a higher
score. On the contrary, as doubling letters or choos-
ing consecutive characters is a weak choice, it is pe-
nalized - the overall score for the sequence is equal to
score for a single building block. The general rules,
as described by the authors of the solution, are shown
in Figure 1. As the users tend to follow some weak
patterns when creating passwords, these basic calcu-
lations are tuned up by detecting and penalizing them.
The list of the weak patterns identified by the algo-
rithm is presented in Figure 2.
3.3 Universally Strong Password
As stated in the previous section, an ideal strong pass-
word should be randomly generated and sufficiently
long. The authors of LPSE propose an 18-characters
long sequence. Let us assume that the characters are
chosen uniformly at random from a 94-piece set con-
sisting of 10 digits, 26 lower- and 26 uppercase let-
ters, and 32 special characters. Then, characters from
all groups should appear proportionally, namely: 2
On the LPSE Password Meter’s Discrepancies among Different Datasets
257

Figure 1: Basic scoring rules, Table 1 from the original
work (Guo and Zhang, 2018).
Figure 2: Common patterns detected by the algorithm, Ta-
ble 2 from the original work (Guo and Zhang, 2018).
digits, 5 lower- and 5 uppercase letters, and 6 special
characters.
When choosing 4-character strings fully at ran-
dom, abcd and 5K%p could be chosen with equal
probability. However, an adversary optimized for use
with human-generated passwords would easily break
the first one. Therefore, we must additionally assume
that the universally strong password does not ”acci-
dentally” follow any weak pattern. The authors of
LPSE propose to assume that no two adjacent charac-
ters come from the same group. We will use this char-
acteristic again later. Under this assumption, the vec-
tor for a universally strong 18-characters long pass-
word is (2, 5, 10, 18, 18).
3.4 Scoring
To provide better accuracy, the algorithm aims to con-
sider three aspects of password composition:
• structure (type and proportions of characters con-
tained)
• length
• editorial distance (number of transformations
needed to transform it into the universally strong
password)
To capture all these characteristics, two measures
are used: the cosine-length similarity for length and
structure, and password distance similarity for the
editorial distance. For their definitions consult the
original LPSE paper. The pair of values is trans-
lated into a score expressed within a 3-level scale
(weak/medium/strong). The algorithm’s authors pro-
posed classification thresholds, based of an analysis
of a leaked passwords dataset. The two similarities
were calculated for passwords previously identified
as strong and weak, and intervals were determined
accordingly. Figure 3 presents the thresholds estab-
lished, s
c
being cosine-length similarity and s
p
- pass-
word distance similarity.
Figure 3: Classification thresholds for password scores, un-
numbered definition from Chapter 4.3 of the original paper
(Guo and Zhang, 2018).
4 DESCRIPTION OF THE
EXPERIMENTS PERFORMED
This section describes the performance evaluation ex-
periments on the LPSE. First, it briefly summarizes
the original experiment. For full description consult
Chapter 4 of (Guo and Zhang, 2018). Then, our ex-
periment is presented. Resources used by our team
can be found at: https://github.com/arucka/
mod_LPSE. Descriptions of the experiments are rel-
evant for understanding the observed discrepancies in
results, discussed later.
4.1 The Original Experiment
The aim of the original experiment was to com-
pare LPSE’s performance with other lightweight pass-
words meters. Believing that a good lightweight me-
ter should yield similar results to a more technologi-
cally advanced one, the authors chose to use PCFG as
the point of reference regarding the ”real” strength of
a password. The other two lightweight meters under
comparison were zxcvbn and PM
1
.
The dataset was composed of passwords coming
from various leaks, mainly of Chinese and English
origin. It was divided into three subsets, the first of
1
http://www.passwordmeter.com/
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
258

which was used to train a PCFG instance, the sec-
ond - to determine LPSE classification thresholds, and
the third one - to compare the performance of the
lightweight meters. Each password in the third set
was scored with all four meters. The scores granted
by each lightweight meter to passwords identified as
weak and strong by the PCFG were summarized. As
it can be observed in Figures 4 and 5, the LPSE’s scor-
ing was the most consistent with PCFG’s.
Figure 4: Classification of strong passwords by LPSE, PM
and zxcvbn. For numerical values see Figure 3 from the
original paper (Guo and Zhang, 2018).
Figure 5: Classification of weak passwords by LPSE, PM
and zxcvbn. For numerical values see Figure 4 from the
original paper (Guo and Zhang, 2018).
4.2 Our Experiment
The general outline of our experiment was the same
as the original. However, we introduced several mod-
ifications. As the original dataset was unavailable, as
well as some of the password sets included, we pre-
pared our own. We chose password leaks with a more
international origin, and prepared two datasets: small
(199 032 passwords) and large (527 163 passwords).
All steps of the experiment were performed on both of
them identically. Originally, our goal was to propose
a modification for the LPSE, therefore we did not in-
clude other lightweight meters, just the original and
modified LPSE. Courtesy of Dr. Guo, we received
the original code, which we slightly corrected due to
compilation errors. We also corrected one minor dis-
crepancy in implementation (one of the bonuses in-
cluded in the algorithm description was not included
in the code). As we did not want to re-establish LPSE
classification thresholds, we skipped this stage of the
original experiment, and divided our datasets in only
two subsets.
Originally, estimation of strength with the PCFG
was performed using a Monte Carlo simulation
method (Dell’Amico and Filippone, 2015). The au-
thors of the LPSE did not provide any details on
their application of this method. Therefore, we chose
to use Dr. Weir’s implementation of the PCFG
and a Monte Carlo simulation script by GitHub user
cwwang15, available in the same repository.
2
The original and modified LPSE, showed almost
identical performance in both our sets. However, it
was significantly different from the results reported in
the original paper. Figures 6 and 7 present a com-
parison of performance of the LPSE in the original
research and our experiment.
Figure 6: Classification of strong passwords by the LPSE in
the three datasets.
Figure 7: Classification of weak passwords by the LPSE in
the three datasets.
Observe that while LPSE’s performance in both
our datasets (small and large) is similar, it is signifi-
cantly worse than the one declared in the original pa-
2
https://github.com/lakiw/pcfg cracker
On the LPSE Password Meter’s Discrepancies among Different Datasets
259

per. This turned our research towards an investigation
of these discrepancies. It is described in the next sec-
tion. From that moment on, our modification of the
LPSE is not considered anymore, and any mention of
the LPSE refers to the original version.
5 INVESTIGATION ON LPSE’S
RESULTS
This section investigates the discrepancies in the
claimed and observed performance of the LPSE. First,
the cause of the differences is examined. Distribution
of our dataset is analyzed and compared to the orig-
inal dataset’s. Then, the possible reasons for differ-
ences among them, including variances in methodol-
ogy, are discussed. This analysis leads to final con-
clusions, provided in the next section.
5.1 Analysis of the Discrepancies
The starting point for our analysis is the high rate of
misclassification of both strong and weak passwords
as medium, which can be observed in Figures 6 and
7. As the LPSE’s classification thresholds were es-
tablished based on a specific dataset, we propose a
hypothesis that they are overfit to it. To verify this, let
us compare the original thresholds (Figure 8) with the
distribution of passwords from our large dataset, re-
garding their strength as assigned by the PCFG. Fig-
ure 9 presents this distribution, color-coded depend-
ing on their PCFG-determined strength. The original
medium interval is outlined in blue for comparison.
Figure 8: Division of the plot of relationship between
cosine-length similarity and password distance similarity
by LPSE’s original thresholds.
Observe that the medium interval is densely oc-
cupied by strong passwords, and that the plot points
Figure 9: Distribution of passwords from the large test set
in terms of their cosine-length similarity and password dis-
tance similarity. Colour indicates strength of the password
as measured by PCFG: green-strong, yellow-medium, red-
weak.
seem to cover one another. Therefore, to obtain better
visibility, let us plot the strong and weak passwords
separately - see Figures 10 and 11.
Figure 10: Distribution of strong passwords from the large
test set in terms of their cosine-length similarity and pass-
word distance similarity.
Notice that the classification thresholds indeed do
not fit the characteristics of our dataset. However,
this is not the matter of simple overfitting, which
could be easily solved by correcting the thresholds’
values. The area common for both strong and weak
passwords is extremely large, and the passwords are
widely spread. This is very different from the distri-
bution presented in the original paper, where strong
and weak passwords occupied much smaller areas of
the plot, which were almost disjoint from one another.
In the original dataset, the distinction between strong
and weak passwords was clear. In our case, it seems
impossible to choose new classification thresholds so
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
260

Figure 11: Distribution of weak passwords from the large
test set in terms of their cosine-length similarity and pass-
word distance similarity.
that the performance will be even close to the orig-
inal one. However, as a scatter plot does not pro-
vide clear data on the density of the passwords, let us
verify this suspicion by re-plotting the same data as
density heatmaps. This will let us observe, whether
the high-density areas of strong and weak passwords
align. The heatmaps are presented in Figures 12 and
13. The plot area most densely populated by strong
passwords is outlined in both Figures for comparison.
Figure 12: Distribution of strong passwords from large set.
The red outline marks the area with the highest density of
strong passwords.
Observe that the most dense groups of strong and
weak passwords indeed overlap, confirming our sus-
picion. It is impossible to propose new thresholds,
that will offer effective classification. As this might
be a sign of a major design flaw in the LPSE, we per-
formed an investigation on the possible reasons for
such results, to ensure no methodological errors were
made during our research. The next section covers
this analysis.
Figure 13: Distribution of weak passwords from large set.
The red outline marks the area with the highest density of
strong passwords for comparison.
5.2 Analysis of the Observed Data
Distributions
Considering the two experiments on LPSE (original
and ours), we propose the following three hypotheses
on the possible reason for the observed differences in
password distributions:
1. There were no significant differences between the
two experiments, and the obtained results are cor-
rect - the dataset used in the original paper was
peculiar.
2. The implementations of the LPSE are different in
the two experiments, which leads to yielding dif-
ferent values of the two similarities for the same
password.
3. The use of the PCFG in the two experiments was
in some way different, leading to it assigning dif-
ferent strength scores to the same password.
The hypotheses will now be discussed in more detail.
5.2.1 Hypothesis 1: The Original Dataset Was
Peculiar
As mentioned earlier, we encountered some obstacles
preventing us from repeating the original experiment
verbatim. A definitive verification whether the experi-
ments were synonymous, would require repeating our
experiment on the original dataset, or the original ex-
periment on our datasets. As this is currently impos-
sible, we cannot confirm nor refute this hypothesis.
5.2.2 Hypothesis 2: The LPSE Implementations
Are Different
The LPSE implementation we received from Dr. Guo
needed several code adjustments to compile, and a
On the LPSE Password Meter’s Discrepancies among Different Datasets
261

small correction. This leads to a suspicion that it
could be a non-final version, and the implementation
of the LPSE used in the original research was some-
how different from ours. We cannot definitively verify
that, however, we performed a code review for a bet-
ter insight. We believe the code correctly implements
the LPSE algorithm described in the paper. Therefore,
there is no reason for the implementations to be sig-
nificantly different. To rule out our small correction
as the source of the mismatch, we also tried to use a
non-corrected LPSE (meaning with no improvements
other than needed to compile), yet its performance
was worse compared to the corrected one. This does
not definitively disprove the hypothesis, however sug-
gests that it is rather unlikely.
5.2.3 Comparison to zxcvbn
As the first and second hypotheses cannot be defini-
tively confirmed nor refuted, we decided to verify zx-
cvbn’s performance in all three datasets for compar-
ison. Having no access to the original dataset, we
had to rely on the results provided by the authors of
the LPSE. For our datasets, we chose an officially
approved Python port of zxcvbn (originally written
in JavaScript), available on GitHub
3
and in official
repository for the pip command. The method of eval-
uating performance was analogous to LPSE’s. The
performance of zxcvbn in the three sets is presented
in Figures 14 - 15 .
Figure 14: Classification of strong passwords by the zxcvbn
in the three datasets.
First, observe that zxcvbn’s performance is more
consistent than LPSE’s. This suggests that the lat-
ter might either be more sensitive to specific charac-
teristics of the evaluated sets (supporting hypothesis
#1) or that its implementations used in the original
and our experiment indeed differed (supporting hy-
pothesis #2). Although this does not speak in favour
of any of the hypotheses, it is worth noting that de-
3
https://github.com/dwolfhub/zxcvbn-python
Figure 15: Classification of weak passwords by the zxcvbn
in the three datasets.
spite the less distinctive distribution of our datasets,
zxcvbn’s results are satisfying. It outperforms LPSE
in correctly classifying strong and weak passwords,
which contributes to enhanced security and building
correct intuitions in users. On the other hand, it shows
slightly higher misclassification rate of strong pass-
words as weak than LPSE, which might cause un-
necessary rejection of good passwords, degrading us-
ability. However, the claim that LPSE outperforms
zxcvbn, which was made by the original authors,
should be considered undermined and further verified
in other datasets.
5.2.4 Hypothesis 3: The PCFG Implementations
Differ
The use of the PCFG in the original paper is described
very vaguely. Apart from citing an article describing
the Monte Carlo simulation algorithm (Dell’Amico
and Filippone, 2015), it does not cover any details.
On our second attempt to contact the authors of the
LPSE paper we were not provided with any details as
well. However, in the further stage of our research,
we managed to retrieve the original script for per-
forming the Monte Carlo estimation by Dell’Amico
and Filippone. While we cannot confirm that it was
used in the original evaluation of the LPSE, it can cer-
tainly be considered correct to use it. Therefore, we
performed a reevaluation of the LPSE for our large
dataset. The results, presented in Figures 16 and 17,
support the initial results of our experiment, obtained
with the script by GitHub user cwwang15. There-
fore, we believe that the implementation of PCFG and
Monte Carlo estimation used in our experiment was
not the cause for discrepancies in the results, and this
hypothesis should be rejected.
ICISSP 2022 - 8th International Conference on Information Systems Security and Privacy
262

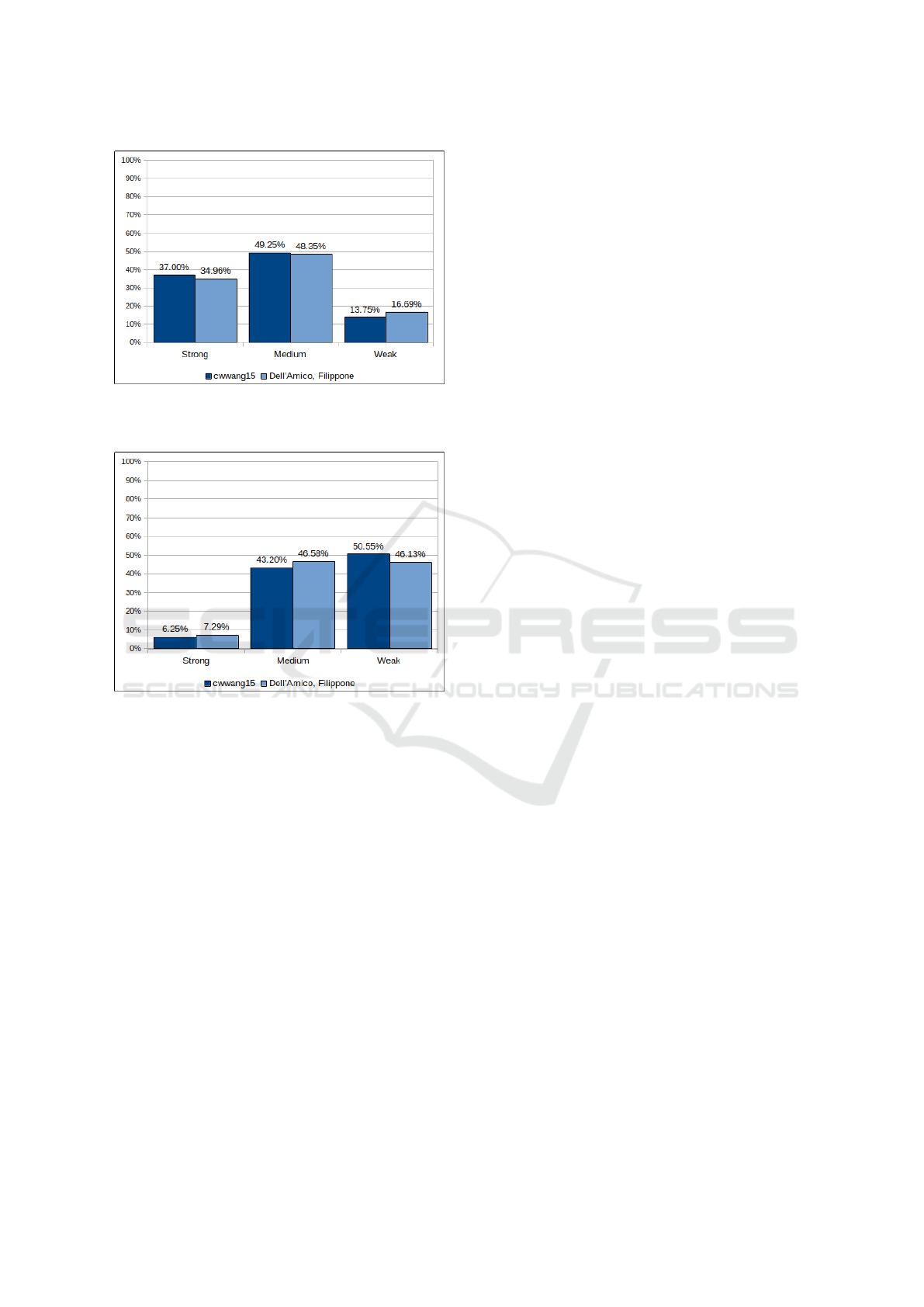
Figure 16: Classification of strong passwords from the large
set, with cwwang15’s and Dell’Amico and Filippone Monte
Carlo scripts used.
Figure 17: Classification of weak passwords from the large
set, with cwwang15’s and Dell’Amico and Filippone Monte
Carlo scripts used.
6 CONCLUSIONS
In this paper, we presented an overview of the prob-
lem of password strength measuring and discussed
performance issues of the LPSE algorithm. Our ex-
periment was explained, and observed discrepancies
in performance were investigated. The findings sug-
gest, that for our datasets, passwords’ characteris-
tics LPSE was based upon do not hold. The mis-
match might be a result of either methodological dif-
ferences between the experiments, or signify major
design flaws in the LPSE. We rejected discrepancies
in using the PCFG as the source of the problem, as we
successfully repeated our results when using another
implementation. We could not confirm, whether the
original implementation of the LPSE was analogous
to ours. Lastly, we also could not verify the origi-
nal results, as the original dataset is not available any-
more. We believe that our findings put LPSE’s quality
in question, and that it should be further examined be-
fore it could be recommended for practical use. Cur-
rently, we suggest to use zxcvbn as the better choice
for a lightweight password meter, as it is better known
and shows more consistent results among datasets. It
also provides better protection from using too weak
passwords. We highly encourage the Readers to ver-
ify our experiment’s results. The resources helpful to
recreate it are provided in the GitHub repository of
this research (https://github.com/arucka/mod_
LPSE).
REFERENCES
Dell’Amico, M. and Filippone, M. (2015). Monte carlo
strength evaluation: Fast and reliable password check-
ing. In Proceedings of the 22nd ACM SIGSAC Con-
ference on Computer and Communications Security,
CCS ’15, page 158–169, New York, NY, USA. Asso-
ciation for Computing Machinery.
Furnell, S. and Esmael, R. (2017). Evaluating the effect
of guidance and feedback upon password compliance.
Computer Fraud And Security, 2017(1):5 – 10.
Guo, Y. and Zhang, Z. (2018). Lpse: Lightweight
password-strength estimation for password meters.
Computers And Security, 73:507 – 518.
Narayanan, A. and Shmatikov, V. (2005). Fast dictionary
attacks on passwords using time-space tradeoff. In
Proceedings of the 12th ACM Conference on Com-
puter and Communications Security, CCS ’05, page
364–372, New York, NY, USA. Association for Com-
puting Machinery.
Oechslin, P. (2003). Making a faster cryptanalytic time-
memory trade-off. In Boneh, D., editor, Advances in
Cryptology - CRYPTO 2003, pages 617–630, Berlin,
Heidelberg. Springer Berlin Heidelberg.
Risk Based Security (2020). 2019 year end report. data
breach quickview.
Weir, M., Aggarwal, S., d. Medeiros, B., and Glodek,
B. (2009). Password cracking using probabilistic
context-free grammars. In 2009 30th IEEE Sympo-
sium on Security and Privacy, pages 391–405.
Wheeler, D. L. (2016). zxcvbn: Low-budget password
strength estimation. In 25th USENIX Security Sympo-
sium (USENIX Security 16), pages 157–173, Austin,
TX. USENIX Association.
On the LPSE Password Meter’s Discrepancies among Different Datasets
263