LABNET: A Collaborative Method for DNN Training and Label

Aggregation

Amirmasoud Ghiassi

1 a

, Robert Birke

2 b

and Lydia Y. Chen

1 c

Delft University of Technology, Delft, The Netherlands

ABB Research, Baden-D

attwil, Switzerland

Keywords:

Crowdsourcing, Deep Learning, Noisy Labels, Label Aggregation.

Abstract:

Today, to label the massive datasets needed to train Deep Neural Networks (DNNs), cheap and error-prone

methods such as crowdsourcing are used. Label aggregation methods aim to infer the true labels from noisy

labels annotated by crowdsourcing workers via labels statistics features. Aggregated labels are the main data

source to train deep neural networks, and their accuracy directly affects the deep neural network performance.

In this paper, we argue that training DNN and aggregating labels are not two separate tasks. Incorporation be-

tween DNN training and label aggregation connects data features, noisy labels, and aggregated labels. Since

each image contains valuable knowledge about its label, the data features help aggregation methods enhance

their performance. We propose LABNET an iterative two-step method. Step one: the label aggregation algo-

rithm provides labels to train the DNN. Step two: the DNN shares a representation of the data features with

the label aggregation algorithm. These steps are repeated until the converging label aggregation error rate. To

evaluate LABNET we conduct an extensive empirical comparison on CIFAR-10 and CIFAR-100 under differ-

ent noise and worker statistics. Our evaluation results show that LABNET achieves the highest mean accuracy

with an increase of at least 8% to 0.6% and lowest error rate with a reduction of 7.5% to 0.25% against existing

aggregation and training methods in most cases.

1 INTRODUCTION

The remarkable success of Deep Neural Networks

(DNNs) in supervised learning models, e.g., in com-

puter vision, natural language processing, and recom-

mender systems, is mainly dependent on data anno-

tated by human knowledge (Imran et al., 2016). It

is drastically time-consuming and expensive to label

each instance by a human expert for massive datasets.

Crowdsourcing platforms have emerged as an ef-

ﬁcient and inexpensive solution for the label anno-

tation task. Since workers in the crowd might have

different expertise levels, the quality of annotated la-

bels is not remarkable (Xu et al., 2017; Yan et al.,

2014). Because the data labeled by crowdsourcing is

used to train DNNs, the label quality has a direct im-

pact on the performance and accuracy of the trained

models. Label aggregation methods aim to infer the

correct labels from noisy annotated data such as stem-

https://orcid.org/0000-0001-6780-0107

https://orcid.org/0000-0003-1144-3707

https://orcid.org/0000-0002-4228-6735

ming from crowdsourcing. In other words, label ag-

gregation methods try to provide high quality labels

for training DNNs. We need to mention here, our fo-

cus is on image classiﬁcation tasks, but our method

has the ability to apply to all datasets that contain

data features. The current solutions consider label

aggregation and image classiﬁcation as two separate

tasks. At the ﬁrst step, the label aggregation algo-

rithm performs data labeling to enhance the quality of

the labels generated by crowdsourcing workers. Next,

the provided dataset, including sample and annotated

label by label aggregation method, is used to train

DNN.

The critical point in the process of labeling, then

learning, is the lack of connection between label ag-

gregation and the DNN training. In addition, the cur-

rent label aggregation, as its name says, only uses la-

bel information to ﬁnd the correct labels without con-

sidering the data features and samples themselves.

In contrast to the current solutions we consider the

label aggregation and DNN training in a collabora-

tive and interrelated manner. In our proposed frame-

work named LABNET, label aggregation algorithms

Ghiassi, A., Birke, R. and Chen, L.

LABNET: A Collaborative Method for DNN Training and Label Aggregation.

DOI: 10.5220/0010770400003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 2, pages 56-66

ISBN: 978-989-758-547-0; ISSN: 2184-433X

and classiﬁcation tasks work together iteratively and

exchange useful knowledge. As mentioned before,

label aggregation algorithms work based on label in-

formation without taking into account data features.

The data features are used to train DNNs, but their

information can be used to aggregate labels. Since

our method is a collaborative process between train-

ing DNN and labels aggregation, DNN extracts a rep-

resentation of data features to share with the label ag-

gregation algorithm as additional information for in-

creasing the quality of annotated labels. Aggregated

labels are used to train DNN as training data, and

DNN performs the classiﬁcation task besides features

extraction for aggregation. In other words, our pro-

posed method interleaves label aggregation and clas-

siﬁcation task such that the feature extraction part can

be useful to both simultaneously.

The majority of label aggregation methods are

iterative-based algorithms. One of the most well-

known method is Expectation–Maximization (Dawid

and Skene, 1979). The Expectation–Maximization

(EM) algorithm is commonly used in aggregation via

maximizing the likelihood of the data. Prior probabil-

ities are an essential part of calculating the data like-

lihood. Numerous probabilistic and statistics mod-

els (Cousineau and Helie, 2013) have studied the im-

pact of different priors on maximum likelihood and,

consequently, EM algorithms. The error rate of aggre-

gated labels directly depends on prior probabilities.

Hence choosing the wrong prior probability leads to

poor performance of the EM algorithm, and as a re-

sult, the number of incorrectly aggregated labels in-

creases.

In LABNET, DNN has two tasks: 1) the traditional

classiﬁcation and, 2) features extraction for aggrega-

tion algorithm. We use the output of the last layer of

the DNN, which is a softmax layer, to map data fea-

tures into a probability vector. In other words, LAB-

NET links data features and labels via the DNN soft-

max output and aggregated labels. Hence LABNET

consists of a classiﬁer and label aggregator. The la-

bel aggregator works based on the EM algorithm, and

the classiﬁer is a DNN, e.g., for image classiﬁcation.

At each iteration, the aggregator provides labels for

input images to train the image classiﬁer. In addition

to learning the image classiﬁer, the classiﬁer repre-

sents each data sample by a softmax vector, which is

considered as the prior probability in the label aggre-

gation algorithm.

Since training the classiﬁer at each iteration of the

EM algorithm would be extremely time-consuming,

we design an algorithm for deciding when to train the

DNN with the latest aggregated labels. After each

iteration of the EM algorithm, we use cross-entropy

function to evaluate the difference between aggre-

gated labels and the classiﬁer prediction at each it-

eration. At each iteration, the value of cross-entropy

is compared to cross-entropy in the previous iteration.

After comparing the cross-entropy of two consecutive

iterations, the training classiﬁer and label aggregation

algorithm will be performed for the next iteration if

the difference is ascending. Otherwise, only label ag-

gregation will be performed.

We evaluate LABNET on two popular image

datasets (Krizhevsky et al., 2009) with synthetic la-

bel noise for each worker. We consider three noise

patterns including uniform, bimodal, and ﬂip noise

under different miss rates for workers. We com-

pare LABNET performance including classiﬁer ac-

curacy and aggregated labels error rate against three

standard methods for aggregation, i.e., EM algorithm

without using softmax as the prior, Minimax Entropy

and Majority Voting. Our results show that LABNET

achieves both high classiﬁcation accuracy and low la-

bel aggregation error rate against baselines methods

under various scenarios with different worker num-

bers, noise patterns, and noise ratios. LABNET out-

performs other baselines accuracy 2% and 3% on av-

erage for CIFAR-10 and CIFAR-100, respectively. In

terms of label aggregation error rate, LABNET re-

duces error rate by 1% and 3% on average against

the baselines for CIFAR-10 and CIFAR-100, respec-

tively.

The contributions of this paper are summarized as

follows.

• LABNET leverages an interactive method for

training DNN and aggregating labels. LABNET

considers the two as collaborative task. Each

step sends its feedback to each other one to im-

prove the performance of the whole framework,

i.e., high DNN accuracy and low aggregation er-

ror rate.

• We estimate the prior probability to use in the

EM algorithm via the softmax output of the DNN

which beneﬁts of using features and labels to-

gether.

• We design an algorithm to decide when to train

the DNN based on the cross-entropy between the

aggregated labels and the labels predicted by the

DNN in the previous training round.

2 RELATED WORK

Robust training DNNs and label aggregation are well-

studied subject areas. Most of the existing robust

learning methods do not take into account collabora-

LABNET: A Collaborative Method for DNN Training and Label Aggregation

tion with label aggregation algorithms.

Robust DNNs consider three different approaches

to distill the impact of wrong labels, including ﬁlter-

ing wrong labels (Han et al., 2018; Yu et al., 2019), es-

timation of noise confusion matrix (Hendrycks et al.,

2018; Patrini et al., 2017) and noise tolerant loss func-

tion (Shu et al., 2019; Wang et al., 2019). Robust

training methods (Li et al., 2020; Shu et al., 2019;

Jiang et al., 2018; Ghiassi et al., 2019; Ghiassi et al.,

2021) mainly focus on the learning task considering

robust architecture and loss adjustment. In robust

training, it does not matter how the data is labeled

and by what process. Hence, in robust training label

aggregation is considered as an entirely separate task.

Label aggregation methods mostly use unsuper-

vised solutions. As an example, (Yin et al., 2017)

introduces an unsupervised method using two neu-

ral networks including a classiﬁer and re-constructor

for label aggregation. We can categorize the aggre-

gation methods into two groups. The ﬁrst group re-

lies on probabilistic inference models (Yang et al.,

2019; Yang et al., 2018), which study the impact of

latent variables on the likelihood of noisy label sam-

ples. (Kim and Ghahramani, 2012; Venanzi et al.,

2014; Simpson et al., 2015; Hong et al., 2021) de-

velop a probabilistic graphical model for label aggre-

gation, and a confusion matrix is considered for eval-

uating each worker. (Liu et al., 2012) works based on

prior approximation via variational inference.

The second group encompasses confusion matrix

based methods. The focus is to ﬁnd how correct labels

are corrupted to noisy labels by each worker (Dawid

and Skene, 1979). GLAD (Whitehill et al., 2009) is

a binary labeling method that infers the true label and

difﬁculty of each sample at the same time. Also, Zhou

et al. (Zhou et al., 2012; Zhou et al., 2014) design a

framework that uses minmax entropy estimator and

assigns a different probabilistic distribution to each

sample-worker pair.

Another aspect of label aggregation is to use a

deep neural network for aggregating crowdsourced

responses. As opposed to the existing unsupervised

method, DeepAgg (Gaunt et al., 2016) is a supervised

model. DeepAgg, instead of using Bayesian algo-

rithms, the label aggregation model relies on DNNs

to encode required information for statistical models.

Another aggregation method is based on a disagree-

ment between the provided labels by workers and pre-

dictions of learning algorithm (Khetan et al., 2018).

The aforementioned studies are limited to label

aggregation without taking into account feature space.

In this paper, we show that the use of data represen-

tation in the label aggregation algorithm reduces the

error and increases the quality of the output labels.

Besides, prior arts do not consider the training pro-

cess and relation with the aggregation algorithm. In

other words, there is useful knowledge that can be

shared between the label aggregation and the train-

ing processes. LABNET is the ﬁrst study that fo-

cuses on model interaction between label aggregation

and training a deep neural network to the best of our

knowledge.

3 METHODOLOGY

Consider the classiﬁcation and label aggregation

problem having training set with N samples D =

{(x

)}

i=1

, where x

is the feature vector of the i

sample and y

= {y

,...,y

} is the set of

labels from different workers w = {1, 2, . . . , K} for the

instance. y

∈ {0,1}

is the corresponding label

vector generated by worker w in the crowdsourcing

setting and C denotes the number of classes.

To label data, it is common practice to use crowd-

sourcing. Crowdsourcing is a cheap and fast method

to label massive data sets compared to labeling by hu-

man experts, but it is less accurate. The accuracy of a

crowd system depends on the ability of inexperienced

workers to identify the correct label. Label aggrega-

tion algorithms are proposed to increase the accuracy

of crowd labels. Thus the aggregated labels are more

accurate than the label sets provided by single work-

ers. After aggregation process, the aggregated labels

Y = { ˆy

, ˆy

,..., ˆy

} are used to train a classiﬁer net-

work. We denote the classiﬁer network prediction as

f (x

x; θ

θ) where θ

θ are the weights of the classiﬁer net-

work. Since the aggregated labels together with the

samples constitute the training data for the neural net-

work, the accuracy of the trained neural network pre-

dictions depend directly on the accuracy of the aggre-

gated labels.

We propose a method leveraging direct coopera-

tive method the classiﬁer network and the label ag-

gregator. The method ﬁrst aggregates labels using the

estimated probabilities by the classiﬁer via the soft-

max layer. After label aggregation using the softmax

output as the prior knowledge in the aggregation algo-

rithm, the network is trained via the aggregated labels.

In other words, the label aggregation algorithm and

the classiﬁer exchange helpful knowledge iteratively.

As a result, both the accuracy of the classiﬁer network

and the accuracy of the aggregated labels increase.

We illustrate the procedure of aggregation and

training the classiﬁer in Figure 1. At the beginning,

each worker assigns a label to each instance based on

its expertise level. In the next step, the label aggre-

gator performs the aggregation task using the EM al-

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

Worker

…

Crowdsourcing

Platform

Label

Aggregator

Unlabeled Samples

Aggregated Labels

Image Classifier

Prediction (softmax)

…

The prior

Figure 1: The label aggregation and training DNN scenario.

gorithm. In the ﬁrst iteration since we have no prior

estimated by the classiﬁer, we use majority voting al-

gorithm to aggregate the labels with which we train

the classiﬁer. After training the classiﬁer, we use it

to infer the softmax vector output for each sample, to

be used as prior by the EM-based aggregation algo-

rithm. EM-based algorithms are commonly used for

label aggregation. EM needs knowledge of the prior

data distribution to estimate the probability of correct-

ness of a label generated by a worker. p

denotes the

prior probability of class label c. In LABNET, we esti-

mate p

via the predicted class probability by the soft-

max layer of the neural network. Hence the inferred

softmax probability vector from each instance is use-

ful knowledge for the EM algorithm. Vice versa, to

train the DNN, we use the labels provided by the EM

algorithm, which selects the labels having maximum

likelihood among the labels provided by the workers.

3.1 Label Aggregation

We consider the scenario shown in Figure 1. To

each data sample x

corresponds a set of labels y

,...,y

} from K different crowd workers. The

label aggregator uses the EM algorithm to estimate

the correct labels. The EM algorithm is an iterative

algorithm, including an E- and an M- step. In the E-

step for each instance i, the algorithm ﬁrst calculates

the probability that the aggregated label ˆy

equals t

given that the label y

generated by worker w equals

l. P

( ˆy

| y

) denotes this probability. Therefore we

have the following expression

( ˆy

= t | y

= l) =

∑

j=1

( ˆy

= t & y

= l)

∑

c=1

( ˆy

= t & y

= c)

(1)

where (.) is the indicator function. In Equation (1),

We count the number of times that worker k labels

item i to l when the aggregated label is t over the

number of classes are labeled by worker k when the

aggregated label is t.

The next stage of the EM algorithm needs the

prior probability of each class. In the classic EM

algorithm these probabilities are calculated as p

∑

i=1

( ˆy

= c) where ˆy

is the aggregated label and

c is the class label. Thus P = {p

, p

,..., p

}

is the set of prior probabilities for each class.

In our proposed method, we replace the prior class

probabilities to make them dependent on the features

extracted by the classiﬁer. As anticipated in Figure 1,

we use the softmax output of the classiﬁer prediction

f (x

x; θ

θ) as set of prior probabilities. The softmax vec-

tor is computed based on image features. Hence, the

prior probabilities from the softmax vector contain in-

formation on the features of the sample data because

the softmax vector is a representation of the input data

in the form of a probability vector. For label aggre-

gation,we use as prior the predicted class probability

across all samples:

∑

i=1

;θ

θ). (2)

where f

x; θ

θ) denotes the softmax value of class c by

the classiﬁer f (x

x; θ

θ). After ﬁnding the prior probabil-

ity based on the proposed method, the EM algorithm

begins maximizing the data likelihood. In the M-step,

the likelihood q

i,c

of each instance i being of class c

is computed as:

i,c

= p

∏

w=1

( ˆy

= c | y

). (3)

LABNET: A Collaborative Method for DNN Training and Label Aggregation

which leverages the Bayes’s theorem. Q

i,1

i,2

,...,q

i,C

} denotes the set of likelihoods for

each data instance i for all C classes. The aggregated

label is the class c having maximum likelihood:

ˆy

= argmax

. (4)

After the M-step the label aggregator passes the set of

aggregated labels

Y = { ˆy

, ˆy

,..., ˆy

} to the training

of the classiﬁer network.

Algorithm 1: LABNET.

1 Input: training set D = {x

x,Y }, Epoch E

max

Iteration I

max

Initialize randomly θ

Y = MajorityVoting(Y ) /* Y

i, j

denotes i

instance from j

worker */

3 Output: The aggregated labels

Y , Trained

network f (x

x, θ

θ)

4 for i = 1,2,...,N do

5 for w = 1, 2, . . . , K do

6 L[ ˆy

][w][y

]+ = 1

7 train = True

8 H

= 0

9 for each iteration t = 1, 2, . . . , I

max

10 if train then

11 for each e = 1, 2, . . . , E

max

12 Train f (x

x, θ

θ) with (x

Y );

13 for each c = 1, 2, . . . ,C do

14 P

∑

i=1

;θ

θ);

15 else

16 for each c = 1, 2, . . . ,C do

17 P

∑

i=1

( ˆy

= c)

Y = ONE-HOT(

Y )

19 H

= −

∑

i=1

˜y

log f (x

;θ

θ)

20 if H

− H

t−1

> 0 then

21 train = True

22 else

23 train = False

24 for i = 1, 2, . . . , N do

25 for w = 1, 2, . . . , K do

26 P

( ˆy

| y

) =

∑

j=1

L[ ˆy

][w][y

]

∑

c=1

L[ ˆy

][w][c]

27 for i = 1, 2, . . . , N do

28 for c = 1, 2, . . . ,C do

29 Q

i,c

= P

∏

w=1

( ˆy

= c | y

)

Y = argmax

3.2 Classiﬁer Training

The data to train the classiﬁer f (x

x; θ

θ) includes fea-

tures vector x

and aggregated labels vector ˆy

from

the aggregator. Hence the loss functions for training

can be written as follows:

ℓ = min

∑

i=1

( f (x

;θ

θ), ˆy

) (5)

where L

(.,.) is the cross entropy loss function:

= −

∑

j=1

log f

) (6)

where

is the aggregated label and f

) is the soft-

max probability for the j

class. These probabilities

represent the data features and are fed back to EM al-

gorithm via Equation (2).

3.3 Making Decision to Train DNN

Training the DNN at each iteration of the EM al-

gorithm would be extremely computation intensive

and unpractical. Therefore, we need to carefully

decide when to train to reduce the computational

load while guaranteeing the accuracy of the classi-

ﬁer and correctness of the aggregated labels. At the

end of each round of the EM algorithm we measure

the (dis)agreement between the DNN predicted labels

and the aggregated labels. If the disagreement in-

creases with respect to the previous iteration, we trig-

gers the training of the DNN to prevent further drifts

between the predicted and aggregated labels.

More in detail at each iteration we calculate the

disagreement suing the cross-entropy function as :

= −

∑

i=1

˜y

log f (x

;θ

θ)

(7)

Equation (7) measures the distance between DNN

predicted and the aggregated labels. Therefore, if

the value of H increases between iteration rounds the

predicetd and aggregated labels are diverging. Hence,

we trigger training of the DNN with the new aggre-

gated labels. Likewise, if the value of H does not

increase between iteration rounds, there is no need to

train DNN at the next iteration.

3.4 End-to-End Training Procedure

Our framework aims to jointly aggregate labels with

low label error rate and train a DNN with high accu-

racy. We describe the whole LABNET and collabo-

ration between DNN and label aggregator in Algo-

rithm 1. In this scenario, we have multiple work-

ers which provide labels for each data instance, thus

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

the input dataset is D = {x

x,Y } (line 1). To initial-

ize the algorithm we need some aggregated labels to

start with. We derive these via simple Majority Voting

(line 2). Before label aggregation, we calculate the

number of labels obtained from each class after ag-

gregation from each worker named L

C×K×C

(line 4-6)

and force training of the classiﬁer f (x

x, θ

θ) (line 7). At

the beginning of each iteration if the train ﬂag is true,

the classiﬁer f (x

x, θ

θ) is trained with the aggregated la-

bels

Y (line 10-12), then we use the softmax output

of f (x

x, θ

θ) as the prior (line 13-14). In case of train

is false, the prior probability for c

class in P vector

equals to the average number of occurrence of class

c into aggregated label set (line 16-17). In each iter-

ation, we calculate the need to train based on Equa-

tion (7) (line 18-23).

Y denotes the one-hot vectors of

aggregated labels

Y , and ˜y

∈

Y is the one-hot vector

for aggregated label of sample i. The label aggregator

method works based on an EM algorithm that starts

with E-step via ﬁnding the conditional probability of

aggregated labels given each worker’s generated label

(line 24-26). The M-step includes ﬁnding the likeli-

hood of each instance and class label (line 27-29). Fi-

nally, the aggregated label is the class with maximum

probability among all classes (line 30). This proce-

dure repeats for each iteration. The aggregated labels

are used to train the DNN and the DNN softmax out-

put used as prior.

4 EVALUATION

4.1 Experiment Setup

Dataset. We consider two different vision datasets in

our experiments to evaluate the performance of our

algorithm against other methods.

• CIFAR-10 (Krizhevsky et al., 2009): contains

60K 32×32 pixels samples. The labels are classi-

ﬁed into 10 categories. Here we use 50K samples

as training data and 10K for testing data.

• CIFAR-100 (Krizhevsky et al., 2009): is simi-

lar to CIFAR-10 except that its labels are grouped

into 100 categories.

Noise and Workers. To simulate workers with

different level of expertise for annotating images, we

use three different noise patterns in our experiments.

• Uniform: This noise corrupts the true label into

another random label with equal probability.

• Bimodal: This noise corrupts the original class

label around two other targeted classes, each

following truncated normal distribution. The

(µ,σ,a,b) includes µ that speciﬁes the target

and σ which controls the spread. a and b denote

the class label boundaries.

• Flip: This noise is generated by ﬂipping the orig-

inal class label to another class with a speciﬁc

probability.

Baselines. We consider three different baselines

for comparison.

• Majority Voting (MV): is a basic label aggre-

gation method which chooses the label with the

highest consensus.

• Expectation Maximization (EM) (Dawid and

Skene, 1979): is an iterative method to estimate

the confusion matrix of workers by maximizing

the likelihood of observed labels. The diagonal

elements show the probability of aggregated label.

• Minimax Entropy (ME) (Zhou et al., 2012):

This method considers a confusion matrix for

workers and encodes their labeling expertise. In

addition, the ME assigns a vector to items and en-

codes their labeling difﬁculty. It uses a minimax

entropy approach to estimate the confusion matrix

and vector together.

We implement all algorithms in Python programming

language using Keras version 2.2.4 and TensorFlow

version 1.12.

Parameters. To conduct our experiments on

CIFAR-10 and CFAR-100, we use an 8-layer CNN

with 6 convolutional layers followed by 2 fully con-

nected layers, and ResNet-44, respectively. All net-

works train with SGD with momentum 0.9, weight

decay 5 × 10

and an initial learning rate of 0.1. For

CIFAR-10 in each iteration, we train the DNN for 120

epochs, and the learning rate is divided by 10 after 40

and 80 epochs. For CIFAR-100, the total number of

epochs is 150, and the learning rate is divided by 10

after 80 and 120 epochs. For the EM algorithm, the

maximum number of iterations is 10. For bimodal

noise, the center of the distribution around classes

= 3.0, µ

= 7.0 with variance σ

= 1.0, σ

= 0.5.

For ﬂip noise in CIFAR-10, we ﬂip similar classes in-

cluding bird → airplane, truck → automobile, deer

→ horse and dog ↔ cat. For CIFAR-100, the 100

classes are categorized into 20 super-classes. Each

super-class consists of 5 sub-classes. We randomly

select two sub-classes in each super-class and ﬂip la-

bels between sub-classes.

Evaluation Metrics. To evaluate the performance

of our proposed model against the baselines, we use

as metric the label aggregation error rate and accuracy

of the trained neural network.

• Aggregation Error Rate: is the percentage of

inferred labels which differ from the true labels.

LABNET: A Collaborative Method for DNN Training and Label Aggregation

(a) Uniform (b) Bimodal (c) Flip

Figure 2: Accuracy of DNN on CIFAR-10 under 60% noise ratio and missing ratio 30%.

(a) Uniform (b) Bimodal (c) Flip

Figure 3: Label aggregation error rate on CIFAR-10 under 60% noise ratio and missing ratio 30%.

The true labels are used only for evaluation not

for training.

• Accuracy: Test accuracy is the percentage of cor-

rect predictions by the DNN on the testing data.

4.2 Number of Workers Impact

4.2.1 CIFAR-10

We summarize the results of CIFAR-10 in terms of

DNN’s accuracy and aggregation error rate for a dif-

ferent number of workers in Figure 2 and Figure 3,

respectively. According to Figure 2a, our method out-

performs all competitors through various numbers of

workers for the uniform noise pattern. When the noise

pattern is bimodal in Figure 2b, LABNET is the most

accurate method against MV, EM, and ME except for

the case of 3 workers that Minimax Entropy is the best

one and our method is the second best result. Also,

for the ﬂip noise in Figure 2c, LABNET achieves the

highest accuracy by 65.59% and 70.12% when num-

bers of workers are 9 and 12, respectively. In the case

of 3 and 6 workers, Minimax Entropy achieves the

best accuracy by 38.88% and 64.24% test accuracy.

Another observation worth mentioning is that the test

accuracy increases with the number of workers for all

cases. In general for LABNET, increasing the num-

ber of workers has the highest and lowest impacts on

the classiﬁer accuracy for the ﬂip and uniform noise

patterns, respectively.

We compare aggregation label error rate in Fig-

ure 3 for three different noise patterns over various

numbers of workers. For uniform noise pattern shown

in Figure 3a, LABNET achieves the lowest error rate

against other rivals by 58.93%, 36.87%, 27.74% and

19.53% for 3, 6, 9 and 12 workers, respectively.

The direct impact of aggregation error rate on

DNN accuracy is shown in Figure 3b and Figure 3c.

The Minimax Entropy has lowest error rate with 3

workers in bimodal noise pattern and the highest

DNN accuracy in Figure 3b and Figure 2b, respec-

tively. Also LABNET achieves the best error rate re-

sults for 6, 9 and 12 workers against the baselines.

Furthermore, we see the same pattern for ﬂip noise in

Figure 2c and Figure 3c which in Minimax Entropy

performs better than other baselines when the number

of workers equals 3 and 6. In addition, the worst re-

sults belong to MV that is the least accurate trained

DNN among all baselines. For the case of 9 and 12

workers, LABNET achieves 32.45% and 25.20% ag-

gregation error rate, respectively, which is the best

method compared to MV, EM, and Minimax Entropy.

The highest impact of increasing workers on error rate

belongs to the ﬂip noise pattern with a reduction of

39.59% for LABNET.

4.2.2 CIFAR-100

CIFAR-100 is more challenging than CIFAR-10 due

to the higher number of classes. The accuracy of

DNN and label aggregation error rate results are

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

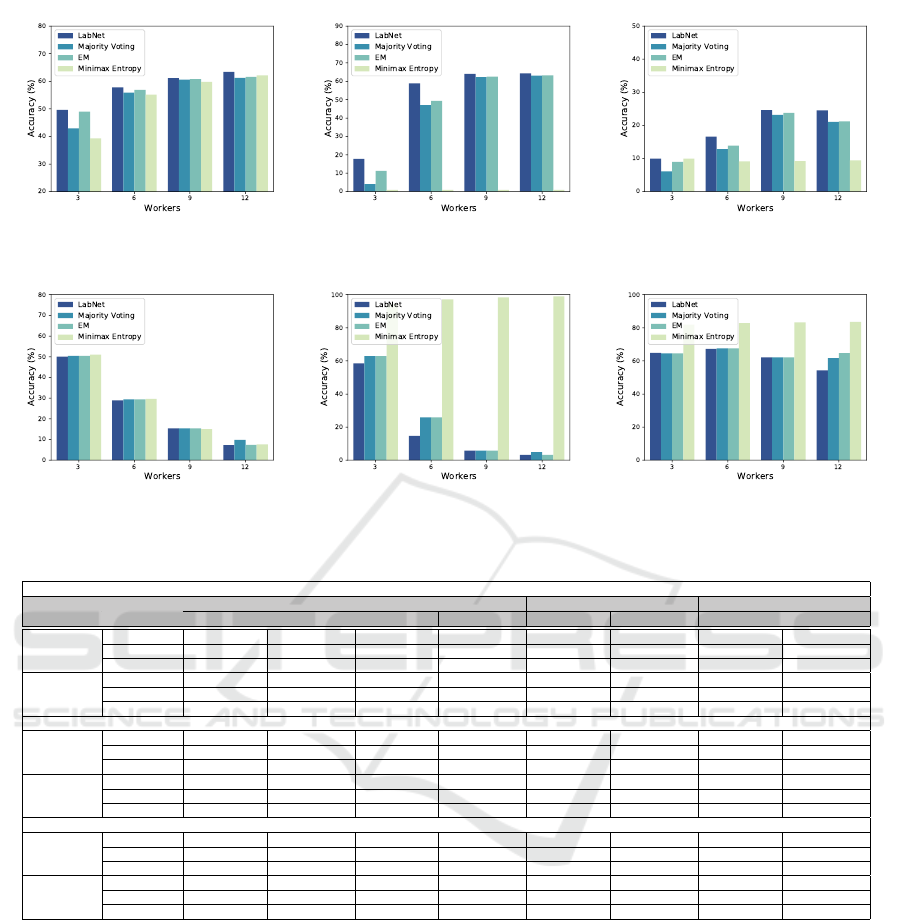
(a) Uniform (b) Bimodal (c) Flip

Figure 4: Accuracy of DNN on CIFAR-100 under 60% noise ratio and missing ratio 30%.

(a) Uniform (b) Bimodal (c) Flip

Figure 5: Label aggregation error rate on CIFAR-100 under 60% noise ratio and missing ratio 30%.

Table 1: Accuracy and error rate for different missing rate on CIFAR-10 with 60% noise ratio.

Noise pattern = Uniform

LABNET MV EM Minimax Entropy

# of Worker Missing rate

Accuracy (%) Error rate (%) Accuracy (%) Error rate (%) Accuracy (%) Error rate (%) Accuracy (%) Error rate (%)

0.0 74.62 ± 0.32 54.51 ± 0.10 71.48 ± 0.29 55.93 ± 0.0 66.17 ± 0.33 59.07 ± 0.12 72.25 ± 0.31 54.87 ± 0.16

0.1 74.11 ± 0.40 56.59 ± 0.05 71.31 ± 0.22 56.75 ± 0.0 70.15 ± 0.38 57.58 ± 0.05 74.17 ± 0.52 56.28 ± 0.08

0.3 73.02 ± 0.25 58.91 ± 0.03 70.44 ± 0.19 60.28 ± 0.0 63.26 ± 0.28 61.17 ± 0.08 71.26 ± 0.19 58.99 ± 0.10

0.0 83.59 ± 0.52 20.75 ± 0.04 81.75 ± 0.38 21.26 ± 0.0 82.12 ± 0.42 20.88 ± 0.05 81.70 ± 0.62 21.15 ± 0.04

0.1 83.31 ± 0.15 20.84 ± 0.03 81.07 ± 0.22 20.96 ± 0.0 82.51 ± 0.13 21.16 ± 0.02 70.85 ± 0.66 21.47 ± 0.09

0.3 81.35 ± 0.19 27.71 ± 0.04 78.72 ± 0.21 33.31 ± 0.0 80.05 ± 0.31 27.71 ± 0.11 80.21 ± 0.27 27.98 ± 0.02

Noise pattern = Bimodal

0.0 76.69 ± 0.31 34.09 ± 0.06 72.44 ± 0.42 44.63 ± 0.0 52.18 ± 0.26 50.71 ± 0.08 78.05 ± 0.38 31.76 ± 0.05

0.1 76.24 ± 0.15 34.49 ± 0.02 73.40 ± 0.37 43.77 ± 0.0 47.03 ± 0.43 54.14 ± 0.07 77.22 ± 0.27 33.79 ± 0.04

0.3 75.39 ± 0.37 35.15 ± 0.03 71.83 ± 0.17 44.92 ± 0.0 48.29 ± 0.36 52.81 ± 0.03 76.44 ± 0.56 33.94 ± 0.11

0.0 87.75 ± 0.21 4.19 ± 0.02 84.43 ± 0.33 11.56 ± 0.0 85.05 ± 0.20 8.51 ± 0.05 86.05 ± 0.18 5.43 ± 0.02

0.1 87.44 ± 0.11 4.2 ± 0.02 83.84 ± 0.34 11.76 ± 0.0 84.55 ± 0.31 8.72 ± 0.04 85.42 ± 0.29 6.37 ± 0.02

0.3 85.52 ± 0.38 7.53 ± 0.01 81.83 ± 0.46 22.86 ± 0.0 84.88 ± 0.25 7.56 ± 0.03 84.47 ± 0.30 9.41 ± 0.04

Noise pattern = Flip

0.0 40.47 ± 0.34 59.17 ± 0.05 30.75 ± 0.29 64.79 ± 0.0 34.73 ± 0.25 64.78 ± 0.02 51.34 ± 0.49 50.39 ± 0.09

0.1 39.89 ± 0.16 59.32 ± 0.03 31.07 ± 0.39 64.79 ± 0.0 32.19 ± 0.10 64.78 ± 0.09 45.76 ± 0.67 55.89 ± 0.08

0.3 38.92 ± 0.37 60.93 ± 0.01 25.15 ± 0.66 68.03 ± 0.0 31.34 ± 0.26 64.80 ± 0.07 38.82 ± 0.41 60.95 ± 0.04

0.0 64.65 ± 0.10 28.56 ± 0.03 18.20 ± 0.43 73.37 ± 0.0 64.39 ± 0.23 30.62 ± 0.02 64.78 ± 0.36 28.43 ± 0.09

0.1 64.64 ± 0.31 29.56 ± 0.02 21.93 ± 0.32 73.37 ± 0.0 64.19 ± 0.53 30.64 ± 0.08 64.21 ± 0.22 29.95 ± 0.12

0.3 64.89 ± 0.69 31.45 ± 0.08 27.94 ± 0.19 70.96 ± 0.0 63.01 ± 0.40 32.33 ± 0.04 63.54 ± 0.37 32.29 ± 0.08

shown in Figure 4 and Figure 5, respectively. The ﬁrst

important observation through the results is the poor

performance of Minimax Entropy for CIFAR-100 be-

cause, for a large number of classes, this method eas-

ily converges to the wrong local optimum. Accord-

ing to Figure 4, the bimodal noise pattern is the most

straightforward pattern, and ﬂip noise is the most

complex one for classiﬁcation and labels aggregation.

As shown in Figure 4a, LABNET achieves the best

accuracy among all methods. The highest difference

between the accuracy of LABNET and second best

method is 1.5% for 12 workers and the least one is

0.4% for 9 workers. For bimodal noise in Figure 4b,

LABNET achieves the highest accuracy for all the sce-

narios with different numbers of workers. The best

accuracy of LABNET equals 64.28% with 12 workers.

In addition, the test accuracy for 3, 6, and 9 workers

are 17.80%, 58.90%, and 63.98%, respectively. Since

the ﬂip noise is the most difﬁcult noise pattern, the

best accuracy of LABNET is 24.73% with 12 work-

ers. Based on the Figure 4c, LABNET outperforms

all the baselines. In LABNET, increasing the num-

ber of workers from 3 to 12 improves the classiﬁer

accuracy 46.48% for the bimodal noise signiﬁcantly

rather than 13.81% and 14.56% for the uniform and

ﬂip noise patterns, respectively.

Figure 5 summarizes the aggregation error rate of

our proposed method and other baselines over differ-

LABNET: A Collaborative Method for DNN Training and Label Aggregation

Table 2: Accuracy and error rate for different missing rate on CIFAR-100 with 60% noise ratio.

Noise pattern = Uniform

LABNET MV EM Minimax Entropy

# of Worker Missing rate

Accuracy (%) Error rate (%) Accuracy (%) Error rate (%) Accuracy (%) Error rate (%) Accuracy (%) Error rate (%)

0.0 48.83 ± 0.28 49.53 ± 0.05 42.89 ± 0.53 50.48 ± 0.0 48.21 ± 0.35 50.37 ± 0.04 39.64 ± 0.28 51.12 ± 0.02

0.1 48.62 ± 0.18 49.55 ± 0.03 42.50 ± 0.29 50.58 ± 0.0 48.03 ± 0.42 50.41 ± 0.06 39.85 ± 0.35 50.92 ± 0.03

0.3 49.65 ± 0.18 50.02 ± 0.03 42.48 ± 0.47 50.64 ± 0.02 48.05 ± 0.59 50.39 ± 0.04 39.31 ± 0.33 51.09 ± 0.03

0.0 64.20 ± 0.16 8.17 ± 0.02 62.14 ± 0.38 8.35 ± 0.0 63.43 ± 0.27 8.33 ± 0.03 62.19 ± 0.14 8.34 ± 0.02

0.1 63.35 ± 0.31 8.19 ± 0.01 61.72 ± 0.41 8.38 ± 0.0 63.21 ± 0.28 8.36 ± 0.02 62.15 ± 0.25 8.38 ± 0.05

0.3 61.16 ± 0.22 15.34 ± 0.02 60.53 ± 0.25 15.42 ± 0.0 60.73 ± 0.39 15.40 ± 0.03 59.78 ± 0.46 15.52 ± 0.05

Noise pattern = Bimodal

0.0 19.34 ± 0.21 54.72 ± 0.03 11.21 ± 0.16 62.86 ± 0.0 11.19 ± 0.36 62.86 ± 0.03 1.05 ± 0.12 92.73 ± 0.04

0.1 18.93 ± 0.27 55.18 ± 0.02 11.85 ± 0.48 62.89 ± 0.0 11.91 ± 0.31 62.87 ± 0.06 1.09 ± 0.17 95.37 ± 0.03

0.3 17.82 ± 0.24 58.49 ± 0.03 4.12 ± 0.31 62.88 ± 0.0 11.32 ± 0.42 62.89 ± 0.04 1.04 ± 0.29 95.38 ± 0.03

0.0 64.89 ± 0.43 3.15 ± 0.03 64.11 ± 0.26 3.19 ± 0.0 64.15 ± 0.28 3.16 ± 0.04 1.03 ± 0.10 98.86 ± 0.02

0.1 64.53 ± 0.14 3.15 ± 0.02 63.20 ± 0.43 3.18 ± 0.0 63.82 ± 0.37 3.17 ± 0.02 1.04 ± 0.09 98.91 ± 0.03

0.3 63.98 ± 0.29 5.76 ± 0.02 62.27 ± 0.36 5.89 ± 0.0 62.48 ± 0.42 5.87 ± 0.02 1.03 ± 0.11 98.39 ± 0.02

Noise pattern = Flip

0.0 11.43 ± 0.28 64.53 ± 0.03 8.88 ± 0.16 64.54 ± 0.0 8.95 ± 0.43 64.54 ± 0.02 10.02 ± 0.33 81.84 ± 0.02

0.1 10.65 ± 0.42 64.53 ± 0.03 9.12 ± 0.28 64.55 ± 0.0 9.14 ± 0.37 64.54 ± 0.01 9.92 ± 0.10 81.84 ± 0.03

0.3 9.98 ± 0.25 64.83 ± 0.02 6.14 ± 0.31 64.91 ± 0.0 8.99 ± 0.20 64.90 ± 0.01 9.76 ± 0.41 81.85 ± 0.09

0.0 25.68 ± 0.46 61.87 ± 0.02 22.06 ± 0.24 63.64 ± 0.0 22.63 ± 0.16 63.62 ± 0.05 9.38 ± 0.57 84.06 ± 0.04

0.1 25.05 ± 0.17 61.95 ± 0.02 21.49 ± 0.40 63.65 ± 0.0 22.58 ± 0.39 63.63 ± 0.02 9.18 ± 0.21 84.07 ± 0.03

0.3 24.65 ± 0.26 62.11 ± 0.01 21.11 ± 0.33 63.77 ± 0.0 22.38 ± 0.14 63.72 ± 0.04 9.17 ± 0.52 83.27 ± 0.03

ent numbers of workers. With respect to the test accu-

racy results in Figure 4, the most accurate method has

the lowest label aggregation error rate in all the cases

with different noise patterns and numbers of work-

ers. For uniform noise, LABNET achieves 50.01%

error rate in the case of 3 workers, which is the low-

est among all methods, although performance of each

method are close to each other. As we mentioned

before, Minimax Entropy suffers from poor perfor-

mance on dataset with large number of classes un-

der bimodal and ﬂip noise patterns which is shown in

Figure 5b and Figure 5c. Through all the noise pat-

terns and different number of workers, LABNET per-

forms as the best method against baselines with gaps

of 7.33%, 3.23% and 54.21% error rate under uni-

form, bimodal and ﬂip noise pattern with 12 workers,

respectively. According to the results of LABNET in

Figure 5, increasing the number of workers has the

most effect on reducing the error for bimodal noise

pattern.

4.3 Impact of Missing Rate on DNN

Accuracy and Label Aggregation

Error Rate

We extensively evaluate LABNET, MV, EM, and Min-

imax Entropy on CIFAR-10 and CIFAR-100, with la-

bel missing rates ranging from 0.0 to 0.3. We also

consider two different numbers of workers: 3 and 9.

We summarize the average test accuracy and label ag-

gregation error rate across three runs for CIFAR-10

and CIFAR-100 in Table. 1 and Table. 2, respectively.

CIFAR-10. As shown in Table. 1, in the case of

uniform noise pattern, LABNET achieves the highest

accuracy in all cases. As we expect, variation of la-

bel missing rate affects DNN accuracy and label ag-

gregation error rate. Increasing the missing rate re-

duces the accuracy of DNN and increases the label

aggregation error rate. In addition, more workers en-

hance the DNN accuracy. According to the results,

we observe an 8.97%, 9.2%, and 8.33% increase in

accuracy by adding six workers to our method for the

missing rate 0.0, 0.1 and 0.3 under uniform noise pat-

tern, respectively. For the case of bimodal noise, Min-

imax Entropy is the best method when three workers

are available. However, with nine workers, LABNET

outperforms all baselines in terms of accuracy and er-

ror rate. According to the results in Table. 1, LAB-

NET performs better aggregation on higher missing

rate under ﬂip noise pattern. Consequently, the ac-

curacy of DNN is higher than other methods in the

higher missing rate.

CIFAR-100. Since CIFAR-100 contains a more

signiﬁcant number of classes than CIFAR-10, label

aggregation is a challenging task. According to the re-

sults in Table. 2, LABNET achieves the highest DNN

accuracy and the lowest aggregation error rate against

other baselines under uniform, bimodal, and ﬂip noise

patterns. The impact of missing rate variation on ac-

curacy and error rate for CIFAR-100 is the same as

the impact of missing rate on CIFAR-10. Another ob-

servation worth mentioning is the signiﬁcant enhance-

ment in Bimodal noise accuracy when the number of

workers changes from 3 to 9. Also, the difference

between LABNET accuracy and other baselines for

CIFAR-100 is signiﬁcantly higher than the results on

CIFAR-10. There exist the same observations for la-

bels aggregation error rate. In other words, our pro-

posed model is signiﬁcantly more accurate on a more

complex dataset under bimodal and ﬂip noise. Fur-

thermore, Minimax Entropy performs label aggrega-

tion poorly for various missing rates equal to 0.0, 0.1,

and 0.3 because of getting stuck in the local optimum

for the case of the biased dataset with a large number

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

of classes to a speciﬁc class. In case of bimodal and

ﬂip noise patterns, EM achieves second best results in

terms of accuracy and error rate.

5 CONCLUSION

Motivated by the need for accurate data labeling of

crowd workers and using the provided labels for train-

ing DNNs, we design an iterative method for label

aggregation and training DNN together. The prior art

performs label aggregation and training classiﬁer in

two separate processes. We propose LABNET that

considers aggregation and training in contact with

each other. In our model, the classiﬁer extracts the

prior knowledge for passing to the aggregation algo-

rithm. Also, the estimated correct labels by aggrega-

tion algorithm are used to train the classiﬁer. In ad-

dition, we design an algorithm to decide when DNN

needs to be trained through the aggregation algorithm

iteration. Compared to the baselines, LABNET out-

performs in most scenarios, especially for in challeng-

ing scenarios with large number of classes.

ACKNOWLEDGEMENTS

This work has been partly funded by the Swiss

National Science Foundation NRP75 project

407540 167266.

REFERENCES

Cousineau, D. and Helie, S. (2013). Improving maximum

likelihood estimation using prior probabilities: A tuto-

rial on maximum a posteriori estimation and an exam-

ination of the weibull distribution. Tutorials in Quan-

titative Methods for Psychology, 9(2):61–71.

Dawid, A. P. and Skene, A. M. (1979). Maximum likeli-

hood estimation of observer error-rates using the em

algorithm. Applied statistics, pages 20–28.

Gaunt, A., Borsa, D., and Bachrach, Y. (2016). Train-

ing deep neural nets to aggregate crowdsourced re-

sponses. In Proceedings of the Thirty-Second Con-

ference on Uncertainty in Artiﬁcial Intelligence. AUAI

Press, page 242251.

Ghiassi, A., Birke, R., Han, R., and Chen, L. Y. (2021).

Labelnet: Recovering noisy labels. In International

Joint Conference on Neural Networks (IJCNN), pages

1–8. IEEE.

Ghiassi, A., Younesian, T., Zhao, Z., Birke, R., Schiavoni,

V., and Chen, L. Y. (2019). Robust (deep) learning

framework against dirty labels and beyond. In Inter-

national Conference on Trust, Privacy and Security in

Intelligent Systems and Applications (TPS-ISA), pages

236–244. IEEE.

Han, B., Yao, Q., Yu, X., Niu, G., Xu, M., Hu, W., Tsang,

I., and Sugiyama, M. (2018). Co-teaching: Robust

training of deep neural networks with extremely noisy

labels. In NeurIPS, pages 8527–8537.

Hendrycks, D., Mazeika, M., Wilson, D., and Gimpel, K.

(2018). Using trusted data to train deep networks on

labels corrupted by severe noise. In NeurIPS, pages

10456–10465.

Hong, C., Ghiassi, A., Zhou, Y., Birke, R., and Chen,

L. Y. (2021). Online label aggregation: A variational

bayesian approach. In Web Conference 2021, WWW

’21, page 1904–1915. ACM.

Imran, M., Mitra, P., and Castillo, C. (2016). Twitter as

a lifeline: Human-annotated twitter corpora for NLP

of crisis-related messages. In Calzolari, N., Choukri,

K., Declerck, T., Goggi, S., Grobelnik, M., Maegaard,

B., Mariani, J., Mazo, H., Moreno, A., Odijk, J., and

Piperidis, S., editors, Language Resources and Evalu-

ation LREC. European Language Resources Associa-

tion (ELRA).

Jiang, L., Zhou, Z., Leung, T., Li, L., and Fei-Fei, L. (2018).

Mentornet: Learning data-driven curriculum for very

deep neural networks on corrupted labels. In ICML,

pages 2309–2318.

Khetan, A., Lipton, Z. C., and Anandkumar, A. (2018).

Learning from noisy singly-labeled data. In ICLR.

Kim, H.-C. and Ghahramani, Z. (2012). Bayesian classiﬁer

combination. In Artiﬁcial Intelligence and Statistics,

pages 619–627.

Krizhevsky, A., Nair, V., and Hinton, G. (2009). Cifar-

10/100 (Canadian Institute for Advanced Research).

Li, J., Socher, R., and Hoi, S. C. (2020). Dividemix: Learn-

ing with noisy labels as semi-supervised learning. In

ICLR.

Liu, Q., Peng, J., and Ihler, A. T. (2012). Variational infer-

ence for crowdsourcing. In Advances in neural infor-

mation processing systems, pages 692–700.

Patrini, G., Rozza, A., Krishna Menon, A., Nock, R., and

Qu, L. (2017). Making deep neural networks robust

to label noise: A loss correction approach. In IEEE

CVPR, pages 1944–1952.

Shu, J., Xie, Q., Yi, L., Zhao, Q., Zhou, S., Xu, Z., and

Meng, D. (2019). Meta-weight-net: Learning an ex-

plicit mapping for sample weighting. In NIPS, pages

1919–1930.

Simpson, E. D., Venanzi, M., Reece, S., Kohli, P., Guiver,

J., Roberts, S. J., and Jennings, N. R. (2015). Lan-

guage understanding in the wild: Combining crowd-

sourcing and machine learning. In Proceedings of

the 24th international conference on world wide web,

pages 992–1002. International World Wide Web Con-

ferences Steering Committee.

Venanzi, M., Guiver, J., Kazai, G., Kohli, P., and Shokouhi,

M. (2014). Community-based bayesian aggregation

models for crowdsourcing. In Proceedings of the 23rd

international conference on World wide web, pages

155–164. ACM.

LABNET: A Collaborative Method for DNN Training and Label Aggregation

Wang, Y., Ma, X., Chen, Z., Luo, Y., Yi, J., and Bailey, J.

(2019). Symmetric cross entropy for robust learning

with noisy labels. In IEEE ICCV, pages 322–330.

Whitehill, J., Wu, T.-f., Bergsma, J., Movellan, J. R., and

Ruvolo, P. L. (2009). Whose vote should count more:

Optimal integration of labels from labelers of un-

known expertise. In Advances in neural information

processing systems, pages 2035–2043.

Xu, Z., Liu, Y., Xuan, J., Chen, H., and Mei, L. (2017).

Crowdsourcing based social media data analysis of ur-

ban emergency events. Multimedia Tools and Appli-

cations, 76(9):11567–11584.

Yan, Y., Rosales, R., Fung, G., Subramanian, R., and Dy, J.

(2014). Learning from multiple annotators with vary-

ing expertise. Machine learning, 95(3):291–327.

Yang, J., Drake, T., Damianou, A., and Maarek, Y. (2018).

Leveraging crowdsourcing data for deep active learn-

ing an application: Learning intents in alexa. In Pro-

ceedings of the 2018 World Wide Web Conference,

pages 23–32.

Yang, J., Smirnova, A., Yang, D., Demartini, G., Lu, Y.,

and Cudr

e-Mauroux, P. (2019). Scalpel-cd: lever-

aging crowdsourcing and deep probabilistic modeling

for debugging noisy training data. In The World Wide

Web Conference, pages 2158–2168.

Yin, L., Han, J., Zhang, W., and Yu, Y. (2017). Aggre-

gating crowd wisdoms with label-aware autoencoders.

In Proceedings of the 26th International Joint Con-

ference on Artiﬁcial Intelligence, pages 1325–1331.

AAAI Press.

Yu, X., Han, B., Yao, J., Niu, G., Tsang, I. W., and

Sugiyama, M. (2019). How does disagreement help

generalization against label corruption? In ICML,

pages 7164–7173.

Zhou, D., Basu, S., Mao, Y., and Platt, J. C. (2012). Learn-

ing from the wisdom of crowds by minimax entropy.

In Advances in Neural Information Processing Sys-

tems, pages 2195–2203.

Zhou, D., Liu, Q., Platt, J., and Meek, C. (2014). Aggre-

gating ordinal labels from crowds by minimax condi-

tional entropy. In International Conference on Ma-

chine Learning, pages 262–270.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence