An Efﬁcient Relax-and-Solve Algorithm for the Resource-Constrained

Project Scheduling Problem

Alireza Etminaniesfahani

, Hanyu Gu

and Amir Salehipour

School of Mathematical and Physical Sciences, University of Technology Sydney, Australia

Keywords:

Relax-and-Solve, Project Scheduling, Resource-Constrained Project Scheduling Problem, RCPSP, Makespan,

Matheuristic.

Abstract:

The resource-constrained project scheduling problem (RCPSP) has a broad range of practical applications,

e.g., in manufacturing, mining, and supply chain, among others(Kreter et al., 2015). Over the last 50 years,

many researchers have tried to solve this challenging NP-hard problem. This paper presents an efﬁcient and

easy-to-implement relax-and-solve matheuristic to solve RCPSP. The proposed method employs constraint

programming in a heuristic framework and uses CPLEX as an optimization solver. This algorithm is tested on

more than 1500 instances from the standard library PSPLIB. Our experimental results show that the proposed

heuristic framework outperforms the CPLEX and provides competitive results compared with the state-of-the-

art techniques.

1 INTRODUCTION

Scheduling a large-scale project characterized by var-

ious activities, complicated precedence constraints

and enormous resource demands is critical and chal-

lenging for managers. One of the primary sources

of delays in projects is the lack of proper project

scheduling (Herroelen and Leus, 2005). Since the

late 1950s, the critical path method (CPM) has been

one of the widely used planning methods that con-

sider precedence constraints and time parameters of

the activities. However, CPM assumes that unlimited

resource is always available, which is not practical in

most of the industrial projects (Liu et al., 2020).

In 1969, Pritsker et al. introduced the Resource-

Constrained Project Scheduling Problem (RCPSP)

(Pritsker et al., 1969), which considers both prece-

dence constraints among the activities and resource

demands of the scheduled activities over time. The

RCPSP and its variants have since been applied to nu-

merous realistic applications in almost all industries,

including job-shop scheduling problems (Demeule-

meester and Herroelen, 1992), mining (Alford et al.,

2007), and supply chain (Liu and Lu, 2017). The wide

applications of the RCPSP and also its computational

https://orcid.org/0000-0002-9780-8262

https://orcid.org/0000-0003-2035-2583

https://orcid.org/0000-0003-4866-1396

complexity as an NP-Hard problem has attracted the

attention of many researchers (Blazewicz et al., 1983;

Rahman et al., 2020) to solve these problems.

Generally, solution methods for the RCPSP can be

categorized as exact algorithms and heuristics-based

approaches (Herroelen et al., 1998). Exact algorithms

can obtain and guarantee optimal solutions, but the

solution time becomes unacceptable as the problem

scale increases (Chen et al., 2021). Heuristic-based

methods are widely used to overcome the computa-

tional limitations of the exact algorithms but have no

guarantee for solution optimality (Kolisch and Hart-

mann, 2006).

Constraint programming (CP) is an exact method

and has been very successful over the last two decades

for solving scheduling problems (Laborie, 2018), and

especially the RCPSP (Liess and Michelon, 2008;

Schutt et al., 2011; Schutt et al., 2015; Kreter et al.,

2017). General CP solvers are also available in both

open-source (Perron and Furnon, 7 19) and commer-

cial (CPLEX, 2017) software.

The performance of CP deteriorates when the

problem size increases (e.g., projects with more than

100 tasks). This motivates us to design a matheuristic

within the recently proposed relax-and-solve (R&S)

framework to exploit the efﬁcient search capability of

CP for small and medium size RCPSP.

The R&S is a matheuristic algorithm that re-

cently developed for scheduling problems (Sale-

Etminaniesfahani, A., Gu, H. and Salehipour, A.

An Efﬁcient Relax-and-Solve Algorithm for the Resource-Constrained Project Scheduling Problem.

DOI: 10.5220/0010772400003117

In Proceedings of the 11th International Conference on Operations Research and Enterprise Systems (ICORES 2022), pages 271-277

ISBN: 978-989-758-548-7; ISSN: 2184-4372

271

hipour, 2017; Salehipour et al., 2018; Ahmadian

et al., 2020; Ahmadian et al., 2021). This method

improves an existing feasible solution by iteratively

relaxing the order constraints (the execution order of

tasks) in the current solution and rescheduling the re-

laxed problem with an MIP solver. Although the size

of the relaxed problem is still large since all jobs are

included, the solution time is signiﬁcantly reduced in

practice. Compared with scheduling problems, the

big challenge to the application of the R&S on RCPSP

is that there is no clear deﬁnition for task orders or

task sequences in a feasible solution. In this paper,

we use time windows, instead of the sequence win-

dow, to select the tasks that will be fully rescheduled,

while for the tasks outside of the window, CP con-

straints such as start-at-end are used to maintain the

relative sequence of tasks.

Because the CP outperforms MIP in solving large-

scale problems and can quickly obtain high quality

solutions (Maleck et al., 2018; Kelareva et al., 2012),

we expect the hybridization of CP and R&S, i.e.,

using CP in R&S framework be helpful for solving

RCPSP.

Related approaches in the literature for solving

mixed-integer programming models include relax-

and-ﬁx and ﬁx-and-optimize. In the relax-and-ﬁx

method, the binary variables in the rolling time win-

dow are divided into two groups, i.e., ﬁxed variables,

and optimized variables. The integrality constraint for

variables out of the rolling window is relaxed (Absi

and van den Heuvel, 2019). The ﬁx-and-optimize

method operates on two groups of variables, namely

ﬁxed variables and optimized variables. A great asset

of ﬁx-and-optimize is that the obtained solutions are

always feasible because it does not relax integrality

constraints (Helber and Sahling, 2010; Escudero and

Romero, 2017).

The main contribution of this study is to propose a

novel matheuristic for decomposing and solving the

RCPSP using a constraint programming solver. In

particular, we

• propose an R&S approach for the RCPSP,

• propose a novel technique to create the relaxed

problems,

• develop a hybrid algorithm combining heuristics

and CP, and

• produce superior results to the state-of-the-art by

solving 1560 problem instances from PSPLIB

(project scheduling problem library) for 30, 60,

and 120 activities (Kolisch and Sprecher, 1997).

The remainder of this paper is organized as follows.

We deﬁne the RCPSP in Section 2, and provide our

R&S method in Section 3. In Section 4, we report the

results of our computational experiments, and Sec-

tion 5 provides some conclusions and future research

directions.

2 PROBLEM DEFINITION AND

FORMULATION

The RCPSP consists of a set of n tasks. Each task

i has a known non-negative duration represented by

. There are also precedence relationships between

tasks, which are commonly modeled as an activity-

on-node network G = (V, A). Each task corresponds

to a node in the vertex set V = {0, 1, . . . , n + 1}, and

the precedence relationship that task i must complete

before task j can start is represented as an arc (i, j)

in the arc set A. Two dummy nodes (tasks) 0 and

n + 1 are added to represent the start and ﬁnish of the

project, respectively. The duration of dummy tasks

i.e., d

and d

n+1

are 0. Graph G is acyclic since only

precedence constraints are modeled.

A ﬁxed set RR of renewable resources is available.

Each resource k ∈ RR has a constant non-negative ca-

pacity R

at any time during planning horizon T . Each

task requires a non-negative amount of r

of each re-

source k ∈ RR. The tasks are non-preemptive, which

means tasks cannot be interrupted once started.

Let S

represent the starting time of the task i, S

0. We aim at minimizing the makespan (the comple-

tion time of the last activity) of the project which is

n+1

. The mathematical model of the RCPSP can be

expressed as follows:

minS

n+1

(1)

subject to

≥ S

+ d

, ∀(i, j) ∈ A, (2)

∑

i∈τ(t)

≤ R

, ∀k ∈ RR, ∀t ∈ {0, . . . , T − 1}, (3)

τ(t) = {i ∈ V |S

≤ t < S

+ d

}, (4)

∈ {0, 1, . . . , T − d

}, ∀i ∈ V, (5)

where T is the available upper bound to the project

duration.

3 THE PROPOSED

RELAX-AND-SOLVE METHOD

In this section, an efﬁcient R&S matheuristic algo-

rithm is proposed for the RCPSP. In this method, a

rolling time window is deﬁned, and during the “re-

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

272

Figure 1: An RCPSP example.

lax” phase, all tasks outside the window are ﬁxed with

each other with respect to the order in the original so-

lution, and only tasks inside the time window can be

reordered. In the “solve” phase, a feasible solution is

obtained by solving the relaxed problem. As we do

not remove the precedence and resource constraints,

the obtained solution is always feasible for the origi-

nal problem. The general R&S algorithm is summa-

rized in Algorithm 1.

Algorithm 1: The R&S algorithm.

Input: A feasible solution for the problem.

while the stopping condition is not met do

Generate a relaxed problem;

Solve the relaxed problem by using an

optimization solver;

end

return the best obtained schedule (the

solution);

In what follows, we discuss the generation of an

initial solution for the problem, the generation of re-

laxed problem in each iteration, and also the stopping

criterion for this algorithm.

3.1 Initial Solution

The CP is an effective method for generating feasi-

ble solutions even for highly constrained problems

(Bockmayr and Hooker, 2005). The successful use of

CP to generate an initial solution is presented in (M.

Pour et al., 2018). We used CPLEX CP solver and set

a short time limit to solve the original problem and

generate a feasible initial solution.

3.2 Generating the Relaxed Problem

We use an example to illustrate the generation of re-

laxed problems. Figure 1 shows a general picture of

a feasible solution while solving a problem by R&S.

The time window in the ﬁgure is used to divide the

tasks into two groups which are treated differently. In

the following, the generation of relaxed problems are

explained.

3.2.1 The Rolling Time Window

A rolling time window is utilized to generate a re-

laxed problem. The larger the time window, the more

tasks are relaxed in each iteration. In the ﬁrst iteration

the time window starts at t = 0 (second). After solv-

ing each relaxed problem, the time window should be

gradually moved forward, and when the whole time

horizon is covered, the time window restarts from

t = 0. For moving forward the time window, a cer-

tain overlap with the current time window should be

considered to let the tasks move in the time horizon.

Otherwise, eliminating the overlap results in restrict-

ing tasks in separate time windows, losing the algo-

rithm’s global searchability, and consequently trap-

ping to a local optimum area. The length of each time

window and the overlap (parameter overlap) of time

windows should be a function of the makespan. This

means both of those parameters should be reduced in

proportion to the makespan’s reduction after each it-

eration. We deﬁned the length of the time window as

follows: (

makespan

) × (1 + overlap). The positive real

value of N to decompose the planning time, and the

value of overlap which is between 0 and 1, should be

set for each problem as explained in section 4.

An Efﬁcient Relax-and-Solve Algorithm for the Resource-Constrained Project Scheduling Problem

273

3.2.2 Tasks Group 1 (G1)

The tasks of the group 1 are those that are completely

outside the time window, which means their ﬁnish

time is less than the minimum of the time window,

or their start time is greater than the maximum of the

time window. In Figure 1, the tasks of group 1 are

G1 = {3, 6, 4, 9, 8, 13}.

To generate a relaxed problem, when the ﬁnish

time (start time) of a task in group 1 is equal to

the start time (ﬁnish time) of another task, then two

tasks are ﬁxed with each other by adding the “start-

at-end” constraints from (CPLEX, 2017). In Fig-

ure 1, the following set of start-at-end constraints is

added to the problem and generate three super tasks:

{(3, 11), (7, 4), (7, 9), (9, 13), (12, 8)}. In this paper,

we refer to the generated tasks by sticking some avail-

able tasks to each other as a super task. The advan-

tage of developing super tasks is reducing the compu-

tations of the problem by forcing some tasks to move

in the time horizon simultaneously. The ﬁrst super

task is generated by tasks 3 − 11, the second one by

tasks 7 − 4 − 9 − 13 and the third one by tasks 12 − 8.

As is clear in Figure 1, task 6 in group 1 is not ﬁxed,

this just may happen for the tasks that start at t = 0

because otherwise tasks start as soon as the resource

constraint and precedence constraints satisfy, which

means it happens right after ﬁnish of a task. We let

task 6 be relaxed, thus the algorithm can efﬁciently

optimize the schedule and ﬁll the gap (between t = 1

and t = 2 if the precedence and resource constraints

are not violated.

3.2.3 Tasks Group 2 (G2)

The tasks in group 2 include the remaining tasks, i.e.,

the tasks that all or some of them are inside the time

window. In the proposed example in Figure 1, the

tasks of group are G2 = {5, 11, 2, 1, 7, 12, 10}.

Tasks group 2 are relaxed to be reordered. It

should be noted that the original precedence and re-

source constraints are always maintained.

3.3 Solving the Relaxed Problem

The solve operation uses the CPLEX CP optimization

solver to solve the relaxed problem. Since the relaxed

problem becomes smaller, it includes just a few tasks

to schedule and can be solved much easier than the

original problem. Moreover, the solution of the re-

laxed problem is always feasible. It should be noted

that the tasks of group 1 can not be reordered, and

because their starting times are not ﬁxed after each it-

eration the starting time of all tasks (including tasks

of group 1) is updated, and the makespan of the origi-

nal problem is updated to the makespan of the relaxed

problem.

3.4 Stopping Criterion

The stopping criterion for this R&S is the total num-

ber of relaxed problem that generated. Also, the opti-

mization solver has a time limit in each iteration, and

as soon as the solver ﬁnds the optimum solution of the

relaxed problem (local optimum for the original prob-

lem) or the computation time exceeds the time limit,

the algorithm goes to the next iteration.

4 COMPUTATIONAL

EXPERIMENTS

In order to evaluate the performance of the proposed

R&S algorithm for solving the RCPSP, we present

the computational results obtained by R&S on 1560

instances from the PSPLIB benchmark (Kolisch and

Sprecher, 1997) with J30, J60 and J120 datasets. The

datasets J30 and J60 each contains 480 instances, and

J120 contains 600 instances. The R&S algorithm is

implemented in Python version 3.6.5 and solved by

the CPLEX CP version 12.10.0.0 (CPLEX, 2017).

Except for the stopping criterion (time limit) for solv-

ing each relaxed problem, all other solver parameters

are set to their default values. The numerical exper-

iments were conducted on an Intel(R) Core™ i7, 2

GHz CPU, and 6GB of RAM under the Windows 10

operating system.

4.1 Parameter Settings

The time limit for CPLEX CP to solve for the initial

solution is set to one second. The computational time

for all experiments is 600 seconds. We set the stop-

ping time of each iteration to 25 seconds. In this way,

we set the maximum computational time of J30, J60

and J120 to 150, 300 and 600 seconds, respectively.

We set overlap = 0.4. To calculate the length of

each time window, we set N = 0.1 × n, i.e., 3, 6 and

12 for J30, J60, J120, respectively. The total num-

ber of relaxed problems generated, i.e., the maximum

number of iterations is set to 2 × N.

4.2 Tests on PSPLIB

In this section, we ﬁrst compare the results from our

R&S method with the results from CPLEX CP and

three other exact methods including, failure directed

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

274

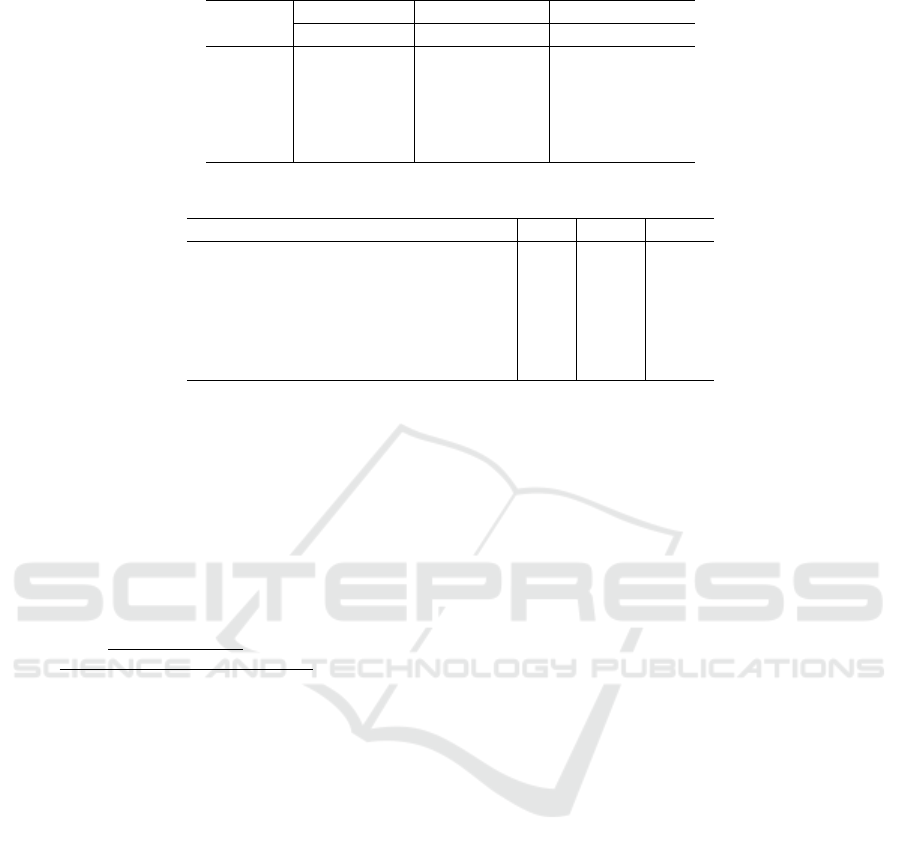
Table 1: Comparison of LCG, FDS, SMT, CPLEX, and R&S on Ct and ∆

J30 J60 J120

Method ∆

Ct ∆

LCG 0 - 2.17 - 9.76 -

FDS 0 0.93s 1.91 67.44s 7.02 322.52s

SMT 0 0.22s 1.88 61.90s 9.55 320.50s

CPLEX 0 4.71s 1.11 52.83s 4.69 350.40s

R&S 0 5.12s 1.06 46.75s 4.63 235.65s

Table 2: Comparison of the state-of-the-art metaheuristics and R&S on ∆

CPM

Algorithm J30 J60 J120

R&S (our proposed method) 0 10.54 31.09

DBGA (Debels and Vanhoucke, 2007) 0.02 10.68 30.69

MA (Rahman et al., 2020) 0 10.55 31.12

GA-FBI (Liu et al., 2020) 0.0 10.56 32.76

COA (Elsayed et al., 2017) 0.0 10.58 31.22

PSO-SS(Koulinas et al., 2014) 0.01 10.68 31.23

search (FDS), lazy clause generation (LCG), and sat-

isﬁability modulo theories (SMT) by (Boﬁll et al.,

2020). In Table 1, for each set of instances, we pro-

vide the average of computational time (Ct).

The lower bound (LB) provides the minimum of

the makespan for each problem. We use the earli-

est start time of the last dummy task as the C

max,LB,p

In Table 1, we report the average deviations from the

best-known lower bound ( ∆

) as follows:

∆

∑

p=P

p=1

max,R&S,p

−C

max,LB,p

× 100%

(6)

where P is the total number instances in an instance

set, and C

max,R&S,p

and C

max,LB,p

are the makespan

obtained by R&S method and the best known lower

bound for each instance, respectively. According to

Table 1, the performance of R&S is superior to solve

J60 and J120 instances because the average deviation

from the best known lower bound is better than other

methods. For J30, all methods can ﬁnd the optimum

solution. Comparing the result of CPLEX as an in-

dependent method with R&S for J60 and J120 illus-

trates the efﬁciency of our proposed algorithm. For

J30, R&S is slower than CPLEX but still ﬁnds op-

timal solutions for all instances. We also compare

our results and the decomposition based genetic al-

gorithm (Debels and Vanhoucke, 2007), and state-of-

the-art metaheuristic methods from (Rahman et al.,

2020) including, memetic algorithm (MA), consoli-

dated optimization algorithm (COA) (Elsayed et al.,

2017), PSO based hyper-heuristic algorithm (PSO-

HH) (Koulinas et al., 2014), and genetic algorithm

using forward-backward improvement (GAFBI) (Liu

et al., 2020). Because in the literature the number

of schedule generated is used as a stopping criterion

which is not applicable to our method, we use the best

results of those methods for 50,000 schedule gener-

ated. The average deviation from the CPM (∆

CPM

)

can be calculated by using Equation (6), where the

lower bound of the makespan, C

max,LB,p

is produced

by CPM. The results summarized in Table 2 illustrates

that our R&S method in comparison with the state-

of-the-art methods can provide competitive results in

a reasonable time. Robust solving methods provide

good solutions for all runs. However, the random pa-

rameters in metaheuristics for solving RCPSPs can re-

sult in different outputs in solving the same problem.

Researchers thus are recommended to report the aver-

age results of several independent runs.

5 CONCLUSION

In this paper, we presented a relax-and-solve (R&S)

matheuristic, which is an efﬁcient and very easy

to implement algorithm to solve the resource-

constrained project scheduling problem (RCPSP). In

this method, the CPLEX CP solver is utilized to solve

the relaxed problems. The results of the tests on 1560

instances from the standard library PSPLIB with 30,

60, and 120 tasks show the capability of this method

to obtain good quality solutions. Future work includes

automating tuning the time window length in each it-

eration and employing local searches to improve the

results. It is also interesting to extend this method

to multi-mode and scheduling problems under uncer-

tainty.

An Efﬁcient Relax-and-Solve Algorithm for the Resource-Constrained Project Scheduling Problem

275

ACKNOWLEDGMENTS

Alireza Etminaniesfahani is the recipient of the UTS

International Research Scholarship (IRS) and UTS

President’s Scholarship (UTSP).

REFERENCES

Absi, N. and van den Heuvel, W. (2019). Worst case anal-

ysis of relax and ﬁx heuristics for lot-sizing prob-

lems. European Journal of Operational Research,

279(2):449–458.

Ahmadian, M. M., Salehipour, A., and Cheng, T. (2021).

A meta-heuristic to solve the just-in-time job-shop

scheduling problem. European Journal of Opera-

tional Research, 288(1):14 – 29.

Ahmadian, M. M., Salehipour, A., and Kovalyov, M.

(2020). An efﬁcient relax-and-solve heuristic for

open-shop scheduling problem to minimize total

weighted earliness-tardiness. Available at SSRN

3601396.

Alford, C., Brazil, M., and Lee, D. H. (2007). Optimisation

in Underground Mining, pages 561–577. SpringerUS,

Boston, MA.

Blazewicz, J., Lenstra, J., and Kan, A. (1983). Schedul-

ing subject to resource constraints: classiﬁcation and

complexity. Discrete Applied Mathematics, 5(1):11–

24.

Bockmayr, A. and Hooker, J. N. (2005). Constraint pro-

gramming. In Aardal, K., Nemhauser, G., and Weis-

mantel, R., editors, Discrete Optimization, volume 12

of Handbooks in Operations Research and Manage-

ment Science, pages 559–600. Elsevier.

Boﬁll, M., Coll, J., Suy, J., and Villaret, M. (2020). Smt

encodings for resource-constrained project schedul-

ing problems. Computers & Industrial Engineering,

149:106777.

Chen, H., Ding, G., Qin, S., and Zhang, J. (2021). A

hyper-heuristic based ensemble genetic programming

approach for stochastic resource constrained project

scheduling problem. Expert Systems with Applica-

tions, 167:114174.

CPLEX, I. I. (2017). version 12.8.0.

Debels, D. and Vanhoucke, M. (2007). A decomposition-

based genetic algorithm for the resource-constrained

project-scheduling problem. Operations Research,

55:457–469.

Demeulemeester, E. and Herroelen, W. (1992). A branch-

and-bound procedure for the multiple resource-

constrained project scheduling problem. Management

Science, 38(12):1803–1818.

Elsayed, S., Sarker, R., Ray, T., and Coello, C. C. (2017).

Consolidated optimization algorithm for resource-

constrained project scheduling problems. Information

Sciences, 418-419:346–362.

Escudero, L. F. and Romero, C. P. (2017). On solving a

large-scale problem on facility location and customer

assignment with interaction costs along a time hori-

zon. TOP: An Ofﬁcial Journal of the Spanish Society

of Statistics and Operations Research, 25(3):601–622.

Helber, S. and Sahling, F. (2010). A ﬁx-and-optimize ap-

proach for the multi-level capacitated lot sizing prob-

lem. International Journal of Production Economics,

123(2):247–256.

Herroelen, W., De Reyck, B., and Demeulemeester, E.

(1998). Resource-constrained project scheduling: A

survey of recent developments. Computers & Opera-

tions Research, 25(4):279–302.

Herroelen, W. and Leus, R. (2005). Identiﬁcation

and illumination of popular misconceptions about

project scheduling and time buffering in a resource-

constrained environment. Journal of the Operational

Research Society, 56(1):102–109.

Kelareva, E., Brand, S., Kilby, P., Thiebaux, S., and Wal-

lace, M. (2012). Cp and mip methods for ship schedul-

ing with time-varying draft. ICAPS 2012 - Proceed-

ings of the 22nd International Conference on Auto-

mated Planning and Scheduling.

Kolisch, R. and Hartmann, S. (2006). Experimental inves-

tigation of heuristics for resource-constrained project

scheduling: An update. European Journal of Opera-

tional Research, 174(1):23–37.

Kolisch, R. and Sprecher, A. (1997). Psplib - a project

scheduling problem library: Or software - orsep oper-

ations research software exchange program. European

Journal of Operational Research, 96(1):205–216.

Koulinas, G., Kotsikas, L., and Anagnostopoulos, K.

(2014). A particle swarm optimization based hyper-

heuristic algorithm for the classic resource con-

strained project scheduling problem. Information Sci-

ences, 277:680–693.

Kreter, S., Rieck, J., and Zimmermann, J. (2015). Models

and solution procedures for the resource-constrained

project scheduling problem with general temporal

constraints and calendars. European Journal of Op-

erational Research, 251.

Kreter, S., Schutt, A., and Stuckey, P. (2017). Using con-

straint programming for solving rcpsp/max-cal. Con-

straints, 22.

Laborie, P. (2018). An Update on the Comparison of MIP,

CP and Hybrid Approaches for Mixed Resource Allo-

cation and Scheduling, pages 403–411. Springer In-

ternational Publishing, Cham.

Liess, O. and Michelon, P. (2008). A constraint program-

ming approach for the resource-constrained project

scheduling problem. Annals of Operations Research,

157(1):25–36.

Liu, J., Liu, Y., Shi, Y., and Li, J. (2020). Solving resource-

constrained project scheduling problem via genetic al-

gorithm. Journal of Computing in Civil Engineering,

34(2):04019055.

Liu, J. and Lu, M. (2017). Optimization on supply-

constrained module assembly process. In IGLC 2017 -

Proceedings of the 25th Annual Conference of the In-

ternational Group for Lean Construction, pages 813–

820. cited By 2.

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

276

M. Pour, S., Drake, J. H., Ejlertsen, L. S., Rasmussen,

K. M., and Burke, E. K. (2018). A hybrid

constraint programming/mixed integer programming

framework for the preventive signaling maintenance

crew scheduling problem. European Journal of Oper-

ational Research, 269(1):341–352.

Maleck, C., Nieke, G., Bock, K., Pabst, D., and Stehli, M.

(2018). A comparison of an cp and mip approach

for scheduling jobs in production areas with time con-

straints and uncertainties. In 2018 Winter Simulation

Conference (WSC), pages 3526–3537.

Perron, L. and Furnon, V. (2019-7-19). Or-tools.

Pritsker, A., Waiters, L. J., and Wolfe, P. (1969). Multi-

project scheduling with limited resources: A zero-one

programming approach. Management Science, 16:93–

108.

Rahman, H. F., Chakrabortty, R. K., and Ryan, M. J. (2020).

Memetic algorithm for solving resource constrained

project scheduling problems. Automation in Con-

struction, 111:103052.

Salehipour, A. (2017). A heuristic algorithm for the

aircraft landing problem. In 22nd International

Congress on Modelling and Simulation. Modelling

and Simulation Society of Australia and New Zealand

Inc.(MSSANZ).

Salehipour, A., Ahmadian, M., and Oron, D. (2018). Ef-

ﬁcient and simple heuristics for the aircraft landing

problem. In Matheuristic 2018 International Confer-

ence.

Schutt, A., Feydy, T., Stuckey, P., and Wallace, M. (2011).

Explaining the cumulative propagator. Constraints,

16:250–282.

Schutt, A., Feydy, T., Stuckey, P. J., and Wallace, M. G.

(2015). A Satisﬁability Solving Approach, pages 135–

160. Springer International Publishing, Cham.

An Efﬁcient Relax-and-Solve Algorithm for the Resource-Constrained Project Scheduling Problem

277