A 3D Matching Method to Compare a Scan to Its Reference using 3D

Registration and Monte Carlo Metropolis Hastings Optimization for

Industrial Inspection Applications

Clément Dubosq

and Andréa Guerrero

Capgemini Engineering R&I France, 4 avenue Didier Daurat, Blagnac, France

Keywords: Point Cloud Registration, 3D Model, 3D Matching, ICP, Monte-Carlo Metropolis Hastings, Point Cloud

Processing, Defect Detection, Automatized Inspection.

Abstract: Currently in industry, inspection tasks are essential to ensure a product efficacity and reliability. Some

automated tools to inspect, i.e. to detect defect exist, but they are not adapted to an industrial inspection

application. Most of industrial inspection is human made. In this article, we propose a new algorithm to match

a 3D point-cloud to its 3D reference to track visual defects. First, we reconstruct a 3D model of an object

using Iterative Closest Points (ICP) algorithm. Then, we propose an ICP initialization based on a Monte Carlo

Metropolis-Hasting optimization to match a partial point-cloud to its model. We applied our algorithm to the

data measured from a Time-of-Flight sensor and a RGB camera. We present the results and performance of

this approach for objects of different complexities and sizes. The proposed methodology shows good results

and adaptability compared to a state-of-the-art method called Go-ICP.

1 INTRODUCTION

Today in industry, inspection remains a complex and

hard task to achieve for an operator. Most of its

activity is done by eye, sometimes in hostile or dark

environment e.g., in a wind turbine nacelle or in a

pipe system for energy distribution. Automatize part

of their task with computer vision or Artificial

Intelligence (AI) will help make their work less

difficult. Such technology assistance should answer

to ground reality of the inspection work:

- These methods must be applicable in real time.

The operator needs the result during its

inspection cycle to buy replacement parts.

- These approaches must be precise. In some fields

like aeronautics.

- These solutions require to treat any object size.

In aeronautics, the operator inspects objects from

a bolt to a turbine.

Online drones, robots or other platforms equipped

with sensors can be used to recover data on the

condition of the object. W. Chen et al., 2020 studied

the state of power lines using a drone using a deep

https://orcid.org/0000-0002-6644-3926

https://orcid.org/0000-0003-3345-1572

learning (DL) approach to classify foreign objects.

Saavedra et al., 2021 also used a DL approach for

analyzing X-Ray images. Overall, classification and

object detection are essentially based on Machine

Learning (ML) technics. However, these methods

efficiency depends on the training database, its

diversity and size. For industrial inspection, this will

imply a large training database for each inspection

application. Yet, to our knowledge, there is no public

database for industrial inspection.

Instead of using ML approach, a well-known

approach consists in comparing a scan of the object

of interest with its no-defect 3D reference. For

example, in Abdallah et al., 2020; Abdallah et al.,

2019, they used Computer-aided design (CAD) as the

no-defect reference. Such approach needs CAD,

which is not always available in industry, especially

in aeronautics where pieces are often replaced by new

models.

In this work, we present our method to compare

an object 3D scans with its reference model to detect

defects. Our goal is to provide an approach fitting the

inspection requirements. Our approach can provide a

518

Dubosq, C. and Guerrero, A.

A 3D Matching Method to Compare a Scan to Its Reference using 3D Registration and Monte Carlo Metropolis Hastings Optimization for Industrial Inspection Applications.

DOI: 10.5220/0010779100003122

In Proceedings of the 11th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2022), pages 518-525

ISBN: 978-989-758-549-4; ISSN: 2184-4313

3D model of the object to have a standard reference,

which means it does not require CADs.

2 RELATED WORK

In this section, we briefly introduce state-of-the-art

methods for evaluate changes between a 3D model

and a partial scan of an object. First, we present

methods creating a 3D model in a section called 3D

reconstruction. Then, we present several methods to

evaluate changes on the object, i.e., 3D matching.

Finally, we will present some optimization methods

to improve 3D matching.

2.1 3D Reconstruction

The literature shows that 3D reconstruction is a

common problem. There is two main approaches

studied: photogrammetry (Bhadrakom, 2016) and

point cloud processing (Bethencourt & Jaulin, 2013).

The first category reconstructs 3D models using set of

2D images and camera information via Structure from

Motion to produce point cloud. Points of interest are

extracted using Scale-invariant Feature Transform

(SIFT). The second category, called point cloud

processing, is mainly based on merging partial point

clouds using 3D matching algorithm (Bethencourt &

Jaulin, 2013). Partial point clouds are usually pre-

matched using interest points extractor like SIFT.

Then, Random Sampling Consensus (RANSAC)

(Zhou et al., 2016) is applied to get a first point cloud

alignment. Finally an Iterative Closest Point (ICP)

(Besl & McKay, 1992) step refines the alignment

estimation. If available, pose estimation can be

improved using Inertial Measurement Unit (IMU).

However, these methods are not suited for

inspection application mostly due to the lack of

precision for photogrammetry, lack of data for ML

approaches, and due to the time cost and adaptability

for existing 3D matching method. To resolve this

issue, we have chosen a simple method. It is based on

existing tools of 3D reconstruction, allowing to obtain

a 3D model of an object under few minutes with a

precision around 1mm. A set of 3D scans are fused to

reconstruct an object based on ICP color (Park et al.,

2017).

2.2 3D Matching

A wide range of algorithms exists for matching two

point-clouds. Each of them has advantages and

limitations. We can cite for example RANSAC

combined with Fast Point Feature Histogram (FPFH)

(Rusu et al., 2009) or Kernel correlation (KC) (Tsin

& Kanade, 2004). However, these approaches suffer

from intrinsic limitations such as the high

computational cost for the most precise ones, or the

non-uniqueness of the minimization solution due to

the high dimensionality problem. Iterative Closest

Point is the widest and commonly used method for

registration (Wang & Zhao, 2017) due to its fitness

and precision. They are many studies to optimize and

to improve ICP (Lamine Tazir et al., 2018; Park et al.,

2017; Pomerleau et al., 2015). This method consists

in minimizing the following criterion:

𝜒



𝑝

⃗





𝑅



𝑝

⃗



𝑡

⃗















(1)

where 𝑝⃗





is the position of the target point cloud, 𝑝⃗



the corresponding points in the source point cloud, 𝑅



is a rotation matrix and 𝑡

⃗

a translation vector. A k-

Nearest Neighbors (k-NN) algorithm evaluates the

pairwise similarity. As shown in the previous

equation, ICP is a self-consistent method which

requires to initialize some parameters. Due to the high

dimensionality of the equation to minimize, local

minima can occur. However, adding constraints to the

problem can help with this issue. We present three

commonly used ICP approaches:

- ICP point-to-point (Pt to Pt) (Arun et al., 1987):

This is the initial approach developed. It is used

as base for every ICPs variants.

- ICP point-to-plan (Pt to Pl) (Besl & McKay,

1992): This variant add surface constrain to

equation (1).

- ICP color (Park et al., 2017): Based on ICP Pt to

Pl, this variant add the RGB information of the

point cloud as another constrain in the

minimization equation.

However, such methods alone require an a priori

to be executed. This implies or to have two scans with

an initial important overlap, or to have an

approximated form of the transformation matrix. To

define the most suited ICP approach for our problem,

a preliminary study was performed on complex object

as a pipeline system. Results for scans matching show

better results for ICP color in term of precision and

overlap between two scans. Color information add a

degree of freedom that help to get optimal 3D

matching. So, we applied ICP color to generate the

3D models used as reference for the object inspection.

2.3 Global Optimization

As we said in the section before, ICP and generally

3D matching methods are sensitive to initialization.

A 3D Matching Method to Compare a Scan to Its Reference using 3D Registration and Monte Carlo Metropolis Hastings Optimization for

Industrial Inspection Applications

519

They are not sufficient to match points in any cases

since these methods can converge to local minima. A

common approach is to use global optimization for

initialization (Linh & Hiroshi, 2015; Yang et al.,

2016). The literature shows different methods. First

category being deterministic optimization methods.

These methods use rigorous optimization providing a

theoretical guarantee to find the best solution. We can

cite Bound and Branch (BnB) as an example of such

approach (Land & Doig, 2010). Yang et al., 2016

proposed an algorithm that make use of BnB

combined with ICP to find global optimal matching

called Go-ICP. In such method, a rough optimization

is done using BnB approach, followed by a fined ICP

optimization. The BnB and ICP procedure is repeated

until convergence is reached. However, these

methods are computationally expensive since they

explore recursively all the possibilities to get the

global minimum. Second category is stochastic

optimization. A well-known example is Monte-Carlo

based simulation. These methods use randomness to

explore all the solution and retain only the best one.

They are easy to implement but require important

computational time to guarantee the optimal solution.

The last category is metaheuristic optimization

methods based on iterative stochastic algorithms.

They use random sampling to extract information of

a given cost function local properties. These methods

allow to get optimal solution but do not assure to find

the optimal solution. Linh & Hiroshi, 2015 proposed

an approach based on simulating annealing

(van Laarhoven & Aarts, 1987) combined with ICP to

do point cloud matching. Their procedure is similar to

Go-ICP procedure in which a simulated annealing is

done instead of BnB. Such approach is not suited due

to possible slow convergence and high risk to be stuck

in local solution for symmetric object and/or plan.

For this work, we used a metaheuristic method of

optimization refer as Monte Carlo Metropolis

Hastings (MCMH) (Hastings, 1970). This method

based on the Markov chain is simple to adapt to our

problem. However, such methods are limited alone

because finding the best matching solution would be

expensive in time cost. In the next section, we explain

our approach which uses MCMH to find an

approximate solution before refinement with ICP.

3 3D MATCHING APPROACH

In this work, we propose a new complete approach to

detect defects by comparing a generated 3D model

with a partial scan. Figure 1 shows the proposed

approach based on 3D registration with ICP and

global optimization. First, we apply preprocessing on

point clouds to clean it. Then a first 3D matching

evaluation is done using MCMH. The 3D matching is

refined with a last ICP color (Park et al., 2017)

calculation. Our solution gives as output a

comparison between the scan and the reference 3D

model.

In a first part, we will present the pre-processing in

which we present cleaning steps of scans before

matching. Then, we will present our matching method

based on MCMH combined with ICP color.

3.1 Pre-process

Scans are cleaned before 3D matching due to possible

outliers created by the sensor used for scan capture.

Cleaning process stands in three steps. First, we

remove the background. Above a certain distance, the

sensor suffers from distortion in the measurement.

Given the a priori of working on a close-by object, we

remove points with a depth over a threshold

dependent of the sensor range sensibility

. Secondly,

if the object is placed on a surface, we remove the

surface. RANSAC is used to estimate plan equation

and to remove points from and below the plan.

Thirdly, we apply a statistical outlier removal method

to remove points considered as noise. We also use

clustering method (Ester et al., 1996) to highlight

cluster of points and discriminate clusters having less

points than an empirically defined threshold (~ 500

points). This allows to only keep the points of the

object of interest.

Figure 1: Scheme of the 3D matching process of our developed approach. We focus in this article on the 3D matching.

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

520

3.2 Scan Matching

We know ICP requires a good initialization to have

good results due to its self-consistent nature (cf.

equation (1)). That is why, usually, ICP methods are

used as a last step for fine registration. To solve our

matching problem, we need a global 3D matching

approach. We show in the related work section that

the optimization field helps to find a global optimal

solution. We present here our approach based on

MCMH combined with ICP to match a misoriented

scan to its 3D reference. We also compare our method

to Go-ICP (Yang et al., 2016) a state-of-the-art

method. Since this last method is based on a

deterministic approach, we assume it should find

correct solution, and so it can be used as a

comparison.

3.2.1 Monte-Carlo Metropolis Hastings

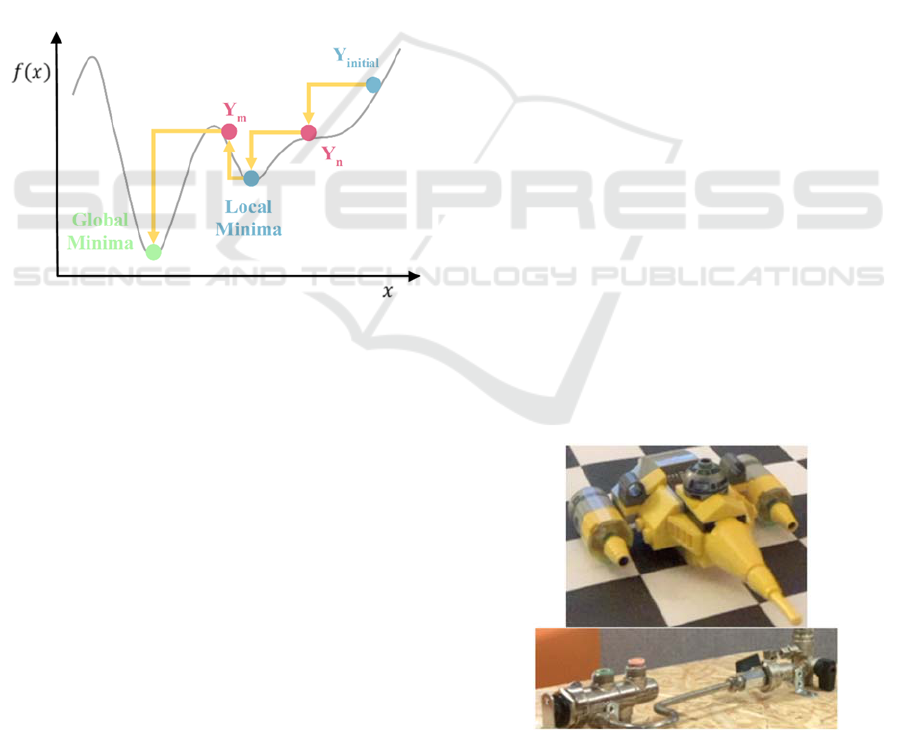
Figure 2: Scheme of the MCMH exploration. MCMH

allows to overcome barrier to find global minima.

As the previous section explains it, MCMH approach

is a meta-heuristic method used for phase spaces

exploration and optimization of cost function. In our

case, phase space corresponds to translation and

rotation spaces to apply on the scan point cloud to

match the 3D model point cloud. The Figure 2

illustrates the approach. Rotation and translation are

initialized with given values (Y

initial

in Figure 2).

Rotation matrix expression is derived from Euler

angle. Then, we apply random variation on rotation

angles and translation elements. A new

transformation is then evaluated (Y

in Figure 2). If

the new obtained configuration minimizes the overlap

between the two points clouds, then the solution is set

as the new reference. Else, in a classical Monte-Carlo

Markov Chain (MCMC) simulation, the solution is

rejected. However, in MCMH an acceptance criterion

is added: The Metropolis-Hastings criteria. It is the

probability of transition between the previous and the

new estimated values of the cost function. Usually,

the probability is expressed as follow:



 exp





𝑓



𝑥







𝑓

𝑥







∗𝛽



 (2)

With 𝛽 the inverse of a fictitious temperature. A

uniformly random number is drawn. If the random

number is lower to the computed probability of

transition, then the new state is kept (as shown with

the kept solution Y

in the Figure 2). Else the state is

finally rejected. This procedure allows to exit local

minimum and to overcome barrier in the phase space.

A new random variation is drawn at each iteration.

This procedure allows to access the global minima.

3.2.2 Hungarian Distance Criteria

To compute a cost function expressing the similarity

between two point clouds, we use pairwise Euclidian

distance between source and target. We compute a

cost matrix which is optimized using the Hungarian

algorithm (Kuhn, 1955). The diagonal of the cost

matrix corresponds to the smallest pairwise distance

between the two considered points clouds. The

MCMH will optimize the value of the cost matrix

trace.

First, cost matrix between points of source and

target is evaluated. Then, we execute the Hungarian

algorithm to solve the assignment problem.

Concretely, solving the problem consists in

performing permutation operation on the cost matrix

to minimize its trace. Each of the diagonal elements

corresponds to the scan and source optimal pairwise.

We compute the trace and divide the value by the

number of diagonal elements. We refer to this value

as the average Hungarian distance in the rest of this

article. The following equation present the equation

to minimize:

Figure 3: Photo of the lego and pipeline systems used for

our tests.

A 3D Matching Method to Compare a Scan to Its Reference using 3D Registration and Monte Carlo Metropolis Hastings Optimization for

Industrial Inspection Applications

521

𝐷

,



𝑁



min

,

𝑇𝑟𝐿



𝐶



𝑅





(3)

Where 𝐷



is the average Hungarian distance we

seek to minimize, 𝑁



is the number of diagonal

elements of the cost matrix 𝐶



, and 𝐿



and 𝑅



are

respectively line and row permutation matrix. With

the MCMH, we seek to minimize this value by

applying variations on rotation and translation.

3.2.3 Our Matching Algorithm

We present below a pseudo-algorithm which explain

the global matching procedure of our approach.

Pseudo-algorithm 1: Our approach based on MCMH

timization

rocedure.

Input: Scan point cloud S and 3D reference model

point cloud M

Output: Optimal transformation T



of S to M

1: Compute topological descriptor of S and M

 S’ and M’

2: Align the center of mass of S’ and M’

3: Compute the initial average Hungarian distance

𝐷



4: Initialize the rotation and translation

5: MCMH algorithm

 Best approximate transformation T





, 𝐷

,

6: Rotation of 180° on Oy axis of S’

7: Perform the same described procedure between line

2 and 5

 Best approximated transformation T





, 𝐷

,

8: if 𝐷

,

𝐷

,

then:

9: | T





 T





10: ICP color evaluation based on T





 Compute T



11: return T



In step 1 of our method, topological descriptor

corresponds to a simplified triangular mesh. Point

clouds are converted into triangular mesh using

Poisson surface reconstruction of Kazhdan et al.,

2006. Simplification of triangular mesh uses voxel

downsampling on vertices. Then we have a simplified

shape of the original point cloud. Vertices from this

shape are used for cost matrix evaluation. This step is

important to reduce computation cost.

First MCMH is computed, followed by a second

MCMH on the same scan rotated by 180° on the Oy

axis. The choice of the Oy axis is motivated by the

idea that the object is placed on a surface. This change

of initial point allows to begin the MCMH procedure

to a different place in the phase space and so, to access

a different path to the global solution. This second

MCMH helps to overcome similarity problem (like in

quasi-symmetric systems).

Table 1: Matching results for the model of lego with our

MCMH approach.

Matching

time (s)

Success

rate

(%)

RMSE

(mm)

Fitness

(%)

Scan 1

13.1 ±

1.4

65.5

0.73 ±

0.04

83.1 ±

1.1

Scan 2

13.2 ±

0.6

71.5

0.66 ±

0.04

91.3 ±

2.3

4 TESTS AND PERFORMANCES

4.1 Technical Settings

Calculations and tests are done on a Mac OS

computer with Intel® Core™ i9 with 8 cores, a

frequency of 2.3 GHz and a RAM of 16 Go. Our code

is developed in python 3.8 using Open3D, NumPy

and SciPy libraries. The data is acquired using frontal

the RGB camera and the ToF sensor (TrueDepth) of

an iPad Pro 11” 2nd generation.

Go-ICP is executed in python, using a cythonized

version of the original code of Yang et al. originally

coded in C++. Calculations were done on a Linux

Ubuntu computer with Intel® Core™ i5 -8365U CPU

@ 1.60GHz 1.90 GHz, with 8Go of RAM.

Table 2: Matching results for the model of pipeline with our

MCMH approach.

Matching

time (s)

Success

rate

(%)

RMSE

(mm)

Fitness

(%)

Scan 1

18.7 ±

1.1

90.5

0.83 ±

0.01

88.1 ±

0.8

Scan 2

16.5 ±

0.8

0.79 ±

0.03

87.4 ±

2.0

4.2 Systems Tested and Parameters

We performed our tests on two objects showed in

Figure 3: a lego and a pipeline system. The lego

object is approximately of 12 cm length, 7 cm width

and 4 cm height. The pipeline object is 30 cm length,

10 cm width and 8 cm height. The last object

represents well the inspection application since it is a

reflective and complex object, made of steel. The lego

is constraining by its size and sets the smallest object

we successfully tested with our approach.

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

522

Table 3: Matching results for the pipeline and the lego models with Go-ICP. MSE Treshold is set to 0.00008. *Due to the

computation time for this scan, only one calculation was performed.

Lego

Time (s)

Success RMSE (mm) Fitness (%)

Scan 1 18.7 ± 0.3

FALSE 0.99 ± 0.01 48.7 ± 2.0

Scan 2 19.9 ± 0.4

TRUE 0.63 ± 0.01 95.3 ± 0.9

eline

Time (s)

Success RMSE (mm) Fitness (%)

Scan 1 20.8 ± 1.3

FALSE 0.994 ± 0.001 55.3 ± 0.6

Scan 2 3471*

FALSE 1.11* 23.1*

We now present the parameter used for the

reconstruction and the global scan matching. We first

begin with the MCMH parameters. Without any a

priori, we must evaluate a large range of translations

and rotations. So, we perform a large exploration in

the first iterations. This allows us to move far enough

from initial position. However, even if it helps to

escape local minima, empirical tests show the need to

restrain the range to access global minima.

Metropolis-Hastings criteria is set to 𝛽  700 ( s e e

equation (2)). MCMH procedure is computed over

10000 iterations. This allows enough sampling of the

phase space to find the best approximate solution.

If luminosity can change during acquisition, we

set the geometric parameter of ICP color 𝜆





1.0. Voxel sizes from the coarse grain to the fine one

are set to [0.01, 0.005, 0.002] for the lego model and

[0.02, 0.01, 0.002] for the pipeline system.

Adaptation of voxel size is needed for coarse to fine

grain approach, depending on the size of the

considered object.

We compare our method with Go-ICP. For this

method, the matching calculations are performed on

the complete point cloud of the scan and the model

without a support plan. We choose to proceed like this

since Go-ICP is combinatory and supposed to assure

a perfect matching. The tests with Go-ICP are

performed using the set of default parameters. Only

the shutoff parameter, here a mean square error

(MSE) threshold, is fixed empirically at 0.00008.

Higher values tested did not gave satisfying results on

all the tests. Lower values increase CPU time above

the hour.

4.3 Scan Matching Performances

We first present the matching results we got for two

different scans of the lego. These two scans are

complex cases due to the low point density on the

object point cloud. We evaluate four performance

criteria: the computation time, the success rate, the

RMSE and the fitness between the scan and the

reference model. Since MCMH is stochastic, we

evaluated 200 runs of our approach to quantify its

robustness. RMSE and fitness are evaluated only for

good results only. We define empirically that a good

match corresponds to a fitness greater than 80%.

Results for the lego are presented in Table 1. We

see our approach has an average success rate for the

matching between 65 and 70% on 200 calculations.

The time cost is about 13 seconds. We also saw

empirically that RMSE and fitness can be used to

evaluate the matching quality. A good matching has

a value over 80% for the fitness and lower than the

millimeter for the RMSE. The fitness is interesting

since it traduces the overlap between the model and

the scan, 100% means a perfect overlap.

We apply the same procedure to the pipeline

model. Results are presented in Table 2. The

computation time of the matching algorithm is 18

seconds. The success rate depends on the complexity

of the scan. For example, the first scan tested show a

rate success of 90.5% and the second, more complex,

70%.

For the Go-ICP method, since this approach is

deterministic, one calculation is enough to get value

for the four performances criteria previously

described. However, stochasticity is added due to our

scan preprocessing, so we evaluate the results on a set

of 20 calculations. The

Table 3 shows the results with

this approach. Go-ICP is supposed to give the best

matching without a priori, but for the two systems we

tested, only one scan matching gives the expected

results. The other tests were not retained since they

converge to wrong solution. Due to its deterministic

aspects, the only possibility to change results should

be to change MSE threshold or initial orientation of

the scans. However, modifying the MSE threshold

does not improve results and requires more time to

converge.

Our approach using MCMH shows interesting

results. We have a ratio of success superior to 80%

for most of the cases. However, difficult scan like

scan 2 of the pipeline has a success rate of 70%, due

to the quasi-symmetry of the object. Such

phenomenon can be explained by the initialization

A 3D Matching Method to Compare a Scan to Its Reference using 3D Registration and Monte Carlo Metropolis Hastings Optimization for

Industrial Inspection Applications

523

before the matching. In term of phase space, the scan

is positioned close to a saddle point. Due to this, in

term of probability, we favor in the first iteration one

side of the pipeline more than the other. In addition,

the barrier between the two regions of the pipeline

should be high. This implies that even with our

metropolis criteria, passing the barrier is difficult.

However, we treat a realistic industrial object, and we

can assure correct matching if we keep only the best

matching over the 200 tests. We already have leads to

get performance improvement like taking the initial

position and orientation of the scan into account

thanks to IMU information. For the lego, we see it is

a difficult case for matching. This is mainly due to the

size and the point density of the scan. It implies less

constrain compared to the pipeline and so, more local

minima.

In term of computational time, our method is

efficient. The complete matching algorithm took

between 10 and 20 seconds for all the tested case. Our

method is faster than Go-ICP. Half of the

computational time is due to the point cloud pre-

processing. For difficult cases, Go-ICP

computational time can explode (~ 1 hour).

Finally, concerning the fitness and the RMSE,

these two values are good performance criteria that

can be used to interpret the matching quality. For

most of the cases, a fitness value over 80% and with

a RMSE below the millimeter means we have a good

matching. In the case where Go-ICP shows good

results, the method has a lower RMSE value and

wider fitness value. Nevertheless, the adaptability

showed by our approach is interesting for inspection

application where objects are complex.

5 CONCLUSIONS

In this work, we proposed a MCMH approach

combined with ICP for the point cloud matching

problem. We showed encouraging results compared

to a state-of-the-art method called Go-ICP. Our

method includes a 3D reconstruction step using ICP

color generating 3D models to compare scans. The

method is efficient on small objects like the lego, and

seems adapted to realistic objects for inspection

problem like the pipeline system.

Our approach still suffers from some limitations,

especially in difficult cases where there is some

symmetry in the object of interest. The simplified

triangular mesh descriptor we used could be too

restrictive for such case, causing some trouble for

matching. Some improvement can be done by

changing the initial position of the scan for the

matching. Parallelization of MCMH can also

conserve efficient results while reducing the actual

computation time of less than 20 seconds, which can

let us consider a quasi-real-time application.

In the future, we plan to use this approach to

perform geometrical comparison between a scan and

its reference model, to highlight the presence of

defects using similarity criterion. Highlighted region

of interest will reveal the presence of defects like

missing pieces, extra pieces or misoriented pieces.

This method could then be used for detection of

foreign objects in aeronautical assembly lines or

missing pieces for maintenance for example. Further

tests on realistic industrial environment, with

different object sizes and complexity, are also

planned to validate the method usability. A last

improvement for this method could be to simulate a

video processing approach through the fusion of

several partial scans to inspect before comparing with

the 3D model. It could improve robustness by adding

more information and increasing artificially the

sensor precision.

REFERENCES

Abdallah, H. B., Orteu, J.-J., Jovancevic, I., & Dolives, B.

(2020). Three-dimensional point cloud analysis for

automatic inspection of complex aeronautical

mechanical assemblies. Journal of Electronic Imaging,

29(4), 041012.

Arun, K. S., Huang, T. S., & Blostein, S. D. (1987). Least-

Squares Fitting of Two 3-D Point Sets. IEEE

Transactions on Pattern Analysis and Machine

Intelligence, PAMI-9(5), 698‑700.

Ben Abdallah, H., Jovančević, I., Orteu, J.-J., & Brèthes, L.

(2019). Automatic Inspection of Aeronautical

Mechanical Assemblies by Matching the 3D CAD

Model and Real 2D Images. Journal of Imaging, 5(10),

81.

Besl, P. J., & McKay, N. D. (1992). Method for registration

of 3-D shapes (P. S. Schenker, Éd.; p. 586‑606).

Bethencourt, A., & Jaulin, L. (2013). 3D Reconstruction

Using Interval Methods on the Kinect Device Coupled

with an IMU. International Journal of Advanced

Robotic Systems, 10(2), 93.

Bhadrakom, B. (2016). As-built 3D modeling based on

structure from motion for deformation assessment of

historical buildings. International Journal of Geomate.

Chen, W., Li, Y., & Li, C. (2020). A Visual Detection

Method for Foreign Objects in Power Lines Based on

Mask R-CNN. International Journal of Ambient

Computing and Intelligence (IJACI), 11(1), 34‑47.

Chen, Y., & Medioni, G. (1992). Object modelling by

registration of multiple range images. Image and Vision

Computing, 10(3), 145‑155.

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

524

Ester, M., Kriegel, H.-P., & Xu, X. (1996). A Density-

Based Algorithm for Discovering Clusters in Large

Spatial Databases with Noise. Kdd, 96(34), 226‑231.

Hastings, W. K. (1970). Monte Carlo sampling methods

using Markov chains and their applications.

Biometrika, 57(1), 97‑109.

Kazhdan, M., Bolitho, M., & Hoppe, H. (2006). Poisson

surface reconstruction. Proceedings of the fourth

Eurographics symposium on Geometry processing,

61‑70.

Kopernicky, M., Kovacovský, M. T., & Gargalık, R.

(2013). 3D Scene Reconstruction Using Partial

RGB+Depth Maps. 6.

Kuhn, H. W. (1955). The Hungarian method for the

assignment problem. Naval Research Logistics

Quarterly, 2(1‑2), 83‑97.

Lamine Tazir, M., Gokhool, T., Checchin, P., Malaterre, L.,

& Trassoudaine, L. (2018). CICP : Cluster Iterative

Closest Point for sparse–dense point cloud registration.

Robotics and Autonomous Systems, 108, 66‑86.

Land, A. H., & Doig, A. G. (2010). An Automatic Method

for Solving Discrete Programming Problems. In M.

Jünger, T. M. Liebling, D. Naddef, G. L. Nemhauser,

W. R. Pulleyblank, G. Reinelt, G. Rinaldi, & L. A.

Wolsey (Éds.), 50 Years of Integer Programming 1958-

2008 : From the Early Years to the State-of-the-Art (p.

105‑132). Springer.

Linh, T. N., & Hiroshi, H. (2015). Global Iterative Closet

Point Using Nested Annealing for Initialization.

Procedia Computer Science, 60, 381‑390.

Nguyen, T.-N., Huynh, H.-H., & Meunier, J. (2018). 3D

Reconstruction With Time-of-Flight Depth Camera and

Multiple Mirrors. IEEE Access, 6, 38106‑38114.

Park, J., Zhou, Q.-Y., & Koltun, V. (2017). Colored Point

Cloud Registration Revisited. 2017 IEEE International

Conference on Computer Vision (ICCV), 143‑152.

Pomerleau, F., Colas, F., & Siegwart, R. (2015). A Review

of Point Cloud Registration Algorithms for Mobile

Robotics. Foundations and Trends in Robotics, 4(1),

1‑104.

Rusu, R. B., Blodow, N., & Beetz, M. (2009). Fast Point

Feature Histograms (FPFH) for 3D registration. 2009

IEEE International Conference on Robotics and

Automation, 3212‑3217.

Saavedra, D., Banerjee, S., & Mery, D. (2021). Detection

of threat objects in baggage inspection with X-ray

images using deep learning. Neural Computing and

Applications, 33(13), 7803‑7819.

Sungjoon Choi, Zhou, Q.-Y., & Koltun, V. (2015). Robust

reconstruction of indoor scenes. 2015 IEEE Conference

on Computer Vision and Pattern Recognition (CVPR),

5556‑5565.

Tsin, Y., & Kanade, T. (2004). A Correlation-Based

Approach to Robust Point Set Registration. In T. Pajdla

& J. Matas (Éds.), Computer Vision—ECCV 2004 (Vol.

3023, p. 558‑569). Springer Berlin Heidelberg.

van Laarhoven, P. J. M., & Aarts, E. H. L. (1987).

Simulated annealing. In P. J. M. van Laarhoven & E. H.

L. Aarts (Éds.), Simulated Annealing : Theory and

Applications (p. 7‑15). Springer Netherlands.

Wang, F., & Zhao, Z. (2017). A survey of iterative closest

point algorithm. 2017 Chinese Automation Congress

(CAC), 4395‑4399.

Yang, J., Li, H., Campbell, D., & Jia, Y. (2016). Go-ICP :

A Globally Optimal Solution to 3D ICP Point-Set

Registration. IEEE Transactions on Pattern Analysis

and Machine Intelligence, 38(11), 2241‑2254.

Zhang, H., Wei, Q., & Jiang, Z. (2017). 3D Reconstruction

of Space Objects from Multi-Views by a Visible

Sensor. Sensors, 17(7), 1689.

Zhou, Q.-Y., Park, J., & Koltun, V. (2016). Fast Global

Registration. In B. Leibe, J. Matas, N. Sebe, & M.

Welling (Éds.), Computer Vision – ECCV 2016 (p.

766‑782). Springer International Publishing.

A 3D Matching Method to Compare a Scan to Its Reference using 3D Registration and Monte Carlo Metropolis Hastings Optimization for

Industrial Inspection Applications

525