Augmenting Reinforcement Learning to Enhance Cooperation in the

Iterated Prisoner’s Dilemma

Grace Feehan

and Shaheen Fatima

Loughborough University, Epinal Way, Loughborough, U.K.

Keywords:

Iterated Prisoner’s Dilemma, Interaction Structure, Multiagent Reinforcement Learning, Mood, Cooperation

Index.

Abstract:

Reinforcement learning algorithms applied to social dilemmas sometimes struggle with converging to mutual

cooperation against like-minded partners, particularly when utilising greedy behavioural selection methods.

Recent research has demonstrated how affective cognitive mechanisms, such as mood and emotion, might

facilitate increased rates of mutual cooperation when integrated with these algorithms. This research has,

thus far, primarily utilised mobile multi-agent frameworks to demonstrate this relationship - where they have

also identiﬁed interaction structure as a key determinant of the emergence of cooperation. Here, we use a

deterministic, static interaction structure to provide deeper insight into how a particular moody reinforcement

learner might encourage the evolution of cooperation in the Iterated Prisoner’s Dilemma. In a novel grid

environment, we both replicated original test parameters and then varied the distribution of agents and the

payoff matrix. We found that behavioural trends from past research were present (with suppressed magnitude),

and that the proportion of mutual cooperations was heightened when both the inﬂuence of mood and the

cooperation index of the payoff matrix chosen increased. Changing the proportion of moody agents in the

environment only increased mutual cooperations by virtue of introducing cooperative agents to each other.

1 INTRODUCTION

Models of human social behaviours, and the socio-

cognitive mechanisms that underlie them, have be-

come a fast focus of researchers in the ﬁeld of com-

puter science in recent years. In particular, they are

of interest both for the improvement of existing algo-

rithms (such as for the focusing of attention in visual

search; (Belkaid et al., 2017) but also in investigating

individual and group behaviours (social network sim-

ulacra being one example). One testing ground for the

development of such artiﬁcial mechanisms are social

dilemmas, as they are relatively well understood, sim-

ple and easy to constrain or build on. In these we ﬁnd

strong methods of studying interpersonal behaviour.

This work builds on previous research on how typ-

ically reward-focused reinforcement learning (RL) al-

gorithms, utilised by a network of agents engaged

in the Iterated Prisoner’s Dilemma (IPD), can be al-

tered using computational socio-cognitive models to

encourage increased cooperation. One of the newer

of these in recent literature has been a model of mood,

with research suggesting that a key determinant of

https://orcid.org/0000-0002-8629-1800

https://orcid.org/0000-0002-6068-2942

the emergence of cooperation within moody dilemma

playing is the interaction environment (or network

structure; Collenette et.al., 2017a). The model has

so far been tested primarily in mobile networks of

moving agents; we instead seek to more clearly es-

tablish how a static and more standardised structure

of interaction affects the moody model’s inﬂuence

on cooperation. The main objective of this paper

is to ﬁnd methods of increasing cooperation in RL

agents playing the IPD. To do this, we evaluate the

behaviour of moody learning agents in a static, reg-

ular, multiagent environment whilst playing against

more traditional RL agents - data on which has not

been explicitly presented in past research. We ﬁrst

summarise the published research on a human-based

model of mood and then examine how behaviour ob-

served in the novel environment compares. We hy-

pothesised that results may follow the data in Col-

lenette et.al. (2017a), and demonstrate that increased

interaction rates dampen cooperation gains, but still

show an increase in cooperation over unaltered RL.

We also investigate two additional factors for in-

creasing cooperation rates; the proportion of oppo-

nents in the environment and a measure of how co-

operative the reward schema is. Results of our sim-

ulations demonstrated that cooperation can indeed

146

Feehan, G. and Fatima, S.

Augmenting Reinforcement Learning to Enhance Cooperation in the Iterated Prisoner’s Dilemma.

DOI: 10.5220/0010787500003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 3, pages 146-157

ISBN: 978-989-758-547-0; ISSN: 2184-433X

be increased by the latter of these factors by up to

15%, whereas the former does not. Our experimen-

tal data are discussed in the context of structures of

interaction, the variables the model utilises, and pos-

sible changes the model’s implementation may need

in this environmental setting. The primary contri-

butions of this research are that we provide direct

evaluation of the moody strategy in static networks

(previously undetailed), test the moody model against

varying quantities of traditional RL opponents to eval-

uate behavioural transference, and test varying payoff

matrices which facilitate comparisons with external

human participant data. The Python code repository

for this paper is available on request.

Beginning with Section 2, we outline the compu-

tational problem space covered by the IPD, and the

justiﬁcation for using it in uncovering social agent be-

haviour. We also describe the RL algorithm SARSA,

and introduce the notion of interaction structures and

how this relates to the moody model to come. Then, in

Section 3 we describe this model of mood (mSARSA)

as it is primarily outlined in Collenette et.al. (2017b),

with deeper presentation of its relevant past perfor-

mance. We also provide the motivation, based on this

literature, for our own experiments. Section 4 pro-

vides the detail of the novel testing environment, pa-

rameters and hypotheses. Finally, Section 5 gives the

data from these experiments, and Section 6 gives the

subsequent analysis, comparisons and conclusions.

Thereafter we propose suggestions for the improve-

ment of the model.

2 BACKGROUND

2.1 Prisoner’s Dilemma

The Prisoner’s Dilemma is a social dilemma in which

players have two behavioural choices available to

them, and typically must choose without direct com-

munication. Cooperate with the partner, and poten-

tially be exploited, or defect (play selﬁshly) against

the partner, which (if mutual) will lead to a lower

round payout than with mutual cooperation. The

Nash Equilibrium of the dilemma, due to the payoff

structure (Table 1), is to defect - but if both players

opt to do this, their score is diminished in compari-

son with what could be achieved. In addition, when

the game is played over many rounds (as in the IPD),

several issues arise. The strong incentive to defect

leads networks to obtain substantially lower payoffs

as a whole than sustained mutual cooperations would

provide. There is also a range of problems involving

how to encourage partners to both trust and continue

Table 1: Payoff matrix for the two-player Prisoner’s

Dilemma game, as used in Collenette et.al. (2017b) and

throughout classic literature. The cooperation index of this

matrix (see Section 3.3) is 0.4.

Partner B (Right)

Cooperate Defect

Cooperate 3,3 0,5

Partner A

(Left)

Defect 5,0 1,1

playing the game with you when you repeatedly de-

fect (Wilson and Wu, 2017). This lends itself to the

motivation for ﬁnding mechanisms that encourage the

evolution of cooperation in artiﬁcial agents.

The payoff values presented in Table 1 have been

used extensively throughout IPD research under dif-

ferent names; Temptation (or T) for a DC outcome,

Reward (or R) for a CC outcome, Punishment (or

P) for a DD outcome and Sucker (or S) for a CD

outcome. In our work, we also refer to these as the

Exploiter, Mutual C, Mutual D and Exploited payoffs

respectively as they provide simpler intuition.

Overall, we ﬁnd a suitable research environment

given two reasons. Firstly, there is well-established

precedent that human networks playing the game do

not defect in the same manner as many game-playing

strategies (Barreda-Tarrazona et al., 2017), and are

more heterogeneous in their behaviours (Fudenberg

et al., 2012). Secondly, there is large potential for

artiﬁcial players to improve from payoff-incentivised

defection with the introductions of novel additions

(as they can already display greedy behaviour; Col-

lenette et.al., 2017b). RL algorithms such as SARSA

have been used to learn behavioural policies for the

IPD (Collenette et.al., 2017b; Yu et.al., 2015; (Gao,

2012), and in general are of interest to computational

neuroscience regarding human behaviour (Shteingart

and Loewenstein, 2014); making them a suitable

methodology for investigating humanlike cooperative

behaviour. In the following section, we detail SARSA

as it relates to social agent research, and then in Sec-

tion 4 we outline how it has been extended further

with a moody model, noting additional factors that

may inﬂuence cooperation behaviour.

2.2 Interaction Structure

One of the primary sources demonstrating the effect a

model of mood has on the emergence of cooperation

within social dilemmas is Collenette et.al. (2018),

a study which concludes that the structure of net-

work connections and interactions inﬂuences how be-

haviours emerge in said network. Here we will out-

line some of the terminology involved and how each

relates to the research at hand. Interaction structures

can be deﬁned as the way agents interact with each

other; in the context of the IPD, interactions occur

Augmenting Reinforcement Learning to Enhance Cooperation in the Iterated Prisoner’s Dilemma

147

between two players when they play a round of the

dilemma game. In our experiments and in much of

the research summarised in Section 3, this is extended

to involve multiple pairs of players in a group, or a

network. Networks can be given in the form of a

graph, where agents in these networks are represented

as nodes and interaction relationships between agents

are represented as edges between nodes. There are

two main forms of network related to the current re-

search (mobile and static), and there are many struc-

tural variations on the graph which represents how

well connected agents are.

In the mobile environments used in the majority of

the model literature, agents move freely around are-

nas with obstacles (dependent on the network type),

intending to replicate the dynamic and uneven inter-

actions of more natural societal networks. These en-

vironments have equivalent static networks with dif-

fering topographical structures; in Collenette et.al.

(2018), for example, the authors include small world

(characterised by high clustering), fully connected

(where all nodes are connected to all other nodes),

random (as the title suggests) and regular networks

(where each node has the same number of edges). The

equivalent in our own experiments would be a static

regular network. As the literature discussed here de-

scribes the effect of increasing mobility, and there

is some disagreement amongst the papers on the ef-

fect of network structure, evaluating both SARSA and

mSARSA in a static regular network may add more

clarity to structural effects. In the learning algorithm

SARSA, agents update world knowledge through hav-

ing game interactions. This makes the nature of those

interactions, how many interactions agents have in the

course of a learning episode, and what information

those interactions provide, critical to this learning.

2.3 SARSA

State-action-reward-state-action (SARSA) is an on-

policy RL algorithm - one that is used throughout

the literature pertaining to the mood model discussed

here. States, in the case of default SARSA as it is used

in this paper, are the histories of interactions with each

partner - the length of which depending on the mem-

ory size afforded to the agent. In our implementation,

up to seven items can be remembered or for larger

items (like the memory of what both players did), 3 or

4 ‘chunks’. Actions are the behaviours available (i.e.

cooperate or defect), and rewards are given by the

payoff matrix used, depending on the outcome of each

individual interaction. Both the default SARSA and

the mSARSA variant use the ε-greedy behaviour selec-

tion mechanism. Algorithmic details and pseudocode

for SARSA can be found in (Sutton and Barto, 2018).

The equation for updating Q (the learned value) for

each state-action combination is given below as it is

pertinent for comparison with the mood-augmented

version presented in Section 3.1.

Let s represent the state, t denote the current

timestep of a learning epoch, a the action taken in that

state, where α is the learning rate (typically 0.1), γ is

the discount factor (typically 0.95), and r is the reward

received:

Q(s

) = Q(s

α[r

t+1

+ γQ(s

t+1

) − Q(s

)]

(1)

Originally selected due to its on-policy nature

conforming with the on-policy characterisation of

mood (Collenette et.al., 2017b), it has the added ben-

eﬁts of being well-established, easy to implement and

computationally light when the state space is smaller

(Collenette et.al.’s methodology yields approximately

216 states, for instance). Application of reinforce-

ment learners is of interest to those researching ar-

tiﬁcial social and cognitive mechanisms in humans;

Shteingart et.al. (2014) discusses the beneﬁts of

model-free temporal difference learners as practical

methodologies for examining and recreating human-

like behaviour, but also the potential lack of intricacy

and depth that model-free algorithms have when at-

tempting to recreate behaviour altered by chemical

neuromodulation (perhaps particularly of relevance to

mood and emotion modelling).

Still, Q-learners are being pursued as viable meth-

ods to model different variations of human processing

(Lin et al., 2019)) and continue to be of use to interdis-

ciplinary research. Bearing these limitations in mind,

we can consider how augmentations to SARSA may

also begin to pursue more complex humaniform mod-

elling. One particular ﬁeld of interest in regards to this

is mood, where there exists a large body of literature

on how mood inﬂuences dilemma reasoning (Palfai

and Salovey, 1993) and cooperative behaviour (Proto

et al., 2017); (Hertel et al., 2000). We will cover one

particular computational model of mood that has been

integrated into the SARSA learning algorithm.

3 RELATED LITERATURE

3.1 Mood Model and Integration with

SARSA

Mood is reliably, if reductively, deﬁned as a task- and

partner-invariant affect spectrum which inﬂuences

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

148

other cognitive processes, dissociated more from cur-

rent events with longer-term effects (Collenette et.al.,

2017b). It is a closely interdependent subsystem with

emotions

and biases many aspects of human percep-

tion.

The moody mSARSA model under analysis here is

primarily outlined in Collenette et.al. (2017b), and

employs a central mechanism by which mood is a

real number between 1 and 100. Higher mood values

are coded as more risky and cooperative, with lower

moods as more rational and defective; in Collenette

et.al., extreme moods (above 90 and below 10) are

implied as characterising mood disorders (mania and

depression, respectively). Mood updates are made

solely around how an agent perceives its current pay-

off (which is adjusted using the Homo Egualis model,

comparing the reward with the opponent’s reward;

(Fehr and Schmidt, 1999), relative to the average pay-

off previously attained. If an agent perceives itself to

be doing poorly in comparison with its past, its mood

will decrease. In Collenette et.al. (2018), this process

is slightly adjusted to facilitate higher moods decreas-

ing more readily (in line with the ease of ﬂuctuation

at lower moods). The mood-altered equation for up-

dating Q for each state-action pair is provided below

(adapted from Collenette et.al., 2017b).

Q(s

) = Q(s

) + α[r

t+1

+ γΨ − Q(s

)] (2)

The rule for the estimation of future rewards (Ψ)

is encapsulated in Equations 3 through 5 (reproduced

from Collenette et.al., 2017b), where m

is the mood

of a given agent i at timestep t (a R between 0 and

100). Mem

is the vector of the set of rewards previ-

ously obtained by that agent when using action a, and

|Mem

| is at maximum 20. Mem

(0) returns the most

recent reward.

= (100 − m

)/100 (3)

= ceil(|Mem

(n)|/α

) (4)

Ψ = (n

∑

Mem

(n))/β

(5)

Mood constrains the depth (denoted with n above)

at which memory is consulted for the average past re-

ward, but also controls the value ε in ε-greedy explo-

ration. When an agent’s mood is below 30 and they

cooperate, or above 70 and they defect, ε increases to

0.9 for that turn and a move is re-selected. Mood is

updated and maintained by the series of Equations 6

Emotions, which are more temporally distinct, varied,

and can be task-relevant (Zulﬁqar and Islam, 2017) also

have an inﬂuence on decision-making; despite their rele-

vance, however, emotions are extraneous to the scope of the

current paper.

through 8 (reproduced from Collenette et.al., 2017b).

Let t denote the current timestep of a learning epoch,

return the payoff of agent i in that timestep, µ

de-

note their average payoff over the elements in Mem

and m

denote their mood. Let j denote agent i’s op-

ponent, and let α = β (as in Collenette et.al., 2017b):

= (100 − m

−1

)/100 (6)

Ω

= µ

− α

· max(µ

− µ

,0)−

· max(µ

− µ

,0)

(7)

= m

t −1

+ (p

− µ

t −1

) + Ω

t −1

(8)

Algorithm 1: mSARSA Pseudocode (Adapted

from Collenette et.al., 2017b).

initialise all Q(states, actions) arbitrarily;

for each episode do

initialise all states;

Choose an action using the policy derived

from Q (ε-Greedy);

for each episode step do

Take the chosen action, observe the

reward and the new state reached;

if mood ≥ 70 and action = ‘D’ OR mood

≤ 30 and action = ‘C’ then

re-select an action under a higher ε

value (0.9)

Choose next action using the policy

derived from Q (ε-Greedy);

Estimate future reward using Equations 3

through 5;

Update Q(s, a) using Equation 2;

Update mood using Equations 6 to 8 ;

Until terminal step;

As Algorithm 1 demonstrates, moody alterations

to the standard SARSA framework are mostly additive,

with the exception of one variable replacement in the

Q-update equation. At each stage of learning mood

value is considered, creating an all-permeating inte-

gration to decision-making. The purpose of the sys-

tem design is a thoughtful combination of a few moti-

vations: it models evidence-based mood in a learner,

where previous focus had been primarily on models of

emotion; it intends to expand understanding on how

human-like mood (and emotion, where applicable) in-

forms decisions in social dilemmas; and it appears to

facilitate increased rates of cooperation in certain sit-

uations, as we will evidence from past research.

One ﬁnal important aspect of the algorithm to note

is that Equation 8 provides the ﬁrst iteration of the

mood update function (MU1) that is utilised in Col-

lenette et.al. (2017b), which this paper will make a

direct comparison with in terms of data. There is a

second iteration of this equation (MU2, see Equation

Augmenting Reinforcement Learning to Enhance Cooperation in the Iterated Prisoner’s Dilemma

149

9), which was developed and deployed in Collenette

et.al. (2018) to facilitate faster mood changes when

poor outcomes are received at higher mood levels.

= m

t −1

+ (p

t −1

− Ω

t −1

) (9)

It is important to note that our implementation (see

Section 4) uses the former of these equations (Equa-

tion 8) in its calculations, for two main reasons. First,

it means we utilise the exact structure of the version

used in Collenette et.al., (2017b), which is the only

source of precise cooperation data for the algorithm

speciﬁcally (and not a mixed population as a whole,

as presented in Collenette et.al., 2018). Secondly, ini-

tial testing with MU2 indicated that it took a lot longer

for the algorithm to run to conversion - if at all, as

it potentially exhibited cyclic behavioural loops. It

did, however, manipulate the mood value much more

effectively than MU1 appeared to do, with the be-

haviour of both possibly exaggerated by the nature of

our environment used. Though full details on our ob-

servations cannot be evaluated here due to constraints,

this may be examined in further work - the limitations

and critique of MU1 where it is relevant to the current

experiments are detailed clearly in Section 6.

3.2 Moody versus Non-Moody

Firstly, it is quite apparent that the addition of the

mood model in previous research scenarios is a posi-

tive one; networks with moody agents achieve greater

proportions of mutual cooperation at behavioural con-

vergence than their non-moody (or even emotional)

counterparts. Moody agents do not necessarily al-

ways attain the greatest utility

but the mechanism

does seem to reduce the self-interest of otherwise

greedy SARSA agents. These agents are typically ren-

dered using Stage (Vaughan, 2008) and perform ran-

dom walks, usually in an environment with central ob-

stacles. On encountering an opponent, they perform

a round of the Prisoner’s Dilemma (or other game, as

relevant) and then move on. It is worth bearing in

mind this setup throughout the following analysis, as

the authors repeatedly comment on how reduced rates

of uncertainty in repeated interaction introduces difﬁ-

culty in sustaining cooperation and removes the threat

of punishment for defecting.

Initial work combining the mood system with the

Ortony, Clore and Collins (OCC) Model of Emo-

tions (Ortony et al., 1988), (Clore and Ortony, 2013)

demonstrated a high rate of effectiveness in the IPD.

In Collenette et.al. (2018), Tit-for-Tat was identiﬁed as

the most successful strategy despite differing environments

and network structures.

In Collenette et.al. (2017b), a three-emotion frame-

work saw an increase in the peak proportion of mutu-

ally cooperative outcomes from approximately 35%

to 100% in some scenarios when the mood model

was added. With the scenarios representing differ-

ent proportions of starting moods (between low, neu-

tral and high) in the environment, it is clear that in

initial testing high mood networks happily cooper-

ate with one another. As discussed later in the pa-

per, however, these are not resilient outcomes, and are

vulnerable to exploitative crashes against pure defec-

tors (versus low mood groups). In these resilience

tests, the percentage of mutual cooperation rose at

best by approximately 16%, which is still a marked

improvement over the 5% initial rate. This paper also

demonstrates the positive visual correlation between

mood value and percentage of mutually cooperative

outcomes, with both rising steadily as more interac-

tions occur.

In a highly mobile environment, the model facil-

itated an increase in the proportion of mutually co-

operative outcomes by at least 40% over the SARSA

equivalent; both when opponents were recognisable

and when their mood labels were directly observable

(Collenette et.al., 2017b). This increase was even

greater when agents possessed no information about

their opponents, with regular SARSA agents attain-

ing only 1.7% mutually cooperative outcomes and

their moody counterparts attaining (at greatest) 78%.

There were equivalent decreases in the proportion

of mutually defective outcomes in these conditions

where mSARSA performed well.

In more explorative network research, the model

was included amongst a very wide variety of other

strategies in a broader selection of topologies. In one

paper, though there is no per-strategy breakdown pro-

vided in the data regarding cooperation or utility gath-

ered, mutual cooperation was maintained at approx-

imately 49% in a mixed strategy environment (Col-

lenette et al., 2018b). Importantly, this paper draws

several key conclusions about the effect network con-

nectivity (and the equivalent physical environments)

has on both cooperation and dilemma playing. Net-

works with random connectivity facilitate the greatest

proportion of mutual cooperation and average pay-

offs to agents, with the mobile environment equiva-

lent providing the same in terms of cooperation, but

performing only approximately as well as the empty

and small world environments. Though the effect on

the mood model speciﬁcally is unknown due to lack

of strategy-by-strategy breakdown, it is important to

note that our environment is most comparable with

the regular static network in Collenette et.al. (2018)

(the mobile equivalent of which is utilised in the ma-

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

150

jority of the tested environments across the papers

discussed). In the terms of connectedness, the reg-

ular static network performed second worst out of the

four constructions (demonstrated lower cooperation

and lower average payoff attained) but attained higher

scores on both metrics in comparison to its mobile

equivalent.

One ﬁnal paper (Collenette et al., 2017a) com-

bines two of these methodologies - the emotional-

moody non-learning model and a variety of differ-

ent network types, similar to Collenette et.al. (2018).

Again, mood shows a strong positive inﬂuence on co-

operation levels over just the OCC framework alone.

Emotional agent networks sustained cooperation al-

most regardless of length of interaction, with starting

level of cooperation having a much larger effect than

the distribution of admiration thresholds (one of the

three emotions used) on the level of cooperation in

the system. Most of the results where initial cooper-

ation was set to 50% resulted in mutual cooperation

proportions within the range of 25% to 40%. On the

other hand, the inclusion of mood increases this range

to between approximately 82% to 100%. Resilience

results are similar to those seen in Collenette et.al.

(2017b), demonstrating low moods as more resistant

to pure defectors in the long run.

3.3 Cooperation Index

Throughout the moody algorithm literature, varia-

tions on the traditional payoff matrix (Table 1) have

not been tested. This is an important factor for an

algorithm modelling humanlike traits, as there exists

work that demonstrates how relational differences be-

tween the payoffs inﬂuences human cooperation rates

in the IPD. In one paper (Wrightsman et al., 1972), the

authors summarise and discuss initial research into a

cooperation index (henceforth referred to as K, as in

Colman et.al., 2018), or formula for characterising the

intensity of the conﬂict the structure of the payoff ma-

trix creates. This text is rather old, but summarises

past work regarding human interactivity with K well;

namely, cooperative behaviour appears to increase as

K increases, with less clear-cut conclusions made re-

garding its inﬂuence on defections (something the au-

thors suggest is primarily inﬂuenced by the T payoff

alone). The equation for K, where each input has been

deﬁned previously in Section 2.1, is given in Equation

10.

K = (R − P)/(T − S) (10)

Other research continues to use K to evaluate pay-

off matrices with humans and compare it to other

models. K has been shown to be a strong cooperation

predictor when values of K are distributed from 0.1

to 0.9 (Hristova and Grinberg, 2005). These authors

again found a consistent increase of cooperation as K

increased, and an inﬂuence of contextual K (that is,

playing other IPD games with high K values around

a speciﬁed target game with a differing K) on cooper-

ation levels. The authors also create a computational

model that utilises subjective expected utility theory,

combined with weightings for the importance of each

outcome type (calculated via average of past payoffs)

to replicate the trends shown in the human data, with

success. One paper reiterates the human conclusions

from this previous work in one of the most recent ref-

erences to K, providing solid basis of connection be-

tween K and cooperation (Colman et al., 2018).

3.4 Summary and Literature Gap

The evidence discussed thus far indicates that the

model has a strong propensity for inducing mutual co-

operation between homogeneous agents, with indirect

data suggesting it possibly assists in the formation of

a stable level of cooperation in heterogeneous strate-

gical groups. It has been ﬂexibly combined with RL

and frameworks of emotional behaviour alike, and in

both cases has allowed for the increase in coopera-

tion. Highly connected networks reduce the effective-

ness of the model as opposed to randomly connected

networks, and with mobility added on top of this, co-

operation is even further diminished in mixed groups.

There is also evidence to suggest that in homogeneous

groups, the inﬂuence of network orientation is much

less important than variables such as starting mood

(though this is in non-learning populations).

Overall, there is a lack of speciﬁc, isolated data

on the performance of the moody learner in a static,

homogeneous environment with regular connectivity,

and no data whatsoever on how moody agents be-

have in environments with varying distributions of

opponents or different payoff matrices. The experi-

mentation in Section 4 seeks to partially rectify this.

For these reasons, we will test mSARSA against itself,

replicating the parameters thoroughly tested in Col-

lenette et.al., (2017b) but under a more consistent in-

teraction structure. We will also substantially evaluate

the two contributing factors outlined (opponent den-

sity and K value) in order to provide a thorough exam-

ination of behavioural outcomes. If we can establish

a baseline of whether mSARSA behaves similarly and

reliably in our environment in comparison with mo-

bile counterparts, we then not only lend weight to the

model’s robustness, but also set precedent for further

experimentation.

Augmenting Reinforcement Learning to Enhance Cooperation in the Iterated Prisoner’s Dilemma

151

4 EXPERIMENTAL EVALUATION

4.1 Design

The environment used for all three of the following

experiments is a regular 2D grid network of 25 agents

who do not change positions between rounds. Grid

positions begin from the bottom left (pos. 1) and in-

crease vertically northwards, ﬁlling out each column

before moving to the next (i.e. top left is pos. 5, top

right is pos. 25). In a single round of the IPD, agents

interact with as many available partners in the four

von Neumann neighbourhood positions, north, south,

east and west (clockwise, in this order). In Interac-

tion Structure experiments, all agents in the grid are

of the same strategy (mSARSA or SARSA). In Strat-

egy Proportion, most agents in the grid are initially

SARSA, with the proportion of agents increased grad-

ually as documented in Table 2. In Payoff Schema,

there are 12 mSARSA agents in the environment to 13

SARSA agents, using the F agent arrangement from

the previous experiment (Table 2).

This structure was designed in MESA (Team,

2021), recreating grid environments from other spa-

tial social dilemmas (Yu et al., 2015). Data pre-

sented are the results of only the inner square grid

of agents (excluding all border players) - this pro-

vides more standardised analysis as these agents will

have the maximum of four partners. Each experiment

consists of 5 learning episodes (experimental periods

in which internal variables are maintained), each con-

sisting of 10,000 time steps. This value was chosen

to compromise between efﬁcient runtime and allow-

ing for any late-phase change of behaviour. Data pre-

sented averages over these learning episodes.

4.2 Parameters

In the base experiment, mSARSA will be tested (as in

Collenette et.al., 2017b) using three levels of state in-

formation - the opponent’s last move, the opponent’s

ID, and the opponent’s mood label - each cumulative

with the last, under the names Stateless, Agentstate

and Moodstate. The parameter mA is intended to re-

ﬂect the ‘extent to which mood inﬂuences behaviour’

(Collenette et.al., 2017b); this takes the form of alter-

ing moody behavioural thresholds chosen each round

and how epsilon is changed. We will test this pa-

rameter with values 0 through 0.8, in increments of

0.4. In the Strategy Proportion and Payoff Schema

experiments, mSARSA utilises just the Moodstate and

mA=0.8 parameters.

In the basic test of Interaction Structure, agents

solely play against opponents of their own strategy

in the grid. In the two experiments following this,

mSARSA agents play the IPD with SARSA agents. The

positions and proportions of agent types in the envi-

ronment for Strategy Proportion tests are outlined in

Table 2, with the Payoff Schema experiments utilising

the Condition F structure from this same table.

Table 2: Parameters used for the Strategy Proportion exper-

iment. The ﬁrst row notes the grid locations of mSARSA

agents in each condition, and the second row displays what

percentage of the whole population the mSARSA agents oc-

cupy.

Condition A B C D E F G H

Grid

Locations

1 9

17,

21,

10,

16,

22,

11,

15,

Network

Proportion (%)

4 4 16 16 32 48 64 80

The independent variable changed in Payoff

Schema is the payoff matrix used, varied both in ac-

tual value size and in size of cooperation index (K)

- a measure used in both Wrightsman et.al. (1972)

and Colman et.al. (2018) (see Table 3). These can be

broadly categorised into three sections; small-value

payoffs (between 0 and 1) with small, medium and

large values of K, the traditional IPD payoff scheme

(Condition 4) and then large-value payoffs (between

0 and 100), again with small, medium and large val-

ues of K. This should provide some insight not only

into inﬂuence of increasing K, but also the actual

value of payoffs themselves. We also investigate the

inﬂuence of increasing K when the T and R payoffs

remain the same - the payoffs used in this portion

of the experiment can be found in Table 4. SARSA

utilises α = 0.1, γ = 0.95 and a linear decay mech-

anism for ε that starts at 0.99 and decays linearly to

0.1 mid-way through each episode. It also uses a state

information proﬁle closest to Stateless with a single-

step memory.

Table 3: Parameters used for the ﬁrst section of the Payoff

Schema experiment. Each column provides the payoff ma-

trix utilitsed by each numbered condition. K is the value of

the Cooperation Index for that payoff matrix column.

Outcome Payoff Value Used

Condition 1 2 3 4 5 6 7

T 0.8 1 1 5 99 56 99

R 0.6 0.9 0.9 3 52 37 98

P 0.5 0.1 0.1 1 51 16 1

S 0 0.6 0 0 0 14 0

K 0.12 0.50 0.80 0.40 0.10 0.50 0.97

4.3 Hypotheses

First and foremost, we wish to evaluate how mSARSA

performs in the environment detailed in Subsection

4.2. According to past research (Collenette et al.,

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

152

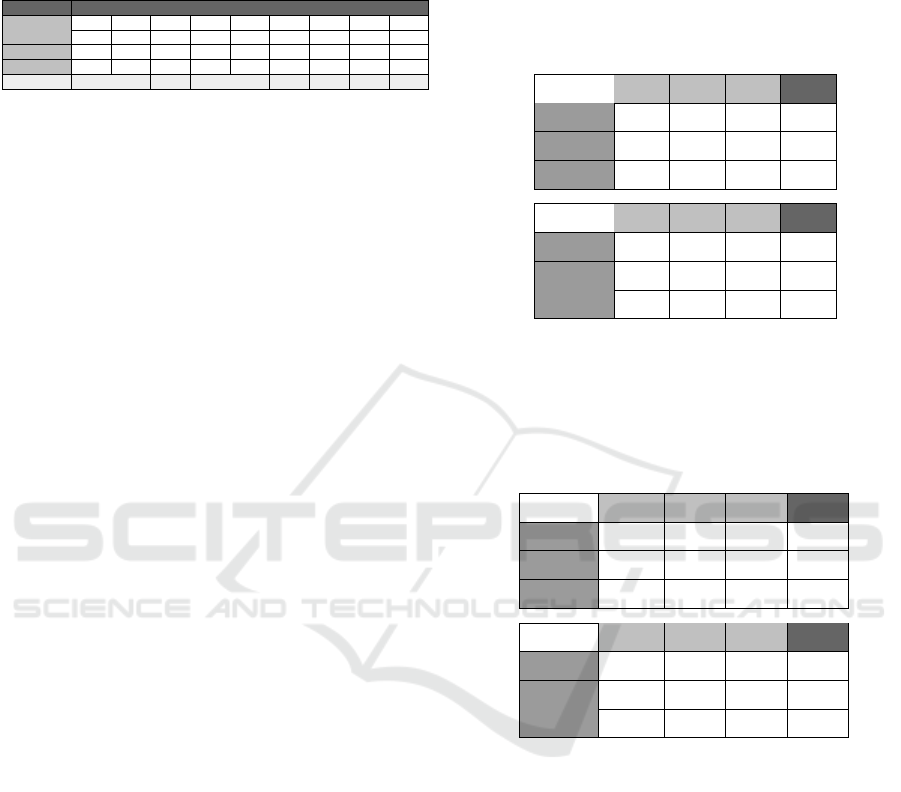
Table 4: Parameters used for the second section of the Pay-

off Schema experiment. Each column provides the payoff

matrix utilitsed by each condition. K is the value of the Co-

operation Index for that payoff matrix column.

Outcome Payoff Value Used

T 52 52 52 52 52 52 52 52 52

R 51 51 51 51 51 51 51 51 51

P 50 50 48 49 49 48 44 43 33

S 42 47 42 47 48 47 42 42 32

K 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

2018a), it is likely with the increased and determin-

istic interaction rate that any increase in the propor-

tion of mutual cooperations may be dampened in

comparison with past research. Given the model’s

overall success in mobile scenarios (Collenette et.al.,

2017b), we expect that increased mood will help raise

proportions of mutual cooperation in our own en-

vironment (over those of standard SARSA counter-

parts) even if this increase is smaller than in mobile

agent research. If we do observe increased propor-

tions of mutual cooperation (in comparison with stan-

dard SARSA), we expect that the model will uphold

similarly when tested with the parameters from Col-

lenette et.al., (2017b). As no prior direct data is avail-

able to make a prediction, we hypothesise that when

mSARSA is played directly against SARSA agents, it

may encourage SARSA to attain more mutually coop-

erative outcomes, based on the mixed-strategy results

of Collenette et.al. (2018). This may only be true,

however, after a critical proportion of mSARSA agents

are present in the environment; the Strategy Propor-

tion experiment serves to evaluate this hypothesis and

search for such value. Lastly, it has been shown in

previous research with human participants in the IPD

that increasing K appears to promote increased rates

of cooperation (see Wrightsman et.al., 1972; Colman

et.al., 2018)). We therefore predict that it is possi-

ble mSARSA may follow this trend, particularly given

that mSARSA utilises actual payoff values more exten-

sively than its competitors. The varying of actual pay-

off values (Conditions 1 through 3 versus Condi-

tions 5 through 7) will serve to evaluate if the K value

is purely responsible for any behavioural changes, or

if payoffs must be chosen carefully in terms of exact

values also.

5 RESULTS

5.1 Interaction Structure

As the primary reference point for the analysis of

these data, we ﬁrst summarise the result data of

the comparable conditions from Collenette et.al.,

(2017b).

Table 5: Proportions of Outcome Types (Mutual Defec-

tions and Mutual Cooperations, respectively) converged to

with 99% conﬁdence intervals in the mobile environment

of past work, summarised from Collenette et.al., (2017b).

S column contains SARSA’s performance, taken from the

Agentstate condition (for comparison with our own SARSA

tests).

Mutual Defection

State Info

0 0.4 0.8 S

Stateless

48.6%

± 1.5

19.7%

± 0.8

1.4%

± 0.1

Agentstate

49.8%

± 1.1

24.3%

± 0.7

6.0%

± 0.5

49.7%

± 1.1

Moodstate

48.4%

± 1.2

24.4%

± 0.6

6.6%

± 0.5

Mutual Cooperation

State Info

0 0.4 0.8 S

Stateless

8.4%

± 0.7

29.7%

± 1.0

78.9%

± 0.5

Agentstate

21.1%

± 0.7

32.1%

± 0.8

63.2%

± 1.2

21.1%

± 0.7

Moodstate

21.3%

± 0.6

31.4%

± 0.8

62.3%

± 1.1

Table 6: Mean Proportions of Outcome Types (Mutual De-

fections and Mutual Cooperations, respectively) averaged

over the last 1000 rounds in the static environment of the

current experiments. S column contains SARSA’s perfor-

mance. * The [Agentstate, 0] condition did not converge on

a ﬁnal stable behaviour on any of the experimental trials.

Mutual Defection

State Info

(SD)

0.4

(SD)

0.8

(SD)

Stateless

85.13%

(0.24)

49.18%

(11.19)

27.54%

(6.98)

Agentstate

81.86%

(23.08)*

49.61%

(12.90)

26.54%

(6.83)

94.99%

(23.40)

Moodstate

85.43%

(22.52)

49.58%

(12.39)

26.80%

(6.63)

Mutual Cooperation

State Info

(SD)

0.4

(SD)

0.8

(SD)

Stateless

0.55%

(0.24)

9.33%

(2.87)

22.38%

(5.52)

Agentstate

2.89%

(4.39)*

9.52%

(3.44)

23.85%

(6.29)

0.07%

(0.04)

Moodstate

1.54%

(2.99)

9.36%

(3.36)

24.09%

(6.44)

Average proportion of mean cooperation (over the

last 1000 rounds) in the moody learning population

followed a similar trend as in the resultant original

data, if greatly reduced in actual value. The inﬂuence

of the Stateless condition does not seem to be present

in the static environment results as in the original mo-

bile data, aside from possibly inﬂuencing Mutual Co-

operations when mA is 0. An increase in information

to the learner generally produced a greater proportion

of mutual cooperation in interactions - as did an in-

crease in the value of mA. Mutual defections simi-

larly decreased as more information became available

and mA increased, reaching a point where it was only

slightly higher than mutual cooperation. Importantly,

the proportions of all outcome types were approxi-

mately equal when mA=0.8; this is observable in Ta-

ble 6 with the similar levels of both mutual defection

Augmenting Reinforcement Learning to Enhance Cooperation in the Iterated Prisoner’s Dilemma

153

Figure 1: Summary graphs for mSARSA versus SARSA,

displaying mean proportion of outcomes in the last 1000

rounds across the experimental conditions given in Table

2. Error bars show one standard deviation from the mean.

Conditions A and D for mSARSA are marked as null as

mSARSA agents were not present in the analysis population.

and mutual cooperation, which persisted through the

non-mutual interactions also.

At all levels, mSARSA performed more mutual co-

operations and less mutual defections than SARSA.

It also showed a higher preference for mutual defec-

tion, and does not experience as many mutual cooper-

ations, at all condition levels compared to the agents

in Collenette et.al., (2017b). The results of a two-

way between-subjects ANOVA on the summed mu-

tual cooperation data from the last 1000 rounds of

each experiment showed a signiﬁcant effect of value

of mA on the total amount of last 1000 rounds of mu-

tual cooperation reached (F (2, 396) = 868.68, p <

0.01), and a signiﬁcant (if weaker) effect of depth of

state information on the same (F (2, 396) = 3.29, p

= .0383). There no statistically signiﬁcant interaction

effect present between the two (at a signiﬁcance level

of p=.05).

5.2 Strategy Proportion

As the proportion of mSARSA increases in the envi-

ronment, SARSA’s proportion of exploitation of its

opponents increases. This increase is directly con-

nected to its interactions with mSARSA agents, as ev-

ident by the low proportion of DC outcomes when

the central SARSA agents are not in contact with any

mSARSA agents (see Conditions A and D, where

the analysed agents are not in direct contact with

mSARSA partners). It maintains a high proportion

of mutual defection throughout, as SARSA primarily

defects in our environment. In the mSARSA popula-

tion, the primary learned outcome types are mutual

defection and Sucker outcomes. As the proportion of

mSARSA in the network increases, mutual coopera-

tion and Temptation outcomes increase - in line with

the previous experiment where populations of entirely

mSARSA have equal proportions of outcome types.

5.3 Payoff Schema

Figure 2: Summary graphs for mSARSA versus SARSA,

displaying mean proportion of outcomes in the last 1000

rounds across the experimental conditions given in Table 4.

Error bars show one standard deviation from the mean.

For the basic comparison of increasing values of K

(whilst maintaining actual payoff values of the T and

R payoffs), it seems that mutual cooperation rises

in mSARSA agents (presumably with other mSARSA

agents, as the SARSA outcome proportions show no

such increase) as K gets larger. Mutual defections

similarly decrease, and the proportion of S payoffs ex-

perienced also increases - meaning that overall, when

K increases, mSARSA displays more cooperative be-

haviour to opponents. Outcomes T and P seem to be

most inﬂuenced when K>=0.7, whereas those of S

and R seem to change from approximately K=0.4.

With SARSA, it appears that behaviour is unaf-

fected by the increase in K, except at high values

(e.g.K>=0.7). This coincides with the point at which

mSARSA begins to be exploited more often (presum-

ably due to an increase in the latter’s cooperation).

Figure 3: Summary graphs for mSARSA versus SARSA,

displaying mean proportion of outcomes in the last 1000

rounds across the experimental conditions given in Table 3.

Error bars show one standard deviation from the mean.

The change in outcome proportions experienced

by the two strategies varies both between the smaller

versus larger payoff values and as the value of K (the

cooperation index) changes (Figure 3).

For mSARSA, it seems both of these manipulations

to the payoff matrix has an inﬂuence on behaviour in

certain ways. As the value of K increases, propor-

tions of mutual defection decrease and proportions

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

154

of Sucker outcomes increase. Mutual cooperations

also increase, whereas proportions of Temptation out-

comes do not appear to show a consistently linear pat-

tern. Despite the classical payoff matrix having a K-

value of 0.4, it does not seem to ﬁt in-trend just under

either of its K=0.5 counterparts (Conditions 2 and 6).

This is possibly due to the size of the payoff values

themselves in Condition 4, which are between 1 and

10 (as opposed to between 0 and 1, and 1 and 100

respectively for the other two categories).

When the actual value of payoffs are greater but

the values of K follow the same trend (minimal, mid-

dling and high), these trends for mSARSA appear to

be replicated but with greater exaggeration.

With SARSA, we see possible similar effects

with the mutual defection and Temptation outcomes,

but these differences may be purely reactive to the

greater changes in mSARSA behaviour. As coopera-

tive behaviour increases with payoff matrix change in

mSARSA, SARSA observes more Temptation payoffs

and slightly less mutual defections. As stated previ-

ously, this effect appears more exaggerated when the

payoff values themselves are larger. SARSA seems

fairly inoculated to changes in the payoff matrix in

our environment, with only small amounts of vari-

ation between conditions and almost none at all in

terms of mutually cooperative or Sucker outcomes.

As mSARSA takes payoffs as a greater factor in each

calculation (such as in the calculation of mood) how-

ever, it appears more inﬂuenced by its values and the

ratio of cooperative payoffs to non-cooperative pay-

offs (K).

6 ANALYSIS, COMPARISON AND

DISCUSSION

In Collenette et.al., (2017b), the primary trends of be-

haviour observed for mSARSA included an overall de-

crease in the proportion of mutual defections at con-

vergence as the value of mA increased, with a like-

wise increase in mutual cooperations. The interaction

of state information is a little more complex. The ad-

dition of more information above Stateless seems to

keep mutual defections a little higher when mA gets

larger, but still largely below the proportion that nor-

mal SARSA mutually defects at. Conversely, addi-

tional information aids mutual cooperation at lower

levels of mA, but ultimately at the highest end (0.8)

an increase in information hinders the proportion of

mutual cooperations. Again, mSARSA still cooperates

much more frequently than SARSA. When we trans-

pose the algorithm into our environment, we observe

a similar, if compressed, trend to that of the original

data. The increased certainty and consistency of inter-

actions in our environment may have led to more ex-

treme proportions in both instances; for example, our

SARSA defects at twice the proportion of the SARSA

in Collenette et.al., (2017b), and mutually cooperates

almost 400 times less (comparing averages). In terms

of mutual defections, behaviour seemed largely unal-

tered by state information but followed the same trend

as in Collenette et.al., (2017b) regarding mA.

Despite similar trends emerging to earlier work,

however, the proportion of non-mutual outcomes

gives us greater insight into how the algorithm func-

tions here. Even though proportions of mutual de-

fection decreased, and mutual cooperations increased,

they evened out to similar proportions overall ( 25%)

- as did non-mutual outcomes. This ‘evening out’ of

all behaviours is unlike that observed in past work,

where mutual cooperation in mSARSA was the clear

dominant outcome. One possible explanation for

these observations comes from how the value of mood

changes within the algorithm in our environment. As

covered in the ﬁnal paragraph of Subsection 3.1, there

are two possible equations to use for updating mood

for each agent - MU1 (Collenette et al., 2017b) and

MU2 (from later work; Collenette et.al., 2018). The

latter of these has no direct data available for it (re-

garding mood changes or behaviour of the algorithm

speciﬁcally), and so is impractical to compare against;

it also exhibits cyclical behaviour of both mood and

resulting behavioural outcomes, taking many more

cycles to attempt to attain convergence (a primary

limitation for our research in terms of time and hard-

ware availability). It does, however, appear to pro-

vide mSARSA with the reactivity necessary for more

diverse behaviour in such a high-interaction environ-

ment. We observed that with MU1, mSARSA agents

rapidly increase in mood to maximum and then very

rarely ﬂuctuate from that position (if they do, the

mood change is inﬁnitesimally small). These ef-

fect may not have been observed in Collenette et.al.,

(2017b) due to the lower rate of interaction and the

lack of guarantee of interacting with the same part-

ner repeatedly. We opted not to utilise MU2 due to

reasons of practicality (after initial testing), but this is

certainly an avenue of future research worth pursuing.

In essence, agents in our own experiments were

therefore always operating at extremely high moods,

meaning that when any agent initially selects defec-

tion, a new behaviour is then re-selected under the

new, higher ε value (0.9), which is high enough to

lead to near-random behaviour selection. Data not re-

ported in Table 6 is that of the non-mutual behaviours

observed, which were at similar levels to both the

mutual outcomes - suggesting that behaviour is more

Augmenting Reinforcement Learning to Enhance Cooperation in the Iterated Prisoner’s Dilemma

155

randomly selected during the ‘converged’ portion of

the experiment (at the very least, within the last 1000

rounds of each test). This is of important note to fu-

ture researchers who opt to use this algorithm, as an

uninformed selection of interaction structure and en-

vironment may lead to differing efﬁcacy.

Effects of increasing the proportion of mSARSA

in the environment are relatively straight-forward. As

mSARSA has a comparatively high propensity to co-

operate, increasing the proportion of mSARSA agents

in the environment increases the likelihood it will be

exposed to agents of its own kind - this explains the

gradual increase of the mutually cooperative and ex-

ploited outcome proportions (the R and S payoffs re-

spectively). We can see this is the case from look-

ing at the SARSA data; in conditions where the anal-

ysed central group of agents were all made up of

SARSA agents that did not come into direct contact

with mSARSA agents (i.e. conditions A and D, where

mSARSA agents were in the outer corners of the grid).

In these conditions, SARSA’s proportion of T pay-

offs is as minimal as its other payoffs (as it primar-

ily plays with like agents, who also defect heavily).

As the proportion of more cooperative (mSARSA) op-

ponents increases, it ﬁnds more opportunities to ex-

ploit. When even 10% of grid agents utilise SARSA,

this signiﬁcantly impacts the outcomes experienced

by mSARSA; they experience twice as many mutual

defections when there are some SARSA agents present

in the environment than when there were none (com-

pared with data from Interaction Structure). This may

suggest that mSARSA is particularly sensitive, in this

environment, to highly defective or pure-defective

partners. Our data also suggest that in our experi-

ments there was no migration of behaviour over time

(at least within the time frame of 10,000 rounds)

- in contrast to our hypotheses, the introduction of

mSARSA to an environment of SARSA did not encour-

age the latter to cooperate more.

One of the more interesting outcomes of the

three experiments dictated here is the interaction of

mSARSA with K, the cooperation index value. Where

we observed approximately 60% mutual defections

and 5% mutual cooperations in Strategy Proportion:

Condition F, when 48% of agents in the environment

were mSARSA, the alteration of the payoff scheme to-

wards a higher K facilitates half as many mutual de-

fections and four times as many mutual cooperations.

The standard payoff matrix (used throughout Strat-

egy Proportion tests) has a K value of 0.4, meaning

that the value of the payoffs themselves only appears

to have decreased the T proportion slightly, and in-

creased the R proportion slightly (in Figure 2 from

in Figure 1). Observing the consistent trend in human

research that an increased K leads to increased rates of

cooperation (Wrightsman et.al., 1972; Colman et.al.,

2018), it is very positive to see that the more human-

like of the two learning algorithms reacts similarly.

The choice of payoff matrix therefore is an important

tool in maximising mutual cooperation in the network

outlined in this research. We also observe an effect of

the size of the actual payoffs themselves on the out-

come behaviours observed, which is critical informa-

tion for future experimentation. mSARSA seems to

display larger changes to its mutual outcomes when

K increases and the actual value of the payoffs them-

selves are large (see Conditions 5, 6, 7 in Figure 3).

7 CONCLUSIONS

Overall, the experiments detailed have thoroughly

tested the mSARSA algorithm presented in Collenette

et.al. (2017b) and Collenette et.al. (2018) with a

novel interaction structure and environment, and also

tested two further dimensions of interest (environ-

mental presence and cooperation index). We ob-

served similar trends to these past works, but also

highlight the limitations of differing versions of the

algorithm within our grid network where possible.

Namely, there was an exaggeration of weaknesses in

the ﬁrst version of the algorithm, which were altered

by the authors in later work but in ways that possi-

bly present further technical issue. The moody al-

ternative to SARSA cooperates more than its standard

counterpart, but is vulnerable to exploitation in its ﬁrst

iteration, meaning that in this particularly intense in-

teraction structure it does not adapt well to poor out-

comes. Additionally, whilst increasing the proportion

of SARSA agents in the environment serves to reaf-

ﬁrm this vulnerability to exploitation, altering the co-

operation index K demonstrated that mSARSA follows

behavioural reactivity to this variable previously ob-

served in humans. This offers afﬁrmation to the de-

sign basis of the variant algorithm, and creates poten-

tial for more accurate human behavioural modelling

in future.

We would next like to perform similar evaluations

with the second iteration of the algorithm and repeat

experiments with K with differing levels of agent con-

nectivity to test for interaction effects. We are cur-

rently evaluating the algorithm in dynamic random

networks as an extension of this. There are also many

avenues of experimentation possible for altered ver-

sions of mSARSA; using alternative methods to evalu-

ate the desirability of an outcome, for example.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

156

ACKNOWLEDGEMENTS

This work was part-funded by UK Research and In-

novation (UKRI) and Loughborough University. We

would like to thank Dr. Joe Collenette and Dr. Katie

Atkinson (University of Liverpool) for their provi-

sion of the code from their implementation of Moody

SARSA, and for their friendly support and communi-

cation.

REFERENCES

Barreda-Tarrazona, I., Jaramillo-Guti

errez, A., Pavan, M.,

and Sabater-Grande, G. (2017). Individual character-

istics vs. experience: An experimental study on coop-

eration in prisoner’s dilemma. Frontiers in Psychol-

ogy, 8.

Belkaid, M., Cuperlier, N., and Gaussier, P. (2017). Emo-

tional metacontrol of attention: Top-down modulation

of sensorimotor processes in a robotic visual search

task. PLoS ONE, 12(9).

Clore, G. L. and Ortony, A. (2013). Psychological construc-

tion in the occ model of emotion. Emotion Review,

5(4):335 – 343.

Collenette, J., Atkinson, K., Bloembergen, D., and Tuyls,

K. (2017a). Environmental effects on simulated emo-

tional and moody agents. The Knowledge Engineering

Review, 32.

Collenette, J., Atkinson, K., Bloembergen, D., and Tuyls,

K. (2017b). Mood modelling within reinforcement

learning. In Proceedings of ECAL’17, pages 106–113.

MIT Press.

Collenette, J., Atkinson, K., Bloembergen, D., and Tuyls,

K. (2018a). Modelling mood in co-operative emo-

tional agents. In Distributed Autonomous Robotic Sys-

tems, volume 6.

Collenette, J., Atkinson, K., Bloembergen, D., and Tuyls,

K. (2018b). On the role of mobility and interaction

topologies in social dilemmas. In Proceedings of Con-

ference on Artiﬁcial Life.

Colman, A. M., Pulford, B. D., and Krockow, E. M. (2018).

Persistent cooperation and gender differences in re-

peated prisoner’s dilemma games: Some things never

change. Acta psychologica, 187:1–8.

Fehr, E. and Schmidt, K. (1999). A theory of fairness, com-

petition, and cooperation. Quarterly Journal of Eco-

nomics, pages 817–868.

Fudenberg, D., Rand, D. G., and Dreber, A. (2012). Slow to

anger and fast to forgive: Cooperation in an uncertain

world. Law & Prosociality eJournal.

Gao, Y. (2012). A reinforcement learning based strategy

for the double-game prisoner’s dilemma. In Proceed-

ings of the First International Conference on Agree-

ment Technologies, volume 918, pages 317–331.

Hertel, G., Neuhof, J., Theuer, T., and Kerr, N. L. (2000).

Mood effects on cooperation in small groups: Does

positive mood simply lead to more cooperation? Cog-

nition and Emotion, 14:441 – 472.

Hristova, E. and Grinberg, M. (2005). Investigation of con-

text effects in iterated prisoner’s dilemma game. In

CONTEX. Lecture Notes in Computer Science, vol-

ume 3554, Berlin, Heidelberg. Springer.

Lin, B., Cecchi, G. A., Bouneffouf, D., Reinen, J., and

Rish, I. (2019). Reinforcement learning models of hu-

man behavior: Reward processing in mental disorders.

ArXiv, abs/1906.11286.

Ortony, A., Clore, G. L., and Collins, A. M. (1988). The

cognitive structure of emotions. New York, NY: Cam-

bridge University Press.

Palfai, T. P. and Salovey, P. (1993). The inﬂuence of de-

pressed and elated mood on deductive and inductive

reasoning. Imagination, Cognition and Personality,

13:57 – 71.

Proto, E., Sgroi, D., and Nazneen, M. (2017). The effect

of positive mood on cooperation in repeated interac-

tion. In The Warwick Economics Research Paper Se-

ries (TWERPS) 1141, University of Warwick, Depart-

ment of Economics.

Shteingart, H. and Loewenstein, Y. (2014). Reinforcement

learning and human behavior. Current Opinion in

Neurobiology, 25:93–98.

Sutton, R. and Barto, A. (2018). Reinforcement Learning:

An Introduction. MIT Press, Cambridge, Mass.

Team, P. M. (2021). projectmesa/mesa. https://github.com/

projectmesa/mesa. Last accessed 03 August 2021.

Vaughan, R. T. (2008). Massively multi-robot simulation in

stage. Swarm Intelligence, 2:189–208.

Wilson, A. J. and Wu, H. (2017). At-will relationships:

How an option to walk away affects cooperation and

efﬁciency. Games Econ. Behav., 102:487–507.

Wrightsman, L. S., O’Connor, J., and Baker, N. J. (1972).

Cooperation and Competition: Readings on Mixed-

Motive Games. Brooks/Cole Pub. Co., Belmont, CA.

Yu, C., Zhang, M., Ren, F., and Tan, G. (2015). Emo-

tional multiagent reinforcement learning in spatial so-

cial dilemmas. IEEE Transactions on Neural Net-

works and Learning Systems, 26:3083–3096.

Zulﬁqar, S. and Islam, A. (2017). Exploring the role of

emotions and moods in decision making: Study on the

use of structured decision approach and intuition. In-

ternational Journal of Engineering and Management

Sciences, 2:140–149.

Augmenting Reinforcement Learning to Enhance Cooperation in the Iterated Prisoner’s Dilemma

157