LSTM-based Abstraction of Hetero Observation and Transition

in Non-Communicative Multi-Agent Reinforcement Learning

Fumito Uwano

Department of Computer Science, Okayama University, 3-1-1, Tsushima-naka, Kita-ku, Okayama, Japan

Keywords:

Multiagent System, Reinforcement Learning, LSTM, Hetero-information, Hetero-transition.

Abstract:

This study focuses on noncommunicative multiagent learning with hetero-information where agents observe

each other in different resolutions of information. A new method is proposed for adapting the time dimen-

sion of the hetero-information from the observation by expanding the Asynchronous Advantage Actor–Critic

(A3C) algorithm. The proﬁt minimizing reinforcement learning with oblivion of memory mechanism was the

previously used noncommunicative and cooperative learning method in multiagent reinforcement learning.

We then insert an long short-term memory (LSTM) module into the A3C neural network to adapt to the time

dimension inﬂuence of the hetero-information. The experiments investigate the performance of the proposed

method on the hetero-information environment in terms of the effectiveness of LSTM. The experimental re-

sults show that: (1) the proposed method performs better than A3C. Without the LSTM module, the proposed

method enabled the agents’ learning to converge. (2) LSTM can adapt the time dimension of the input infor-

mation.

1 INTRODUCTION

Multiagent Reinforcement Learning (MARL) con-

trols some agents in groups to learn cooperative ac-

tion, such as in warehouses where robot agents coop-

erate with each other to manage the delivery of sup-

plies. In this case, MARL must decrease the complex-

ity of communication to achieve the desired coopera-

tion and enable the robots to solve real-world prob-

lems. In previous work, Kim et al. discussed a practi-

cal scenario for each agent to communicate with other

agents in real-world reinforcement learning tasks and

proposed a multiagent deep reinforcement learning

(DRL) framework called SchedNet (Kim et al., 2019).

Du et al. expanded the focus to the dynamic na-

ture of communication and the correlation between

agents’ connections to propose a learning method to

obtain the topology (Du et al., 2021). Those works

are efﬁcient and straightforward, but the agents them-

selves cannot do complex tasks based on real-world

problems, especially in a dynamic environment. In

contrast, Raileanu et al. proposed self–other model-

ing (SOM) method to enable agents to learn coopera-

tive policy through predicting others’ purpose or goals

based only on the observation (Raileanu et al., 2018).

Ghosh et al. argued that the premise of SOM requires

https://orcid.org/0000-0003-4139-2605

the behaviors and types of all agents be presented as

a problem and proposed AdaptPool and AdaptDQN

as cooperative learning methods without using this

premise (Ghosh et al., 2020). However, these meth-

ods are based on static environment and require all

purposes to be given. Uwano et al. proposed a method

called proﬁt minimizing reinforcement learning with

oblivion of memory (PMRL-OM) as a noncommu-

nicative and cooperative learning method in a mul-

tiagent dynamic environment (Uwano and Takadama,

2019).

In addition, by communicating with other agents

and predicting their behaviors, the agents can learn

appropriate and cooperative actions (Raileanu et al.,

2018; Ghosh et al., 2020). In MARL, however, agents

can observe the same resolution information, e.g.,

the environmental situation and other agents’ actions

(i.e., if some agents can observe high-resolution in-

formation, then the other agents can also observe the

same information). This can become an issue because

all agents cannot be guaranteed to observe the same

resolution of information about each other in the real

world. For example, all vehicles using car navigation

systems must cooperate (in planning routes) appro-

priately with each other because the optimal routes

are inﬂuenced by other vehicles’ route planning and

trafﬁc jams; therefore, the vehicles cannot observe

172

Uwano, F.

LSTM-based Abstraction of Hetero Observation and Transition in Non-Communicative Multi-Agent Reinforcement Learning.

DOI: 10.5220/0010795700003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 1, pages 172-179

ISBN: 978-989-758-547-0; ISSN: 2184-433X

information with different resolutions. Uwano de-

scribed the different information resolutions as “het-

ero information” (Uwano, 2021), and discussed the

relationship between the network topology of DRL

and abstraction of input–output information. Al-

though they discuss the hetero-information in inputs,

the transition is important in MARL. Recently, the re-

sults for hetero-information did not converge; that is,

the agents could not stably learn cooperative actions

(Uwano, 2021).

Based on this background, this paper focuses

on the hetero-transition caused by the hetero-

information. Hetero-transition refers to the different

transitions between observations and the actual sit-

uation. Thus the problem expands from the hetero-

information to the hetero-transition. In addition, this

paper proposes a noncommunicative and cooperative

learning method using the unstable hetero-transition

in a dynamic environment. In particular, this pa-

per proposes a new method to expand the Asyn-

chronous Advantage Actor–Critic (A3C) algorithm to

adapt the hetero-information from observations us-

ing the PMRL-OM mechanism as the previous non-

communicative and cooperative learning method in

MARL. We then an LSTM module into the A3C neu-

ral network to adapt to the time dimension inﬂuence

on the hetero-information. In the experiment, this pa-

per employed a maze problem where the starting and

goal locations change after several steps in the grid

world and either of the agents sense only the hetero-

information and investigated the agents’ performance

in solving the problem.

This paper is organized as follows: A3C and

PMRL-OM are introduced in Sections 2 and 3, re-

spectively. The proposed new method combined both

A3C and PMRL-OM as explained in Section 4. Fur-

thermore, the problem and unstableness are explained

in Section 5. The experimental details and discussions

are described in Section 6. Finally, the conclusions

are presented in Section 7.

2 ASYNCHRONOUS ADVANTAGE

ACTOR–CRITIC

The A3C algorithm (Mnih et al., 2016) is a DRL

method where the system copies the agents and envi-

ronments, and then executes trials asynchronously to

acquire an optimal policy immediately. This paper ex-

plains the details of A3C based on (Fujita et al., 2019),

where the implementation is similarly employed in

the experimental section of this paper as described

previously (Mnih et al., 2016). The copied agents ex-

ecute backpropagation of the primary agent with the

loss of parameters as the learning result. They then

initialize themselves and synchronize the current pa-

rameters from that of the primary agent and repeat the

presented processes.

In DRL, state s or sensed information to detect the

state is input to the network and the policy π or state–

action value Q(s,a) is output from the network. DRL

approximates the true policy π or true state–action

value Q(s, a) and action a throughout the process to

learn by backpropagation from the loss between the

output and true value. As for A3C, the agent esti-

mates the appropriate values of the policy π(a

;θ)

and state value V (s

;θ

) using the neural network, as

well as shares them to the copied agents, which calcu-

late the loss of the parameters θ and θ

to update ones

of the neural network. A3C learns from the state s

or some information to detect s as input to output the

policy π(a

;θ) and state value V (s

;θ

) as respec-

tively “Actor” and “Critic.”

The policy loss dθ and state value loss dθ

are

deﬁned as Equations (1) and (4), respectively.

dθ ← dθ + ∇

′

logπ



;θ

′



A(s

, a

;θ, θ

)

+ β∇

′

H(π



;θ

′



), (1)

A(s

, a

;θ, θ

) =

k−1

∑

j=0

i+ j

+ γ

V (s

i+k

;θ

) −V (s

;θ

(2)

R ← r

+ γR, (3)

dθ

← dθ

∂(R −V (s

;θ

′

))

∂θ

′

. (4)

Where the losses θ

′

and θ

′

are for the copied agent.

In a certain steps i, the state, action and reward are

denoted by s

, a

, and r

, respectively. Updating θ

′

uses the entropy function H(π(s

;θ

′

)) multiplied by

the factor β. In the advantage function A(s

, a

;θ, θ

the calculation includes the future reward multiplied

by the discount factor γ. The copied agents update the

original parameter using Equations (1) and (4).

3 PROFIT-MINIMIZING

REINFORCEMENT LEARNING

WITH OBLIVION OF MEMORY

To learn multiagent cooperation without communica-

tion in an environment of dynamic change, Uwano

et al. proposed the PMRL-OM mechanism (Uwano

and Takadama, 2019), which is based on Q-learning

and enables cooperation by managing the reward in

dynamic change environments. The agents can iden-

tify the largest spent steps when they reach all goals

LSTM-based Abstraction of Hetero Observation and Transition in Non-Communicative Multi-Agent Reinforcement Learning

173

through the optimal steps, e.g., the PMRL-OM mech-

anism enables all agents to reach the farthest goals in

the maze problem. While that might result in each

agent crashing into each other, the agent that reached

the goal ﬁrst yield it to other agents by trying to reach

other goals and avoiding crashing and managing the

goals whenever accidents occur.

Figure 1: Overview of PMRL-OM.

The PMRL-OM mechanism updates the agent’s

memory as the environment changes and controls the

reward values for each agent to reach all goals in the

shortest time (Figure 1). In this ﬁgure, Agents A

and B are learning to reach the appropriate goals with

each other by tuning their own reward values. Thus,

Agents A and B reached goals X and Y, respectively.

Using an internal reward design as the reward tuning

mechanism and updating the goal values as the goal

selection are explained in the next subsection.

3.1 Internal Reward Design

Generally, an agent learns based on environmental re-

wards or a reward signal communicated by the agent

when it achieves its purpose. However, the internal

reward design can remake the reward, or the reward

signal is used as the internal reward in the agents’

learning process. PMRL-OM estimates the internal

reward to enable agents to reach the appropriate goals

by learning. The next subsection, “goal value updat-

ing,” explains how to decide the appropriate goals.

Let the goal g be the appropriate goal, then the inter-

nal reward is calculated using Equation (5) as follows:

= max

′

∈G,g

′

̸=g

′

−t

+ δ, (5)

where ir

is the internal reward of the goal g, γ is the

discount rate in Q-learning, g

′

is the certain goal in

the goal set G in which all goals are included, and

′

is the external reward of the goal g

′

. The vari-

ables t

and t

′

are the minimum number of steps until

the agent has reached the goals g and g

′

, respectively.

Note that the internal reward is calculated for only the

appropriate goal g and those of the other goals are set

by the external rewards.

Equation (5) calculates discounted expected re-

wards as Q-values to each goal in the Q-learning pro-

cess and sets the internal reward of the appropriate

goal to be larger than any other goal. For example,

Figure 2 shows three goals denoted by the money

pouches, the arrows show the actions to achieve the

goals, and the variables indicate the Q-values. An in-

ternal reward ir

is set by the agent to facilitate other

agents to achieve the goal g. Thus, ir

should be set

as follows:

> max



, r



(6)

Let the difference between the left- and right-hand

sides be δ; thus, the equation can be transformed as

follows:

= max



, r



+ δ (7)

= max



−t

, r

−t



+ δ (8)

Let the arbitrary goal be g

′

and Equation (8) is the

same as Equation (5). Therefore, the internal reward

design can lead the agent to the appropriate goal.

3.2 Goal Value Updating

The goal value can be used by agents to select the

appropriate goal. The value is converged to the mini-

mum number of steps for each goal to achieve the goal

that takes the longest time to achieve (i.e., the farthest

goal in the maze problem). The agent then learns how

to reach the goal with the maximum value using this

internal reward. Equation (9) denotes the goal value

update functions. Let t

and ξ be the minimum num-

ber of steps for the appropriate goal g and constant

value. Note that ξ is a positive integer value greater

than 0 and ξ indicates how much emphasis is given

to the current minimum number of steps in the goal

value: if ξ is small, the minimum numbers of steps are

emphasized; otherwise an increased minimum num-

bers of steps is emphasized in the goal value. At the

end of every iteration, if the agent has received the

reward, the goal value is updated by the top function;

otherwise, it is updated by the bottom function. Using

these equations, all agents aim to reach the farthest

goal. After that the agents set their internal rewards to

reach that goal:

(

bid

ξ−1

bid

i f received rewards

bid

ξ−1

bid

otherwise

(9)

Figure 2: Internal reward design.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

174

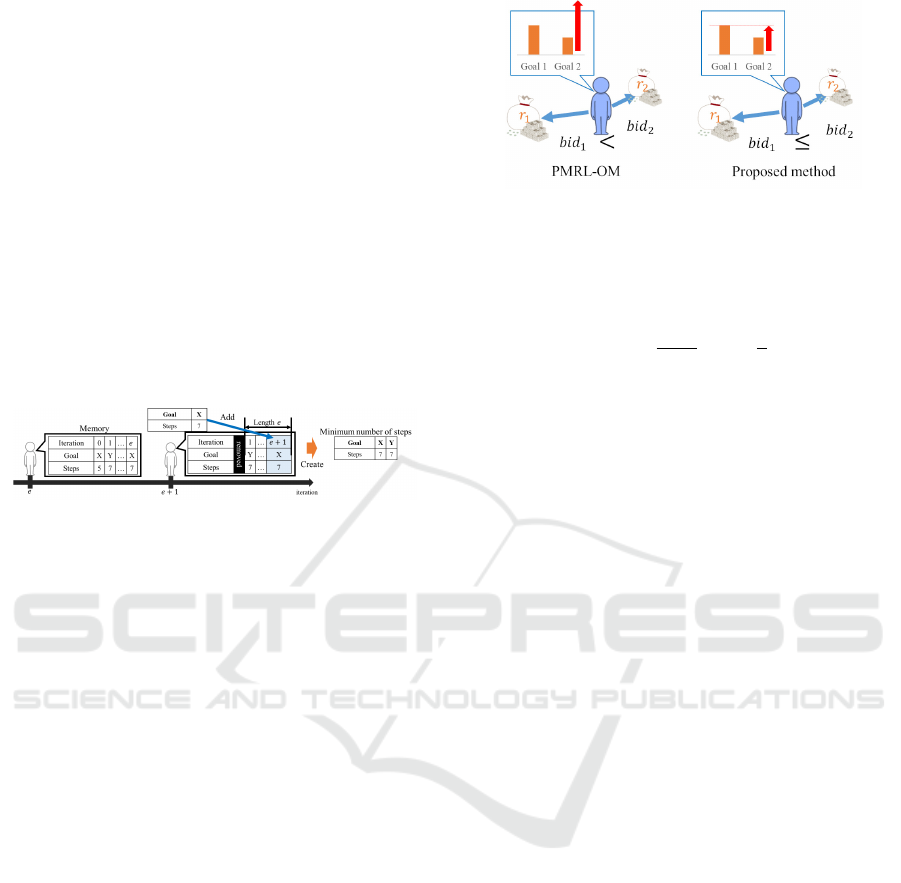
3.3 Memory Management

To use the minimum number of steps, PMRL-OM

counts the steps to each goal throughout the entire it-

eration. However, PMRL-OM stores the steps in or-

der because its memory is ﬁnite and older data might

degrade. Figure 3 shows the memory management

using PMRL-OM. The word balloon and the human

ﬁgure at its tail denote the memory and agent, re-

spectively. The bottom arrow indicates the continu-

ous iterations using the iteration e to e + 1. Given the

memory length e, the agent repeats the actions of stor-

ing the current iteration, counting the current number

of steps, and when it reached the goal until the stack

length of the data is less than the memory length e. If

the stack length is over e, the agent removes the oldest

data from its memory.

Figure 3: Memory management of PMRL-OM.

4 PROPOSED METHOD

The proposed method is expanded from A3C in

the hetero-observation and hetero-transition using the

PMRL-OM mechanism. The goal value and inter-

nal reward design are added to the A3C algorithm,

which is modiﬁed to adapt to the hetero-observations.

The A3C neural network is replaced with the LSTM-

based network to adapt to the hetero-transitions. This

section explains the presented three modiﬁcations

and describes the shared parameters in the proposed

method: that is, the goal values and minimum num-

bers of steps, which can promote learning and prevent

any inﬂuence of the hetero-information by helping the

agents to ervise their own information from the shared

data.

4.1 Modiﬁcation of Goal Value Design

The A3C is a policy-based algorithm, where the agent

performs actions based on the policy π. Thus, the goal

value function must be expanded in the case when the

memory (explained in Subsection 3.3) is empty. In

this situation, PMRL-OM sets the maximum number

of steps to t

in Equation (9) instead of the minimum

number. Thus, the agent is inﬂuenced to reach the un-

memorized goal. However, the maximum number of

steps is too large for the A3C algorithm to enable the

agent to avoid becoming absorbed in the goal because

Figure 4: Difference in the goal value updating.

the algorithm does not employ ε-greedy action selec-

tion, unlike PMRL-OM. Thus, the proposed method

modiﬁes the goal value update function from Equa-

tion (9) to Equation (10) as follows:

bid

ξ − 1

bid

, (10)

φ =







max

′

bid

′

i f memory is empty

else i f received rewards

0 otherwise

(11)

This modiﬁcation adds a process if the memory

is empty, and the goal value is updated by the max-

imum value of all goal values. Figure 4 shows the

effect of the proposed method when updating the goal

value when the data for Goal 2 is empty. The left- and

right-hand sides denote PMRL-OM and the proposed

method. The word balloons are inside the agents and

the graphs denote the goal values and their dynamics.

PMRL-OM helps the agent to reach Goal 2 even if

Goal 2 cannot be reached by overvaluation. The pro-

posed method sets the goal values at the same level;

thus, the goal value for Goal 2 cannot be greater than

or equal to the other goal values. If Goal 2 is not valu-

able, the proposed method can recover quickly. Oth-

erwise, the goal value for Goal 2 can exceed the goal

value for the other goals.

4.2 Modiﬁcation of Internal Reward

Design

The internal reward design of the proposed method

uses the same function of PMRL-OM as follows;

however, the parameters differ:

= max

′

∈G,g

′

̸=g

′

−t

+ δ (12)

where the discount rate γ is used in the A3C algo-

rithm and the reward r

′

is the external reward. As

for A3C, the internal reward can maintain its ratio-

nality because of Equations (1) and (4). Equation

(1) ﬁnally converges to the advantage value shown in

Equation (2). Thus the internal reward can keep the

gradient and large–small relationship between select-

ing actions in its policy. Equation (4) is used in the

same manner.

LSTM-based Abstraction of Hetero Observation and Transition in Non-Communicative Multi-Agent Reinforcement Learning

175

4.3 LSTM-based Network

The proposed method replaces the A3C neural net-

work to adapt the hetero-information from hetero-

observations and hetero-transitions. An LSTM layer

is then inserted into the network. Figure 5 shows the

overview of the modiﬁed network. In the network

model, the red line denotes an LSTM layer and the top

graphic shows the difference between an agent’s ob-

servation and the actual situation. Although the pre-

vious network comprises only dense layers, it can ab-

stract the hetero-information in its inputs, but it can-

not adapt to the hetero-information from the hetero-

transition. This hetero-transition is because of the dif-

ferent transitions between the hetero-observation and

the actual situation. At the top of this graphic, the

agent cannot observe the movement to the left and in-

puts the same information.

LSTM (Hochreiter and Schmidhuber, 1997) is a

kind of recurrent neural network used to learn about

the current situation using one-step-back inputs to

adapt to the time-sequential data. This paper replaces

a part of the network to adapt to the hetero-transition.

That is, the proposed method enables the agent to

catch up with the actual change in the situation using

LSTM to continuously learn the same input.

5 PROBLEM AND

UNSTABLENESS

5.1 Maze Problem

In this paper, the agents train and practice on grid

world mazes. The maze problems in the grid worlds

are shown in Figure 6. On the left-hand side, the

agent departs from the “Start” square to reach the

Figure 5: Vertical and horizontal abstraction in modiﬁca-

tion.

“Goal” square based on the available rewards. On

the right-hand side, the two agents depart from the

squares labeled “Start A” and “Start B” to reach the

goals named “Goal X” and “Goal Y.” Although the

agents can acquire the same reward value for each

goal, the reward values accumulate when both agents

reach different goals. The agents attempt to avoid hit-

ting each other by avoiding being in the same square,

including the goal square. The agents input informa-

tion with one-hot vector using ﬁve dimensions: road,

wall, goal, agent on road, and other in the even case,

but only Agent A departs from “Start A.”

Figure 6: Environment.

5.2 Unstableness

There are two kinds of unstableness: hetero-

information and the dynamic environment. This pa-

per focuses on maze problems that include both kinds

of unstableness.

5.2.1 Hetero-information

Hetero-information denotes the situation where

agents have different input resolutions because of

their individual sensor differences and different sen-

sors in the same situation, among others. For vehi-

cle navigation, each vehicle senses different resolu-

tion information; i.e., the same environmental states

might be divided and the example becomes more dif-

ﬁcult.

Figure 7 represents an example of hetero-

information, with sensing in basic MARL on the

right-hand side and sensing hetero-information on

the left-hand side. The blue agent can move front,

back, left, and right to reach the light-red goal square

in the grid world. Although the agent can be given

any information for all states in basic MARL, it

uses one-fourth of all states because four states are

observed as one state in the hetero-information case.

Figure 7 shows that the agent can observe the back

right-hand goal but cannot observe the front left-hand

goal. Therefore, the hetero-information case means

that agents cannot sense with low resolution, but can

sense that something includes their goals.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

176

Figure 7: Hetero information observation.

Figure 8: Dynamic environment.

5.2.2 Dynamic Environment

This paper focuses on the dynamics of the start and

goal locations for the environmental change, which

inﬂuence the state transition function. Figure 8 shows

an example of the dynamic change. The location of

agents and goals are changed after some steps and the

reward is not changed. The environmental change oc-

curred once in a trial and the modiﬁed method aims to

learn a cooperative policy based on the environmental

change.

6 EXPERIMENT

6.1 Experimental Setup

To investigate the effectiveness, this paper compared

the proposed methods where the network has an

LSTM module or not using the A3C algorithm in the

maze problem (Figure 8). The environmental change

happened after half of all the steps and Agent B only

senses the hetero-information. The network topology

differs for each agent: that is, Agent A has a hid-

den and dense layer of 16 nodes, while Agent B has

256 nodes in the proposed method without the LSTM

module. The hidden layer of Agent B is replaced by

an LSTM layer in the proposed method. Note that the

A3C algorithm is based on (Fujita et al., 2019). The

evaluation criteria are the spent step until all agents

have reached the goal and the agents’ acquired re-

wards.

6.2 Parameters

The setting parameters are summarized on Table 1.

The total number of steps is 20 million (ﬁrst line) and

the copied agent learns every 25 steps as a maximum

until 250 steps (second and third lines). The number

of copied agents is 32 (fourth line). The parameters

α, γ, and β are set by 0.0007, 0.99, and 0.01 (i.e., the

ﬁfth, sixth, and seventh lines, respectively). Finally,

the internal reward gap δ is 1, and the number of ex-

ternal reward values is 10 for all goals (last lines).

Table 1: Experimental parameters.

Horizon of steps 20,000,000

Horizon of steps for copied agent 250

Horizon of steps in an iteration 25

Processes 32

Learning rate α 0.0007

Discount rate γ 0.99

Rate β 0.01

Internal reward gap δ 1

External reward value 10

6.3 Results

Figures 9, 10, and 11 show the spent steps until all

agents have reached the goal and the acquired re-

wards of both agents using A3C and the proposed

method, respectively. The vertical and horizontal axes

denote the results and episodes, respectively. The

blue, orange, and green lines indicate the resulting

trajectories of 100 moving episodes using the A3C

and the proposed methods (called “A3C,” “Proposed

method,” and “Proposed method (no LSTM)” in Fig-

ures 9, 10, and 11, respectively).

Although the results are not clearly different from

each other, they show that the proposed method is

slightly better than any other method before the en-

vironmental change. After the change, the proposed

method can converge to the minimum number of

steps. In particular, the variance of the results using

the A3C algorithm and the proposed method without

the LSTM module is larger than that of the proposed

method. As for the acquired rewards, the results are

obtained in the same manner as the spent step and the

convergence of the proposed method is better.

6.4 Discussion

Those results show that the proposed method per-

forms better than PMRL-OM to enable the agents to

learn optimal policies.

6.4.1 Effectiveness of LSTM

In this section, we discuss which layers should be in-

serted using LSTM through an experiment comparing

LSTM-based Abstraction of Hetero Observation and Transition in Non-Communicative Multi-Agent Reinforcement Learning

177

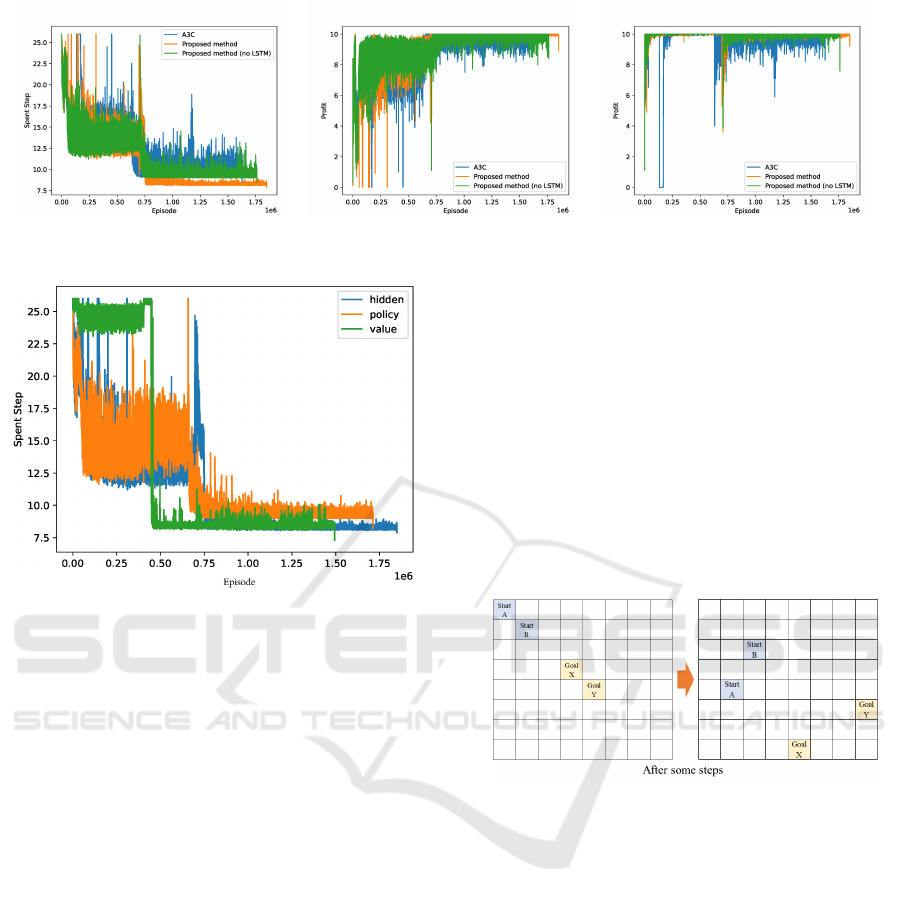
Figure 9: Result of spent step. Figure 10: Result of proﬁt (Agent A). Figure 11: Result of proﬁt (Agent B).

Figure 12: Results of spent steps (in the experiment of

LSTM).

the agents’ performance with different LSTM posi-

tions in the proposed method. There are three cases:

(1) one is the proposed method; (2) another is which

network uses the inserted LSTM in the previous pol-

icy output; and (3) the other is for the value output.

Figure 12 shows the experiment results. The verti-

cal and horizontal axes denote the spent steps and

episodes, respectively. The blue, orange, and green

lines indicate the resulting trajectories of 100 mov-

ing episodes for the cases (1), (2), and (3) (“hidden,”

“policy,” and “value,” respectively). The hidden re-

sult is the best, while the policy result is better than

value. However, the value result is better than the

policy result after the environmental change, it is the

worst because the agents cannot learn a cooperative

policy. This ﬁnding is because the state value en-

ables the A3C algorithm for stable learning to con-

verge the agents’ learning results to the worst result.

Therefore, case (1) enables the agents to abstract the

hetero-transition information in their input. In case

(2), LSTM cannot abstract the policy output by insert-

ing the previous policy output. Because the environ-

mental change occurred according to the total number

of steps; this happened late during the situation where

the agents using the proposed method can achieve the

change using smaller steps than any other agents for

each episode.

6.4.2 Limitation of Hetero Information

In Figure 9, the convergence is different between be-

fore and after the environmental change because the

ﬁrst maze is more difﬁcult than the other mazes. In

particular, it is difﬁcult for Agent A to reach Goal

Y for 14 translations using hetero-observation. Thus,

the proposed method has a limitation of scale when

using the hetero-transition. In this section, we ex-

amine the comparison of the proposed method and

that without the LSTM module in the different mazes

(Figure 13, where the setup is in the same manner as

subsections 6.1 and 6.2.)

Figure 13: Simple environment.

Figure 14 shows the result. The vertical and hor-

izontal axes denote the spent step and episodes, re-

spectively. The blue and orange lines indicate the

resulting trajectories of 100 moving episodes with

the proposed method and without the LSTM mod-

ule (called “LSTM” and “Dense”), respectively. From

these results, the result of the proposed method with-

out the LSTM module obtains some steps. On the

other hand, the agents cannot cooperate with each

other in some steps, e.g., in 0.75e + 6, before the

experimental change, and the result could not con-

verge to the minimum number of spent steps after

that. On the other hand, the proposed method enables

the agents to learn to cooperate and the optimal pol-

icy and convergence. The environmental change oc-

curred by the total number of steps, which happened

late in the situation where the agents using the pro-

posed method can reach the change with fewer steps

than any others for each episode.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

178

Figure 14: Spent step results (in the simple maze experi-

ment).

7 CONCLUSION

This paper proposed a method based on the previous

noncommunicative and cooperative learning method

(PMRL-OM) based on DRL (A3C) in a multiagent

system within an unstable environment in terms of

hetero-transitions using different transitions accord-

ing to the difference between observed and recent sit-

uations. The proposed method inserts an LSTM mod-

ule into the A3C neural network. The experiments

compared the proposed method with A3C and with-

out the LSTM module. The derived results were as

follows: (1) the proposed method performs better than

the A3C algorithm and without the LSTM module. In

particular, the proposed method enables the agents’

learning to converge; (2) LSTM can adapt the time

dimension of the input information.

This paper showed that the proposed method can

not only adapt the hetero-transition of input informa-

tion, but should also adapt the hetero-transition of out-

put information. In particular, the hetero-transition

should be assumed as a partially observable Markov

decision process (POMDP), but the proposed method

performs as a Markov decision process. Therefore,

we will expand the proposed method to POMDP to

adapt the hetero-observations in the future.

ACKNOWLEDGEMENTS

This research was supported by JSPS Grant on

JP20K23326.

REFERENCES

Du, Y., Liu, B., Moens, V., Liu, Z., Ren, Z., Wang, J.,

Chen, X., and Zhang, H. (2021). Learning Correlated

Communication Topology in Multi-Agent Reinforce-

ment Learning, page 456–464. International Founda-

tion for Autonomous Agents and Multiagent Systems,

Richland, SC.

Fujita, Y., Kataoka, T., Nagarajan, P., and Ishikawa, T.

(2019). Chainerrl: A deep reinforcement learning li-

brary. In Workshop on Deep Reinforcement Learning

at the 33rd Conference on Neural Information Pro-

cessing Systems.

Ghosh, A., Tschiatschek, S., Mahdavi, H., and Singla, A.

(2020). Towards Deployment of Robust Cooperative

AI Agents: An Algorithmic Framework for Learning

Adaptive Policies, page 447–455. International Foun-

dation for Autonomous Agents and Multiagent Sys-

tems, Richland, SC.

Hochreiter, S. and Schmidhuber, J. (1997). Long short-term

memory. Neural Comput., 9(8):1735–1780.

Kim, D., Moon, S., Hostallero, D., Kang, W. J., Lee, T.,

Son, K., and Yi, Y. (2019). Learning to schedule com-

munication in multi-agent reinforcement learning.

Mnih, V., Badia, A. P., Mirza, M., Graves, A., Lillicrap,

T. P., Harley, T., Silver, D., and Kavukcuoglu, K.

(2016). Asynchronous methods for deep reinforce-

ment learning. CoRR, abs/1602.01783.

Raileanu, R., Denton, E., Szlam, A., and Fergus, R. (2018).

Modeling others using oneself in multi-agent rein-

forcement learning. In Dy, J. and Krause, A., editors,

Proceedings of the 35th International Conference on

Machine Learning, volume 80 of Proceedings of Ma-

chine Learning Research, pages 4257–4266, Stock-

holmsmassan, Stockholm Sweden. PMLR.

Uwano, F. (2021). A cooperative learning method for

multi-agent system with different input resolutions. In

4th International Symposium on Agents, Multi-Agents

Systems and Robotics.

Uwano, F. and Takadama, K. (2019). Utilizing observed

information for no-communication multi-agent rein-

forcement learning toward cooperation in dynamic en-

vironment. SICE Journal of Control, Measurement,

and System Integration, 12(5):199–208.

LSTM-based Abstraction of Hetero Observation and Transition in Non-Communicative Multi-Agent Reinforcement Learning

179