
Deep-Learning-based Fuzzy Symbolic Processing with Agents
Capable of Knowledge Communication
Hiroshi Honda
a
and Masafumi Hagiwara
b
Faculty of Science and Technology, Keio University, Yokohama, Japan
Keywords: Deep Learning, Explainable Artificial Intelligence, Fuzzy, Prolog, Reinforcement Learning,
Symbolic Processing.
Abstract: The authors propose methods for reproducing deep learning models using a symbolic representation from
learned deep reinforcement learning models and building agents capable of knowledge communication with
humans. It is difficult for humans to understand the behaviour of agents using deep reinforcement learning,
and to inform agents of the state of the environment and to receive actions from the agents. In this paper,
fuzzified states of the environment and agent actions are represented by rules of first-order predicate logic,
and models using symbolic representation are generated by learning such rules. By replacing deep reinforce-
ment learning models with models using a symbolic representation, it is possible for humans to inform the
state of the environment and add rules to the agents. As a result of the experiments, the authors can reproduce
trained deep reinforcement learning models with high match rate for two types of reinforcement learning
simulation environments. Using reproduced models, the authors build agents that can communicate with hu-
mans that have yet be realized thus far. This proposed method is the first case of building agents capable of
knowledge communication with humans using trained reinforcement learning models.
1 INTRODUCTION
In recent years, research on explainable artificial
intelligence (XAI) (Lipton, 2018; Montavon et al.,
2018; Alejandro et al., 2020) modeled by white-box
machine learning for interpretation by humans has
been actively conducted. XAI research is also being
conducted with a particular focus on reinforcement
learning (Sequeira and Gervasio, 2019; Fukuchi et al.,
2017; Lee, 2019; Waa et al., 2018; Madumal et al.,
2019; Coppens et al., 2019).
However, research on symbolic processing with
neural networks (Cohen, 2016; Minervini et al., 2018;
Rocktaschel and Riedel, 2017; Serani and d'Avila
Garcez, 2016; Sourek et al., 2015; Minervini et al.,
2020; Dong et al., 2019; Cingillioglu and Russo,
2018; Honda and Hagiwara, 2019) has been actively
conducted. Symbolic processing has the advantage of
being easy for humans to understand because it uses
symbols for knowledge representation.It has become
possible to use a large amount of data on the Web,
and with the improved learning ability of neural
a
https://orcid.org/0000-0002-9171-5663
b
https://orcid.org/0000-0002-6171-0618
networks through deep learning, research on
symbolic processing with neural networks.
It is difficult for humans to understand the
behaviour of agents using deep reinforcement
learning, and to inform agents of the state of the
environment and to receive actions from the agents.
Therefore, in this paper, we propose a method for
reproducing deep learning models using a symbolic
representation from trained reinforcement learning
models and to build agents capable of knowledge
communication with humans. Using symbolic
representations for knowledge representation makes
it easier for humans to understand models, and
humans can also write rules. It is difficult for humans
to interpret continuous values of states immediately,
and humans express states ambiguously using
language. In this paper, fuzzified states of
environments and agent actions are represented by
rules of first-order predicate logic, and models using
symbolic representation are generated by learning
them. Then, by replacing deep reinforcement learning
models with models using symbolic representation, it
172
Honda, H. and Hagiwara, M.
Deep-Learning-based Fuzzy Symbolic Processing with Agents Capable of Knowledge Communication.
DOI: 10.5220/0010796300003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 3, pages 172-179
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
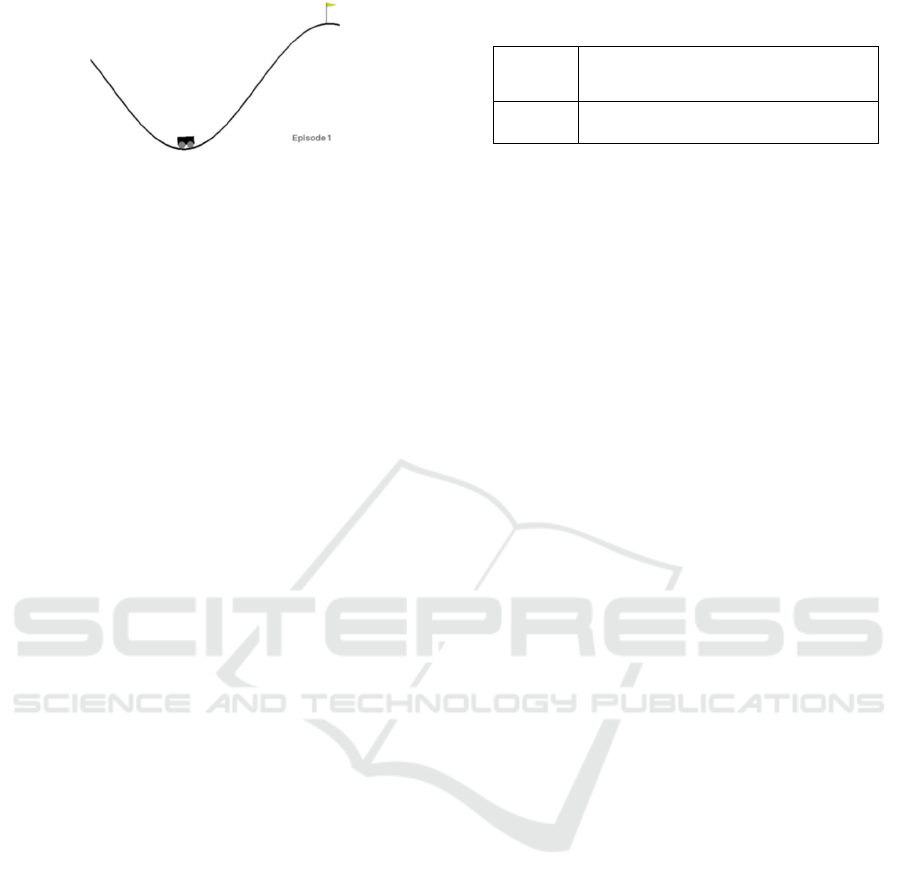
Figure 1: Environment of MountainCar-v0.
is possible for humans to inform the states of the
environment and add rules to the agents. Since the
fuzzy symbolic representations differ from person to
person, we think that the learning cost will be lower
if the trained reinforcement learning models are
reproduced instead of symbolizing the training data in
advance before performing reinforcement learning.
Furthermore, the ability of symbolic processing using
deep learning is so powerful that we believe that it can
reproduce deep reinforcement learning models.
This paper makes the following contributions:
Trained reinforcement learning models are re-
produced with models using symbolic represen-
tations that are easy for humans to understand.
Agents capable of knowledge communication
with humans are built.
This proposed method is the first case of building
agents capable of knowledge communication with
humans using trained reinforcement learning models.
We believe that this proposal can contribute to
practical applications, such as coaching for people
using agents acquired through reinforcement
learning. Specifically, an application that coaches
driving a car or playing video games can be
considered.
We begin by reviewing related research in Section
2. In Section 3, we describe the symbolic
representation of the reinforcement learning model.
In Section 4, we propose agents capable of knowledge
communication. Finally, in Section 5, we report the
experimental results of the proposed system.
2 RELATED WORK
2.1 Explainable Artificial Intelligence
In the field of explainable reinforcement learning,
research is being conducted to generate another
model to explain the first model, with the aim of
allowing humans to understand the output of both
models (Sequeira and Gervasio, 2019; Fukuchi et al.,
2017; Lee, 2019; Waa et al., 2018; Madumal et al.,
2019; Coppens et al., 2019). Among them, there are
studies using a structural causal model (Madumal et
Table 1: Actions and statuses of MountainCar-v0.
Action Accelerate to the left : 0
Do not accelerate : 1
Accelerate to the
r
igh
t
: 2
Status
Car position : -1.2 – 0.6
Car velocity : -0.07 – 0.07
al., 2019) and studies using soft decision trees
(Coppens et al., 2019). However, such studies
generate models for explanation, and it is difficult to
use the generated models instead of reinforcement
learning models.
2.2 Symbolic Processing with Neural
Networks
After the emergence of deep learning, deductive and
inductive inferences based on first-order predicate
logic were studied using graph neural networks
(Cohen, 2016; Minervini et al., 2018; Rocktaschel
and Riedel, 2017; Serani and d'Avila Garcez, 2016;
Sourek et al., 2015; Minervini et al., 2020). Further-
more, studies using feedforward networks (Dong et
al., 2019) and recurrent neural networks (Cingillioglu
and Russo, 2018; Honda and Hagiwara, 2019; Honda
and Hagiwara, 2021) have been conducted.
3 SYMBOLIC
REPRESENTATION OF
REINFORCEMENT LEARNING
MODEL
We use Prolog (Bratko, 1990), a subsystem of first-
order predicate logic for symbolic processing, to sym-
bolize the input and output of the reinforcement learn-
ing models described. Reinforcement learning as-
sumes a Markov property, which is the property in
which the next states depend only on the current states
and actions. Therefore, it can be explained that the ac-
tions at a certain point in time are the result of the
models interpreting the states at a certain point in
time. When these are represented by the rules of
Prolog, the head of the rules is the action, and the
body of the rules is the conjunction of the states.
Figure 1 shows the environment of MountainCar-
v0, which is one of the simulation environments for
reinforcement learning provided by OpenAI Gym
(Brockman et al., 2016). MountainCar-v0 aims at
learning the agent to move the car to the top of the
mountain. Table 1 shows the actions and states of
MountainCar-v0. The outputs are actions with
discrete values of 0, 1, or 2.
Deep-Learning-based Fuzzy Symbolic Processing with Agents Capable of Knowledge Communication
173

Figure 2: Example of variable B represented by a crisp
membership function.
The input and output of the reinforcement
learning model of MountainCar-v0 can be
represented by Prolog rules, as shown in Equation (1).
action(X,A):-position(X,B),speed(X,C). (1)
In this equation, “action” indicates the action of the
agent, “position” represents the position of the car,
and “speed” is the speed of the car. The variable X is
the number of trials, variable A is the type of action,
variable B is the linguistic variable indicating the
degree of the position, and variable C is a linguistic
variable indicating the degree of the speed. Because
an action is a discrete value, the variable A takes three
types of values, i.e., “push_left,” “stay,” and
“push_right.” The position and speed of the car are
continuous values and are converted into linguistic
variables B and C, respectively.
The membership functions of the fuzzy theory are
used to convert continuous values into linguistic
variables. Figure 2 shows an example of variable B,
represented by a crisp membership function. If the
value of the car position is negative, the car is on the
left, and if it is positive, it is on the right. If the car is
on the left, variable B takes a value of “very left,”
“left,” or “a little left.” The boundary of the crisp set
on the left is the quantile of the observed negative car
position. By contrast, Figure 3 shows an example of
variable B, represented by a trapezoidal membership
function. If the car is on the left, variable B takes the
value of “very left,” “left,” or “a little left.” The
apexes of the trapezoidal set on the left are the
quantiles of the observed negative car positions.
Variable C can also be represented using the
membership functions in the same way as variable B.
Equation (2) shows an example of a rule based on
the input and output of the reinforcement learning
model.
action(10,push_right):-
position(10,very_left),
speed(10,slowl
y_
to
_
the
_
left).
(2)
Figure 3: Example of variable B represented by a trapezoi-
dal membership function.
This rule indicates the car is pushed to the right if,
during the 10th trial, the position of the car is “very
left” and the speed of the car is “slowly to the left.”
4 PROPOSED AGENTS
CAPABLE OF KNOWLEDGE
COMMUNICATION
4.1 Generation of Models using
Symbolic Representation
This subsection describes the generation of models
using symbolic representations. To generate a model
using a symbolic representation, we use data that rep-
resent the input and output of the trained reinforce-
ment learning models. Here, the linguistic variables
that are converted from the states of continuous val-
ues take up to five levels for both the positive and
negative values. In the semantic differential (SD)
(Osgood et al., 1957; Osgood et al., 1975) approach,
which is a method of impression used in evaluation
experiments, adjective pairs are expressed on a scale
of five or seven levels. In addition, the Likert scale
(Likert, 1932) often uses a 5-level scale. Therefore, in
this paper, we assume that the scale of the degree of
easy human discrimination reaches up to five levels.
For example, in MountainCar-v0, if the position of
the car is positive and is represented using 5-level val-
ues, the linguistic variables are “very small right,”
“small right,” “right,” “large right,” and “very large
right.”
The recurrent neural network proposed in Honda
and Hagiwara, 2019 was used to learn the symbolically
represented data. They compared the recurrent neural
network with the Transformer (Vaswani et al., 2017),
and the recurrent neural network performed better.
Therefore, the recurrent neural network is also used in
our proposed system. In this paper, to infer the output
from the input of the reinforcement learning model, the
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
174
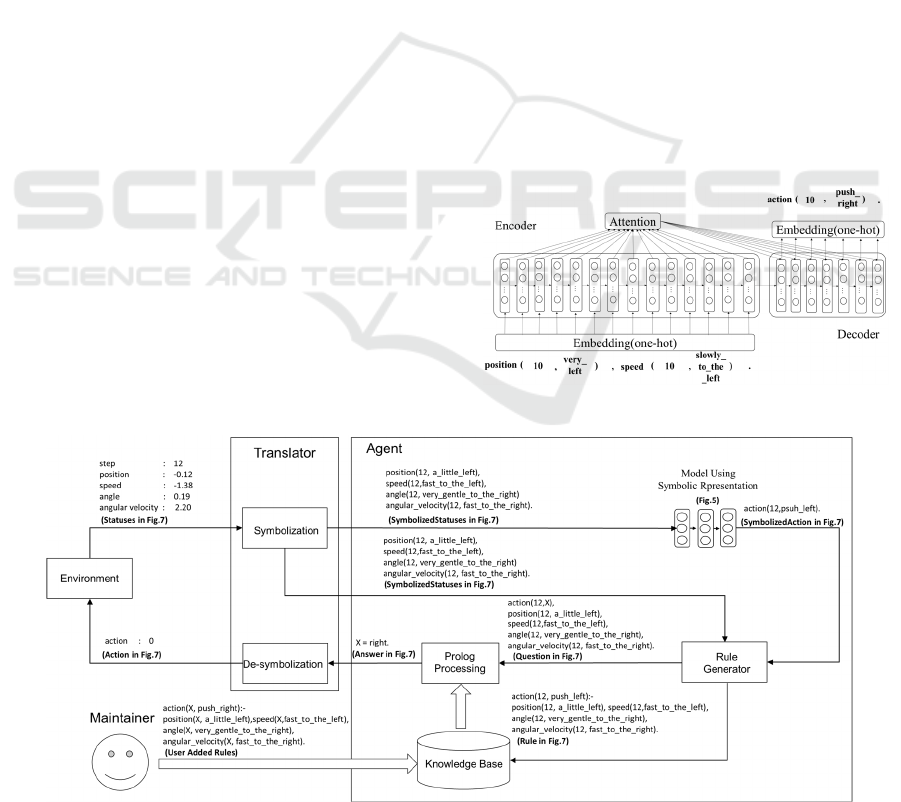
recurrent neural network is trained such that when the
body of the Prolog rule is input, the head of the Prolog
rule is output.
Figure 4 shows the recurrent neural network
proposed in this paper. First, in the input embedding
layer, the word sequence of the body is converted into
a one-hot vector. Second, the one-hot vector is passed
to Seq2Seq with an attention mechanism (Bahdanau
et al., 2015). The attention mechanism improves the
performance of Seq2Seq by inferring which part of
the input data is important. Seq2Seq with an attention
mechanism also consists of an encoder and decoder.
When the encoder receives an input sequence, it
produces a compressed vector. The attention
mechanism calculates the degree of attention given to
each word in the input sequence based on the context
of the output sequence. A weight that depends on the
degree of attention is added to the compression
vector. When the decoder receives vectors from the
encoder and attention mechanism, it generates an
output sequence. Long short-term memory (LSTM)
(Hochreiter and Schmidhuber, 1997) was used for the
encoder and decoder. We apply Bi-LSTM, which is
capable of handling future and past information at the
encoder. The Bi-LSTM consists of three layers and
has a 128-dimensional output layer. A stateless
LSTM that does not inherit short-term memory is
applied to the decoder. The stateless LSTM has a 128-
dimensional output layer and uses Maxout
(Goodfellow et al., 2013) as the activation function.
Finally, the output of Seq2Seq with an attention
mechanism is passed to the output embedding layer,
embedded in one-hot layer, and thereafter produced
as the word string of the head.
For the learning used in this paper, the dropout
rate was set to 0.1, the batch size was set to 128, and
learning was conducted for 20 epochs. Using Adam
(Kingma and Ba, 2014) as the optimizer, the
parameters were set to α = 0.001, β
1
= 0.9, β
2
= 0.999,
and eps = 1e-08.
Taking the rule of Equation (2) as an example, the
model is trained such that Equation (4) is output when
Equation (3) is input.
position(10,very_left),
speed(10,slowl
y_
to
_
the
_
left).
(3)
action(10,push
_
ri
g
ht). (4)
4.2 Agents Capable of Knowledge
Communication
This subsection describes agents capable of
knowledge communication incorporated into models
using a symbolic representation. Agents capable of
knowledge communication can reflect human inten-
tions on already trained models by inputting the rules
described by humans. It is also possible for humans
to interpret the states of the environment and convey
them to the agents.
Figure 5 shows agents capable of knowledge
communication incorporated into models using a
symbolic representation. The “Environment” in Fig-
ure 5 is a simulation environment for reinforcement
Figure 4: Model using symbolic representation.
Figure 5: Agents capable of knowledge communication.
Deep-Learning-based Fuzzy Symbolic Processing with Agents Capable of Knowledge Communication
175

Figure 6: Translator and agent algorithm.
Table 2: Actions and statuses of CartPole-v1.
Action Push to the left : 0
Push to the right : 1
Status
Cart position : -2.4 – 2.4
Cart velocity : -Inf – Inf
Pole angle : -41.8 – 41.8
Pole angula
r
velocity : -Inf
–
Inf
learning. The “Agent” in Figure 5 is an agent capable
of knowledge communication. The “Translator” in
Figure 5 converts the states of the “Environment”
from numerical values into a symbolic representation,
and converts the symbolically represented acts of the
“Agent” into numerical values. The “Translator” can
be realized programmatically, but when realized by
humans, it becomes possible to directly convey the
states of the environment to the agent. The
“Maintainer” in Figure 5 is a human who adds rules
to the “Agent.” The rules added by “Maintainer” take
precedence over the rules generated by the model
inside the “Agent.”
Figure 6 shows the algorithm of the “Translator”
and “Agent.” Here, CartPole-v1, which is a
simulation environment for reinforcement learning
provided by OpenAI Gym (Brockman et al., 2016), is
described as an example. Figure 7 shows the
environment of CartPole-v1. CartPole-v1 aims to
move the cart to balance the pole and prevent it from
tipping over. Table 2 shows the actions and states of
CartPole-v1.
When the “Translator” receives the states from the
“Environment,” the “Translator” symbolizes them
using the method described in Section 3
(Symbolization in Figure 5, and line 1 in Figure 6).
When the “Agent” receives the symbolized states, the
“Agent” inputs them into the “model using symbolic
representation” and outputs the symbolized action
(Model Using Symbolic Representation in Figure 5,
and line 2 in Figure 6). Next, a question and a rule are
generated from the symbolized states and the
symbolized action (Rule Generator in Figure 5, and
line 3 in Figure 6). If the symbolized states are as in
Equation (5) and the symbolized action is as indicated
in Equation (6), the generated rule is as shown in
Equation (7) and the question is as indicated in
Equation (8). The question is a conjunction of
symbolized states and symbolic action.
Figure 7: Environment of CartPole-v1.
position(12,a_little_left),
speed(12,fast_to_the_left),
angle(12,very_gentle_to_the_right),
an
g
ular
_
velocit
y
(12,fast
_
to
_
the
_
ri
g
ht).
(5)
action(12,push
_
left). (6)
action(12,push_left):-
position(12,a_little_left),
speed(12,fast_to_the_left),
angle(12,very_gentle_to_the_right),
an
g
ular
_
velocit
y
(12,fast
_
to
_
the
_
ri
g
ht).
(7)
action(12,X), position(12,a_little_left),
speed(12,fast_to_the_left),
angle(12,very_gentle_to_the_right),
an
g
ular
_
velocit
y
(12,fast
_
to
_
the
_
ri
g
ht).
(8)
The generated rules are added to the knowledge base
(Knowledge Base in Figure 5, and line 4 in Figure 6),
and the ”Maintainer” stores rules such as in Equation
(9) in advance in the knowledge base.
action(X,push_right):-
position(X,a_little_left),
speed(X,fast_to_the_left),
angle(X,very_gentle_to_the_right),
an
g
ular
_
velocit
y
(X,fast
_
to
_
the
_
ri
g
ht).
(9)
For example, if the angle of the pole is greatly
tilted to the left and the pole will fall regardless of
how it is controlled with the cart, suppose you want
to knock the pole down as soon as possible. In such a
case, the “Maintainer” should store in advance the
rules for moving the cart to the right when the angle
of the pole increases to the left, as shown in Equation
(9).
Prolog processing refers to the knowledge base
and answers the question (Knowledge Base in Figure
5, and line 5 in Figure 6). The rules generated by the
“Agent” are added after the rules stored by the
“Maintainer” in the knowledge base. Therefore, even
if there are multiple answers to the question, the result
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
176

Table 3: Dataset obtained from reinforcement learning
models of MountainCar-v0.
DQN DDQN
Training Data 124,753 99,937
Validation Data 16,219 12,436
Test Data 15,846 12,613
Table 4: Results of calculating the match rates from models
using the symbolic representation of MountainCar-v0.
Reinforce-
ment
Learning
Algorithm
Member-
ship Func-
tion
Number of Lin-
guistic Valua-
bles
Match Rate
DQN
Crisp
Pos.=1, Neg.=1 0.8565
Pos.=2, Neg.=2 0.9231
Pos.=3, Neg.=3 0.9598
Pos.=4, Neg.=4 0.9363
Pos.=5, Neg.=5 0.9773
Trapezoid
Pos.=2, Neg.=2 0.8942
Pos.=3, Neg.=3 0.9300
Pos.=4, Neg.=4 0.9539
Pos.=5, Neg.=5 0.9665
DDQN
Crisp
Pos.=1, Neg.=1 0.9418
Pos.=2, Neg.=2 0.9390
Pos.=3, Neg.=3 0.9726
Pos.=4, Neg.=4 0.9742
Pos.=5, Neg.=5 0.9743
Trapezoid
Pos.=2, Neg.=2 0.9244
Pos.=3, Neg.=3 0.9386
Pos.=4, Neg.=4 0.9432
Pos.=5, Neg.=5 0.9481
Table 5: Dataset obtained from reinforcement learning
models of CartPole-v1.
DQN DDQN
Training Data 136,386 141,269
Validation Data 16,919 17,564
Test Data 17,190 17,933
of the rule stored by the “Maintainer” in the
knowledge base is output first. Finally, the
“Translator” de-symbolizes the answer received from
the “Agent” such that it can be input into the
“Environment” (De-symbolization in Figure 5, and
line 6 in Figure 6) If the answer is Equation (10), it
will be zero because it means “pushed to the right.”
X=right. (10)
The de-symbolized act is passed to the
“Environment.”
5 EVALUATION EXPERIMENTS
The models were trained using two types of reinforce-
ment learning simulation environments, and the
agents incorporating them were built. In this section,
we discuss the experimental results.
5.1 Experiments using
MountainCar-V0
Agents were built by reproducing models using sym-
bolic representations from the reinforcement learning
models of MountainCar-v0. Two types of reinforce-
ment learning algorithms were used: deep Q network
(DQN) (Mnih et al., 2013) and double deep Q net-
work (DDQN) (Hado et al., 2016). Both DQN and
DDQN models were trained until the average reward
for one episode exceeded 160. The maximum number
of trials per episode was 200. DQN spent 7,800 epi-
sodes and DDQN spent 3,200 episodes to learn
MountainCar-v0.
Table 3 shows the dataset obtained from the
trained reinforcement learning models. We repeated
trials with the trained models to build the dataset. The
dataset contained the states and acts for each number
of trials. The dataset was randomized and divided into
training data, validation data, and test data. Table 4
shows the results of calculating the match rates from
the model using the symbolic representation trained
from the dataset in Table 3. To generate models using
a symbolic representation, we created multiple data
from the dataset in Table 3 using membership
functions that varied the number of linguistic
variables for the position and speed of the car. Two
types of membership functions, i.e., the crisp type and
the trapezoid type described in Section 3, were used.
The continuous values of the states were converted
into linguistic variables by the method described in
Subsection 4.1. Here, the match rate is the rate at
which the output obtained by inputting the state of the
test data into the models using the symbolic
representation exactly matches the behavior of the
test data.
5.2 Experiments using CartPole-V1
Agents were built by reproducing models using sym-
bolic representations from the reinforcement learning
models of CartPole-v1. Two types of reinforcement
learning algorithms were used: DQN and DDQN.
Both DQN and DDQN models were trained until the
average reward for one episode exceeded 200. The
maximum number of trials per episode was 200. DQN
spent 2,187 episodes and DDQN spent 820 episodes
to learn CartPole-v1.
Table 5 shows the dataset obtained from the
trained reinforcement learning models. We repeated
trials with the trained models to build the dataset. The
dataset contained states and acts for each number of
trials. The dataset was randomized and divided into
training data, validation data, and test data. Table 6
Deep-Learning-based Fuzzy Symbolic Processing with Agents Capable of Knowledge Communication
177

shows the results of calculating the match rates from
the model using the symbolic representation trained
from the dataset in Table 5. To generate models using
a symbolic representation, we created multiple data
from the dataset in Table 5 using membership
functions that varied the number of linguistic
variables for the position and speed of the cart, and
the angle and angular velocity of the pole. Two types
of membership functions, i.e., the crisp type and
trapezoid type described in Section 3, were used. The
continuous values of the states were converted into
linguistic variables by the method described in
Subsection 4.1.
5.3 Discussion
In the experimental results of both MountainCar-v0
and CartPole-v1, the reinforcement learning algo-
rithm showed high match rates for both DQN and
DDQN. Therefore, our proposed method is consid-
ered effective, regardless of the reinforcement learn-
ing algorithm applied. Furthermore, since the dataset
was randomized, the reproduced models have Mar-
kov property the same as reinforcement learning
models.
The experimental results of both MountainCar-v0
and CartPole-v1 tended to increase the match rates as
the number of linguistic variables increased. This is
thought to be because a larger number of linguistic
variables resulted in a greater number of rules that can
be represented. By contrast, when the crisp
membership functions were used, the match rate of
MountainCar-v0 was 0.9773 and the match rate of
CartPole-v1 was 0.9123 within the range of up to five
linguistic variables. When the trapezoid membership
functions were used, the match rate of MountainCar-
v0 was 0.9665 and the match rate of CartPole-v1 was
0.9080 within the range of up to five linguistic
variables. Within the range of up to five linguistic
variables, which are assumed to be easy for humans
to distinguish, all match rates were high.
Furthermore, the experimental results of both
MountainCar-v0 and CartPole-v1 showed high match
rates for both the crisp membership functions and the
trapezoidal membership functions. When humans
observe the states of the environment and represent
symbols, ambiguity occurs, and thus it is considered
practical to use trapezoidal membership functions. In
the case of the trapezoidal membership functions, the
match rates were almost the same as those of the crisp
functions, even though the linguistic variables were
stochastically selected.
Table 6: Results of calculating the match rates from models
using the symbolic representation of CartPole-v1.
Reinforcement
Learning
Algorithm
Membership
Function
Number of
Linguistic
Valuables
Match Rate
DQN
Crisp
Pos.=1, Neg.=1 0.8593
Pos.=2, Neg.=2 0.8850
Pos.=3, Neg.=3 0.8934
Pos.=4, Neg.=4 0.8921
Pos.=5, Neg.=5 0.8901
Trapezoid
Pos.=2, Neg.=2 0.8697
Pos.=3, Neg.=3 0.8700
Pos.=4, Neg.=4 0.8789
Pos.=5, Neg.=5 0.8753
DDQN
Crisp
Pos.=1, Neg.=1 0.9002
Pos.=2, Neg.=2 0.8991
Pos.=3, Neg.=3 0.9063
Pos.=4, Neg.=4 0.9048
Pos.=5, Neg.=5 0.9123
Trapezoid
Pos.=2, Neg.=2 0.9012
Pos.=3, Neg.=3 0.9001
Pos.=4, Neg.=4 0.9026
Pos.=5, Neg.=5 0.9080
6 CONCLUSION
We proposed methods for reproducing deep learning
models using symbolic representations from deep re-
inforcement learning models and for building agents
capable of knowledge communication with humans.
In this paper, fuzzified states of environments and
acts of agents are represented by rules of first-order
predicate logic, and models using symbolic represen-
tation are generated by learning them through recur-
rent neural networks. Then, by replacing deep rein-
forcement learning models with models using sym-
bolic representations, it is possible for humans to in-
form the states of the environment and add rules to
the agents.
We believe that this proposal can contribute to
practical applications of coaching such as driving a
car and playing video games. Our proposal suggests
that agents will be able to develop human skills.
Future work will consider applying our proposal
to various reinforcement learning simulation
environments, such as when the agent's actions take
continuous values, when the states are represented by
images, and when the rules are required negative
literals.
REFERENCES
Alejandro, A., Natalia, D., Javier, S., Adrien, B., Siham, T.,
Alberto, B., Salvador, G., Sergio, G., Daniel, M., Ri-
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
178

chard, B., Raja, C., and Francisco, H., (2020). Explain-
able Artificial Intelligence (XAI): Concepts, taxono-
mies, opportunities and challenges toward responsible
AI, Information Fusion, volume 58, pages 82-115.
Bahdanau, D., Cho, K., and Bengio, Y., (2015). Neural ma-
chine translation by jointly learning to align and trans-
late, in ICLR, San Diego, CA, USA.
Bratko I., (1990). Prolog Programming for Artificial Intel-
ligence. 2nd ed., Addison-Wesley Publishing Company,
USA, pages 597.
Brockman, G., Cheung, V., Pettersson, L., Schneider,
Schulman, J., Tang, J., J., and Zaremba, W., (2016).
Openai gym, arXiv preprint arXiv: 1606.01540.
Cingillioglu, N. and Russo, A., (2018). DeepLogic: To-
wards end-to-end differentiable logical reasoning,
arXiv preprint arXiv: 1805.07433.
Cohen, W., (2016). Tensorlog: A differentiable deductive
database, arXiv preprint arXiv: 1605.06523.
Coppens, Y., Efthymiadis, K., Lenaerts, T., Nowe, A., Mil-
ler, T., Weber, R., and Magazzeni, D., (2019). Distilling
deep reinforcement learning policies in soft decision
trees, in Proc. of the IJCAI 2019 Workshop on Explain-
able Artificial Intelligence, pages 1-6.
Dong, H., Mao, J., Lin, T., Wang, C., Li, L., and Zhou, D.,
(2019). Neural logic machines, in Proc. of International
Conference on Learning Representations, New Orle-
ans, Louisiana, USA.
Fukuchi, Y., Osawa, M., Yamakawa, H., and Imai, M.,
(2017). Autonomous selfexplanation of behavior for in-
teractive reinforcement learning agents, in Proc. of the
5th International Conference on Human Agent Interac-
tion - HAI ’17. ACM Press.
Goodfellow, I., Warde-Farley, D., Mirza, M., Courville, A.,
and Bengio, Y., (2013). Maxout networks, in Proc. of
the 30th International Conference on Machine Learn-
ing, Atlanta, Georgia, USA.
Hado, H., Arthur, G., and David, S., (2016). Deep rein-
forcement learning with double Q-learning, Thirtieth
AAAI Conference on Artificial Intelligence, volume 30,
number 1.
Hochreiter, S. and Schmidhuber, J., (1997). Long short-
term memory, Neural Computation, volume 9, number
8, pages 1735-1780.
Honda, H. and Hagiwara, M., (2019). Question answering
systems with deep learning-based symbolic processing,
in IEEE Access, volume 7, pages 152368-152378.
Honda, H. and Hagiwara, M., (2021). Analogical Reason-
ing With Deep Learning-Based Symbolic Processing,
in IEEE Access, volume 9, pages 121859-121870.
Kingma, D. and Ba, J., (2014). Adam: A method for sto-
chastic optimization, arXiv preprint arXiv: 1412.6980
.
Lee, J. H., (2019). Complementary reinforcement learning
towards explainable agents, arXiv preprint arXiv:
1901.00188.
Likert, R., (1932). A technique for the measurement of atti-
tudes, Archives of Psychology, volume 140, number 55.
Lipton, Z.C., (2018). The mythos of model interpretability,
Communications of the ACM, volume 61, number 10,
pages 36-43.
Madumal, P., Miller, T., Sonenberg, L., and Vetere, F.,
(2019). Explainable reinforcement learning through a
causal lens, arXiv preprint arXiv: 1905.10958.
Minervini, P., Bosnjak M., Rocktschel, T., and Riedel, S.,
(2018). Towards neural theorem proving at scale, arXiv
preprint arXiv: 1807.08204.
Minervini, P., Riedel, S., Stenetorp, P., Grefenstette, E., and
Rocktäschel, T., (2020). Learning Reasoning Strategies
in End-to-End Differentiable Proving, in Proc. of the
37th International Conference on Machine Learning,
PMLR 119, pages 6938-6949.
Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., Anto-
noglou, I., Wierstra, D., and Riedmiller, M. (2013).
Playing Atari with deep reinforcement learning, arXiv
preprint arXiv:1312.5602.
Montavon, G., Samek, W., and Muller, K.R., (2018) Meth-
ods for interpreting and understanding deep neural net-
works, Digital Signal Processing, volume 73, pages 1-
15.
Osgood, C. E., Suci, G., and Tannenbaum, P., (1957). The
measurement of meaning, Urbana, IL: University of Il-
linois Press.
Osgood, C. E., May, W. H., and Miron, M. S., (1975).
Cross-Cultural Universals of Affective Meaning, Ur-
bana, IL: University of Illinois Press.
Rocktaschel, T. and Riedel, S., (2017). End-to-end differ-
entiable proving, in Proc. of the NIPS 30, pages 3788-
3800.
Sequeira, P. and Gervasio, M., (2019). Interestingness ele-
ments for explainable reinforcement learning: Under-
standing agents, capabilities, and limitations, arXiv pre-
print arXiv: 1912.09007.
Serani, L. and d'Avila Garcez, A. S., (2016). Logic tensor
networks: Deep learning and logical reasoning from
data and knowledge, in Proc. of the 11th International
Workshop on Neural-Symbolic Learning and Reason-
ing (NeSy’16) co-located with the Joint Multi-Confer-
ence on Human-Level Artificial Intelligence (HLAI
2016), New York City, NY, USA.
Sourek, G., Aschenbrenner, V., Zelezny, F., and Kuzelka,
O., (2015). Lifted relational neural networks, in Proc.
of the NIPS Workshop on Cognitive Computation: Inte-
grating Neural and Symbolic Approaches co-located
with the NIPS 29, Montreal, Canada.
Vaswani,A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,
L., Gomez, A., Kaiser, L., and Polosukhi, I., (2017). At-
tention Is All You Need, in Proc. of the NIPS 31
, pages
5998–6008.
Waa, J., Diggelen, J., Bosch, K., and Neerincx, M., (2018).
Contrastive explanations for reinforcement learning in
terms of expected consequences, IJCAI-18 Workshop
on Explainable AI (XAI), volume 37.
Deep-Learning-based Fuzzy Symbolic Processing with Agents Capable of Knowledge Communication
179
