Whale Optimization-based Prediction for Medical Diagnostic

Ali Asghar Rahmani Hosseinabadi

, Mehdi Sadeghilalimi

, Morteza Babazadeh Shareh

Malek Mouhoub

1 a

and Samira Sadaoui

University of Regina, 3737 Wascana Parkway, Regina, Canada

Islamic Azad University, Babol Branch, Babol, Iran

Keywords:

Feature Importance, Meta-heuristics Optimization, Nature-inspired Techniques, Combinatorial Optimization,

Supervised Learning.

Abstract:

This study aims to improve disease detection accuracy by incorporating a discrete version of the Whale Opti-

mization Algorithm (WOA) into a supervised classiﬁcation framework (KNN). We devise the discrete WOA

by redeﬁning the related components to operate on discrete spaces. More precisely, we redeﬁne the notion of

distance (between individuals in WOA), and propose a random exploration function to include more diversity.

The latter includes the random move deﬁned in the WOA algorithm, as well as two other random techniques

based on the crossover and mutation operators. To assess the performance of our proposed method, we con-

ducted experiments on two benchmark medical datasets. The results demonstrate the efﬁcacy of the hybrid

approach, WOA+KNN.

1 INTRODUCTION

Nowadays, automated diagnostic systems are an inte-

gral part of numerous medical applications. Initially,

researchers adopted machine learning algorithms to

assist physicians in their decision-making tasks. More

recently, researchers were motivated to incorporate

meta-heuristic optimization methods to improve the

prediction outcome and reduce false alarms. For

instance, the authors in (Shankar and Manikandan,

2019) proposed a new approach combining the Grey

Wolf Optimization Algorithm (GWOA) with Fuzzy

Logic. First, the diagnostic model is formed based on

a set of Fuzzy rules. Then this set of rules is opti-

mized using GWOA, which is found to be more efﬁ-

cient than the Ant Colony Optimization (ACO) algo-

rithm. In (Alirezaeia et al., 2019), the authors utilized

K-means for clustering patient data and removing out-

liers. Then, they developed four multi-objective meta-

heuristic optimization methods that are integrated into

a Support Vector Machine (SVM) classiﬁer to select

the features more accurately. The experimental re-

sults demonstrated that the accuracy increased signiﬁ-

cantly. The study in (Bhuvaneswari and Manikandan,

2018) proposed a new diagnostic system by devising

a classiﬁer called “Temporal Feature Selection and

https://orcid.org/0000-0001-7381-1064

Temporal Fuzzy Ant Miner Tree”. A modiﬁed version

of the Genetic Algorithm was also utilized in the pro-

posed method, to increase diagnosis detection. This

new method has a high detection capability compared

to other techniques. Lastly, the work in (Giveki and

Rastegar, 2019) adopted the RBF-based Neural Net-

work together with the Harmony Search optimization

algorithm to improve efﬁciency in medical diagnos-

ing. Combining these two methods showed a higher

performance.

This present study is preliminary work on enhanc-

ing machine learning algorithms to improve med-

ical diagnostic performance. Following on previ-

ous research works, we develop a hybrid approach

based on the Whale Optimization Algorithm (WOA)

(Mirjalili and Lewis, 2016) and K-Nearest Neighbors

(KNN) algorithm to tackle disease diagnostic more

efﬁciently. Generally speaking, we determine the op-

timal weights of the predictive features using the dis-

cretization of WOA, train KNN on the weighted data,

and test the learned model on unseen data. For this

purpose, we incorporate a discrete version of WOA

intending to optimize the weights of the feature space

of the training medical datasets. We deﬁne the dis-

crete version of WOA by redeﬁning the related com-

ponents to operate on discrete spaces. In addition,

we devise a random function to better conduct the

exploration phase. This latter is based on the Ge-

Hosseinabadi, A., Sadeghilalimi, M., Shareh, M., Mouhoub, M. and Sadaoui, S.

Whale Optimization-based Prediction for Medical Diagnostic.

DOI: 10.5220/0010802200003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 3, pages 211-217

ISBN: 978-989-758-547-0; ISSN: 2184-433X

211

netic Algorithm’s operators to add more diversity. We

note that various discrete variants of WOA have been

reported in the literature. These variants have been

mainly deﬁned to tackle speciﬁc learning problems

including: image segmentation (Aziz et al., 2017),

parameter tuning of neural networks (Aljarah et al.,

2018), parameter estimation of solar cells (Oliva et al.,

2017), and classical combinatorial problems such as

the Knapsack problem (Li et al., 2020) and the Trav-

eling Salesman Problem (TSP) (Zhang et al., 2021).

The main difference between our proposed method

and the above variants is regarding the discretization

of the equations guiding the WOA, as well as the op-

erator we suggest to conduct better exploration. In

this regard, we propose a function that performs one

of the following three random movements depending

on the value of a given random parameter: (1) shrink-

ing towards a random whale, (2) a crossover with a

random whale, and (3) a random mutation. Our main

objective is to improve medical diagnosis by opti-

mizing the WOA ﬁtness function during the training

phase.

We fully implement our hybrid approach

WOA+KNN using the MATLAB toolkit. We utilize

two benchmark medical diagnostic datasets to evalu-

ate the proposed method performance: the diabetic

Type 2 dataset (called PID) and the electrocardio-

gram dataset (called ECG200). We select these

two datasets given that they are challenging; both

are of small size, which may under-ﬁt the learned

classiﬁcation models, and the second dataset’s size is

relatively small compared to its dimensionality.

We organize the paper as follows. The follow-

ing section describes the original WOA (Mirjalili and

Lewis, 2016). Section 3 explains the discretization

of WOA and its integration into a supervised classi-

ﬁcation framework. Section 4 evaluates the proposed

hybrid approach using the two medical datasets. Fi-

nally, Section 5 lists concluding remarks and ideas for

future works.

2 WHALE OPTIMIZATION

ALGORITHM (WOA)

WOA is a population-based algorithm drawn from

the collective hunting of whales (humpback whales)

representing potential solutions (Mirjalili and Lewis,

2016; Sangaiah et al., 2020). In this regard, the forag-

ing behavior of whales is performed via crating bub-

bles in a spiral manner. Whales movement towards

the prey follows an exploitation/exploration strategy

(Mirjalili and Lewis, 2016). Exploitation is achieved

through shrinking encircling and spiral motions. In

the former, each whale approaches the prey by ro-

tating around it. In the second method, each whale

approaches the prey by following a spiral curve. Fol-

lowing the assumption that the prey’s position is the

same or close to the one of the Best Whale (BW),

each of the other whales will update its position dur-

ing a shrinking encircling motion, through the follow-

ing equations deﬁned in (Mirjalili and Lewis, 2016).

D = |CX

∗

(t) − X(t)|

X(t + 1) = X

∗

(t) − AD

(1)

In the above, t and t + 1 are the current and the

next iterations, respectively. X

∗

and X are respec-

tively the position of BW and a given whale. A and C

are computed as follows.

A = 2ar − a

C = 2r

(2)

a and r are random parameters in [0,2] and [0,1],

respectively. Note that a decreases at each iteration

from 2 to 0 to achieve shrinking. The Spiral motion

is obtained through the following equation (Mirjalili

and Lewis, 2016).

X(t + 1) = D

′

cos(2πl) + X

∗

(t) (3)

In the above, l is a random number in [-1,1], b is

a constant used to set the spiral curve. The distance

between each whale and the prey, D

′

, is computed as

follows (Mirjalili and Lewis, 2016).

′

= |X

∗

(t) − X(t)| (4)

In exploration, each whale searches for the prey

randomly by updating its position according to a ran-

domly chosen whale (instead of moving towards BW,

as done above in shrinking encircling and spiral mo-

tion). The related equations for the random move are

as follows (Mirjalili and Lewis, 2016).

D = |CX

rand

(t) − X(t)|

X(t + 1) = X

rand

(t) − AD

(5)

In the above, X

rand

is a randomly chosen whale.

Given the above equations guiding the exploita-

tion and exploration strategies, the WOA algorithm

works as follows. A random number named p is taken

from [0,1]. If p is greater or equal to 0.5, then the

whale moves in spiral motion. Otherwise, we need

to check the value of A. If |A| is less or equal to 1,

then the shrinking encircling operation will be exe-

cuted. Otherwise, the whale will move randomly as

described above. Note that at the beginning of the al-

gorithm, the value of A is likely greater than 1, which

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

212

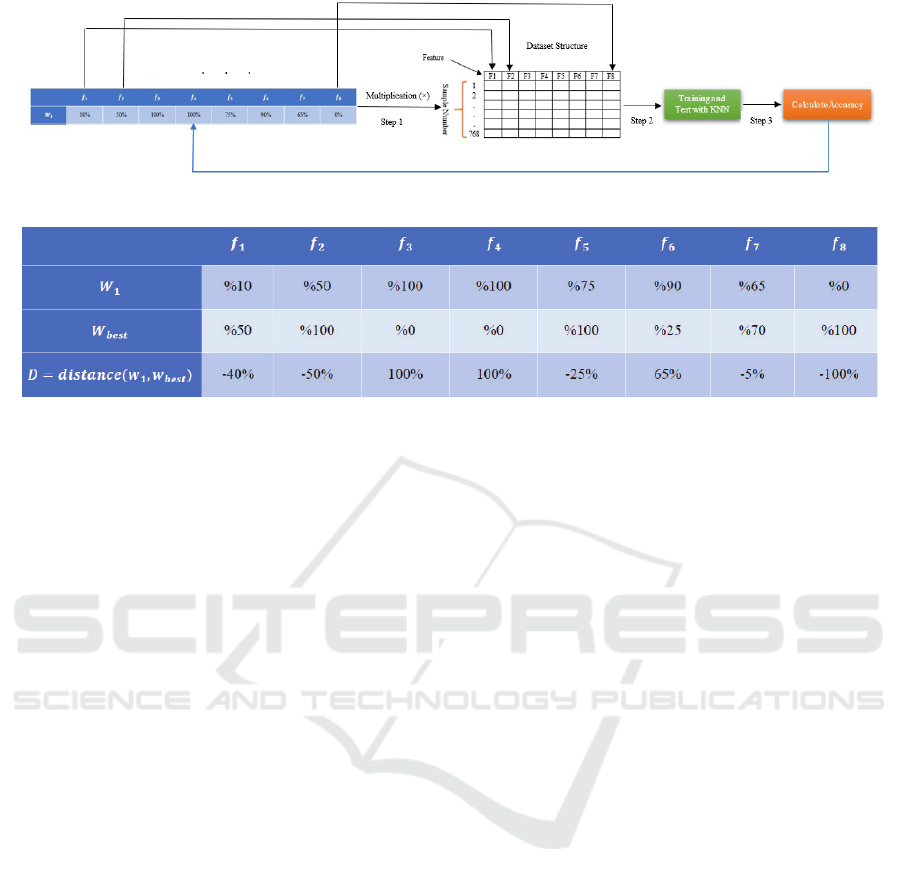
Figure 1: Process of calculating the accuracy (ﬁtness) of an individual.

Figure 2: Distance between two individuals.

will allow more exploration. Then, as the value of a

decreases, the value of A will often become less than

1, which will favor more shrinking. This reﬂects the

behaviour of the algorithm with more exploration at

the beginning, followed by more exploitation at the

end.

Given that WOA was proposed to solve con-

tinuous optimization problems (Mirjalili and Lewis,

2016), we need to adapt it to discrete spaces to be

able to tune the weights of the features of the patient

dataset. The discretization of the different compo-

nents of WOA is described in the next section.

3 DISCRETIZATION OF WOA

3.1 Individual Representation and

Fitness Function

Each individual (whale) is represented with a vec-

tor of weights, each corresponding to the degree of

importance/participation of the related KNN feature.

For instance, if the weight (degree of importance) of

a given feature is 100%, then the latter should be fully

present in the classiﬁcation. A weight of 0% indicates

that the feature should not be considered in the clas-

siﬁcation. If the weight is equal to 50%, then the fea-

ture should participate in the classiﬁcation with half

of its power. The length of the vector is equal to the

dimensionality of the dataset. The left table in Fig-

ure 1 shows an example of a vector corresponding to

a dataset with eight features. The ﬁtness function of a

given whale (individual) corresponds to the accuracy

of the KNN model using the weights (features degree

of importance) listed in the corresponding vector. Fig-

ure 1 shows how the ﬁtness (accuracy) is computed,

through the following three steps.

1. The value of each feature weight is multiplied by

the corresponding feature column of the dataset.

For example, the weight of the ﬁrst feature (10%)

is multiplied by the 768 samples in the ﬁrst col-

umn.

2. The classiﬁcation will be performed by KNN al-

gorithm according to the vector of weights, fol-

lowing 60% for training and 40% for testing, for

instance.

3. The obtained accuracy will be considered as the

corresponding ﬁtness value.

3.2 Distance, Spiral and Shrinking

Functions

We deﬁne the distance between two individuals as the

pairwise difference between the entries in the related

vectors. Note that the distance is not symmetric. Fig-

ure 2 shows an example of a distance between two

individuals.

Shrinking and spiral functions are implemented

based on the equations we listed in the previous sec-

tion, and the new notion of distance we deﬁned above.

More precisely, at each step of the algorithm, the dis-

tance is calculated according to equations 1 or 4 (for

each pair of features in both X

∗

(t) and X(t + 1)) and

a percentage, A, of the result will be subtracted from

∗

(t) to get the value for X(t + 1). This will allow

X(t) to get closer to X

∗

(t) via shrinking or spiral mo-

tion.

Whale Optimization-based Prediction for Medical Diagnostic

213

Figure 3: Example of crossover function with crossover point equals to 3.

3.3 Exploration: Random Function

Rather than having one random function (as described

in the previous section) where whales move toward a

random one via shrinking, we deﬁne a random func-

tion offering more diversity. The pseudo-code, listed

in Figure 4, performs one of the following three op-

erations, depending on the value of a given random

parameter rand: shrinking (toward a random whale,

as in the traditional WOA described in the previous

section), crossover, or mutation. The crossover func-

tion performs a 1-point crossover (according to a ran-

dom crossover point) between W

and another ran-

domly selected whale (W

). The mutation function

selects some values from W

and then changes them

randomly.

Random Function (W

)

rand = a random number in [0, 1];

randomly select W

if (rand < 0.25)

= shrinking(W

);

elseif (0.25 ≤ rand < 0.5)

= crossover(W

);

else (rand ≥ 0.5)

= mutation(W

);

return W

;

Figure 4: Pseudo-code of the random function.

4 VALIDATION

4.1 PID Dataset

Through a well-known benchmark dataset, the Pima

Indian Diabetes (PID) (Giveki and Rastegar, 2019),

we assess our hybrid method’s performance. The PID

dataset consists of 768 patients, where all are females

aged at least 21 years old. The balanced dataset has

eight numerical features listed in Table 1. The target

class is either diabetic or healthy. Since the features

possess different scales, we normalize all of them to

the range of [0, 1]. We tune the WOA’s parameters as

presented in Table 2. We train the KNN classiﬁer with

the training dataset (70%) and then assess its predic-

tive performance on the testing dataset (30%).

Table 1: Features of PID Dataset (Giveki and Rastegar,

2019).

Feature Diagnosis Unit

#1 Number of pregnancies Integer

#2 Plasma glucose concentration Mg/dl

#3 Diastolic blood pressure mmHg

#4 Triceps skin fold thickness Mm

#5 2-h serum insulin MuU/mL

#6 Body mass index Kg/m

#7 Diabetes pedigree function Integer

#8 Age Year

Table 2: Parameter Tuning for PID Dataset.

Parameter Deﬁnition Value

n Number of whales 200

k Number of whale movements 500

prob Possibility of changing rand(100)

whale cell

a Change the discovery phase 2

to optimization

train Percentage of learning data 70%

The best solution for the diabetes diagnostic re-

turned by the WOA+KNN method is exposed in Ta-

ble 3. We observe that the two features “Plasma glu-

cose concentration” (F2) and “Blood pressure” (F3)

are the most important to identify diabetes. The least

relevant feature is the “Amount of insulin” (F5). The

values of the columns in the normalized PID dataset

must be multiplied by the optimal values of Table 3 to

increase the detection accuracy. As observed in Table

4, WOA+KNN outperforms KNN across all the qual-

ity metrics, with an increase of 9.84% in Accuracy

and 12.22% in F1-score. This increase is important in

medical diagnostic to increase the disease diagnostic.

Table 3: Best Solution for PID Dataset.

F1 F2 F3 F4 F5 F6 F7 F8

39 52 52 11 2 47 22 35

One of the essential points to consider in the pro-

posed algorithm is the trend of changes in the best

answer’s value. To this end, the best whale’s ﬁt value,

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

214

Table 4: Predictive Performance with/without optimization for PID Dataset.

Classiﬁer Accuracy Recall Precision F1-Score

WOA+KNN 91.29 92.79 91.18 91.97

KNN 81.45 81.29 78.27 79.75

(a)

(b)

Figure 5: (a) Change in amount of ﬁt to the best answer, (b)

Process of changes in ﬁt of all whales.

in each round of the algorithm, is kept in an array,

and a diagram is then drawn from it. Figure 5 de-

picts the best ﬁt changes during the 500 rounds of the

algorithm run. As we can observe, the ﬁt value is

optimized gradually during run-time. After each it-

eration, the next optimization occurs at a greater dis-

tance. In fact, the higher the performance of the al-

gorithm, the more difﬁcult the optimization response

becomes. The whale’s hunting inspires the WOA be-

havior. Consequently, its function should be such that,

eventually, all the whales get closer to the prey. In

other words, at the end of the algorithm, all whales

must be close to the optimal whale. This approach

should happen progressively. Figure 5 illustrates the

process of changes in the ﬁt of all the whales. As

seen in the ﬁgure, the whales are initially far from the

optimal answer but eventually move around the best

whales.

4.2 ECG200 Dataset

Table 5: Parameter Tuning for ECG200 Dataset.

Parameter Deﬁnition Value

n Number of whales 100

k Number of whales’ movements 100

prob Possibility of changing rand(100)

whale cell

a Change the discovery phase 2

to optimization

train Percentage of learning data 50%

We experiment with the proposed approach this

time using a higher dimensional dataset, called

ECG200, described in (Ding et al., 2008). ECG200 is

the most frequently used benchmark dataset for eval-

uating time-series. It consists of 200 ECG signals and

96 quantitative features. For each timestamp, a record

reﬂects one heartbeat signal. Out of the 200 records,

133 were annotated as Normal, while 67 as Abnormal

(cardiac disease). The imbalanced class distribution

ratio is low, so no need to re-balance the dataset.

We apply WOA+KNN to the EGC dataset and set

the parameters presented in Table 5. The method op-

timizes the weights of the entire feature space, and in

Table 6, among the 96 features, we expose the top 40

features and their weights. Features F#8 and F#28 are

the most relevant to the target class.

In Table 7, we compute the average for each met-

ric for ten runs. The hybrid method WOA+KNN

attained high Accuracy of 97% and F1-Score of

97.67%, even though we are dealing with high dimen-

sionality. The outcome of the KNN classiﬁer with-

out any feature optimization is only 89% for Accu-

racy and 88% for F1-score. As seen, using the meta-

heuristic optimization technique improved the KNN

classiﬁcation performance. However, WOA+KNN

took much more time, which is expected.

The research (Anowar et al., 2021) adopted dif-

ferent categories of feature extraction methods, such

as unsupervised vs. supervised, linear vs. non-linear,

and manifold vs. random projection, which is com-

bined with the supervised classiﬁcation framework

Whale Optimization-based Prediction for Medical Diagnostic

215

Table 6: Best Solution For ECG200 Dataset (top 40 features).

F1 F2 F3 F4 F6 F8 F11 F14 F15 F16

55 32 51 38 57 87 38 45 75 32

F17 F21 F24 F25 F28 F29 F31 F32 F33 F36

78 44 45 50 96 30 52 30 40 38

F37 F38 F41 F42 F44 F46 F51 F56 F62 F65

71 31 80 67 41 55 58 57 70 32

F66 F67 F72 F75 F77 F78 F79 F81 F85 F93

35 59 62 34 58 38 44 46 69 38

Table 7: Predictive Performance with/without optimization for ECG200 Dataset.

Classiﬁer Accuracy Recall Precision F1-Score Time

WOA+KNN 97 98.43 96.93 97.67 180s

KNN 89 88 89 88.49 4s

(a) (b)

(c)

Figure 6: (a): Best whale’s ﬁtness in each round, (b): Whales’ ﬁtness in each round, (c): Whales’ movement in each round.

Kernel SVM. More precisely, the authors assessed

and compared the performances of KPCA, LDA,

MDS, SVD, LLE, ISOMAP, LE, ICA, t-SNE us-

ing the same electrocardiography dataset. The high-

est F1-score of 90.03% was obtained with the Ker-

nel PCA+Kernel SVM. Therefore, the WOA+KNN

approach may outperform dimensionality reduction

methods.

Figure 6(a) shows the ﬁtness value of the best

whale in each round. At the beginning of the al-

gorithm, the best ﬁtness is 92% but in less than 10

rounds, we reach the promising ﬁtness of 95%. The

nest improvement is somewhere between 50 and 60.

The last optimization is after round 60 and beyond

that there is no any optimization that occurred. Fi-

nally, the last and best ﬁtness after 100 rounds of exe-

cution is 97%. Figure 6(b) depicts the value of ﬁtness

of all the whales. Due to the highly random behav-

ior of algorithm in the early rounds, the ﬁtness values

of solutions are highly scattered, but gradually the al-

gorithm moves from exploration phase to exploitation

phase and as a result all the ﬁtness values tend to be

optimized. In the last round, all the solutions are near

the best answer. Figure 6(c) shows the difference in

whale motion at each stage of motion. The vertical

axis is the sum of the current and previous differences

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

216

of the whale vector. Here, the whales move quickly in

the middle of the algorithm and get close to the prey.

5 CONCLUSION AND FUTURE

WORK

Our study is ongoing research that aims to improve

medical diagnostic performance by fusing a discrete

version of the meta-heuristic optimization method

WOA with supervised classiﬁcation. We designed the

discrete WOA by redeﬁning the related components

for discrete spaces and a new exploration function to

include more diversity. The whale ﬁtness is calculated

based on the classiﬁcation accuracy using the KNN

classiﬁer. The feature space is re-scaled based on the

whales’ values before the learning task. The experi-

mental results demonstrated that the WOA+KNN ap-

proach increased the performance of machine learn-

ing algorithms.

One exciting but challenging research direction is

to incorporate WOA and other nature-inspired tech-

niques (Mouhoub and Wang, 2008; Bidar et al.,

2018a; Abbasian et al., 2011; Bidar et al., 2018b;

Hmer and Mouhoub, 2016) to the incremental learn-

ing setting where the classiﬁer is updated gradually

with new observations but without re-training from

scratch.

REFERENCES

Abbasian, R., Mouhoub, M., and Jula, A. (2011). Solving

graph coloring problems using cultural algorithms. In

Murray, R. C. and McCarthy, P. M., editors, Proceed-

ings of the Twenty-Fourth International Florida Arti-

ﬁcial Intelligence Research Society Conference, May

18-20, 2011, Palm Beach, Florida, USA. AAAI Press.

Alirezaeia, M., Niaki, S. T. A., and Niaki, S. A. A. (2019).

A bi-objective hybrid optimization algorithm to re-

duce noise and data dimension in diabetes diagnosis

using support vector machines. Expert Systems with

Applications, 127:47–57.

Aljarah, I., Faris, H., and Mirjalili, S. (2018). Opti-

mizing connection weights in neural networks us-

ing the whale optimization algorithm. Soft Comput.,

22(1):1–15.

Anowar, F., Sadaoui, S., and Selim, B. (2021). Concep-

tual and empirical comparison of dimensionality re-

duction algorithms (PCA, KPCA, LDA, MDS, SVD,

LLE, ISOMAP, LE, ICA, t-SNE). Computer Science

Review, 40:100378.

Aziz, M. A. E., Ewees, A. A., and Hassanien, A. E. (2017).

Whale optimization algorithm and moth-ﬂame opti-

mization for multilevel thresholding image segmenta-

tion. Expert Systems with Applications, 83:242–256.

Bhuvaneswari, G. and Manikandan, G. (2018). A novel

machine learning framework for diagnosing the type 2

diabetics using temporal fuzzy ant miner decision tree

classiﬁer with temporal weighted genetic algorithm.

Computing, 100:759––772.

Bidar, M., Kanan, H. R., Mouhoub, M., and Sadaoui,

S. (2018a). Mushroom reproduction optimization

(mro): a novel nature-inspired evolutionary algorithm.

In 2018 IEEE congress on evolutionary computation

(CEC), pages 1–10. IEEE.

Bidar, M., Sadaoui, S., Mouhoub, M., and Bidar, M.

(2018b). Enhanced ﬁreﬂy algorithm using fuzzy pa-

rameter tuner. Comput. Inf. Sci., 11(1):26–51.

Ding, H., Trajcevski, G., Scheuermann, P., Wang, X., and

Keogh, E. (2008). Querying and mining of time

series data: Experimental comparison of representa-

tions and distance measures. Proc. VLDB Endow.,

1(2):1542–1552.

Giveki, D. and Rastegar, H. (2019). Designing a new ra-

dial basis function neural network by harmony search

for diabetes diagnosis. Optical Memory and Neural

Networks, 28(4):321—-331.

Hmer, A. and Mouhoub, M. (2016). A multi-phase hybrid

metaheuristics approach for the exam timetabling. In-

ternational Journal of Computational Intelligence and

Applications, 15(04):1–22.

Li, Y., He, Y.-C., Liu, X., Guo, X., and Li, Z. (2020).

A novel discrete whale optimization algorithm for

solving knapsack problems. Applied Intelligence,

50:3350–3366.

Mirjalili, S. and Lewis, A. (2016). The whale optimization

algorithm. Advances in Engineering Software, 95:51

– 67.

Mouhoub, M. and Wang, Z. (2008). Improving the ant

colony optimization algorithm for the quadratic as-

signment problem. In 2008 IEEE Congress on Evo-

lutionary Computation, pages 250–257. IEEE.

Oliva, D., Abd El Aziz, M., and Ella Hassanien, A. (2017).

Parameter estimation of photovoltaic cells using an

improved chaotic whale optimization algorithm. Ap-

plied Energy, 200:141–154.

Sangaiah, A. K., Hosseinabadi, A. A. R., Shareh, M. B., Bo-

zorgi Rad, S. Y., Zolfagharian, A., and Chilamkurti,

N. (2020). Iot resource allocation and optimization

based on heuristic algorithm. Sensors, 20(2).

Shankar, G. S. and Manikandan, K. (2019). Diagnosis of

diabetes diseases using optimized fuzzy rule set by

grey wolf optimization. Pattern Recognition Letters,

125:432–438.

Zhang, J., Hong, L., and Liu, Q. (2021). An improved

whale optimization algorithm for the traveling sales-

man problem. Symmetry, 13(1).

Whale Optimization-based Prediction for Medical Diagnostic

217