Veriﬁable Executable Models for Decomposable Real-time Systems

Callum M

Coll

1 a

, Vladimir Estivill-Castro

2 b

, Morgan M

Coll

1 c

and René Hexel

1 d

School of Information and Communication Technology, Grifﬁth University, Brisbane, Australia

Departament de Tecnologies de la Informació i les Comunicacions, Universitat Pompeu Fabra, Barcelona 08018, Spain

Keywords:

Safety-critical Teal-time Systems, Model-driven Development, Executable Models, Formal Veriﬁcation.

Abstract:

Formally veriﬁable, executable models allow the high-level design, implementation, execution, and validation

of reliable systems. But, unbounded complexity, semantic gaps, and combinatorial state explosion have dras-

tically reduced the use of model-driven software engineering for even moderately complex real-time systems.

We introduce a new solution that enables high level, executable models of decomposable real-time systems.

Our novel approach allows veriﬁcation in both the time domain and the value domain. We show that through

1) the use of a static, worst-case execution time, and 2) our time-triggered deterministic scheduling of arrange-

ments of logic-labelled ﬁnite-state machines (LLFSMs), we can create succinct Kripke structures that are ﬁt

for formal veriﬁcation, including veriﬁcation of timing properties. We leap further and enable parallel, non-

preemptive scheduling of LLFSMs where veriﬁcation is feasible as the faithful Kripke structure has bounded

size. We evaluate our approach through a case study where we fully apply a model-driven approach to a hard

time-critical system of parallel sonar sensors.

1 INTRODUCTION

Model-driven software engineering (MDSE) has pro-

gressed remarkably (Bucchiarone et al., 2020; Buc-

chiarone et al., 2021) in creating executable models

that deﬁne behaviour at a high level. However, with

the same ease as generating high level behaviours, it

is possible for these to have semantic variants and

thus, formal veriﬁcation of the model results in cases

where correctness properties hold for some scenar-

ios, but not others (Besnard et al., 2018). This hap-

pens even for a current version of fUML (Guermazi

et al., 2015). Another anomaly with executable mod-

els of UML (fUML) is that race conditions, or exe-

cution paths may diverge, depending on the order of

construction, even if the same model editor is used

to construct the executable model, since there still

are some constructs with ambiguous semantics (Pham

et al., 2017; Estivill-Castro 2021).

Despite the advances in testing approaches, such

as test-driven development (Mäkinen and Münch,

2014) and continuous integration (Hilton et al., 2016),

testing only proves the existence of defects, not their

https://orcid.org/0000-0002-9373-0875

https://orcid.org/0000-0001-7775-0780

https://orcid.org/0000-0003-4217-7210

https://orcid.org/0000-0002-9668-849X

nonexistence, whereas formal methods (in particular

model checking) can ensure the correctness of the

software. Thus, it would seem natural that executable

models constructed under MDSE should be suitable

for model checking. In Section 2 we provide a new

perspective into the challenges for veriﬁcation in the

time domain. This analysis not only reviews the state

of the art, but in Section 3 we show why time-domain

veriﬁcation with an arbitrary scheduler results in large

sets of possible time-points and further state space ex-

plosion. State space explosion is a major inhibitor to

more widely adopted model-checking to verify exe-

cutable models. Although event-driven programming

has been extremely productive for many types of sys-

tems, it is fundamentally a best-effort approach and

it cannot ensure it meets hard deadlines (Lamport,

1984). Formal veriﬁcation is signiﬁcantly more fea-

sible for time-triggered systems than for event-driven

systems (Furrer, 2019).

In Section 4 we analyse the advantages of logic-

labelled ﬁnite-state machines (LLFSMs) to reduce

state space explosion in the time-domain. For now,

consider LLFSMs as UML state-charts where events

can no longer label transitions but only guards can.

While this seems to be a restriction, LLFSMs re-

main Turing-complete and there is no loss of expres-

sive power. Moreover, we indicate how the machines

182

McColl, C., Estivill-Castro, V., McColl, M. and Hexel, R.

Veriﬁable Executable Models for Decomposable Real-time Systems.

DOI: 10.5220/0010812200003119

In Proceedings of the 10th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2022), pages 182-193

ISBN: 978-989-758-550-0; ISSN: 2184-4348

can be statically analysed and scheduled in a time-

triggered fashion. As a result, rather than a machine

waiting in a state for an event to trigger a transition

(which leads to all the issues and complications of the

Run-To-Completion (RTC) semantics (Eriksson et al.,

2003; OMG, 2019; Samek, 2008; Drusinsky, 2006;

Selic et al., 1994)), machines are running the activi-

ties in their states when their turn arrives. This sub-

tle change results in a massive reduction of the state-

space for the model checker. Moreover, because we

can perform static analysis and scheduling, we can

not only verify correctness properties in the value-

domain, but also in the time domain. It may seem

surprising that one is willing to trade the ease of de-

velopment of an event-driven approach for the more

elaborate planning of a schedule in the time-triggered

approach. We argue that for embedded systems, the

event-driven approach (akin to the notion of an inter-

rupt, where the handler suspends the current code)

may not be suitable. Take, for example, the com-

munication channels between the programmable real-

time units (PRUs) and the ARM processors of TI’s

BeagleBone-Black (Molloy, 2014). Here, all syn-

chronisation is through polling the status of Boolean

ﬂags. There often are no operating systems for bare-

metal microcontrollers such as the PRUs, not even a

real-time OS. In Section 5 we present a novel time-

triggered alternative to schedule an arrangement so

that the behaviours execute under controlled concur-

rency. Moreover, we show that modelling with LLF-

SMs facilitates the construction of a schedule. A core

contribution is that we show how we formally verify

that this schedule results in a system that meets prop-

erties in the time domain as well as in the value do-

main. Section 6 describes the design of parallel, non-

preemptive scheduling that is also veriﬁable. Sec-

tion 7 illustrates the approach with a timing-critical

system of parallel sonar sensors before we conclude

in Section 8.

2 VERIFYING TIME

2.1 Veriﬁcation of Executable Models

Formal veriﬁcation is paramount when designing

complex systems, particularly in the domain of

safety-critical real-time systems. MDSE has long

been promising (Selic, 2003) to overcome the lim-

itations of traditional programming languages while

rigorously expressing executable concepts (Mellor,

2003). Executable models strive to remove the dan-

ger of human translation error and ensure that the ex-

ecution semantics corresponds to the target system.

However, formal veriﬁcation of executable models is

not ideal: as system complexity grows, current ap-

proaches quickly reach their limits, as the compo-

sition of a complex system from multiple subsys-

tems results in a combinatorial state explosion (Seshia

et al., 2018). Model checking veriﬁes abstractions as

a workaround to this problem, but the veriﬁed model

is only indicative of what actually runs, introducing a

semantic gap.

Formal veriﬁcation of a model that does not cor-

respond to its implementation is informative, but po-

tentially worthless. The challenge within real-time

systems is that, in addition to correctness in the

value domain, correctness in time is vital. A value-

domain failure means that an incorrect value is pro-

duced while a temporal failure means that a value

is computed outside the intended interval of real-

time (Kopetz, 2011, Page 139). Temporal veriﬁcation

is hard, as it must consider all timing combinations

of all possible tasks across all potential schedules.

Such combinations result in an unviable state space

explosion, requiring simplifying assumptions in ex-

isting approaches for formal veriﬁcation, dangerously

widening the semantic gap.

Time must be treated as a ﬁrst-order quantity

that can be reasoned upon to verify that a sys-

tem will be able to meet its deadlines (Stankovic,

1988). While UML proﬁles such as MARTE (An-

dré et al., 2007), and speciﬁc languages and tools

such as AADL (Feiler et al., 2005) enable require-

ments engineering of real-time systems, the event-

driven nature and the adoption of the RTC semantics

prevails around UML; thus we still have to see ex-

ecutable (Pham et al., 2017) and formally veriﬁable

models without semantic gaps (Besnard et al., 2018)

or serious restrictions to speciﬁc subsets (Zhang et al.,

2017; Berthomieu et al., 2015). Alternatively the RTC

semantics must be simpliﬁed signiﬁcantly (Jin and

Levy, 2002; Kabous and Nebel, 1999). Till August

2020, Papyrus™ (Guermazi et al., 2015) (the most

UML 2 compliant tool), only had an incomplete Moka

prototype for executing UML state charts. Papyrus

Real Time (Papyrus-RT) UML models show discrep-

ancies with their nuXmv simulation (Sahu et al.,

2020), even in the value domain (let alone the time do-

main) and the (non real-time) C/C++ code of Papyrus-

RT requires a runtime system (RTS) and a C/C++

Development Toolkit (CDT) that use non-real time

Linux concurrency features. Thus, MDSE fails to

guarantee time-related correctness properties.

Veriﬁable Executable Models for Decomposable Real-time Systems

183

2.2 Models of Time

When performing model checking, the system is rep-

resented as a formal model M that corresponds, with-

out semantic gaps, to a transition system known as a

Kripke structure. A model checker veriﬁes whether

the model M meets some speciﬁcation φ (D’Silva

et al., 2008) by examining the Kripke structure. The

speciﬁcation is created through the use of speciﬁ-

cation languages, usually some form of temporal

logic (Alur et al., 1993). However, a prevalent con-

cern for the extended impact of MDSE is whether the

technical difﬁculties of translating models into code

result in errors due to subtleties in meaning (Selic,

2003) and dangerous semantic gaps (Besnard et al.,

2018). The modelling tool must be able to guarantee

that the semantics deﬁned by the model is the same

when the model is implemented (Mellor, 2003).

Finite-state machines are ubiquitous in modelling

the behaviour of software systems, appearing in

prominent systems modelling tools and languages

such as the UML (OMG, 2012), SysML (Friedenthal

et al., 2009), or timed automata (Alur and Dill, 1994).

In these modelling tools, transitions are usually la-

belled with an event e that triggers the transition.

Model checking approaches that follow these event-

triggered semantics typically use an idealised view of

events that puts aside some of the realities of cyber-

physical systems (Lee, 2008). Often, model checking

tools take the view that events occur on a sparse (or

discrete) time base and that no event can occur while

the system is already processing another event (Alur

and Dill, 1994). Most real-time systems are cyber-

physical systems where events can originate from the

environment (which is not in the sphere of control of

the computer system), meaning that events originate

on a dense (or continuous) time base and may orig-

inate while the computer system is processing other

events (Kopetz, 1992). Importantly, the computer sys-

tem must decide on what happens to events that occur

while the computer system is processing other events.

Are they to be placed on a queue to be processed

later? What priority criteria shall be used to order

events on the queue? Is the queue bounded or un-

bounded? How does the computer system process si-

multaneous events? In rare circumstances such as an

event shower, does the computer system drop events?

And if so, does the computer system choose which

events to drop? Even training materials for certiﬁca-

tion on UML are ambiguous.

“Events that are not processed off the pool are gen-

erally dropped. They will need to be resent to the

state machines for them to be considered. The or-

der the events are examined from the pool is not

speciﬁed, though the pool is usually considered an

event queue” (Chonoles, 2017).

Model checking approaches using event-triggered

ﬁnite-state semantics often leave these issues un-

deﬁned. This can cause the resulting system

to signiﬁcantly deviate from the semantics of the

model (von der Beeck, 1994).

The only way to discern the timing of event-

triggered systems is to consider all combinations

of temporal effects of all possible events and event

handlers (Kopetz, 1993). The nature of the non-

deterministic scheduling of the system based around

when events arrive requires considering all possible

combinations. That is, the uncontrollability of the or-

der and frequency of environment events results in un-

controllable concurrency of event handlers, challeng-

ing the capability to reason about timely behaviour

for event-triggered systems particularly when design-

ing temporally accurate real-time systems (Lee et al.,

2017; Furrer, 2019).

3 STATE EXPLOSION

A model checker must inspect all possible execu-

tion paths through a program relevant to the prop-

erties tested. For event-triggered systems, accurate

veriﬁcation should include conﬁguration of all event

queues. However, most veriﬁcation tools ignore this

issue (Bhaduri and Ramesh, 2004).

When time veriﬁcation is required, this must also

take into consideration the execution time of tasks. A

worst-case execution time (WCET) analysis is manda-

tory to ensure deadlines will be met under all circum-

stances. However, the WCET can be prohibitively

complex to analyse when composing a complex sys-

tem from a diversity of subsystems. The execution

time of tasks falls within a range [BCET, WCET]

where BCET is equal to the best-case execution time.

Non-deterministic scheduling based on event occur-

rence and ordering introduces a further state explo-

sion, as any event-triggered task may be executed at

any point in time and in any order. Veriﬁcation must

therefore ensure that timing deadlines will be met for

any chain of events, where each task responding to an

event takes an execution time somewhere between the

BCET and WCET. To verify such a system, each time

point within this range must be considered, as the sys-

tem behaviour may change, depending on the order-

ing of events. When subsystems communicate using

events, the ordering of events becomes important.

Moreover, a subsystem may generate more events,

which must be handled, causing greater delays. Since

the timing of the system may change depending on

MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development

184

the ordering of when events happen, all possible event

combinations must be veriﬁed they meet all deadlines.

Timed automata attempt to deal with this issue by us-

ing region automata (Alur et al., 1993, p. 18). This

breaks up the range of possible execution times into

sub-ranges which are used to verify properties under

different combinations of time limits. While timed

automata ameliorate this issue, the technique cannot

remove it altogether. Since state space explosion still

remains, the more complex a system becomes, the

more combinations must be veriﬁed. Consider a se-

quence of events e

→ e

→ ... → e

. Even when

we know that the processing of an individual event e

takes some time t

such that BCET

≤ t

≤ WCET

and thus the sequence would be handled no later than

∑

i=0

WCET

, what guarantees can we offer regarding

handling event e

, for each i? The following lemma

can be veriﬁed by induction.

Lemma 1. For all i,

∑

j=0

WCET

−

∑

j=0

BCET

≤

i+1

∑

j=0

WCET

−

i+1

∑

j=0

BCET

That is, the range of possible time points increases

monotonically with more events. Moreover, the over-

all amount t of processing time for the sequence of

events is therefore t = t

when processing only one

event e

. However, if the order of events is arbitrary,

and event e

arrives somewhere during the handling

of the previous i − 1 events, event e

waits on a ﬁrst-in

ﬁrst-out queue anywhere between

∑

j=0

BCET

and

∑

j=0

WCET

with numerous partitions possible for

the handling of earlier events. From this discussion,

we can see that the amount of clock values that must

be considered by the veriﬁcation to ensure bounds

on the lag for handling an event increases with the

length of the event sequence. Moreover, even under

the optimistic assumption that the overhead of event

queuing does not prevent determination of the spe-

ciﬁc BCET and WCET bounds for each task, the pos-

sibility to trigger subsequent events causes an over-

all multiplicative effect (and thus, combinatorial state

explosion) that quickly will make time veriﬁcation in-

feasible for most systems.

4 DETERMINISM WITH LLFSMs

In our approach, we will take advantage of the deter-

ministic schedule for Logic-Labelled Finite-State Ma-

chines (LLFSMs) (Estivill-Castro et al., 2012). LLF-

SMs constitute executable models, enabling model-

driven development. Even with a minimal action lan-

guage (with assignment and integers), LLFSMs are

Turing complete. Thus, there are programs for which

some properties are not veriﬁable. However, we ac-

cept this is analogous to verifying any system that

is implemented using a Turing-complete language.

We leave open the particular language used for state

actions. However, if a detailed semantics is to be

considered, we can choose IMP (Winskel, 1993) for

the action language compatible with model checkers

such as NuSMV and nuXmv. The important aspect is

that LLFSMs have a deterministic semantics, because

they do not label transitions with events.

Rather than an uncontrolled concurrency at the

mercy of events popping out in the environment or

the system itself, LLFSMs offers controlled concur-

rency and a deterministic schedule. An arrangement

of LLFSMs is ordered and represents a system. Each

LLFSM consists of a ﬁnite set S of states and starts

with an initial state s

. The system starts with the

initial state of the ﬁrst LLFSM in the arrangement.

Each transition is labelled with some Boolean logic

expression instead of an event. This fundamentally

changes the model of state execution. Each current

state is not sleeping (as is the case with the event-

triggered ﬂavoured versions of ﬁnite-state machines)

and is instead, periodically scheduled. Each transition

is a member of an ordered sequence of transitions. For

the current state, the logical conditions on each tran-

sition are therefore evaluated sequentially, in a deter-

ministic order, from the ﬁrst transition to the last.

All states have sections that may contain source

code. The sections that execute when the current state

is scheduled constintute a ringlet, and are determined

as follows. The OnEntry section of a state is executed

when the LLFSM ﬁrst transitions to that state. Con-

versely, OnExit is executed when a transition ﬁres, i.e.

the Boolean expression of some outgoing transition

evaluates to true. Alternatively, if no transition ﬁres,

the code in the Internal section gets executed.

A common schedule is to assign the token of exe-

cution in a round-robin fashion (Estivill-Castro et al.,

2012). However, since a LLFSM ringlet may execute

differently for the same current state, ringlets have

variable duration and are executed one after another

resulting again in a large number of time boundary

values to consider by model-checkers. It would ap-

pear that LLFSMs do not resolve the state explosion

alluded before. However, in Section 5 we will show

how to we can utilise the deterministic order of LLF-

SMs execution to obtain timing guarantees.

Coll et al. showed (M

Coll et al., 2017) that

actual practical implementations of executable LLF-

SMs can be obtained using the Swift programming

language. These implementations have demonstrated

the generation of efﬁcient Kripke structures from ex-

ecutable LLFSMs, which can be used for formal ver-

Veriﬁable Executable Models for Decomposable Real-time Systems

185

iﬁcation in the value domain. The size of these

Kripke structures is minimised through a combina-

tion of strict type-checking rules in combination with

functional programming concepts such as referential

transparency and how communication is modelled be-

tween LLFSMs (M

Coll et al., 2017). Recall that a

ringlet represents a single execution of a single state

within a single LLFSM. The execution of a single

ringlet can be made atomic (M

Coll et al., 2018)

through the use of context snapshots of the external

variables. The external variables represent variables

that are in the sphere of control of the environment,

e.g., representing the value of sensors. Before the

ringlet is executed, a snapshot of the external vari-

ables is taken. The state that is executed (along with

all transition checks) acts on this snapshot. The state

reads and manipulates variables of the snapshot and

then, when the state has ﬁnished executing, writes

the snapshot back out to the environment. This over-

comes inconsistencies where the external variables

may change during the execution of a state, as the

state is only ever acting on the snapshot. This also

simpliﬁes the Kripke structure as the execution of the

state becomes atomic. Since the only way that the

LLFSM can communicate with the sensors/actuators

is through the use of the external variables, the only

Kripke States that matter are those that represent the

conﬁguration of the LLFSM before and after (but not

during) the execution of the state.

We take this idea of an atomic ringlet further, by

introducing the notion of decomposing Kripke struc-

tures into smaller individual structures. LLFSMs that

do not communicate are thus able to be veriﬁed in-

dependently within the value domain. However, vari-

ations in the timing of a schedule for LLFSMs must

be resolved if we are to achieve the same effect for

time-domain veriﬁcation.

5 TIME VERIFICATION

We deﬁne the WCET of an LLFSM (denoted

WCET

LLFSM

) as the largest WCET of the set of

all possible ringlets of the LLFSM. Conversely, the

BCET of the LLFSM (denoted BCET

LLFSM

) is equal

to the smallest BCET of the set of all possible ringlets

of the LLFSM. Note that since state sections in LLF-

SMs do not have control structures, these values can

be obtained by static analysis.

The time-triggered model of computation parti-

tions and separates large systems into subsystems

through small, stable interfaces (Kopetz, 1998). Im-

portant here is the concept of a temporal ﬁre-

wall (Kopetz and Nossal, 1997) that allows arrest-

ing the effects of timing dependencies at the sub-

system level, effectively limiting the cumulation of

unbounded propagation (Lamport, 1984) of temporal

dependencies and uncertainty. This has led to the con-

cept of a time-triggered architecture that allows limit-

ing complexity by designing distributed components

around strict, temporal interface constraints (Kopetz

and Bauer, 2003).

Using the sequential static schedule of LLFSM

means that the actual execution time of the sched-

ule cycle would, therefore, fall within a range

[BCET

, WCET

]. We eliminate this range by

changing the schedule to now use a time-triggered se-

mantics. To the best of our knowledge, this is the ﬁrst

case in the literature of time-triggered schedules con-

taining LLFSMs. To this effect, each LLFSM now

executes within its allotted time slot.

Each time slot is large enough to cover the WCET

of the executing LLFSM. The arrangement of LLF-

SMs still gets dispatched in a round-robin fashion,

however, each time slot is triggered at speciﬁc points

in time. Since the time slot is large enough to cover

the WCET of the LLFSM, most of the time, each

LLFSM will ﬁnish with some laxity. The system will

execute the ringlet of the next machine at the start of

its time slot, effectively fusing the WCET and BCET

to a single value (the slot duration).

Initial

var a: Int = 2

var b: Int = 3

var result: Int

onEntry

onExit

result = a + b

internal

Terminal

onEntry

onExit

internal

after_ms(20)

(a) The Sum LLFSM.

Initial

onEntry

sleep_ms(30)

onExit

internal

Terminal

onEntry

onExit

internal

true

(b) The Sleeping LLFSM.

Figure 1: Two LLFSMs executing together.

Importantly, the snapshots of the external vari-

ables are taken at the start, immediately upon enter-

ing the time slot and immediately before exiting the

time slot. This effectively reduces the time it takes

for values in the external variables from reaching the

sensors/actuators to a single, deterministic value that

can be measured during WCET analysis. The effects

of this strategy ﬂow onto the timing of the schedule

cycle. Importantly, this makes the timing of every

schedule cycle deterministic and veriﬁable. Since the

schedule is made up of a few static time slots that

do not change, and we can consider the BCET

and

WCET

equal to the slot duration, the earlier state

explosion disappears. With this approach we then

generate the input for a time transition system (TTS)

which can be evaluated by nuXmv. A TTS in noth-

ing more than a Kripke structure with edges labelled

with durations. nuXmv can represent clocks and ver-

MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development

186

ify time-domain properties on the corresponding TTS.

5.1 An Illustrative Example

Considering the LLFSMs shown in Fig. 1 as an ex-

ample. The Sum LLFSM can be reduced to adding

two numbers a and b together and store the sum in

result. However, only after 20 milliseconds, will

the initial state add the numbers together. Since

the computation of the sum is in the OnExit action

of the state, the result value will only be com-

puted just as the system LLFSM transitions to the

Terminal state. The after_ms(20) statement re-

turns a Boolean value indicating whether 20 millisec-

onds have elapsed since the LLFSM ﬁrst started exe-

cuting the Initial state. The OnEntry action of the

Initial state of the Sleeping LLFSM takes 30 mil-

liseconds to execute. Once it ﬁnishes executing the

OnEntry section, it checks its transitions, ﬁnds that

the transition marked with true is valid, and will tran-

sition to its Terminal state.

When executing these LLFSMs, we must ﬁrst

evaluate the WCET of each LLFSM. This will be used

to determine the amount of time allocated to the time

slot for each LLFSM. Let us assume we have anal-

ysed the WCET of the Sum LLFSM to be 5 millisec-

onds. This value would represent the ringlet where

the after_ms(20) transition evaluates to true and the

LLFSM transitions and executes the OnExit action.

For the Sleeping LLFSM, assuming the WCET is 35

milliseconds for instance, captures the ringlet where

the OnEntry action is executed and the system transi-

tions to the Terminal state.

Sum Timeslot

Sleeping Timeslot

|-WCET

Sum

-| |-WCET

Sleeping

Figure 2: The schedule of the two LLFSMs.

Fig. 2 shows how these values result in a static

schedule with two time slots. To perform the veriﬁca-

tion of this schedule, we label the edges of the graph

with time values (Markey and Schnoebelen, 2004).

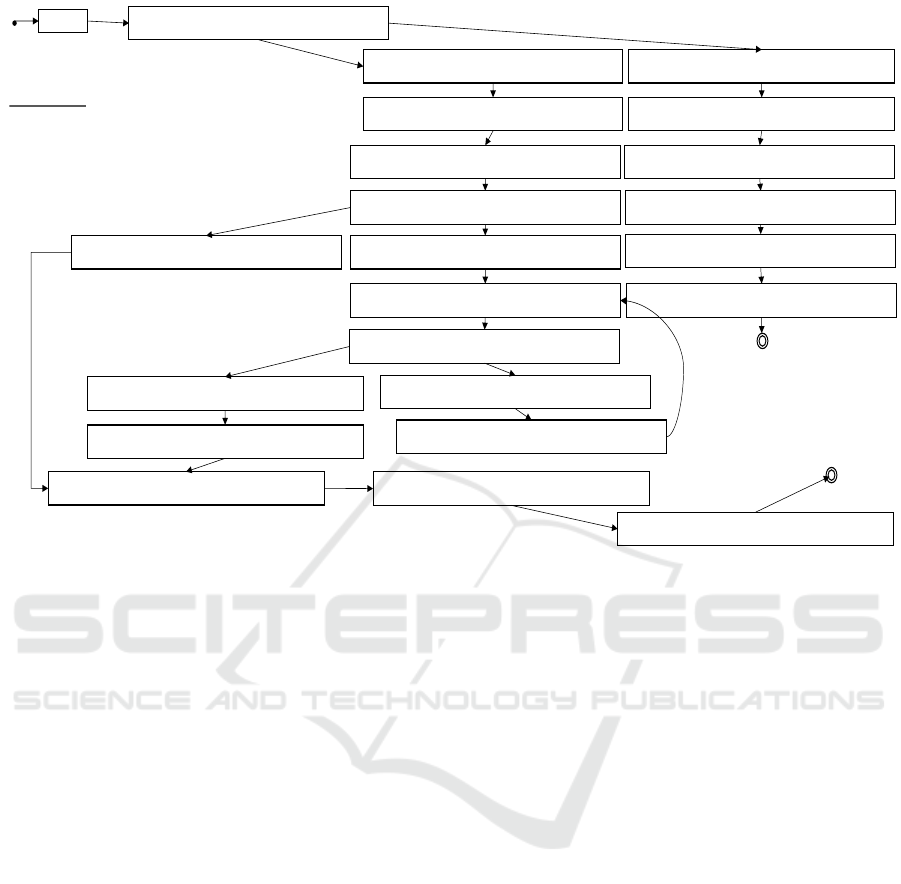
Fig. 3 shows the corresponding Kripke structure.

The resulting Kripke structure demonstrates the

advantage of the time-triggered approach. Each node

contains an evaluation of all variables for all LLFSMs

that have been scheduled, and the program counter

(pc) which indicates which LLFSM is currently exe-

cuting. This program counter is qualiﬁed into R (read)

nodes and W (write) nodes. These nodes capture a

snapshot of the external variables, or save the snap-

shot to external output variables, respectively. The

edge between these nodes is labelled with the amount

of time between the reading and writing of the snap-

shots, and is equal to the amount of time allotted to

the time slot. Recall that the activity reads a snapshot

of the external variables immediately upon entering

the time slot and then saves the snapshot immediately

before exiting the time slot. The snapshots are there-

fore read at the start of the time slot and written at the

end of the time slot.

Handling timing transitions (such as

after_ms(20)) is delicate. Taking the example

of the Sum LLFSM, we can see that the conﬁguration

of the LLFSM remains the same until 20 milliseconds

have passed. In other words, this means that only

the clock is changing in the LLFSM. In the Kripke

structure, we deal with this issue by converting the

Kripke structure into a time transition system (TTS)

which can be evaluated by nuXmv. The TTS is made

up of several clocks which are reset at certain points

throughout the graph. The main clock c : R represents

the clock which governs when an edge is available to

be taken. We achieve this with the sync : R variable

that deﬁnes the amount of time that must elapse

before transitioning. To this effect, the clock c gets

set to 0, and sync gets set to the amount of time to

wait before transitioning, every time an edge is taken

in the graph.

For example, consider the Sum LLFSM, which

has a time slot of 5 milliseconds. The amount of time

it takes for the system to start executing the LLFSM

within its time slot — represented by the R node —

until the end of the time slot — represented by the

W node — is therefore 5 milliseconds. In the Kripke

structure, the R node thus sets the clock c to 0 and sets

the sync value to 5000, representing 5000 microsec-

onds in this case. The clock c will increase with time

until it reaches the designated 5000 microseconds rep-

resented by the evaluation of sync and causes a tran-

sition to the W node. We use a similar approach to

transition from the W node to the next R node. By util-

ising the c and sync variables, we can create discrete

transition points within the graph which semantically

match the timing of the scheduler when executing the

LLFSMs using time slots.

To handle the a f ter_ms transitions, each LLFSM

within the TTS is also allocated a clock. The clock

for the LLFSM is used to represent the amount of

time that the LLFSM remains within the current state.

The Sum LLFSMs clock c

Sum

here is used to stipu-

late when the LLFSM moves from the Initial state

to the Terminal state. The c

Sum

clock only resets

when the LLFSM transitions to a new state. This

means that as long as the LLFSM remains in the same

state, the c

Sum

clock will continue to increase. The

after_ms(20) transition which limits the LLFSM to

Veriﬁable Executable Models for Decomposable Real-time Systems

187

pc = initial

SL = {cS = Initial,ringlet = {sEOE = true}}, SM = {cS = Initial,ringlet = {sEOE = true},

states = {Initial = {a = 2,b = 3,result = nil}}}, pc = SM.Initial.R

Abbreviations

SL=Sleeping

SM=Sum

cS=Current State

sEOE = shouldExecuteOnEntry

SL = {cS = Initial,ringlet = {sEOE = true}}, SM = {cS = Initial,ringlet = {sEOE = false},

states = {Initial = {a = 2,b = 3,result = nil}}}, pc = SM.Initial.W

SM.clock := 0

SL = {cS = Initial,ringlet = {sEOE = true}}, SM = {cS = Terminal,ringlet = {sEOE =true},

states = {Initial = {a = 2,b = 3,result = 5}}}, pc = SM.Initial.W

SL = {cS = Initial,ringlet = {sEOE = true}}, SM = {cS = Initial,ringlet = {sEOE = false},

states = {Initial = {a = 2,b = 3,result = nil}}}, pc = SL.Initial.R

SL = {cS = Initial,ringlet = {sEOE = true}}, SM = {cS = Terminal,ringlet = {sEOE =true},

states = {Initial = {a = 2,b = 3,result = 5}}}, pc = SL.Initial.R

5000,SM.clock ≤ 20000

5000,SM.clock > 20000

5000,SL.clock := 0 5000,SL.clock := 0

SL = {cS = Terminal,ringlet = {sEOE = true}}, SM = {cS = Initial,ringlet = {sEOE =false},

states = {Initial = {a = 2,b = 3,result = nil}}}, pc = SL.Initial.W

SL = {cS = Terminal,ringlet = {sEOE=true}}, SM = {cS = Terminal,ringlet = {sEOE=true},

states = {Initial = {a = 2,b = 3,result = 5}}},pc = SL.Initial.W

3500035000

SL = {cS = Terminal,ringlet = {sEOE = true}}, SM = {cS = Initial,ringlet = {sEOE = false},

states = {Initial = {a = 2,b = 3,result = nil}}},pc = SM.Initial.R

SL = {cS = Terminal,ringlet = {sEOE=true}}, SM = {cS = Terminal,ringlet = {sEOE=true},

states = {Initial = {a = 2,b = 3,result = 5}}}, pc = SM.Terminal.R

SM.clock := 0

SL = {cS = Terminal,ringlet = {sEOE = true}}, SM = {cS = Initial,ringlet = {sEOE = false},

states = {Initial = {a = 2,b = 3,result = nil}}}, pc = SM.Initial.W

SL = {cS = Terminal,ringlet = {sEOE=true}}, SM = {cS = Terminal,ringlet= {sEOE=false},

states = {Initial = {a = 2,b = 3,result = 5}}}, pc = SM.Terminal.W

SL = {cS = Terminal,ringlet = {sEOE=true}}, SM = {cS = Terminal,ringlet = {sEOE=true},

states = {Initial = {a = 2,b = 3,result = 5}}},pc = SM.Initial.W

5000

5000,SM.clock > 20000

5000,SM.clock ≤ 20000

SL = {cS = Terminal,ringlet = {sEOE = false}}, SM = {cS = Initial,ringlet = {sEOE = false},

states = {Initial = {a = 2,b = 3,result = nil}}}, pc = SL.Terminal.W

SL = {cS = Terminal,ringlet = {sEOE=false}}, SM={cS = Terminal,ringlet = {sEOE=false},

states = {Initial = {a = 2,b = 3,result = 5}}}, pc = SL.Terminal.W

3500035000

SL = {cS = Terminal,ringlet = {sEOE = false}}, SM = {cS = Initial,ringlet = {sEOE =false},

states = {Initial = {a = 2,b = 3,result = nil}}}, pc = SM.Initial.R

SL = {cS = Terminal,ringlet = {sEOE = false}}, SM = {cS = Initial,ringlet = {sEOE = false},

states = {Initial = {a = 2,b = 3,result = nil}}}, pc = SM.Initial.W

SL = {cS = Terminal,ringlet = {sEOE = false}}, SM = {cS = Initial,ringlet = {sEOE = false},

states = {Initial = {a = 2,b = 3,result = nil}}}, pc = SL.Terminal.R

SL = {cS = Terminal,ringlet = {sEOE=false}}, SM = {cS = Terminal,ringlet = {sEOE=true},

states = {Initial = {a = 2,b = 3,result = 5}}}, pc = SM.Initial.W

SL = {cS = Terminal,ringlet = {sEOE=false}}, SM = {cS = Terminal,ringlet = {sEOE=true},

states = {Initial = {a = 2,b = 3,result = 5}}}, pc = SM.Initial.W

SL = {cS = Terminal,ringlet = {sEOE = false}}, SM = {cS = Terminal,ringlet = {sEOE=true},

states = {Initial = {a = 2,b = 3,result = 5}}}, pc = SL.Terminal.W

5000,SM.clock ≤ 20000

5000,SM.clock > 20000

5000

35000

5000

35000

SL = {cS = Terminal,ringlet = {sEOE =false}}, SM = {cS = Terminal,ringlet = {sEOE=true},

states = {Initial = {a = 2,b = 3,result = 5}}}, pc = SM.Terminal.R

SL = {cS = Terminal,ringlet = {sEOE =false}}, SM = {cS = Terminal,ringlet = {sEOE=false},

states = {Initial = {a = 2,b = 3,result = 5}}}, pc = SM.Terminal.W

SM.clock := 0

5000

Figure 3: Illustration of the entire Kripke structure of the 2-LLFSMs executable model.

transition only after 20 milliseconds can be expressed

in the TTS by creating a guard on the edge leading to

the R node corresponding to the ﬁrst ringlet when the

LLFSM moves to the Terminal state. The guard is ex-

pressed by an evaluation on the c

Sum

clock with the

usual sync and c guards: c

Sum

> 20000 ∧ c = sync.

Since the LLFSM is not part of a hierarchy and

does therefore not communice, we can apply the opti-

misation discussed earlier and further minimise this

Kripke structure by creating isolated Kripke struc-

tures. These isolated Kripke structures have 5 and 7

nodes respectively. When creating the isolated Kripke

structures, it is important to maintain the timing of

the schedule. Therefore, although the isolated Kripke

structures are able to eliminate nodes of unrelated

LLFSMs, thus avoiding a combinatorial state explo-

sion, they must include the time of the schedule cycle.

This is to account for the timing of all the other LLF-

SMs that are executing, without requiring them to be

included in the Kripke structure.

6 PARALLEL EXECUTION

We now extend our ideas to enable parallel execu-

tion. By utilising a combination of a static sched-

ule and module isolation, we can signiﬁcantly reduce

and minimise Kripke structures so that scheduling be-

comes deterministic and timing veriﬁcation becomes

possible. Here we use the same techniques to allow

LLFSMs to execute in parallel.

LLFSMs may exert control over other LLF-

SMs within an LLFSM-hierarchy (Estivill-Castro and

Hexel, 2013a). LLFSMs may also share access to

external variables without concurrency issues. Both

of these features constitute communication lines be-

tween LLFSMs. We leverage the use of an algorithm

that identiﬁes subsystems that can be veriﬁed inde-

pendently, and has been utilised for efﬁcient model

checking and failure mode effects analysis (FMEA)

of safety-critical systems (Estivill-Castro and Hexel,

2013b). Here we build on that algorithm to allow par-

titioning of a system into subsystems that can run in

parallel while maintaining veriﬁability of the system

as a whole in both the time and value domain.

In our earlier example, the Sum and the Sleeping

LLFSMs are not part of a hierarchy and do not use

external variables, thus enabling the creation of iso-

lated Kripke structures. Since these conditions en-

able parallel execution, these two LLFSMs, can exe-

cute simultaneously on at least two cores. The corre-

sponding isolated Kripke structures would reduce the

amount of time between W and R nodes to 0, since the

other LLFSM is executing on a separate core, there

is no wait time. When the dependencies between

all LLFSMs are known, we create a static schedule

MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development

188

for each core. We follow (Estivill-Castro and Hexel,

2013b) and create a dependency graph that details the

dependencies that each LLFSM uses to communicate.

Fig. 4 illustrates this.

We use a dependency graph following Holt’s no-

tation (Holt, 1972). Nodes A, B, C, D and E each

represent an LLFSM. The nodes E

and E

represent

external variables. The edges of the nodes represent

communication lines. The lines between the LLFSMs

represent the hierarchical owner/slave relationship be-

tween them. Therefore, in Fig. 4, A controls B and

C. The lines connecting the LLFSMs to the external

variables represent LLFSMs that have access to this

particular set of external variables. Importantly, we

extend the semantics of external variables to provide

read-only and write-only semantics. The lines marked

with «read» only read the external variables (sensors).

Any lines marked with «write» (though none appear

in this example) only write to the external variables

(actuators). Those lines that remain unmarked (the

line between A and E

for example) follow the orig-

inal semantics where the LLFSMs can both read and

write to the external variables.

This extended semantics facilitates a more ﬁne-

tuned scheduling strategy. In Fig. 4, nodes A and

D can execute at the same time. This is achieved

through a shared snapshot of external variables E

Since the LLFSMs do not write to the snapshot but

simply read it, they are able to execute their ringlet si-

multaneously, which reads from a shared snapshot of

external variables E

. If one of the LLFSMs were to

write to the snapshot, then this would constitute a race

condition. This is why A and E cannot share a snap-

shot of external variable E

. Furthermore, we cannot

schedule A, B and C simultaneously as A may exert

control over B and C during the execution. We can,

however, schedule B and C simultaneously since they

are not communicating, and neither are C, D, and E.

Thus, many equivalent schedules are possible.

It is vital that we maintain the use of a static sched-

ule, which allows solving of the NP-hard schedul-

ing problem (Xu and Parnas, 1990) pre-runtime. We

can then verify that the schedule satisﬁes all con-

straints depicted by the dependency graph before

run-time. Importantly, it has been shown that such

«read»

Figure 4: Example of a dependency graph.

Start Time Length Task Core

0 30 A 1

30 30 C 1

60 40 B 1

0 50 D 2

50 30 E 2

Core 1

Core 2

C B

Figure 5: A possible schedule.

non-preemptive real-time scheduling can be done ef-

ﬁciently across multi-core processors with shared

caches (Xiao et al., 2017). Fig. 5 shows a possible

conﬁguration of a schedule for a dual-core system.

As depicted in the ﬁgure, we can see that the

schedule may contain synchronisation points where

multiple LLFSMs communicate. Recall that A reads

from E

but also reads from and writes to E

. A

also controls B and C. A is a particularly contentious

LLFSM to schedule as it communicates with many

nodes within the dependency graph. However, we

need to be able to schedule LLFSMs in parallel with

A is executing as to take advantage of the dual-core

system. We can, therefore, execute A and D together.

Once A has ﬁnished executing on the ﬁrst thread, we

can immediately start executing C. Note, that C is

triggered while D is still running on the second thread.

Once D has ﬁnished executing, we can also immedi-

ately start executing E on the second thread since E

has no dependencies shared with C. When C has ﬁn-

ished executing, we can then immediately start exe-

cuting B. This may seem to introduce a race condi-

tion. However, since B is writing to the external vari-

ables E

after the snapshot is taken by E, it cannot

inﬂuence the execution of E. Note that after execut-

ing E, the second thread must wait some time to ﬁnish

at the same time as the ﬁrst thread and thus complete

the scheduled cycle. This resulting laxity is indicated

by the black box after E.

We follow the earlier procedure to create a Kripke

structure. We create 3 isolated Kripke structures:

1. one containing LLFSMs A, B and C,

2. one containing LLFSM D, and

3. one containing LLFSM E.

The cycle time equals the maximum of the cumula-

tive WCETs across cores, and the timed Kripke struc-

ture must account for any laxity on the other cores.

The time between C and B would thus be included in

the transition from the W node of C to the R node of

B. Similarly, for the other Kripke structures, the left-

over time of the schedule cycle labels the transitions

from the W node to the next R node for the D Kripke

structure. For E, the Kripke structure would contain

the execution time of D as well as the laxity at the end

of the schedule.

Veriﬁable Executable Models for Decomposable Real-time Systems

189

7 THE SONAR CASE STUDY

We will now illustrate, in a realistic case study, the ad-

vantages of our MDSE approach of time-domain ver-

iﬁcation of executable models. To this end, we imple-

ment an embedded sonar sensor system that is a vital,

often safety-critical, real-time component in systems

ranging from automotive driver-assist systems to au-

tonomous vehicles and robots.

The model represents a vehicle with several sonar

sensors that measure the distance to potential obsta-

cles. Each sonar sensor covers a section in space

around the vehicle and the sonars are displaced to

prevent propagating signals from interfering. In our

implementation, we use the sonars on a differential

robot to determine the distance to an object. Still, the

notions discussed here are applicable to comparable

sensors that contain emitters and receivers and mea-

sure distance through time-of-ﬂight, e.g. in systems

such as self-driving cars.

The sonar’s operation must record the time it takes

for the signal to travel from the emitter to the object,

and then from the object back to the receiver. The dis-

tance reported is directly proportional to the time, and

its precision and reliance/obsolescence relates to strict

execution timing requirements. Notably, the timing

can vary by orders of magnitude and is in the sphere

of control of the environment (e.g. the changing dis-

tance to an approaching obstacle), rather than the real-

time computer system.

We now show that we can meet strict timing re-

quirements while designing a modular, decomposable

system, i.e. can be composed of individual modules

for each sensor. Moreover, our resulting model will

be scalable, i.e. be able to utilise the module isolation

algorithm from the previous section to avoid combi-

natorial state explosion when generating the corre-

sponding Kripke structure.

While such a state explosion could be avoided if

we implemented this model through a non-preemptive

schedule of measuring tasks, in reality, this is not fea-

sible. Such a solution would cycle through the sonar

sensors by sending out a pulse, waiting for that pulse

to return, calculating the distance, and then executing

a similar task for the subsequent sensor. This is in-

feasible because the act of reading from a sonar sen-

sor involves emitting a pulse and then waiting for that

pulse to return. The further an object is from the sen-

sor, the longer it takes for the pulse to return. Un-

fortunately, this has dire consequences. This is be-

cause it takes an indeterminate amount of time before

the sonar pulse returns (inﬁnity, if there is no obsta-

cle). Even if we bound the time by a maximum dis-

tance, the upper bound for each measurement is or-

ders of magnitude higher than the lower bound when

an obstacle is close. Now imagine a scenario where

task 1 is associated with a clear sensor (i.e. taking its

maximum amount of time). Task 1 is scheduled prior

to task 2 that measures the distance to a rapidly ap-

proaching obstacle. It is easy to envision that the no-

obstacle WCET for Task 1 would cause Task 2 to miss

its deadline resulting in a late sighting.

Switching to a pre-emptive schedule is not scal-

able, as the corresponding models suffer from the

aforementioned combinatorial state explosion. Thus,

we employ our time-triggered approach, which allows

us to create a simple model that will give accurate

readings with deterministic timing and bounded er-

rors. To this end, we have created a system of repli-

cated LLFSMs. Consider the LLFSM depicted in

Fig. 6, operating on a single sonar sensor to produce a

distance calculation. An arrangement of three of these

machines constitutes an executable model that in our

case was then deployed on an Atmel ATmega32U4

Microcontroller, operating at 16MHz, that interfaces

with three external sonar sensors.

In the Setup state, a machine sets up the appropri-

ate pins for reading and writing. Writing to the output

pin in the Skip_Garbage state creates the sonar sig-

nal. The next states are called Wait_For_Pulse_Start,

ClearTrigger and Wait_For_Pulse_End and use the

numloops variable to count the number of ringlets the

machine executes while waiting for the sonar wave to

reﬂect and register at the input pin. The next states

calculate the distance and transition back to the Setup

states to take a new reading.

Our static schedule calculates the distance by re-

lating time to the number of ringlets executed in our

machine. Since our schedule executes one ringlet in

each machine in turn, the time that the signal travels is

related to the length of the schedule cycle. Since we

have replicated our machines, the WCETs, and thus

the time slots, are of the same length and our sched-

ule cycle is simply 3 × WCET.

In our experiments, the WCET, including dispatch

overhead, was 244µs for each of these machines.

Therefore, the machines time slots are taken from the

following table.

Start Time (µs) Length (µs) Machine

0 244 I

244 244 II

488 244 III

Our overall cycle time is 732µs, which produces a

constant, upper error bound of approximately 13cm.

While this demonstrates that we can achieve a

constant error bound while retaining the ability of

MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development

190

Initial

onEntry

triggerPin = 3; echoPin = 2;

distance = 65535; // invalid reading

double NUMBER_OF_MACHINES = 3.0;

SCHEDULE_LENGTH = 0.000244 * NUMBER_OF_MACHINES; // 244 us per machine

SPEED_OF_SOUND = 34300.0; // cm/s

SONAR_OFFSET = 40.0;

uint16_t MAX_DISTANCE = 400;

double MAX_TIME = static_cast<double>(MAX_DISTANCE * 2) / SPEED_OF_SOUND;

maxloops = static_cast<uint16_t>(ceil( MAX_TIME / SCHEDULE_LENGTH));

onExit

numloops = 0;

internal

FSM Variables

uint8_t echoPin;

uint8_t triggerPin;

uint16_t distance;

uint16_t numloops;

uint16_t maxloops;

uint8_t inputPort;

uint8_t inputBit;

double SCHEDULE_LENGTH;

double SPEED_OF_SOUND;

double SONAR_OFFSET;

Setup_Pin

onEntry

pinMode(echoPin, INPUT);

pinMode(triggerPin, OUTPUT);

digitalWrite(triggerPin, LOW);

onExit

digitalWrite(echoPin, LOW);

Internal

SetupMeasure

onEntry

inputBit = digitalPinToBitMask(echoPin);

inputPort = digitalPinToPort(echoPin);

onExit

internal

Skip_Garbage

onEntry

onExit

digitalWrite(triggerPin, HIGH);

++numloops;

internal

++numloops;

Wait_For_Pulse_End

onEntry

onExit

internal

++numloops;

Calculate_Distance

onEntry

distance = static_cast<uint16_t>(max(static_cast<double>(numloops) * SCHEDULE_LENGTH * SPEED_OF_SOUND/2.0 - SONAR_OFFSET, 0.0));

onExit

numloops = 0;

internal

WaitForPulseStart

onEntry

onExit

++numloops;

internal

++numloops;

ClearTrigger

onEntry

digitalWrite(triggerPin, LOW);

onExit

++numloops;

internal

++numloops;

LostPulse

onEntry

distance = 65535;

onExit

numloops = 0;

internal

true

numloops >= maxloops || (*portInputRegister(inputPort) & inputBit) != inputBit

after_ms(1)

numloops >= maxloops

(*portInputRegister(inputPort) & inputBit) == inputBit

numloops >= maxloops

(*portInputRegister(inputPort) & inputBit) != inputBit

true

Figure 6: The Sonar LLFSM.

model checking in both the value and time domains,

we can further improve this by leveraging our ap-

proach to schedule these LLFSMs in parallel. This is

trivially achievable through module isolation, as the

LLFSMs do not share any dependencies. To this end,

we have created an implementation in the Swift lan-

guage for LLFSMs. This shows that our approach al-

lows not only to utilise a language such as C/C++, but

that it may leverage modern programming languages

such as Swift. Creating an implementation in Swift

provides high-level concepts such as functional pro-

gramming, protocol-oriented design, as well as addi-

tional type safety. Our approach is capable of exe-

cuting not only on just embedded devices, but other

platforms such as desktop or mobile devices.

We use a whiteboard middleware (Estivill-Castro

et al., 2014) to represent sensor input in simulation.

The schedule for the 3 parallel LLFSMs uses a similar

dispatch table, but, the start time of each time slot is 0.

This is because we can leverage a system with at least

three cores, allowing us to schedule these LLFSMs at

the same time. The result of this approach is that the

WCET of the schedule cycle decreases, thus decreas-

ing the amount of error associated with the amount of

time an LLFSM would have to wait before it would be

able to execute its next ringlet. This reduces the error

by a third, since each LLFSM would not have to wait

for other LLFSMs to ﬁnish executing their ringlet.

We have generated Kripke structures for both

the sequential and the parallel schedule for the

three sonar machines utilising the swift version of

the Sonar LLFSM. For each variant, 3 separate

isolated Kripke structures were generated each

representing a single sonar LLFSM. In the repository

https://github.com/mipalgu/SonarKripkeStructures

one can ﬁnd nuXmv source ﬁles containing the

Kripke structures as well as graphviz versions which

enable the visualisation of the Kripke structures.

Each of the nuXmv ﬁles contains the timed transition

systems for the evaluation of LTL proofs in both

the value and time domains. For example, consider

the proof of Fig. 7, which stipulates that the sonar

machine will always calculate a distance (or fail to

detect any obstacles) within 35 ms.

LTLSPEC

G pc = "Sonar23-Setup_Pin-R" ->

time_until( pc = "Sonar23-LostPulse-W" |

pc = "Sonar23-CalculateDistance-W"

) <= 35000

Figure 7: The LTL Speciﬁcation For a Guaranteed Result

Delivery Time Interval.

Veriﬁable Executable Models for Decomposable Real-time Systems

191

8 CONCLUSION

We have demonstrated a MDSE approach for veri-

ﬁable and executable models of decomposable real-

time systems. We have shown that a time-triggered

model can overcome the combinatorial state explo-

sion and unbounded delays often associated with

event-triggered systems. We can isolate subsystems

to formally verify system execution time bounds, with

the associated ability to handle events within a given

deadline. This has been achieved by creating tem-

poral ﬁrewalls between the subsystems involved, us-

ing a static time slot based scheduler. We have fur-

ther demonstrated that this approach can be extended

to parallel, non-preemptive schedules across multi-

ple processor cores. By identifying dependencies be-

tween subsystems, we are able to identify communi-

cation dependencies between the subsystems and cre-

ate ﬁne-tuned schedules.

Our techniques have successfully been applied in

a real-time system case study of vehicular sonar sen-

sors. Through the introduction of the time-triggered

scheduler, we have mitigated the issues that forced

the timing of critical tasks from being tightly coupled

to what is occurring in the environment, i.e. outside

their sphere of control. In doing so, we have shown

how the design of a system can be achieved at a high

level, through an executable model that can be de-

composed into isolated modules, which enables veri-

ﬁcation through much smaller Kripke structures, even

when utilising a parallel schedule.

REFERENCES

Alur, R., Courcoubetis, C., and Dill, D. (1993). Model-

checking in dense real-time. Information and Compu-

tation, 104(1):2 – 34.

Alur, R. and Dill, D. (1994). A theory of timed automata.

Theoretical Computer Science, 126(2):183–235.

André, C., Mallet, F., and de Simone, R. (2007). Modeling

time(s). Model Driven Engineering Languages and

Systems, p. 559–573, Springer Berlin.

Berthomieu, B., Bodeveix, J.-P., Dal-Zilio, S., Filali, M.,

Le Botlan, D., Verdier, G., and Vernadat, F. (2015).

Real-time model checking support for AADL. CoRR,

abs/1503.00493.

Besnard, V., Brun, M., Jouault, F., Teodorov, C., and

Dhaussy, P. (2018). Uniﬁed LTL veriﬁcation and em-

bedded execution of UML models. 21th ACM/IEEE

Int. Conf. on Model Driven Engineering Languages

and Systems, MODELS ’18, p. 112–122, NY, USA.

Bhaduri, P. and Ramesh, S. (2004). Model checking of stat-

echart models: Survey and research directions.

Bucchiarone, A., Cabot, J., Paige, R. F., and Pierantonio, A.

(2020). Grand challenges in model-driven engineer-

ing: an analysis of the state of the research. Software

and Systems Modeling, 19(1):5–13.

Bucchiarone, A., Ciccozzi, F., Lambers, L., Pierantonio, A.,

Tichy, M., Tisi, M., Wortmann, A., and Zaytsev, V.

(2021). What is the future of modeling? IEEE Soft-

ware, 38(02):119–127.

Chonoles, M. J. (2017). OCUP 2 Certiﬁcation Guide

Preparing for the OMG Certiﬁed UML 2.5 Profes-

sional 2 Foundation Exam. Morgan Kaufmann, Cam-

bridge, MA 02139.

Drusinsky, D. (2006). Modeling and Veriﬁcation Us-

ing UML Statecharts: A Working Guide to Reactive

System Design, Runtime Monitoring and Execution-

based Model Checking. Newnes.

D’Silva, V., Kroening, D., and Weissenbacher, G. (2008).

A survey of automated techniques for formal software

veriﬁcation. IEEE Trans. Computer-Aided Design of

Integrated Circuits and Systems, 27(7):1165–1178.

Eriksson, H.-E., Penker, M., Lyons, B., and Fado, D.

(2003). UML 2 Toolkit. Wiley.

Estivill-Castro, V. (2021). Tutorial Activity Diagrams With

Moka And Unsafe Race Conditions YouTube mipalgu

www.youtube.com/watch?v=P1KX2dBjmO8

Estivill-Castro, V. and Hexel, R. (2013a). Arrange-

ments of ﬁnite-state machines - semantics, simulation,

and model checking. MODELSWARD, p. 182–189.

SciTePress.

Estivill-Castro, V. and Hexel, R. (2013b). Module isola-

tion for efﬁcient model checking and its application

to FMEA in model-driven engineering. 8th Int. Conf.

on Evaluation of Novel Approaches to Software Engi-

neering, p. 218–225.

Estivill-Castro, V., Hexel, R., and Lusty, C. (2014). High

performance relaying of C++11 objects across pro-

cesses and logic-labeled ﬁnite-state machines. Sim-

ulation, Modeling, and Programming for Autonomous

Robots, p. 182–194. Springer.

Estivill-Castro, V., Hexel, R., and Rosenblueth, D. A.

(2012). Failure mode and effects analysis (FMEA)

and model-checking of software for embedded sys-

tems by sequential scheduling of vectors of logic-

labelled ﬁnite-state machines. 7th IET Int. Conf. on

System Safety.

Feiler, P. H., Lewis, B., Vestal, S., and Colbert, E. (2005).

An overview of the SAE architecture analysis & de-

sign language (AADL) standard: A basis for model-

based architecture-driven embedded systems engi-

neering. Architecture Description Languages, p. 3–

15, Boston, MA. Springer US.

Friedenthal, S., Moore, A., and Steiner, R. (2009). A Prac-

tical Guide to SysML: The Systems Modeling Lan-

guage. Morgan Kaufmann, CA, USA.

Furrer, F. (2019). Future-Proof Software-Systems: A Sus-

tainable Evolution Strategy. Springer, Berlin.

OMG (2019). Precise semantics of UML state machines

(PSSM). www.omg.org/spec/PSSM/1.0.

Guermazi, S., Tatibouet, J., Cuccuru, A., Seidewitz, E.,

Dhouib, S., and Gérard, S. (2015). Executable mod-

eling with fUML and Alf in Papyrus: Tooling and ex-

periments. 1st Int. Workshop on Executable Modeling

MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development

192

co-located with ACM/IEEE 18th Int. Conf. on Model

Driven Engineering Languages and Systems (MOD-

ELS 2015), vol. 1560, p. 3–8. CEUR-WS.org.

Hilton, M., Tunnell, T., Huang, K., Marinov, D., and Dig,

D. (2016). Usage, costs, and beneﬁts of continuous

integration in open-source projects. 31st IEEE/ACM

Int. Conf. on Automated Software Engineering, ASE

2016, p. 426–437, NY, USA.

Holt, R. C. (1972). Some deadlock properties of computer

systems. ACM Computing Surveys, 4(3):179–196.

Jin, D. and Levy, D. C. (2002). An approach to schedu-

lability analysis of UML-based real-time systems de-

sign. 3rd Int. Workshop on Software and Performance,

WOSP ’02, p. 243–250, NY, USA. ACM.

Kabous, L. and Nebel, W. (1999). Modeling hard real time

systems with UML the OOHARTS approach. 2nd Int.

Conf. on The Uniﬁed Modeling Language: Beyond the

Standard, UML’99, page 339–355, Berlin, Springer-

Verlag.

Kopetz, H. (1992). Sparse time versus dense time in dis-

tributed real-time systems. 12th Int. Conf. on Dis-

tributed Computing Systems, p. 460–467.

Kopetz, H. (1993). Should responsive systems be event-

triggered or time-triggered? IEEE Trans. Information

and Systems, E76-D(11):1325–1332.

Kopetz, H. (1998). The time-triggered model of compu-

tation. 19th IEEE Real-Time Systems Symposium, p.

168–177.

Kopetz, H. (2011). Real-Time Systems: Design Principles

for Distributed Embedded Applications. Springer, 2nd

edition.

Kopetz, H. and Bauer, G. (2003). The time-triggered archi-

tecture. Proc. of the IEEE, 91(1):112–126.

Kopetz, H. and Nossal, R. (1997). Temporal ﬁrewalls in

large distributed real-time systems. 6th IEEE Com-

puter Society Workshop on Future Trends of Dis-

tributed Computing Systems, p. 310–315.

Lamport, L. (1984). Using time instead of timeout for fault-

tolerant distributed systems. ACM Trans. Program-

ming Languages and Systems, 6:254–280.

Lee, E., Reineke, J., and Zimmer, M. (2017). Abstract

PRET machines. 2017 IEEE Real-Time Systems Sym-

posium, p. 1–11.

Lee, E. A. (2008). Cyber physical systems: Design chal-

lenges. 2008 11th IEEE Int. Symp. on Object and

Component-Oriented Real-Time Distributed Comput-

ing (ISORC), p. 363–369.

Mäkinen, S. and Münch, J. (2014). Effects of test-driven de-

velopment: A comparative analysis of empirical stud-

ies. Software Quality. Model-Based Approaches for

Advanced Software and Systems Engineering, p. 155–

169, Cham. Springer.

Markey, N. and Schnoebelen, P. (2004). Symbolic model

checking for simply-timed systems. Formal Tech-

niques, Modelling and Analysis of Timed and Fault-

Tolerant Systems, p. 102–117, Berlin, Springer.

Mellor, S. J. (2003). Executable and translatable UML. Em-

bedded Systems Programming, 16(2):25–30.

Molloy, D. (2014). Exploring BeagleBone: Tools and Tech-

niques for Building with Embedded Linux. Wiley.

Coll, C., Estivill-Castro, V., and Hexel, R. (2017). An

OO and functional framework for versatile semantics

of logic-labelled ﬁnite state machines. 12th Int. Conf.

on Software Engineering Advances, p. 238–243.

Coll, C., Estivill-Castro, V., and Hexel, R. (2018). Versa-

tile but precise semantics for logic-labelled ﬁnite state

machines. Int. J. on Advances in Software, 11(3 &

4):227–238.

Pham, V. C., Radermacher, A., Gérard, S., and Li, S.

(2017). Complete code generation from UML state

machine. 5th Int. Conf. on Model-Driven Engineering

and Software Development, MODELSWARD 2017,

Porto, Portugal, 2017, p. 208–219. SciTePress.

Sahu, S., Schorr, R., Medina-Bulo, I., and Wagner, M. F.

(2020). Model translation from Papyrus-RT into the

nuXmv model checker. Software Engineering and

Formal Methods. SEFM 2020 Collocated Workshops

- ASYDE, CIFMA, and CoSim-CPS, volume 12524 of

LNCS, p. 3–20. Springer.

Samek, M. (2008). Practical UML Statecharts in C/C++,

Second Edition: Event-Driven Programming for Em-

bedded Systems. Newnes, Newton, MA, USA.

Selic, B. (2003). The pragmatics of model-driven develop-

ment. IEEE Software, 20(5):19–25.

Selic, B., Gullekson, G., and Ward, P. T. (1994). Real-Time

Object-Oriented Modeling. John Wiley, USA.

Seshia, S. A., Sharygina, N., and Tripakis, S. (2018). Mod-

eling for veriﬁcation. Handbook of Model Checking.,

p. 75–105. Springer.

Stankovic, J. A. (1988). Misconceptions about real-time

computing: a serious problem for next-generation sys-

tems. Computer, 21(10):10–19.

OMG (2012). Information technology - Object Man-

agement Group Uniﬁed Modeling Language (OMG

UML), Infrastructure. ISO/IEC 19505-1:2012(E).

ISO.

von der Beeck, M. (1994). A comparison of statecharts

variants. Formal Techniques in Real-Time and Fault-

Tolerant Systems, p. 128–148, Berlin. Springer.

Winskel, G. (1993). The Formal Semantics of Programming

Languages: An Introduction. MIT Press, USA.

Xiao, J., Altmeyer, S., and Pimentel, A. (2017). Schedu-

lability analysis of non-preemptive real-time schedul-

ing for multicore processors with shared caches. IEEE

Real-Time Systems Symposium, p. 199–208.

Xu, J. and Parnas, D. L. (1990). Scheduling processes

with release times, deadlines, precedence and exclu-

sion relations. IEEE Trans. on Software Engineering,

16(3):360–369.

Zhang, F., Zhao, Y., Ma, D., and Niu, W. (2017). Formal

veriﬁcation of behavioral AADL models by stateful

timed CSP. IEEE Access, 5:27421–27438.

Veriﬁable Executable Models for Decomposable Real-time Systems

193