
Performance Analysis for Threshold-based N-Systems with
Heterogeneous Servers
Le Anh Thu
1 a
and Tuan Phung-Duc
2 b
1
Public Policy Program, VNU Vietnam Japan University, My Dinh Campus, Nam Tu Liem, Hanoi,Vietnam
2
Department of Policy and Planning Sciences, Faculty of Engineering, Information and Systems, University of Tsukuba,
1-1-1 Tennodai, Tsukuba, Ibaraki 305-8573, Japan
Keywords:
Multi-skilled Servers, Threshold Policy, Matrix Analytic Method, Administrative Services.
Abstract:
Driven by the need to develop methods for minimizing operational delays at public administration agencies,
this paper considers problems involving routing and staffing in these agencies. We examine a threshold-based
N-System of two queues with capacities C
1
= ∞ and C
2
< ∞, respectively. We use the matrix analytic method
to obtain the steady-state probabilities, the performance measures, and the optimal threshold values in terms
of the system parameters. Our numerical experiments reveal that the mean response time is sensitive to the
stability condition, and the effectiveness of the threshold policy depends on the customer arrival rate.
1 INTRODUCTION
Almost everyone has waited for days or weeks to get
an identity card, a driver’s license, a visitor visa, a
business registration certificate, etc. Waiting lines or
queues are known as common phenomena in admin-
istrative services due to the inadequate resources in
public administrations and rising demand for these
services, typically in Immigration Department, Busi-
ness Registration Office, etc. Queues exist mainly due
to the limited resources of the system. Customer ar-
rivals cannot be scheduled or controlled since the cus-
tomers usually arrive randomly. Moreover, customer
service times are independent random variables; some
individuals take a short time, while others require a
long period. It can be seen that queueing phenom-
ena lead to three common problems: (i) Customer
satisfaction declines due to the discomfort of spend-
ing hours in a crowded waiting room to access the
services; (ii) The employees endure the overloaded
work stress, which reduces the efficiency and quality
of work; (iii) Worsening relationships between cus-
tomers and staff, and leading to more disputes.
Waiting time has been identified as the critical
factor influencing customer satisfaction, and conse-
quently, decreasing delays has become a focus in op-
timizing the efficiency of public services (Osborne
a
https://orcid.org/0000-0002-1474-134X
b
https://orcid.org/0000-0002-5002-4946
et al., 2013). Allocating human resources based on
staff capacity is an effective solution for optimizing
staff performance and, as a result, reducing waiting
time. The complexity of work in administrative ser-
vices varies, and so do the qualifications of the staff.
Experienced employees are advantageous in terms of
performance in highly complex jobs; however, their
performance tends to decline quickly in non-complex
tasks when they become bored. Meanwhile, inexpe-
rienced employees are under pressure as their skills
are not well-matched to their job duties (Hunter and
Thatcher, 2007).
Motivated by these situations, we consider an N-
design multi-server queueing system that serves two
types of customers in two queues. This system em-
ploys two groups of servers: employees trained to
handle low complexity tasks and more experienced
employees who can handle all tasks. The switching
policy of the model is based on the skills of two dif-
ferent types of employees and the thresholds of two
queues. Similar configurations are found in various
settings, including international call centers (single-
language and multilingual servers), emergency med-
ical departments (life-threatening injuries and oth-
ers), etc. The problem of optimal allocation of cus-
tomers between queues in queueing systems to mini-
mize waiting time has received much attention. As for
the routing and staffing issues, we refer to the survey
paper by Gans et al. (2003).
The model used in this paper is related to the
Thu, L. and Phung-Duc, T.
Performance Analysis for Threshold-based N-Systems with Heterogeneous Servers.
DOI: 10.5220/0010812800003117
In Proceedings of the 11th International Conference on Operations Research and Enterprise Systems (ICORES 2022), pages 137-144
ISBN: 978-989-758-548-7; ISSN: 2184-4372
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
137
stochastic service systems belonging to a class of
models named ”lane section” that was first pro-
posed by Schwartz (1974). Stanford and Grassmann
(1993) considered a similar model of N-design bilin-
gual server system with both specialized and flexible
servers. They presented an exact performance anal-
ysis to determine the minimum number of bilingual
servers required. Due to the computational complex-
ity of this method, only comparatively small systems
can be solved. A closely related model is the paper
by Li and Yue (2016). The authors examined the N-
design call center with two types of users in which pri-
mary users have non-preemptive priority. The state-
space division method has been employed to divide
an infinite number of system states into several finite
states and obtain the steady-state probability equation
of the system. Shumsky (2004) presented an approx-
imate analysis of a queueing model of the multi-skill
call center in N-design, which has a fixed priority
strategy. The approximate analysis provides reason-
able accuracy while reducing the computational bur-
den of large service centers.
A matrix analytic method has been successfully
applied to the entire state space to obtain exact perfor-
mance measures. Morozov et al. (2021) examined a
modified Erlang loss system with two classes of cus-
tomers, in which the primary users take precedence
over secondary users. The authors assumed that the
probability distribution of service time is the expo-
nential distribution, then studied the model in depth
by matrix analysis method to evaluate the influence
of the input parameters on the secondary user perfor-
mance. Perel and Yechiali (2017) studied a closely
related system consisting of two non-identical M/M/1
queues controlled by a threshold-based switching pol-
icy. Jolles et al. (2018) expanded the model of Perel
and Yechiali by adding a switchover time policy.
In order to find the mean number of customers in
each queue, the authors formulated the system as a
Quasi-Birth-and-Death (QBD) process. Similar to
the method in Latouche and Ramaswami (1999), they
studied the steady-state behavior of the system and
obtained the rate matrix by applying the matrix ana-
lytic method.
In this paper, we consider the staffing problem of
the N-design model using the matrix-analytic method.
Though queueing analysis has been used in public ser-
vices, this is the first analytical result for public ad-
ministration service models with multiple servers in
N-design. The matrix-analytic method allows us to
derive the stability condition and effects of the input
parameters on the mean response time and users’ per-
formance. The advantage of this method is to pro-
vide systematically specific calculation formulas to
analyze more complicated models while not requir-
ing complex data. Therefore, our model is suitable
for providing evidence to evaluate administrative ser-
vice performance and compare alternatives quickly.
The rest of the paper is structured as follows. In
Section 2, we describe our model with a focus on the
switching policy, while in Section 3, the matrix an-
alytic method is applied to derive performance mea-
sures of the system in steady-state. In Section 4, we
present the results of numerical experiments to show
insights into the performance of our system and vari-
ous phenomena that occur due to a result of changes
in parameters. Section 5 concludes the paper.
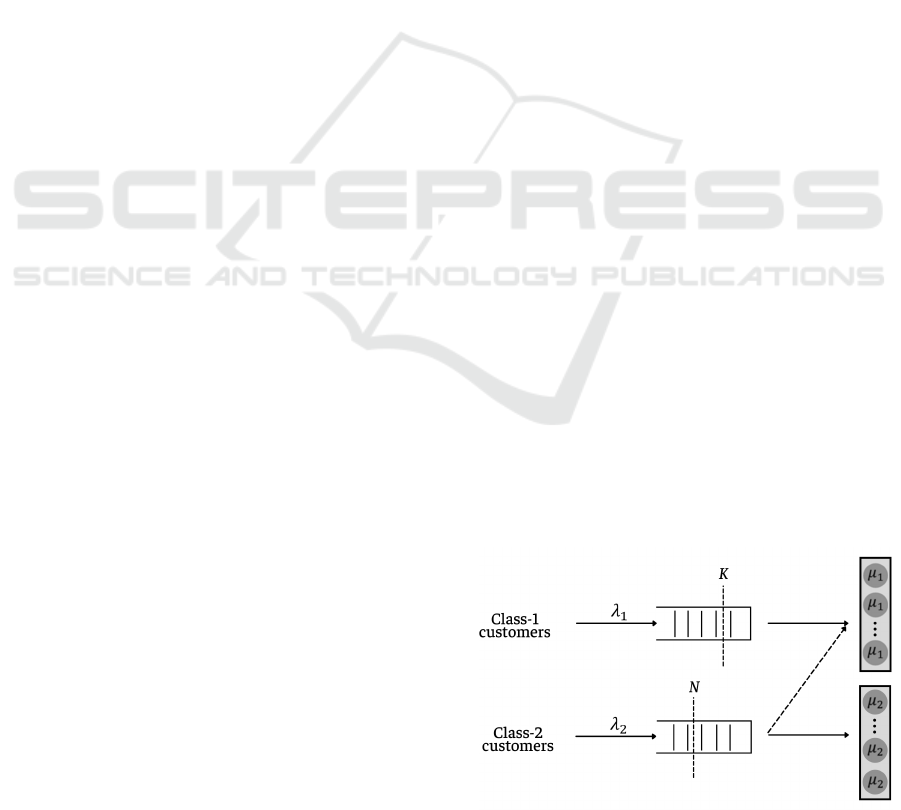
2 MODEL DESCRIPTION
We consider an N-design system that serves two
classes of customers with c
1
and c
2
servers, respec-
tively. The arrival processes are assumed to be the
Poisson processes with arrival rates λ
1
and λ
2
, respec-
tively, and the servers have exponential distributions
with mean 1/µ
i
for class-i customers, i = 1,2. The
server’s switching policy is threshold-based.
We assume that number of customers in Queue 1
(Q
1
) is not limited while Queue 2 (Q
2
) can accom-
modate up to N
max
< ∞ customers including the ones
in service. Let C
i
denote the capacity (the maximum
number of customers accommodated in the system) of
Q
i
, i = 1,2. We then have C
1
= ∞, and C
2
= N
max
< ∞.
If the two capacities C
1
and C
2
are infinite, a com-
pletely different approach is required to solve this
problem. For Q
1
, the threshold level is K ≥ c
1
, while
for Q
2
, it is N, c
2
≤ N ≤ N
max
. Denote by Q
i
(t) the
number of customers in Q
i
, i = 1, 2 at time t.
If a customer arrives at Q
2
and sees this queue al-
ready has N customers, this customer will transfer to
Q
1
. At that time, if Q
1
already has K customers, Q
1
will not accept customers from Q
2
, and that customer
will return to Q
2
. The system is illustrated in Figure
1.
Figure 1: The N-design multi-server queueing system.
ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems
138

3 THE QBD PROCESS
In this section, we calculate the stationary distri-
bution of the Markov process to obtain the cor-
responding stationary performance measures. The
two-dimensional process {(Q
1
(t),Q
2
(t)),t ≥ 0} is a
continuous-time Markov Chain with the state space
S given by S = {(i, j) ∈ N × {0,1, .. ., N
max
}}. The
system can be formulated as a Quasi-Birth-and-Death
process (QBD) with the infinitesimal generator Q
given as
Q =
B
0
C 0 0 0 ·· · ·· · ·· · ·· · ·· · ··· ·· ·
A
1
B
1
C 0 0 ···
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 A
2
B
2
C 0 ·· ·
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 ·· · 0 A
c
1
B
c
1
C 0 ·· ·
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 .. . ... 0 A
c
1
B
K−1
C 0 ...
.
.
.
.
.
.
0 0 .. . ... 0 0 A
c
1
B
K
C
K
0 .. .
.
.
.
0 0 ··· ·· · · ·· 0 0 A
c
1
B
K
C
K
0 .. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
,
where 0 is a (N
max+1
)×(N
max+1
) zero matrix, and A
i
,B
i
,B
K
,C,C
K
are (N
max+1
)×(N
max+1
) block matrices given
by
A
i
=
min(i, c
1
)µ
1
0 0 0
0 min(i, c
1
)µ
1
0 0
.
.
.
.
.
.
.
.
.
.
.
.
0 .. . 0 min (i,c
1
)µ
1
,
for i < c
1
, and A
i
= A
c
1
for i ≥ c
1
.
B
i
=
b
i,0
λ
2
0 0 .. . . .. . .. .. . .. . .. . 0
µ
2
b
i,1
λ
2
0 .. . . .. . .. .. . .. . .. . 0
0 2µ
2
b
i,2
λ
2
0 .. . ... . .. . .. . .. 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 ... 0 c
2
µ
2
b
i,c
2
λ
2
0 .. . .. . .. . 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 ... .. . .. . 0 c
2
µ
2
b
i,N−1
λ
2
0 .. . 0
0 ... .. . .. . 0 0 c
2
µ
2
b
i,N
0 .. . 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 ... .. . .. . . .. ... .. . 0 c
2
µ
2
b
i,N
max−1
0
0 ... .. . .. . . .. ... .. . ... 0 c
2
µ
2
b
i,N
max
,
for i = 0, 1,2, ...,K − 1, where b
i,n
= − [λ
1
+ λ
2
+ min (i;c
1
)µ
1
+ min (n;c
2
)µ
2
].
B
K
=
b
i,0
λ
2
0 0 .. . . .. .. . 0
µ
2
b
i,1
λ
2
0 .. . . .. .. . 0
0 2µ
2
b
i,2
λ
2
0 .. . ... 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 ... 0 c
2
µ
2
b
i,c
2
λ
2
.. . 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 ... .. . .. . 0 c
2
µ
2
b
i,N
max
−1
λ
2
0 ... .. . .. . . .. 0 c
2
µ
2
b
i,N
max
,
Performance Analysis for Threshold-based N-Systems with Heterogeneous Servers
139

for i = K,K + 1,K + 2,... ,B
i
= B
K
, where
b
i,n
= − [λ
1
+ λ
2
+ min (i;c
1
)µ
1
+ min (n;c
2
)µ
2
],
for n = 0, 1,. ..,N
max
− 1, and
b
i,N
max
= − [λ
1
+ min (i;c
1
)µ
1
+ min (n;c
2
)µ
2
].
C =
λ
1
0 0 ... .. . . .. 0
0 λ
1
0 ... ... . .. 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0
.
.
. 0 λ
1
0 ... 0
0 .. . ... 0 λ
1
+ λ
2
... 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 .. . ... ... ... 0 λ
1
+ λ
2
,
where the diagonal element C(i, i) is given by
C(i, i) = λ
1
, for i = 0,1, .. .,N − 1,
C(i, i) = λ
1
+ λ
2
, for i = N,N + 1,. .. ,N
max
.
C
K
=
λ
1
0 0 0
0 λ
1
0 0
.
.
.
.
.
.
.
.
.
.
.
.
0 . .. 0 λ
1
.
Let M = A
c
1
+ B
K
+C
K
, then
M =
m
0
λ
2
0 0 . . . . .. 0
µ
2
m
1
λ
2
0 .. . . .. 0
0 2µ
2
m
2
λ
2
0 .. . 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 ... 0 c
2
µ
2
m
c
2
λ
2
...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 ... .. . .. . 0 c
2
µ
2
m
N
max
,
where the diagonal elements of M is given by
m
i
= −(min(i, c
2
)µ
2
+ λ
2
), for i = 0,1, .. .,N
max
− 1,
and m
N
max
= −c
2
µ
2
.
Let π
M
= (π
M,i
;i = 1, 2,. .. ,N
max
) be the stationary
probability vector of the matrix M, i.e., π
M
M = 0
and π
M
e = 1, where e denotes the column vector
of ones, whose dimension is determined upon context.
The stability condition of such a QBD, (see Theorem
1.7.1, Neuts (1994)) can be obtained by the condition
π
M
C
K
e < π
M
A
c
1
e.
This stability condition can be transformed as
λ
1
< c
1
µ
1
. (1)
Let π(i,n) = P(Q
1
(t) = i, Q
2
(t) = n), for i ∈ N and
n = 0,1, ...,N
max
denote the stationary probability of
the Markov chain.
We define
π
(1)
i
= (π
i,0
,π
i,1
,. .. ,π
i,N
max
), for i = 0,1,2,...,
π
(2)
n
= (π
0,n
,π
1,n
,π
2,n
,. ..) , for n = 0,1,2,..., N
max
.
According to Matrix-analytic-method (Latouche and
Ramaswami (1999); Phung-Duc et al. (2010)), we
have
π
(1)
i
= π
(1)
K
R
i−K
, i > K, (2)
π
(1)
i
= π
(1)
i−1
R
(i)
, i = K,K − 1, ...,1, (3)
where R is the minimal non-negative solution of
C
K
+ RB
K
+ R
2
A
c
1
= 0, (4)
and
R
(i)
= −C(B
i
+ R
(i+1)
A
i+1
)
−1
, for i = K − 1,K − 2, ... , 1,
(5)
given that
R
(K)
= −C(B
K
+ RA
c
1
)
−1
. (6)
Then, π
0
is the solution of the following equations
π
(1)
0
B
0
+ R
(1)
A
1
= 0,
π
(1)
0
I +
K−1
∑
i=1
i
∏
j=1
R
( j)
+
K
∏
j=1
R
( j)
!
(I − R)
−1
!
e = 1,
(7)
where we use I to denote the (N
max
+ 1) × (N
max
+ 1)
identity matrix. The first and the second equation in
(7) represent the boundary equations at level 0, and
the normalization condition, respectively.
Let E[L
i
] denote the average number of customers in
the system in Q
i
, i = 1,2. We then obtain the mean
queue length of Q
1
and Q
2
as follows
E [L
1
] =
∞
∑
i=1
π
(1)
i
ie
=
K−1
∑
i=1
π
(1)
i
ie +
∞
∑
i=K
π
(1)
i
ie
=
K−1
∑
i=1
π
(1)
i
ie +
∞
∑
i=K
π
(1)
K
R
i−K
ie
=
K−1
∑
i=1
π
(1)
i
ie + π
(1)
K
∞
∑
i
0
=0
R
i
0
i
0
+ K
e
=
K−1
∑
i=1
π
(1)
i
ie + π
(1)
K
∞
∑
i
0
=0
R
i
0
Ke + π
(1)
K
∞
∑
i
0
=0
R
i
0
i
0
e
ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems
140

=
K−1
∑
i=1
π
(1)
i
ie + π
(1)
K
(I − R)
−1
Ke + π
(1)
K
R
∞
∑
j=1
R
j−1
je
=
K−1
∑
i=1
π
(1)
i
ie + π
(1)
K
(I − R)
−1
Ke + π
(1)
K
R[(I − R)
−1
]
2
e
=
K−1
∑
i=1
π
(1)
i
ie + π
(1)
K
[(I − R)
−1
K + R[(I − R)
−1
]
2
]e,
(8)
E [L
2
] =
N
max
∑
n=0
π
(2)
n
ne
=
K−1
∑
n=0
π
(1)
n
+ π
(1)
K
I + R + R
2
+ ···
!
f
=
K−1
∑
n=0
π
(1)
n
+ π
(1)
K
(I − R)
−1
!
f ,
(9)
where f = (0, 1,2, ...,N
max
)
T
.
Let E[L] be the total average number of customers in
the system in both queues, then
E[L] = E [L
1
] + E [L
2
]. (10)
We obtain the mean number of busy servers, E[S
i
], in
Q
i
, i = 1, 2 as follows
E[S
1
] =
c
1
−1
∑
i=1
π
(1)
i
ie + c
1
∞
∑
j=c
1
π
(1)
j
e
=
c
1
−1
∑
i=1
π
(1)
i
ie + c
1
K−1
∑
j=c
1
π
(1)
j
e + c
1
∞
∑
j
0
=K
π
(1)
j
0
e
=
c
1
−1
∑
i=1
π
(1)
i
ie + c
1
K−1
∑
j=c
1
π
(1)
j
e + c
1
∞
∑
j
0
=K
π
(1)
K
R
j
0
−K
e
=
c
1
−1
∑
i=1
π
(1)
i
ie + c
1
K−1
∑
j=c
1
π
(1)
j
e + c
1
π
(1)
K
(I − R)
−1
e
=
c
1
−1
∑
i=1
π
(1)
i
ie +
K−1
∑
j=c
1
π
(1)
j
+ π
(1)
K
(I − R)
−1
!
c
1
e.
(11)
E[S
2
] =
c
2
−1
∑
i=1
π
(2)
i
ie + c
2
N
max
∑
j=c
2
π
(2)
j
e
=
K−1
∑
n=0
π
(1)
n
+ π
(1)
K
(I − R)
−1
!
g,
(12)
where g is a (N
max
+ 1) × 1 column vector given by
g = (0, 1,2, ...,c
2
− 1,c
2
,. .. ,c
2
)
T
.
Denote by E[T
i
] the throughput of Q
i
, i = 1,2, that are
E[T
1
] = E[S
1
] × µ
1
=
c
1
−1
∑
i=1
π
(1)
i
ie + c
1
∞
∑
j=c
1
π
(1)
j
e
!
µ
1
< c
1
∞
∑
i=1
π
(1)
i
eµ
1
= c
1
µ
1
, (13)
E[T
2
] = E[S
2
] × µ
2
. (14)
Then the throughput of the system is given by
E[T ] = E[T
1
] + E[T
2
]. (15)
Furthermore, due to Little’s law, we obtain the mean
response time E[R
i
] in Q
i
, i = 1,2, respectively, as
follows
E[R
i
] =
E[L
i
]
E[Ti]
, for i = 1,2. (16)
The mean system response time is given by
E[R] =
E[L]
E[T ]
. (17)
For reference, we compare with a baseline model,
i.e., two parallel queues without the threshold policy.
In the absence of threshold policy (K = 0), our
system becomes a system of an M/M/c
1
queue and
an M/M/c
2
/N
max
queue.
According to Medhi (2002), the probability of zero
customers in the system in Q
1
is calculated by
π
(1)
o
=
c
1
−1
∑
n=0
(λ
1
/µ
1
)
n
n!
+
(λ
1
/µ
1
)
c
1
c
1
!(1 − λ
1
/(c
1
µ
1
))
!
−1
.
The condition for the stability of Q
1
is λ
1
/(c
1
µ
1
) < 1.
The mean number of customers in the system in Q
1
is
given by
E[L
1
] =
λ
1
µ
1
+
ρ
1
1 − ρ
1
C
c
1
,
λ
1
µ
1
, (18)
where ρ
1
=
λ
1
c
1
µ
1
, and C
c
1
,
λ
1
µ
1
=
(λ
1
/µ
1
)
c
1
c
1
!(1−λ
1
/(c
1
µ
1
))
π
(1)
0
is referred to as Erlang’s C formula.
Then, the mean response time in Q
1
can be obtained
by
E[R
1
] =
E[L
1
]
λ
1
. (19)
According to Shortle et al. (2018), the probability of
zero customers in the system in Q
2
is given by
π
(2)
o
=
c
2
−1
∑
n=0
ρ
n
2
n!
+
ρ
c
2
2
c
2
!
(N
max
− c
2
+ 1)
−1
,
for
ρ
2
c
2
= 1, and
Performance Analysis for Threshold-based N-Systems with Heterogeneous Servers
141
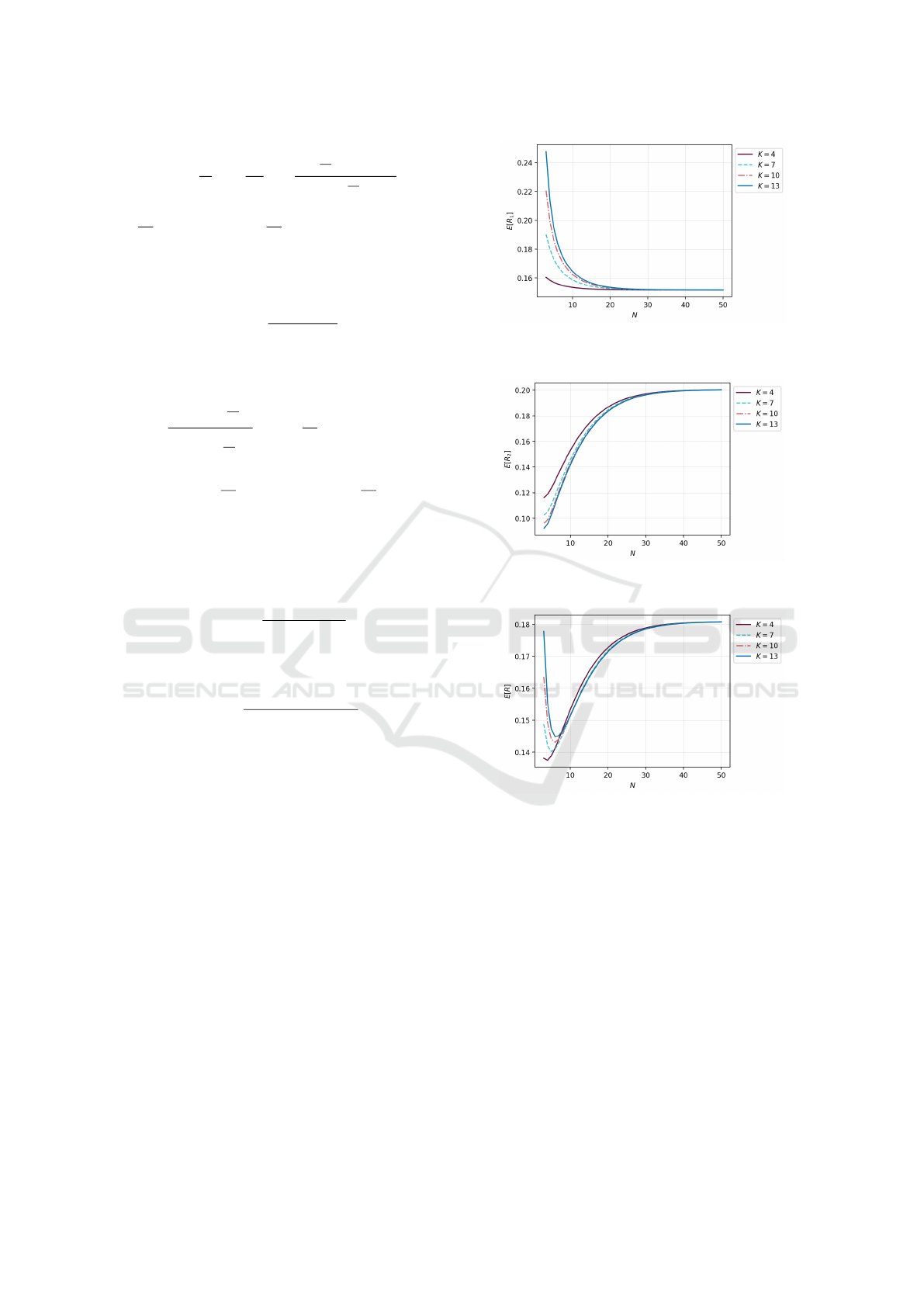
π
(2)
0
=
"
c
2
−1
∑
n=0
ρ
n
2
n!
+
ρ
c
2
2
c
2
!
1−
ρ
2
c
2
N
max
−c
2
+1
1−
ρ
2
c
2
!#
−1
,
for
ρ
2
c
2
6= 1, where ρ
2
=
λ
2
µ
2
.
Denote by P
N
max
the blocking probability of Q
2
which
means that Q
2
can satisfy atmost N
max
flow units, then
P
N
max
=
π
(2)
0
ρ
N
max
2
c
N
max
−c
2
2
c
2
!
.
The mean number of customers in the system in Q
2
is
calculated as
E[L
2
] =
π
(2)
o
ρ
c
2
2
ρ
2
c
2
c
2
!
1 −
ρ
2
c
2
2
"
1 −
ρ
2
c
2
N
max
−c
2
+1
−
1 −
ρ
2
c
2
(N
max
− c
2
+ 1)
ρ
2
c
2
N
max
−c
2
#
+ ρ
2
(1 − P
N
max
).
(20)
The mean system response time in Q
2
can be obtained
by
E[R
2
] =
E[L
2
]
λ
2
(1 − P
N
max
)
. (21)
We obtain the mean system response time E[R] in the
case without threshold policy as follows
E[R] =
E[L
1
] + E[L
2
]
λ
1
+ λ
2
(1 − P
N
max
)
. (22)
4 NUMERICAL INSIGHTS
This section presents several numerical experiments
of the results obtained in Section 3 to find insights
into the performance of our system. For fixed λ
1
=
20, λ
2
= 30, µ
1
= 8, µ
2
= 12, c
1
= 4, c
2
= 3, and
N
max
= 50, we show how the performance measures
change according to the thresholds (K,N). Under the
same settings, we also compute these performance
measures in the case without threshold policy (K = 0)
using the classical M/M/c and M/M/c/m models.
Figure 2 reflects the changes in the mean response
time of class-1 customers against Q
2
’s threshold. The
mean response time of class-1 customers decreases
when N goes up to a specific value for a fixed K, then
remains unchanged as N continues to increase. Mean-
while, Figure 3 shows the exact opposite trend in the
response time of class-2 customers. It is noticeable
that the mean amount of time that class-2 customers
spend in the system depends more on N than on K.
Figure 2: The mean response time of class-1 customers
against the Q
2
’s threshold.
Figure 3: The mean response time of class-2 customers
against the Q
2
’s threshold.
Figure 4: The mean system response time against the Q
2
’s
threshold.
Figure 4 indicates that the mean system response
time E[R] drops as N goes up to certain thresholds,
then rises again sharply before remaining unchanged
when N is at very high values. For small values of N,
E[R] goes down as N increases and K decreases. This
occurs since the servers in Q
2
may remain idle even if
there are waiting customers in Q
1
, including class-2
customers, leading to an increase in the mean system
response time. In this experiment, E[R] reaches the
minimum at 0.1374 when the value of N is 4, and K
is 4. Moreover, the mean response time of the system
without threshold policy is 0.1808, which is higher
than it is in the case of the optimal threshold policy.
For fixed K = 4 and N = 3,9, we show the changes
in the performance measure E[R] against λ
1
and λ
2
,
ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems
142

while all other parameters remain unchanged. We
also illustrate the changes in these performance mea-
sures against λ
1
and λ
2
in the absence of threshold
policy, thereby finding that a non-threshold policy is
not optimal for our system. We recall that the stability
condition in both cases with and without the threshold
policy is given by λ
1
< c
1
µ
1
= 32.
Figure 5: The mean system response time E[R] against the
arrival rate of class-1 customers (λ
2
= 30).
Figure 5 illustrates how the mean system response
time E[R] changes according to the arrival rate of
class-1 customers. The mean system response time is
large when class-1 customers arrive more frequently,
especially as λ
1
is asymptotic to the value c
1
µ
1
. The
mean system response time is highly sensitive to these
values of λ
1
, while changes in N and K at that time
have no significant effect on E[R]. Therefore, as the
arrival rate of class-1 customers approaches the stable
threshold, increasing the number of servers in Q
1
is
required to reduce the mean system response time.
Figure 6: The mean system response time E[R] against ar-
rival rate of class-2 customers (λ
1
= 20).
Figure 6 shows the changes in the mean system
response time E[R] against λ
2
in both cases with and
without the threshold policy. The performance mea-
sure E[R] in these two cases shares the same trend
when λ
2
changes. It can be seen that applying the
threshold policy significantly reduces the mean sys-
tem response time as the arrival rate of class-2 cus-
tomers is large enough. If class-2 customers arrive
more frequently, the mean system response time is
large, especially within a specific range of values of
λ
2
. However, when λ
2
reaches a certain threshold,
the mean system response time E[R] will stop grow-
ing because the capacity of Q
2
is limited to N
max
.
Figure 7: Throughput of Q
1
against arrival rate of class-2
customers (λ
1
= 20).
Figure 7 indicates the impact of the arrival rate
of class-2 customers on the throughput of Q
1
. In the
case of the threshold policy, the throughput E[T
1
] re-
mains unchanged at λ
1
when λ
2
goes up to certain
thresholds, then rises sharply as λ
2
continues to in-
crease before remains stable at a value of c
1
µ
1
(see
the condition (13)) when class-2 customers arrive at
very high rates.
Figure 8: Throughput of Q
2
against arrival rate of class-1
customers (λ
2
= 30).
Figure 8 reflects the changes in the throughput of
Q
2
against λ
1
when λ
2
is fixed. Under the threshold
policy, the throughput of Q
2
closely approaches the
value of λ
2
when λ
1
is asymptotic to the value of c
1
µ
1
.
For large values of N, the throughput of Q
2
is insen-
sitive to the arrival rate of class-1 customers. Obvi-
ously, with the threshold policy, the throughput of Q
1
is greater than or equal to λ
1
, whereas the through-
put of Q
2
is less than or equal to λ
2
because class-
2 customers can transfer from Q
2
to Q
1
. In the ab-
sence of threshold policy, the throughputs E[T
1
] and
E[T
2
] equal the arrival rates of class-1 and class-2 cus-
tomers, respectively.
Performance Analysis for Threshold-based N-Systems with Heterogeneous Servers
143

5 CONCLUSIONS
This paper has considered the routing and staffing
problems of an administrative agency in an N-design
model that serves two types of customers. Using the
matrix analytic method, we have derived the steady-
state probabilities and the performance measures. We
then have determined the optimal threshold values ac-
cording to the system parameters. We have found
that the threshold policy is highly effective when the
arrival rate of class-1 customers is low and the ar-
rival rate of class-2 customers is high. When λ
1
ap-
proaches the critical value satisfying the stability con-
dition or λ
2
is relatively small, increasing the num-
ber of servers combined with changing the threshold
policy is the solution to reduce the mean system re-
sponse time. As a result, we have provided a ba-
sis for reallocating resources when the customer ar-
rival rate changes. Our findings could be used in
decision-making, managing resources in administra-
tive services, and related applications. It will be help-
ful to expand the analysis of our model to the case
when both capacities are infinite.
ACKNOWLEDGEMENTS
The research of Tuan Phung-Duc was supported in
part by JSPS KAKENHI Grant Numbers 18K18006,
21K11765.
REFERENCES
Gans, N., Koole, G., and Mandelbaum, A. (2003). Tele-
phone call centers: Tutorial, review, and research
prospects. Manufacturing & Service Operations Man-
agement, 5(2):79–141.
Hunter, L. W. and Thatcher, S. M. (2007). Feeling the heat:
Effects of stress, commitment, and job experience on
job performance. Academy of Management Journal,
50(4):953–968.
Jolles, A., Perel, E., and Yechiali, U. (2018). Alternating
server with non-zero switch-over times and opposite-
queue threshold-based switching policy. Performance
Evaluation, 126:22–38.
Latouche, G. and Ramaswami, V. (1999). Introduction
to matrix analytic methods in stochastic modeling.
SIAM.
Li, C.-Y. and Yue, D.-Q. (2016). The staffing problem of
the n-design multi-skill call center based on queuing
model. In Advances in computer science research, 3rd
International Conference on Wireless Communication
and Sensor Network, volume 44, pages 427–432.
Medhi, J. (2002). Stochastic models in queueing theory.
Elsevier.
Morozov, E. V., Rogozin, S., Nguyen, H., and Phung-Duc,
T. (2021). Modified erlang loss system for cognitive
wireless networks. arXiv preprint arXiv:2103.03222.
Neuts, M. F. (1994). Matrix-geometric solutions in stochas-
tic models: an algorithmic approach. Courier Corpo-
ration.
Osborne, S. P., Radnor, Z., and Nasi, G. (2013). A new the-
ory for public service management? toward a (public)
service-dominant approach. The American Review of
Public Administration, 43(2):135–158.
Perel, E. and Yechiali, U. (2017). Two-queue polling sys-
tems with switching policy based on the queue that is
not being served. Stochastic Models, 33(3):430–450.
Phung-Duc, T., Masuyama, H., Kasahara, S., and Taka-
hashi, Y. (2010). A simple algorithm for the rate ma-
trices of level-dependent qbd processes. In Proceed-
ings of the 5th international conference on queueing
theory and network applications, pages 46–52.
Schwartz, B. L. (1974). Queuing models with lane selec-
tion: a new class of problems. Operations Research,
22(2):331–339.
Shortle, J. F., Thompson, J. M., Gross, D., and Harris, C. M.
(2018). Fundamentals of queueing theory, volume
399. John Wiley & Sons.
Shumsky, R. A. (2004). Approximation and analysis of a
call center with flexible and specialized servers. OR
Spectrum, 26(3):307–330.
Stanford, D. A. and Grassmann, W. K. (1993). The bilin-
gual server system: A queueing model featuring fully
and partially qualified servers. INFOR: Information
Systems and Operational Research, 31(4):261–277.
ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems
144
