Ontology-based Detection of Inconsistencies in UML/OCL Models

Shan Lu

, Alexey Tazin

, Yanji Chen

, Mieczyslaw M. Kokar

and Jeff Smith

Department of Electrical and Computer Engineering, Northeastern University, Boston, Massachusetts 02115, U.S.A.

Sierra Nevada Corporation, Sparks, Nevada 89434, U.S.A.

Keywords:

UML/OCL Models, OCL Constraints, Consistency Checking, Ontology-based Method, State Machine

Diagrams.

Abstract:

Consistency checking of UML/OCL models is a challenging issue in software development. In this paper,

we discuss an OWL/ontology-based method to detect the inconsistencies in the UML/OCL models as the ﬁrst

step of requirement change management. Speciﬁcally, we map the UML/OCL models to OWL, so that the

consistency of the corresponding ontology can be checked by OWL reasoners automatically. We propose a set

of mapping rules to interpret the components of UML state machine diagrams, along with OCL constraints,

to OWL DL. Towards this objective, we demonstrate three consistency reasoning tasks over a state machine

diagram using OWL reasoners. In each case, the result of reasoning is accompanied by an explanation of the

logic behind the decision.

1 INTRODUCTION

There are two main advantages of using an ontology

in software engineering. First, ontologies provide

common vocabularies of given domains that can

be shared between software developers for different

software applications. Second, once the model of the

software and the user requirements are represented as

an ontology in OWL (WC3, 2004), the requirement

satisfaction can be veriﬁed automatically using an

inference engine.

In this paper, we are focusing on the latter issue.

However, instead of proving that user requirements

are satisﬁed, we will show some “reasonable

assurances” to the developer that the model is correct,

reserving full veriﬁcation of requirement satisfaction

as future work.

2 PROBLEM STATEMENT

Uniﬁed Modeling Language (UML) is a widely used

industry standard language that provides graphical

notation for software design speciﬁcation in the early

phases of software development. Systems Modeling

Language (SysML) is an extension of a subset of

the UML. However, UML/SysML models alone are

not expressive enough to represent constraints on

the modeling concepts. Object Constraint Language

(OCL) is used to express constraints in UML/SysML

models. Many UML/SysML tools support adding

OCL constraints in UML class diagrams and SysML

block diagrams. However, none of the tools supports

the semantics checking of the constraints. In other

words, the UML/SysML tools do not check if the

model is correct according to these constraints.

To support the software developers with

automated reasoning capabilities when developing

the model of the software, we use an ontology-

based method to reason about the correctness

of a UML/SysML model with OCL constraints.

Speciﬁcally, we map UML class diagrams (or

SysML block diagrams), state machine diagrams,

and OCL constraints to OWL (WC3, 2004), and

check the consistency of the corresponding ontology

by running an OWL inference engine. Although

signiﬁcant amount of research on mapping UML

models to ontologies has been reported, almost all of

the researchers limit their scope of investigation to

class diagrams. There is a lack of widely accepted

mapping rules for the mapping of UML behavior

diagrams to OWL.

In this paper, we propose a set of mapping rules

to interpret the components of UML state machine

diagrams, along with OCL constraints, to OWL DL.

The novelty of our approach is the identiﬁcation

and implementation of a more complete mapping

of UML/SysML to OWL, than what is included

194

Lu, S., Tazin, A., Chen, Y., Kokar, M. and Smith, J.

Ontology-based Detection of Inconsistencies in UML/OCL Models.

DOI: 10.5220/0010814500003119

In Proceedings of the 10th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2022), pages 194-202

ISBN: 978-989-758-550-0; ISSN: 2184-4348

with current CASE tools to support deeper model

veriﬁcation. There are a few papers on the mapping

of the UML/SysML behavior diagrams to OWL

DL, however, they either use a non-OCL logic,

a restricted set of OCL operators and/or do not

support formal proof. Our mapping rules have

two advantages: (1) they show how to translate

both basic state machine elements (including states,

transitions, events, actions, guards, and triggers)

and OCL constraints in the state machine diagrams

(including the OCL invariants in states and guards)

to OWL, and (2) the OCL to OWL translation rules

cover relational operators (e.g equivalent, greater/less

than) between variables.

The existing research on consistency checking

of UML state machine diagrams focuses on the

contradictions between: (1) the UML metamodel and

state machine speciﬁcations, and (2) state machine

diagrams and other types of diagrams. Veriﬁcation

that state machine diagrams are not contradictory

with the requirements expressed as OCL constraints is

also a very important issue in software development.

In this paper, we check for contradictions between

OCL constraints in state machine diagrams. We

demonstrate this capability on three exemplary

inference tasks.

The rest of this paper is organized as follows. In

Section 3, we review some of the existing literature

related to our work. In Section 4, we show the

OWL axiom usage in reasoning about SysML block

diagrams. In Section 5, we propose a set of mapping

rules to interpret the components of state machine

diagrams along with OCL constraints to OWL DL,

and demonstrate three reasoning tasks using OWL

reasoners. Finally, Section 6 summarizes our work.

3 RELATED WORK

We group our literature review into four categories.

Classiﬁcation of Inconsistency in UML Models:

Consistency checking of UML/SysML models is an

important step in MBSE-based system development.

The appropriate deﬁnitions of types of consistency are

still an open research topic, c.f., Ahmad and Nadeem

(2010); Elaasar and Briand (2004); Usman et al.

(2008). One of the UML consistency classiﬁcations

is horizontal vs. vertical consistency. Horizontal

consistency, also called intra-model consistency,

means the lack of contradictions between different

diagrams at the same level of abstraction. Vertical

consistency, also called inter-model consistency,

means the lack of contradictions between different

diagrams at different levels of abstraction. Another

basic classiﬁcation of consistency in UML is syntactic

vs. semantic consistency. Syntactic consistency refers

to the relation between UML diagram speciﬁcations

and a UML metamodel, whether the syntax of a given

diagram is compatible with the syntax prescribed by

the metamodel. Semantic consistency refers to the

meaning of UML diagrams, i.e., to the notion of

truth - whether any contradictions in the model do

not exist and whether a concept can be instantiated.

Other methods of consistency classiﬁcation were also

discussed in the literature, e.g., static versus dynamic

consistency, multi-level consistency, and the nature of

errors.

In this paper, we focus on the consistency of UML

models that include requirements expressed in OCL.

Since the OCL constraints capture the semantics

of the domain, our approach falls in the semantic

validation category.

Consistency Checking Via Mapping to Formal

Languages: Many approaches rely on the mapping

UML/SysML models to a formal languages and

automatic proof engines that are used for reasoning

on these models. While many recent papers propose

mapping of UML to OWL, most of the papers

seem to ignore the fact that UML and OWL have

different semantics. This issue was ﬁrst discussed

in (Baclawski et al., 2001), where the authors

identiﬁed similarities and differences between UML

and DAML (DARPA Agent Markup Language). To

close the gap between the two representations, the

authors proposed extending UML by adding two

metamodel elements called Property and Restriction,

where a property is a grouping of association ends

and a restriction is a classiﬁer for objects. The

recommendation from the (Baclawski et al., 2001)

paper has not materialized primarily due to the fact

that UML has not been modiﬁed as suggested in the

paper. Moreover, DAML became OWL.

UML2Alloy (Anastasakis and Ray, 2010;

Przigoda and Drechsler, 2016) maps UML/OCL

models to Alloy notations, and then the Alloy model

is automatically analysed by the Alloy Analyzer.

Alloy is an object modeling language based on First

Order Logic (FOL), offering declaration syntax

compatible with graphical object oriented models,

and state-based formulas. However, Alloy models do

not provide semantic notations which are necessary

during the analysis phase of software development

(Dwivedi and Rath, 2018).

USE (Gogolla et al., 2008, 2007) includes an

interpreter for a subset of UML and OCL. It provides

its own UML/OCL user interface and lets one check

constraints (invariants and pre- and post-conditions).

That is, it checks model states (snapshots) making

Ontology-based Detection of Inconsistencies in UML/OCL Models

195

sure invariants are not contradictory. However, this

is not a formal system and it uses a custom UI that

does not support XMI import/export.

Rehman et al. (Latif et al., 2018, 2019) modeled

a smart parking and a sewage systems using UML

activity diagrams, translating them to automata-based

models, and then to temporal logic of actions. A

(TLA)-based formal method was utilized to validate

and verify system properties using the TLA+ toolbox

(Lamport, 2021). The toolbox includes a proof

system and a high level language to generate TLA

code. TLA+ is a good tool for verifying code

simulating state machines, it is not clear how it could

be used for model analysis, which was our objective.

Automated Reasoning on UML/OCL conceptual

Schemas (AuRUS) (Rull et al., 2013) is a standalone

application which allows verifying and validating

UML/OCL conceptual schemas speciﬁed in

ArgoUML. Veriﬁcation consists in determining

whether the schema satisﬁes a set of well-known

desirable properties such as class liveliness or

non-redundancy of integrity constraints. However,

AuRUS only validates the structural part of a schema.

Validation of the behavioral part of a schema is not

supported.

There are many other methods surveyed in

(Ahmad and Nadeem, 2010; Usman et al., 2008)

that are based on a formal language. In particular,

the authors considered mapping UML models to

DL. None of the methods reviewed in that paper

check the consistency of the OCL constraints. Some

researchers pursue veriﬁcation of consistency, e.g.,

Filipovikj (2019); Mahmud et al. (2016), but not of

UML/SysML models.

Ontology-based Consistency Checking: In

(Parreiras et al., 2007), the authors investigate the

method called TwoUse to integrate a UML model

and an OWL ontology. Since OWL classes can not

be exploited through OCL expressions, the authors

propose an extension to the OCL basic library, called

OCL-DL, to permit operations to call the OWL

reasoner. In OCL-DL, the authors propose new

operations which rely on reasoning engine services

to extend the boundaries of OCL towards OWL.

However, their method only focuses on UML class

diagrams.

In (Berardi et al., 2005), the authors represent

class diagram operations using three ways: (1)

FOL n-ary predicate that has to satisfy some FOL

assertions. (2) DLR-ifd (variation of DL) where the

operation is represented as an n-ary relation. (3)

ALCQI (variation of DL) where the approach is based

on reiﬁcation and an operation is expressed as an

atomic concept - ALCQI roles. Our approach to class

diagram mapping is in line with (Berardi et al., 2005).

Mapping Behavior Models to OWL DL: The

method in (Van Der Straeten et al., 2002) translates

UML state machines and OCL constraints to DLR -

an expressive Description Logic (DL) that supports

n-ary relations. The basic idea is that the states and

transitions in a state diagram are mapped to primitive

concepts in DL. We have not found tool support for

the translation. Also, the translation of OCL to OWL

does not allow relational operators between variables.

In (Gr

oner and Staab, 2010), the authors describe

a transformation of UML statechart primitives to

OWL DL. In their transformation, a speciﬁc state

is deﬁned by a class expression constrained by

transitions and state conditions. A speciﬁc transition

is deﬁned by an intersecting class expression standing

for the source, target, event and guard of this

transition. However, this work does not support

translation of OCL constraints.

In (Khan and Porres, 2015; Khan et al., 2013), the

authors translate both the UML class and statechart

diagrams of a model to a single ontology, and analyze

the consistency and satisﬁability of the model using

OWL reasoners. However, the authors do not provide

any translation of transitions in the statechart diagram.

Moreover, translation of OCL to OWL does not allow

relational operators between variables.

The method in (Belgueliel et al., 2014) represents

state machine using OWL individuals. It is difﬁcult

to extend this method for OCL support, since the

mapping of OCL to OWL that we use is class-based.

The detailed comparison of theses mapping rules

is shown in Table 2.

4 OWL REASONING ABOUT

SysML BLOCK DIAGRAMS

An ontology is an explicit, formal speciﬁcation of a

shared conceptualization (Gruber, 1993). Ontologies

include ﬁve basic components to represent the

knowledge of a domain: (1) Classes: groups of things

that share common characteristics; (2) Relations:

the ways in which classes can be related to one

another; (3) Constraints: determining which values

are allowed for relations; (4) Axioms: logical

statements or assertions about classes, relations,

and constraints; (5) Instances: the things that the

ontology describes. Web Ontology Language (OWL)

is a family of standardized ontology languages with

formal semantics to formalize ontologies. Prot ´eg ´e

(Stanford University, 2020) is a popular open-source

ontology editor and knowledge base framework. We

used Prot ´eg ´e to develop our ontologies.

MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development

196

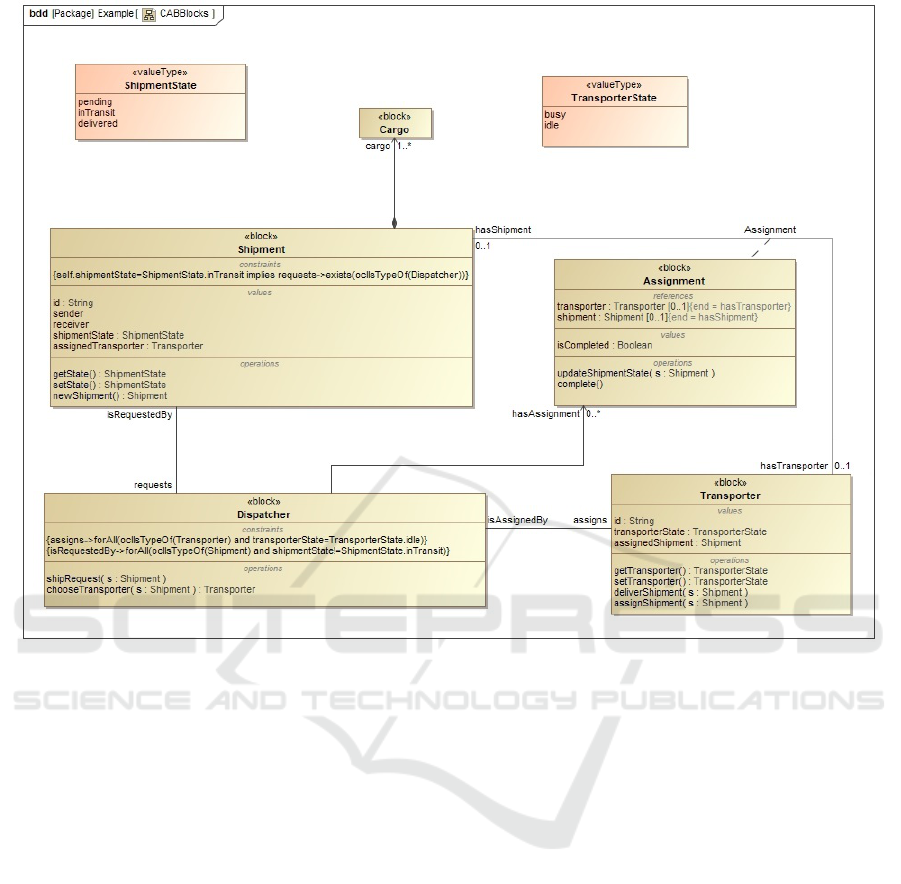
Figure 1: SysML Block Diagram of the CAB Model.

We used the Cameo Concept Modeler plugin

(NoMagic, 2021) for Cameo Enterprise Architecture

to translate SysML block diagrams to OWL. Then

we used rules to translate OCL contraints to OWL.

In this paper, we only consider a subset of OCL

constraints, namely OCL invariants. OCL invariants

were manually translated into OWL 2 DL axioms

based on (Parreiras et al., 2007) and (Fu et al., 2017).

Speciﬁcally, for a block diagram, the OCL invariants

of a block are translated into OWL object property

restrictions. OWL DL provides three types of class

axioms to construct a class description: SubclassOf,

EquivalentClasses, DisjointClasses that can be used

for checking consistency.

Generalization associations between two blocks

are translated into SubclassOf axioms of the

corresponding OWL classes. Moreover, OCL

invariants of a block are translated into SubclassOf

axioms of the corresponding OWL class. In DL, we

represent this as C

⊑ C

. When such a subclass

axiom is part of an OWL model, for any individual

x of C

, the fact (x rdf:type C

) is inferred by an OWL

reasoner. If the class description of C

has conﬂicts

with the class description of C

, the OWL reasoner

will detect this as an inconsistency.

Generalizations with the “Equivalent Class”

stereotype in SysML are translated into

EquivalentClass axioms of the corresponding

OWL classes. In DL, we represent this as C

≡ C

. If

the class description of C

has conﬂicts with the class

description of C

(i.e., the sets of the individuals from

these two classes do not fully overlap), the OWL

reasoner will detect this as an inconsistency.

Dependencies with the “Disjoint With” stereotype

in SysML are translated into DisjointClasses axioms

of the corresponding OWL classes. In DL, we

represent this as C

≡ ¬C

. In such a case, if the

class description of C

has any overlap with the class

description of C

, the OWL reasoner will detect this

as an inconsistency.

Here we consider an example based on the Cloud

Agility Baseline (CAB) (DARPA, 2021) that SNC

and Northeastern developed to provide an adaptable

framework which can be molded to meet typical

Logistics and Cloud applications and changes to those

requirements. Figure 1 shows the SysML block

diagram of the CAB model. The question we are

investigating in this paper is - how do we verify the

correctness of the CAB model, e.g., are the state

machines of the CAB correct?

Ontology-based Detection of Inconsistencies in UML/OCL Models

197

Figure 2: Main Structure of the CAB Ontology.

Table 1: Principles of mapping of OCL to OWL.

Invariant OWL DL

Context C

: p →

f orAll(oclIsTypeO f (C

))

⊑ ∀p.C

Context C

: p →

exists(oclIsTypeO f (C

))

⊑ ∃p.C

Context C

: attr1 = C

⊑ ∀p.C

Context C

: attr1! = C

⊑ ¬∃p.C

Cameo translates the six blocks in the CAB

SysML model and the associations between them

to the classes and properties in the CAB ontology.

Figure 2 shows the main structure of the CAB

ontology in Prot ´eg ´e. However, the Cameo mapping-

to-OWL capability is very limited and the automatic

translation lost some information in translation. We

extended the automatically generated CAB ontology

by mapping the OCL constraints in the Dispatcher

block and the Shipment block into OWL restrictions

for the corresponding classes manually (shown in

Figures 3 and 4). In this step, we followed the

mapping principles shown in Table 1. Finally, we

ran the OWL reasoner. It identiﬁed the semantic

inconsistency of the model: the Shipment block is

equivalent to Nothing, i.e., the OWL class is not

satisﬁable (it cannot have any individuals).

5 MAPPING RULES

The main concepts of state machines are state,

transition, event, guard and action. These concepts

are mapped to OWL following the rules shown in

Table 2. A simple state is mapped to a class

expression in OWL. The classes are constrained by

transitions and state invariants expressed in OCL.

All the state classes are disjoint. In OWL, each

transition of a state machine diagram is represented

by an intersection of class expressions for the source

state, target state, event and guard of this transition.

In addition, our translation introduces relational

operators between variables.

Figure 3: OWL Restrictions for the Dispatcher Class.

Figure 4: OWL Restrictions for the Shipment Class.

5.1 A Mapping Example

The statechart diagram in Figure 5 describes the

behavior of the Dispatcher block from Figure 1. The

six states are mapped to six OWL classes. The OWL

DL representations of the OCL constraints on the

states are shown in the following DL expressions.

Allocating ≡Waiting ⊔ GettingTransporters

⊔ MakingAssignment

(1)

MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development

198

Table 2: UML State Machine Diagram to OWL Mapping Rules Comparison.

State Machine

Component

oner and

Staab (2010)

Van

Der Straeten

et al. (2002)

Khan and

Porres (2015)

Belgueliel

et al. (2014)

Our Mapping

Rule

State

Simple

State

Class Class Subclass of

the class of

the object

Individual Class

Composite

State

Superclass

of substate

classes

Superclass

of substate

classes

Superclass

of substate

classes

Individual Superclass

of substate

classes

Initial

State

Class Class Class Individual Class

Final State Class Class Class Individual Class

OCL

invariants

None None OWL object

property

restrictions

None OWL object

property

restrictions

Transition Class Class None Individual Class

Event Class Class None Individual Class

Action None Class None Individual Class

Guard Class Class None Individual Class

Guard expressed

in OCL invariants

None None None None OWL object

property

restrictions

Figure 5: Dispatcher Statechart.

Allocating ⊑ ∃isRequestedBy.Shipment (2)

Complete ⊑ ∀isRequestedBy.1Shipment (3)

Waiting ⊑ ∀hasAssignment.0Assignment (4)

GettingTransporters ⊑ ∃hasAssignment.(

Assignment⊓ ≥ hasTransporter.1Transporter)

(5)

MakingAssignment ⊑ ∃hasAssignment.(

Assignment ⊓∀hasShipment.1Shipment⊓

∀hasTransporter.1Transporter)

(6)

The six transitions are also mapped to six

OWL classes. The transition from Waiting

to GettingTransporters is triggered by the

event shipRequest. So the transition class

Ontology-based Detection of Inconsistencies in UML/OCL Models

199

WaitingToGettingTrans is deﬁned as:

WaitingToGettingTrans ≡

∃ f sm.triggeredBy.{shipRequest}

(7)

WaitingToGettingTrans ⊑ ∃ f sm.hasSource.Waiting

⊓ ∃ f sm.hasTarget.GettingTransporters0

(8)

GettingTransporters state has two outgoing

transitions. After the operation chooseTransporter of

the dispatcher is invoked, if the returned transporter

state is busy, the state stays at GettingTransporters.

Otherwise, the state transits to MakingAssignment.

So the two transition classes are deﬁned as:

GettingTrans ≡

∃ f sm.triggeredBy.chooseTransporter

⊓ ∃( f sm.hasGuard. f sm.EvalCmp.EQ

⊓ ∃ f sm.hasLe f tExpr.{transporterState}

⊓ ∃ f sm.hasRightExpr.{busy})

(9)

GettingTrans ⊑

∃ f sm.hasSource.GettingTransporters

⊓ ∃ f sm.hasTarget.GettingTransporters

(10)

GettingTransToMakingAssignment ≡

∃ f sm.triggeredBy.chooseTransporter

⊓ ∃( f sm.hasGuard. f sm.EvalCmp.EQ

⊓ ∃ f sm.hasLe f tExpr.{transporterState}

⊓ ∃ f sm.hasRightExpr.{busy})

(11)

GettingTransToMakingAssignment ⊑

∃ f sm.hasSource.GettingTransporters

⊓ ∃ f sm.hasTarget.MakingAssignment

(12)

From the state MakingAssignment, after the

dispatcher invokes the operation assignShipment,

if the deliverShipment is true, then the state of the

dispatcher goes back to Waiting.

MakingAssignmentToWaiting ≡

∃ f sm.triggeredBy.assignShipment

⊓ ∃( f sm.hasGuard. f sm.EvalCmp.EQ

⊓ ∃ f sm.hasLe f tExpr.{deliverShipment}

⊓ ∃ f sm.hasRightExpr.{true})

(13)

MakingAssignmentToWaiting ⊑

∃ f sm.hasSource.MakingAssignment

⊓ ∃ f sm.hasTarget.Waiting

(14)

5.2 OWL Reasoning with State

Machine Diagrams

In order to check the consistency of the state machine

in Figure 5, we translate the state machine along with

OCL constraints to OWL (as shown in Section 5.1).

In order to show different types of inconsistencies of

constraints, we deﬁned three reasoning tasks.

The ﬁrst OWL reasoning task is to check if the

OCL invariants of all the states are consistent. The

state invariants that may cause the object violate

the constraints imposed on state diagrams in the

UML superstructure speciﬁcation of state machine

are considered to be inconsistent invariants. For

example, for the composite state Allocating, the OCL

constraint of the state invariant is:

isRequestedBy− > size() > 0 (15)

which means the dispatcher is in Allocating state if

it is requested by at least one shipment (Figure 6).

The Waiting state is a substate of Allocating. The

substate should not have a conﬂicting invariant with

the composite state. Adding the following invariant

to the Waiting state:

isRequestedBy− > size() = 0 (16)

would imply being in the Waiting state even if there

was no request by any shipment (Figure 7). Thus,

such two OCL constraints are inconsistent, and thus

there can not be a state individual that can satisfy both

the constraints of Allocating and the constraints of

the Waiting states. When we run the OWL reasoner

in Prot ´eg ´e, it will identify the semantic inconsistency

of the OWL axioms in Allocating class and Waiting

class.

Figure 6: Allocating. Figure 7: Waiting.

The second OWL reasoning task is to check

whether only one transition can be taken out of a

state, i.e., whether the state machine is deterministic.

For a state with more than one possible outgoing

transition, e.g., GettingTransporters, the state that

has two outgoing transitions GettingTrans and

GettingTransToMakingAssignment, adding the guard:

assigns.transporterState = busy (17)

MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development

200

to both transitions, would make the choice of a

transition not unique. In OWL, two outgoing

transitions are represented by two disjoint

transition classes and should have disjoint guards.

Otherwise, the OWL reasoner will identify semantic

inconsistency because an individual can not belong

to both a type and its complement. The inconsistent

result is shown in red in Figures 8 and 9.

Figure 8: Outgoing Transition1.

Figure 9: Outgoing Transition2.

The third OWL reasoning task is to check if

the state machine contains deadlocks. A deadlock

happens when two or more processes have conﬂicting

resource needs. In this paper, we consider a simple

deadlock case: for a state with only one outgoing

transition, the guards on this outgoing transition of

a state are mutually exclusive. In other words, if the

guards on the only outgoing transition of a state can

not be satisﬁed at the same time, the state machine for

the object will be stuck in this state. For example, for

the transition from MakingAssignment to Waiting, if

we add the guards as follows:

assigns.deliverShipment = true,

assigns.deliverShipment = f alse

(18)

once the state machine of the dispatcher object gets

into MakingAssignment, it will not be able to get

out of this state because the deliverShipment attribute

can not be both true and false at the same time.

When we run the OWL reasoner, it will identify the

semantic inconsistency of the OWL axioms in the

MakingAssignmentToWaiting class that represents the

transition, as shown in red in Figure 10.

Figure 10: MakingAssignmentToWaiting Transition.

6 CONCLUSIONS

In this paper, we discuss an ontology-based method to

reason about the correctness of UML/SysML models

that include OCL constraints on state machines.

Speciﬁcally, we map the UML/SysML models with

OCL constraints to OWL and check the consistency

of the corresponding ontology by running an OWL

inference engine. We propose a set of rules

for mapping components of UML state machine

diagrams along with OCL constraints to OWL DL.

We also demonstrate three examples of reasoning

tasks in which OWL axioms are used for consistency

checking of state machine diagrams. Our work is

aimed at providing the software developer with some

reasonable assurances about the correctness of the

model in the system modeling stage of software

development. This is the ﬁrst step of requirement

change management. In the future, we plan to

extend the scope of our approach to a more complete

and automatic veriﬁcation of UML state machine

speciﬁcations with OCL constraints as well as both

theoretical analysis and experimental validation of the

correctness of the mapping rules.

ACKNOWLEDGEMENTS

This research was supported by a grant from

the Defense Advanced Research Projects Agency

(DARPA). The views, opinions and/or ﬁndings

expressed are those of the authors and should not

be interpreted as representing the ofﬁcial views or

policies of the Department of Defense or the US

Government. The authors wish to acknowledge

contributions from the whole IDAS team, and in

particular James Hove and Everett Pompeii of SNC.

Ontology-based Detection of Inconsistencies in UML/OCL Models

201

REFERENCES

Ahmad, M. A. and Nadeem, A. (2010). Consistency

checking of UML models using Description Logics:

A critical review. In 2010 6th International

Conference on Emerging Technologies (ICET), pages

310–315. IEEE.

Anastasakis, Bordbar, G. and Ray (2010). On challenges of

model transformation from UML to Alloy. Software

and Systems Modeling, 9(69).

Baclawski, K., Kokar, M. K., Kogut, P. A., Hart, L.,

Smith, J., Holmes, W. S., Letkowski, J., and Aronson,

M. L. (2001). Extending UML to support ontology

engineering for the semantic web. In International

Conference on the Uniﬁed Modeling Language, pages

342–360. Springer.

Belgueliel, Y., Bourahla, M., and Brik, M. (2014). Towards

an ontology for UML state machines. Lecture Notes

on Software Engineering, 2(1):116.

Berardi, D., Calvanese, D., and De Giacomo, G. (2005).

Reasoning on UML class diagrams. Artiﬁcial

intelligence, 168(1-2):70–118.

DARPA (2021). Intent-Deﬁned Adaptive Software (IDAS).

https://www.darpa.mil/program/intent-deﬁned-

adaptive-software; Accessed: 2021-08-30.

Dwivedi, A. K. and Rath, S. K. (2018). Transformation

of Alloy Notation into a Semantic Notation. ACM

SIGSOFT Software Engineering Notes, 43(1):1–6.

Elaasar, M. and Briand, L. (2004). An overview of

UML consistency management. Carleton University,

Canada, Technical Report SCE-04-18.

Filipovikj, P. (2019). Automated Approaches for Formal

Veriﬁcation of Embedded Systems Artifacts. PhD

thesis, M

alardalen University.

Fu, C., Yang, D., Zhang, X., and Hu, H. (2017). An

approach to translating ocl invariants into owl 2

dl axioms for checking inconsistency. Automated

Software Engineering, 24(2):295–339.

Gogolla, M., Bttner, F., and Kuhlmann, M. (2008). System

modeling with USE (UML-based speciﬁcation

environment).

Gogolla, M., B

uttner, F., and Richters, M. (2007). Use: A

UML-based speciﬁcation environment for validating

UML and OCL. Science of Computer Programming,

69(1-3):27–34.

oner, G. and Staab, S. (2010). Specialization and

validation of statecharts in OWL. In International

Conference on Knowledge Engineering and

Knowledge Management, pages 360–370. Springer.

Gruber, T. R. (1993). A translation approach to portable

ontology speciﬁcations. Knowledge acquisition,

5(2):199–220.

Khan, A. H. and Porres, I. (2015). Consistency of UML

class, object and statechart diagrams using ontology

reasoners. Journal of Visual Languages & Computing,

26:42–65.

Khan, A. H., Rauf, I., and Porres, I. (2013). Consistency

of UML class and statechart diagrams with state

invariants. In MODELSWARD, pages 14–24.

Lamport, L. (2021). The tla+ toolbox. https://lamport.

azurewebsites.net/tla/toolbox.html; Accessed: 2021-

01-04.

Latif, S., Rehman, A., and Zafar, N. A. (2018). Modeling

of Sewerage System Linking UML, Automata and

TLA+. In 2018 International Conference on

Computing, Electronic and Electrical Engineering

(ICE Cube), pages 1–6.

Latif, S., Rehman, A., and Zafar, N. A. (2019). NFA

Based Formal Modeling of Smart Parking System

Using TLA +. In 2019 International Conference on

Information Science and Communication Technology

(ICISCT), pages 1–6.

Mahmud, N., Seceleanu, C., and Ljungkrantz, O. (2016).

ReSA Tool: Structured Requirements Speciﬁcation

and SAT-based Consistency-checking. In Proceedings

of the Federated Conference on Computer Science and

Information Systems, pages 1737 – 1746. IEEE.

NoMagic (2021). Cameo concept modeler 2021x

plugin documentation. https://docs.nomagic.com/;

Accessed: 2021-09-09.

Parreiras, F. S., Staab, S., and Winter, A. (2007). TwoUse:

Integrating UML models and OWL ontologies.

Citeseer.

Przigoda, Soeken, W. and Drechsler (2016). Verifying the

structure and behavior in UML/OCL models using

satisﬁability solvers. IET Cyber-Physical Systems:

Theory and Applications, 1:49–59.

Rull, G., Farr

e, C., Queralt, A., Teniente, E., and Urp

ı,

T. (2013). Aurus: explaining the validation of

UML/OCL conceptual schemas. Software & Systems

Modeling, 14.

Stanford University (2020). Prot ´eg ´e. http://protege.

stanford.edu/; Accessed: 2021-08-30.

Usman, M., Nadeem, A., Kim, T.-h., and Cho, E.-s. (2008).

A survey of consistency checking techniques for UML

models. In 2008 Advanced Software Engineering and

Its Applications, pages 57–62. IEEE.

Van Der Straeten, R., Van, R., and Straeten, D. (2002).

Using Description Logic in Object-Oriented Software

Development.

WC3 (2004). OWL Web Ontology Language: Overview.

https://www.w3.org/TR/owl-features/; Accessed:

2021-08-30.

MODELSWARD 2022 - 10th International Conference on Model-Driven Engineering and Software Development

202