Online Heuristic Approach for Efﬁcient Allocation of Limited COVID-19

Testing Kits

Muhammad Alfas S. T.

and Shaurya Shriyam

Department of Mechanical Engineering, Indian Institute of Technology, Delhi, India

Keywords:

COVID-19 Testing, Resource Management, Pooled Testing, Multi-armed Bandit, Online Dynamic Allocation.

Abstract:

Testing kit scarcity plays an important role in aggravating any epidemiological response against pandemics

such as COVID-19, especially for resource-constrained countries. Better decision-making tools are essential

to assist policymakers in containing the disease from spreading to a large extent despite limited resource

availability. We propose a testing kit allocation framework that comprises three components: estimation of

time-varying prevalence rates using empirical Bayes model, testing kit allocation using multi-armed bandit

algorithms, and pooled testing technique to extract the maximum utility from the available testing kits. We

conduct simulation experiments based on real-world data and obtain results to demonstrate the enhanced

efﬁciency in detecting COVID-19 cases. We conclude that Bayesian estimation of prevalence coupled with

bandit-based allocation performs signiﬁcantly well. We also identify scenarios under which pooled testing

offers a strong advantage.

1 INTRODUCTION AND

LITERATURE REVIEW

COVID-19 has enormously disrupted the normal

functioning of vital aspects of society across the

planet and has essentially exposed several weak spots

in our preparedness against highly contagious respi-

ratory viral diseases. Unlike the global trend, India

witnessed a gradual increase in the number of cases in

the ﬁrst wave (Jain et al., 2021). In the initial phases

when community transmission has not yet started, in-

creased testing may help detect and isolate potential

super-spreaders and thus keep the viral spread under

manageable levels. But since during this phase, the

availability of reliable testing kits is scarce, optimal

allocation of testing kits becomes critical to ﬂatten the

curve.

The pooled testing technique may help tackle this

challenge. In this technique introduced by Dorf-

man (1943), people are divided into groups, and each

group is allocated one testing kit. If there is even one

infected person in a group, that group’s sample will

give a positive result. Individuals belonging to the

positive groups are tested again but in smaller groups.

When the disease prevalence is low, pooling may be

https://orcid.org/0000-0003-1483-1182

https://orcid.org/0000-0003-2135-9103

very effective (Guha et al., 2021).

Deckert et al. (2020) proposed two approaches for

pooling, viz. a routine high-throughput technique,

and a novel context-sensitive technique. Mutesa et al.

(2020) proposed an algorithm for pooled testing based

on hypercubic geometry. Hanel and Thurner (2020)

computed group sizes to minimize the number of

false positives. Contrary to the common approaches,

Ghosh et al. (2020) proposed a single round pooling

technique. Although pooling may be more advanta-

geous than traditional approaches, its utility becomes

limited for large population sizes.

Besides pooled testing, another way to improve

testing is the optimal allocation of testing kits. Buhat

et al. (2021) used a non-linear programming model to

allocate COVID-19 testing kits in Philippines. This

model incorporates demographic factors but is not

suitable for dynamic allocation. Du et al. (2021) pro-

posed an optimal allocation strategy based on preva-

lence probability estimation. Prevalence rate or sim-

ply prevalence is the fraction of people infected in a

community by a disease. Usually, the daily test posi-

tivity rate (TPR), which is the fraction of people who

tested positive out of the total number of people tested

in a day is used as a prevalence rate indicator. But

it is highly unlikely that the people who were tested

will give a true representation of the entire population

because the tested fraction mostly comprises symp-

Alfas, M. and Shriyam, S.

Online Heuristic Approach for Efﬁcient Allocation of Limited COVID-19 Testing Kits.

DOI: 10.5220/0010818600003117

In Proceedings of the 11th International Conference on Operations Research and Enterprise Systems (ICORES 2022), pages 329-336

ISBN: 978-989-758-548-7; ISSN: 2184-4372

329

tomatic individuals and those who come in contact

with COVID-positive patients. Yang et al. (2020) es-

timate prevalence using a representative randomized

sample method claiming that the actual prevalence is

two or three times more. Bastani et al. (2021) use an

empirical Bayes model to estimate prevalence for pas-

senger arrival at Greek airports by making use of the

past two weeks’ testing data.

The major conﬂict to allocate testing kits lies in

choosing between locations where estimated preva-

lence is high and those with lower prevalence esti-

mates. Such exploration-exploitation trade-off sce-

narios are usually modeled as multi-armed bandit

(MAB) problems. Several solution strategies have

been developed including UCB1, Thompson sam-

pling and Gittins index (Chapelle and Li, 2011).

While computing the exact Gittins index is compu-

tationally intractable, Bastani et al. (2021) modeled

COVID-19 testing kit allocation as bandit problem

and solved it using optimistic Gittins index method.

To validate the efﬁcacy of an allocation frame-

work, we need to estimate the number of undetected

cases in a region. Several studies have been conducted

to estimate undetected cases. Lau et al. (2020) inves-

tigate the undetected cases globally using the corre-

lation between Healthcare Access and Quality Index

and COVID-19 prevalence. Pedersen and Meneghini

(2020) used an epidemic dynamics model to estimate

the number of undetected cases in Italy. B

ohning et al.

(2020) propose a capture-recapture method to ﬁnd out

the undetected cases.

In this paper, we propose a framework for

COVID-19 testing kit allocation to maximize the uti-

lization of limited resources. This framework com-

prises (i) prevalence estimation model (ii) allocation

model based on MAB (iii) pooling testing plan gen-

eration. The prevalence estimation model is based

on the empirical Bayes method. For MAB, we used

two solution methods, viz. Thompson Sampling (TS)

and optimistic Gittins index. We also considered two

types of pooling by (i) limiting the maximum number

of testing rounds to two, and (ii) placing no limit.

2 PROBLEM DESCRIPTION

The objective of the testing kit allocation problem is

to maximize the number of infected individuals de-

tected. We assume that if one testing kit is used for

each person, the number of infected persons detected

will be the total number of tests done times the preva-

lence rate. Indian healthcare system comprises hospi-

tals at different levels in a hierarchical fashion (Shoaib

and Ramamohan, 2021). The availability of testing

kits in a hospital may depend on several factors and

we may also have to take into account the specially

designated testing labs besides the normally operating

hospitals (Mohd et al., 2021). We assume that every

city has a single testing lab to which the allocated kits

are supplied by a central authority and where pooled

testing is performed.

The pooled testing is performed over multiple

rounds and initially, the people who need to be tested

are divided into blocks and one testing kit is allocated

per block. Then, in the next round of testing, peo-

ple from the positively tested blocks are further sub-

divided into smaller blocks. This process is repeated

until no block tests positive or we reach the stage of

individual testing. When we place no limits on the

number of testing rounds, the decision problem in-

cludes computing the number of rounds as well as

the block sizes for each round. These two parame-

ter speciﬁcations deﬁne what we shall refer to as the

pooling scheme. When there is a speciﬁed value for

the number of testing rounds, only the block sizes

for each round need to be computed. Mutesa et al.

(2020) reported that the pooled sample gives positive

results even if diluted with 100 negative samples, so

for the present study we assume pooled testing to be

efﬁciently scalable for testing a large cohort.

Now consider city c and take a particular day de-

noted by t following the usual convention of denoting

a time step. Let n

rct

and b

rct

respectively denote the

number of testing blocks and the size of each testing

block for the r

round of testing. The ﬁrst round of

testing clubs all the samples together and tests them.

Thus, the total number of people who have been tested

in the country is given by max

∑

t=1

∑

c=1

1ct

Here C is the total number of cities competing for

testing kits and T is the time horizon. If ρ

is the

prevalence rate for city c for time step t, the objective

of the allocation problem may be rewritten as follows

max

∑

t=1

∑

c=1

1ct

(1)

If K

and R

respectively denote the number of test-

ing kits allocated by the central authority to and the

number of testing rounds conducted in city c at time

step t, then we obtain a constraint as follows

∑

r=1

rct

≤ K

∀c = 1,··· ,C,t = 1, · ·· ,T (2)

If K

is the total number of testing kits available with

central authority for allocation at time step t, then we

obtain another constraint as follows

∑

c=1

∑

r=1

rct

≤ K

∀t = 1,··· ,T (3)

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

330

In pooled testing, the ﬁnal round involves individ-

ual testing. Also in each round except the ﬁrst, tests

are only repeated for blocks that tested positive in the

previous round. So if p

rct

be the proportion of blocks

that tested positive in r

round, these two constraints

are written as follows

= 1 ∀c = 1,··· ,C; t = 1, · ·· ,T (4)

r+1,ct

= p

rct

∀r = 1,··· ,R

− 1; c; t (5)

The nonlinear nature of the proposed problem makes

it difﬁcult to ﬁnd the optimal answers efﬁciently even

if we obtain the data of infected persons and the pre-

vailing infection rate.

3 DATA COLLECTION

The testing kits are allocated by a central authority to

the cities every day. Thus to develop the proposed al-

location framework, the daily data of testing kit avail-

ability are required. An empirical Bayes model is

used to compute the prevalence for each city and the

estimate is updated daily. For this purpose, we require

the daily data of the number of tests conducted and the

number of positive cases detected.

COVID19-India API (COVID19India, 2021) pro-

vides data for the number of tested, infected, recov-

ered, and deceased people on daily basis in time-

series format. This API portal is not ofﬁcial but con-

solidates information from various sources including

the ofﬁcial ones. Since lab-level data is not avail-

able and we already assumed one lab per city, so we

only collect city-level data. Based on data availabil-

ity, we selected ﬁve Indian cities, viz. Ahmedabad,

Bengaluru, Chennai, Delhi, and Jaipur, for testing our

framework.

Data before July 1, 2020, are deleted because suf-

ﬁcient data are not available for that period. The data

is obtained in cumulative form. From the cumula-

tive data, daily numbers are found by successive dif-

ferencing. There were also missing data for which

imputation was done using the Last Observation Car-

ried Forward (LOCF) method which ﬁlls the missing

values based on the most recent data points available

(Heyting et al., 1992).

Similarly, we created another dataset comprising

65 Indian cities by additionally including 60 more

cities mostly from semi-urban and rural areas which

quite expectedly led to a much larger variance among

the demographic factors. We chose July 1, 2020, as

the starting date for collecting data in both cases. But

unlike the ﬁve-city dataset, where data was recorded

until October 31, 2020, we stopped data collection

for the 65-city dataset on August 30, 2020, because

of computational restrictions. We perform extensive

computational experiments on the ﬁve-city dataset to

determine suitable parameter values which were then

deployed on the 65-city dataset.

4 ALLOCATION FRAMEWORK

We describe the three components of the proposed al-

location framework in the following sections. A sum-

mary of the allocation framework is depicted as Algo-

rithm 1.

Algorithm 1: Testing Kit Allocation.

Input: Set of cities: C; data of past D days; testing kits

available centrally on a speciﬁc day: K

Output: Testing kit allocation: a

∀c = 1,·· · ,C; Number

of persons that get tested using the allocated kits in

each city; Pooled testing schemes of all cities

1: for c = 1 : C do

2: Estimate prevalence using empirical Bayes

3: Base-level kit allocation to each city:

←

100

4: Posterior update of prevalence parameters using

Equations 10 or 11

5: end for

6: K ← K(1 −

100

)

7: while K > 0 do

8: Compute bandit-based dynamic allocation indices

for all cities

9: c

← max

{DAI(c)}

10: a

← a

+ 1

11: Posterior update of prevalence parameters using

Equations 10 or 11 K ← K − 1

12: end while

13: for c = 1 : C do

14: Find pooled testing capacity using Algorithm 3

15: Find pooled testing scheme using Algorithm 2

16: end for

4.1 Prevalence Estimation

Prevalence denotes the proportion of the population

in a city that is infected by the SARS-CoV-2 virus at

a particular time step and is the sole criterion adopted

in the present framework to decide how many testing

kits are allocated to each city. We use an empirical

Bayes method to estimate prevalence. The event of a

person getting a positive test result shall be modeled

as a Bernoulli random variable taking the prevalence

rate to be the probability of success. Consequently,

for the set of all persons living in a city, we shall use

the binomial distribution to model the number of pos-

itive cases.

Online Heuristic Approach for Efﬁcient Allocation of Limited COVID-19 Testing Kits

331

Since we assume the collected data to follow a bi-

nomial distribution, we apply a prior on its parameter,

viz. the probability of success in the form of a beta

distribution as per the standard Bayes paradigm. The

two parameters for the beta distribution are updated

daily using the data of past D days. If S

persons are

tested in city c on day t, and if I

is the number of

positive cases, then the prevalence rate for the city c

for the day t

are written as follows

(D)

∑

−D

t=t

−1

∑

−D

t=t

−1

(6)

Applying the strong law of large numbers to the mean

and variance formula of beta distribution as shown by

Bastani et al. (2021), we may come up with two esti-

mators

and

as follows

∑

c=1

∑

c=1

(D)

− 1)

(D)

− 1)

(7)

Then the prior estimates for the parameters of the beta

distribution are computed as follows

(1 −

)

−

= α

(1 −

)

(8)

Thereafter, the posterior estimates are straightforward

to compute using conjugacy

= α

+ I

(D)

= β

+ S

(D)

− I

(D)

(9)

If the estimated prevalence rate is very low, the bi-

nomial variable is approximated by a Poisson dis-

tribution for which the gamma distribution serves as

the conjugate prior. The shape and scale parameters

of the prior gamma distribution are intuitively set as

k = I

(D)

and θ = 1 but even this simple choice turns

out to be very effective.

4.2 Bandit Allocation

After estimating the prevalence and obtaining the test-

ing kit availability data, the allocation process is mod-

eled as a multi-armed bandit problem. There are sev-

eral solution methods available for the bandit problem

but we use the two most popular ones, viz. optimistic

Gittins index and Thompson sampling.

When we strictly follow the bandit methods and

some cities turn out to record far fewer cases than oth-

ers, then the standard implementation of bandit algo-

rithms are found to stop allocating testing kits to those

cities which may have an adverse domino effect later

because, in the next few days, the number of cases in

such dormant cities may aggravate resulting in poor

detection performance. To remedy this situation, we

decided to equally distribute a fraction (denoted as

q%) of the available testing kits among all cities ﬁrst

while the remaining testing kits are distributed as per

the bandit method. Even if q = 0 this method outper-

forms the baseline method discussed later.

The Thompson sampling method proceeds by ran-

domly sampling a value from the most recently es-

timated posterior distribution for each city’s preva-

lence. Then the city whose randomly sampled value is

maximum gets assigned a testing kit. The parameter

values depending on whether beta or gamma distri-

bution was selected are changed for the selected city

using the posterior update Equations 10 and 11 where

ρ is the estimated prevalence rate and a is the num-

ber of testing kits allocated (Lynch, 2007). The entire

process is repeated until all testing kits are used up.

= α + aρ β

= β + a(1 − ρ) (10)

= k + aρ θ

aθ + 1

(11)

In the Gittins index method, everything remains the

same as in the Thompson sampling method except

that instead of randomly sampling values we compute

dynamic allocation indices for each city. More specif-

ically, we use compute optimistic Gittins index from

(Gutin and Farias, 2016). For the beta prior, it is com-

puted using Equation 12 where F is the cumulative

distribution function and γ is the discount rate set to

0.9 in this paper.

λ =

α + β



1 − γF

α+1,β

(λ)



+ γλ



1 − F

α,β

(λ)



(12)

4.3 Pooled Testing

After the testing kits are allocated to the cities by the

central authority, we need to estimate the number of

people who got tested and those who showed a posi-

tive coronavirus (COVID-19) test result. For this pur-

pose, we develop a simulation model which computes

the pooling scheme and also determines the number

of testing kits required τ

∗

to test S people in a city

whose prevalence rate is estimated to be ρ.

This pooled testing simulator is described in Al-

gorithm 2 where r denotes the index of testing round

as before, S

denotes the number of persons who need

to be tested in that round, and p

is the number of

positive-tested blocks in round r. If patient samples

are not pooled as in the standard way of testing, then

the number of tests required τ

∗

would simply be equal

to the number of persons who need to be tested. We

use the variable τ

to keep track of the number of tests

performed in the previous round whereas τ tracks the

total number of testing kits needed for that particular

pooling scheme.

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

332

Initially, we start by assuming S testing kits will

sufﬁce for the city population and setting the num-

ber of testing rounds to be two. We ﬁrst compute

the maximum block size for the ﬁrst round (b

) and

set the second round block size to be one (b

) as per

usual. The simulator then tries to identify whether the

two-stage pooling offers any advantage. If two-stage

pooling is better than no pooling at all, then we try to

test whether three-stage pooling would be even better

for which we need to compute the maximum block

size for the second round (b

This process of adding testing rounds continues

until we stop getting a reduction in the number of

testing kits required. If the number of testing rounds

is capped for technical reasons, we encode this con-

straint (r ≤ R) in the beginning to reduce extrane-

ous computations. In such a case, the block sizes

({b

: r = 1,··· ,R}) would be the only variable that

needs to be determined using the above approach.

Algorithm 2: Simulation Algorithm for Pooled Testing.

Input: Population size of city: S; current estimated

prevalence rate: ρ

Output: Minimum number of testing kits required to test

the speciﬁed population size: τ

∗

; Number of testing

rounds: R = max(r); Number of individual samples to

be pooled in each round: b

∀r = 1, ··· ,R

1: τ

← 0

2: τ ← S

3: r ← 1

4: b

← 2

5: S

← S

6: Generate array of size S whose ρ% elements are

randomly designated as covid-positive

7: while true do

8: while true do

9: Update minimum estimate: τ

∗

← τ

10: Divide S

into equal blocks of size b

11: Number of testing kits used: τ

← S

12: Find number of blocks p

that tested positive by

simulation

13: Number of individual tests required:

← p

× b

14: Total testing kits utilized: τ ← τ

+ τ

15: if τ < τ

∗

then

16: Increase block size: b

← b

+ 1

17: else

18: break

19: end if

20: end while

21: if b

> 2 then

22: τ

← τ

+ τ

23: Increase number of rounds: r ← r + 1

24: Persons that need to be tested again: S

25: else

26: break

27: end if

28: end while

Now we shall describe how we may make use of

the pooled testing simulator to estimate how many

positive cases were detected in a city. We already

know the number of testing kits allocated to the city.

So to ﬁnd out the maximum number of people that

may be tested using pooled testing with the assigned

number of testing kits K given that the prevalence rate

is known, we use the iterative Algorithm 3. We be-

gin with a naive estimate of the number of people S

that may be tested and then in each iteration, we es-

timate the number of testing kits τ required for these

S people under the best-suited pooling scheme which

Algorithm 2 tells us. If τ happens to be less than the

available number of testing kits K, then the number of

people under consideration S is increased and we do

this in steps of powers of 10.

Algorithm 3: Iterative Algorithm to Estimate Number of

Persons Tested.

Input: Testing kits allocated to city: K; current estimated

prevalence rate: ρ

Output: Number of persons that may get tested S

∗

1: S

∗

← K

2: S ← K

3: m ← blog

(K)c

4: while m > 0 do

5: τ ← number of testing kits required for conducting

pooled testing of S persons (Algorithm 2)

6: if τ < K then

7: S

∗

← S

8: S = S + 10

9: else

10: m = m − 1

11: end if

12: end while

5 SIMULATION EXPERIMENTS

We primarily conduct our experiments on the 5-city

dataset with a time horizon of 100 days. To validate

the model, we compute the detection rate as the ratio

of the number of detected cases to the number of in-

fected individuals. After obtaining the daily number

of detected cases from the data, we estimate the num-

ber of undetected cases using the capture-recapture

method proposed by B

ohning et al. (2020) according

to which if the new cases detected on day t is I(t) and

if D(t) denotes the number of deaths that day, then

the bias-corrected number of undetected cases is esti-

mated using Equation 13. Here I(t − 1) is the number

of cases detected on day t − 1.

U(t) =

I(t)(I(t) − 1)

1 + max{0,I(t − 1) − D(t)}

(13)

We select the existing allocation done by the

Online Heuristic Approach for Efﬁcient Allocation of Limited COVID-19 Testing Kits

333

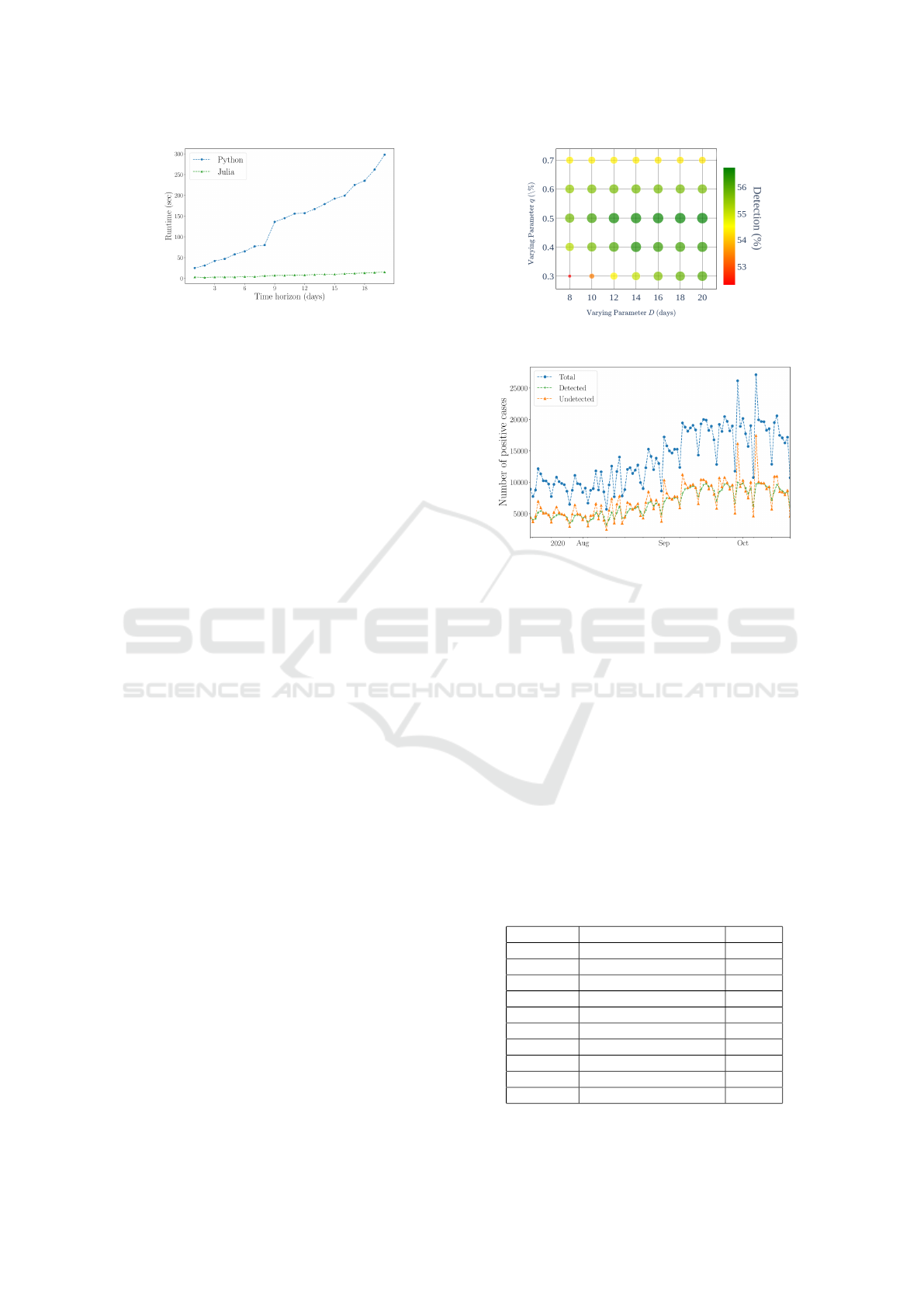
Figure 1: Runtime comparison between Python and Julia.

authorities as the baseline method and compare it

against different combinations of prevalence estima-

tion and allocation methods that were explained ear-

lier. We denote the Thompson sampling method using

beta-binomial and gamma-Poisson distribution mod-

els by BBTS and GPTS respectively. The optimistic

Gittins index method using the beta-binomial distri-

bution model shall be denoted by BBGI. We consider

two types of pooled testing models: (i) where the

maximum number of testing is limited to two denoted

by R2 (ii) where there is no restriction on the number

of rounds denoted by RX.

Thus, we shall consider a total of nine feasi-

ble combinations during our simulation experiments,

viz. BBTS, BBTSR2, BBTSRX, GPTS, GPTSR2,

GPTSRX, BBGI, BBGIR2, and BBGIRX. The entire

framework is primarily coded in Python 3.6.9 but cer-

tain parts like the iterative algorithm which turned out

to be signiﬁcantly time-consuming in Python had to

be ported over to Julia 1.5.3 in order to leverage Ju-

lia’s fast computational performance. Figure 1 shows

runtime in seconds for running the iterative algorithm

for R2 pooling. The 5-city dataset was experimented

with by varying the time horizon. We clearly observe

that Python requires around 300 seconds to ﬁnish a

20-day model whereas Julia took 15 seconds for the

same. The simulation results were obtained on a sin-

gle core (serial execution) on an Intel i3-5005U CPU

2.4 GHz with 4GB memory, running elementary OS

5.1.7 Linux.

6 RESULTS

The allocation framework rests primarily on two im-

portant parameters: D which is used to estimate the

prior distribution, and q which denotes the fraction of

testing kits allocated equally to all cities. We found

suitable values for both by iteratively searching the

parameter space as shown in Figure 2. Thus, D is

taken to be between twelve and twenty days while

50% seems to be the best value chosen for q.

Let us now consider the estimation of the number

Figure 2: Effect of parameters D and q on detection rate.

Figure 3: Comparing number of detected cases and unde-

tected cases where total cases is the sum of both.

of undetected cases. Based on the method described

by B

ohning et al. (2020), the number of undetected

cases is estimated using Equation 13, and the actual

number of infections turned out to be 1.7 to 2.8 times

more than that was detected. Figure 3 contrasts the

difference between the number of undetected and de-

tected cases.

We have used the fraction of positive cases de-

tected from among the infected individuals as the

metric for comparison among nine different alterna-

tives possible from the proposed allocation frame-

work. The detection ratios of COVID-19 cases for

all ten models have been averaged over the ten exper-

iments and the collected statistics are shown in Table

1. The sources of randomness are random sampling

in the TS method and random pooling.

Table 1: Comparison of ten allocation strategies.

Method Average Detection (%) SD(%)

GPTSRX 69.84 0.0331

GPTSR2 69.56 0.0092

BBTSRX 68.45 0.0531

BBTSR2 68.24 0.0381

BBGIRX 68.14 0.0238

BBGIR2 67.93 0.0246

GPTS 55.25 0.0003

BBTS 54.42 0.0077

BBGI 54.32 0

Baseline 48.55 0

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

334

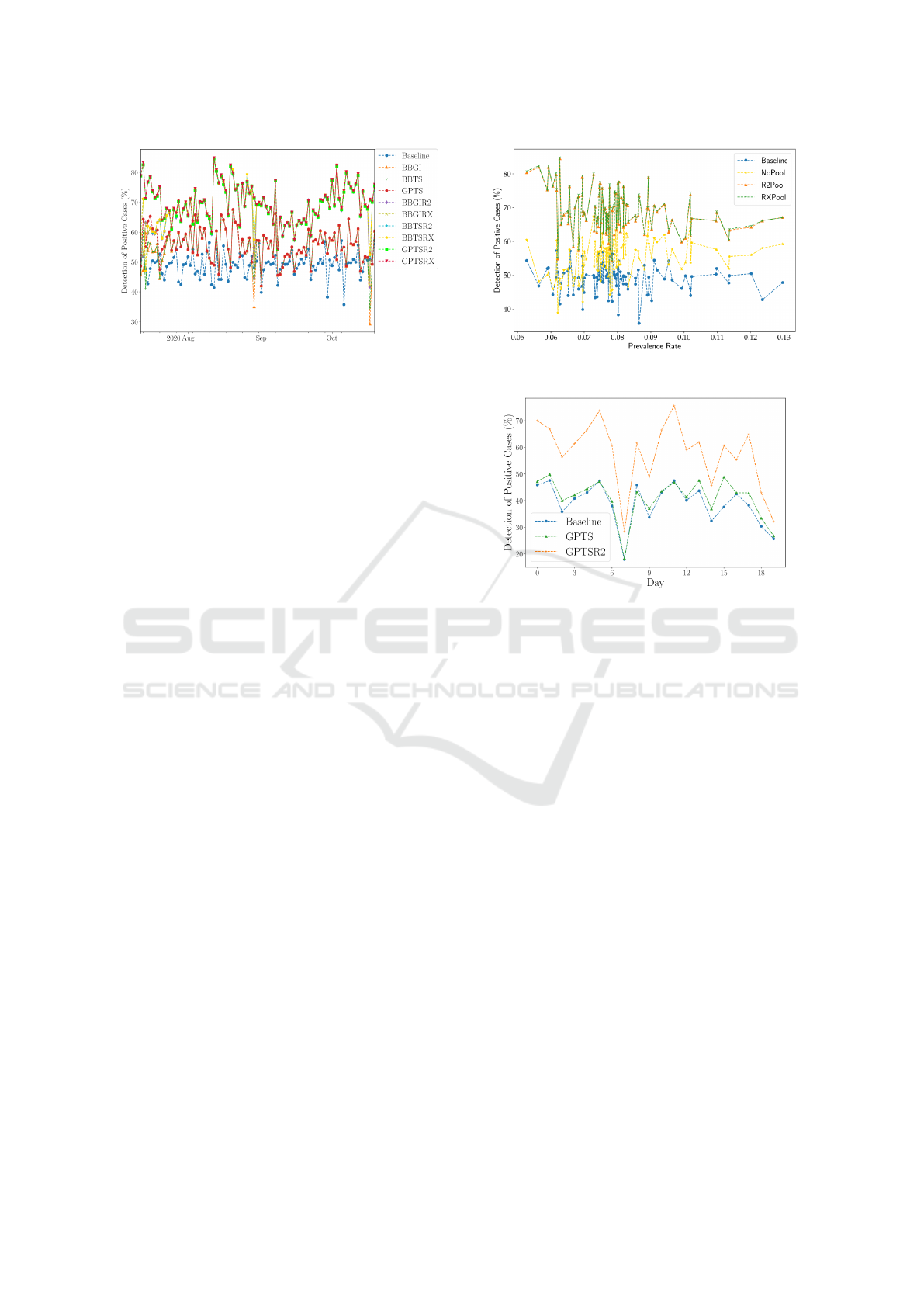
Figure 4: Daily detection rate for ten allocation strategies.

From Table 1, we observe that the MAB-based

models perform signiﬁcantly better than the base-

line method. The Thompson sampling based mod-

els performed slightly better than the optimistic Git-

tins index based models. Similarly, the gamma-

Poisson models performed slightly better than the

beta-binomial models. Since we are dealing with

modeling count data of persons arriving for testing

in time-series format, it is usually expected for such

processes that the past history of detected cases plays

no role in predicting the future chances of obtain-

ing a positive result (memoryless property). In addi-

tion, when the number of infected individuals is suf-

ﬁciently low compared to the population size of city,

then the likelihood of the count data being best ap-

proximated as coming from a Poisson process is high.

This is reafﬁrmed by the observed results.

Figure 4 shows the detection performance for all

ten models over the 100 days conﬁrming the trend we

observed in Table 1. The obvious point to stress from

these observations is that the pooled testing paradigm

leads to major efﬁciency gain over plain individual-

ized testing methods.

Also, the performance difference between two-

round pooling (R2) and multi-round (RX) models is

very small and so, for all practical purposes, it is ad-

visable to stick to two-stage pooled testing. So even

though we explored the multi-round pooled testing

models by assuming that the standard pooled testing

technique is scalable, it may not be technologically

feasible to have the sample collected from a single

patient undergo multiple rounds of testing. Neverthe-

less, our algorithm on average only suggests a maxi-

mum of three or four rounds.

Figure 5 shows that although at lower prevalence

rates, the pooling detects as many as 80% of the

infected individuals if the prevalence rate is high,

say more than 10%, then the difference between no-

pooling and pooling strategies becomes much lower.

This shows that once the disease has spread through

society in large numbers, the advantages afforded to

Figure 5: Effect of prevalence on detecting positive cases.

Figure 6: Detection performance for 65-city dataset.

us by the pooled testing technique are lost. But during

the initial phases of the pandemic, pooled testing may

indeed turn out to be a very effective tool for policy-

makers to contain the disease spread.

Based on the results from the ﬁve-city dataset,

three models, viz. GPTS, GPTSR2, and the baseline

method are used for the 65-city dataset over a period

of 20 days. The bandit model (GPTS) outperformed

baseline method which detects about 36.64% of the

infected cases; for GPTS, detection is about 38.83%;

for GPTSR2, it is 54.64%. The daily detection per-

formance is visualized in Figure 6. The overall detec-

tion rate is lower than for the ﬁve-city dataset. This

is primarily due to higher prevalence, poorer report-

ing of cases, larger lags in reporting test results, and

a higher proportion of undetected cases. The analy-

sis of the 65-city dataset reveals that on average there

are 2.8 times more undetected cases whereas, for the

ﬁve-city dataset, the undetected cases were on aver-

age about 2 times more.

7 CONCLUSION AND FUTURE

WORK

We demonstrated that bandit-based allocation strate-

gies outperform naive strategies that would allocate

Online Heuristic Approach for Efﬁcient Allocation of Limited COVID-19 Testing Kits

335

testing kits directly on the basis of test positivity rates,

and show good performance when combined with

pooled testing. It must also be noted that pooled test-

ing offers excellent advantages if prevalence rates are

low but the advantage starts dissipating as prevalence

rates begin to rise. We observed that two-stage pooled

testing is sufﬁcient for the prevalence rates that show

up in the collected data, and introducing more test-

ing rounds does not lead to signiﬁcant gains. We shall

use a compartmental model to track the disease preva-

lence at different locations as part of future work.

Exploring the usefulness of agent-based modeling to

handle the increased model complexity shall be inter-

esting.

ACKNOWLEDGEMENTS

The authors acknowledge the contributions of under-

graduate students Aditya Sahu and Kanishk Jain at

IIT Delhi towards data collection and cleaning.

REFERENCES

Bastani, H., Drakopoulos, K., Gupta, V., Vlachogiannis,

J., Hadjicristodoulou, C., Lagiou, P., Magiorkinis, G.,

Paraskevis, D., and Tsiodras, S. (2021). Efﬁcient and

Targeted COVID-19 Border Testing via Reinforce-

ment Learning. SSRN.

ohning, D., Rocchetti, I., Maruotti, A., and Holling, H.

(2020). Estimating the undetected infections in the

Covid-19 outbreak by harnessing capture–recapture

methods. International Journal of Infectious Dis-

eases, 97:197–201.

Buhat, C. A. H., Duero, J. C. C., Felix, E. F. O., Rabajante,

J. F., and Mamplata, J. B. (2021). Optimal alloca-

tion of COVID-19 test kits among accredited testing

centers in the Philippines. Journal of healthcare in-

formatics research, 5(1):54–69.

Chapelle, O. and Li, L. (2011). An empirical evaluation of

thompson sampling. Advances in neural information

processing systems, 24:2249–2257.

COVID19India (2021). Covid19-India API. 2021 [online]

available at: https://www.data.covid19india.org. Ac-

cessed on: 2nd October.

Deckert, A., B

arnighausen, T., and Kyei, N. N. (2020).

Simulation of pooled-sample analysis strategies for

COVID-19 mass testing. Bulletin of the World Health

Organization, 98(9):590.

Dorfman, R. (1943). The detection of defective members of

large populations. The Annals of Mathematical Statis-

tics, 14(4):436–440.

Du, J., Beesley, L. J., Lee, S., Zhou, X., Dempsey, W., and

Mukherjee, B. (2021). Optimal diagnostic test allo-

cation strategy during the COVID-19 pandemic and

beyond. Statistics in Medicine.

Ghosh, S., Rajwade, A., Krishna, S., Gopalkrishnan, N.,

Schaus, T. E., Chakravarthy, A., Varahan, S., Appu,

V., Ramakrishnan, R., Ch, S., et al. (2020). Tapestry:

a single-round smart pooling technique for COVID-19

testing. medRxiv.

Guha, P., Guha, A., and Bandyopadhyay, T. (2021). Appli-

cation of pooled testing in estimating the prevalence of

COVID-19. Health Services and Outcomes Research

Methodology.

Gutin, E. and Farias, V. F. (2016). Optimistic gittins indices.

In Proceedings of the 30th International Conference

on Neural Information Processing Systems, NIPS’16,

page 3161–3169.

Hanel, R. and Thurner, S. (2020). Boosting test-efﬁciency

by pooled testing for SARS-CoV-2—Formula for op-

timal pool size. PLoS One, 15(11):e0240652.

Heyting, A., Tolboom, J., and Essers, J. (1992). Statisti-

cal handling of drop-outs in longitudinal clinical tri-

als. Statistics in medicine, 11(16):2043–2061.

Jain, V. K., Iyengar, K. P., and Vaishya, R. (2021). Differ-

ences between ﬁrst wave and second wave of COVID-

19 in India. Diabetes & Metabolic Syndrome: Clinical

Research & Reviews.

Lau, H., Khosrawipour, V., Kocbach, P., Mikolajczyk,

A., Ichii, H., Schubert, J., Bania, J., and Khosraw-

ipour, T. (2020). Internationally lost COVID-19 cases.

Journal of Microbiology, Immunology and Infection,

53(3):454–458.

Lynch, S. M. (2007). Introduction to applied Bayesian

statistics and estimation for social scientists. Springer

Science & Business Media.

Mohd, S., Mustafee, N., Madan, K., and Ramamohan, V.

(2021). Leveraging healthcare facility network simu-

lations for capacity planning and facility location in a

pandemic. Available at SSRN 3794811.

Mutesa, L., Ndishimye, P., Butera, Y., Souopgui, J.,

Uwineza, A., Rutayisire, R., Ndoricimpaye, E. L.,

Musoni, E., Rujeni, N., Nyatanyi, T., et al. (2020). A

pooled testing strategy for identifying SARS-CoV-2 at

low prevalence. Nature, pages 1–5.

Pedersen, M. G. and Meneghini, M. (2020). Quantifying

undetected COVID-19 cases and effects of contain-

ment measures in Italy. ResearchGate Preprint, 10.

Shoaib, M. and Ramamohan, V. (2021). Simulation model-

ing and analysis of primary health center operations.

SIMULATION.

Yang, M.-J., Seegert, N., Gaulin, M., Looney, A., Orleans,

B., Pavia, A., Stratford, K., Samore, M., and Alder, S.

(2020). What is the Active Prevalence of COVID-19?

Available at SSRN 3734463.

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

336