GAMS: Graph Augmentation with Module Swapping

Alessandro Bicciato and Andrea Torsello

Department of Environmental Sciences, Informatics and Statistics, Ca’ Foscari University of Venice, Italy

Keywords:

Augmentation, Motif, Swapping.

Abstract:

Data augmentation is a widely adopted approach to solve the large-data requirements of modern deep learning

techniques by generating new data instances from an existing dataset. While there is a huge literature and

experience on augmentation for vectorial or image-based data, there is relatively little work on graph-based

representations. This is largely due to complex, non-Euclidean structure of graphs, which limits our abilities

to determine operations that do not modify the original semantic grouping.

In this paper, we propose an alternative method for enlarging the graph set of graph neural network datasets by

creating new graphs and keeping the properties of the originals. The proposal starts from the assumptions that

the graphs compose a set of smaller motifs into larger structures. To this end, we extract modules by grouping

nodes in an unsupervised way, and then swap similar modules between different graphs reconstructing the

missing connectivity based on the original edge statistics and node similarity. We then test the performance

of the proposed augmentation approach against state-of-the-art approaches, showing that on datasets, where

the information is dominated by structure rather than node labels, we obtain a signiﬁcant improvement with

respect to alternatives.

1 INTRODUCTION

Deep Learning techniques have proved to be effective

in tackling a wide range of real-world tasks due to

their ability to effectively learn low- to medium-level

representation for the problems at hand, and to pro-

vide more complex decision boundaries to reﬂect the

complexity of the problems. However, this results in

generally much larger hypothesis spaces and a greater

tendency to over-ﬁtting what in general needs to be

balanced by means of much larger amounts of train-

ing data. One approach to make up for the large data

requirements of these approaches is data augmenta-

tion, i.e. the generation of new plausible that simu-

lates a re-sampling of the space of possible training

instances, by transforming and recombining the exist-

ing data. Augmentation operations are easily devised

for computer vision and natural language process-

ing tasks where one can express nuisance data trans-

formations that modify the input without modifying

the original semantic grouping. For example, object

translation and rotation, occlusion, and background

substitutions can readily be used on object detection

tasks to increase the number of training images. For

more general vectorial data nuisance, transformations

can be harder to deﬁne, but one can use continuity

assumptions to artiﬁcially increase the sample den-

sity of the feature space. However, even continuity

assumptions have to be given up when dealing with

graphs-based representations.

Graphs have long been used as a powerful abstrac-

tion for a wide variety of real-world data where struc-

ture plays a key role, from collaborations (Lima et al.,

2014) to biological data (Gilmer et al., 2017; Ye et al.,

2015). While Graph Neural Networks (GNNs) have

gained increasing traction in the machine learning

community for being able to effectively tackle clas-

siﬁcation problem abstracted in terms of graphs, the

increased complexity of deep models expresses itself

in these approaches as well, resulting in a tendency to

over-ﬁtting and beyond what can be addressed with

simple dropout techniques, to the point that represen-

tations of nodes belonging to different classes become

indistinguishable when stacking multiple layers, seri-

ously hurting the model accuracy (Chen et al., 2019).

In general, this leads to a requirement for large dataset

that can be harder to come by than in the case of im-

ages and text, since graph-based representation reside

at a higher semantic level and cannot be acquired as

easily.

However, data augmentation techniques for

graphs is still under-researched, with most methods

performing simple node and edge edit operations

with little consideration of the larger structure of the

Bicciato, A. and Torsello, A.

GAMS: Graph Augmentation with Module Swapping.

DOI: 10.5220/0010822400003122

In Proceedings of the 11th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2022), pages 249-255

ISBN: 978-989-758-549-4; ISSN: 2184-4313

249

graphs. In this paper we propose a novel augmenta-

tion approach called Graph Augmentation with Mod-

ule Swapping (GAMS) which tries to automatically

detect coherent portions of the graphs motifs and aug-

ment the dataset producing new graphs by swapping

similar motifs between different graphs. The idea be-

hind this approach is that the structural representa-

tions do satisfy some form of compositionality rule

just like image and text data, and it is formed by

the composition of several simpler coherent substruc-

tures loosely connected with one another according to

some unknown compositionality rule. Under this as-

sumption, swapping the modules is equivalent to in-

terchanging base substructures into existing composi-

tion templates.

2 STATE OF THE ART

Approaches for augmenting graph data are relatively

limited and mostly consist in heuristics to select

which elements of the structure (nodes/edges) to per-

turb in order to generate a new graph from a sin-

gle sample. One of the simplest and most used ap-

proaches for graph augmentation is graph perturba-

tion, which consists in a series of edge addition or

removal operations between existing nodes of a sin-

gle graph. This presents several degrees of freedom

and a large number of parameters. In particular, edge

selection can be random or follow a given heuristic,

making this more of a meta-approach with several dif-

ferent instances depending on the perturbation strat-

egy adopted. Perturbation approaches are in general

simple to implement and fast in their execution. How-

ever, in their simplest incarnation they give little to no

control over what part of the structure gets modiﬁed,

resulting in graphs that have very little to do with the

originals, and which do not maintain the underlying

semantic label. For instance, the algorithm might add

several edges in a sparse area of the graph or remove

them from a dense area resulting in graphs that are

very dissimilar from the original.

The simplest instance of edge perturbation is

given by DropEdge (Rong et al., 2019), which con-

sists in randomly dropping edges of the input graph

for each training iteration. This method was designed

to alleviate over-ﬁtting and over-smoothing when

training Graph Convolutional Networks (GCNs).

Through DropEdge, we are actually generating differ-

ent randomly deformed copies of the original graph,

thus increasing randomness and diversity of the in-

put data, reducing the risk of over-ﬁtting. Second,

DropEdge can also be treated as a message passing

reducer. In GCNs, the message passing between adja-

cent nodes is conducted along edge paths. Removing

certain edges renders node connections sparser, thus

avoiding over-smoothing to some extent when GCN

goes very deep (Rong et al., 2019). This algorithm is

well suited for deep learning algorithms, with DropE-

dge being executed at the end of each training epoch,

generating the new dataset for the next epoch.

The AdaEdge algorithm (Chen et al., 2019) op-

timizes the graph topology based on the model pre-

dictions. The method consists in iteratively training

GNN models and conduct edge remove/add opera-

tions based on the prediction to adaptively adjust the

graph for the learning target. Experimental results

in general cases show that this method can signiﬁ-

cantly relieve the over-smoothing issue and improve

model performance, which further provides a com-

pelling perspective towards better GNNs performance

(Chen et al., 2019). More speciﬁcally, GNNs are

trained on the original graph and then the graph topol-

ogy is adjusted based on the prediction result of the

model by deleting inter-class edges and adding intra-

class edges. The GNN is then retrained on the updated

graph, and the topology optimization and model re-

training are iterated multiple times.

The GAUG (Zhao et al., 2020) methods follow a

similar concept to DropEdge and AdaEdge, driving

the augmentation based on the results of the trained

classiﬁer. The goal is to improve node classiﬁca-

tion by mitigating propagation of noisy edges. Neural

edge predictors like GAE (Kipf and Welling, 2016)

are able to latently learn class-homophilic tenden-

cies in existent edges that are improbable, and nonex-

istent edges that are probable (Zhao et al., 2020).

GAUG key idea is to leverage information inherent in

the graph to predict which non-existent edges should

likely exist, and which existent edges should likely be

removed in the graph G to produce modiﬁed graph(s)

to improve model performance.

• GAUG-M: this procedure starts using an edge pre-

dictor function to obtain edge probabilities for all

possible and existing edges in G. The role of the

edge predictor is ﬂexible and can generally be re-

placed with any suitable method. Then we use

the predicted edge probabilities, we deterministi-

cally add (remove) new (existing) edges to create

a modiﬁed graph G

, which is used as input to a

GNN node-classiﬁer.

This method is tough for modiﬁed-graph setting,

i.e. when we apply one or multiple graph trans-

formation operation f : G → G

, such that G

re-

places G for both training and inference.

• GAUG-O: it is complementary to GAUG-M be-

cause it is applied for original-graph setting, i.e.

when we apply many transformations f

: G → G

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

250

0.8 0.6 0.4

0.5

0.9 0.3

0.6 0.7 0.5

↔ C'

Take 2 graphs from the

dataset

Divide in clusters

Compare the clusters and

select the most similar

HKS on the nodes of the

selected clusters

Associate the nodes of one

cluster to the ones of the other

Build new graphs

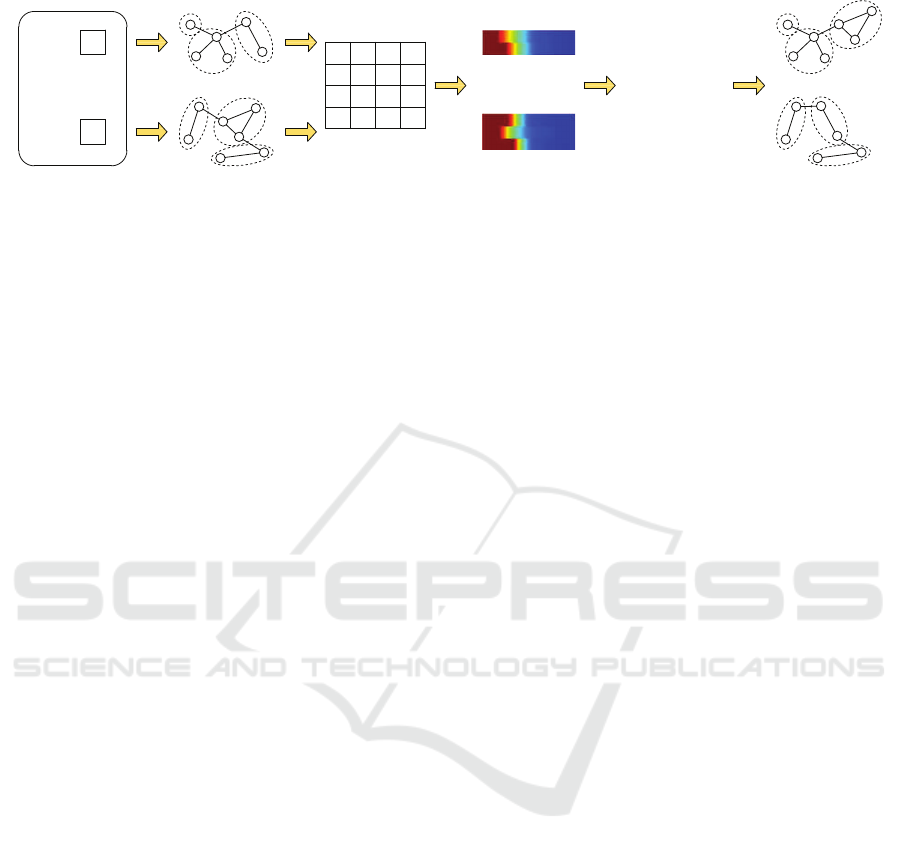
Figure 1: Schematic representation of the algorithm.

for i = 1...N, such that G ∪ {G

}

i=1

may be used

in training, but only G is used for inference.

The method of computation reminisces of the two

steps of GAUG-M and it also uses an edge pre-

diction module for the beneﬁt of node classiﬁca-

tion and aims to improve model generalization.

It does not require discrete speciﬁcation of edges

to add/remove, is end-to-end trainable, and uti-

lizes both edge prediction and node-classiﬁcation

losses to iteratively improve augmentation capac-

ity of the edge predictor and classiﬁcation capac-

ity of the node classiﬁer GNN.

Note that both AdaEdge and GAUG are designed

for node classiﬁcations scenarios, where the whole

dataset consists of a single graph, and the classiﬁer

produces a label per node. This way the classiﬁca-

tion response can be localized in the structure and can

be used to drive the edit operations. However, in a

graph classiﬁcation scenario, where the dataset con-

sists of several graph and the task is to classify the

graph themselves, the label cannot be as directly used

to drive the augmentation.

GraphCL (You et al., 2021) is a recent augmen-

tation technique mainly used for learning unsuper-

vised, semi-supervised and supervised representation

of graph data, for both node classiﬁcation and graph

classiﬁcation tasks. The approach is based on a graph

contrastive learning (GraphCL) framework that can

combine four different augmentation methods: node

dropping, edge perturbation, attribute masking and

subgraph.

• Node Dropping: Given the graph G, node drop-

ping randomly discards a speciﬁed proportion of

vertices along with their connections. The under-

lying idea behind this is that ”occluding” a small

portion of vertices does not affect the semantic la-

beling G;

• Edge Perturbation: perturbs the connectivities in

G by randomly adding or dropping a given ratio of

edges. The underlying idea is that that the seman-

tic label of G has a level of robustness to variation

in the edge connectivity patterns;

• Attribute Masking: attribute masking eliminates

some vertex attributes, forcing the model to re-

cover them using contextual information. The

underlying assumption is that model predictions

should be robust with respect to missing partial

vertex attributes.

• Subgraph: This method samples a subgraph from

G using random walk. It assumes that the seman-

tics of G is preserved in its (partial) local struc-

ture.

The purpose of the GraphCL framework is to produce

graph representations of similar or better generaliz-

ability, transferability, and robustness compared to the

competing approaches.

3 CLUSTERING

AUGMENTATION

Our proposed graph augmentation algorithm is de-

signed for a graph classiﬁcation task. The idea be-

hind the proposal is that, just like images and text,

graph representations are obtained through the com-

position of smaller structural components, motifs, that

are in general internally more coherent than the rest of

the structure. The goal of a deep classiﬁer is then to

implicitly capturing both these motifs and their com-

positional rules. In our proposal, with a schematic

representation in Figure 1, we extract the motifs in

an unsupervised way through a graph-clustering ap-

proach, thus we partition each graph in the dataset

into a ﬁxed number of clusters C. Let G

= (V

)

and G

= (V

) be two graphs belonging to the

same semantic class, with V

and V

being the node

sets, and E

⊆ V

×V

and E

⊆ V

×V

the edge sets

of the two graph. Then we ﬁnd the pair of motifs, one

from each graph, that are most similar to one another,

and swap them rebuilding the connections with the

rest of the graphs’ nodes. This gives us two new per-

turbed graphs G

and G

to be added to the training

set.

More generally, given a set D

of graphs having

GAMS: Graph Augmentation with Module Swapping

251

Table 1: Overview of the datasets tested.

Dataset # Graphs Classes Avg. Nodes Avg. Edges Avg. Degree

DD 1178 2 284.32 715.66 2.517

MUTAG 188 2 17.93 19.79 1.103

PROTEINS 1113 2 39.06 72.82 1.864

ENZYMES 600 6 32.63 62.14 1.904

MSRC 21 563 20 77.52 198.32 2.558

NCI1 4110 2 29.87 32.30 1.081

IMDB-MULTI 1500 3 13.00 65.94 5.072

COLLAB 5000 3 74.49 2457.78 32.994

REDDIT-BINARY 2000 2 429.63 497.75 1.158

the same label `, we can partition the graph in the

set, and augment the set by performing high similar-

ity swaps between partition of all the same-labeled

graphs.

The ﬁrst step of our approach is to partition the

nodes of each graph into clusters. The subgraphs

induced by each partition are candidates for our ex-

tracted motifs. Any suitable clustering approach can

be used for motif extraction, but in our implementa-

tion we used the spectral clustering implementation

provided by the Scikit Learn library, which is a vari-

ation of the normalized cut algorithm (Shi and Malik,

2000).

After the extraction of the motif candidates we

measure the similarity between each pair of motif

using the Weisfeiler-Lehman Kernel (Weisfeiler and

Lehman, 1968). The key idea of the Weisfeiler-

Lehman kernel is to replace the label of each vertex

with a multiset label, consisting of the original label

of the vertex and the sorted set of labels of its neigh-

bors. The resultant multiset is then compressed into

a new, short label. This relabeling procedure is then

repeated for h iterations.

Using the resulting kernel to the second cluster,

we get the transformation, i.e. the degree of similarity

between the pair of clusters.

With the motif similarities to hand, we can per-

form the swap. Given two graph with he same class

label, we select and swap the most similar clusters

from one graph to the other. Once the graph and mo-

tifs to be swapped are selected, we need a way to re-

stitch the motifs to the new graph, i.e. re-create the

connectivity between the swapped-in motif and the

rest of the graph. This is done by taking all the edges

outgoing from the motif and connecting them to the

node in the new graph that is most similar to the node

the edge was originally connected to.

More formally, let G

= (V

) and G

) be the two graphs, and assume we decided

to swap motif M

= (V

) from G

with motif

= (V

) with V

⊆ V

, E

= E

∩ V

. Let E

⊥

and E

⊥

be the set of edges connecting

and M

with the rest of the respective graphs, i.e.

⊥

= {(u,v) ∈ E

|u ∈ M

and v 6∈ M

} (1)

⊥

= {(u,v) ∈ E

ku ∈ M

and v 6∈ M

Then, to stitch M

into G

\ M

, for every (u,v) ∈

we ﬁnd the node v

∈ V

most similar to v

and create an edge from u to v

in the new graph.

The similarity between the nodes in the two struc-

ture can be gauged by any measure incorporating

structural information and/or vertex attributes. In

out experiments we used the Heat Kernel Signa-

ture (H

ormann, 2014) to characterize the structure

around each node and used the cosine similarity to

measure the similarity between the signatures.

Once the similarities between all nodes in V

and V

\ V

are computed, we cast the problem

of matching the outgoing connections in E

with

\ V

as a bipartite matching problem, thus ﬁnd-

ing the set of nodes in V

to which to connect

the outgoing edges E

⊥

from motif M

. The same is

performed in reverse to stitch M

into G

\ M

. In our

implementation we used the auction algorithm (Bert-

sekas, 1992) to solve the bipartite matching problem.

The code for our approach is available at

https://gitlab.com/ripper346-phd/graph-cluster-

augmentation.

4 RESULTS

To test the effectiveness of the augmentation al-

gorithm we applied a graph convolutional network

(GCN) to several graph classiﬁcation tasks and tested

the performance after augmenting the training set by

different amount. The model used embeds each node

by performing multiple rounds of message passing;

aggregate node embeddings into a uniﬁed graph em-

bedding (readout layer); train a ﬁnal classiﬁer on the

graph embedding. The readout layers took the aver-

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

252

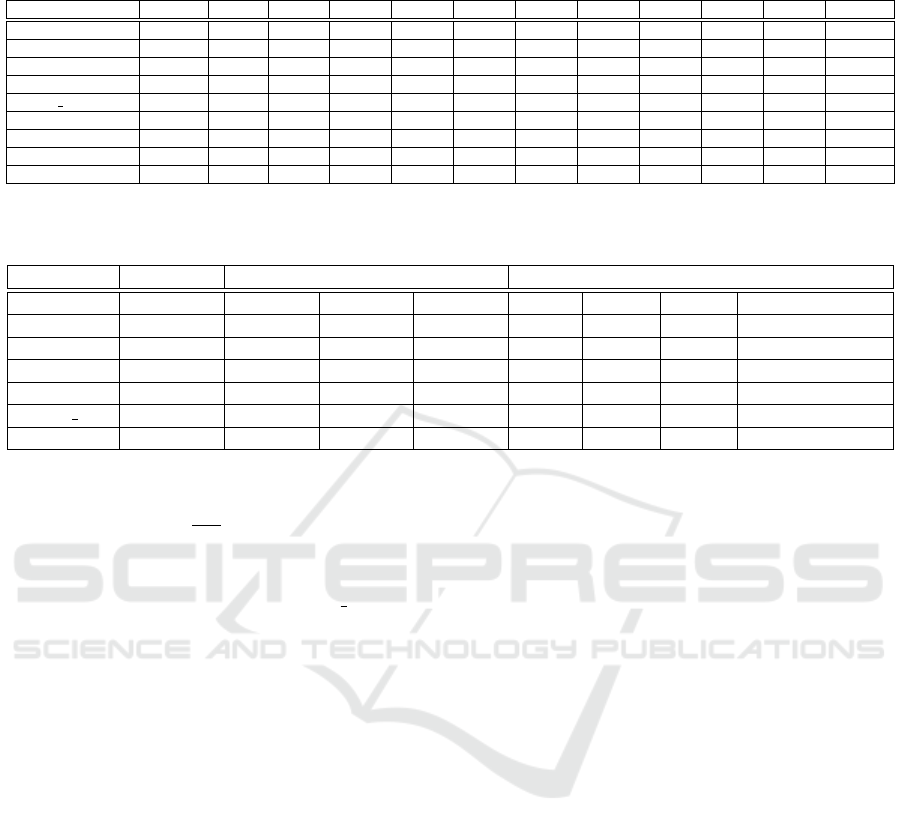
Table 2: Test accuracy of 200th epoch of class classiﬁcation training with increasing number of graphs. The bold numbers are

the best results.

Datasets Original +50% +100% +200% +300% +400% +500% +600% +700% +800% +900% +1000%

DD 0.6907 0.7288 0.7055 0.6945 0.7878 0.8091 0.7381 0.8176 0.8256 0.7973 0.8141 0.8750

MUTAG 0.7368 0.8421 0.7763 0.7876 0.7616 0.8989 0.8230 0.8561 0.9070 0.8525 0.8298 0.8575

PROTEINS 0.7315 0.6543 0.6898 0.6836 0.7269 0.7185 0.7091 0.7070 0.6950 0.7078 0.7079 0.7378

ENZYMES 0.3500 0.2961 0.2594 0.2821 0.2432 0.2433 0.2640 0.2120 0.2652 0.2815 0.2617 0.2453

MSRC 21 0.8761 0.9231 0.8717 0.9467 0.9246 0.9520 0.9630 0.9556 0.9512 0.9635 0.9565 0.9677

NCI1 0.6910 0.6285 0.6582 0.6215 0.6176 0.6441 0.6341 0.6318 0.6242 0.6381 0.6346 0.6337

IMDB-MULTI 0.3967 0.3756 0.3850 0.3944 0.3975 0.4189 0.4373 0.4728 0.4329 0.4646 0.4485 0.4603

COLLAB 0.7240 0.7113 0.7480 0.7547 0.7733 0.7700 - - - - - - - - - - - - - - - - - -

REDDIT-BINARY 0.7575 0.8033 0.8300 - - - - - - - - - - - - - - - - - - - - - - - - - - -

Table 3: Test accuracy of 200th epoch of class classiﬁcation training with increasing number of graphs compared to three

different GraphCL runs. The bold numbers are the best results.

Datasets Untouched GraphCL GAMS

random 4 random 3 random 2 +50% +100% +300% best

DD 0.6907 0.5847 0.5339 0.6186 0.7288 0.7055 0.7878 0.8750 (+1000%)

MUTAG 0.7368 0.7368 0.6842 0.5263 0.8421 0.7763 0.7616 0.9070 (+700%)

PROTEINS 0.7315 0.5964 0.5830 0.6457 0.6543 0.6898 0.7269 0.7378 (+1000%)

ENZYMES 0.3500 0.1917 0.2083 0.2667 0.2961 0.2594 0.2432 0.2961 (+50%)

MSRC 21 0.8761 0.6637 0.6814 0.7168 0.9231 0.8717 0.9246 0.9677 (+1000%)

NCI1 0.6910 0.5182 0.4927 0.5049 0.6285 0.6582 0.6176 0.6582 (+100%)

age of node embeddings:

|V |

∑

v∈V

(L)

(2)

We performed the tests on different datasets:

D&D, Mutag, Proteins, Enzymes, MSRC 21, NCI1,

COLLAB, IMDB-Multi and Reddit-Binary. Table 1

provides a brief overview of the datasets used.

In our experiments we divided each graph into

ﬁve clusters and then recombined the motifs increas-

ing the size of the training set by increasing amounts,

starting from an increase off 50% all the way to an

increase of 1000% of the original size. Table 2 shows

the results of the classiﬁcation on the test set using

GCN classiﬁers trained on the augmented training set

and on the original unaugmented training set. The

best result for each dataset is in bold. From this table

we can see that the augmentation provides an advan-

tage in most datasets, with some datasets exhibiting a

dramatic increase in performance after the augmenta-

tion procedure. It is worth noting that the best results

are for datasets containing bigger and denser graphs,

where the structural component is more determinant

in classiﬁcation. On the other hand, with datasets

such as ENZYMES and NCI1, which are generally

sparser and with more complex vertex attributes, the

augmentation seems to not provide any advantage.

Also, neither the classiﬁcation nor the node match-

ing and stitching approaches that we adopted make

use of the vertex attributes, and more attribute-aware

might improve the results on these datasets. Nonethe-

less, it is important to note that for all datasets the

performance has a clear increasing trend as the level

of augmentation increases. This can also be seen in

Figure 2 where we display the classiﬁcation perfor-

mance at the varying training epochs for various lev-

els of augmentation of the training set. We can see

that large augmentations increase convergence speed

and reduce the volatility of the accuracy throughout

the training process, as well as increase the ﬁnal per-

formance of the network.

We compared the results obtained with our

augmentation approach with the semi-supervised

GraphCL. In particular we use three runs of GraphCL:

• random4: use the degree feature, one hot degree

feature with max degree 100, a

feature, and

with random selection between node dropping,

edge perturbation, attribute masking and subgraph

methods;

• random3: use the degree feature, one hot degree

feature with max degree 100, a

feature, and with

random selection between node dropping, edge

perturbation and subgraph methods;

• random2: use the degree feature, one hot degree

feature with max degree 100, a

feature, and with

random selection between node dropping and sub-

graph methods.

In Table 3 we can see the results on some of the

datasets used for GAMS. The results of our algorithm

are always better than those obtained with GraphCL

(for clarity in the table we compared only to +50%,

+100%, +300% but we can still take all the results of

GAMS from Table 2), even in those instances where

GAMS: Graph Augmentation with Module Swapping

253

Figure 2: Accuracy results of the test set for the datasets’ graph classiﬁcation training with 5 cluster division. For clarity it is

shown the moving average of the results with W = 10. The red curve is the untouched dataset training, the other curves are the

augmented runs, where the darker the color the bigger is the augmentation. In the legend are reported the number of graphs

added to the original dataset.

ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods

254

GAMS decreases the performance with respect to the

original training set, conﬁrming the hypothesis that

in these datasets the structure is not as important for

classiﬁcation.

5 CONCLUSION

In this paper, we presented a new method for graph

augmentation. This method, works under the assump-

tion that the graphs are formed by composing simpler

cohesive substructures (motifs), and operates by ex-

tracting and swapping these substructures from train-

ing graph with the same label. This provides an aug-

mentation approach that is data-driven, in the sense

that the swapped-in motifs are directly observed from

the dataset, but that not require to be learned nor it

is in any way coupled with the learning algorithm

adopted for the ﬁnal classiﬁcation problem.

Our experimental evaluation showed that the ap-

proach is capable of providing very substantive in-

creases in performance for datasets where the struc-

tural information is determinant for classiﬁcation,

consistently yielding better results than competing ap-

proaches at the state of the art, and in some instances

allowing state-of-the-art classiﬁcation performances

even with a simple GCN scheme.

REFERENCES

Bertsekas, D. P. (1992). Auction algorithms for network

ﬂow problems: A tutorial introduction. LIDS-P-2108.

Chen, D., Lin, Y., Li, W., Li, P., Zhou, J., and Sun, X.

(2019). Measuring and relieving the over-smoothing

problem for graph neural networks from the topologi-

cal view. arXiv:1909.03211.

Gilmer, J., Schoenholz, S. S., Riley, P. F., Vinyals, O., and

Dahl, G. E. (2017). Neural message passing for quan-

tum chemistry. In International conference on ma-

chine learning, pages 1263–1272. PMLR.

ormann, T. (2014). Heat kernel signature.

Kipf, T. N. and Welling, M. (2016). Variational graph au-

toencoders. arXiv:1611.07308.

Lima, A., Rossi, L., and Musolesi, M. (2014). Coding to-

gether at scale: Github as a collaborative social net-

work. In Eighth international AAAI conference on we-

blogs and social media.

Rong, Y., Huang, W., Xu, T., and Huang, J. (2019). Drope-

dge: Towards deep graph convolutional networks on

node classiﬁcation. arXiv:1907.10903v4.

Shi, J. and Malik, J. (2000). Normalized cuts and image

segmentation. IEEE Trans. on Pattern Analysis and

Machine Intelligence, 22(8):888–905.

Weisfeiler, B. and Lehman, A. A. (1968). A reduction of

a graph to a canonical form and an algebra arising

during this reduction. Nauchno-Technicheskaya Infor-

matsia, pages 2(9):12–16.

Ye, C., Comin, C. H., Peron, T. K. D., Silva, F. N., Ro-

drigues, F. A., Costa, L. d. F., Torsello, A., and Han-

cock, E. R. (2015). Thermodynamic characterization

of networks using graph polynomials. Physical Re-

view E, 92(3):032810.

You, Y., Chen, T., Sui, Y., Chen, T., Wang, Z., and Shen,

Y. (2021). Graph contrastive learning with augmenta-

tions. arXiv:2010.13902v3.

Zhao, T., Liu, Y., Neves, L., Woodford, O., Jiang, M., and

Shah, N. (2020). Data augmentation for graph neural

networks. arXiv:2006.06830v2.

Zhou, J., Shen, J., Yu, S., Chen, G., and Xuan, Q. (2020).

M-evolve: Structural-mapping-based data augmenta-

tion for graph classiﬁcation. CoRR, abs/2007.05700.

GAMS: Graph Augmentation with Module Swapping

255