GAN-based Intrinsic Exploration for Sample Efﬁcient Reinforcement

Learning

gay Kamar

, Nazım Kemal

Ure

1,2

and G

ozde

Unal

1,2

Faculty of Computer and Informatics, Istanbul Technical University, Istanbul, Turkey

Artiﬁcial Intelligence and Data Science Research Center, Istanbul Technical University, Istanbul, Turkey

Keywords:

Deep Learning, Reinforcement Learning, Generative Adversarial Networks, Efﬁcient Exploration in Rein-

forcement Learning.

Abstract:

In this study, we address the problem of efﬁcient exploration in reinforcement learning. Most common ex-

ploration approaches depend on random action selection, however these approaches do not work well in en-

vironments with sparse or no rewards. We propose Generative Adversarial Network-based Intrinsic Reward

Module that learns the distribution of the observed states and sends an intrinsic reward that is computed as high

for states that are out of distribution, in order to lead agent to unexplored states. We evaluate our approach in

Super Mario Bros for a no reward setting and in Montezuma’s Revenge for a sparse reward setting and show

that our approach is indeed capable of exploring efﬁciently. We discuss a few weaknesses and conclude by

discussing future works.

1 INTRODUCTION

In reinforcement learning, an agent learns which ac-

tion to take depending on the current state by trying

to maximize the reward signal provided by the envi-

ronment (Sutton and Barto, 2018). The agent is not

given any prior information about the environment

or which action to take, but instead, it learns which

actions return more reward in a trial-and-error man-

ner. To do so, agents are usually incentivized to ex-

plore the state-action space before committing to the

known rewards in order to avoid exploitation of a non-

optimal solution.

Most common approaches to exploration, such as

ε-greedy in Deep-Q-Network (DQN) (Mnih et al.,

2013), adding Ornstein–Uhlenbeck to action in Deep

Deterministic Policy Gradient (DDPG) (Lillicrap

et al., 2016) or maximizing entropy over the ac-

tion space in Asynchronous Advantage Actor-Critic

(A3C) (Mnih et al., 2016), rely on increasing the

probability of a random action. This approach works

ﬁne in an environment with dense reward signals.

However, in sparse or no reward settings, the agent

fails to ﬁnd a reward signal to guide itself, thus fail-

ing to ﬁnd a solution.

Related works have focused on providing an ex-

tra intrinsic reward to the agent in addition to the

extrinsic reward, i.e. the reward from the environ-

ment. Prediction-based exploration models estimate

the novelty of an observation by learning the environ-

ment dynamics and assigning higher rewards to the

observation which the future of it can not predict well,

i.e. it makes the agent act ”curiously” (Schmidhuber,

1991; Pathak et al., 2017; Stadie et al., 2015). In an-

other work, environment dynamics is modeled using

variational inference and the novelty of a state is mea-

sured through prediction using this model (Houthooft

et al., 2016). (Pathak et al., 2019) proposed a frame-

work with multiple dynamic models, and the intrinsic

reward is calculated by the disagreement between the

dynamic models.

Another set of methods are based on count-based

exploration, by counting the number of times a state is

visited and encouraging the agent to visit less-visited

states. However, if the state space is high dimen-

sional, it is not feasible to keep track of all the states.

Recent studies proposed density models to approx-

imate how frequently a state is visited (Bellemare

et al., 2016; Ostrovski et al., 2017; Zhao and Tresp,

2019). (Tang et al., 2017) beneﬁted from hashing in

order to shrink the state-space to keep the count of the

visitations to states.

In ”Random Network Distillation (RND)”, fea-

tures of an observation are calculated through a ﬁxed,

randomly initialized network and another network is

trained to predict these features, with the error being

264

Kamar, D., Üre, N. and Ünal, G.

GAN-based Intrinsic Exploration for Sample Efﬁcient Reinforcement Learning.

DOI: 10.5220/0010825500003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 2, pages 264-272

ISBN: 978-989-758-547-0; ISSN: 2184-433X

the intrinsic reward (Burda et al., 2019). ”Never Give

Up” adds on to RND by a memory-based episodic re-

ward module, where they keep the embeddings of the

states observed in the current episode and compare the

new states to the ones in the memory, discouraging the

agent to visit the same states in the episode, while also

using RND for the long-term exploration (Badia et al.,

2020). DORA framework creates an identical MDP to

the task at hand with E-values ﬁxed to 0 instead of Q-

values for every state-action pair, and assigns a bonus

intrinsic reward for how well the framework can pre-

dict the E-value in the current state (Choshen et al.,

2018).

Instead of computing an intrinsic reward, (Ecoffet

et al., 2021) proposes ”Go-Explore”, a method that

focuses on exploring until a solution is found before

starting policy learning. In ”Go-explore”, a memory

is maintained to keep the visited states, which are en-

coded into lower-sized cells, and periodically, a state

is selected from the memory to go back to and ex-

plore from. Selection of the state is probabilistic,

however, the probabilities are assigned using a heuris-

tic, which tries to assign higher probabilities to ”in-

teresting” states, i.e. states that have better chances

to lead to a good exploration. Once a solution is

found through exploration, the agent goes through a

robustiﬁcation phase using imitation learning. A sim-

ilar idea named ”Diverse Trajectory-conditioned Self-

Imitation Learning (DTSIL)” is proposed by (Guo

et al., 2019), where they train a policy using Self-

Imitation Learning (Oh et al., 2018) to follow trajec-

tories stored in a memory, which lead agent to less-

frequently-visited states, in order to learn a policy for

exploring the environment.

This study follows the trend of providing an in-

trinsic reward to the agent by using Generative Ad-

versarial Networks (GAN) (Goodfellow et al., 2014).

GANs consist of two networks: a generator G tasked

with generating synthetic data similar to real data, and

a discriminator D tasked with measuring the proba-

bility of the input being real to discriminate real and

generated data. Both G and D have tasks adversarial

to each other as G tries to fool D that the data it gen-

erates is real, and D tries to successfully detect data

generated by G. The convergence of GAN happens

when G is able to generate data indistinguishable to

D, and D has 50% accuracy of detecting fake data,

meaning D starts to randomly guess. G’s ability to

generate new data comes from its learning and ﬁtting

to the distribution of the real data, therefore, in the-

ory, with the right input, G should be able to generate

exactly the same sample from the original data distri-

bution. This idea is realized in the anomaly detection

task in (Schlegl et al., 2017) and (Schlegl et al., 2019),

in which, after the training of GAN, G is forced to

generate the query sample and an anomaly score is

assigned by measuring the difference between gener-

ated and query sample. A high anomaly score means

the query sample is an out-of-distribution sample. In-

spired by this work (Schlegl et al., 2019), we propose

a GAN-based exploration method for reinforcement

learning, where a GAN is trained using the visited

state observations. The trained G is used to assign an

intrinsic reward to the agent, and unobserved novel

states are assigned higher rewards due to them not be-

ing in the distribution of the observed states used in

GAN’s training.

A recent study has also utilized GANs for the task

of exploration (Hong et al., 2019) by using D to dis-

tinguish between visited and novel states. However,

their approach trains G less frequently so that D does

not lose the ability to distinguish between fake and

real data. This approach has two weaknesses: (a)

G needs to train just good enough to incentivize D

to improve itself, but not good enough so that GAN

does not reach convergence, and with the right hy-

perparameter setup, the task of keeping this balance

is hard to accomplish; and (b) D is trained to sepa-

rate real data from what G generates, however, there

is no guarantee on how D will act on an unseen in-

stance, resulting in unreliable feedback. In our pro-

posed method, the GAN is trained to convergence so

that G is able to generate data similar to real states,

and an encoder E is trained to map a newly observed

state to the latent noise space, to then be regenerated

by G. The difference between the observed state and

the generated state is then fed as the intrinsic reward

to the learning agent. We chose to use GANs for this

task because (a) with this approach, learning the dy-

namics of the environment is not required, we are only

interested in learning the distribution of the observed

states, and (b) GANs are very widely studied and its

use-cases have expanded to many areas. We believe

that GANs can be integrated into reinforcement learn-

ing and showcasing a successful application will open

the gates for the future studies.

We evaluate our proposed method on Mon-

tezuma’s Revenge, an Atari game that is notoriously

hard to explore due to rewards being very sparse and

difﬁcult to reach from the initial position by random

exploration (Bellemare et al., 2016). In addition to the

sparse reward setting, we also evaluate our method

in a no-reward setting in the game of Super Mario

Bros. (Kauten, 2018). We show by that using only

the intrinsic reward, the agent is capable of exploring

the environment. We discuss how the method can be

further improved and invite readers to build upon the

proposed method.

GAN-based Intrinsic Exploration for Sample Efﬁcient Reinforcement Learning

265

Figure 1: A general reinforcement learning framework with our proposed GAN-based Intrinsic Reward Module (GIRM).

At each time step t, agent observes a state s

from the environment MDP M , chooses an action depending on its policy π,

and receives an extrinsic reward r

from the environment and an intrinsic reward r

from GIRM. In GIRM, the encoder E

maps s

to the input noise space of the generator G and outputs E(s

). G generates a synthetic state G(E(s

)) and the error

measured between s

and G(E(s

)) is then sent to the agent as an intrinsic reward. Operation − in the GIRM module is not

necessarily subtraction, but could be any function that computes the residual between s

and G(E(s

)). L

is used for training

the Encoder.

2 PRELIMINARIES

Generative Adversarial Networks. Proposed by

(Goodfellow et al., 2014), Generative Adversarial

Networks (GAN) is a framework that consists of two

neural networks, called generator and discriminator,

competing against each other in order to train the gen-

erator to be able to generate synthetic data similar to

real data. Discriminator D is optimized to detect if the

input sample is real or generated, and the generator G

tries to fool the discriminator by generating data sim-

ilar to the real data x from an input noise z sampled

from a distribution p

. D outputs the probability of

the input being real data, and is originally optimized

to maximize logD(x) + log(1 −D(G(z))) while G is

optimized to minimize log(1 −D(G(z))). In an opti-

mal training, G is able to learn the distribution of the

real data and can sample new synthetic data from the

same distribution.

Reinforcement Learning. In reinforcement learning,

environments are modeled by a Markov Decision Pro-

cess (MDP), deﬁned as M = (S , A, R , P , ρ

), where

S is the set of states, A the set of actions, R the reward

function, P the state transition probability distribution

and ρ

the distribution of the initial state. Given a

state s

in t

time step, the agent takes an action a

according to its policy π(s

), receives a reward r

and

observes the next state s

t+1

. The aim is to ﬁnd a pol-

icy π∗ that maximizes the expected total discounted

reward,

∗

= argmax

π(s

),P



∑



(1)

where γ ∈ [0, 1) is the discount factor that determines

the weight of rewards in the distant future compared

to present.

Exploration in Reinforcement Learning. One of

the longstanding problems of reinforcement learning

is to explore the environment efﬁciently before agent

exploits a sub-optimal but positive reward it receives.

The most common approaches for exploration depend

on diversifying action selection, meaning that agent

ideally performs a random action in a state it did not

previously observe, rather than sticking to a single ac-

tion. These approaches do not necessarily guide agent

to unvisited states, but occasionally lets the agent take

a random action that might guide it to a better reward.

However, if the reward signals in an environment are

sparse or nonexistent, the policy π’s behaviour will be

random at any state as the agent does not encounter a

reward signal to guide itself. In such problems, an

efﬁcient exploration method is necessary to discover

unvisited states in order to ﬁnd the sparse rewards to

learn the π

∗

3 EXPLORATION GUIDED BY

GAN-BASED INTRINSIC

REWARD MODULE

Inﬂuenced by the anomaly detection framework of

(Schlegl et al., 2019), we propose a ”GAN-based In-

trinsic Reward Module (GIRM)” in order to incen-

tivize the policy learning agent to explore unvisited

states. To do so, at every time-step, in addition to

the extrinsic reward received from the environment

, GIRM will also feed the agent with an intrinsic

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

266

reward r

, which will be higher for the unexplored

states. Policy of the agent is then updated to maximize

the total reward, r

= r

+ r

. Providing an intrinsic

reward is especially important for the environments

with sparse or no rewards, because in such environ-

ments, the agent usually fails to ﬁnd the states with

rewards and it needs reinforcement to ﬁnd the set of

actions that will maximize the total reward received.

With the intrinsic reward, the agent will now be re-

inforced into exploring the environment to ﬁnd the

extrinsic rewards. Figure 1 illustrates the proposed

GIRM-enhanced reinforcement learning framework.

The ﬁrst goal of GIRM is to learn the distribution

of the visited states. To that end, we train a GAN with

the visited states as the train data, using the improved

WGAN architecture (Gulrajani et al., 2017). Since

the generator G is trained to minimize the divergence

between G’s sample distribution and the distribution

of the training data, G is trained to ﬁt to the distribu-

tion of the visited states, i.e. G learns the mapping

z →G(z) where G(z) is a synthetic state similar to the

visited states.

After training of the GAN is complete, an encoder

E is trained to learn the mapping s

→ z, i.e. E maps

the state s

to the input noise distribution of G. The

aim is to ﬁnd the z that is mapped to a G(z) which is

the most similar synthetic state in the distribution of

G, to the input state s

. To that aim, ﬁrst, we deﬁne

an MSE loss to minimize the difference between the

input s

and the recreated image G(z) = G(E(s

)):

min

L (s

) =

−G(E(s

))k

(2)

where n is the number of dimensions in the state

space (if states are images, n represent the number

of pixels). As pointed in (Schlegl et al., 2017) and

(Schlegl et al., 2019), the discriminator D is able

to learn the feature representations of the inputs in

an intermediate layer, and in addition to the loss in

Eq. 2, minimizing the difference between the fea-

ture encodings of the training data and the recreated

data improves the training of E. Therefore, we adapt

the loss of feature encodings of s

and G(E(s

) as

) =

kf (s

) − f (G(E(s

)))k

and ﬁnalize the

loss function for E as:

min

L (s

)+L

) =

−G(E(s

))k

kf (s

) − f (G(E(s

)))k

(3)

where f is the output of an intermediate layer in D,

number of the dimensions in the feature represen-

tations, and λ is a hyperparameter scaling the feature

representation loss. After E is trained, as illustrated

in Fig. 1, for an observed state by the agent s

, the

intrinsic reward is computed as:

−G(E(s

))k

, (4)

which is the MSE between s

and G(E(s

). If s

is a

frequently visited state, it will belong to the distribu-

tion learned by G, therefore it can be recreated and

will be low. On the contrary, if s

is an unvisited

state, the difference between s

and G(E(s

) will be

signiﬁcant and r

will be high, reinforcing the agent

to explore towards s

. Notice that, we do not mul-

tiply r

with a constant scalar to scale it. It is true

that in different environments, the scale of the intrin-

sic rewards will be different, however as the distri-

bution of the visited states change, so will the scale

of intrinsic rewards. Therefore, instead of a constant

scalar, we calculate the exponentially weighted mov-

ing average(EMA) and variance(EMV ) of the rewards

as:

EMA =

(

, if t = 1

α ∗r

+ (1 −α) ∗EMA, otherwise

(5)

EMV =











0, if t = 1

α ∗(r

−EMA)

(1 −α) ∗EMV

, otherwise

(6)

and then, standardize the intrinsic reward:

−EMA

√

EMV

. (7)

In this study, we used α = 0.01. The standard-

ization ensures that the distribution of the rewards

will have the same mean and variance throughout the

training and in different environments. In Eq. 7, the

intrinsic reward is standardized to have a mean of 0

and a variance of 1, and in this study, we used this

equation for standardization, however the equation

can be modiﬁed to have different mean and variance if

needed. With the standardization of r

, the optimiza-

tion problem in Eq. 1 becomes:

∗

= argmax

π(s

),P



∑

+ r

)



. (8)

GIRM is trained periodically during the policy

learning. To do so, the states observed by the agent

are stored in a memory M = s

, s

, ..., s

with a pre-

deﬁned capacity N. As soon as M reaches full ca-

pacity, we stop policy learning of the agent, and train

GIRM with the data stored in M using stochastic gra-

dient descent. After training of the GIRM is ﬁnished,

M’s content is cleared and the policy learning, as well

GAN-based Intrinsic Exploration for Sample Efﬁcient Reinforcement Learning

267

Figure 2: A full view of the ﬁrst level in the game Super Mario Bros. Player starts at the left side of the level and only perceives

the surroundings of the character it is controlling, while the camera is always centered at the character in the horizontal-axis.

To complete the level, the player needs to reach the castle at the far right of the level. With no reward given, a reinforcement

learning agent only depends on exploration to ﬁnd the end of the level.

Figure 3: First room in the game Montezuma’s Revenge.

The player starts the game in this room and needs to col-

lect the key ﬁrst, and then go to one of the doors to escape

from the room. Only rewards are received when a key is

grabbed or a door is unlocked. The player needs to com-

plete a complex set of actions to reach the key, as it needs

to climb down two stairs, jump to a rope, avoid an enemy,

and then climb up a stair while avoiding death. The camera

is static, the player has the full view of the room and it only

changes when the player goes to another room.

as storing observed states to M, restarts. Every time

M reaches full capacity, the GIRM is trained with the

new data as the distribution of visited states keeps

changing during the policy learning. Since GIRM

consists of only random networks before the ﬁrst time

M is full, GIRM does not provide an intrinsic reward

until the ﬁrst training phase, and the agent only re-

ceives the extrinsic rewards from the environment.

Until the ﬁrst training phase of GIRM is ﬁnished, we

use exploration by randomly selected actions. More-

over, the ﬁrst time M is full, GIRM is trained for larger

number of epochs to train it until convergence. After-

wards, GIRM is ﬁne-tuned with the newly observed

data for a lesser number of epochs.

4 EXPERIMENTS

4.1 Experimental Setup

As the baseline reinforcement learning algorithm, we

used Advantage Actor-Critic (A2C), a synchronous

version of A3C (Mnih et al., 2016) in the experi-

ments. The main difference between A2C and A3C

is, while in A3C, there are a number of workers with

their own network weights asynchronously working

and updating a global network, in A2C, workers send

transition synchronously, and share one global net-

work. In our experiments, we used sixteen workers

synchronously running their own environments. For

both A2C and GIRM, observed state visuals are con-

verted to grayscale from RGB and resized to 84×84.

The actor-critic network has 3 convolutional layers,

followed by a fully connected layer. First convolu-

tional layer has 32 ﬁlters of 8×8 kernel size with

stride 4, second convolutional layer has 64 ﬁlters of

4×4 kernel size with stride 2, the third convolutional

layer has 64 ﬁlters of kernel size 3×3 with stride 1

and ﬁnally, the fully connected layer has 512 hidden

units. Each layer has Leaky ReLU as its activation

function with a negative slope of 0.01. The output of

the fully connected layer is then sent to two separate

fully connected layers, one of them selecting the ac-

tion(actor) and the other predicting the value of the

state(critic).

As depicted in Figure 1, the GIRM consists of 3

networks: generator G, discriminator D and encoder

E. The size of the input noise is 128 for G, and it

is created as a 2D input, with the size 1 ×1 and 128

channels. G consists of 5 transposed convolutional

layers, with 64 ﬁlters in the ﬁrst 4 layers and 1 ﬁlter in

the last layer, each ﬁlter having a kernel size of 4 ×4.

D consists of 6 convolutional layers with 64 ﬁlters in

the ﬁrst 5 layers and 1 ﬁlter in the last, with kernel

sizes of 4, 5, 5, 3, 1, and 5, respectively. The output of

the ﬁrst 5 layers of D is also used as the intermediate

feature representation for the training of E. Finally, E

is formed with 5 convolutional layers with 64 ﬁlters

in the ﬁrst 4 layers and 128 ﬁlters in the last, which is

the size of the input noise. Kernel Sizes are 4, 5, 5,

3, and 5, respectively. All three networks use Batch

Normalization (Ioffe and Szegedy, 2015) at the end of

each layer except the ﬁnal ones. Hidden layers in D

and E are activated with Leaky ReLU with a negative

slope of 0.2, and hidden layers of G uses ReLU as the

activation function, except the ﬁnal layer which uses

tanh as its activation function.

For all the networks, we used ADAM optimizer

(Kingma and Ba, 2014) to update the weights. For

training the actor-critic network, learning rate is 2.5 ∗

−4

and for the networks in GIRM module, learn-

ing rate is 10

−4

. β

= 0.9 and β

= 0.999 for all the

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

268

Table 1: Comparison of agents in Super Mario Bros. in terms of furthest point they explored and percentage of the states that

are further from certain point out of all of the states they visited in horizontal axis.

Method # of Frames Furthest Visited visited > 500 visited > 1000 visited > 1500

A2C 32M 1673 41.3% 2.3% 0.1%

A2C+GIRM 8M 3150 (End of level) 60.3% 21.5% 4.1%

networks.

To evaluate our proposed module, we set up two

environments, one of which has sparse reward signals

and the other has no reward signal other than the one

in the goal state. We evaluate our module by running

an agent with and without the module and compare

the results. Later on, we compare our results with the

other studies in the ﬁeld.

First of the environments is the game Super Mario

Bros. (Kauten, 2018). Fig. 2 shows the full layout of

the ﬁrst level, which is the level our agent is trained

in. The agent can only partially observe the environ-

ment, as the states include only the surroundings of

the character it’s controlling. The initial position is at

the far left side of the level and the goal position is the

ﬂag next to the castle at the far right side. In this en-

vironment, we disable all the extrinsic rewards other

than the one given for reaching the goal state. With-

out an extrinsic reward, the agent depends only on its

exploration strategy, and with random exploration, it

is a signiﬁcantly hard task to go past the ﬁrst few ob-

stacles, let alone reach the goal state.

The second environment is the game Mon-

tezuma’s Revenge, which is notoriously hard to solve

for an AI agent due to its sparse rewards. Fig. 3

shows the room the player starts in. In order to re-

ceive the ﬁrst extrinsic reward signal, the player needs

to navigate to the key. However, the agent needs to

select a speciﬁc set of actions in order to reach the

key, as a fall from any height results in death, so the

agent needs to navigate the character to jump to the

middle platform, climb down the stairs, jump to the

rope and to the platform on right, climb down the sec-

ond stairs, avoid the enemy and ﬁnally climb up the

stairs. Producing an action set randomly to carry out

all these tasks is especially hard. Differing from Su-

per Mario Bros, the observed environment does not

change with the movement of the agent and the back-

ground stays static until the agent moves to a differ-

ent room. This provides a different challenge to the

GIRM, as the generated image by the generator G

will have the same background whether the state is

visited or not, until a new room is explored, and r

calculated in Eq. 4 will only have small differences

between states. Standardization in Eq. 7 is especially

important in this type of environments to make the

computed for visited and unvisited states have a

meaningful difference.

4.2 Results and Discussion

Super Mario Bros. Table 1 compares the agents

trained with A2C with and without GIRM module,

by the distance they covered in horizontal axis in the

ﬁrst level of the game Super Mario Bros. With no re-

ward signal received, the agent only depends on its

exploration strategy to ﬁnd the goal state of the envi-

ronment. In the case of no GIRM module, a strategy

to maximize the entropy of the actions is used (Mnih

et al., 2016). Results show that when GIRM is in-

troduced, the agent can ﬁnd the goal state, whereas

without it, the agent can only reach nearly half point

of the level and it can only visit there once.

In Mario, as shown in Fig. 2, in order to explore

the environment, the agent needs to go right consis-

tently. When there is no extrinsic reward, exploration

depends only on the observation of new environmen-

tal elements and vertical movement does not provide

new information and is only useful for overcoming

obstacles. Since the intrinsic rewards from the GIRM

are higher in the unobserved states that are on the

right side of the level, the agent eventually needs to

learn to go right in order to explore efﬁciently. As

shown in Table 1, the visited states by the agent with

GIRM that are further from half point of the level

amounts to 4.1% of all visited states. Through the

observed rewards from GIRM in the ﬁrst part of the

level, the agent learns to go right as it receives higher

rewards from the states on the right side of the map

and through this learnt policy, the agent manages to

ﬁnd the end of the level without roaming around in

the second half of the level. Even though there is no

extrinsic reward, through the rewards from the GIRM,

our agent learns to explore the environment by learn-

ing to move right until the end of the episode, show-

ing that it is capable of efﬁcient exploration. This is

an important trait for the agent to have, as, through the

usage of the GIRM, we show that the agent can learn

how to explore efﬁciently in the speciﬁc environment

setting it is in.

Montezuma’s Revenge. An exceptionally hard-to-

solve environment, it is very crucial to explore efﬁ-

ciently and ﬁnd the rewards in Montezuma’s Revenge.

Our agent trained with the GIRM has shown capable

of doing so, guided to rewards and achieved better

scores than the baseline A2C agent, as shown in Fig.

4. Agent trained without the GIRM was capable of

GAN-based Intrinsic Exploration for Sample Efﬁcient Reinforcement Learning

269

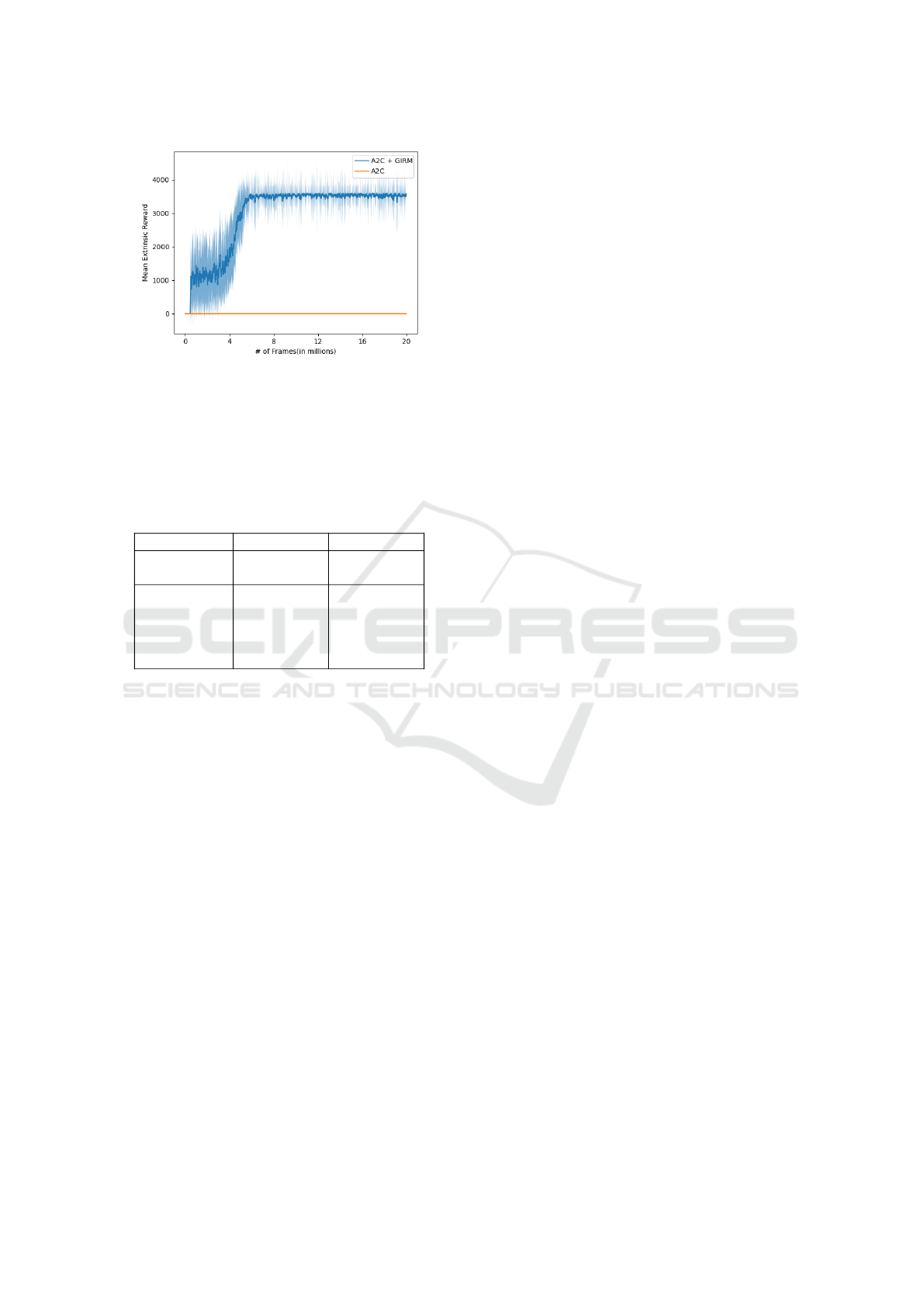
Figure 4: Mean scores during the training of A2C and A2C

+ GIRM in Montezuma’s Revenge.

Table 2: Comparison of our results in Montezuma’s Re-

venge against DQN-GAEX (Hong et al., 2019), Go-explore

(Ecoffet et al., 2021), NGU (Badia et al., 2020), RND

(Burda et al., 2019) and DTSIL (Guo et al., 2019). Scores

are reported by the authors of the methods, except the base-

line result from A2C and our method, GIRM. Bold indicates

the best result.

Method # of Frames Mean Score

A2C 20M 0

A2C+GIRM 20M 3,594

DQN-GAEX 200M 420

Go-explore 12B 43,791

NGU 35B 10,400

RND 16B 10,070

DTSIL 3.2B 22,616

ﬁnding the reward for grabbing key in the ﬁrst room

very few times, and in those cases, it could not ﬁnd

its way out of the room to receive further rewards.

Agent trained with the GIRM has shown its capabil-

ity to further explore the environment, ﬁnding rewards

in the other rooms as well. However, it should be

noted that an early convergence happens as the agent

could not break out of the score of 3600. We observed

that the agent found a 3000 reward for killing an en-

emy and started to exploit that big reward rather than

exploring. This shows that even though our GIRM

guides the agent into exploration, exploiting extrinsic

rewards when the difference between intrinsic and ex-

trinsic rewards is high could not be avoided. Results

in Table 2 further shows that our method is capable

of exploring and matching the results of some of the

works in the literature but could not beat the perfor-

mances of the state-of-the-art.

Another factor affecting the performance of the

GIRM is the static background observation in the

rooms, resulting in small differences between the ob-

served state and the regenerated state by the generator

G(even if the observed state is novel) as long as the

agent stays in the same room, because the only differ-

ence between state observations is the position of the

character. We addressed this problem by introducing

exponentially weighted moving average (EMA) and

variance (EMV ) in Section 3 to make even very small

differences into meaningful intrinsic rewards. How-

ever, when the agent manages to ﬁnd new rooms in

the level, the difference for calculating intrinsic re-

ward grows bigger, which also increases EMA and

EMV . This results in small differences being not sig-

niﬁcant enough anymore, hindering the exploration in

an already observed room. Nevertheless, as shown

by the results in both Super Mario Bros. and Mon-

tezuma’s Revenge, we can conclude that our pro-

posed GIRM is capable of incentivizing the agent into

exploring, heavily outperforming the random explo-

ration approaches that are most commonly used in

the literature, however, we also identiﬁed a few afore-

mentioned weaknesses as well.

Sample Efﬁciency of GIRM. As explained, GIRM

is trained when the memory M that stores observed

states is full and the ﬁrst training phase of GIRM oc-

curs for a larger number of epochs in order to train

it until convergence. This leads to optimized net-

works in the GIRM even after the ﬁrst training phase

and GIRM becomes capable of computing accurate

intrinsic rewards, i.e. rewards that are higher for

unobserved states. Because of this, to start leading

the agent into exploring the environment efﬁciently,

GIRM needs only the amount of data M initially

stored. Our reported results in Table 1 and Table 2

uses only 8 million and 20 million of frames for each

respective environment. Especially in Montezuma’s

Revenge, as also shown in Table 2, recent studies have

beneﬁted from billions of frames even for efﬁcient ex-

ploration. Our method proves to be sample efﬁcient,

as it successfully provides the necessary intrinsic rein-

forcement for the agent with signiﬁcantly less amount

of data.

5 CONCLUSION AND FUTURE

WORK

Common exploration strategies work well when re-

ward signals are dense, however an additional incen-

tive is needed in environments with sparse or no re-

wards. In this work, we proposed the ”GAN-based

Intrinsic Reward Module (GIRM)” to compute an in-

trinsic reward for a reinforcement learning agent, in

order to incentivize the agent to explore the environ-

ment it is in. GIRM is trained so that the intrinsic re-

ward is higher for the novel or less-frequently-visited

states to guide the agent into exploring the environ-

ment. The memory mechanism that we employ in

the training of GIRM provides an adaptation to the

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

270

changing distribution in the observed environment.

Since GIRM is an extension module, it can be ap-

plied to any reinforcement learning algorithm. In this

work, we used Asynchronous Actor-Critic (A2C) as

the baseline algorithm, comparing agents trained with

and without GIRM.

We show GIRM’s capability of exploration in a

sparse reward and a no reward setting. We used Super

Mario Bros. (Kauten, 2018) for the no reward set-

ting and show that the agent trained with GIRM pro-

vides the necessary intrinsic reward so that the agent

explores and completes the level and outperforms the

agent without GIRM. Our agent does so by learning

the pattern of going right in order to ﬁnd unexplored

states. For the sparse reward setting, we evaluated

our agent in Montezuma’s Revenge, an atari game

that’s been recently used for benchmarking in rein-

forcement learning, due to its difﬁculty. While the

agent trained without GIRM is not capable of escap-

ing the initial room, with the addition of GIRM, our

agent explores multiple rooms throughout the envi-

ronment, achieving a mean score of 3954. On the

one hand, we show that GIRM provides a more ef-

ﬁcient exploration strategy, but on the other hand, we

observe that our agent converges early, beginning to

exploit the high rewards from the environment.

We also identify another weakness of GIRM

through Montezuma’s Revenge: standardizing re-

wards through the usage of EMA and EMV turns

small differences between the observed novel state

and regenerated state into meaningful intrinsic re-

wards, however, as the agent begins to explore new

rooms, the already high difference between regener-

ated and novel states gets higher, which also increases

the distribution EMA and EMV represents, there-

fore GIRM loses the capability of assigning meaning-

ful rewards to novel states in the frequently visited

rooms. In the future, we would like to address this

problem. A potential solution could be leaving out

the very high or very low intrinsic reward when up-

dating EMA and EMV , treating them as an anomaly.

Furthermore, a more efﬁcient reward scaling method

could be investigated.

Another future direction is to make use of GANs

to train a model to learn the dynamics of the envi-

ronment, instead of the distribution of observations.

Since the dynamics throughout the environment do

not change drastically, a model that learns the dy-

namics might have a better generalization property

throughout the environment. This idea is not a direct

improvement to GIRM, but instead, we recommend

an idea to utilize GANs in the efﬁcient exploration

problem in reinforcement learning with a different ap-

proach.

ACKNOWLEDGEMENTS

This work is supported by Istanbul Technical Univer-

sity BAP Grant NO: MOA-2019-42321.

REFERENCES

Badia, A. P., Sprechmann, P., Vitvitskyi, A., Guo, Z. D.,

Piot, B., Kapturowski, S., Tieleman, O., Arjovsky,

M., Pritzel, A., Bolt, A., and Blundell, C. (2020).

Never give up: Learning directed exploration strate-

gies. CoRR, abs/2002.06038.

Bellemare, M. G., Srinivasan, S., Ostrovski, G., Schaul, T.,

Saxton, D., and Munos, R. (2016). Unifying count-

based exploration and intrinsic motivation. In Pro-

ceedings of the 30th International Conference on Neu-

ral Information Processing Systems, NIPS’16, page

1479–1487, Red Hook, NY, USA. Curran Associates

Inc.

Burda, Y., Edwards, H., Storkey, A., and Klimov, O. (2019).

Exploration by random network distillation. In 7th In-

ternational Conference on Learning Representations

(ICLR 2019), pages 1–17. Seventh International Con-

ference on Learning Representations, ICLR 2019 ;

Conference date: 06-05-2019 Through 09-05-2019.

Choshen, L., Fox, L., and Loewenstein, Y. (2018). Dora the

explorer: Directed outreaching reinforcement action-

selection. ArXiv, abs/1804.04012.

Ecoffet, A., Huizinga, J., Lehman, J., Stanley, K. O., and

Clune, J. (2021). First return, then explore. Nature,

590(7847):580–586.

Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B.,

Warde-Farley, D., Ozair, S., Courville, A., and Ben-

gio, Y. (2014). Generative adversarial nets. In Ghahra-

mani, Z., Welling, M., Cortes, C., Lawrence, N., and

Weinberger, K. Q., editors, Advances in Neural Infor-

mation Processing Systems, volume 27. Curran Asso-

ciates, Inc.

Gulrajani, I., Ahmed, F., Arjovsky, M., Dumoulin, V., and

Courville, A. C. (2017). Improved training of wasser-

stein gans. In Guyon, I., Luxburg, U. V., Bengio, S.,

Wallach, H., Fergus, R., Vishwanathan, S., and Gar-

nett, R., editors, Advances in Neural Information Pro-

cessing Systems, volume 30. Curran Associates, Inc.

Guo, Y., Choi, J., Moczulski, M., Bengio, S., Norouzi,

M., and Lee, H. (2019). Efﬁcient exploration with

self-imitation learning via trajectory-conditioned pol-

icy. ArXiv, abs/1907.10247.

Hong, W., Zhu, M., Liu, M., Zhang, W., Zhou, M., Yu, Y.,

and Sun, P. (2019). Generative adversarial exploration

for reinforcement learning. In Proceedings of the First

International Conference on Distributed Artiﬁcial In-

telligence, DAI ’19, New York, NY, USA. Association

for Computing Machinery.

Houthooft, R., Chen, X., Duan, Y., Schulman, J., De Turck,

F., and Abbeel, P. (2016). Vime: Variational informa-

tion maximizing exploration.

GAN-based Intrinsic Exploration for Sample Efﬁcient Reinforcement Learning

271

Ioffe, S. and Szegedy, C. (2015). Batch normalization: Ac-

celerating deep network training by reducing internal

covariate shift. CoRR, abs/1502.03167.

Kauten, C. (2018). Super Mario Bros for OpenAI Gym.

GitHub.

Kingma, D. and Ba, J. (2014). Adam: A method for

stochastic optimization. International Conference on

Learning Representations.

Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T.,

Tassa, Y., Silver, D., and Wierstra, D. (2016). Con-

tinuous control with deep reinforcement learning. In

Bengio, Y. and LeCun, Y., editors, ICLR.

Mnih, V., Badia, A. P., Mirza, M., Graves, A., Lillicrap, T.,

Harley, T., Silver, D., and Kavukcuoglu, K. (2016).

Asynchronous methods for deep reinforcement learn-

ing. In Balcan, M. F. and Weinberger, K. Q., editors,

Proceedings of The 33rd International Conference

on Machine Learning, volume 48 of Proceedings of

Machine Learning Research, pages 1928–1937, New

York, New York, USA. PMLR.

Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,

Antonoglou, I., Wierstra, D., and Riedmiller, M. A.

(2013). Playing atari with deep reinforcement learn-

ing. CoRR, abs/1312.5602.

Oh, J., Guo, Y., Singh, S., and Lee, H. (2018). Self-

imitation learning. In Dy, J. and Krause, A., editors,

Proceedings of the 35th International Conference on

Machine Learning, volume 80 of Proceedings of Ma-

chine Learning Research, pages 3878–3887. PMLR.

Ostrovski, G., Bellemare, M. G., van den Oord, A., and

Munos, R. (2017). Count-based exploration with neu-

ral density models. In Proceedings of the 34th Inter-

national Conference on Machine Learning - Volume

70, ICML’17, page 2721–2730. JMLR.org.

Pathak, D., Agrawal, P., Efros, A. A., and Darrell, T. (2017).

Curiosity-driven exploration by self-supervised pre-

diction. In Proceedings of the 34th International Con-

ference on Machine Learning - Volume 70, ICML’17,

page 2778–2787. JMLR.org.

Pathak, D., Gandhi, D., and Gupta, A. (2019). Self-

supervised exploration via disagreement. In ICML.

Schlegl, T., Seeb

ock, P., Waldstein, S., Schmidt-Erfurth,

U., and Langs, G. (2017). Unsupervised anomaly de-

tection with generative adversarial networks to guide

marker discovery. pages 146–157.

Schlegl, T., Seeb

ock, P., Waldstein, S. M., Langs, G., and

Schmidt-Erfurth, U. (2019). f-anogan: Fast unsuper-

vised anomaly detection with generative adversarial

networks. Medical Image Analysis, 54:30–44.

Schmidhuber, J. (1991). Curious model-building control

systems. In [Proceedings] 1991 IEEE International

Joint Conference on Neural Networks, pages 1458–

1463 vol.2.

Stadie, B. C., Levine, S., and Abbeel, P. (2015). Incentiviz-

ing exploration in reinforcement learning with deep

predictive models. CoRR, abs/1507.00814.

Sutton, R. S. and Barto, A. G. (2018). Reinforcement Learn-

ing: An Introduction. The MIT Press, second edition.

Tang, H., Houthooft, R., Foote, D., Stooke, A., Chen, X.,

Duan, Y., Schulman, J., De Turck, F., and Abbeel,

P. (2017). #exploration: A study of count-based ex-

ploration for deep reinforcement learning. In Pro-

ceedings of the 31st International Conference on Neu-

ral Information Processing Systems, NIPS’17, page

2750–2759, Red Hook, NY, USA. Curran Associates

Inc.

Zhao, R. and Tresp, V. (2019). Curiosity-driven expe-

rience prioritization via density estimation. CoRR,

abs/1902.08039.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

272