Narrative Economics of the Racetrack: An Agent-Based Model of

Opinion Dynamics in In-play Betting on a Sports Betting Exchange

Rasa Guzelyte

and Dave Cliff

Department of Computer Science, University of Bristol, Bristol BS8 1UB, U.K.

Keywords:

Agent-Based Model, Betting Exchange, Opinion Dynamics, Track-racing, Narrative Economics.

Abstract:

We present ﬁrst results from a new agent-based model (ABM) of a sports-betting exchange (such as those op-

erated by BetFair, BetDdaq, and SMarkets, among other companies) in which each agent holds a dynamically-

varying opinion about some uncertain future event (such as which competitor will win a particular horse race)

and in which all agents interact with the betting exchange to ﬁnd counterparties holding an opposing view

with whom they can then enter into a bet with. We extend methods from Opinion Dynamics (OD) research to

give each agent an opinion at any particular time which is inﬂuenced partially by local interactions with other

agents (as is common in the OD literature), partially by globally available information (as published to all by

the betting exchange) and partially by the progressive reduction in uncertainty in the system (i.e., eventually

all agents know which horse has won the race). Our work here is motivated by the prize-winning ICAART2021

paper of Lomas & Cliff, who integrated OD methods with ABMs of ﬁnancial markets to explore issues in Nar-

rative Economics, an approach recently proposed and popularised by Nobel Laureate Robert Shiller, but here

we explore a signiﬁcantly different type of market: a betting market (which has strong similarities to a ﬁnan-

cial market for tradeable derivative contracts such as futures or options). The novel contributions of this paper

are centred on the extension of OD methods to situations in which there is a mix of local and global inﬂuence,

and in which uncertainty progressively reduces to zero. We present results from our initial proof-of-concept

implementation. The Python source-code for our ABM is freely available on Github for other researchers to

replicate and extend the work reported here.

1 INTRODUCTION

In recent years Nobel Laureate Robert Shiller has in-

troduced and popularised the concept of Narrative

Economics (Shiller, 2017; Shiller, 2019), where eco-

nomic phenomena that would otherwise be hard to

explain using the tools of traditional economics are

explained instead with reference to the narratives, the

stories, that economic agents believe and tell them-

selves and each other about the nature of the eco-

nomic system that they are acting within: inter alia,

Shiller uses this to shed insightful light on the other-

wise hard-to-understand stratospheric rise in value of

cryptocurrencies such as Bitcoin.

At ICAART2021 the prize for Best Paper was

awarded to Lomas & Cliff for their work on a novel

agent-based model (ABM) of narrative economics

in a contemporary electronic ﬁnancial market (Lo-

mas, 2020; Lomas and Cliff, 2021) which took meth-

https://orcid.org/0000-0002-1306-7680

https://orcid.org/0000-0003-3822-9364

ods developed in the research literature on Opin-

ion Dynamics (OD) and integrated them with long-

established agent-based models of trader-agents in-

teracting within an accurate model of a contempo-

rary electronic ﬁnancial exchange such as Nasdaq or

NYSE. Lomas & Cliff argued that Shiller’s concept

of a narrative can be nothing more than an opinion

put into words, thereby justifying the link with OD

research; their study of opinionated agents trading in

a ﬁnancial market enabled empirical ABM studies of

narrative economics, because the opinions held by the

trader-agents affected the prices that they quoted in

the market; by deliberately injecting positive or neg-

ative narratives/opinions into the population and al-

lowing them to spread via speciﬁc OD models, the

effects of such changes in narrative on the subsequent

dynamics of prices in the markets could be studied.

In this paper we present ﬁrst results from our

newly-developed ABM which is inspired by and com-

plementary to that of Lomas & Cliff. Like Lomas

& Cliff, we study populations of opinionated agents

Guzelyte, R. and Cliff, D.

Narrative Economics of the Racetrack: An Agent-Based Model of Opinion Dynamics in In-play Betting on a Sports Betting Exchange.

DOI: 10.5220/0010834800003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 1, pages 225-236

ISBN: 978-989-758-547-0; ISSN: 2184-433X

225

that interact with one another via an exchange, how-

ever in our research the exchange is not a ﬁnancial

exchange, but is instead a betting exchange. Betting

exchanges, an innovation from the dot-com boom of

the late 1990s, have been a massive disruptor of the

global betting/bookmaking industry over the past two

decades. The primary innovator in this space was

the British company called Betfair, whose founders

recognised that just as a ﬁnancial exchange acts as

a platform that enables traders to seek and identify

potential counter-parties to trade with (i.e., the ex-

change matches buyers to sellers, and sellers to buy-

ers), so the same technology could be used to enable

bettors to seek and identify potential counter-parties

to a bet (i.e., the exchange matches bettors who want

to bet that some event E will happen, to bettors who

want to bet that E will not happen). The development

of high-technology online betting exchanges enabled

further innovation, introducing a new type of betting

that would have been difﬁcult or impracticable to im-

plement without computerised technology: speciﬁ-

cally, betting exchanges developed the capability to

offer so-called in-play (or in-game or in-race) betting,

where bettors can continue to bet on the outcome of

an event such as a horse-race after it has started, with

betting continuing potentially right up until the mo-

ment that the event ends and the winner is known.

As with the work of Lomas & Cliff, we use estab-

lished methods from the OD literature to give change-

able opinions to the agents in our ABM, but our

agents are opinionated bettors rather than Lomas &

Cliff’s opinionated traders. To do this, we have used

a newly-developed ABM of a betting exchange with

in-play betting on track-racing events such as horse-

races or sports-car races. This model is the open-

source Bristol Betting Exchange (BBE) described by

(Cliff, 2021; Cliff et al., 2021), various implementa-

tions of which are freely available on GitHub. BBE

offers a minimal abstract simulation of a track-race

event, sufﬁcient to make the dynamics of the simu-

lated betting exchange interestingly realistic, and in-

cludes a base set of types of different betting strate-

gies: bettor-agents can each be instantiated with one

of these strategies, which vary in their degree of ra-

tionality and in their accuracy of predicting the ﬁnal

outcome of the race.

The behavior of human bettors, as individuals and

in aggregate (i.e., as populations of bettors) has long

been studied by economists and psychologists inter-

ested in how we make economic decisions in situa-

tions of risk and uncertainty. An extensive literature

survey is presented in (Cliff, 2021) which reveals that,

to the best of our knowledge, the work we report here

is the ﬁrst ever ABM exploration of narrative eco-

nomics and opinion dynamics in a betting context.

In our model, over the duration of any one experi-

ment, each agent interacts with some number of other

agents in the population, with each atomic event being

a pairwise interaction between two agents. When two

agents (denoted here as A1 and A2) interact, the opin-

ion of A1 might be altered in response to the opin-

ion of A2, and/or the opinion of A2 might alter in re-

sponse to the opinion of A1. Whether the opinions of

A1 and/or A2 alter at all, and how much they change

by if they do, depends on the particular OD model in

use. This approach, of agents privately communicat-

ing with one another in pairs and their opinions pos-

sibly altering in response, is entirely standard within

the OD literature: indeed, in the vast majority of OD

papers, that is all that is studied. The link between

this mainstream style of OD and narrative economics

was established by (Lomas and Cliff, 2021) to which

the reader is referred for further details. Because in

this paper we move beyond the mainstream OD ap-

proach, we will denote this aspect of the OD model in

our system as the local opinions for each bettor: that

is, this inﬂuence on the bettor’s opinion comes from

local interactions with other bettors. However, in our

model this is not the only inﬂuence.

In real life, we might meet a friend for a chat over

morning coffee, and our friend might tell us her hot tip

for which horse is going to win a race tomorrow; in

the course of the rest of the day, we might meet other

people and pass on our friend’s tip to them: in the

course of these interactions, peoples’ opinions about

the outcome of tomorrow’s race are altered via their

private local interactions. However, surely this is not

the only factor of signiﬁcance. There are two other

additional factors that we model here.

The ﬁrst additional factor is one that we refer to

as the global opinion available to an individual bettor.

In contrast to tips passed among friends, anyone who

looks at the betting exchange’s real-time information

about the market for tomorrow’s horse-race can read-

ily see the aggregated opinions of very large numbers

of bettors, each of whom is sufﬁciently sure of their

opinions that they have put money down, i.e. paid a

stake for their bet into the exchange, in the expecta-

tion that their personal opinion is correct. In this way,

an individual bettor’s opinion can be inﬂuenced by the

combined opinions of everyone who has placed a bet

in the exchange’s market for that event, i.e. the over-

all market sentiment. If our friend’s hot tip is that

horse H1 will win the race, but currently the vast ma-

jority of bets, or of total money wagered, is indicating

a common belief that a different horse H2 will instead

win, we may well come to doubt the wisdom of our

tipster friend, and so in this way our opinion can be

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

226

changed to some extent (maybe more, maybe less) by

the global information available to us.

The second additional factor is speciﬁc to the na-

ture of gambling (and is shared in the ﬁnancial mar-

kets for tradable ﬁnancial derivatives such as futures

and options contracts), and that is the ﬁnality of the

outcome of the event becoming known: eventually,

one horse or another crosses the ﬁnishing line ﬁrst,

and the race is over, and the winner is known. Our

opinion of which horse will win might change from

time to time in the run-up to the start of the race, as

a consequence of the effects of local and global opin-

ion inﬂuences, but once the race is actually running,

once it is in-play, we can see for ourselves how each

horse is doing: our opinions of which horse will win

could change much faster during the race itself, and

yet eventually all rational observers of the race con-

verge on the same opinion of which horse will actu-

ally win, because at the inﬁnitesimal moment before

the ﬁrst horse crosses the ﬁnish-line all rational ob-

servers must hold the opinion that the lead horse will

in fact win the race.

We refer to this as the inﬂu-

ence of the event on the agents’ opinion, or simply

the event-opinion.

The novel contributions of this paper are centred

on the extension of OD methods to situations in which

there is a mix of local and global inﬂuence, and in

which uncertainty progressively reduces to zero. Our

focus here is solely on the opinion dynamics of in-

play betting. Source-code for our ABM has been

freely released on Github for other researchers to

replicate and extend the work reported here.

Fur-

ther discussion, and extensive additional results are

available in (Guzelyte, 2021), from which this paper

is abridged.

In Section 2 we give more details of the back-

ground of this work. Section 3 reviews the few

papers in the OD literature that are relevant to

the issues that we face in our ABM (the num-

ber of papers is small because the vast majority of

BBE ignores the real-world phenomena of photo-

ﬁnishes and dead-heats: in our ABM we know the position

of the competitors, their distances along the track, to arbi-

trary spatial accuracy and no two competitors can ever be at

exactly the same position.

See: https://github.com/Guzelyte/TBBE OD.

Both authors worked on this research in the UK where

gambling as described herein is entirely legal, and where

the major betting-exchange operators pay corporate taxes to

the government, which contribute to the funds available for

enabling research such as this to be conducted in publicly-

funded universities. We recognise that in other countries,

in other cultures, gambling is viewed as immoral and/or is

illegal, and that readers from such backgrounds might ﬁnd

the morality of the work described here to be questionable.

work in the OD literature seems to be focused on

agents whose opinions are never objectively evalu-

able as either true or false). Section 4 explains our

OD model of bettor-agents with opinions dynami-

cally inﬂuenced by other agents’ locally-expressed

and globally-expressed opinions, and by the event-

opinion. After that, we brieﬂy show illustrative results

from our system in Section 5 and then draw conclu-

sions in Section 6.

2 BACKGROUND

2.1 Betting and Exchanges

In 2020 the global gambling industry had reportedly

reached a value of US$67billion and was projected to

more than double by 2028 (Fortune, 2021). While

the growth of the industry is largely driven by the

general increase in popularity of digital technologies

and its associated beneﬁts, the COVID-19 pandemic

has notably accelerated the adoption of internet-based

gambling with government-mandated restrictions and

temporary closures of non-essential services includ-

ing casinos, betting parlours and other ofﬂine gam-

bling sites. At the time of writing this paper, gambling

in the USA is being signiﬁcantly liberalised, with re-

strictions being lifted and new markets opening up.

The introduction of electronic betting exchanges

in the late 1990s proved to be a major disruptor for

the global betting industry, which previously relied al-

most exclusively on traditional bookmaking. Unlike

bookmakers, a betting exchange does not take the op-

posing view of customers, but rather acts as a facil-

itator platform that aggregates all bets placed on an

event and efﬁciently matches bettors with competing

views on the outcome, in exchange for some commis-

sion fee (typically fees are charged only to winners of

bets). The way betting exchanges operate is closely

analogous to stock exchanges, where instead of buy-

ing and selling stocks, people can place bets that are

referred to either as backs (wagers that some outcome

of an event will happen) or lays (wagers that an event-

outcome will not happen). In much the same way that

a ﬁnancial exchange publishes a global (available to

all) real-time display of aggregated and anonymised

orders currently sat at the exchange and awaiting ac-

ceptance by a counterparty, so betting exchange plat-

forms also provide customers with a public summary

of placed bets over all available outcomes – this is

referred to within the gambling industry as the mar-

ket for that event. In addition to the introduction of

in-play betting, described in Section 1, another im-

portant innovation enabled by electronic betting ex-

Narrative Economics of the Racetrack: An Agent-Based Model of Opinion Dynamics in In-play Betting on a Sports Betting Exchange

227

changes allows bettors to gamble on the movement of

odds and changes in the distribution of stake-money

for a particular event.

Notably, most betting exchanges offer their users

charge-free API access, which can be utilised for cre-

ating custom automated betting strategies. Given his-

toric time-series data on different event markets, cus-

tomers may apply Artiﬁcial Intelligence (AI) and Ma-

chine Learning (ML) approaches for developing and

testing various approaches for proﬁtable future bet-

ting. Methods that are commonly and successfully

used for similar tasks like identifying trading signals

in ﬁnancial markets such as Deep Learning Neural

Networks (see e.g. (Goodfellow et al., 2017)) re-

quire access to large quantities of training data to

learn from. Such data is available from some betting

exchanges, but it is usually offered at a premium fee

and, for some machine learning methods, even if all

of the data held by the exchange was available at zero

cost, there may simply be insufﬁcient data to effec-

tively train a large network. That is, given the relative

recency of the introduction of betting exchanges, the

right kind of data can be unattainable at any price, due

to the massive volumes required.

Shortages of training data are not uncommon in

contemporary ML, and in various application areas

the introduction of synthetic data generators (SDGs)

has proven to be a successful remedy. In brief, an

SDG is a source of ML training data that is synthe-

sized, but which is statistically such a close match

to the relevant real-world data-sets that from the per-

spective of the ML system the fact that the data is syn-

thetic makes no difference to the outcome. For further

details and examples of SDGs, see (El Emam et al.,

2021; Cao et al., 2021; Wood et al., 2021). The open-

source Bristol Betting Exchange (BBE), described in

the next section, is a recently-introduced SDG for in-

play betting-exchange data, which we use here as the

platform for our experiments in studying opinion dy-

namics in populations of bettors.

2.2 BBE

BBE was introduced in a paper by Cliff (Cliff, 2021),

where it is classed as a constructive SDG model, i.e.

one which is intended to generate data-sets that pre-

serve the original data’s key statistical features, and

for which the ground-truths are known and explain-

able. This means that in addition to providing de-

sired quantities of synthetic betting data it also sim-

ulates the sports event that generated those particular

betting outcomes. Currently, BBE consists of simu-

lated track-racing (e.g., horse racing) events only and

includes the betting-exchange matching-engine and a

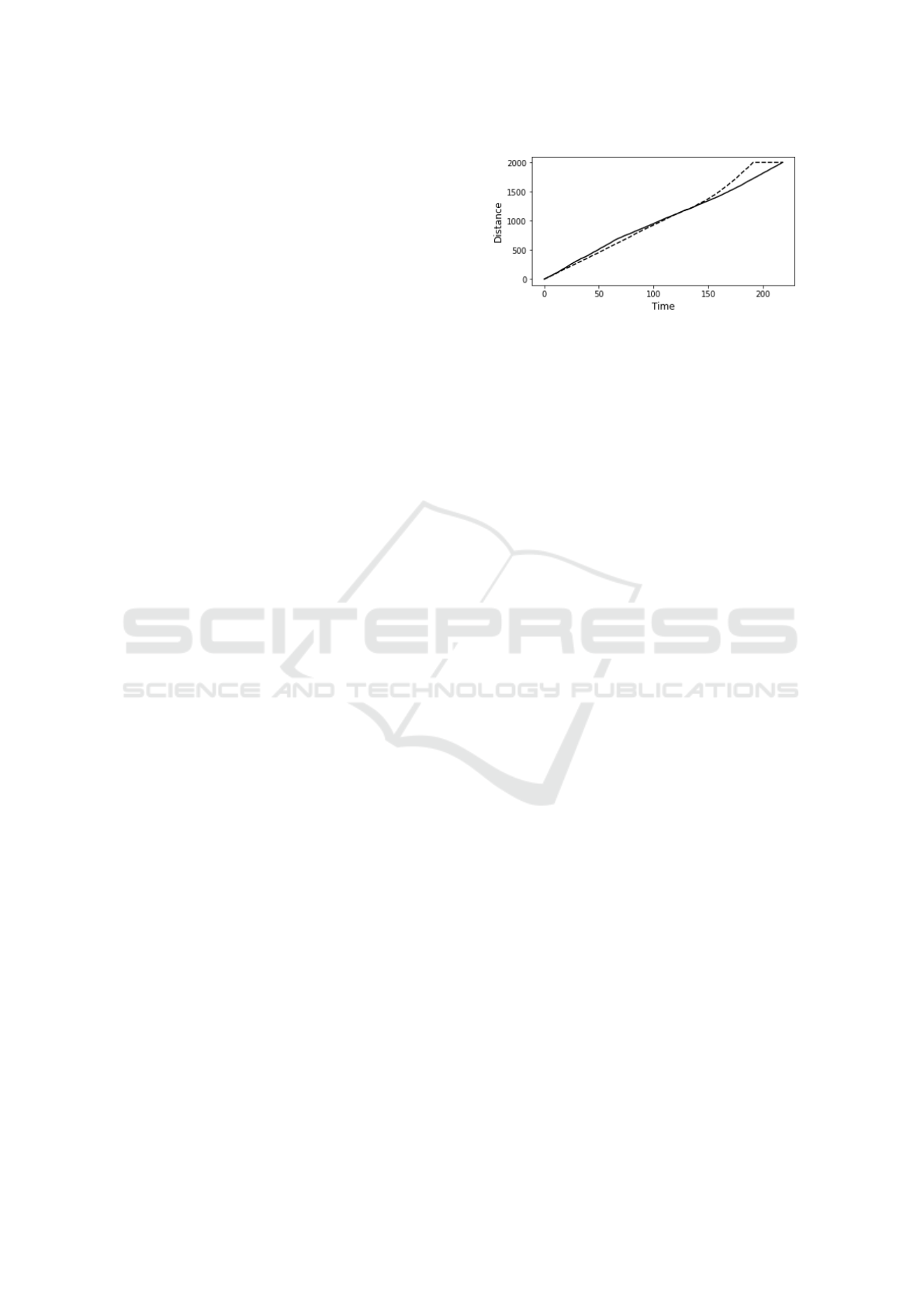
Figure 1: Competitor distance-time (d

/t) graph of a 2000m

two-competitor race. Competitor C0 (dashed line) wins the

race, reaching the race-distance ﬁrst, and then ceases to

move (creating the horizontal trace at the end of its d

plot), while competitor C1 (solid line) initial leads the race

but eventually comes in second place.

population of agent-based bettors that can post backs

and lays on the exchange’s market for that event.

The rationale for, and architecture of, BBE are docu-

mented at length in (Cliff, 2021), to which the reader

is referred for full details.

BBE models some number of competitors (e.g.,

horses) racing along a track that is topologically lin-

ear, so that the primary variable of concern for any

one competitor is how far along the track it has trav-

elled: once that distance exceeds the race-distance,

that competitor has crossed the ﬁnish-line. We use

(t) to denote the distance travelled along the race-

track by competitor c at time t. Each competitor is

modelled as a point on the line (i.e.. it has no spatial

extent) but the speed at which a competitor C1 moves

forward can be affected by the distance between it and

any nearby competitors in front (which may block

C1, slowing it down) and behind (which may “spur

on” C1, causing it to deliver a burst of speed as they

close in). Figure 1 visualises a two-horse race as a

plot of distance over time (d

/t) for each of the com-

petitors, but this wastes a lot of whitespace. Fig-

ure 2 shows a different projection of the same race-

data, in which all competitor’s race-distances at each

timestep of the simulated race are treated as a cloud of

data-points, and the linear regression line is calculated

for that cloud: the linear-regression line is then sub-

tracted from each competitor’s d

/t data, to show the

residual distance (RD); in the RD plot the moment-

by-moment changes in relative distance between the

competitors are much easier to see. The coincident

nature of the plots for C0 and C1 in Figure 2 around

t = 100 to t = 110 show C0 being blocked by C1,

something that is much less clear in Figure 1.

A variety of simple types of BBE bettor-agent

strategy are described by (Cliff, 2021): these vary in

their sophistication, and in the accuracy of their pre-

dictions. The simplest strategy of all is the Zero In-

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

228

Figure 2: Competitor residual distance (RD) graph of the

same 2000m two-competitor race as shown in Figure 1. The

residual distances are calculated as the difference between

each competitor’s distance at t and the linear regression

(LR) line at t where the LR line is created ex post from all

competitors’ positions for each time-step in the race. This

visualisation method better illustrates ﬁne-grained changes

in relative distance between the competitors, for instance

the period where C0 (dashed line) is blocked by C1 (solid

line) from t = 115 to t = 135 is much clearer in this plot.

telligence (ZI) bettor, which selects one competitor

at random, using a uniform distribution (i.e., so the

choice of competitor is equiprobable over the set of

competitors for a particular race), and sticks with that

choice for the rest of the race. ZI is very simple to im-

plement, and is very often wrong. At the other end

of the BBE spectrum is a Rational Predictor strat-

egy known as RP(d), because this strategy makes d

attempts at simulating the race, given all available in-

formation, and then estimates each competitor’s prob-

ability of winning the race using simple frequentist

statistics (e.g., if d = 20 and competitor C0 wins the

race in 3 of the 20 simulations, then the RP(d) bet-

tor’s estimate of C0’s probability of winning the race

is 3/20=15%). For in-play betting, RP(d) bettors can

re-calculate their d simulations at any time that the

race is in progress, simulating the race forward in

time from its current state, and magically taking no

simulation-time at all to do so – in this sense, they

are as wholly unrealistic as the assumptions of ratio-

nality in most economist’s models prior to the reali-

sations that actual human rationality is bounded, and

that much of human behavior is irrational.

A follow-up paper (Cliff et al., 2021) sum-

marises three separate BBE implementations using

varying levels of technical complexity developed

by (Hawkins, 2021), (Keen, 2021), and (Lau-Soto,

2021), and each of these presented their ﬁrst empir-

ical results. In the work we report here, we adapted

and extended the (Keen, 2021) BBE implementation,

integrating OD for bettor-agents.

2.3 Bettor Opinion Dynamics

Cliff’s (2021) paper that ﬁrst introduced the BBE plat-

form proposes that such interactive agent-based simu-

lated betting environments are well-suited as test-beds

and experimentation platforms for studying narrative

economics as a form of opinion dynamics (OD); the

links from OD to Shiller’s narrative economics were

ﬁrst argued for by (Lomas and Cliff, 2021). OD is a

socio-physics sub-ﬁeld mainly aimed at understand-

ing the way group opinions are formed, how they

evolve, and whether a consensus is reached. One

novel contribution of our paper here is that it describes

the ﬁrst attempt to integrate opinion dynamics into

the BBE platform by implementing a way for bet-

tors to record, share and update their sentiment about

the event market (an opinion about whether a speciﬁc

competitor is going to win the race or not). Specif-

ically, six classes of agent bettors with zero or min-

imal levels of intelligence, which are present in the

BBE platform, get integrated with a way to initiate

independent opinions for each agent and update those

initial opinions using one or more of three previously-

established OD models: Bounded Conﬁdence (BC)

(Krause, 2000; Hegselmann and Krause, 2002); Rel-

ative Agreement (RA) (Deffuant et al., 2002; Mead-

ows and Cliff, 2012) and Relative Disagreement (RD)

(Meadows and Cliff, 2013).

These three models have previously been ex-

plored in the OD literature mainly for understand-

ing how groups reach consensus under various sce-

narios, which ignores any situations where a ground

truth opinion is ultimately established and shared with

the population: much of the OD literature seems cu-

riously ﬁxated on the dynamics of opinions in situ-

ations where the opinions of the agents are entirely

subjective, and can never be proven true or false, right

or wrong. Certainly there are some important aspects

of real-world opinions, such as politics or religion, or

which is the greatest of all time football team, etc,

where there is no objective test that can be applied to

establish truth or falsehood. But it seems strange that

so little work has been published in the OD literature

in which the opinions are actually about something

tangible, opinions that can subsequently be proven

to be right or wrong. In addition, the existing OD

models allow the population of agents to converge to

multiple ﬁnal opinions, forming a different consen-

sus shared within each group. Since in our track-

race events at the end of each race a single unique

winner is almost always established, OD models for

bettors have to take this into consideration. For ex-

ample, during in-play betting for horse-racing, as the

race progresses bettors’ opinions on which horse is

Narrative Economics of the Racetrack: An Agent-Based Model of Opinion Dynamics in In-play Betting on a Sports Betting Exchange

229

going to win will change based on the observable evo-

lution of the race. In every case, as the race comes to

an end, each individual bettor’s opinion should con-

verge to the same ground truth that one particular

horse won and that none of the other horses did. Be-

cause of these considerations, for our work the BC,

RA and RD models are used only to represent the in-

ﬂuence on opinions of private bettor-to-bettor conver-

sations, the local opinion factor. Additional factors

affecting bettor opinions are introduced to create our

novel OD model that tends towards the ﬁnal ground

truth (the winner being known) with varying levels of

conﬁdence given the information available to the bet-

tor at that time. In our survey of the OD literature

we have found only one related idea, ﬁrst explored

by (Hegselmann and Krause, 2002), which involved

the introduction of truth-seeker agents. A full review

of literature that discusses opinion dynamics with the

presence of truth is included in Section 3.

Once the mechanism for tracking bettor sentiment

is established, the integrated BBE environment is then

used to explore the evolution of bettor-agent opin-

ion dynamics for various speciﬁc event scenarios and

bettor populations. The controlled and reproducible

nature of BBE simulations allows the exploration of

how different bettor groups react in the same event

market (i.e., keeping the track-race evolution con-

stant) and how the presence of other bettor classes

inﬂuence the opinion dynamics.

3 RELATED WORK

Space constraints prevent us from providing a com-

prehensive review of all relevant literature: for in-

depth reviews that form the background to our work

reported here, see (Cliff, 2021) and (Guzelyte, 2021);

and for an extensive review of opinion dynamics

research see (Dong et al., 2018), which cites 157

sources and the text of which does not include the

word “truth” even once. Here we focus on review-

ing the small number of papers in the large canon of

OD work that deals with truth-seeking agents.

3.1 Ground Truth in Opinion Dynamics

The well-known opinion dynamics models provide a

reasonable approach for exploring consensus and po-

larisation cases among voters or followers of religious

faiths, where opinions are personal, subjective, and

largely unaffected by references to objective truths.

These models, however, do not consider the presence

of a ground truth opinion in their logic. Speciﬁcally,

the BC, RA and RD models have no mechanism that

would represent the truth or falsehood of an opinion,

which means that while the agents will converge to

some ﬁnal opinion or multiple fragmented opinions,

it cannot be used to study social exchange processes

that involve discussions about a known fact.

To explore the opinion dynamics of bettors, the

concept of ground truth is relevant because each BBE

event that is bet upon has a deﬁned end-time when

some winner is announced. Regardless of what each

individual bettor thought the winner would be at the

start, as the race progresses all bettors have to update

their opinions incorporating new information about

the advancing race and then as the winner crosses the

ﬁnish line ﬁnish the population of agents should all

share the same single opinion, the true opinion, about

who the winner is. Below is a brief overview of aca-

demic literature that extends opinion dynamics mod-

els to include a notion of truth.

3.2 Truth-seeking Agents

Hegselmann and Krause (Hegselmann et al., 2006)

extended and modiﬁed the BC model by introducing

a new type of truth-seeking agent. They analyse the

chances of agents reaching the truth under a cognitive

division of labour, where some number of individuals

in the population are truth seekers. To account for the

true opinion, the extended BC model introduces two

parameters: the true opinion T ∈ [0,1] ∈ R; and α

the

strength of “attraction” to the truth for i

agent. This

gives the following equation for the Hegselmann-

Krause Bounded Conﬁdence (HKBC) truth seekers in

a population of N

agents:

(t + 1) = α

T + (1 − α

) f

(t));1 ≤ i ≤ N

. (1)

Here, the opinion of agent i is given by two compo-

nents: α

T , the objective component (how attracted

the agent is to truth); and (1 − α

), the social compo-

nent (how easily the agent is socially inﬂuenced from

truth) given f

as the function of current opinion pro-

ﬁle x

(t). When α

= 0 Equation 1 gives the origi-

nal BC model speciﬁcation (Krause, 2000), where the

agent’s opinions are updated following only the so-

cial process and the truth does not play any role. With

reference to the terminology we have developed for

our model of OD in populations of bettors, HKBC’s

social component corresponds naturally to our local

component; and our global component corresponds

to something conceptually part-way between HKBC’s

objective (1 − α

) and social α

T .

HKBC assumes that the truth T is one and only

one, which is a reasonable assumption for modelling

our agent bettors as there is only ever one winner of

a race in BBE. HKBC also assumes that truth is cer-

tain from the outset and does not change through time,

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

230

which fares poorly in any attempt to map HKBC onto

a betting event (i.e., an opinion about who will be the

winner of the race is eventually either true or false;

a bettor might plausibly hold a true opinion about

which competitor has the highest likelihood of win-

ning at current time in the race given all currently

available information). So, clearly our chosen prob-

lem domain stretches HKBC beyond breaking point,

and something better is needed.

(Malarz, 2006) extended the RA model (Deffuant

et al., 2002) using the same logic as HKBC by in-

corporating truth and showed that quantitatively both

models give the same results. HKBC was also later re-

visited by (Liu and Mo, 2018), who explored the role

that information noise plays in populations with truth-

seeking agents, and concluded that small amounts of

noise help agents achieve the truth while higher noise

obstructs the truth-seeking process.

3.3 Truth Persuasion

(Friedkin and Bullo, 2017) explored how truth

is reached during intellectual group debates, and

showed that for intellectual debates with some true

opinion, a deeper level of persuasion is associated

with truth statements. The authors argue that those

agents that hold the factually correct opinion will as-

sert a higher level of persuasion over other agents

during discussions where agents share not only their

opinions but also the underpinning calculative logic

of those opinions. This was shown to be true for de-

centralised populations split into independent groups

with one-true versus many-false calculative logics

present, given that individuals understand the rele-

vant science and mathematics for that logic. How-

ever, Friedkin and Bullo conclude that the truth does

not win when large-enough social movements elevate

the presence of some false calculative logic, due to

majority inﬂuence. (Tsang et al., 2015) also proposes

that a higher-level of persuasion is present with truth

statements, attributing this to the power of the righ-

teous argument: “it is easier to convince someone of

the truth than the falsehood”.

4 OPINIONATED BETTORS

4.1 A Three-factor OD Model

Earlier in this paper we introduced the distinction

between three inﬂuences on a bettor-agent’s overall

opinion: local, global and event. It is reasonable to

think that each of these factors would have a differ-

ent impact on individual bettors, that the bettors’ in-

dividual sensitivity to these inﬂuences would be het-

erogeneous. For example, some bettors might be very

susceptible to the conversations they are having with

other bettors about which competitor is likely to win,

while other bettors might be more easily swayed by a

change in the overall market sentiment about the com-

petitors (e.g., by observing a sudden increase in back

odds for a competitor).

For simplicity in the explanation that follows, we

talk in terms of a single bettor b forming an overall

opinion about a competitor of interest, a single spe-

ciﬁc competitor in the race. The model we describe

here in those terms generalises naturally to multiple

bettors each forming an opinion on multiple com-

petitors. Also, note that one bettor’s overall opinion

about a speciﬁc competitor of interest can intuitively

be viewed as their estimated probability of that com-

petitor winning the event (see (Guzelyte, 2021) for

further explanation).

In our model the opinion of bettor b at time t is

denoted by o

(t) and is a weighted linear combination

of all three elements of opinion-inﬂuence: the local,

denoted by Λ

(t) ∈ [0, 1] ∈ R; the global, denoted by

(t) ∈ [0, 1] ∈ R; and the inﬂuence of the event itself,

denoted by E(t) ∈ [0,1] ∈ R.

The overall opinion of bettor b at time t + 1 can

then be deﬁned as follows:

(t + 1) = α

b,1

(t)Λ

(t) +

b,2

(t)Γ

(t) +

b,3

(t)E(t)

Where the α

b,i

(t) ∈ [0,1] ∈ R; i ∈ {1,2,3} are time-

varying weights that the bettor places on their local,

global and event opinion-inﬂuences at time t respec-

tively, such that:

∑

i=1

b,i

(t) = 1.

4.2 Event Opinion

Unlike local and global impact on overall opinion,

which could stay consistent throughout the race, the

event opinion element is expected to have an increas-

ing impact on bettor’s opinions as the event proceeds

towards its ending. This is because any distance dif-

ferences between competitors become more material

to the outcome of the race as it is coming to the end.

As such, in our model the impact of event opinion

on overall opinion is increasing throughout the race.

Since at time=0 the race has not yet started and at ﬁn-

ish time a winner is established, the impact of event

opinion should start at 0 and reach 1 (100% of over-

all opinion), which can be interpreted as every bet-

tor’s opinion at the end of the game matching the

actual outcome of the game. As the weight α

in-

creases, the ratio between α

and α

could stay the

Narrative Economics of the Racetrack: An Agent-Based Model of Opinion Dynamics in In-play Betting on a Sports Betting Exchange

231

same or vary for each bettor during the race. In

the work reported here the ratio between local and

global weights (α

and α

) is kept the same, while

the event opinion weight (α

) increases according to

3,b

(t) = d

max

(t)/D

∗

, where D

∗

is the total length of

the race-track and:

max

(t) = max(d

(t) : ∀c) (2)

i.e., d

max

(t) is the distance of the competitor in the

lead at time t. This gives α

(0) = 0 and α

∗

) =

1, where T

∗

is the time at which the ﬁrst competitor

crosses the ﬁnish line, i.e. for which d

max

∗

) = D

∗

4.3 Global Opinion

The global element of the overall bettor’s opinion

models the extent to which they are inﬂuenced by the

overall market sentiment. Betting exchanges offer all

bettors publicly accessible information on the aggre-

gated odds at which each of the competitors are being

backed and laid at any given time. Since the over-

all opinion of the bettor can intuitively be viewed as

their estimated probability for a competitor of interest

to win, the global opinion element could be deﬁned

as the market’s estimated probability of the competi-

tor winning as inferred by the bettor. Given that each

bettor has access to the best (lowest) odds at which

each of the competitors is being backed, their global

opinion can be deﬁned as follows:

(t) =

bβ

(t)c

(3)

Where bβ

(t)c denotes the lowest back-odds offered

in the betting market for competitor c at time t. Since

all market participants will observe the same market

odds, the global opinion component of individual bet-

tor opinions will not vary per bettor.

4.4 Local Opinion

Local opinion represents a bettor-speciﬁc channel of

information that is private to them. In our model this

factor is split into two segments: the bettor’s default

strategy (i.e. how it forms an opinion in the absence

of any local OD interactions with other agents) and

the OD effects of private conversations with other

agents. Speciﬁcally, the bettors will engage in agent-

to-agent conversations about the competitor of inter-

est and update their opinions using one of the well-

established opinion dynamics models BC, RA, or RD

as discussed above, following the same logic as in the

opinionated traders introduced by (Lomas and Cliff,

2021). For increased realism, bettor-to-bettor con-

versations are set to be between two individual bet-

tors and the duration of any one conversation is some

number of seconds set by a random function, such that

the durations of all conversations are IID.

All opinionated bettors that we have experimented

with thus far have as their default strategy, their

default opinion-formation mechanism, the method

known as RP(d) introduced by (Cliff, 2021) and

described above in Section 2.2: this strategy uses

simple frequentist statistics to calculate probability

mass estimates over the space of possible outcomes

from d IID race-simulations. As this can be quite

computationally-intensive, an RP(d) bettor also in-

cludes a speciﬁcation of how frequently it is to up-

date its estimates: useful results can be had when

the updates occur once every few seconds, although

for more responsive bettors the frequency can be in-

creased, at the expense of overall simulation runtimes.

Therefore, our opinionated bettors have two lo-

cal opinion factors running in parallel: the conver-

sations (OD interactions) that run continuously, but

take a speciﬁed length of time to have an impact on

the local opinion; and the RP(d) repeated simulation

runs that impact the local opinion whenever new odds

are estimated. To describe the process of updating lo-

cal opinion of a bettor, two functions are introduced:

(t) for assigning the inﬂuence that update in strat-

egy has on local opinion and C

(t) for assigning the

inﬂuence that a conversation has on local opinion.

The inﬂuence of strategy on local opinion for bet-

tor b will be deﬁned by a strategy weight, denoted

by σ

. Given a strategy weight of 0, the bettor’s lo-

cal opinions will completely ignore any information

from strategy and represent only the impact of conver-

sations, while with strategy weight equal to 1, every

time the bettor updates their strategy, previous local

opinion is completely ignored and becomes equal to

strategy opinion. S

(t) for bettor b can therefore be

expressed as:

(t)

= σ

(t)

+ (1 − σ

)Λ

(t)

Where Γ

(t) is the lowest back-odds bβ

(t)c con-

verted into an opinion value, per Equation 3.

A conversation’s impact on local opinion will be

calculated using one of the opinion dynamics models,

either BC, RA, or RD as introduced in Section 2.3.

An example using the BC model is shown below for

bettors b1 and b2:

(t)

= wΛ

(t)

+ (1 − w)Λ

(t)

, (4)

s.t. Λ

(t)

− Λ

(t)

≥ δ, for δ deﬁned per the stan-

dard BC model.

The full process of updating local opinion using

functions S

(t) and C

(t) is then outlined in pseudo

code in Algorithm 1, in which U(r

min

max

) is used

to denote a random variable drawn from a uniform

distribution over the range [r

min

max

] ∈ R.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

232

Algorithm 1: Calculate local opinion

(t)

Require: t < T

∗

Ensure: 0 <= local opinion

(t)

<= 1

if t = 0 then

local opinion

(t)

← neutral opinion

n ← 1

← U(2, 6)

k ← 0

else

local opinion

(t)

← local opinion

(t − 1)

conversation end time ←

∑

if t = conversation end time then

local opinion

(t) ← C

(t)

n ← n + 1

← U(2, 6)

end if

if t = s × k then

local opinion

(t)

← S

(t)

k ← k + 1

end if

Where s is set time time interval for RP(d) strategy

refreshes, n is the index-count of the current conver-

sation, and r is the length of the current conversation.

The random generation of conversation length here is

limited to be between 2 and 6 seconds, however this

can be varied as appropriate.

4.4.1 Event Opinion, Revisited

The event-inﬂuence on the bettor’s overall opinion

models the bettor’s observation of the ongoing race

and their interpretation of how each of the competitors

is performing. Given the speed and distance position

of each of the competitors at time t of the race, an es-

timate of which competitor is most likely to win the

race can be derived. For simplicity, as a ﬁrst approxi-

mation, the event opinion is calculated as a function of

competitor c’s distance along the track at time t (i.e.,

(t)), time elapsed (i.e., t itself), and total length of

the race (denoted by D

∗

). Since the signiﬁcance of

differences between competitor distances at time t is

dependent on the total length of the race track, the

value of interest is the proportion of distance remain-

ing for each competitor at t; this value is squared to

introduce a nonlinear exaggeration of the differences

between the competitors as they are nearing the ﬁnish

line.

(t) =



∗

− d

(t)



The values of v

(t) for each competitor are then used

to determine the function for event opinion as the pro-

portion of all squared distances remaining by each of

Figure 3: Time-series from the opinionated bettors in the

population gambling on the race illustrated in Figures 1 and

2, showing the bettor’s opinion of competitor C0. Local

inﬂuence on opinions is updated using the Relative Agree-

ment model. Bettors are initialised with random variation

in their various weight coefﬁcients, giving rise to variation

in initial opinions, but as the race progresses, opinions con-

verge and the variance reduces, until the point where C0

crosses the ﬁnish-line, at which point all bettors hold the

identical (ground-truth opinion) that C0 is the winner.

the competitors from the total, as shown below:

(t) =

(t)

∑

c=1

(t)

The event opinion for each competitor is then de-

cided by using function f

(t) until the ﬁrst competitor

crosses the ﬁnish line. Once a winner is established,

the event opinion is equal to either 0 or 1 based on the

outcome of the race:

(t) =











(t), if d

max

(t) < D

∗

;

1, if d

(t) = d

max

(t) = D

∗

;

0, otherwise.

5 RESULTS

Here we present only a single set of illustrative re-

sults to demonstrate the rich opinion dynamics that

our ABM is able to exhibit: for extensive illustration

and discussion of this and several other related sets of

our results, see (Guzelyte, 2021).

Figures 1 and 2 showed a race over 2,000m, be-

tween two competitors C0 and C1, ﬁrst as a conven-

tional distance-time plot, and then as a residual dis-

tance plot, respectively. Figure 3 shows the time-

series for the opinions of each of the opinionated

bettors active on the betting exchange during the in-

play betting over the duration of this race, in the case

where C0 is the competitor of interest. As can be seen,

the spread of opinions tightens as the race progresses,

and when C0 crosses the ﬁnish line as the winner,

each bettor holds the same opinion, the ground-truth

provided by the event having been resolved.

Narrative Economics of the Racetrack: An Agent-Based Model of Opinion Dynamics in In-play Betting on a Sports Betting Exchange

233

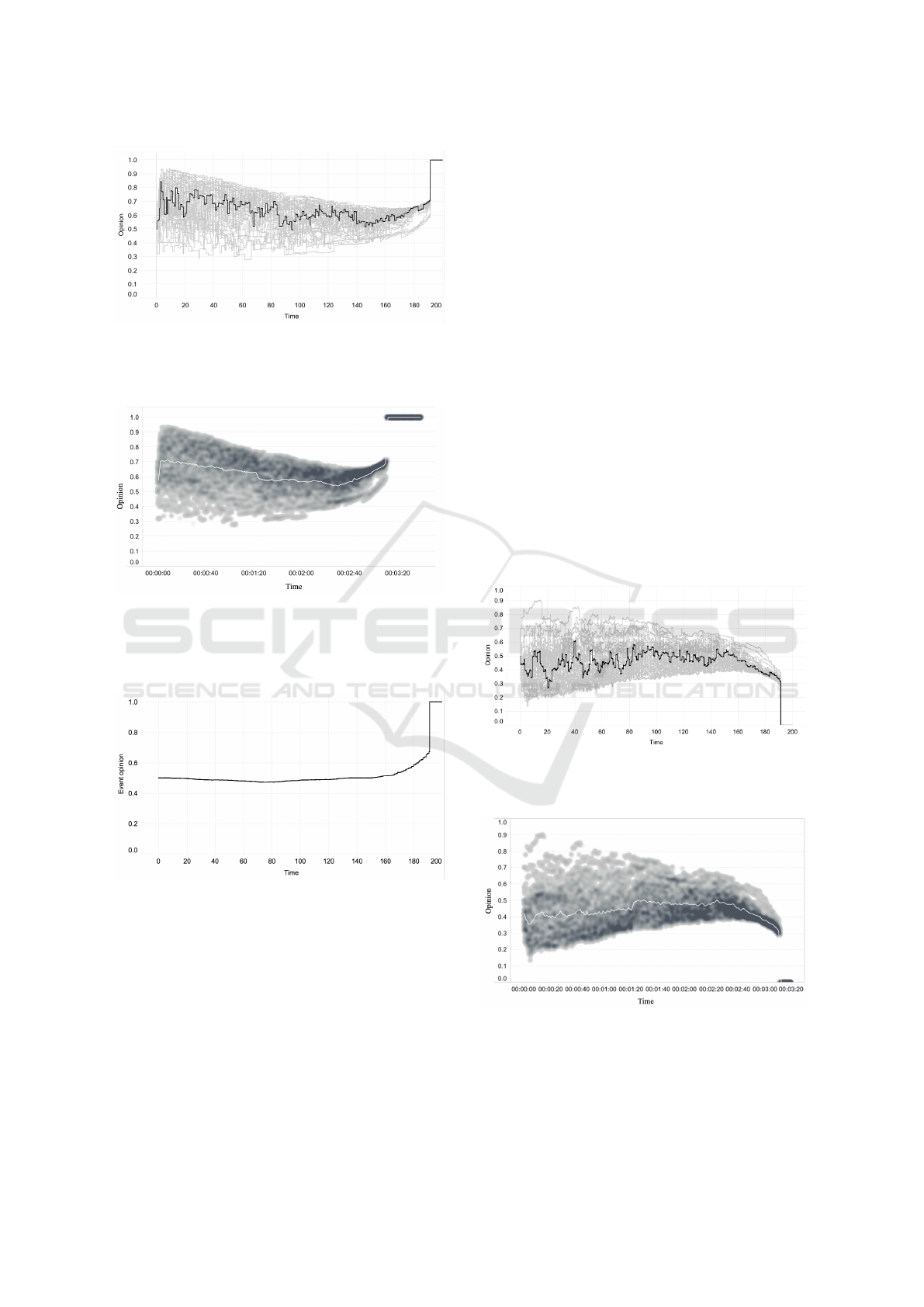
Figure 4: This plot shows the same set of time-series as

Figure 3, but with the temporal evolution of one randomly-

chosen bettor’s opinion over the duration of the race high-

lighted, for clarity.

Figure 5: Overall bettor opinions density plot for competitor

C0, a different projection of the data shown in Figure 3. The

population’s collective opinions are displayed as a gray-

scaled density plot over time, and a white line shows the

average opinion over time.

Figure 6: Event-opinion for competitor C0 over the dura-

tion of the race illustrated in Figures 1 and 2; see text for

discussion.

Figure 3 is something of a spaghetti-plot, with the

nature of an individual bettor’s opinion evolution over

the course of the event being obscured, and with no

clear indication of the central tendency of the popula-

tion. To remedy this, Figure 4 shows exactly the same

data as in Figure 3, but with the temporal evolution

of the opinion of a single randomly-chosen bettor

highlighted for clarity; and Figure 5 is the same data

as in Figure 3, as a grayscale density-plot and with the

population’s mean opinion value shown by the

pale line.

To help disentangle the spaghetti-plot of Figure 3,

in Figure 4 we highlight the opinion of a single ran-

domly chosen opinionated bettor from Figure 3. Fi-

nally, Figure 6 shows the event-opinion for C0 in this

race: for the ﬁrst half of the race this holds steady

at approximately 0.5, but once C0 pulls into the lead,

the event-opinion for C0 rises steadily until C0 actu-

ally crosses the ﬁnish line, at which point the event

opinion jumps to one.

For comparison, we can separately re-run exactly

the same race, in terms of the moment-by-moment po-

sitions of the competitors, and instead compute and

record the opinion dynamics in the population of bet-

tors when they are focused on C1 (who initially leads

the race, but is overtaken and ﬁnishes in second place)

as the competitor of interest. This requires a second

separate simulation session, because our ABM is cur-

rently conﬁgured to only ever record the bettors’ opin-

ions on a single speciﬁc competitor of interest. Fig-

ures 7 to 9 show a single bettor’s opinion on C1, a

plot of the population density and mean opinion for

C1, and the event-opinion for C1, respectively.

Figure 7: Temporal evolution of whole-population (gray)

and single-bettor opinion (black) for the race of Figures 1

and 2, re-simulated with C1 as the competitor of interest.

Figure 8: Population opinion density plot for competitor

C1, plotted as for Figure 8.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

234

Figure 9: Event-opinion for competitor C1 over the duration

of the race illustrated in Figures 1 and 2.

6 CONCLUSION

To the best of our knowledge, this paper is the ﬁrst to

describe the application of long-established opinion

dynamics (OD) models within an agent-based model

(ABM) of a contemporary sports-betting exchange.

Motivated by Shiller’s work on Narrative Economics,

and by Lomas & Cliff’s paper at ICAART2021, our

ABM serves as a platform for exploring the interplay

between the opinions that bettors hold about the out-

come of an event that they are betting on, where those

opinions can be expressed both locally (i.e., as nar-

ratives, as stories or statements, that the bettors pri-

vately tell each other about their belief in which out-

come will occur) and globally (i.e., as monetary bets

on speciﬁc outcomes, placed at the betting exchange,

and visible in aggregate and anonymised form to all

participants in the exchange’s ‘market’ for that event,

showing the distribution of bets over the space of pos-

sible outcomes for the event). If one bettor saying to

another “I am sure horse H1 will win” is a (local, pri-

vate) expression of an opinion, then surely if that bet-

tor instead says nothing at all while silently placing a

$100 back-bet on H1 at the exchange then that bettor

is still expressing an opinion: the placing of the bet is

a private act, but the existence of the bet immediately

becomes globally visible to all (albeit in anonymised

form).

Although our ABM of a betting exchange is min-

imal, even with such a simple model it is necessary to

extend OD methods beyond those that have been pre-

viously published, and not only because in our model

the bettor-agents need to balance the inﬂuence of lo-

cal and global expressions of opinions: the other fac-

tor that takes our model beyond the conﬁnes of tra-

ditional OD models is that our bettor agents need to

deal with the realities of the event itself, which is ini-

tially uncertain but will eventually have a deﬁnite out-

come. As the event progresses, the space of possible

outcomes progressively reduces in scope, until only

one outcome (the actual outcome) has nonzero prob-

ability. We know of no OD models that have been

developed which explore and accommodate the inter-

play between local and global opinions about the out-

come of some uncertain future event, and the actual

event outcome itself, in the way described here.

In this paper we have reported our earliest results,

and this model remains very much a work in progress

that we will be developing further in coming months:

there are many avenues of future work that we in-

tend to explore within the context of this model, and

we have made our source-code freely available on

GitHub to enable other researchers to replicate and

extend the work described here.

REFERENCES

Cao, J., Chen, J., Hull, J., Poulos, Z., and Zhang, D.

(2021). Synthetic data: A new regulatory tool. SSRN:

3908626.

Cliff, D. (2021). BBE: Simulating the Microstructural Dy-

namics of an In-Play Betting Exchange via Agent-

Based Modelling. SSRN 3845698.

Cliff, D., Hawkins, J., Keen, J., and Lau-Soto, R. (2021).

Implementing the BBE agent-based model of a sports-

betting exchange. In Affenzeller, M., Bruzzone, A.,

Longo, F., and Petrillo, A., editors, Proceedings of the

33rd European Modelling and Simulation Symposium

(EMSS2021), pages 230–240.

Deffuant, G., Neau, D., and Amblard, F. (2002). How

can extremism prevail? A study based on the rela-

tive agreement interaction model. Journal of Artiﬁcial

Societies and Social Simulation, 5(4):1.

Dong, Y., Zhan, M., Kuo, G., Ding, Z., and Liang, H.

(2018). A survey on the fusion process in opinion dy-

namics. Information Fusion, 43:57–65.

El Emam, K., Mosquera, L., and Hoptroff, R. (2021). Prac-

tical Synthetic Data Generation: Balancing Privacy

and the Broad Availability of Data. O’Reilly.

Friedkin, N. E. and Bullo, F. (2017). How truth wins in

opinion dynamics along issue sequences. Proceedings

of the National Academy of Sciences, 114(43):11380–

11385.

Goodfellow, I., Bengio, Y., Courville, A., and Bach, F.

(2017). Deep Learning. MIT Press.

Guzelyte, R. (2021). Exploring opinion dynamics of agent-

based bettors in an in-play betting exchange. Master’s

thesis, Department of Engineering Mathematics, Uni-

versity of Bristol.

Hawkins, J. (2021). Design and implementation of a simu-

lated betting exchange: Generating synthetic data for

use in discovering proﬁtable betting strategies. Mas-

ter’s thesis, University of Bristol, Department of Com-

puter Science; SSRN 3876312.

Hegselmann, G. and Krause, U. (2002). Opinion dynamics

and bounded conﬁdence: models, analysis and simu-

lation. Journal of Artiﬁcial Societies and Social Sim-

ulationn, 5(3):2.

Narrative Economics of the Racetrack: An Agent-Based Model of Opinion Dynamics in In-play Betting on a Sports Betting Exchange

235

Hegselmann, R., Krause, U., et al. (2006). Truth and cogni-

tive division of labor: First steps towards a computer

aided social epistemology. Journal of Artiﬁcial Soci-

eties and Social Simulation, 9(3):10.

Fortune Business Insights (2021). Online Gambling

Market Size, Share & COVID-19 Impact Analysis,

by type, by devices, and regional forecast, 2021-

2028. https://www.fortunebusinessinsights.com/

online-gambling-market-104803.

Keen, J. (2021). Discovering transferable and proﬁtable al-

gorithmic betting strategies within the simulated mi-

crocosm of a contemporary betting exchange. Mas-

ter’s thesis, University of Bristol, Department of Com-

puter Science; SSRN 3879677.

Krause, U. (2000). A discrete nonlinear and non-

autonomous model of consensus formation. In Elaydi,

S., Ladas, G., Popenda, J., and Rakowski, J., editors,

Communications in Difference Equations: Proc. 4th

International Conference on Difference Equations,

pages 227–236. Overseas Publishers Association.

Lau-Soto, R. (2021). An agent-based model of a betting ex-

change via a single-threaded and object-oriented im-

plementation. Master’s thesis, University of Bristol,

Department of Computer Science; SSRN 3874192.

Liu, J. and Mo, L. (2018). Noise-Induced Truth Seeking of

Heterogeneous Hegselmann-Krause Opinion Dynam-

ics. Advances in Mathematical Physics, 8702152:1–6.

Lomas, K. (2020). Exploring narrative economics: A novel

simulation platform that integrates automated traders

with opinion dynamics. Master’s thesis, University of

Bristol Department of Computer Science.

Lomas, K. and Cliff, D. (2021). Exploring narrative eco-

nomics: An agent-based modeling platform that in-

tegrates automated traders with opinion dynamics. In

Rocha, A.-P., Steels, L., and van den Herik, J., editors,

Proceedings of the 13th International Conference on

Agents and Artiﬁcial Intelligence (ICAART2021), vol-

ume 1, pages 137–148. SciTePress.

Malarz, K. (2006). Truth seekers in opinion dynamics mod-

els. International Journal of Modern Physics C, 17.

Meadows, M. and Cliff, D. (2012). Reexamining the Rela-

tive Agreement Model of Opinion Dynamics. Journal

of Artiﬁcial Societies and Social Simulation, 15(4):4.

Meadows, M. and Cliff, D. (2013). The Relative Disagree-

ment Model of Opinion Dynamics: Where Do Ex-

tremists Come From? 7th International Workshop on

Self-Organizing Systems (IWSOS), pages 66–77.

Shiller, R. (2017). Narrative Economics. Technical Report

2069, Cowles Foundation, Yale University.

Shiller, R. (2019). Narrative Economics: How Stories Go

Viral & Drive Major Economic Events. Princeton Uni-

versity Press.

Tsang, A., Doucette, J. A., and Hosseini, H. (2015). Vot-

ing with social inﬂuence: Using arguments to uncover

ground truth. In Proceedings of the 2015 Interna-

tional Conference on Autonomous Agents and Multia-

gent Systems, pages 1841–1842.

Wood, E., Baltrusaitis, T., Hewitt, C., Dziadzio, S., John-

son, M., Estellers, V., Cashman, T., and Shotton, J.

(2021). Fake it till you make it: face analysis in the

wild using synthetic data alone. ArXiv:2109.15102.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

236