Analysis of Computational Efficiency in Iterative

Order Batching Optimization

Johan Oxenstierna

1,2 a

, Jacek Malec

and Volker Krueger

Dept. of Computer Science, Lund University, Lund, Sweden

Kairos Logic AB, Lund, Sweden

Keywords: Order Picking, Order Batching Problem, Computational Efficiency, Warehousing.

Abstract: Order Picking in warehouses is often optimized through a method known as Order Batching, wherein several

orders can be assigned to be picked by the same vehicle. Although there exists a rich body of research on

Order Batching optimization, one area which demands more attention is that of computational efficiency,

especially for warehouses with unconventional layouts and vehicle capacity configurations. Due to the NP-

hard nature of Order Batching, computational cost for optimally solving large instances is often prohibitive.

In this paper we focus on approximate optimization and study the rate of improvement over a baseline solution

until a timeout, using the Single Batch Iterated (SBI) algorithm. Modifications to the algorithm, trading

computational efficiency against increased memory usage, are tested and discussed. Existing and newly

generated benchmark datasets are used to evaluate the algorithm on various scenarios. On smaller instances

we corroborate previous findings that results within a few percentage points of optimality are obtainable at

minimal CPU-time. For larger instances we find that solution improvement continues throughout the allotted

time but at a rate which is difficult to justify in many operational scenarios. The relevance of the results within

Industry 4.0 era warehouse operations is discussed.

1 INTRODUCTION

Order Picking is the process in which human pickers

or vehicles (henceforth vehicles) retrieve sets of

products (orders) from locations in a warehouse.

Order Batching is a method in which vehicles can be

assigned to pick several orders at a time. Order

Batching can be formulated as an optimization

problem known as the Order Batching Problem

(OBP) (Gademann et al., 2001) or the Joint Order

Batching and Picker Router Problem (JOBPRP)

(Valle et al., 2017), where the Picker Router Problem

is a Traveling Salesman Problem (TSP) applied in a

warehouse environment (Ratliff & Rosenthal, 1983).

We consider the OBP and JOBPRP versions

equivalent if solutions to the OBP are assumed to

include TSP solutions (henceforth we use the term

OBP to refer to this version). There are several further

versions and focus areas in OBP’s, including

dynamicity, traffic congestion, depot setups and

https://orcid.org/0000−0002−6608−9621

https://orcid.org/0000−0002−2121−1937

https://orcid.org/0000−0002−8836−8816

obstacle layouts. One area in need of more attention

is computational efficiency. As will be laid out in

Section 2, computational efficiency is considered

important in OBP-related research, but detailed

discussions are sparse and there are significant

differences in how CPU-times and timeouts are used.

Although the variability of OBP’s and results

concerning computational efficiency is high, we

believe more research in this domain is warranted.

We delimit our work to OBP’s where the aim is to

minimize aggregate distances, and as measurement of

computational efficiency we use the rate with which

aggregate distance is reduced through CPU-time over

a baseline solution. We use a distance based OBP cost

because this is the predominant Key Performance

Indicator (KPI) in OBP benchmark datasets.

Although a KPI based on capital cost is what is

mostly sought by warehouse management, it is

difficult to work with: There are a multitude of

complex and variable features that go into capital,

Oxenstierna, J., Malec, J. and Krueger, V.

Analysis of Computational Efﬁciency in Iterative Order Batching Optimization.

DOI: 10.5220/0010837700003117

In Proceedings of the 11th International Conference on Operations Research and Enterprise Systems (ICORES 2022), pages 345-353

ISBN: 978-989-758-548-7; ISSN: 2184-4372

345

such as time-based aspects of work, traffic

congestion, maintenance, ergonomics etc. A distance

based KPI makes it easier to generate instances and

solutions in a more generalizable and reproducible

way.

For experimentation we use the approximate

optimizer Single Batch Iterated (SBI), to which we

introduce novel search heuristics that permit stronger

solution improvement at the cost of increased

memory usage. We only work with CPU-times in the

range 0 – 300 seconds. Results are compared with

previous work by Aerts et al. (2021) and Henn &

Wäscher (2012b), who have proposed approximate

optimization results for sets of smaller instance sizes.

For smaller instances we also assess SBI against

optimal results on the Foodmart dataset (Briant et al.

2020). For larger instances we introduce a new

dataset and make it available on a public repository

(Section 5.1). For instance generation we use the

TSPLIB format (Hahsler & Kurt, 2007). As far as we

are aware, there exists no standard benchmark format

in OBP research, rendering experiments difficult to

reproduce. Further discussions on how to represent

key OBP features in reproducible data is highly

relevant. This would allow for more data-driven

evaluation of algorithmic performance, for example

when investigating computational efficiency. Our

research aims are as follows:

1. To investigate the importance of

computational efficiency in OBP

optimization.

2. To analyse computational efficiency of an

approximate OBP optimizer on both existing

and new test-instances and to discuss results

in the light of previous work.

2 LITERATURE REVIEW

In this section we first present how the OBP and some

of its key features are formulated in the literature.

Then we present commonly used OBP optimization

algorithms and heuristics. Finally, we present how

computational efficiency has been motivated and

evaluated in different OBP scenarios.

As several studies have pointed out, the Order

Batching Problem (OBP) shares significant

similarities with the more well-known Vehicle

Routing Problem (VRP) (Cordeau et al., 2007; Valle

et al., 2017; Valle & Beasley, 2019). Aerts et al.

(2021), distinguish three points of separation between

the OBP and the standard VRP:

1. Order-integrity constraint: In the OBP the

products belonging to an order may only be picked by

one vehicle, whereas there exists no concept of orders

or order-integrity in the standard VRP.

2. Number of visits constraint: In the OBP the

same location may be visited several times by various

vehicles, whereas a location may only be visited once

in the standard VRP.

3. Obstacle-layout: In the OBP it is assumed that

there exists an obstacle layout, whereas there is no

such assumption in the standard VRP.

Concerning the latter point, most of the research on

the OBP assumes that the warehouse uses a

conventional layout, which means racks are arranged

with parallel aisles (between racks) and parallel cross-

aisles (between sections of racks). If these conditions

are not met the layout is unconventional (see Figure 1).

Aerts et al. argue that the OBP can be modelled as

a Clustered VRP (CluVRP) with weak cluster

constraints. Weak cluster constraints mean that a

vehicle may visit the locations in several clusters of

locations in any sequence. The CluVRP was first

introduced by Defryn & Sörensen (2017) and is

according to Aerts et al. equivalent to the OBP since

clusters can be mapped as orders. In experiments they

utilize this problem on a conventional layout

warehouse and on OBP scenarios involving up to 100

orders.

Figure 1: Examples of a conventional (top) and

unconventional (bottom) layout warehouse, and example

OBP’s with four orders. The colored diamonds denote

origin and destination locations. The colored dots denote

products and the orders which they belong to. In the

solutions (right of the arrows), one vehicle is assigned to

pick the red and lime orders and a second vehicle is

assigned to pick the blue and green orders.

For conventional layouts, proposed optimization

algorithms include integer programming (Valle et al.,

2017), clustering (Kulak et al., 2012), datamining

(Chen & Wu, 2005), dynamic programming (Briant

et al., 2020) meta-heuristics and heuristics: Examples

of meta-heuristics include Variable Neighborhood

Search (Aerts et al., 2021), Tabu Search (Henn &

Wäscher, 2012b), Ant Colony Optimization (Li et al.,

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

346

2017) and Genetic Algorithms (Cergibozan & Tasan,

2020). The heuristic algorithms can be divided into

three categories: Priority rule-based algorithms,

savings algorithms and seed algorithms (Henn et al.,

2010). Priority-rule based algorithms build batches by

sorting orders according to a heuristic, for example

First-Come-First-Serve, First-Fit or Best-Fit. In

savings algorithms batches with single orders are first

initialized and evaluated. Then, pairs, triplets and

larger collection of orders are constructed and the

combination with the best total result is retrieved

(Henn & Wäscher, 2012a). In seed algorithms batches

are generated in two phases: Seed selection and order

addition. In seed selection, an initial seed order is

chosen and then orders are added to the seed. There

are several proposals for how to choose the first seed

and add orders to it (Ho et al., 2008). One example is

the Sequential Minimal Distance (SMD) heuristic

(Sharp & Gibson, 1992), where the sum of minimal

distances between products in the seed order and

remaining orders is computed:

𝑆𝑀𝐷



𝑠,𝑜



𝑚𝑖𝑛

∈

𝑑



,

∈

𝑜∈𝒪,𝑜∉𝑏,𝑠∈𝑏,

(1)

where 𝑠 denotes a seed order in batch 𝑏, where 𝑜

denotes an order which does not exist in 𝑏, and where

𝑖 and 𝑗 denote products in order 𝑠 and 𝑜 respectively.

Whenever there are more than two products in a

batch, we assume some form of TSP algorithm is used

within the OBP algorithm. For conventional layouts,

the highly efficient S-shape or Largest Gap

algorithms are commonly used (Henn, 2012;

Roodbergen & Koster, 2001). We are not aware of

any attempts to extend these to unconventional

layouts. Given a distance matrix is provided,

however, TSP’s can be optimized reasonably fast

using e.g. OR-tools (Kruk, 2018) or Concorde (D.

Applegate et al., 2002; D. L. Applegate et al., 2006).

Computational efficiency in OBP optimization

can be motivated in two general ways. The first

concerns the direct impact of CPU-time on warehouse

operations. In models where orders are coming in to

the warehouse dynamically, for example,

optimization should ideally be faster than the time it

takes a vehicle to finish a picking round (Henn, 2012;

Scholz et al., 2017). Otherwise, vehicles must wait in

an idle state at the depot. Dynamic models are

generally more realistic than static ones (incoming

orders are there assumed to be known beforehand).

The literature still tends to model OBP’s as static

since dynamicity incurs more complexity (Scholz et

al., 2017).

The second motivation for computational

efficiency stems from a system architecture

perspective and how an OBP optimization module

can integrate with a Warehouse Management System

(WMS) without leading to higher optimization costs

in a more indirect sense. As an example, if an OBP

module is deployed on the cloud as a 3

party

software service (SaaS) there are some advantages

with short CPU-times: A WMS client may be more

interested in buying a service if it is safe and simple

to integrate and this is made easier with short CPU-

times (Esposito et al., 2016). Furthermore, rental cost

of servers can be assumed to rise with CPU-time and

this also motivates more efficiency in regard to CPU-

times (Naumenko & Petrenko, 2021).

The efficiency considerations described above are

rarely considered of central importance in the broader

literature on the OBP, however. CPU times are

chosen to be “tolerable” (Kulak et al., 2012),

“reasonable” (Bozer & Kile, 2008), “acceptable” or

“realistic” (Aerts et al., 2021), but often lack in

explanations of what these terms actually entail.

Some examples are provided below for how

researchers have used CPU-times and timeouts in

optimization experiments with OBP’s.

For approximate optimization, Henn & Wäsher

(Henn & Wäscher, 2012a) use timeouts between 1 –

180 seconds for a heuristic optimizer and OBP’s

where 40 – 100 unassigned orders are to be batched.

Aerts et al. (2021), set timeouts between 1 and 60

seconds on the same instance set and propose a meta-

heuristic algorithm specifically designed to terminate

at around 60 seconds, since solution improvement is

found to be insignificant beyond that point. Both

Aerts et al. and Henn & Wäscher’s algorithms come

to within 5% of the best solution overall within the

first 10% of optimization time. Scholz et al. (2017)

experiment with instances of similar size but in a

dynamic setting and report a much lower efficiency:

70% of maximum allowed CPU-time is necessary to

reach within 5% of best solution overall. Efficiency

also decreases non-linearly with instance size in their

results: For 10 orders their optimizer needs 2 seconds,

for 100 orders it needs 11 minutes, and for 200 orders

60 minutes. Henn (2012) also presents an algorithm

for dynamic OBP’s and sets it to self-terminate after

60 seconds, partly due to operational considerations

(to avoid vehicles from idling at the depot). Many

publications do not present concrete results for

timeouts or rate of solution improvement, or a low

number of experiments (Azadnia et al., 2013; Bué et

al., 2019; Jiang et al., 2018). Kulak et al. (2012) and

Li et al. (2017), for example, present highly efficient

meta-heuristic optimizers, but use only 5 to 10

instances and do not show their rate of solution

improvement. For authors presenting algorithms

Analysis of Computational Efﬁciency in Iterative Order Batching Optimization

347

capable of finding optimal solutions to static OBP’s,

Henn & Wäscher (2012b), set timeouts between 2 –

1328 seconds for instances with up to 60 orders.

Gademann et al. (2001), set timeouts to 10 – 30

minutes for up to 100 orders. Valle et al. (2017) and

Briant et al. (2020), on the Foodmart dataset, present

timeouts in the range 300 seconds to 2 hours for 20-

30 orders.

These examples show that computational

efficiency in OBP experiments is difficult to judge

generally. Choice of static or dynamic modelling,

optimal versus approximative optimization,

experimental setup, instance sizes and the technology

level of used software and hardware, are all factors

that can have a complex effect on results in this

regard.

3 PROBLEM FORMULATION

We define the OBP objective as the assignment of

batches to vehicles such that the aggregate distance

needed to pick the batches is minimized. Each batch

𝑏 consists of a set of orders 𝑏∈2

𝒪

,𝑏∅ where

each 𝑜∈𝒪 is a subset of products 𝑜∈2

𝒫

,𝑜∅.

Each product 𝑝∈𝒫 is a set which includes a unique

product identifier, an order identifier, weight 𝑤 and

volume 𝑣𝑜𝑙, 𝑤,𝑣𝑜𝑙∈ ℝ



. The sum of weight,

volume or number of orders in a batch can be

retrieved with function 𝑞



𝑏



,𝑞∈𝑤,𝑣𝑜𝑙,𝑘. The x,

y location coordinates of all products is defined as set

ℒ

𝒫

, and the location of a product is retrievable with

function 𝑙𝑝. The locations of the products in an

order are retrievable with function 𝑙



𝑜



∪

∈

𝑙



𝑝



and all locations in a batch are retrievable with

function 𝑙



𝑏



∪

∈

𝑙



𝑜



. We define a single origin

location for all vehicles 𝑙



, a single destination

location 𝑙



and a set of polygonal obstacle location

sets ℒ

𝒰

. The aggregate of all locations is ℒ𝑙



∪

𝑙



∪ℒ

𝒫

∪ℒ

𝒰

We build undirected graph 𝐺𝑉,𝐸. Each

vertex in 𝑉 represents a unique location in ℒ and

function 𝑣



𝑙



gives a vertex for a location and 𝑙



𝑣



gives a location for a vertex. The vertices in batch 𝑏

includes the origin and destination vertices 𝑣



𝑏





𝑣



𝑙





∪𝑣𝑙



𝑏



∪𝑣



𝑙





. 𝐸 represents the set of all

Euclidean edges between all locations that

circumvent obstacles in ℒ

𝒰

. Distance matrix 𝐷 and

shortest paths between all edges is computed using

the Floyd-Warshall algorithm. How 𝐸 and shortest

paths can be constructed with polygonal obstacles is

beyond the scope of this paper; for details see

(Rensburg, 2019). We also permit several products to

be assigned to the same location in our model. This

can be useful to help reduce the memory footprint of

𝐺. The path to pick batch 𝑏 is retrievable with the

following function:

𝑇



𝑏



𝑣









,𝑛

𝑣



𝑏

|

(2)

𝑣





𝑣



𝑖1

𝑣



1𝑖𝑛

𝑣



𝑖𝑛

(3)

and represents the solution to a Traveling

Salesman Problem (TSP). The distance of 𝑇𝑏 is

retrievable with function

𝐷



𝑏





∑

𝑑





















,𝑖,𝑗∈

ℤ



,𝑗𝑖1,𝑖

𝑇𝑏

, where 𝑑 represents entries

in distance matrix 𝐷. Vehicles are defined as 𝑚∈ℳ

where each vehicle has capacities expressed in weight

𝑤, volume 𝑣𝑜𝑙 and number of orders 𝑘. The scenario

where a vehicle 𝑚 is assigned a batch, order, and/or

product location is defined with binary variables 𝑥



𝑥



and 𝑥



, respectively. We then formulate the

OBP as follows:

𝑚𝑖𝑛𝐷



𝑏



𝑥



∈ℬ

𝑚∈ℳ

s.t.

(4)

𝑥



∈

ℳ

1,∀𝑜∈𝒪

(5)

𝑥



∈







𝑥



,∀𝑜∈𝒪,𝑚∈ℳ

(6)

𝑞



𝑏



𝑞



𝑚



𝑥



,𝑏∈ℬ,

𝑞∈𝑤,𝑣𝑜𝑙,𝑘,𝑚∈ℳ

(7)

where (4) states the objective, i.e., minimize

distances for all generated batches ℬ , where (5)

enforces order-integrity, where (6) enforces all

locations in all orders to be visited at least once and

where (7) ensures vehicle capacities are never

exceeded. Since this OBP is highly intractable we

also formulate a less ambitious objective in the single

batch OBP:

𝑎𝑟𝑔𝑚𝑖𝑛

∈ℬ

𝐷



𝑏



(8)

Here the aim is to find a single batch for an already

selected vehicle. For this case we also enforce the

single batch to come as close as possible to vehicle

capacity: ∃𝑞𝑞



𝑏



𝑞



𝑜



 𝑞



𝑚



,∀𝑜∈𝒪,𝑜∉

𝑏,𝑞∈𝑤,𝑣𝑜𝑙,𝑘.

4 OPTIMIZATION ALGORITHM

SingleBatchIterated (SBI) (Algorithm 1) is a heuristic

multi-phase optimizer. In the core of the algorithm

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

348

unassigned orders 𝒪 are iteratively sent as input to the

SMD (Sequential Minimal Distance) seed function,

together with distance matrix 𝐷, a randomly chosen

available vehicle and a variable seed index. The SMD

function builds a single batch 𝑏 by first selecting a

seed order according to the seed index and adding

orders to it according to minimal distances (Equation

1). Batch 𝑏 is then removed from the set of

unassigned orders and the procedure repeats until all

orders have been batched into ℬ. An approximate

solution to the OBP can thus be obtained by pre-

selecting vehicles and approximately solving a single

batch OBP for that vehicle (Equation 8).

Algorithm 1: Single Batch Iterated (SBI).

The path to visit all locations in batch 𝑏∈ℬ, 𝑇



𝑏



and its distance, 𝐷



𝑏



, is computed using the OR-

tools TSP optimization suite

, in function TSP

. OR-

tools is set to finish quickly by using a number of

iterations parameter, which is set to grow linearly

with number of vertices in the TSP. If the aggregate

distance was found to be lower than the best result so

far, the TSP’s are optimally solved using Concorde

If the aggregate distance is still lowest, the solution is

stored as the best result.

The algorithm self-terminates after |𝒪| outer

loops (or after a manually set timeout of 300 seconds

in our experiments). Since the number of calls to

SMD is approximately cubic to number of orders:

𝒪

|∑|

𝒪

𝑖



,𝑖∈



|𝒪|  1



, we use an SMD order-

https://developers.google.com/optimization/routing/tsp,

collected 13-09-2021.

http://www.math.uwaterloo.ca/tsp/concorde/index.html,

collected 16-09-2021.

https://pagesperso.g-scop.grenoble inp.fr/~cambazah/

batching/, collected 04-05-2021.

order enumerated matrix, which is populated through

the optimization procedure: If SMD between two

orders does not exist in the matrix, it is computed and

pushed to the matrix. Once the value is stored it is

subsequently queried. Caching SMD’s this way

reduces number of calls to SMD from cubic to square,

at an insignificant increase of memory usage (~25

megabytes for 5000 orders assuming 8 bits per cell in

the matrix). It should be noted that this only works for

an SMD algorithm where the seed is defined as a

single order, which cannot provide more than a noisy

estimate of the subsequent TSP solution distance for

batches with more than two orders. We still deem

pairwise order-order SMD caching is suitable, since

distance estimates are inaccurate even if SMD’s for

larger collections of orders are computed (TSP

optimization is required for accurate estimates).

Caching could also be used to store all generated

single batches and their solved TSP’s in a hash tree or

equivalent, to prevent the same TSP to be optimized

twice (memoization). We leave an implementation of

this for future work, but there are likely gains to be

made in general by storing and reusing results from

the most expensive parts of the algorithm.

5 EXPERIMENTS

5.1 Benchmark Datasets

The publicly shared datasets Foodmart

, L6_203

and

L09_251

are used for experimentation. Foodmart

was introduced by Valle et al. (2017) and models a

warehouse with a conventional layout with a

maximum of 8 aisles and 3 cross-aisles. A feature in

Foodmart is that vehicles carry bins and that vehicle

capacity is expressed as a volume unit per bin. If an

order cannot fit in a single bin, splitting it between

different bins is permitted. SBI is not specifically

designed to optimize for this feature (an extra bin

packing problem within the OBP), so a greedy

heuristic module is appended to the optimizer for the

Foodmart experiment (for details see Oxenstierna et

al., 2021).

L6_203 and L09_251 model scenarios for up to

six unconventional warehouse layouts and multiple

depots. In these instances, vehicle capacity is

https://github.com/johanoxenstierna/OBP_instances, co-

llected 23-09-2021.

https://github.com/johanoxenstierna/L09_251, collected

10-06-2021.

Analysis of Computational Efﬁciency in Iterative Order Batching Optimization

349

expressed in number of orders. To allow for some

degree of comparability between L6_203 and

Foodmart, we chose to exclude the largest six

instances in Foodmart (100 – 5000 orders). Apart

from these the number of orders is similar between

Foodmart and L6_203. For larger instances we

instead use L09_251, where number of orders range

between 50 – 1000.

Number of orders only gives a rough idea of how

much CPU-time might reasonably be needed to

optimize an OBP instance. Number of products and

vehicle capacities are further examples of features

that have a considerable impact. To classify instances

by size, we use the amount of computational time SBI

requires to obtain a baseline solution: 0-2, 2-5, 5-7 or

7-10 seconds. The resulting number of instances for

the four classes are as follows: 0-2 s: 395, 2-5 s: 191,

5-7 s: 88, 7-10 s: 32. For all our experiments we use

Intel Core i7-4710MQ 2.5 GZ 4 cores, 16 GB RAM.

5.2 Experiment Results

Aggregations of all results are presented in Table 1,

Figure 2 and Figure 3. In Figure 2, the average

improvement rate from the baseline is shown for the

four instance size classes. The shades around the lines

represent 95% confidence intervals.

Figure 2: Optimization time versus relative OBP distances

in percentages, for four instance size classes.

The solution improvement rates for smaller instances

(blue and orange) generally corroborate those of

Henn & Wäscher (2012b) and Aerts et al. (2021):

Improvements are significant in the initial stage of

optimization (1-4% improvement over baseline

within the first 10% of optimization) and then taper

off. In our case all instances with up to 100 orders

require no more than 2 seconds to obtain a baseline.

Within this class we also note SBI always self-

terminates within 10 seconds (in figures 2 and 3 we

show this by cutting the blue curve at 10 seconds; it

could also have been extended as a horizontal line

beyond 10 seconds).

The Foodmart instances fit within the smallest

class and there we compare against optimal results in

Briant et al. (2020): On average, a gap to optimality

of 2.3% was achieved after a maximum of 10

seconds. The gap between the baseline solution and

the best solution found was 3.2% on Foodmart. On

generated instances in L6_203 the corresponding gap

was 3.5%.

For our larger instance classes (2-10 seconds to

find a baseline solution), the pattern is similar, but

more time is needed to reach the same percentage

improvement over the baseline. This is expected since

fewer candidate solutions can be generated for larger

instances within the same CPU-time (more

computational time is needed by the SMD and TSP

functions to generate a solution).

In terms of absolute distance rate of improvement,

we first standardize the data such that the average

pick round is of similar length between the three

datasets. The absolute distance improvements for the

four instance size classes are shown in Figure 3:

Figure 3: Optimization time versus standardized absolute

distance savings, for four instance size classes.

Only toward the end of the maximum allotted CPU-

time we observe larger absolute gains for larger

OBP’s. As solution space grows, the probability of

SBI finding a strong baseline decreases and possible

improvement percentages can therefore be assumed

to be higher for larger instances. As we can see in

Figure 3, the red curve, for example, starts with the

least amount of distance saved compared to the other

curves, but ends with the most amount of distance

saved. The time to get there is 4 minutes, however.

This is explainable since larger instances require

more time to produce candidate solutions. Since there

are only 32 instances in the class of largest instances,

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

350

more data would be needed to investigate this pattern

further and to narrow the confidence intervals. The

less regular pattern and larger confidence interval in

the red curve is primarily assumed to be due to the

fewer number of data points.

Concerning rate of solution improvement, we can

see that it decreases to less than ~1% / minute after

the initial gains taper off after 30 – 60 seconds (Figure

2). In terms of standardized distance, this is on

average equivalent to around 18% of the length of a

single batch TSP solution (~12 standardized distance

units).

As discussed in Section 2, generalization of results

is difficult due to the high variability of OBP

scenarios. Overall, we believe 1% / min is a slow rate

of improvement and that it would be difficult to

justify in many scenarios, especially when

considering various indirect advantages of short

CPU-times (Section 2).

6 CONCLUSION

We investigated computational efficiency in

approximate Order Batching Problem (OBP)

optimization, both in previous work and in an

experiment involving the Single Batch Iterated (SBI)

optimizer. In previous work, computational

efficiency is rarely discussed in detail, especially for

warehouses with various types of obstacle layouts. It

is an important topic, however, affecting costs in real

warehouse operations both directly and indirectly.

Suitable modifications to the SBI optimizer and its

usage of the Sequential Minimal Distance (SMD)

heuristic, where more computational efficiency is

achieved at the cost of more memory, were tested and

discussed. For OBP instances with up to 100 orders

and a few seconds of CPU-time, SBI yielded

distances only a few percentage points higher than

results obtained when optimization was set to run for

up to five minutes. The result corroborates previous

research claims: Fast approximate optimization is a

practicable choice in many common OBP scenarios.

For larger instances, with 100 – 1000 orders, more

time was required to obtain similar savings. The

standardized absolute distance saved through the

optimization procedure was shown to grow very

similarly for all instance sizes, which may seem

counterintuitive. The SBI algorithm only constructs

weak batches (with products located far from each

other) whenever there are few orders left to select

from (SMD prevents this in other cases). Since this

phenomenon occurs an equal number of times

regardless of instance size, the amount of possible

solution improvement in larger instances is relatively

low. This is a feature specific to SBI and other

optimizers may avoid this issue, while facing others.

Regardless of instance size, we conclude that

spending extra CPU-time to obtain a result a few

percentage points better than a baseline might be

justified, but at the same time it needs to be weighed

against the less measurable and indirect costs that

come with lower computational efficiency.

Unfortunately, that type of analysis is usecase-

dependent and difficult to generalize.

For future work we believe the investigation can

be widened to include more optimizers which are

compared side by side. We also believe there are

significant savings to be made in optimization if more

memory is allocated to store and reuse parts of

expensive computations. Modeling of OBP’s and

data-driven performance evaluation are also of

primary importance. Currently there exists no

standard format for OBP benchmark datasets and this

poses a serious threat to scientific reproducibility.

Since there are many possible versions of OBP’s, the

community should discuss how OBP benchmark data

can best be built to balance realism with simplicity

and reproducibility. Until then it will remain

challenging to concretely and fairly judge the

computational efficiency of OBP optimizers.

ACKNOWLEDGEMENTS

This work was partially supported by the Wallenberg

AI, Autonomous Systems and Software Program

(WASP) funded by the Knut and Alice Wallenberg

Foundation. We also convey thanks to Kairos Logic

AB for software.

REFERENCES

Aerts, B., Cornelissens, T., & Sörensen, K. (2021). The

joint order batching and picker routing problem:

Modelled and solved as a clustered vehicle routing

problem. Computers & Operations Research, 129.

Applegate, D., Cook, W., Dash, S., & Rohe, A. (2002).

Solution of a Min-Max Vehicle Routing Problem.

INFORMS Journal on Computing, 14, 132–143.

Applegate, D. L., Bixby, R. E., Chvatal, V., & Cook, W. J.

(2006). The traveling salesman problem: A

computational study. Princeton university press.

Azadnia, A. H., Taheri, S., Ghadimi, P., Samanm, M. Z. M.,

& Wong, K. Y. (2013). Order Batching in Warehouses

by Minimizing Total Tardiness: A Hybrid Approach of

Weighted Association Rule Mining and Genetic

Algorithms. Scientific World Journal.

Analysis of Computational Efﬁciency in Iterative Order Batching Optimization

351

Bozer, Y. A., & Kile, J. W. (2008). Order batching in walk-

and-pick order picking systems. International Journal

of Production Research, 46(7), 1887–1909.

Briant, O., Cambazard, H., Cattaruzza, D., Catusse, N.,

Ladier, A.-L., & Ogier, M. (2020). An efficient and

general approach for the joint order batching and picker

routing problem. European Journal of Operational

Research, 285(2), 497–512.

Bué, M., Cattaruzza, D., Ogier, M., & Semet, F. (2019). A

Two-Phase Approach for an Integrated Order Batching

and Picker Routing Problem (pp. 3–18).

Cergibozan, Ç., & Tasan, A. (2020). Genetic algorithm

based approaches to solve the order batching problem

and a case study in a distribution center. Journal of

Intelligent Manufacturing, 1–13.

Chen, M.-C., & Wu, H.-P. (2005). An association-based

clustering approach to order batching considering

customer demand patterns. Omega, 33(4), 333–343.

Cordeau, J.-F., Laporte, G., Savelsbergh, M., & Vigo, D.

(2007). Vehicle Routing. In Transportation, handbooks

in operations research and management science (Vol.

14, pp. 195–224).

Defryn, C., & Sörensen, K. (2017). A fast two-level

variable neighborhood search for the clustered vehicle

routing problem. Computers & Operations Research,

83, 78–94.

Esposito, C., Castiglione, A., & Choo, K.-K. R. (2016).

Challenges in Delivering Software in the Cloud as

Microservices. IEEE Cloud Computing, 3(5), 10–14.

Gademann, A. J. R. M. (noud), Van Den Berg, J. P., & Van

Der Hoff, H. H. (2001). An order batching algorithm

for wave picking in a parallel-aisle warehouse. IIE

Transactions, 33(5), 385–398.

Hahsler, M., & Kurt, H. (2007). TSP – Infrastructure for the

Traveling Salesperson Problem. Journal of Statistical

Software, 2, 1–21.

Henn, S. (2012). Algorithms for on-line order batching in

an order picking warehouse. Computers & Operations

Research, 39(11), 2549–2563.

Henn, S., Koch, S., Doerner, K. F., Strauss, C., & Wäscher,

G. (2010). Metaheuristics for the order batching

problem in manual order picking systems. Business

Research, 3(1), 82–105.

Henn, S., & Wäscher, G. (2012a). Tabu search heuristics

for the order batching problem in manual order picking

systems. European Journal of Operational Research,

222(3), 484–494.

Henn, S., & Wäscher, G. (2012b). Tabu search heuristics

for the order batching problem in manual order picking

systems. European Journal of Operational Research

222(3), 484–494.

Ho, Y.-C., Su, T.-S., & Shi, Z.-B. (2008). Order-batching

methods for an order-picking warehouse with two cross

aisles. Computers & Industrial Engineering, 55(2),

321–347.

Jiang, X., Zhou, Y., Zhang, Y., Sun, L., & Hu, X. (2018).

Order batching and sequencing problem under the pick-

and-sort strategy in online supermarkets. Procedia

Computer Science, 126, 1985–1993.

Kruk, S. (2018). Practical Python AI Projects:

Mathematical Models of Optimization Problems with

Google OR-Tools. Apress.

Kulak, O., Sahin, Y., & Taner, M. E. (2012). Joint order

batching and picker routing in single and multiple-

cross-aisle warehouses using cluster-based tabu search

algorithms. Flexible Services and Manufacturing

Journal, 24(1), 52–80.

Li, J., Huang, R., & Dai, J. B. (2017). Joint optimisation of

order batching and picker routing in the online retailer’s

warehouse in China. International Journal of

Production Research, 55(2), 447–461.

Naumenko, T., & Petrenko, A. (2021). Analysis of

Problems of Storage and Processing of Data in

Serverless Technologies. Technology Audit and

Production Reserves, 2(2), 58.

Oxenstierna, J., Malec, J., & Krueger, V. (2021). Layout-

Agnostic Order-Batching Optimization. International

Conference on Computational Logistics, 115–129.

Ratliff, H., & Rosenthal, A. (1983). Order-Picking in a

Rectangular Warehouse: A Solvable Case of the

Traveling Salesman Problem. Operations Research, 31,

507–521.

Rensburg, L. J. van. (2019). Artificial intelligence for

warehouse picking optimization—An NP-hard problem

[Master’s Thesis]. Uppsala University.

Roodbergen, K. J., & Koster, R. (2001). Routing methods

for warehouses with multiple cross aisles. International

Journal of Production Research, 39(9), 1865–1883.

Scholz, A., Schubert, D., & Wäscher, G. (2017). Order

picking with multiple pickers and due dates –

Simultaneous solution of Order Batching, Batch

Assignment and Sequencing, and Picker Routing

Problems. European Journal of Operational Research,

263(2), 461–478.

Sharp, G. P., & Gibson, D. R. (1992). Order batching

procedures. European Journal of Operational

Research, 58.

Valle, C. A., & Beasley, B. A. (2019). Order batching using

an approximation for the distance travelled by pickers.

European Journal of Operational Research.

Valle, C. A., Beasley, J. E., & da Cunha, A. S. (2017).

Optimally solving the joint order batching and picker

routing problem. European Journal of Operational

Research, 262(3), 817–834.

ICORES 2022 - 11th International Conference on Operations Research and Enterprise Systems

352

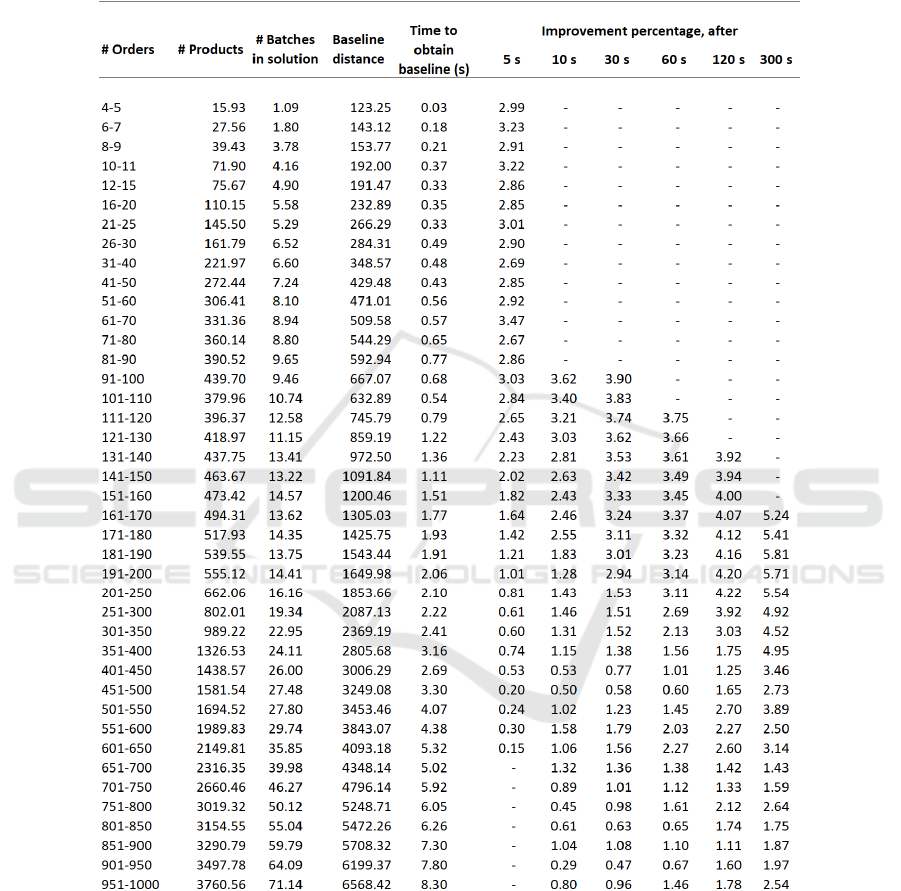
APPENDIX

Table 1: Aggregation of test-instance results into categories based on number of orders in the OBP’s. Within each category

the average over all results is shown. Whenever the optimizer (SBI) failed to obtain a result within the specified time, or when

it self-terminated, a minus sign (-) is shown. The distances shown are standardized.

Analysis of Computational Efﬁciency in Iterative Order Batching Optimization

353