Machine-checked Verification of Cognitive Agents
Alexander Birch Jensen
a
DTU Compute - Department of Applied Mathematics and Computer Science, Technical University of Denmark, Richard
Petersens Plads, Building 324, DK-2800 Kongens Lyngby, Denmark
Keywords:
Cognitive Agent Systems, Formal Verification, Isabelle/HOL.
Abstract:
The ability to demonstrate reliability is an important aspect in deployment of software systems. This applies
to cognitive multi-agent systems in particular due to their inherent complexity. We are still pursuing better
approaches to demonstrate their reliability. The use of proof assistants and theorem proving has proven itself
successful in verifying traditional software programs. This paper explores how to apply theorem proving to
verify agent programs. We present our most recent work on formalizing a verification framework for cognitive
agents using the proof assistant Isabelle/HOL.
1 INTRODUCTION
In the deployment of software systems we are often
required to provide assurance that the systems operate
reliably. Cognitive multi-agent systems (CMAS) con-
sist of agents which incorporate cognitive concepts
such as beliefs and goals. Their dedicated program-
ming languages enable a compact representation of
complex decision-making mechanisms. For CMAS
in particular the complexity of these systems often
exceeds that of procedural programs (Winikoff and
Cranefield, 2014). This calls for us to develop ap-
proaches that tackle the issue of demonstrating relia-
bility for CMAS.
The current landscape reveals testing, debugging
and formal verification such as model checking as the
primary approaches to demonstrating reliability for
CMAS (Calegari et al., 2021). This landscape has pri-
marily been dominated by work on model checking
techniques and exploration of better testing methods
(Jongmans et al., 2010; Bordini et al., 2004). How-
ever, if we take a deeper look, we find promising
work on theorem proving approaches (Alechina et al.,
2010; Shapiro et al., 2002). Combining testing and
formal verification has also been suggested as their in-
dividual strengths and weaknesses complement each
other well (Winikoff, 2010).
A proof assistant is an interactive software tool
which assists the user in developing formal proofs,
often by providing powerful proof automation. State-
of-the-art proof assistants have proven successful in
a
https://orcid.org/0000-0002-7298-2133
verification of software and hardware systems (Ringer
et al., 2019), but their potential use in the context of
CMAS is yet to be uncovered. The major strength of
a proof assistant is that every proof can be trusted as
it is checked by the proof assistant’s kernel. Exactly
which proof assistant someone prefers is highly sub-
jective. In this paper our work is carried out in the
Isabelle/HOL proof assistant (Nipkow et al., 2002).
In the present paper, we formalize existing work
on a verification framework for agents programmed
in the language GOAL (de Boer et al., 2007; Hindriks
and Dix, 2014; Hindriks et al., 2001; Hindriks, 2009).
The work we present is an extension of previous work
(Jensen, 2021a; Jensen et al., 2021; Jensen, 2021b;
Jensen, 2021c). Section 2 elaborates on the contribu-
tions of this previous work.
The contribution of this paper is threefold:
• we present and describe how a temporal logic can
be used to prove properties of agents specified in
the agent logic,
• we demonstrate how this is achieved in practice
by proving a correctness property for a simple ex-
ample program, and finally
• we improve upon our previous work with a fo-
cus on concisely delivering the main results of the
formalization in a format more friendly to those
unfamiliar with proof assistants.
The paper is structured as follows. Section 2
places this work into context with related work. Sec-
tion 3 provides an overview of the structure of the
formalization. Section 4 describes the GOAL lan-
Jensen, A.
Machine-checked Verification of Cognitive Agents.
DOI: 10.5220/0010838700003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 1, pages 245-256
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
245

guage and its formalization. Section 5 describes how
to specify agents in a Hoare logic and how this trans-
lates to the low-level semantics. Section 6 introduces
a temporal logic on top of the agent logic and de-
scribes how this can be used to prove temporal prop-
erties of agents. Section 7 demonstrates the use of the
verification framework by means of a simple example
program. Finally, Section 8 discusses limitations and
further work and concludes on the paper.
This paper contains a number of Isabelle/HOL
listings from the formalization source files referenced
below, all of which have been verified. In a few cases,
their presentation in this paper has been altered in mi-
nor ways for the sake of readability. For absolute pre-
cision, please refer to the full source which is publicly
available online:
https://people.compute.dtu.dk/aleje/#public
2 RELATED WORK
The ability to demonstrate reliability of agent systems
and autonomous systems has emerged as an impor-
tant topic, perhaps sparked by the reemergence of a
broader interest in AI. The following quote from a re-
cent seminar establishes this point (Dix et al., 2019):
The aim of this seminar was to bring together
researchers from various scientific disciplines,
such as software engineering of autonomous
systems, software verification, and relevant
subareas of AI, such as ethics and machine
learning, to discuss the emerging topic of the
reliability of (multi-)agent systems and au-
tonomous systems in particular. The ultimate
aim of the seminar was to establish a new
research agenda for engineering reliable au-
tonomous systems.
The work presented in this paper embraces this
perspective as we apply software verification tech-
niques using the Isabelle/HOL proof assistant to ver-
ify agents programmed in the language GOAL.
The main approaches to agent verification can be
categorized as testing, model checking and formal
verification. Our approach falls into the latter cate-
gory.
Testing is in general more approachable as it does
not necessarily require advanced knowledge of verifi-
cation systems. The main drawback is that it is non-
exhaustive as tests explore a finite set of inputs and be-
haviors. In (Koeman et al., 2018), the authors present
a testing framework that automatically detects failures
in cognitive agent programs. Failures are detected
at run-time and are enabled by a specification of test
conditions. While the work shows good promise, the
authors note that more work needs to be dedicated to
localizing failures.
Model checking is a technique where a system de-
scription is analyzed with respect to a property. It
is then checked that all possible executions of the
system satisfy this property. Model checking is cur-
rently considered the state-of-the-art approach to an
exhaustive demonstration of reliability for CMAS. In
(Dennis and Fisher, 2009; Dennis et al., 2012), we
are presented with a verification system for agent
programming languages based on the belief-desire-
intention model. In particular, an abstract layer maps
the semantics of the programming languages to a
model checking framework thus enabling their veri-
fication. The framework as a whole consists of two
components: an Agent Infrastructure Layer (AIL)
and an Agent Java Pathfinder (AJPF) which is a ver-
sion of the Java Pathfinder (JPF) model checker (Java
Pathfinder, 2021). The work contains a few exam-
ple implementations. In particular, the semantics of
the agent programming GOAL is mapped to AIL.
While this remains purely speculative, it would be in-
teresting to explore whether our formal verification
approach could be generalized to an abstract agent in-
frastructure such as AIL.
Formal verification is a technique where proper-
ties are proved with respect to a formal specification
using methods of formal mathematics. Because of the
amount of work involved in conducting formal proofs
and their susceptibility to human errors, such tech-
niques are often applied with a theorem proving soft-
ware tool such as a proof assistant. If the proof assis-
tant is trusted, this in turn eliminates human errors in
proofs while automation greatly reduces the amount
of work required. The main drawback is the expert
knowledge required to work with such software sys-
tems. In (Gomes et al., 2017), the authors verify cor-
rectness for a class of algorithms which provides con-
sistency guarantees for shared data in distributed sys-
tems. (Ringer et al., 2019) provides a survey of the
literature for engineering formally verified software.
We have not been able to find related work that com-
bines verification of agents with the use of proof as-
sistants. We hope that the work presented in this pa-
per can contribute to breaking the ice and stimulating
interest in the potential of proof assistants for verifi-
cation of agents.
We finally relate the contributions of this paper to
our previous work. In (Jensen, 2021a), we outlined
how to mechanically transform GOAL program code
into the agent logic for GOAL formalized in this pa-
per. In the present paper, we have not pursued the idea
of formalizing this transformation in Isabelle/HOL.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
246

The example we present in Section 7 is based on ac-
tual program code, but has been significantly sim-
plified for the sake of readability to hide program-
ming quirks that do not translate elegantly and be-
cause our focus is on the Isabelle/HOL formalization.
In (Jensen et al., 2021), we argued for the use of the-
orem proving to verify CMAS and presented early
work towards formalizing the framework. In (Jensen,
2021b), we go into the details of our early work on the
formalization. In particular, there is more attention on
the intricate details of formalizing the mental states of
agents. Due to the sheer complexity and volume of
the formal aspects we need to cover in the present pa-
per, we cannot here dedicate attention to every detail.
In (Jensen, 2021c), the emphasis is on formalizing ac-
tions and their effect on the mental state, and how to
reason about such actions. The present paper is a for-
malization of the verification framework in its entirety
and covers the most important aspects.
3 FORMALIZING GOAL IN
ISABELLE/HOL
The framework formalization is around 2400 lines
of code in total (178 KB) and loads in a few sec-
onds. The BW4T example formalization is around
1100 lines of code in total (95 KB) and loads in about
a minute. We want to emphasize that the example has
not been optimized. With proper optimization, we ex-
pect the loading time for the example to be just a few
seconds as well. The loading times have been tested
on a modern laptop.
The Gvf Logic theory sets up a framework for
propositional classical logic, including a definition
of semantics and a sequent calculus proof system.
The Gvf Mental States theory introduces the defini-
tion of mental states and a logic for reasoning about
mental states which is defined as a special case of
propositional logic. The Gvf Actions theory intro-
duces concepts of agents, actions, transitions and
traces. The Gvf Hoare Logic theory introduces a
Hoare logic for reasoning about the (non-)effects of
actions on mental states. The Gvf Agent Specification
theory sets up a framework for specifying an agent
using Hoare triples and a Hoare triple proof system.
The Gvf Temporal Logic theory introduces a tempo-
ral logic to reason about temporal properties of spec-
ified agents. Finally, the Gvf Example BW4T theory
proves the correctness of a simple example agent pro-
gram.
Figure 1 illustrates the high-level components of
the formalization and how they interact.
4 LOGIC FOR AGENTS
In this section, we describe a formalization of the
GOAL language.
From the Gvf Logic theory, we import a number
of key definitions and proofs:
•
0
a Φ
P
: Datatype for propositional logic formulas
with an arbitrary type
0
a of atoms.
• |=
P
: Semantic consequence for
0
a Φ
P
.
• `
P
: Sequent calculus proof system for
0
a Φ
P
.
The meaning of Γ |=
P
∆ is that the truth of all for-
mulas in the list of formulas Γ implies that at least one
formula is true in the list of formulas ∆.
The standard form of propositional logic, using
string symbols for atoms, is denoted by the derived
type Φ
L
. Here, the semantics are defined over a model
which maps string symbols to truth values.
Theorem 4.1 (Soundness of `
P
). The proof system `
P
is sound with respect to the semantics of propositional
logic formulas |=
P
:
Γ `
P
∆ =⇒ Γ |=
P
∆
Proof. By induction on the proof rules of `
P
.
4.1 Mental States of Agents
We are now interested in formalizing a state-based se-
mantics for GOAL. The state of an agent program is
determined by the mental state of the agent. A men-
tal state is modelled as two lists of formulas: a be-
lief base and a goal base. The belief base formulas
describe what the agents believe to be true while the
goal base formulas describe what the agents want to
achieve.
type-synonym mental-state = (Φ
L
list × Φ
L
list)
The original formulation describes these as sets,
but we have chosen to work with lists. There are ad-
vantages and disadvantages to either approach.
Usually, we distinguish between the beliefs of the
agent and the static knowledge about its world. In
this setup, static knowledge is incorporated into the
beliefs.
Due to limitations of the simple type system, we
need a definition to formulate the special properties of
a proper mental state:
definition is-mental-state :: mental-state ⇒ bool (∇) where
∇ M ≡ let (Σ, Γ) = M in ¬ Σ |=
P
⊥ ∧
(∀γ∈set Γ. ¬ Σ |=
P
γ ∧ ¬ |=
P
(¬ γ))
The above states that the belief base should be
consistent, that no goal should be entailed by the be-
lief base and that goals should be achievable.
Machine-checked Verification of Cognitive Agents
247

Agent program
Agent specification
- Agent Hoare triples
- Satisfiability problem
- Sound proof system
Verified temporal
properties of agents
Logic for GOAL
Temporal logic
- Formula type
- Trace semantics
Hoare logic
- Hoare triples for actions
- Definition of semantics
Actions
- Agent type
- Enabledness of actions
- Proof rules and semantics
- Proof of soundness
- Transitions and traces
Mental states
- Mental state definition
- Mental state formulas
Propositional logic
- Definition of semantics
- Sound proof system
Access to proof environmentsProve agent satisfiability
Prove Hoare triples
Figure 1: Visualization of the verification framework components.
The special belief and goal modalities, B and G re-
spectively, enable the agent’s introspective properties
as defined by their semantics:
(Σ, -) |=
M
B Φ = (Σ |=
P
Φ)
(Σ, Γ) |=
M
G Φ =
(¬ Σ |=
P
Φ ∧ (∃γ∈set Γ. |=
P
(γ −→ Φ)))
The language of mental state formulas Φ
M
can be
perceived of as a special form of propositional logic
where an atomic formula is either a belief or goal
modality. This approach allows us to exploit the type
variable
0
a for atoms where the model is defined via
the semantics of the belief and goal modalities.
We extend the proof system for propositional logic
`
P
with additional rules and axioms for the belief and
goal modalities given in Table 1 to obtain a proof sys-
tem for mental state formulas `
M
.
Table 1: Properties of beliefs and goals.
R
M
-B |=
P
Φ =⇒ `
M
B Φ
A1
M
`
M
B (Φ −→ ψ) −→ B Φ −→ B ψ
A2
M
`
M
¬ (B ⊥)
A3
M
`
M
¬ (G ⊥)
A4
M
`
M
B Φ −→ ¬ (G Φ)
A5
M
|=
P
(Φ −→ ψ) =⇒
`
M
¬ (B ψ) −→ G Φ −→ G ψ
Theorem 4.2 (Soundness of `
M
). The proof system
`
M
is sound with respect to the semantics of mental
state formulas |=
M
for any proper mental state (∇ M):
∇ M =⇒ `
M
Φ =⇒ M |=
M
Φ
Proof. By induction on the proof rules and using The-
orem 4.1.
Notice that we assume ∇ M which is necessary for
the proof rules to hold semantically. Furthermore, in
the soundness theorem for `
M
, there are no premises
on the left-hand side. This is deliberate, as we want to
match the formal notation for the semantics of mental
states that takes on the left-hand side a mental state,
i.e. M |=
M
Φ. We can solve this problem by incorpo-
rating premises in the target formula Φ by the use of
implication, i.e. for premises p
1
, p
2
, ... we have for
the semantics M |=
M
p
1
−→ p
2
−→ . . . −→ Φ.
4.2 Selecting and Executing Actions
In order to formalize a state-based semantics for
GOAL, we need a notion of transitions between men-
tal states of agents. We assume that agents themselves
are the only ones capable of changing their mental
state. As such, we can model transitions where an
action executed in a given mental state has a predeter-
mined outcome.
The low-level actions of GOAL are the basic ac-
tions. A basic action may be one of the two GOAL
built-in actions for directly manipulating the goal
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
248

base, or a user-defined action which is specific to the
agent program:
datatype cap = basic Bcap | adopt Φ
L
| drop Φ
L
The type Bcap is some type for identifying actions, in
our case the type for strings.
An action transforms the mental state in which it
is executed. In fact, for any action different from adopt
and drop it is sufficient to consider only a transforma-
tion of the belief base as the effect on the goal base
can be derived from the semantics of GOAL.
The transformation of mental states is partially de-
fined by a function T of the type Bcap ⇒ mental-state
⇒ Φ
L
list option: given a mental state and an action
identifier, optionally a new belief base is returned.
That T only optionally returns a new belief base is
a result of the fact that a basic action may not be en-
abled in a given state. Notice that T is only concerned
with the agent specific actions, namely those with an
effect on the belief base.
The full effect on the mental state of executing a
basic action is captured by a function M :
fun mental-state-transformer :: cap ⇒ mental-state ⇒
mental-state option (M ) where
M (basic n) (Σ, Γ) = (case T n (Σ, Γ) of
Some Σ
0
⇒ Some (Σ
0
, [ψ←Γ. ¬ Σ
0
|=
P
ψ])
| - ⇒ None)
M (drop Φ) (Σ, Γ) = Some (Σ, [ψ←Γ. ¬ [ψ] |=
P
Φ])
M (adopt Φ) (Σ, Γ) = (if ¬ |=
P
(¬ Φ) ∧ ¬ Σ |=
P
Φ then
Some (Σ, List.insert Φ Γ) else None)
The case for agent specific actions captures the de-
fault commitment strategy where goals are only re-
moved once achieved.
On top of basic actions we introduce the notion of
a conditional action. A conditional action consists of
a basic action and a condition ϕ, denoted ϕ  do a. This
condition is specified as a mental state formula which
is evaluated in a given mental state. The action can
only be executed if the condition is met. As such, the
enabledness of a conditional action depends on both
T and ϕ. The set of conditional actions for an agent is
denoted Π.
Combining the notion of conditional actions and a
mental state transformer gives rise to the concept of a
transition between two states due to the execution of
an action, captured by the following definition:
definition transition :: mental-state ⇒ cond-act ⇒
mental-state ⇒ bool (- →- -) where
M →b M
0
≡ b ∈ Π ∧ M |=
M
(fst b) ∧
M (snd b) M = Some M
0
In the formalization, a conditional action b is a tu-
ple and fst b gives its condition while snd b gives its
basic action. The definition states that a transition M
→(ϕ  do a) M
0
exists if ϕ  do a is in Π, the condition
ϕ holds in M and M
0
is the resulting state.
A run of an agent program can be understood as
a sequence of mental states interleaved with condi-
tional actions (M
0
, b
0
, M
1
, b
1
, . . . , M
i
, b
i
, M
i+1
, . . .). We
do not consider the use of a stop criterion and instead
assume the program to continue indefinitely. It is not
a criterion for scheduled actions (those in the trace)
to necessarily be enabled and thus executed. In such
cases, we have M
i
= M
i+1
. We call a possible run of
the agent a trace. The codatatype command allows for
a coinductive datatype:
codatatype trace = Trace mental-state cond-act × trace
We further define functions st-nth and act-nth
which give the i-th state and conditional action of a
trace, respectively.
Analogous to mental states, our definition of a
trace includes all elements of the simple type, so we
need a definition:
definition is-trace :: trace ⇒ bool where
is-trace s ≡ ∀i. (act-nth s i) ∈ Π ∧
(((st-nth s i) →(act-nth s i) (st-nth s (i+1))) ∨
¬(∃M. (st-nth s i) →(act-nth s i) M) ∧
(st-nth s i) = (st-nth s (i+1)))
The definition requires that for all M
i
, b
i
, M
i+1
ei-
ther a transition M
i
→b
i
M
i+1
exists or the action is not
enabled and M
i
= M
i+1
. The definition makes it ex-
plicit that if a transition exists from M
i
then it is to
M
i+1
.
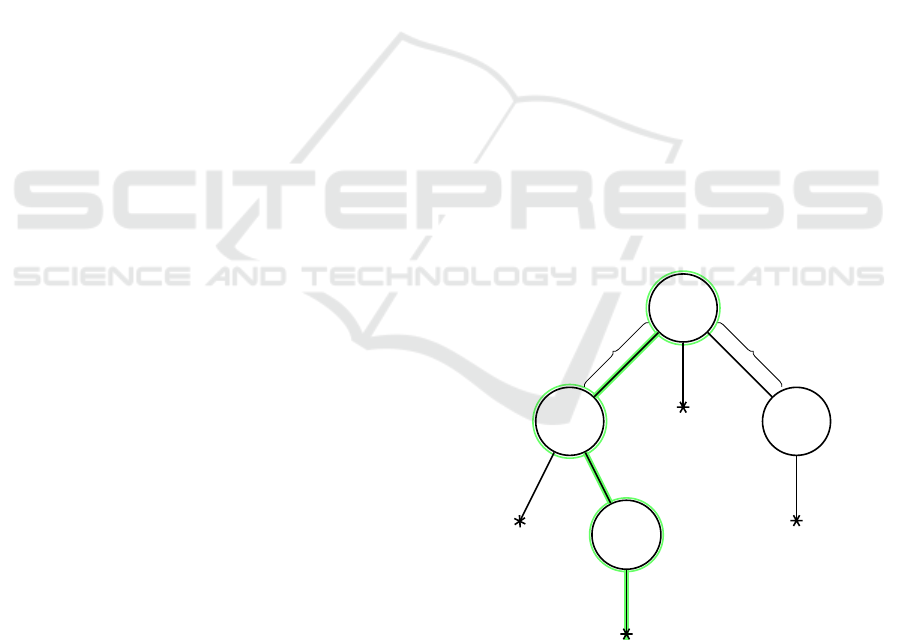
Figure 2 illustrates the set of all traces and high-
lights a single trace.
M
0
M
0,0
...
M
0,n
M
0,0,n
... ...
...
M
0
→b
0
M
0,0
M
0
→b
n
M
0,n
Figure 2: Visualization of the set of all traces, highlighting
a single trace.
For any scheduling of actions by the agent, we as-
sume weak fairness. Consequently, we have that the
traces are fair:
definition fair-trace :: trace ⇒ bool where
Machine-checked Verification of Cognitive Agents
249

fair-trace s ≡ ∀ b ∈ Π. ∀ i. ∃ j > i. act-nth s j = b
At any point in a fair trace, for any action there
always exists a future point where it is scheduled for
execution. The meaning of an agent is defined as the
set of all possible fair traces starting from a predeter-
mined initial state M
0
:
definition Agent :: trace set where
Agent ≡ {s . is-trace s ∧ fair-trace s ∧ st-nth s 0 = M
0
}
With the newly introduced terminology, it be-
comes rather straightforward to express the seman-
tics of the new components in formulas regarding en-
abledness:
M |=
E
(enabled-basic a) = (a ∈ Cap ∧ M a M 6= None)
M |=
E
(enabledond b) = (∃M
0
. (M →b M
0
))
Here, Cap is the set of the agent’s basic actions.
For the second case, a similar check is built-in to the
transition definition.
We introduce the shorthand notation ϕ[s i] for eval-
uating the mental state formula ϕ in the i-th state of a
trace s.
An extended proof system `
E
is obtained by in-
cluding the rules of Table 2 which state syntactic
properties of enabledness.
Table 2: Enabledness of actions.
E1
E
(ϕ  do a) ∈ Π =⇒
`
E
enabled (ϕ  do a) ←→ (ϕ ∧ enabledb a)
E2
E
`
E
enabledb (drop Φ)
R3
E
¬ |=
P
(¬ Φ) =⇒
`
E
¬ (B
E
Φ) ←→ enabledb (adopt Φ)
R4
E
|=
P
(¬ Φ) =⇒ `
E
¬ (enabledb (adopt Φ))
R5
E
∀M. ∇M −→ T a M 6= None =⇒
`
E
enabledb (basic a)
Theorem 4.3 (Soundness of `
E
). The proof system `
E
is sound with respect to the semantics of mental state
formulas including enabledness |=
E
for any proper
mental state (∇ M):
∇ M =⇒ `
E
ϕ =⇒ M |=
E
ϕ
Proof. By induction on the proof rules and using The-
orem 4.2.
4.3 Hoare Logic for GOAL
To reason about transition steps due to execution of
actions, we set up a specially tailored Hoare logic.
By means of Hoare triples, we can specify the ef-
fect of executing an action using mental state formu-
las as pre- and postconditions. We distinguish be-
tween Hoare triples for basic actions and conditional
actions, but as becomes apparent later, there is a close
relationship between the two. We introduce the usual
Hoare triple notation: {ϕ} a {ψ} for basic actions
and {ϕ} υ  do b {ψ} for conditional actions. The no-
tation masks two constructors for a simple datatype
hoare-triple consisting of two formulas and a basic or
conditional action.
We now give the semantics of Hoare triples. The
pre- and postconditions can only be evaluated given
a current mental state. However, for the definition of
the semantics we quantify over all mental states. In
other words, a Hoare triple is only true if it holds at
any point in the agent program:
|=
H
{ ϕ } a { ψ } = (∀ M.
(M |=
E
ϕ ∧ (enabledb a) −→ the (M a M) |=
M
ψ) ∧
(M |=
E
ϕ ∧ ¬(enabledb a) −→ M |=
M
ψ))
|=
H
{ ϕ } (υ  do b) { ψ } = (∀ s ∈ Agent. ∀ i.
(ϕ[s i] ∧ (υ  do b) = (act-nth s i) −→ ψ[s (i+1)])
The first case is for basic actions. In any state, if
the precondition is true, the postcondition should hold
in the state obtained by executing the action a. Other-
wise, it should hold in the same state as the action is
not enabled and thus not executed. The second case
is for conditional actions. The case is analogous, but
the enabledness of the action, and thus whether the
successor state is unchanged, is implicit due to the
definition of traces.
Lemma 4.4 (Relation between Hoare triples for basic
and conditional actions).
|=
H
{ ϕ ∧ ψ } a { ϕ
0
} =⇒
∀ s ∈ Agent. ∀ i. ((ϕ ∧ ¬ψ) −→ ϕ
0
)[s i] =⇒
|=
H
{ ϕ } (ψ  do a) { ϕ
0
}
Proof. We need to show ϕ
0
[s (i+1)]. We can assume
(ϕ[s i] ∧ (υ  do b) = (act-nth s i). We then distinguish
between the cases of whether ψ[s i] holds. If it holds,
the basic action Hoare triple can be used to infer ϕ
0
[s
(i+1)]. If it does not hold, the result follows from the
second assumption as the action a is not enabled and
thus st-nth s i = st-nth (i+1).
Lemma 4.4 is used to prove Theorem 5.3.
5 SPECIFICATION OF AGENTS
In this section, we are concerned with the specifica-
tion of agent programs using Hoare triples and find-
ing a Hoare system to be able to derive Hoare triples
for the specified agent program. Because the low-
level semantics of GOAL is not based on Hoare logic,
we need to show that the low-level semantics can be
derived from an agent specification based on Hoare
triples. More specifically, it suffices to show that it
is possible to come up with a definition of T which
satisfies all the specified Hoare triples.
We define an agent specification as a list:
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
250

type-synonym ht-specification = ht-spec-elem list
The elements of such a list are tuples containing
an action identifier, a mental state formula which is
the decision rule for the action and lastly a list of
Hoare triples which specify the frame and effect ax-
ioms for the action:
type-synonym ht-spec-elem = Bcap × Φ
M
× hoare-triple
list
We have not touched upon this earlier, but frame
axioms specify what does not change when executing
an action and effect axioms specify what does change,
i.e. what are the effects of executing the action. An-
other note is that we only allow a single decision rule
in our setup. We could allow for multiple rules per
action. Instead, we assume that if there are multiple
rules they have been condensed to a single rule using
disjunction.
5.1 Satisfiability Problem
Our task is now to show that a low-level semantics can
be derived from a specification, i.e. that there exists
some T which complies with the specification. This
may also be seen as a model existence problem which
has already been studied for other areas of logic. An-
other perspective on this problem is to consider it as
a satisfiability problem, or equivalently that there are
no contradictions.
The definition of satisfiability is split into two
parts, quantifying over any proper mental state and
every element of the specification:
definition satisfiable :: ht-specification ⇒ bool where
satisfiable S ≡ ∀ M. ∇ M −→
(∀s ∈ set S. sat-l M s ∧ sat-r M s)
The first part is concerned with those mental states
where the action in question is enabled:
fun sat-l :: mental-state ⇒ ht-spec-elem ⇒ bool where
sat-l M (a, Φ, hts) = (M |=
M
Φ −→ (∃Σ. sat-b M hts Σ))
When the action is enabled, for all states there
should exist a belief base which satisfies all Hoare
triples for this action:
definition sat-b :: mental-state ⇒ hoare-triple list ⇒ Φ
L
list ⇒ bool where
sat-b M hts Σ ≡
(¬ fst M |=
P
⊥ −→ ¬ Σ |=
P
⊥) ∧
(∀ht ∈ set hts. M |=
M
pre ht −→
(Σ, [ψ←snd M. ¬ Σ |=
P
ψ] ) |=
M
post ht)
For a belief base to be satisfiable in this context, we
require:
1. that the consistency is preserved, and
2. that the postcondition holds in the new mental
state if the precondition holds in the current men-
tal state (the new goal base is derived by removing
achieved goals from the current goal base).
The second part of the satisfiability definition is
concerned with those mental states where the action
in question is not enabled:
fun sat-r :: mental-state ⇒ ht-spec-elem ⇒ bool where
sat-r M (-, Φ, hts) =
(M |=
M
¬ Φ −→
(∀ht ∈ set hts. M |=
M
pre ht −→ M |=
M
post ht))
In such a case the postcondition should hold in the
same state if the precondition holds.
Because of the way we have set up the specifi-
cation type, a definition is-ht-specification ensures that
the specification is satisfiable and that each element
reflects the specification of a distinct action.
We briefly mentioned that satisfiability entails the
existence of a T which matches the agent specifica-
tion. To show this, we first define what it means for a
T to comply with an agent specification:
definition complies :: ht-specification ⇒ bel-upd-t ⇒ bool
where
complies S T ≡ (∀s∈set S. complies-hts s T ) ∧
(∀n. n /∈ set (map fst S) −→ (∀M. T n M = None))
Again we can define this for each element of spec-
ification individually. Furthermore, we require that
T is only defined for action identifiers present in the
specification.
definition complies-hts :: (Bcap × Φ
M
× hoare-triple list)
⇒ bel-upd-t ⇒ bool where
complies-hts s T ≡ ∀ ht∈set (snd (snd s)).
is-htb-basic ht ∧ (∀M. ∇M −→
complies-ht M T (fst (snd s)) (the (htb-unpack ht)))
The following definition has a convoluted syntax.
Essentially, we quantify over all proper mental states
and assert compliance for each Hoare triple:
fun complies-ht :: mental-state ⇒ bel-upd-t ⇒ Φ
M
⇒
(Φ
M
× Bcap × Φ
M
) ⇒ bool where
complies-ht M T Φ (ϕ, n, ψ) =
((M |=
M
Φ ←→ T n M 6= None) ∧
(¬ (fst M) |=
P
⊥ −→ T n M 6= None −→
¬the (T n M) |=
P
⊥) ∧
(M |=
M
ϕ ∧ M |=
M
Φ −→
the (M ∗ T (basic n) M) |=
M
ψ) ∧
(M |=
M
ϕ ∧ M |=
M
¬ Φ −→ M |=
M
ψ))
Note that in the preceding definition, M ∗ T cor-
responds to the mental state transformer M where T
is not fixed by the agent. Furthermore, the definition
packs a number of important properties:
1. that the formula ϕ is the sole factor for enabled-
ness of the action,
2. that consistency is preserved for belief bases, and
lastly
3. that it matches the semantics of the Hoare triple.
Arguably, the definitions of satisfiability and com-
pliance could be optimized for readability and less re-
dundancy.
Machine-checked Verification of Cognitive Agents
251

We now show that compliance is entailed by sat-
isfiability. An interesting partial result is that because
each element of specification is for a distinct action,
the existence of a (partial) T can be shown for each
action and used to show the existence of a T for the
full specification:
Lemma 5.1 (Disjoint compliance). The existence of
a T for each element of the specification can be used
to show the existence of a T for the full specification.
is-ht-specification S =⇒
∀s∈set S. ∃ T . complies-hts s T =⇒
∃T . complies S T
Proof. Since there is no overlap between each partial
T
x
obtained from the assumptions, we combine the
partial functions into a single function T which com-
plies with the specification by construction.
We then prove that for any specification which fol-
lows the definition (most importantly, it is thus satis-
fiable) there exists a compliant T .
Lemma 5.2 (Compliance). There exists a belief up-
date function T for any proper agent specification
which is satisfiable.
is-ht-specification S =⇒ ∃T . complies S T
Proof. By construction of a T for each specification
element using the definition of satisfiable bases and
ultimately using Lemma 5.1.
5.2 Derived Proof System
Our primary focus is on proving the truth of partic-
ular Hoare triples. Exactly how this plays into prov-
ing properties of agents becomes apparent later. To
this end, we need a Hoare logic proof system. While
we can state the general proof rules for Hoare triples,
as well as axioms regarding pre- and postconditions
involving the special belief and goal modalities, the
most important properties of any agent program de-
pend on the agent specification. The user needs to
specify a number of effect and frame axioms. They
state what is changed and what is not changed by
executing the action. Outside of the general rules
for proving Hoare triples, we include a special im-
port rule which allows for any of the specified Hoare
triples as axioms. The soundness of the import rule
follows directly from the compliance of T .
The proof system is defined inductively:
inductive derive
H
:: hoare-triple ⇒ bool (`
H
) where
The import rule allows for a specified Hoare triple
as an axiom:
(n, Φ, hts) ∈ set S =⇒ { ϕ } (basic n) { ψ } ∈ set hts =⇒
`
H
{ ϕ } (basic n) { ψ }
The persist rule states that a goal persists as either
a belief or goal unless it is dropped:
¬ is-drop a =⇒ `
H
{ G Φ } a { B Φ ∨ G Φ }
The inf rule states that nothing happens if the pre-
condition implies that the action is not enabled:
|=
E
(ϕ −→ ¬(enabledb a)) =⇒ `
H
{ ϕ } a { ϕ }
The following rules state important properties of
the adopt and drop actions:
`
H
{ B Φ } (adopt ψ) { B Φ }
`
H
{ ¬ (B Φ) } (adopt ψ) { ¬ (B Φ) }
`
H
{ B Φ } (drop ψ) { B Φ }
`
H
{ ¬ (B Φ) } (drop ψ) { ¬ (B Φ) }
¬ |=
P
(¬ Φ) =⇒ `
H
{ ¬ (B Φ) } (adopt Φ) { G Φ }
`
H
{ G Φ } (adopt ψ) { G Φ }
¬ |=
P
(ψ −→ Φ) =⇒
`
H
{ ¬ (G Φ) } (adopt ψ) { ¬ (G Φ) }
|=
P
(Φ −→ ψ) =⇒ `
H
{ G Φ } (drop ψ) { ¬ (G Φ) }
`
H
{ ¬(G Φ) } (drop ψ) { ¬ (G Φ) }
`
H
{ ¬(G (Φ ∧ ψ)) ∧ (G Φ) } (drop ψ) { G Φ }
Finally, we have the structural rules:
`
H
{ ϕ ∧ ψ } a { ϕ
0
} =⇒ |=
M
(ϕ ∧ ¬ψ −→ ϕ
0
) =⇒
`
H
{ ϕ } (ψ  do a) { ϕ
0
}
|=
M
(ϕ
0
−→ ϕ) =⇒ `
H
{ ϕ } a { ψ } =⇒
|=
M
(ψ −→ ψ
0
) =⇒ `
H
{ ϕ
0
} a { ψ
0
}
`
H
{ ϕ
1
} a { ψ
1
} =⇒ `
H
{ ϕ
2
} a { ψ
2
} =⇒
`
H
{ ϕ
1
∧ ϕ
2
} a { ψ
1
∧ ψ
2
}
`
H
{ ϕ
1
} a { ψ } =⇒ `
H
{ ϕ
2
} a { ψ } =⇒
H
{ ϕ
1
∨ ϕ
2
} a { ψ }
Due to the sheer number of proof rules, proving
the soundness of the system becomes quite involved.
Theorem 5.3 (Soundness of `
H
). The Hoare system
`
H
is sound with respect to the semantics of Hoare
triples |=
H
.
`
H
H =⇒ |=
H
H
Proof. By induction on the proof rules. The import
rule follows directly from Lemma 5.2. The rule for
conditional actions follows from Lemma 4.4. The re-
maining rules follow from the semantics of mental
states |=
E
and the semantics of Hoare triples |=
H
.
6 PROVING CORRECTNESS
In this section, we describe how to prove temporal
properties of agents by means of a temporal logic
which is constructed on top of the logic for GOAL.
Ultimately, we show that proofs of certain liveness
and safety properties can be reduced to proofs of
Hoare triples in the Hoare logic.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
252

6.1 Temporal Logic
We start by setting up a datatype for temporal logic
formulas with just two temporal operators and where
the type variable
0
a allows for any type of atoms:
datatype
0
a Φ
T
=
F (⊥
T
) |
Atom
0
a |
Negation
0
a Φ
T
(¬
T
) |
Implication
0
a Φ
T
0
a Φ
T
(infixr −→
T
60) |
Disjunction
0
a Φ
T
0
a Φ
T
(infixl ∨
T
70) |
Conjunction
0
a Φ
T
0
a Φ
T
(infixl ∧
T
80) |
init |
until
0
a Φ
T
0
a Φ
T
The Boolean operators each have a subscript to
avoid ambiguity, e.g. −→
T
for implication.
Additional temporal operators can be defined by
combining the existing ones. The always operator 
states that the operand remains true forever:
definition always ::
0
a Φ
T
⇒
0
a Φ
T
() where
ϕ ≡ ϕ until ⊥
T
The eventuality operator  states that the operand is
true at some point:
definition eventuality ::
0
a Φ
T
⇒
0
a Φ
T
() where
ϕ ≡ ¬
T
( (¬
T
ϕ))
The unless operator states for ϕ unless ψ that if ϕ be-
comes true then it remains true until ψ becomes true:
definition unless ::
0
a Φ
T
⇒
0
a Φ
T
⇒
0
a Φ
T
where
ϕ unless ψ ≡ ϕ −→
T
(ϕ until ψ)
In the following, the type Φ
T M
is for temporal
logic with the belief and goal modalities as atoms.
The semantics of temporal logic for agents is evalu-
ated in terms of a trace s and a natural number i, in-
dicating that the formula is to be evaluated in the i-th
state of trace s:
s, i |=
T
⊥
T
= False
s, i |=
T
(Atom x) = ((Atom x)[s i]
M
)
s, i |=
T
(¬
T
p) = (¬ (s, i |=
T
p))
s, i |=
T
(p −→
T
q) = ((s, i |=
T
p) −→ (s, i |=
T
q))
s, i |=
T
(p ∨
T
q) = ((s, i |=
T
p) ∨ (s, i |=
T
q))
s, i |=
T
(p ∧
T
q) = ((s, i |=
T
p) ∧ (s, i |=
T
q))
s, i |=
T
init = (i = 0)
s, i |=
T
(ϕ until ψ) = ((∃ j ≥ i. s, j |=
T
ψ ∧
(∀k ≥ i. j > k −→ s, k |=
T
ϕ)) ∨ (∀k ≥ i. s, k |=
T
ϕ))
The Boolean operators are defined using Isabelle’s
operators. Identical results can be achieved using the
more traditional if-then-else constructs if one desires
a more programming-like style. The case for atoms
simply delegates the task to the semantics functions
for mental state formulas. The case for init is true
when i = 0, i.e. when we are at the very first state of
the trace. The more complicated case for until war-
rants further explanation: either ϕ remains true until a
future point j where ψ becomes true, or ϕ remains true
forever.
6.2 Liveness and Safety Properties
There is a close relationship between proving Hoare
triples and proving liveness and safety properties of
an agent. Concerning safety, we can show that ϕ is
a stable property by proving ϕ unless F. In case we
also have init −→ϕ, we say that ϕ is an invariant of
the agent program. We now prove that, due to the
unless operator, this safety property can be reduced to
proving a Hoare triple for each conditional action.
Theorem 6.1. After executing any action from Π ei-
ther ϕ persists or ψ becomes true and we can con-
clude ϕ unless ψ and conversely.
∀(υ  do b) ∈ Π. |=
H
{ ϕ ∧ ¬ ψ } (υ  do b) { ϕ ∨ ψ })
←→ Agent |=
T
ϕ unless ψ
Proof. The −→ direction is shown by contraposition
where the semantics of temporal logic leads us to a
contradiction. The ←− direction is shown by a case
distinction of |=
M
ϕ in some arbitrarily chosen state.
Liveness properties involve showing that a partic-
ular state is always reached from a given situation. A
certain subclass of these properties is captured by the
ensures operator:
definition ensures ::
0
a Φ
T
⇒
0
a Φ
T
⇒
0
a Φ
T
where
ϕ ensures ψ ≡ (ϕ unless ψ) ∧
T
(ϕ −→
T
ψ)
Here, ϕ ensures ψ informally means that ϕ guaran-
tees the realization of ψ.
Also for the ensures operator we can show that it
can be reduced to proofs of Hoare triples.
Theorem 6.2. The proof of an ensures property can
be reduced to the proof of a set of Hoare triples.
∀b ∈ Π. |=
H
{ ϕ ∧ ¬ ψ } b { ϕ ∨ ψ } =⇒
∃b ∈ Π. |=
H
{ ϕ ∧ ¬ ψ } b { ψ } =⇒
Agent |= ϕ ensures ψ
Proof. From the fact that any trace in Agent is a fair
trace, we obtain a contradiction using the semantics
of temporal logic |=
T
and of Hoare triples |=
H
.
Finally, we introduce the temporal operator 7→
(“leads to”). The property ϕ 7→ ψ is similar to ensures
except that it does not require ϕ to remain true until
ψ is realized. It is defined from the ensures operator
inductively:
inductive leads-to :: Φ
T M
⇒ Φ
T M
⇒ bool (infix 7→ 55)
where
base: ∀s ∈ Agent. ∀i. s, i |=
T
(ϕ ensures ψ) =⇒ ϕ 7→ ψ |
imp: ϕ 7→ χ =⇒ χ 7→ ψ =⇒ ϕ 7→ ψ |
disj: ∀ϕ ∈ set ϕ
L
. ϕ 7→ ψ =⇒ disL ϕ
L
7→ ψ
The rule imp states a transitive property and disj
states a disjunctive property. The function disL forms
a disjunction from a list of formulas:
Machine-checked Verification of Cognitive Agents
253

fun disL::
0
a Φ
T
list ⇒
0
a Φ
T
where
disL [] = ⊥
T
|
disL [ϕ] = ϕ |
disL (ϕ # ϕ
L
) = ϕ ∨
T
disL ϕ
L
We can prove that the temporal operator 7→ can be
used to state a correctness property for agents.
Lemma 6.3. The proof of a certain class of temporal
properties can be reduced to a proof of the “leads to”
operator 7→.
ϕ 7→ ψ =⇒ ∀s ∈ Agent. ∀ i. s, i |=
T
(ϕ −→
T
ψ)
Proof. By induction on the rules and using the seman-
tics of temporal logic |=
T
.
Lemma 6.3 is used to prove that temporal logic
statements of the form P 7→ Q in fact state temporal
properties of agents.
7 AN EXAMPLE AGENT
In this section, we showcase how to use the verifica-
tion framework in Isabelle/HOL to prove the correct-
ness of a simple agent which can solve a simple task
to collect a block. Informally, the agent initially is
located in a special dropzone location where a block
is to be delivered. The agent must go to a room con-
taining such a block. Before the agent can pick up a
block, it must move right next to it. Finally, the agent
must return to the dropzone and deliver the block.
The belief base of the initial mental state is:
[ in-dropzone, ¬ in-room, ¬ holding, ¬ at-block ]
The goal base of the initial mental state is:
[ collect ]
The initial belief and goal bases capture the initial
configuration:
• The agent is located in the dropzone.
• Naturally, the agent is therefore not in a room con-
taining a block, and consequently also not next to
a block.
• The agent is not holding a block.
• The goal of the agent is to collect a block.
Furthermore, our example agent has a number of
available actions:
• go-dropzone: The agent moves to the dropzone.
• go-room: The agent moves to a room containing a
block.
• go-block: When in a room containing a block, the
agent moves right next to the block.
• pick-up: If the agent is right next to a block, the
agent will pick it up.
• put-down: If the agent is carrying a block, the
agent will put it down.
Each action has a condition which states when the
action can be performed. This is specified by the fol-
lowing formulas for enabledness:
enabled(go-dropzone) ≡ B in-room ∧ B holding
enabled(go-room) ≡ B in-dropzone ∧ ¬ (B holding)
enabled(go-block) ≡ B in-room ∧ ¬ (B at-block) ∧
¬ (B holding)
enabled(pick-up) ≡ B at-block ∧ ¬ (B holding)
enabled(put-down) ≡ B holding ∧ B in-dropzone
Because of the simplicity of our example, only
one of these conditions is true in any given state. In
other words, there is only ever one meaningful action.
Furthermore, we must specify effect axioms for
the actions. In our case, each action has exactly one
effect axiom:
{ B in-room ∧ B holding } go-dropzone { B in-dropzone }
{ B in-dropzone ∧ ¬ (B holding) } go-room { B in-room }
{ B in-room ∧ ¬ (B at-block) ∧ ¬ (B holding) }
go-block { B at-block }
{ B at-block ∧ ¬ (B holding) } pick-up { B holding }
{ B in-dropzone ∧ B holding } put-down { B collect }
Since we do not have the space to go through the
details, the specification of frame axioms and proofs
of invariants has been left out of the paper.
We define the belief update function as some T
which complies with the specification. We are al-
lowed to do this if we can prove that such a speci-
fication exists.
definition T
x
≡ SOME T . complies S
x
T
We need to prove that our different example com-
ponents actually compose a single agent program:
interpretation bw4t:
single-agent-program T
x
(set Π
x
) M
0
x
S
x
The requirements of a single agent program has
not been described earlier. It requires showing the ex-
istence of some T which complies with the specifica-
tion. This is due to the definition of T
x
using SOME
which is based on Hilbert’s epsilon operator i.e. the
axiom of choice. The main issue is thus to show the
satisfiability of the specification due to Lemma 5.2.
The proof is rather lengthy and is not shown here.
The main point of interest is the proof of the state-
ment involving the “leads to” operator:
lemma B in-dropzone ∧ ¬ (B at-block) ∧ ¬ (B holding) ∧
G collect 7→ B collect
This captures that the desired state, where the
agent believes to have collected the block, is reached
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
254

from the initial configuration of the agent. The in-
ductive definition of the operator makes it possible to
split the proof into subproofs for each step:
have in-dropzone ∧ ¬ (B at-block) ∧ ¬ (B holding) ∧ G
collect 7→ B in-room ∧ ¬ (B at-block) ∧ ¬ (B holding) ∧ G
collect
. . .
moreover have B in-room ∧ ¬ (B at-block) ∧ ¬ (B holding)
∧ G collect 7→ B in-room ∧ B at-block ∧ ¬ (B holding) ∧
G collect
. . .
moreover have B in-room ∧ B at-block ∧ ¬ (B holding) ∧
G collect 7→ B in-room ∧ B holding ∧ G collect
. . .
moreover have B in-room ∧ B holding ∧ G collect 7→ B
in-dropzone ∧ B holding ∧ G collect
. . .
moreover have B in-dropzone ∧ B holding ∧ G collect 7→
B collect
. . .
ultimately show ?thesis using imp by blast
Every step in the proof above is achieved by a sin-
gle action; again this is due to the simplicity of the
example. We can easily conceive of programs which
have multiple paths to the desired state in which case
all paths need to be considered.
Due to Lemma 6.3, the proof of B in-dropzone ∧
¬ (B at-block) ∧ ¬ (B holding) ∧ G collect 7→ B collect
shows a correctness property of our simple example
agent.
8 CONCLUSIONS
We have presented a formalization of a verification
framework for GOAL agents in its entirety. Further-
more, we have demonstrated how it can be applied to
an agent specified in the agent logic by means of a
simple example.
There are still a number of issues for our atten-
tion in the future. As was clear in our earlier work,
the original formulation of the verification framework
has some limitations. First, the framework is lim-
ited to single agent programs. Long term, the aim
is to verify programs with multiple communicating
agents. To this end, we want to explore how exist-
ing work on extending the framework can be inte-
grated into our Isabelle/HOL formalization (Bulling
and Hindriks, 2009). Second, the agent logic is lim-
ited to propositional logic which not only causes an
inconvenience in specifying complex agent programs,
but also means that certain things cannot be modelled.
Outside of extending the framework, there are also
a number of usability concerns to address. This has
little theoretical significance, but it would be inter-
esting to experiment with providing more means of
automation for conducting proofs of agent properties.
While we did not have the space to show the proofs of
our example agent in full details, we note that it can
become quite tedious to conduct these proofs manu-
ally. Due to the complexity of the structures involved
in the proofs, the automation of Isabelle/HOL is not
geared towards such proofs out-of-the-box. Further
work is required to enable more automation.
Nevertheless, the present paper demonstrates that
a theorem proving approach to verifying agents is fea-
sible. Furthermore, because we have formalized the
framework in a proof assistant, we are able to provide
a high level of assurance as everything is checked by
Isabelle/HOL. In conclusion, we are excited to see the
future potential of the framework enabled by the ca-
pabilities of Isabelle/HOL.
ACKNOWLEDGEMENTS
Koen V. Hindriks has provided valuable insights
into the details of GOAL. Jørgen Villadsen, Frederik
Krogsdal Jacobsen and Asta Halkjær From have com-
mented on drafts.
REFERENCES
Alechina, N., Dastani, M., Khan, A. F., Logan, B., and
Meyer, J.-J. (2010). Using Theorem Proving to Ver-
ify Properties of Agent Programs. In Specification
and Verification of Multi-agent Systems, pages 1–33.
Springer.
Bordini, R., Fisher, M., Wooldridge, M., and Visser, W.
(2004). Model Checking Rational Agents. Intelligent
Systems, IEEE, 19:46–52.
Bulling, N. and Hindriks, K. V. (2009). Towards a Verifica-
tion Framework for Communicating Rational Agents.
In Multiagent System Technologies, 7th German Con-
ference, MATES 2009, Hamburg, Germany, Septem-
ber 9-11, 2009. Proceedings, Lecture Notes in Com-
puter Science, pages 177–182. Springer.
Calegari, R., Ciatto, G., Mascardi, V., and Omicini, A.
(2021). Logic-Based Technologies for Multi-Agent
Systems: Summary of a Systematic Literature Re-
view. In Proceedings of the 20th International Confer-
ence on Autonomous Agents and Multiagent Systems,
AAMAS ’21, pages 1721––1723. International Foun-
dation for Autonomous Agents and Multiagent Sys-
tems.
de Boer, F. S., Hindriks, K. V., van der Hoek, W., and
Meyer, J.-J. (2007). A verification framework for
agent programming with declarative goals. Journal
of Applied Logic, 5:277–302.
Dennis, L., Fisher, M., Webster, M. P., and Bordini, R. H.
(2012). Model checking agent programming lan-
guages. Automated Software Engineering, 19:5–63.
Machine-checked Verification of Cognitive Agents
255

Dennis, L. A. and Fisher, M. (2009). Programming Verifi-
able Heterogeneous Agent Systems. In Programming
Multi-Agent Systems, pages 40–55. Springer.
Dix, J., Logan, B., and Winikoff, M. (2019). Engineer-
ing Reliable Multiagent Systems (Dagstuhl Seminar
19112). Dagstuhl Reports, 9(3):52–63.
Gomes, V. B. F., Kleppmann, M., Mulligan, D. P., and
Beresford, A. R. (2017). Verifying strong eventual
consistency in distributed systems. Proc. ACM Pro-
gram. Lang., 1(OOPSLA).
Hindriks, K. V. (2009). Programming Rational Agents in
GOAL. In Multi-Agent Programming: Languages,
Tools and Applications, pages 119–157. Springer.
Hindriks, K. V., de Boer, F. S., van der Hoek, W., and
Meyer, J.-J. (2001). Agent Programming with Declar-
ative Goals. In Intelligent Agents VII Agent The-
ories Architectures and Languages, pages 228–243.
Springer.
Hindriks, K. V. and Dix, J. (2014). GOAL: A Multi-agent
Programming Language Applied to an Exploration
Game. In Agent-oriented software engineering, pages
235–258. Springer.
Java Pathfinder (2021). https://github.com/javapathfinder/
jpf-core/wiki. Accessed: 2021-11-22.
Jensen, A. (2021a). Towards Verifying a Blocks World for
Teams GOAL Agent. In Rocha, A., Steels, L., and
van den Herik, J., editors, Proceedings of the 13th In-
ternational Conference on Agents and Artificial Intel-
ligence, volume 1, pages 337–344. Science and Tech-
nology Publishing.
Jensen, A. (2021b). Towards Verifying GOAL Agents in
Isabelle/HOL. In Rocha, A., Steels, L., and van
den Herik, J., editors, Proceedings of the 13th Inter-
national Conference on Agents and Artificial Intelli-
gence, volume 1, pages 345–352. Science and Tech-
nology Publishing.
Jensen, A., Hindriks, K., and Villadsen, J. (2021). On Us-
ing Theorem Proving for Cognitive Agent-Oriented
Programming. In Rocha, A., Steels, L., and van
den Herik, J., editors, Proceedings of the 13th Inter-
national Conference on Agents and Artificial Intelli-
gence, volume 1, pages 446–453. Science and Tech-
nology Publishing.
Jensen, A. B. (2021c). A theorem proving approach to for-
mal verification of a cognitive agent. In Matsui, K.,
Omatu, S., Yigitcanlar, T., and Rodriguez-Gonz
´
alez,
S., editors, Distributed Computing and Artificial In-
telligence, Volume 1: 18th International Conference,
DCAI 2021, Salamanca, Spain, 6-8 October 2021,
volume 327 of Lecture Notes in Networks and Sys-
tems, pages 1–11. Springer.
Jongmans, S.-S., Hindriks, K., and Riemsdijk, M. (2010).
Model Checking Agent Programs by Using the Pro-
gram Interpreter. In Computational Logic in Multi-
Agent Systems, pages 219–237.
Koeman, V., Hindriks, K., and Jonker, C. (2018). Automat-
ing failure detection in cognitive agent programs. In-
ternational Journal of Agent-Oriented Software Engi-
neering, 6:275–308.
Nipkow, T., Paulson, L., and Wenzel, M. (2002).
Isabelle/HOL — A Proof Assistant for Higher-Order
Logic. Springer.
Ringer, T., Palmskog, K., Sergey, I., Gligoric, M., and Tat-
lock, Z. (2019). QED at Large: A Survey of Engineer-
ing of Formally Verified Software. Foundations and
Trends in Programming Languages, 5(2-3):102–281.
Shapiro, S., Lesp
´
erance, Y., and Levesque, H. J. (2002). The
Cognitive Agents Specification Language and Verifi-
cation Environment for Multiagent Systems. In Pro-
ceedings of the First International Joint Conference
on Autonomous Agents and Multiagent Systems: Part
1, AAMAS ’02, pages 19–26. Association for Com-
puting Machinery, New York, NY, USA.
Winikoff, M. (2010). Assurance of Agent Systems: What
Role Should Formal Verification Play? In Dastani,
M., Hindriks, K. V., and Meyer, J.-J. C., editors, Speci-
fication and Verification of Multi-agent Systems, pages
353–383. Springer US, Boston, MA.
Winikoff, M. and Cranefield, S. (2014). On the Testability
of BDI Agent Systems. Journal of Artificial Intelli-
gence Research, 51:71–131.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
256