Post-hoc Diversity-aware Curation of Rankings

Vassilis Markos

and Loizos Michael

1,2

Open University of Cyprus, Nicosia, Cyprus

CYENS Center of Excellence, Nicosia, Cyprus

Keywords:

Diversity, Preferences, Ranking, Shufﬂing.

Abstract:

We consider the problem of constructing rankings that exhibit a prescribed level of diversity. We take a black-

box view of the ranking procedure itself, and choose, instead, to post-hoc curate any given ranking, deviating

from the original ranking only to the extent allowed by any given constraints. The curation algorithm that we

present is oblivious to how diversity is measured, and returns shufﬂed versions of the original rankings that are

optimal in terms of their exhibited level of diversity. Our empirical evaluation on synthetic data demonstrates

the effectiveness and efﬁciency of our methodology, across a number of diversity metrics from the literature.

1 INTRODUCTION

The over-abundance of options in practically any facet

of modern life makes it unrealistic for any individ-

ual to meaningfully consider them all. An often-used

technology-mediated solution is to present these op-

tions in a ranked manner, as in the case of receiving a

ranked list of results when posing a web search query.

Although these rankings might capture some form

of preference that is centrally deﬁned by the technol-

ogy provider (e.g., ranking higher a well-connected

web page), it is generally the case that the preferences

expressed in rankings are adapted, through machine

learning, to the individual who is consuming the rank-

ings. Since the learning itself happens by observing

the choices that the individual makes through those

rankings, it is not surprising that this process leads to

echo chambers, where the individual and the learning

algorithm reinforce each other in a narrower and nar-

rower view of what is to be ranked (or ranked higher).

Although such echo chambers are already inher-

ently problematic, they can be even more so when

what is being ranked are other individuals. Such could

be the case, for instance, in social networking sites,

where the linear manner in which one’s “friends”

might be presented might lead, through the reinforce-

ment effect mentioned above, to one interacting with

only a “selected few”, exacerbating social stereotyp-

ing, biases against minorities, and discrimination.

Such considerations are particularly relevant in the

context of the EU-funded project “WeNet: The In-

ternet of Us”, which seeks to design and develop a

machine-mediated platform that connects a requester

with potential volunteers who can help the former ad-

dress a given task. To reduce the risk of the aforemen-

tioned issues arising, the project embraces diversity-

awareness as a core principle in machine-mediation.

Diversity-awareness should not be taken to imply

that maximum diversity is always desirable; instead,

it implies that diversity should be carefully balanced

in each particular context. Indeed, deciding when di-

versity should be promoted to ensure inclusion, and

when it should be restricted to ensure protection, is

an ethically-challenging question (Helm et al., 2021).

Accordingly, this work takes the position that how

diversity is measured, and the level of diversity that

should be exhibited by a ranking, are externally deter-

mined and given. Our proposed approach seeks, then,

to demonstrate how that diversity can be achieved by

curating a given ranking. The ranking itself is also as-

sumed to be externally determined, which in the case

of the WeNet project would correspond to a ranking

expressing the user’s preferences, as learned by ob-

serving the user interact within the WeNet platform.

Since deviating considerably from this given ranking

(while promoting or restricting the level of diversity

with respect to what is already present) would antag-

onize the purpose of having a user-speciﬁc ranking to

begin with, we assume that we are provided with con-

straints on what constitutes an acceptable deviation.

Given the above, our proposed curation algorithm

proceeds to shufﬂe the given ranking, while respect-

ing the given constraints, towards achieving a level of

diversity that is as close to the given speciﬁcations as

Markos, V. and Michael, L.

Post-hoc Diversity-aware Curation of Rankings.

DOI: 10.5220/0010839600003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 2, pages 323-334

ISBN: 978-989-758-547-0; ISSN: 2184-433X

323

possible. We prove that the algorithm returns optimal

rankings, in a formally speciﬁed sense, and we empir-

ically demonstrate its effectiveness and efﬁciency.

2 RELATED WORK

In what follows we review some of the most widely

used ranking methodologies and metrics of diversity.

2.1 Ranking Methodologies

An early but popular learning-to-rank methodology is

RankNet (Burges et al., 2005), where a Neural Net-

work learns a ranking function from observed pairs

(A,B) that are labeled by target probabilities P

that

A is preferred over B. RankNet uses a probabilistic

ranking cost function based on the target probabilities,

which it seeks to minimize using gradient descent.

A well-known variant of RankNet is DirectRank

oppel et al., 2019), which seeks to learn a quasi-

order (i.e., reﬂexive, anti-symmetric, transitive) re-

lation over an attribute space by observing pairwise

comparisons of attributes. Since this is beyond what

a standard Neural Network could do, DirectRank em-

ploys two identical Neural Networks that are trainable

on pairwise comparisons, and appropriately enhances

them and combines their outputs via an extra neuron.

In (Cakir et al., 2019), another Neural Network

based learning-to-rank methodology, FastAP, is pre-

sented. FastAP is a Deep Learning method that is

based on an algorithm that computes Average Preci-

sion (AP) signiﬁcantly faster than other approaches

— average precision is deﬁned as the (continuous or

discrete, accordingly) convolution of ranking preci-

sion with ranking recall. The architecture of FastAP

relies on learning a Deep Neural Network that maps

entities into a d-dimensional Euclidean space and is

optimized for AP. The contribution of the above work

is mostly focused on two axes: (i) a new signiﬁcantly

faster way to compute AP given a ranking is provided,

based on discretizing the underlying convolution and

using a histogram-based approach and; (ii) introduc-

ing a new learning strategy regarding mini-batching,

were batches are collected so as to form difﬁcult prob-

lems — i.e., they contain, among others, some highly

similar entities — so as to reduce time complexity

(namely, introducing harder learning examples helps

avoiding larger batches during the training phase).

In (Pfannschmidt et al., 2018), there are presented

two neural-based context-sensitive ranking method-

ologies that allow for a ranking to take into account

information regarding the ranked items and possible

underlying relations. The two methodologies pre-

sented, First-Aggregate-Then-Evaluate-Net (FATE-

Net) and First-Evaluate-Then-Aggregate-Net (FETA-

Net), both rely on computing a ranking score function

which maps pairs of the form (a,A), where a is an en-

tity and A a set of entities (i.e., a context), to a rank-

ing score. The difference between FETA and FATE is

that in FETA all scores for each entity are computed

using a ranking function that takes into account pair-

wise (in the simplest case) dependencies between en-

tities, while in FATE, a representative for each context

is computed ﬁrst, followed by the computation of the

ranking scores, according again to a context depen-

dent ranking (utility) function. (Oliveira et al., 2018)

present a ranking/comparison methodology which re-

lies on the analysis of paired comparison data. The

novelty introduced by (Oliveira et al., 2018) is that,

in contrast to other works, the comparison function

— i.e., the function used to infer whether a is more

preferred than b — is assumed to be only partially

known. Namely, it is assumed that the comparison

function belongs in a class of functions and make no

other assumptions regarding its form — in the ex-

periments presented in (Oliveira et al., 2018), this

class consists of all the functions whose inverse is a

polynomial of some certain degree with a bounded

support. Given the above assumptions, a new com-

parison/ranking methodology is presented, PolyRank,

which transforms the comparison learning problem

into an efﬁciently solvable Least-Squares problem.

Perhaps the most close in spirit to our work is

the learning-to-rank approach PRM (Personalized Re-

ranking Model) (Pei et al., 2019). PRM is a method-

ology that relies on re-ranking ranked lists accord-

ing to personalized criteria for a certain user. Like

our work, PRM can be appended on top of any rank-

ing methodology. Unlike our work, however, which

simply receives a ranked list, PRM expects to receive

ranking scores for each entity in an attribute space. It

takes into account the output of the ranking process

as well as relations among the ranked entities and the

user’s preferences/history (explicitly described) and

re-computes ranking scores, thus yielding a new rank-

ing that adheres to the user’s personal preferences.

2.2 Diversity Metrics

In this subsection we shall present in detail ways

in which diversity may be quantiﬁed. To begin

with, measures of diversity have been widely stud-

ied, especially within the context of Ecosystem Biol-

ogy as well as in other ﬁelds, such as business hu-

man resources management. Hence, there are nu-

merous metrics that measure diversity from certain

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

324

viewpoints and under certain assumptions. Here we

will discuss many already existing metrics as well as

present ways in which they could be utilized during a

ranking process with diversity in mind.

Starting with basic metrics, the most common one

is richness (Colwell, 2009), deﬁned as the number of

different classes present in a certain sample of entities

S. More formally, richness(S), is deﬁned as follows:

richness(S) := #{p ∈ P : p ∩ S 6= ∅}. (1)

A normalized version of richness, where we divide by

the total number of classes in X, is the following one:

richness(S) :=

richness(S)

. (2)

As one may observe, richness captures only

vaguely one of the many meanings diversity has in

everyday language as well as in several applications.

A simple way to obtain more meaningful informa-

tion regarding a sample’s diversity is through the

so-called Berger-Parker Index, BP(S), (Berger and

Parker, 1970), which corresponds to the maximum

abundance ratio of S, i.e.:

BP(S) := max

i=1,...,n

, (3)

where S is assumed to be partitioned into classes

,...,C

} and p

/#S, i = 1,...,n, are the cor-

responding relative frequencies. In order to facilitate

comparison with other metrics we will discuss later

on, we shall use the following version of BP(S) which

is increasing with respect to sample diversity:

BP(S) := 1 − BP(S). (4)

Another way to measure diversity is to introduce

more sophisticated metrics, such as Simpson’s Index

(Simpson, 1949) — often referred to as Herﬁndahl-

Hirschmann Index (HHI) in economics (Herﬁndahl,

1950). Simpson’s index, given a sample, S, parti-

tioned into classes {C

,...,C

}, represents the prob-

ability two randomly chosen entities to belong to the

same class. So, if p

, i = 1,. . . , n, are the relative fre-

quencies of all classes, C

, as above, then Simpson’s

Index, λ(S), equals:

λ(S) :=

∑

i=1

. (5)

In the same probabilistic view of diversity, one

may also deﬁne Shannon’s Index (Spellerberg and Fe-

dor, 2003), which coincides with Shannon’s entropy,

i.e.:

H(S) := −

∑

i=1

ln p

. (6)

The idea of Shannon’s Index is that, the more uni-

formly distributed sample entities are, the more di-

verse a sample should be considered, since it is more

difﬁcult to guess to which class a randomly drawn en-

tity would belong (Shannon, 1948). Indeed, Shan-

non’s Index is equal to 0 in cases where all classes but

one are empty, while it attains its maximum value,

lnn, for p

/n, i = 1,...,n.

A natural normalization would be to divide H(S)

by its maximum value, ln n, obtaining the following

normalized version of Shannon’s Index:

H(S) :=

H(S)

lnn

. (7)

Other more complex metric of diversity are the so-

called Hill numbers (Hill, 1973). Hill numbers are

given by the following formula, where q is a parame-

ter of the metric:

D(S) :=

∑

i=1

/1 − q

. (8)

Observe that for q = 1, equation (8) cannot be com-

puted, in which case we compute the corresponding

limit as q → 1, as shown in equation (9)

D(S) := e

H(S)

. (9)

The above metric, also referred to as effective number

of species, true diversity or gamma-diversity in Biol-

ogy, corresponds to the number of equally abundant

classes required to achieve the same average propor-

tional abundance as in S (Chao et al., 2010; Colwell,

2009).

While Hill numbers are used in Biology to mea-

sure species diversity at a global scale, there also other

metrics that allow for computing diversity at a more

local scale — e.g. in smaller natural habitats or in

local departments of businesses. One of the most

popular choices is alpha-diversity, (Whittaker, 1960),

which is deﬁned as follows:

(S) :=

∑

i=1

∑

j=1

q−1

j|i

/1 − q

. (10)

In the above, n is the total number of classes, as pre-

viously, while k corresponds to the total number of

local components — e.g., local habitats. Also, p

j|i

is the relative frequency of class C

at component i

while p

is the relative size of component i in S. Based

on alpha diversity, which is of local nature, another

popular diversity metric is beta-diversity, (Whittaker,

1960; Tuomisto, 2010), which is deﬁned as the ratio

between total and local diversity, namely:

(S) =

D(S)

(S)

. (11)

Another conceptualization of diversity is under-

standing diversity as the opposite of similarity. In this

Post-hoc Diversity-aware Curation of Rankings

325

sense, a natural choice could be to deﬁne diversity of

a given sample S as:

div(S) :=

∑

1≤i< j≤#S

i j

sim(x

)

. (12)

In the above, sim is any (normalized) similarity met-

ric deﬁned on S and w

i j

are non-negative weights that

sum to 1, while x

∈ S. Some choices for sim,

among others, could be L

metrics, cosine similarity,

etc.

3 POST-HOC SHUFFLING

In this section we present and discuss an abstract

framework that shufﬂes a given ranking to improve

its diversity according to a given metric µ. We start

by presenting an unconstrained version of the algo-

rithm where the shufﬂed ranking can differ arbitrarily

from the initial ranking, and then show how to extend

that to obey given constraints.

Let X = {x

,...,x

} be a ﬁnite set and consider

a ranking function r, i.e., a function that maps X to

a vector r(X). Now, let us assume that µ is a certain

metric we would like to monitor in r(X) — e.g., the

diversity of some part(s) of the returned ranked list.

More precisely, let without loss of generality µ take

values in [0,1] and let D ∈ P ([0,1])

be a sequence

of sets of µ’s desired values for each initial part of a

ranking r(X ) of the elements of a set X. For instance,

D in case of a set X = {x

} could have the

following form:

D = ({0.47}, [0.33, 0.65], {0.56, 0.89}, {1}) . (13)

So, if r(X) = (x

) is a ranking of X, D

informs us that it is desired that µ(r(X )

) = 0.47,

µ(r(X )

) ∈ [0.33,0.65], µ(r(X )

) ∈ {0.56,0.89} and

µ(r(X )

) = 1, where by r(X)

we denote the list con-

taining the ﬁrst i elements in r(X ).

Then, given a set X = {x

,...,x

} and a ranking,

r(X ), of it, we would like to shufﬂe r(X) or, equiv-

alently, provide an alternative ranking r

∗

such that

each initial part r

∗

(X)

of r

∗

(X) satisﬁes the condi-

tion µ(r

∗

(X)) ∈ D. However, it is not difﬁcult to see

that this is not possible in most cases. So, a more

realistic goal would be to demand that r

∗

(X) is not

globally inferior to any other ranking r(X). Formally,

we ﬁrst deﬁne D-loss, L

∗

), or simply L(r

∗

) when

D is obvious from the context, as follows:

L(r

∗

) := (dist(µ(r

∗

(X)

),D

))

i=1

. (14)

That is, L(r

∗

) is the sequence of distances of µ com-

puted at each initial part of r

∗

(X) from D

(the i-th set

in D). Given that, we shall say that a ranking r

dom-

inates another ranking r

if the following two condi-

tions hold:

L(r

)(i) ≤ L(r

)(i), for every i ∈ {1, . . . , n} (15)

L(r

)(i

) < L(r

)(i

), for some i

∈ {1, . . .,n} (16)

Given the above deﬁnition, a reasonable goal would

be to compute a shufﬂed ranking r

∗

that is not dom-

inated by any other shufﬂed ranking r

in the above

sense; i.e., the shufﬂed ranking r

∗

is Pareto optimal.

A simple method to determine r

∗

is given by Al-

gorithm 1, where at each iteration we compute the

next element of r

∗

(X) by sorting all unranked ele-

ments of X by ascending distance from D

, dist(µ(X \

∗

(X)), D

), and appending the ﬁrst element of that

list to r

∗

(X). Sorting is performed according to Algo-

rithm 2.

Algorithm 1: Diversity-aware shufﬂing.

1: procedure SHUFFLE(X, µ, D)

2: µRank ← ∅

3: for i = 1, . . . , X.length do

4: x

∗

← SORTBY(X,µRank,µ,D

)[0]

5: µRank[i] ← x

∗

6: end for

7: return µRank

8: end procedure

Algorithm 2: SORTBY sorting algorithm.

1: procedure SORTBY(X, µRank,µ,D

)

2: dists ← ∅  Empty dictionary.

3: for x ∈ X \ µRank do

4: dists[x] ← dist(µ(µRank ∪ {x}),D

)

5: end for

6: return dists.sortByValue()  Sort keys.

7: end procedure

Algorithm 1 performs a greedy search for the best

candidate to append next to the generated ranking as

described above. At this point we should remark that,

while SHUFFLE does not take the ranking function r

into account, is utilized in SORTBY at each iteration

as a tie-breaker. That is, from all the possible x ∈ X

that may satisfy x = argmin

x∈X\µRank

dist(µ(µRank ∪

{x}),D), we prefer the one ranked higher by r.

In the following lemma we state two obvious, yet

important, properties that the returned ranking, µRank

has:

Lemma 1. Given a set X = {x

,...,x

}, a ranking

function r, a metric µ and a sequence of desired val-

ues of µ, D, SHUFFLE as described in Algorithm 1

returns a ranking r

∗

(X) which satisﬁes the following

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

326

two conditions:

dist(µ(r

∗

(X)

),D) = min

x∈X

dist(µ({x}),D

) (17)

dist(µ(r

∗

(X)

),D) = min

Y ⊆X , #Y=i

∗

(X)

i−1

⊆Y

dist(µ(Y ),D

) (18)

for each i = 2,...,n.

Proof. Regarding r

∗

(X)

, it is chosen in order to sat-

isfy (17). Now, for some i ≥ 2 we observe that if

Y ⊆ X is such that #Y = i and r

∗

(X)

i−1

⊆ Y , then,

again, r

∗

(X)

i−1

∪ {x

∗

} — where x

∗

is determined as

in Algorithm 1 — satisﬁes the following inequality:

dist(µ(r

∗

(X)

i−1

∪ {x

∗

}),D

) ≤ dist(µ(Y ),D

). (19)

So, r

∗

satisﬁes both (17) as well as (18).

Using the above, we may now prove the follow-

ing:

Theorem 1. Given a set X = {x

,...,x

}, a ranking

function r, a metric µ and a sequence of desired val-

ues of µ, D, SHUFFLE returns a ranking r

∗

(X) that is

Pareto optimal.

Proof. Follows directly from Lemma 1.

As one may easily observe, the above method fa-

vors µ over r. That is, we only utilize our initial rank-

ing as a tie-breaker — which could naturally lead to

completely ignoring r in case no ties occur — while

we focus on keeping µ as close as possible to the set of

desired values, D. While in some scenarios this may

be our target behavior, there are also cases where pre-

serving µ is only a secondary objective compared to

yielding an accurate ranking according to some given

ranking function, r. A natural solution to this issue

is to allow for a strict constrain capturing how r

∗

(X)

can deviate from r(X), let us denote it by R(r

∗

,r) or

simply R.

Before we proceed with the rest of our framework,

we shall remark at this point that we consider restric-

tions R that are monotonic with respect to the involved

rankings’ initial parts in the following sense: if R is

violated for some initial part r

(X)

of r

(X), then it

is also violated for each initial part r

(X)

for j > i.

This demand, while restricting the possible choices

for R, is aligned with the idea that when it comes to

ranking, it is the ﬁrst positions that matter the most,

so we would like to exclude the case where a ranking

violates R in some initial positions while it does not

entirely do so.

So, instead of returning a ranking, r

∗

, that is

Pareto optimal among all the possible rankings, we

seek to compute a ranking, r

∗

, that is Pareto optimal

among all possible rankings that respect R.

In this direction, we can design a variation of Al-

gorithm 1 that yields a shufﬂed ranking that respects

R and at the same time is Pareto optimal, in the above

setting. Namely, given a set X, a ranking function r,

a metric µ, a sequence of sets of desired values of µ,

D, as well as a deviation restriction R, we aim to ﬁnd

a ranking r

∗

(X) such that µ(r

∗

(X)) is close to D —

where “close” is understood in the context of Pareto

optimality — and at the same time r,r

∗

do not violate

R. This is achieved by Algorithm 3, which is actu-

ally a backtracking search for r

∗

, with R serving as

the backtracking condition.

Algorithm 3: Constrained diversity-aware shufﬂing.

1: procedure SHUFFLE2(X,r,µ,D,R)

2: rank ← r(X)

3: µRank ← ∅

4: i ← 0

5: f ront ← SORTBY(X, µRank,µ,D

)  Stack.

6: while f ront 6= ∅ do

7: next ← f ront.pop()

8: µRank.append(next)

9: i ← i + 1

10: if R(µRank, rank) is violated then

11: µRank.pop()

12: i ← i − 1  Backtrack.

13: else if X \µRank = ∅ then

14: return µRank  Found shufﬂing.

15: else

16: children ← SORTBY(X, µRank,µ,D

)

17: f ront.push(children.reverse())

18: end if

19: end while

20: return False  Failed to ﬁnd shufﬂing.

21: end procedure

We shall now make some remarks regarding Algo-

rithm 3. To begin with, observe that, when expanding

our partial ranking, µRank, we push all elements re-

turned by SORTBY in reverse order so as to ensure

that the most ﬁtting item computed by SORTBY is ex-

amined ﬁrst. Also, SHUFFLE2 is actually an extension

of SHUFFLE since, in case we set R to be a restriction

that may never be violated, then Algorithm 3 returns

the same shufﬂing of X that Algorithm 1 would re-

turn.

As one may expect, we can prove that, indeed,

µRank lies on the Pareto Frontier. Namely, we have

the following:

Theorem 2. Given a set X = {x

,...,x

}, a ranking

function r, a metric µ and a sequence of desired values

of µ, D, SHUFFLE2 returns a ranking r

∗

(X) such that

∗

is Pareto optimal among all rankings r

∈ R (X)

that respect R(r

,r).

Post-hoc Diversity-aware Curation of Rankings

327

Proof. We will proceed with reductio ad absurdum.

Let a ranking r

such that all the above three condi-

tions hold and, speciﬁcally, let i

be the minimum in-

dex such that:

dist(µ(r

(X)

),D

) < dist(µ(r

∗

(X)

),D

). (20)

Since we also have that:

dist(µ(r

(X)

),D

) ≤ dist(µ(r

∗

(X)

),D

) (21)

for every i = 1,...,n and i

is the minimum index

such that the inequality in (21) is strict, we have that

for every i = 1,...,i

− 1 it holds:

dist(µ(r

(X)

),D

) = dist(µ(r

∗

(X)

),D

) (22)

Equation (22) means that calling SORTBY with

X, r

∗

(X)

−1

,µ and D

as arguments yields a list

where all elements of r

∗

(X)

−1

∪r

(X)

−1

are ranked

below the i

-th element in r

(X), let x

. Furthermore,

Equation (20) ensures that x

∗

is ranked higher in the

returned list than x

∗

6= x

, where by x

∗

we denote the

-th element of r

∗

(X). However, this means that

(see Algorithm 3, line 7) x

is processed prior to x

∗

so, since x

is not the i

-th element of the returned

ranking, r

∗

(X), we infer that R is violated by r

(X)

which is a contradiction, since R(r

,r) is assumed to

hold. So, r

∗

satisﬁes indeed all three conditions.

So, SHUFLE2 computes, indeed, a shufﬂing of

r(X ) that, given R, is optimal with respect to all other

soft restrictions about µ.

4 EXPERIMENTS

In this section we shall present some experiments con-

ducted on synthetic data with our main purpose being

studying Algorithm 3 and its behavior with respect

to its hyperparameters on the special case where µ is

some diversity metric. Namely, we examine the scala-

bility of Algorithm 3 as well as how different choices

of D and R affect its behavior — either combined or

separately. At ﬁrst we present our data generation

protocol and then we proceed with explaining which

speciﬁcations we decided to make to our framework.

At last, we present and discuss the results of our ex-

periments.

4.1 Data Construction

In these experiments, we study our diversity aware

ranking framework with two goals in mind: (i) to ex-

amine the effect the choice of our framework’s hy-

perparameters has on its behavior and; (ii) to exam-

ine any differences the diversity metrics we have pre-

sented may have in practice. For the purposes of

these experiments, we have generated two synthetic

datasets, P

and P

. Regarding P

, it consists of N

randomly generated samples of points in [0,1]

. and

each sample is generated under the following proto-

col:

1. At ﬁrst, a set of M points in [0,1]

, call it C, is

generated — the points in C will serve as cluster

centers.

2. Then, for each cluster center, c

, in C, a sam-

ple of n

points is generated, under a uniform

distribution on the 

sphere with center c

and radius r

min

i6=k



∞

). Also, we

choose n

randomly from a triangular distribution

Trig(n

min

max

) with mode δ =

min

max

We chose for n

to be a random variable since having

clusters of ﬁxed size would have direct implications

for our dataset’s diversity according to most met-

rics. Speciﬁcally, in our experiments, we set M = 4,

min

= 0 and n

max

= 10. That is, P

contains 10 clus-

ters with each cluster containing from 0 to 40 points.

Now, given the above data, we assign to each sample

S of D a randomly chosen target point t(S) ∈ [0,1]

which will serve as the target point of each ranking,

as we shall present below.

Regarding P

, it is signiﬁcantly larger than P

since it consists of 17 sets, with each set containing

N = 10 samples, as in P

. However, while in P

we did

not monitor the total number of points in each sample

— i.e., each sample in P

may contain from 0 to 400

points — we did so in all samples in P

. Namely, ev-

ery set of samples in P

contains samples with exactly

K elements, where K = 15, 20, . . . , 95. Then, given

K we determine how many elements each of the ﬁve

clusters of a sample contains by randomly selecting a

partition of K into ﬁve non-negative integers.

4.2 Empirical Setting

Our shufﬂing framework, as described above is quite

abstract, so, we needed to make some speciﬁcations

in order to implement and test it. To begin with, we

chose our deviation restriction, R, to be a simple ex-

pression of the form d(r

∗

,r) ≤ d

max

, where d is a

metric deﬁned on permutations (rankings) and d

max

is some ﬁxed threshold provided to our algorithm.

Namely, we chose the 

metric, which is deﬁned as

follows:



) :=

∑

k=1

(k) − r

(k)|. (23)

So, for instance, for n = 5, let two rankings of

X = {1, 2, 3, 4,5} be r

= (3, 5, 1, 4, 2) and r

(3,5,2,4,1). Then, have 

) = 2 while, if r

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

328

(4,1,3,2,5), we have 

) = 12. We preferred



over other permutation metrics, mostly due to its

simplicity and intuitive interpretation in the context

of ranking — i.e., the total “displacement” of each

entity.

At this point we should mention that across all ex-

periments we chose to use a normalized version of the



metric. Namely, for given n, 

in S

attains a max-

imum value of

−1

, so the normalized 

distance,

denoted by



, is deﬁned follows:



) :=

−1



). (24)

Regarding the metric µ used, we used the diversity

metrics shown in Table 1. We did not include α and

β diversities in our study since our datasets did not

have a structure that would allow us to do so. We also

chose to exclude Hill numbers since in the most used

cases in bibliography, q is set to either 0, or 1 or 2,

(Chao et al., 2010), which in each case reduces to a

function

of some of the metrics presented in Table 1.

Table 1: Diversity metrics used in A Series Experiments.

Method Tag

Richness R

Berger-Parker Index BP

Simpson’s Index λ

Shannon’s Index H

Another parameter that needed to be speciﬁed was

D, for which we considered two different scenarios:

(i) each set of D to be a singleton containing the same

value and; (ii) each set of D to be a singleton contain-

ing a randomly chosen value, with all choices being

pairwise independent.

Lastly, we chose a simple ranking function r

across all experiments, which ranked all points in a

sample by ascending distance to each sample’s target

point. As our distance in this case we preferred the

usual Euclidean Distance.

Given the above speciﬁcations, we performed the

following sets of experiments:

1. Set A consisted of experiments using dataset P

where we allowed for a single value for D for each

sample win [0,1] with a 0.05 step while we al-

lowed for d

max

to similarly vary from 0 to 1.

2. Set B consisted of experiments using dataset P

Namely, for q = 0,

D coincides with richness, for q =

D is just a function of Shannon’s Index, namely

D =

exp(−H) while for q = 2,

D is the inverse of Simpson’s

Index (Chao et al., 2010).

where D took random sequences as values and

max

took values from 0 to 1 with a 0.05 step.

3. Set C consisted of experiments using dataset P

where D took random sequences as values and

max

took values from 0 to 1 with a 0.05 step.

Experiments of Set A where used to study the be-

havior of Algorithm 3 in a general setting and ver-

ify that its behavior is the expected one, as described

by Theorem 2. Regarding experiments in Set B, we

wanted again to test the behavior of Algorithm 3 but,

this time, under a more general protocol of determin-

ing D, so as to further support the results found in Set

A. Regarding Set C, we wanted to study properties of

Algorithm 3 related to scalability as well as determine

whether trends observed in smaller datasets — sets A

and B — were also present at a larger scale.

4.3 Results

We shall now present the results of our experiments.

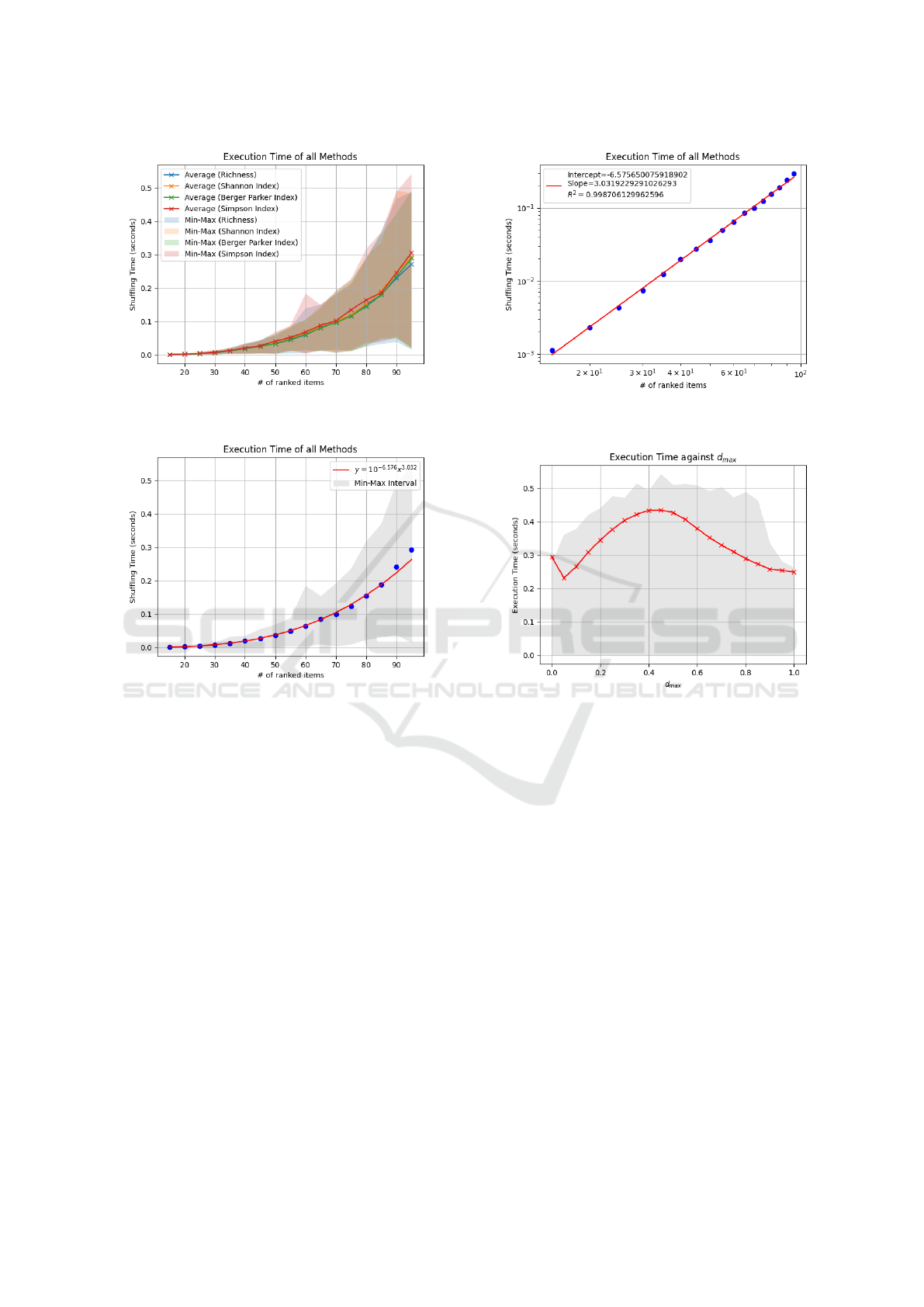
To begin with, in Figure 1a we observe that the choice

of the diversity metric does not seem to affect the

overall computation time since average computation

times seem to be identical while minimum and max-

imum values also do not seem to differ signiﬁcantly.

This was more or less expected since computing the

diversity of a set is not time-demanding when com-

pared to SHUFFLE2’s backtrack search while also all

four diversity metrics have similar time complexities.

As a result we choose to aggregate over all diver-

sity quantiﬁcation methods in the rest three plots pre-

sented in Figure 1.

In Figure 1b we observe that the average execu-

tion time is quite well ﬁtted by a straight line in log-

log axes (R

> 0.99), which implies that execution

time grows polynomially with respect to input size, n.

Namely, as shown in Figure 1c, the average execution

time of SHUFFLE2 in Set C was asymptotically cubic

with respect to n. Since, the worst-case complexity of

our backtrack searching algorithm is Θ(n!), having an

implementation that has a signiﬁcantly lower average

time complexity is quite surprising and would require

further investigation.

One fact that could contribute to this unexpected

efﬁciency is that in all experiments we allowed for

max

to vary signiﬁcantly, so, one may argue that the

low observed average time complexity is due to e.g.,

lower execution time of searches for higher values of

max

. However, as shown in Figure 1d, this is not

true since, while there is some expected variation of

the execution time of SHUFFLE2 with respect to d

max

it is not signiﬁcant enough to account for a notable

decrease of average execution time.

Post-hoc Diversity-aware Curation of Rankings

329

(a) Scalability of Shufﬂe2 with respect to all diversity

metrics.

(b) Average execution time across all diversity metrics

(Log-Log).

alongside the ﬁtting polynomial, y = 10

−6.576

3.032

(d) Average execution time vs deviation threshold, d

max

Figure 1: Scalability results regarding SHUFFLE2.

Another interesting feature observed in Figure 1d

is an initial spike for d

max

= 0. We can provide two

reasons for this spike — possibly among others. At

ﬁrst, d

max

= 0 means that we have to look for the ini-

tial ranking r throughout the entire search space, so

even in this case we have to explore some possibly

signiﬁcant part of the search tree. On the other hand,

in each experiment conducted d

max

= 0 was the ﬁrst

case examined after the dataset was loaded, so this

initial spike might be a result of caching the dataset in

memory for the rest values of d

max

, as well.

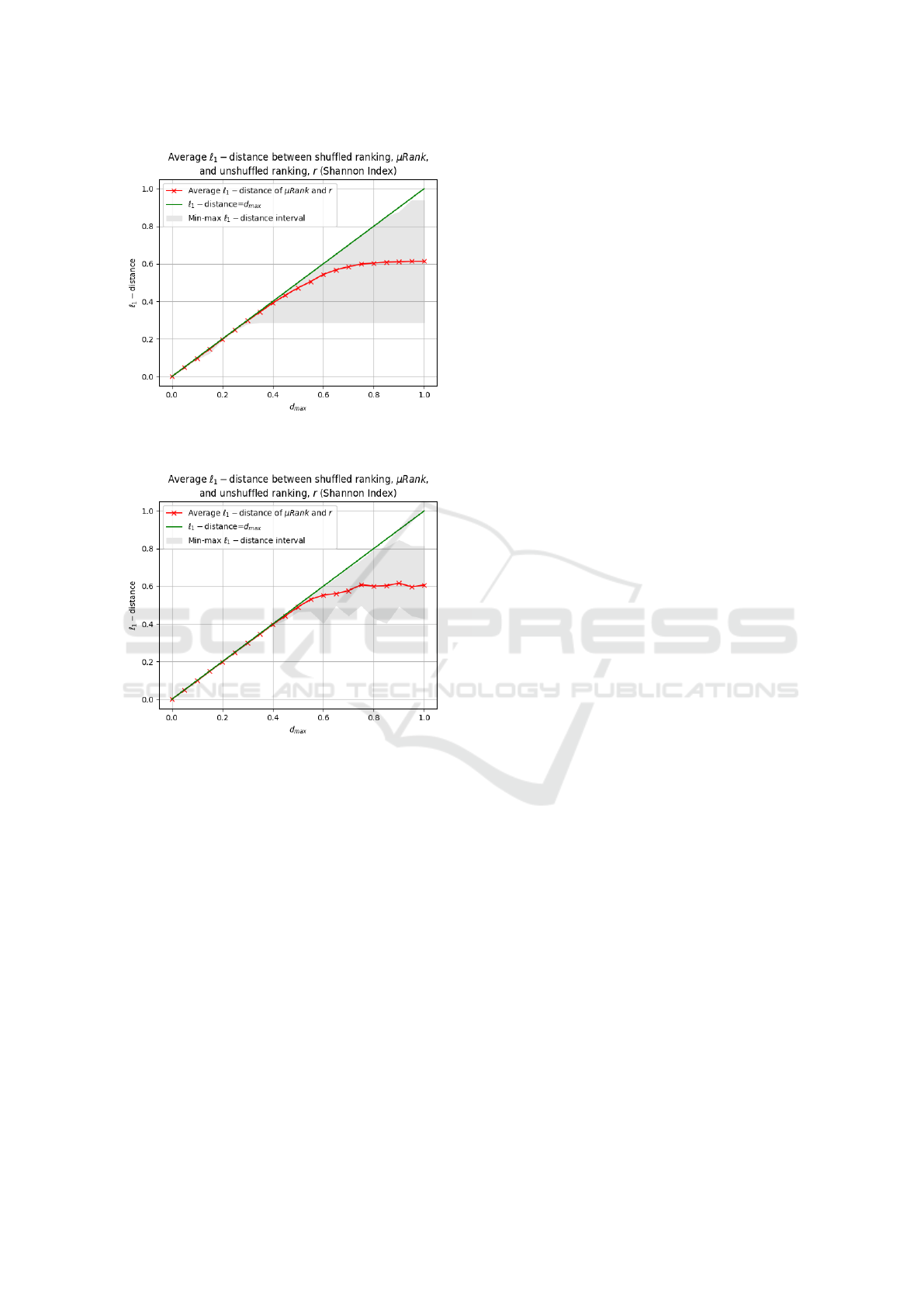
Next, we examine how much the ranking returned

by SHUFFLE2 deviates from the initial ranking, r —

see Figure 2. Starting from Set A, we observe that

using all four metrics, the algorithm initially returns

a shufﬂed ranking r

∗

that seems to take as much dis-

tance allowed from r as possible, while after around

max

= 0.4 in all four cases of Set A the distance be-

tween r and r

∗

converges to a value around 0.6 —

Figure 2a demonstrates the case of Shannon Entropy,

while using any of the rest metrics yielded similar re-

sults. Since SHUFFLE2 for d

max

= 1 is actually Al-

gorithm 1, we also infer from the above results that

an empirical estimation of the maximum average de-

viation from the initial ranking r using Algorithm 1

is slightly above 60% as quantiﬁed using 

as our

metric. Similarly, in the case of Set B — Figure

2b again demonstrates the case of Shannon Entropy,

while using any of the rest metrics yielded similar re-

sults — we observe the very same behavior, but for

the maximum and minimum values of 

∗

,r) which

are less diverse than those in Set A. This may be ex-

plained by the different way we have chosen D in each

case, since in Set A the values of D were ordered and

strictly determined — D was constant across all initial

parts, r

∗

(X)

— while in Set B it was allowed to vary

randomly with i.

At this point, observe that in both plots in Fig-

ure 2 the distance between r

∗

and r is virtually in-

creasing even past the 0.4 limit we described above.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

330

(a) 

distance between r

∗

and r using Shannon’s Index

as diversity index (Set A).

(b) 

distance between r

∗

and r using Shannon’s Index

as diversity index (Set B).

Figure 2: Results from experiment sets A and B regarding

the deviation of the returned ranking, r

∗

, from the initial

ranking, r, as measured using the 

ranking metric.

One may have expected that a virtually unconstrained

search for the Pareto optimal shufﬂing would termi-

nate in more or less the same time, however, as d

max

increases, so does the part of the search graph that

SHUFFLE2 is allowed to search, which can explain

why execution time is increasing with d

max

, even if at

a slower rate after some certain point.

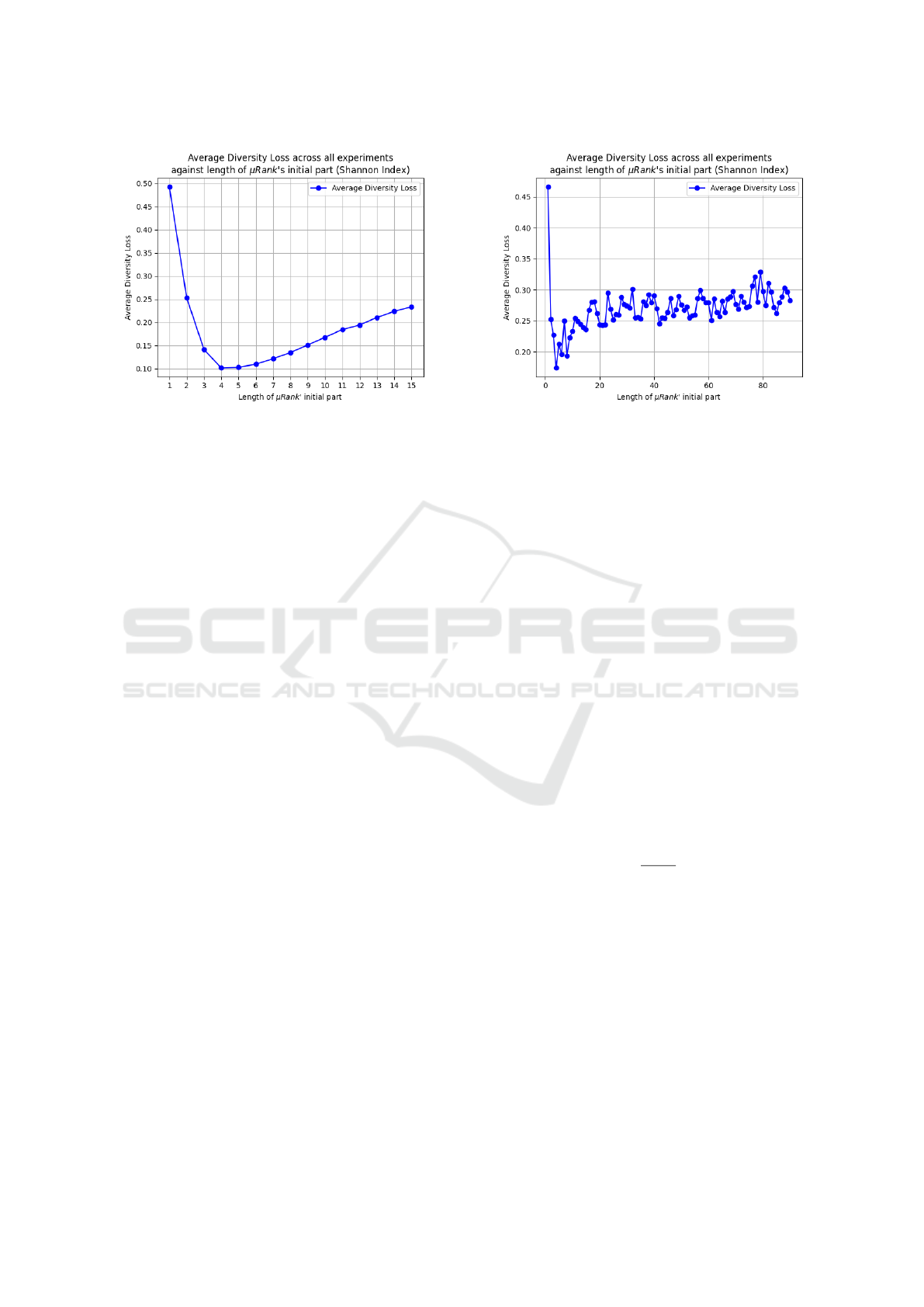
Since in all experiments we deﬁned µ to be a diver-

sity metric, we will refer to D-loss as deﬁned in Equa-

tion (14) as diversity loss. In Figure 3 we present, at

ﬁrst, the average diversity loss in the ﬁrst set of ex-

periments (Set A) — Figure 3a — where we observe

a similar trend across all diversity metrics — the cor-

responding curves for the rest metrics were similar to

the one shown in Figure 3a. Namely, initially L is

quite high, then it approaches zero for some of the ﬁrst

initial parts of the returned ranking and, eventually, it

grows again away from zero. This behavior is repli-

cated at a larger scale in Set C — Figure 3b — where

we allowed for rankings to contain each 95 elements

— instead of 15 we present in Figure 3a. Again, av-

erage diversity loss drops for the ﬁrst initial parts for

each metric while then it rises to some higher value.

The more vivid variation of average diversity loss we

observe in the results of Set C is attributed mostly to

D taking random values compared to Set A where D

took a single value across each sample. We also pro-

duced plots for the rest subsets of Set C — namely,

for rankings of length l = 15,20, . . . , 95 — but they

all were more or less truncated versions of Figure 3b.

4.4 Diversity Loss

This trend observed in Figure 3 is of special interest so

we shall further elaborate on it. As we have discussed

in the description of our framework — see Section

3 for more details — adhering to the restrictions im-

posed by D is treated as a soft restriction throughout

Algorithm 3. That is, we do not expect that the shuf-

ﬂed ranking returned by SHUFFLE2 will be globally

optimal with respect to diversity loss, L, but, as we

proved in Theorem 2, each shufﬂed ranking returned

is Pareto optimal. However, as we observe in Figure

3, in all cases of diversity metrics we have a similar

trend. Namely, L is initially relatively high, it then

drops close to zero for the ﬁrst initial parts of the re-

turned ranking and then it rises again away from the

desired levels of diversity determined by D for the last

parts of the returned shufﬂed ranking.

The above behavior is expected, given the metrics

we have at our disposal. To begin with, given a set,

X, and a a diversity metric, µ, each ranking of X, let

r(X ), has the same diversity as X since none of the

metrics we used is sensitive to the order in which el-

ements appear in X — this is a natural feature of a di-

versity metric since it quantiﬁes the diversity of a pop-

ulation/sample at a given time/time interval. Also, as

we include more of X’s elements into our ranking we

expect µ(r(X)

) to be approximately div(X) since, for

large sets, introducing another element does not affect

diversity dramatically — at least not when quantify-

ing it using the metrics discussed in Section 2.2. As a

result, we are not able to guarantee adherence to D

far as large values of i are concerned, which is clearly

depicted in all ﬁgures in Figure 3. Also, the same ap-

plies to singletons, since the diversity of a singleton

takes some trivially constant value under all the met-

rics presented in Section 2.2.

Post-hoc Diversity-aware Curation of Rankings

331

(a) Average diversity loss (L) using Shannon’s Index as

diversity metric (Set A).

(b) Average diversity loss (L) using Shannon’s Index as

diversity metric (Set C).

Figure 3: Average Diversity Loss (L) across experiments of sets A and C.

So, the only values of i for which we could rea-

sonably expect that µ(r

∗

(X)

) ≈ D

are those closer to

bur larger than 1. As shown in Figure 3, this is in-

deed the case since, using any metric, we achieve a

minimum diversity loss for such values of i. At this

point we should also observe that the fact that each

ranked sampled contains elements from (at most) four

classes plays an important role. Namely, with less

than four — or richness(X), in general — items the

values diversity may take — with any metric but for

richness in mind — are more restricted than when

there are more — but not much more — items in the

sample. Intuitively, this happens because, especially

when richness(X) is not large, modifying the diver-

sity of a sample boils down to adding a few items

to it. On the contrary, when there are too few items

in a sample, diversity values are more “sparsely” dis-

tributed in [0, 1] while when the cardinality of a sam-

ple is much larger than richness(X), adding a few

items does not signiﬁcantly affect its diversity. Bear-

ing these in mind, it is expected that a sample is more

ﬂexible in manipulations of its diversity when it con-

tains roughly as many items as the classes available.

Less items lead to less ﬂexibility as well as much

more.

This trend is also reﬂected in the distance the rank-

ing r

∗

returned by Algorithm 3 has from r, as shown

in Figure 2. Namely, for tighter values of d

max

observe that r

∗

takes as much distance as possible

in order to minimize diversity loss as much as pos-

sible. In these cases there is an expected trade-off be-

tween adherence to r and diversity, which is attributed

mostly to the following two factors: (i) ﬁrst, the rank-

ing methodology we chose in all our experiments was

promoting similarity in the ﬁrst positions of the re-

turned rankings while, at the same time it compro-

mised diversity and; (ii) second, diversity is inher-

ently opposite to similarity in the sense that a set that

is considered diverse should contain elements that are

dissimilar to each other above some certain threshold.

Bearing in mind the above, we can easily explain the

observed trade-off between diversity and adherence to

the initial ranking we provide to SHUFFLE2.

To shed more light on the above behavior

of SHUFFLE2 let us consider a setting where

X = {a

}, where a, b denote the

classes of the corresponding elements and r(X ) =

). Also, let us consider that we

measure diversity using Richness and that our de-

sired diversity values are D = (1,1,1,0, 0, 0), i.e., we

care about the ﬁrst half of the list being highly di-

verse while we have no demands regarding the list’s

last elements. Then, it is not difﬁcult to see that

any ranking, r

∗

(X), containing at least one a and

at least one b would yield a diversity loss vector

L(r

∗

) = (1,0,0, 0, 0, 0). However, a ranking such as

∗

(X) = (a

) has an 

distance from

r(X ) equal to 

∗

,r) =

1+2+3

≈ 0.353. That is, in

order to achieve a highly diverse shufﬂing, we had to

deviate from our initial ranking at about 35%.

5 DISCUSSION

Our work raises certain issues and suggests possible

directions for future work that we discuss below.

5.1 Determining D in Practice

Our developed framework assumes that D, the desired

level of diversity, is externally provided, with each of

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

332

its components, associated to an initial part of the con-

structed ranking, being a set or interval of values. Al-

though we have not fully explored this ﬂexibility in

our empirical setting, both of these features could be

useful in practical applications, where one would at-

tempt to actually determine what D should be.

A ﬁrst approach to determining D could be to

measure the diversity µ(X) of the set X of options

that are available, and set each component of D to

equal {µ(X )}. This would effectively ask for some

form of uniformity of the diversity exhibited in any

initial part of a ranking presented to the user. Thus,

the user would not only wish for the entire list of op-

tions presented to them to be diverse, but also for the

ﬁrst handful of results in that ranking — which prac-

tically is what a user gets to see when making their

choice — to also be equally diverse.

Variations are, of course, possible. Instead of in-

sisting on uniformity, the user could ask that each ini-

tial part of the ranking is at least as diverse as the en-

tire list by setting each component of D to equal the

interval [µ(X),1], so that the shufﬂing algorithm will

not seek to demote diversity of a part of the ranking

if this happens to be higher than µ(X). Analogously,

the user may wish to relax the minimum bound on the

diversity and replace the interval [µ(X), 1] with, say,

[µ(X)/2, 1], insisting that some diversity is minimally

and uniformly required in each part of the ranking.

An interesting direction for future research would

be to determine D using actual user feedback in real

scenarios. Namely, it would be interesting to see to

what extent and under what conditions users desire

ranked lists presented to them to be diverse and, on

top of that, what part of the list is of signiﬁcant im-

portance — for instance, in typical web search tasks,

the ﬁrst page of the returned results is usually of the

highest signiﬁcance to a user.

One approach to learning the diversity that a user

may be seeking in their ranked options is to track the

user’s past choices from ranked lists. The precise

choice from each speciﬁc ranking can, naturally, be

used as a signal of how the user wishes the options to

be ranked to begin with. But in addition, looking at

the choices C

of the user after t rounds of being pre-

sented with a ranking and making a choice, one could

consider the diversity µ(C

) of C

as an indication of

the level of diversity that the user would wish to see

in subsequent rounds of rankings. Setting each com-

ponent of D to equal µ(C

), and presumably updating

D over time as C

is computed for larger and larger

values of t would capture this intuition.

A more involved solution would be to maintain a

list of user choices as above, but partitioned based on

the position in the ranking of each choice made. So,

if during round t a user chooses option at position i

in their presented ranking, then that option would be

added to list C

. D would then be deﬁned by setting its

i-th component to equal µ(C

). Further accounting for

the amount of data within each list C

of choices, one

could insist that each component of D is some conﬁ-

dence interval around µ(C

), whose size is determined

by the size of C

. This would then be able to capture

situations where a user might signal that different lev-

els of diversity are desired for different initial parts

of the ranking; e.g., no diversity preference for the

ﬁrst handful of results (so that the original ranking is

maintained), but then maximum diversity in the sec-

ond handful of results (so that the user can explore

alternatives that might be less preferred according to

the original ranking, but are highly diverse).

5.2 Measuring Shufﬂing Deviation

A choice that we made for the purposes of our em-

pirical evaluation was to implement the deviation re-

striction, R, required by Algorithm 3, through the use

of 

as a simple to compute yet informative way to

quantify distance between two ranked lists. As we

explained in Section 4.2, 

is naturally interpreted

as the total “displacement” required to transit from a

ranking r

to another ranking r

. However, what mat-

ters in most occasions a ranking is used, is the ﬁrst

part of the returned ranked list. So, 

may not be the

most appropriate choice since it does not make a dis-

tinction between changes in the ﬁrst, middle or last

places of a ranking r. A natural adaptation of 

ac-

commodating the above is to introduce weights, w

∑

k=1

= 1, such that moving the ﬁrst, say, element

of r(X) three places down the list matters more than

moving the 15

element to position 18.

Other than distance-based deviation constraints

that apply globally on a ranked list, it would also be

meaningful to explore more complex restrictions R,

including ones that are not necessarily based on dis-

tance metrics. For instance, in some scenarios a user

may wish to explicitly state that the initial handful of

options in the original ranking should not be shufﬂed

and that subsequent options could be shufﬂed more

the later in the ranking they appear.

5.3 Efﬁcient Search of Shufﬂings

In the implementation of Algorithm 3, as used in

the empirical evaluation presented in Section 4, we

adopted a greedy breadth-ﬁrst strategy to search the

space of all shufﬂings of r(X). The only heuristic we

have implemented in order to alter the order nodes

are expanded is, as mentioned in Section 3, that when

Post-hoc Diversity-aware Curation of Rankings

333

sorting any remaining items using SORTBY we break

any ties that may occur using r, expecting that an item

ordered at a higher position in r(X) will lead to a shuf-

ﬂed ranking r

∗

(X) with smaller 

distance from r.

However, there is plenty of space for further im-

provement in this direction. To begin with, SHUF-

FLE2’s performance may be enhanced by introduc-

ing Forward Checking. Since after each expansion

of the generated ranking, µRank, the remaining chil-

dren nodes are fewer than in the previous iteration,

Forward Checking may lead to signiﬁcant parts of the

search tree to be pruned. Moreover, one may also de-

ploy more sophisticated search techniques such as A

∗

or other heuristic or stochastic search methods in or-

der to further reduce the running time of SHUFFLE2.

6 CONCLUSIONS

Motivated by the widespread use of ranking to fa-

cilitate the choices of individuals, and the real dan-

ger of ending up creating echo chambers with poten-

tially grave implications in social settings, this work

has proposed and empirically evaluated a post-hoc ap-

proach for the diversity-aware curation of rankings.

Our next steps include the integration of our method-

ology in the context of the WeNet platform, and its

evaluation on data coming from the platform’s users.

ACKNOWLEDGMENTS

This work was supported by funding from the EU’s

Horizon 2020 Research and Innovation Programme

under grant agreements no. 739578 and no. 823783,

and from the Government of the Republic of Cyprus

through the Deputy Ministry of Research, Innovation,

and Digital Policy.

REFERENCES

Berger, W. H. and Parker, F. L. (1970). Diversity of Plank-

tonic Foraminifera in Deep-Sea Sediments. Science,

168(3937):1345–1347.

Burges, C., Shaked, T., Renshaw, E., Lazier, A., Deeds, M.,

Hamilton, N., and Hullender, G. (2005). Learning to

Rank Using Gradient Descent. In Proceedings of the

22nd International Conference on Machine Learning,

ICML ’05, page 89–96, New York, NY, USA. Associ-

ation for Computing Machinery.

Cakir, F., He, K., Xia, X., Kulis, B., and Sclaroff, S. (2019).

Deep Metric Learning to Rank. In IEEE Conference

on Computer Vision and Pattern Recognition (CVPR),

pages 1861–1870.

Chao, A., Chiu, C.-H., and Jost, L. (2010). Phylogenetic

Diversity Measures Based on Hill Numbers. Philo-

sophical transactions of the Royal Society of London.

Series B, Biological sciences, 365:3599–609.

Colwell, R. (2009). Biodiversity: Concepts, Patterns, and

Measurement, pages 257–263. Princeton Univ. Press.

Helm, P., Michael, L., and Schelenz, L. (2021). Diversity by

Design: Balancing Protection and Inclusion in Social

Networks.

Herﬁndahl, O. (1950). Concentration in the US Steel Indus-

try. In Unpublished doctoral dissertation.

Hill, M. O. (1973). Diversity and Evenness: A Unifying

Notation and Its Consequences. Ecology, 54(2):427–

432.

oppel, M., Segner, A., Wagener, M., Pensel, L., Karwath,

A., and Kramer, S. (2019). Pairwise Learning to Rank

by Neural Networks Revisited: Reconstruction, The-

oretical Analysis and Practical Performance. CoRR,

abs/1909.02768.

Oliveira, I. F. D., Ailon, N., and Davidov, O. (2018). A New

and Flexible Approach to the Analysis of Paired Com-

parison Data. Journal of Machine Learning Research,

19(60):1–29.

Pei, C., Zhang, Y., Zhang, Y., Sun, F., Lin, X., Sun, H.,

Wu, J., Jiang, P., Ou, W., and Pei, D. (2019). Per-

sonalized Context-aware Re-ranking for E-commerce

Recommender Systems. CoRR, abs/1904.06813.

Pfannschmidt, K., Gupta, P., and H

ullermeier, E. (2018).

Deep Architectures for Learning Context-dependent

Ranking Functions.

Shannon, C. E. (1948). A Mathematical Theory of Com-

munication. The Bell System Technical Journal,

27(3):379–423.

Simpson, E. H. (1949). Measurement of Diversity. Nature,

163(4148):688–688.

Spellerberg, I. and Fedor, P. (2003). A Tribute to Claude

Shannon (1916–2001) and a Plea for More Rigorous

use of Species Richness, Species Diversity and the

‘Shannon–Wiener’ Index. Global Ecology & Bio-

geography, 12:177–179.

Tuomisto, H. (2010). A Consistent Terminology for Quan-

tifying Species Diversity? Yes, It Does Exist. Oecolo-

gia, 164(4):853–860.

Whittaker, R. H. (1960). Vegetation of the Siskiyou Moun-

tains, Oregon and California. Ecological Mono-

graphs, 30(3):279–338.

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

334