
Exploiting Ontology to Build Bayesian Network
Ahmed Mabrouk, Sarra Ben Abbes, Lynda Temal, Ledia Isaj and Philippe Calvez
LAB CSAI ENGIE, 4 Rue Jos
´
ephine Baker, 93240 Stains, France
Keywords:
Bayesian Network Structure, Ontology, Expert Knowledge, Learning, Dependencies, Renewable Energies.
Abstract:
Exploiting experts’ domain knowledge represented in the ontology can significantly enhance the quality of
the Bayesian network (BN) structure learning. However, in practice, using such information is not a trivial
task. In fact, knowledge encompassed in ontologies doesn’t share the same semantics as those represented in
a BN. To tackle this issue, a large effort has been devoted to create a bridge between both models. But, as far
as we know, most state-of-the-art approaches require a Bayesian network-specific ontology for which the BN
structure could be easily derived. In this paper, we propose a generic method that allows deriving knowledge
from ontology to enhance the learning process of BN. We provide several steps to infer dependencies as well
as orientations of some edges between variables. The proposition is implemented and applied to the wind
energy domain.
1 INTRODUCTION
Over the last three decades, probabilistic graphical
models (PGMs) such as Bayesian networks (Pearl,
1988) are considered as one of the most successful
tools for reasoning about beliefs in many real-world
applications (cancer diagnosis, robotics, machine di-
agnosis, etc). Unlike many state-of-the-art predictive
models such as random forests, support vector ma-
chine (SVM), BN provides a prominent model that
enables to represent complex systems using graphi-
cal and probabilistic formalisms (easy for humans to
understand). The graphical structure encodes a set of
dependencies among random variables. The proba-
bilistic part is composed of a set of conditional prob-
ability tables to represent uncertainties. Both compo-
nents are jointly used to perform automated reasoning
under uncertainty by enabling to answer efficiently a
very wide range of diagnosis queries (Pearl, 2014).
Ontology, also represented by a graphical model,
is well known to be the best way to represent knowl-
edge in a domain of discourse according to different
points of view and purposes. It allows representing
explicitly and formally existing entities in an appli-
cation domain. Ontology formalization can use De-
scription Logic (DL) language, which is based on
First-order logic to describe concepts, relationships,
and constraints. It then enables us to make inferences.
Both models appear to be useful to perform rea-
soning and domain knowledge explanation using dif-
ferent paradigms. Intuitively, we believe that com-
bining BNs and ontologies gives rise to provide high
expressiveness and more reliable reasoning under un-
certainty. In this sense, several approaches have been
proposed to create a bridge between both models.
Basically, they can be divided into three categories:
(i) introducing additional notations to represent prob-
abilistic values in the ontology (Yang and Calmet,
2005; Zhang et al., 2009; Carvalho et al., 2010;
Mohammed et al., 2016), (ii) exploiting the seman-
tic richness of the ontology to guide the BN learn-
ing (Fenz, 2012; Jeon and Ko, 2007; Ishak et al.,
2011a; Messaoud et al., 2013), and (iii) using BN
results to enrich the ontology (Ishak et al., 2011b;
Wang, 2007). In this paper, we are interested in ex-
ploiting the knowledge in the ontology within the BN
structure learning. Unlike classical methods which,
naively rely on ontological relationships to identify
dependencies between variables, our approach ex-
ploits in an intelligent way existing knowledge to de-
duce more efficient dependencies in the BN. To do
so, we propose a generic method that allows deriving
key knowledge from ontology. This method is based
on a set of rules allowing to infer dependencies and
edges orientation in an original way. The rest of this
paper is organized as follows. In section 2 we give the
main definitions of BN and ontology models. In sec-
tion 3, we discuss the most common state-of-the-art
approaches dedicated to exploit ontologies during the
BN learning phase. Then, in section 4, we describe
our new approach and justify its correctness within
the wind turbine domain. Its efficiency is highlighted
through experiments in section 5. Finally, a conclu-
sion and some future works are given in section 6.
578
Mabrouk, A., Ben Abbes, S., Temal, L., Isaj, L. and Calvez, P.
Exploiting Ontology to Build Bayesian Network.
DOI: 10.5220/0010840400003122
In Proceedings of the 11th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2022), pages 578-585
ISBN: 978-989-758-549-4; ISSN: 2184-4313
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 BACKGROUND
In this section, we present the main definitions and
semantics of BN and ontology models.
2.1 Bayesian Network
Definition 1 (Bayesian network). A BN is a pair
(G, Θ) where G = (V, E
G
) is a directed acyclic graph
(DAG), V represents a set of random variables
1
, E
G
is
a set of arcs, and Θ = {θ
V
i
|Pa(V
i
)
}
V
i
∈V
is the set of con-
ditional probability tables (CPTs) of the nodes / ran-
dom variables V
i
in G given their parents Pa(V
i
), i.e.
θ
V
i
|Pa(V
i
)
= P(V
i
|Pa(V
i
)). The BN encodes the joint
probability over V as:
P(V) =
∏
V
i
∈V
P(V
i
|Pa(V
i
)) (1)
Eq.1 is also called the chain rule or the general
product rule. BN provides a mechanism for exploit-
ing structure in high-dimensional joint distributions
to describe them compactly, and in a way that al-
lows them to be constructed and utilized effectively.
By their graphical structure, BNs encode an indepen-
dence model, i.e., a set of conditional independences
between random variables, characterized by the d-
separation property:
Definition 2 (d-separation). Two nodes V
i
and V
j
are
said to be d-separated in G by a set of nodes Z ⊆ V \
{V
i
,V
j
}, which is denoted by V
i
⊥
G
V
j
|Z, if, for every
trail (directed path) linking V
i
and V
j
in G, there exists
a node S on the trail such that one of the following
conditions holds:
1. S has converging arrows on the trail and neither
S nor any of its descendants are in Z;
2. S does not have converging arrows on the trail
and S ∈ Z.
In other words, any independence reported by d-
separation is satisfied by the underlying distribution.
When two variables V
i
and V
j
are not d-separated by
Z ⊂ V, they are said to be d-connected. With these
definitions, relationships encoded in a BN can be seen
as a flow in the graph. The d-separation tells us when
influence from V
i
can “flow” through Z to affect our
beliefs about V
j
.
2.2 Ontology
Ontologies are complex artifacts (composed of con-
cepts, hierarchical relations, and roles) that are built
1
By abuse of notation, we use interchangeably V
i
∈ V to
denote a node in the BN or the voltage of bus i
according to different points of view and purposes.
The most widely cited definition of an ontology is a
formal, explicit specification of a shared conceptual-
ization, used to help humans and machines to share
common knowledge (Gruber, 1993; Guarino, 1995).
This definition highlights the following characteris-
tics of an ontology:
• Conceptualization: defines the objects, con-
cepts, and other entities that are assumed to ex-
ist in some area of interest and the relationships
that hold among them (Genesereth and Nilsson,
1987). A conceptualization is an abstract, simpli-
fied view of the world that we wish to represent
for some purpose (Gruber, 1993) .
• Explicit: corresponds to the precise definition of
the concepts and the constraints of their use.
• Formal: refers to the fact that the expressions
must be machine-readable.
• Shared: refers to a common understanding of do-
main knowledge among people or agents.
An ontology is formally defined by
O = (C, 6
C
, R, 6
R
, A)
• C and R are two disjoint sets whose elements are
respectively called Concepts (e.g. Room, Build-
ing) and Relations (e.g.part-of, sub-Zone-of ).
• 6
C
is a partial order over C, called concept hier-
archy or taxonomy (is-a)
• 6
R
is a partial order over R, called a hierarchy of
relations (e.g.sub-Zone-Of 6
R
part-Of )
• A a set of axioms and inferences rules (e.g. Phys-
ical Entity part-of Only Physical Entity)
3 RELATED WORK
In our paper, we shall focus our discussion on the use
of ontology to construct a BN structure. In this con-
text, several approaches have been developed for as-
sisting in eliciting knowledge from ontology and then
derive a BN (Bucci et al., 2011; Helsper and Van
Der Gaag, 2002). In (Devitt et al., 2006), authors
expose a direct correspondence between BN formal-
ism and the original domain ontology: (i) concepts
→ nodes, (ii) concepts attributes → CPTs, and (iii)
inheritance relations → arcs. The main drawback of
this approach is that it requires BN-specific ontology
extensions. (Fenz, 2012) proposed a semi-automatic
approach composed of the following steps: (i) selec-
tion of relevant classes, individuals, and properties (ii)
creation of the BN structure (iii) construction of the
CPTs, and (iv) incorporation of existing knowledge
Exploiting Ontology to Build Bayesian Network
579

facts. In this work, the BN is built from a security
ontology describing threat, vulnerability, and control
dependencies. The author extends the basic idea of
(Devitt et al., 2006) to a more generalized framework
by introducing the following analogies: (i) axioms
→ BN nodes scales and weights, and (ii) instances
→ findings. To generate a BN, (Fenz, 2012) devel-
oped a Prot
´
eg
´
e plug-in called Bayesian Network Tab
(BNTab)
2
. A key issue in the proposed approach is
that it works only with boolean (or binary) variables,
so the application scope is limited to restricted real-
world domains. Moreover, this approach doesn’t take
into account the meaning of the ontology relations to
identify the more significant ones that fit better with
the dependency semantic in the BN. In (Jeon and Ko,
2007), a semi-automatic approach of BN construc-
tion for diagnosing diseases in the e-health domain
is proposed. This method starts by generating nodes
in a BN based on a set of selected concepts from the
e-health ontology. Then, developers identified valid
links among nodes in the BN based on a meta-model
that represents cause-and-effect relationships among
ontologies. This approach demonstrates several is-
sues. First, it requires the presence of causal rela-
tionships between ontologies which are not always
tractable in practice. Second, the links generating step
ends up with a complex BN structure in the form of
a hierarchical graph. Such topology is not suitable
for all applications. In (Messaoud et al., 2013), au-
thors present SemCaDo (Semantical Causal Discov-
ery) algorithm for integrating ontological knowledge
for learning causal BNs. The SemCaDo algorithm
takes an observational dataset and a corresponding
ontology as inputs. In the first phase, causal relations
are extracted from the ontology and then integrated
in the form of constraints (white lists) during BN
structure learning. Then, the second phase optimizes
the orientation of the remaining undirected edges in
the complete partially directed graph (CPDAG) using
a semantic distance calculus provided by the ontol-
ogy. Finally, the algorithm re-iterates over the sec-
ond phase if there are still some non-directed edges
in the graph. All discovered causal links will be
introduced as semantic causal relations between the
corresponding ontology concepts. BN and OWL In-
tegration Framework (ByNowLife) (Setiawan et al.,
2019) is a framework proposed to integrate BN with
OWL by providing an interface for probabilistic rea-
soning information through SPARQL queries. This
approach consists of transforming logical information
contained in an ontology into a BN and vice-versa.
This framework is composed of three main parts:
2
https://protegewiki.stanford.edu/wiki/Bayesian
Network Tab (BNTab) 1.1.3
(1) application, which allows querying the Knowl-
edge Base in SPARQL format for logical reasoning
and hasProbValueOf special property for probabilis-
tic reasoning, (2) reasoner, which involves two com-
ponents; logical reasoner and probabilistic reasoner,
and (3) knowledge base, contains the domain ontol-
ogy and BN knowledge. The main drawback of the
two last approaches is that causal relations in the on-
tology are not always available. In addition, semantic
characteristics of ontological relations are not taken
into consideration during BN construction.
4 PROPOSED APPROACH
In this section, we describe a new approach that ex-
ploits in an efficient way the knowledge capitalized in
ontologies to enhance BN structure learning results.
We justify the correctness of our approach based on
the wind turbine example.
4.1 Problem Formalization
Although BNs are seldom constructed entirely by ex-
perts, the knowledge given by these latter can still
prove to be a useful source of information that should
be exploited by BN learning algorithms. In this con-
text, the ontology can be particularly helpful since
it represents explicit knowledge. While the com-
plementarity between ontology and BN mights seem
trivial in general, it turns out that the joint use of both
models can be subject to many issues. In fact, rela-
tions between concepts do not necessarily encode a
dependence/independence between concepts. There-
fore, generate automatically a BN graphical struc-
ture from a given ontology, appears completely in-
tractable. To tackle this issue, we propose a semi-
automatic solution to facilitate knowledge elicitation
from ontology and knowledge-guided BN structure
learning. The general pipeline of the proposed ap-
proach is summarized as follows:
1. identify a set of relations that encapsulate a de-
pendence property between concepts,
2. compute dependence scores between concepts
based on selected relationships,
3. build an initial BN skeleton
3
based on the com-
puted scores,
4. orient some edges in the skeleton using the seman-
tic of selected relationships in the ontology,
3
a skeleton of the BN is the DAG where arcs are substi-
tuted by (undirected) edges.
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
580

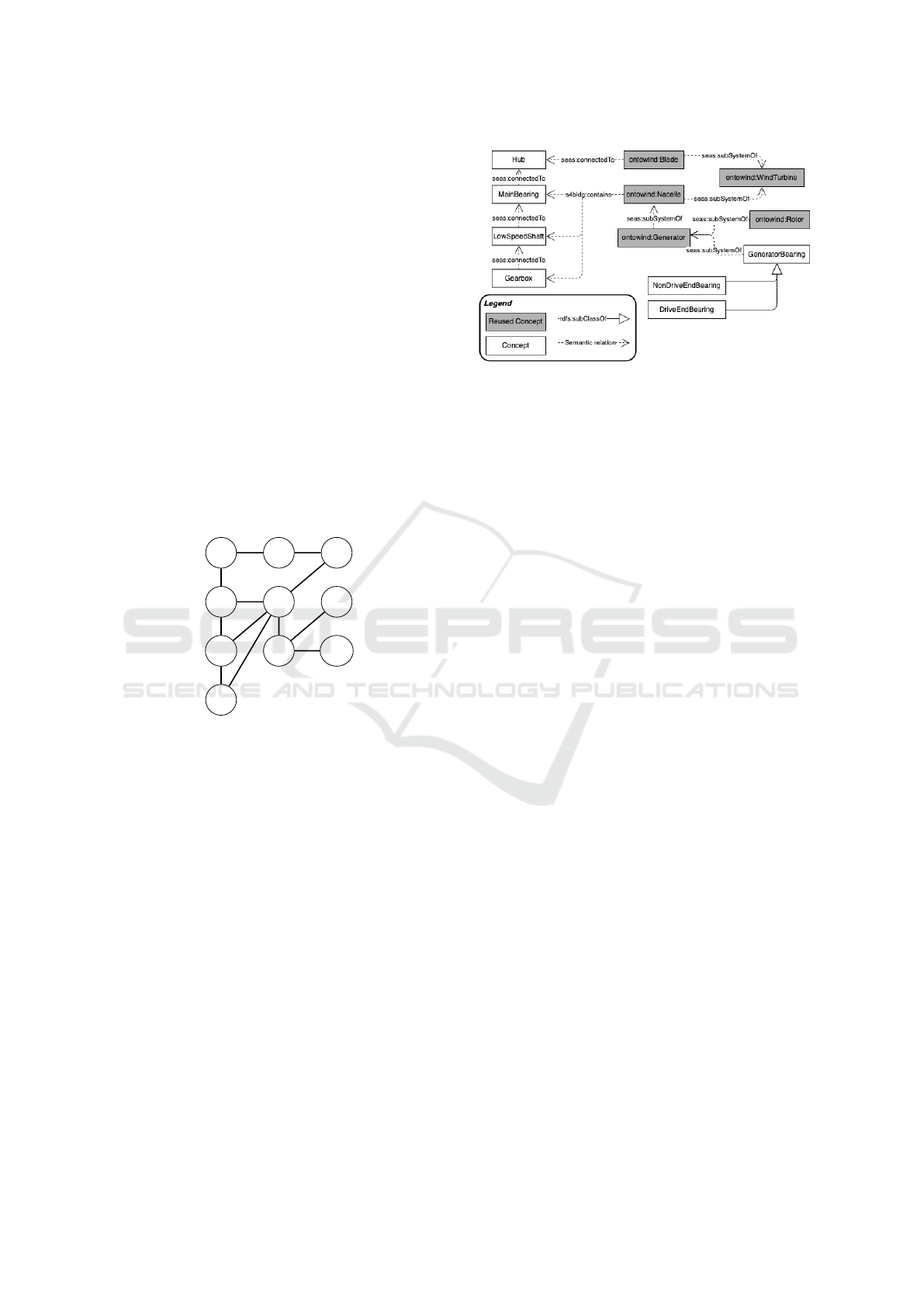
Figure 1: Selected Relations used in the Wind Turbine On-
tology.
5. refine the resulted BN through the use of observa-
tional data and a score-based approach.
In the following, we discuss in greater detail each of
the previous steps. To facilitate understanding, we ap-
ply our approach on the wind turbine domain.
4.2 Identification of Key Relationships
As discussed previously, the BN model allows repre-
senting conditional independencies as a DAG. In fact,
conditional independencies could be directly inferred
from the BN graph via the d-separation criterion. In
this context, we need to extract relevant relations from
the ontology that provide novel insights about vari-
able interactions (dependence, causality, etc.). To
identify these relations called R
dep
⊆ R, it is quite
natural to ask questions to one or multiple experts,
following this format: Given a relation R
i
∈ O, is our
belief about the state of the concept C
i
(resp. C
j
)
is influenced when we have an observation regard-
ing the concept C
j
(resp. C
i
)? The binary decision
(yes/no) returned by the expert for this question in-
dicates whether the relationship should be considered
to capture dependencies between variables. After the
accumulation of all of these binary answers, we end
up the first step of our approach with the selected
relations shown in figure1. As can be easily seen,
the selected relationships focus mainly on the loca-
tion (s4bldg:contains (resp. s4bldg:isContainedIn))
as well as the set of connections between the different
components (seas:connectedTo, seas:subSystemOf
(resp. seas:hasSubSystem))
4
. According to the ex-
pert, the lower the semantic distance between two
components (or concepts in the ontology) in the sys-
tem, the greater dependent they are. For example,
since the concept Main Bearing is connected to the
concept Hub in the ontology, it is likely that, if the
temperature of the Main Bearing is high, the temper-
ature of the Hub will get higher as well, or vice-versa.
The same idea applies to the other selected relations.
4
Note that subSystemOf of can inferred from hasSub-
System if it is not explicitly mentioned in O Same thing for
the relation contains according to iscontainedIn
In this step, SPARQL queries were used to extract
concepts linked by the selected relationships from O
as described in the algorithm1.
Algorithm 1: Dependency triples extraction.
1: Input: Ontology O, Selected relations R
dep
2: Output: Set T of extracted triples
3: for R
k
in R
dep
do
4: Perform SPARQL query:
5: SELECT ??C
i
?C
j
WHERE {
?C
i
rdfs:subClassOf ?S .
?S a owl:Restriction; owl:onProperty R
k
;
owl:someValuesFrom k owl:allValuesFrom ?C
j
.
}
6: Add < C
i
, R
k
,C
j
> to T
7: end for
8: return T
4.3 Dependence Scores Calculation and
BN Skeleton Building
In this section, we explain how the extracted infor-
mation from O can be exploited during the different
BN construction steps. Given the extracted triples
T, we merely generate a graph G, where edges are
weighted by the strength of dependency w
k
that ev-
ery relation R
k
represents, i.e., an undirected edge in
G is inserted between nodes V
i
(corresponds to C
i
)
and V
j
(corresponds to C
j
)
5
if < C
i
, R
k
,C
j
>∈ T or
< C
j
, R
k
,C
i
>∈ T. In the example of wind turbine,
the selected relations were ranked by the experts ac-
cording to the dependency semantic, as follows: the
relation contains
6
(resp. isContainedIn) transcribes
a stronger dependency between concepts, as certain
components are contained in another one, followed
by subSystemOf (resp. hasSubSystem), and finally
connectedTo. For these relations, the assigned de-
pendency weights are: w
contains
(resp. w
isContainedIn
)
← 1, w
subSystemO f
(resp. w
hasSubSystem
) ← 1.2, and
w
connectedTo
← 1.4. Figure 2 depicts an example of
a weighted graph resulting from the ontology shown
in figure3. Based on the resulted graph, we compute
the dependence between any two nodes V
i
and V
j
in
G (denoted by dep(V
i
,V
j
)) as:
dep(V
i
,V
j
) =
1
shortPath
G
(V
i
,V
j
)
(2)
The shortest path between nodes V
i
and V
j
(shortPath
G
(V
i
,V
j
)) is calculated using the weighted
5
We use V
i
to denote nodes in the weighted graph rather
than C
i
in order to be consistent with BN notations
6
For simplicity, in the rest of the paper, we remove the
prefix part from all concepts and relationships.
Exploiting Ontology to Build Bayesian Network
581
Dijkstra’s algorithm(Dijkstra et al., 1959). From the
given results, we deduce dependency strengths be-
tween all pairs of nodes in G. For instance, the depen-
dence strength between Main Bearing and Generator-
Bearing (dep(MB, GBe)) is equal to 0.29 (see Fig.2).
The obtained results were approved by the wind tur-
bine experts. Using dependency scores, we can there-
fore build an initial skeleton of the BN. Remind that
edges in the BN represent probabilistic dependencies
(or correlations) between nodes. In this case, an edge
E
V
i
,V
j
is inserted in the BN if and only if dep(V
i
,V
j
)
is greater than some defined threshold k:
E
V
i
,V
j
=
Accept if dep(V
i
,V
j
) ≥ k
Re ject else.
With all these rules, our approach ends up this first
step by constructing an initial skeleton of the BN us-
ing dependencies information derived from the ontol-
ogy. In this phase, the expert domain can check and
then correct the automatically detected edges between
variables if needed.
H B
WT
N
R
GBeG
MB
LSS
GB
1.2
1.2
1.4
1.4
1.4
1.2 1.2
1.2
1
1
1
1.4
Figure 2: Extracted weighted graph from ontology using
the selected relations where H: Hub, B: Blade, WT: Wind
Turbine, N: Nacelle, R: Rotor, GBe: Generator bearing, G:
Generator, MB: Main Bearing, LSS: Low Speed Shaft, and
GB: GearBox.
In the next section, we will describe how we can de-
termine the orientations of some edges and how we
exploit such information to make the BN learning,
more reliable.
4.4 Knowledge-guided BN Structure
Learning
We start by explaining how certain edges in the skele-
ton are oriented based on the semantic of relationships
in O. Then, we use a score-based algorithm to refine
the BN. For example, if we consider the dependency
semantic encapsulated in subSystemOf and contains
relations, an ordering ≺ over the associated variables
(corresponding to concepts), can be inferred. The
relation subSystemOf is used to represent the com-
position of different systems. These systems can be
Figure 3: Extract of Wind Turbine ontology.
divided into two categories: mechanical and electri-
cal sub-systems. According to the wind turbine on-
tology, the mechanical component has the following
sub-systems: wind turbine blade, the rotor, the na-
celle, etc. Regarding the electrical component, it is
composed of the generator and the power electronic
converter, etc.. Both sub-systems are also composed
of a set of smaller sub-systems. Thus, the subSys-
temOf can be considered as a relationship linking a
component to smaller ones, which makes it usable per
se as a prior about corresponding variables (or con-
cepts) ordering. To illustrate this idea, let us consider
an extract of the wind turbine ontology as shown in
figure3. Based on the subSystemOf property, the fol-
lowing ordering can be deduced:
Nacelle ≺ Generator ≺ Generator-bearing ≺ ...
Intuitively, the ordering ≺ over variables is very use-
ful to define the list of parents for some variables in
the constructed skeleton. For this purpose, a node V
i
is set as a parent of node V
j
(i.e., V
i
→ V
j
) only when
V
i
≺ V
j
and they are connected in the skeleton. It
should be emphasized that the variables ordering de-
duced from the relation subSystemOf is acyclic since
a variable V
i
cannot be at the same time a subSystemOf
and hasSubSystem with the same variable V
j
. Accord-
ing to the expert, this approach is quite reasonable
in practice since the impact is generally more impor-
tant from the global component to the more specific
one. For instance, a high temperature of the nacelle
implies that the temperature of all its subsystems are
also high. The opposite scenario does not necessarily
hold in practice. The relation contains depicts the set
of mechanical/electronic elements that a component
may contain. Thus, an ordering over variables that
satisfies the position of each component w.r.t. the oth-
ers can be deduced. Note that both relations subSys-
temOf and contains (resp. hasSubSystem and isCon-
tainedIn) may be linked to the same concepts. Impor-
tantly, these ordering results do not contradict each
other, because their semantics are very close. If two
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
582

concepts C
i
and C
j
are linked by contains and subSys-
temOf, the following properties are satisfied:
< C
i
, subSystemO f ,C
j
>→ @ < C
j
, contains,C
i
>
(3)
< C
i
, contains,C
j
>→ @ < C
i
, subSystemO f ,C
j
>
(4)
With all these properties, our approach converts the
skeleton G into a partially directed graph (PDAG) us-
ing Algorithm2. For the remaining undirected edges,
we select arbitrarily orientations. At this point, our
algorithm has constructed an initial DAG of the BN.
The obtained DAG is then refined through a score-
based search algorithm. In our wind turbine case, we
used a SCADA data to learn the final BN. During the
search phase, we pick the resulted DAG from the on-
tology as a starting point and we compute its score.
After that, we consider all the neighbor graphs of G
in the search space — all of the legal (without cy-
cle) networks obtained by applying a single operator
(edge deletion, edge addition, or edge reversal) to G
— and compute the score for each of them given the
dataset. We then consider the change that leads to
the best improvement. We continue this process until
no modification improves the score. During this re-
finement process, there are two ways to consider the
knowledge derived from the ontology:
• scenario 1: enable the learning algorithm to mod-
ify the initial DAG deduced from O.
• scenario 2: consider the ontology-based oriented
edges as constraints that we want to enforce, i.e.,
the algorithm is not allowed to modify these arcs.
Algorithm 2: Construct an initial PDAG-BN.
1: Input: BN skeleton G, Ontology O
2: Output: PDAG-BN G
3: ≺
1
= order(O, subSystemOf)
4: ≺
2
= order(O, contains)
5: ≺= {≺
1
∪ ≺
2
}
6: for each E
V
i
,V
j
in E
G
do
7: if V
i
≺ V
j
then
8: E
G
← (V
i
→ V
j
)
9: end if
10: if V
j
≺ V
i
then
11: E
G
← (V
j
→ V
i
)
12: end if
13: end for
14: return G
5 EXPERIMENTAL RESULTS
This section is dedicated to present the use-case and
highlight the impact of ontology’s knowledge in the
BN learning process.
5.1 Wind Turbine Use Case
In this paper, we evaluate our approach using the
data from supervisory control and data acquisition
(SCADA) of wind turbines. This data represents a
cost-effective way to monitor wind turbine compo-
nents for early failures and performance issues. In our
experiment, we used the SCADA data coming from
La Haute Borne wind farm between 2013 and 2016.
This data is composed by a massive amounts of time-
series that are stored, manipulated, and filtered via
the DARWIN Platform of ENGIE
7
. Overall, 210095
records have been generated during this period. In
this section, we focus our attention on the study of
the main components of the wind turbine such as na-
celle, generator, gearbox, etc
8
. To build the BN, we
also used the wind turbine ontology (see an extract in
Fig.3), designed within H2020 European project. For
each concerned concept (nacelle, generator, gearbox,
etc.), we extract all the concepts that are related to
it with the selected relations as described in our ap-
proach (subSystemOf (resp. hasSubSystem), contains
(resp. isContainedIn), and connectedTo).
In the following, both knowledge resources (SCADA
data and ontology) are exploited to derive a BN model
representing wind turbine system.
5.2 Evaluation of the Approach
We evaluate the performance of our approach w.r.t.
the quality of the detected relationships for a set of
selected temperature variables (gearbox and nacelle).
For each record in the data, we predict the value of the
temperature classes given the observations about the
explanatory variables in the BN. The evaluation of the
BN’s classification task is been carried out using the
10-fold cross-validation procedure and the expected
loss estimation. We studied the impact of the ontol-
ogy knowledge integration on the predictions qual-
ity and the computation time. To make the compar-
ison evaluation more thorough, in our experiments,
we vary the following parameters:
• the size of the dataset,
• the dependence threshold k,
7
https://digital.engie.com/solutions/darwin
8
By abuse of notation, we use the word Gear and Gen to
denote respectively gearbox and generator.
Exploiting Ontology to Build Bayesian Network
583

• the scenario of the score-based setting (see the end
of section 4.4).
All experiments are performed on a 1.9GHz Intel
Core i7 computer with 16GB of memory running
Windows 10. Our approach has been implemented
using the bnlearn R package (Scutari, 2009) and
Prot
´
eg
´
e tool
9
. We start by building the initial BN
DAG using the information in the ontology. Note that
we have done the matching between SCADA tem-
perature variables and the ontological entities (con-
cepts/relations). For example: the generator temper-
ature, which is a variable in SCADA, is represented
in the ontology by this triple <Generator, hasTem-
perature, Temperature>. Table 1 mentions an extract
of detected dependencies between SCADA variables
using the ontology. In these results, we observe a
strong dependency between temperatures of nacelle
and gearbox oil sump (equal to 1). A high depen-
dency is also observed between rotor bearing and na-
celle temperatures.
Table 1: An extract of dependency computed scores.
Var1 name Var2 name Score
Nacelle temp Gear oil temp 1
Gear inlet temp Gear oil temp 1
Rotor bear temp Nacelle temp 1
Converter torque Torque 0.83
Gear bear 1 temp Gear oil temp 0.83
Gear bear 2 temp Gear oil temp 0.83
Hub temp Rotor bear temp 0.71
Gear inlet temp Nacelle temp 0.5
Rotor bear temp Gear oil temp 0.5
Gear inlet temp Gear bear 1 temp 0.45
Gear inlet temp Gear bear 2 temp 0.45
Nacelle temp Gear bear 1 temp 0.45
Nacelle temp Gear bear 2 temp 0.45
Gen stator temp Gen bear 1 temp 0.42
Gen stator temp Gen bear 2 temp 0.42
Gen stator temp Nacelle temp 0.42
Gen bear 1 temp Nacelle temp 0.42
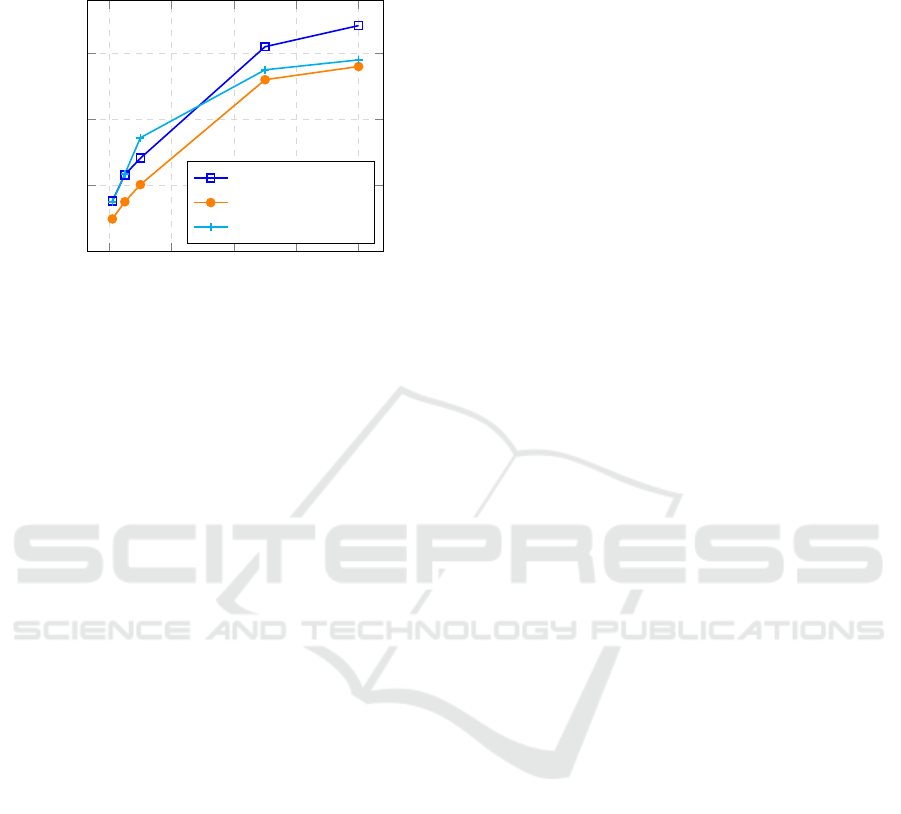
Figure 4 displays the expected loss for the gear-
box inlet temperature prediction using models learned
with the hill-climbing algorithm (HC) alone, and our
approach without and with constraints, respectively
denoted by sc=1 and sc=2. We fixed the threshold
k = 0.2. As can be observed, our approach always
outperforms the simple HC method, whatever the size
of the dataset. For a dataset size equal to 10000, the
expected loss of our approach with scenarios 1 and 2
is actually lower than that of the HC by ∼ 6% and ∼
5%. These results can be explained by the fact that our
9
https://protege.stanford.edu/
approach rules enable us to detect key dependencies
with gearbox inlet temperature variable, hence obtain-
ing better predictions.
0 2 4
6
8
·10
4
0.1
0.2
0.3
0.4
0.5
Sample size
Expected Loss
HC
HC, sc=1, k=0.2
HC, sc=2, k=0.2
Figure 4: Gearbox inlet temperature prediction errors.
Figure 5 shows results for nacelle temperature pre-
dictions. As can be seen, our approach using con-
straints got better results than the simple use of HC
algorithm. Our approach with scenario 1 (sc=1) is al-
ways outperformed by the simple use of HC, in this
case. These results happened because we enable the
refinement score-based algorithm to modify our ini-
tial DAG (derived mostly from the ontology), which
may lead to loose some key relationships.
0 2 4
6
8
·10
4
0
0.2
0.4
Sample size
Expected Loss
HC
HC, sc=1, k=0.2
HC, sc=2, k=0.2
Figure 5: Nacelle temperature prediction errors.
Figure 6 depicts runtimes associated with each al-
gorithm according to the data size parameter. As ex-
pected, except for the case where the data size is equal
to 10000, our approach (sc=1 and sc=2) is mostly
faster than HC. This is explained by the use of ini-
tial knowledge derived from the ontology which op-
timizes the DAG search space. For data size equal
to 80000, our approach with scenarios 1 and 2 are
ICPRAM 2022 - 11th International Conference on Pattern Recognition Applications and Methods
584
respectively about ∼19% and ∼16% faster than the
only use of HC.
0 2 4
6
8
·10
4
0
10
20
30
Sample size
Expected Loss
HC
HC, sc=1, k=0.2
HC, sc=2, k=0.2
Figure 6: Runtime w.r.t. the data size.
6 CONCLUSION AND FUTURE
WORKS
In this paper, we proposed a new generic method for
the BN learning structure by exploiting the knowl-
edge in the ontology. Our method is divided into sev-
eral steps: (i) constructing a weighted graph from the
ontology (ii) deriving dependencies and constructing
the BN skeleton (iii) orienting edges using the seman-
tic of relations in the ontology (iv) refining the BN via
a scored based algorithm. By integrating knowledge
from the ontology, our approach leads to a significant
improvement in terms of runtime computations and
expected loss results. The proposed approach can be
easily applied to other domains. As future works, our
current approach can be extended by integrating addi-
tional knowledge from ontologies and also by refining
these latter through the use of BN results (adding re-
lationships, uncertainty, etc.). Additional experimen-
tations on more complex real-world datasets will be
also explored.
REFERENCES
Bucci, G., Sandrucci, V., and Vicario, E. (2011). Ontologies
and bayesian networks in medical diagnosis. In 2011
44th Hawaii International Conference on System Sci-
ences, pages 1–8. IEEE.
Carvalho, R. N., Laskey, K. B., and Costa, P. C. (2010).
Pr-owl 2.0–bridging the gap to owl semantics. Uncer-
tainty reasoning for the semantic web II, pages 1–18.
Devitt, A., Danev, B., and Matusikova, K. (2006). Con-
structing bayesian networks automatically using on-
tologies. Applied Ontology, 1.
Dijkstra, E. W. et al. (1959). A note on two problems
in connexion with graphs. Numerische mathematik,
1(1):269–271.
Fenz, S. (2012). An ontology-based approach for construct-
ing bayesian networks. Data & Knowledge Engineer-
ing, 73:73–88.
Genesereth, M. R. and Nilsson, N. J. (1987). Logical Foun-
dations of Artificial Intelligence. San Francisco, CA,
USA.
Gruber, T. R. (1993). A translation approach to portable
ontology specifications. Knowledge Acquisition,
5:199–220.
Guarino, N. (1995). Formal ontology, conceptual analysis
and knowledge representation. International Journal
Human Computer Study, 43(5-6):625–640.
Helsper, E. M. and Van Der Gaag, L. C. (2002). Building
bayesian networks through ontologies. In ECAI, vol-
ume 2002, page 15th.
Ishak, M. B., Leray, P., and Amor, N. B. (2011a). Ontology-
based generation of object oriented bayesian net-
works. In BMAW 2011, pages 9–17.
Ishak, M. B., Leray, P., and Amor, N. B. (2011b). A
two-way approach for probabilistic graphical models
structure learning and ontology enrichment. In KEOD
2011, pages 189–194.
Jeon, B.-J. and Ko, I.-Y. (2007). Ontology-based semi-
automatic construction of bayesian network models
for diagnosing diseases in e-health applications. In
2007 Frontiers in the Convergence of Bioscience and
Information Technologies, pages 595–602. IEEE.
Messaoud, M. B., Leray, P., and Amor, N. B. (2013). Ac-
tive learning of causal bayesian networks using on-
tologies: a case study. In The 2013 International Joint
Conference on Neural Networks (IJCNN), pages 1–8.
IEEE.
Mohammed, A.-W., Xu, Y., and Liu, M. (2016).
Knowledge-oriented semantics modelling towards un-
certainty reasoning. SpringerPlus, 5(1):1–27.
Pearl, J. (1988). Probabilistic reasoning in intelligent sys-
tems : networks of plausible inference / Judea Pearl.
Morgan Kaufmann Publishers San Mateo, Calif.
Pearl, J. (2014). Probabilistic reasoning in intelligent sys-
tems: networks of plausible inference. Elsevier.
Scutari, M. (2009). Learning bayesian networks with the
bnlearn r package. arXiv preprint arXiv:0908.3817.
Setiawan, F. A., Budiardjo, E. K., and Wibowo, W. C.
(2019). Bynowlife: a novel framework for owl and
bayesian network integration. Information, 10(3):95.
Wang, Y. (2007). Integrating uncertainty into ontology
mapping. In The Semantic Web, pages 961–965.
Springer.
Yang, Y. and Calmet, J. (2005). Ontobayes: An ontology-
driven uncertainty model. In International Conference
on Computational Intelligence for Modelling, Control
and Automation and International Conference on In-
telligent Agents, Web Technologies and Internet Com-
merce (CIMCA-IAWTIC’06), volume 1, pages 457–
463. IEEE.
Zhang, S., Sun, Y., Peng, Y., Wang, X., et al. (2009).
Bayesowl: A prototype system for uncertainty in se-
mantic web. In Proceedings of the International Con-
ference on Artificial Intelligence.
Exploiting Ontology to Build Bayesian Network
585
