Highways in Warehouse Multi-Agent Path Finding: A Case Study
Vojt
ˇ
ech Ryb
´
a
ˇ
r
a
and Pavel Surynek
b
Faculty of Information Technology, Czech Technical University, Th
´
akurova 9, 160 00 Praha 6,Czech Republic
Keywords:
Multi-Agent Path Finding (MAPF), Highways, Conflict-Based Search (CBS).
Abstract:
Orchestrating warehouse sorting robots each transporting a single package from the conveyor belt to its des-
tination is a NP-hard problem, often modeled Multi-agent path-finding (MAPF) where the environment is
represented as a graph and robots as agents in vertices of the graph. However, in order to maintain the speed
of operations in such a setup, sorting robots must be given a route to follow almost at the moment they obtain
the package, so there is no time to perform difficult offline planning. Hence in this work, we are inspired by
the approach of enriching conflict-based search (CBS) optimal MAPF algorithm by so-called highways that
increase the speed of planning towards on-line operations. We investigate whether adding highways to the
underlying graph will be enough to enforce global behaviour of a large number of robots that are controlled
locally. If we succeed, the slow global planning step could be omitted without significant loss of performance.
1 INTRODUCTION
Logistics centres that are organised in such a way that
small sorting robots can operate in them, are starting
to become widespread. Their undeniable advantages
include higher speed in sorting larger quantities of
shipments and significant savings in human labour.
Such logistics centres are organized the following
way: a human operator or a robot arm takes a package
from, e.g., a conveyor belt. Then the operator (robot
arm) uses the optical recognizing system to examine
the package to determine its destination cage. Then
the operator (robot arm) loads the package to a sorting
robot which is capable of carrying just one package.
Once the sorting robot is loaded with the package, it
takes off for its destination. When the sorting robot
arrives at its destination, it unloads the carried pack-
age to a hole in the ground, which is an entrance to a
cage below the floor. We present a screenshot taken
from an illustrative YouTube video
1
in Figure 1.
This approach, where the operator stands in one
place and the robots with the load come to him and
leave again after the operator performs a simple op-
eration, was popularized by the Kiva robots (Wurman
et al., 2008). In contrast to them, the sorting robot we
consider in this paper only transports a single package
at a time.
a
https://orcid.org/0000-0003-0552-3997
b
https://orcid.org/0000-0001-7200-0542
1
https://youtu.be/jwu9SX3YPSk
Figure 1: Real world instance of the warehouse sorting
robots concept.
To ensure that the process of planning the individ-
ual routes of each sorting robot does not cause delays
that slow down the orchestration of the entire sort-
ing process in the logistics centre (and thus largely
reduce the main advantage of why logistics centres of
this type are being built), it is necessary that finding
the route for each robot, whether from where it has
been assigned a parcel and a destination cage, or back
to where it can load a new parcel, is a matter of mo-
ments.
As it makes no sense to employ just one sorting
robot in the whole warehouse, it is important to find
a suitable route that would take into account other
robot operations in the same warehouse space. This
routing problem in the warehouse can be abstracted
274
Rybá
ˇ
r, V. and Surynek, P.
Highways in Warehouse Multi-Agent Path Finding: A Case Study.
DOI: 10.5220/0010845200003116
In Proceedings of the 14th International Conference on Agents and Artificial Intelligence (ICAART 2022) - Volume 1, pages 274-281
ISBN: 978-989-758-547-0; ISSN: 2184-433X
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

as so-called Multi-agent path finding (MAPF) (Ryan,
2007; Silver, 2005; Kornhauser et al., 2009; Surynek,
2009). The task in MAPF is to navigate agents in a
graph from their starting vertices to given individual
goal vertices so that agent do not collide with each
other (that is, they neither share a vertex nor traverse
an edge in the opposite directions).
Such a problem has an optimal solution in terms
of the number of actions (movements), but finding
the optimal solution is NP-hard (Yu and LaValle,
2013; Surynek, 2010). With dozens to hundreds sort-
ing robot operation in current warehouses, this is a
substantial limitation. Conflict-Based Search (CBS)
(Sharon et al., 2015a) or SAT (Surynek, 2019) can
serve as well-established algorithms to obtain a glob-
ally optimal solution.
In this paper, we would like to compare how an
optimal solution obtained by the CBS algorithm per-
forms compared to the most simple algorithm we
could define that would ensure that robots do not
block each other so that their planned routes and col-
lision avoidance make movement around the ware-
house impossible.
Our approach is inspired by (Cohen and Koenig,
2016). There the authors enhance low-level CBS
search (explained in Section 2.1) with predefined
preferable set of edges called highways. The second
source of inspiration is agent-based modeling (ABM)
(Castiglione, 2009) which aims at achieving complex
global behaviour of a group of agents via local con-
trol of individual agents. Here the behaviour we want
to achieve is that agents reduce collisions with each
other and the cost of the global plan is close to the
optimum.
We use the highway idea but remove the the global
planning step. All edges in our warehouse abstraction
(described in Section 3) will be made directed. In-
stead of global planning, each robot will check the
robots in its neighbourhood to avoid collisions. Thus
will follow simple local rules, however the environ-
ment is enhanced via highways which we believe can
make these simple rules efficient.
1.1 Related Work
There are many approaches to solving optimalthe
MAPF problem optimally as well as bounded sub-
optimally. The solutions may be found via reduction
(often also called compilation) of the MAPF problem
to propositional satisfiability (SAT) (Kautz and Sel-
man, 1999; Surynek et al., 2016) or to other estab-
lished formalism for modeling and solving NP-hard
problems (Lam et al., 2019)
Different stream of approaches is represented by
search-based algorithms that model the MAPF di-
rectly and suggest dedicated algorithm. Some of the
state-of-the-art algorithms include Increasing Cost
Tree Search - ICTS (Sharon et al., 2013), Conflict-
based Search - CBS (Sharon et al., 2015b), and Im-
proved CBS – ICBS (Boyarski et al., 2015) and mode.
Most of optimal algorithms have their bounded sub-
optimal variants that trade-off optimality for the speed
of solving.
2 MULTI-AGENT PATH FINDING
In MAPF, the time is discretized into time steps. The
configuration of agents A = {a
1
,a
2
,...,a
k
} in vertices
of the graph G = (V, E) at timestep t is denoted as s
t
.
Each agent a
i
has a start position s
0
(a
i
) ∈ V and a goal
position s
+
(a
i
) ∈ V .
Formally, a MAPF instance is a tuple Σ = (G =
(V,E),A,s
0
,s
+
) where s
0
: R → V is an initial config-
uration of agents and s
+
: A → V is a goal configura-
tion of agents. A solution for Σ is a sequence of con-
figurations S (Σ) = [s
0
,s
1
,...,s
µ
] such that s
t+1
results
from valid movements from s
t
for t = 1,2,...,µ − 1,
and s
µ
= s
+
. Orthogonally to this, the solution can be
represented as a set of paths for individual agents that
do not conflict with each other.
At each time step a agent can either move to an
adjacent location (vertex) or wait in its current loca-
tion. The task is to find a sequence of move/wait ac-
tions for each agent a
i
, moving it from s
0
(a
i
) to s
+
(a
i
)
such that agents do not conflict, i.e., do not occupy
the same location at the same time and do not traverse
the same edge in opposite directions. An example of
MAPF instance and its solution is shown in Figure 2.
path(a
1
) =
[v
1
, v
4
, v
7
, v
8
, v
9
]
Cost = 4
path(a
2
) =
[v
3
, v
6
, v
5
, v
4
, v
7
]
Cost = 4
SoC = 8
MAPF
s
0
(a
1
) = v
1
s
+
(a
1
) = v
9
s
0
(a
2
) = v
3
s
+
(a
2
) = v
7
v
1
a
1
a
2
v
2
v
3
v
4
v
5
v
6
v
7
v
8
v
9
a
1
a
2
v
1
v
4
v
7
v
2
v
5
v
8
v
3
v
6
v
9
Figure 2: An MAPF instance with two agents a
1
and a
2
.
Often various cumulative objectives are optimized
in MAPF. We will develop all concepts in this paper
for the sum-of-costs objective, one of the most fre-
quently used, formally defined as follows:
Definition 1. (Sum-of-Costs). Sum-of-costs denoted
SoC is the summation, over all agents, of the number
of time steps required to reach the goal. Formally,
SoC =
∑
k
i=1
cost(path(a
i
)), where cost(path(a
i
)) is
an individual path cost of agent a
i
connecting s
0
(a
i
)
Highways in Warehouse Multi-Agent Path Finding: A Case Study
275

calculated as the number of edge traversals and wait
actions.
2
Observe that in the sum-of-costs we accumulate
the cost of wait actions for agents not yet reaching
their goal vertices. A feasible solution of a solvable
MAPF instance can be found in polynomial time (Ko-
rnhauser et al., 1984).
Finding an optimal solution with respect to the
sum-of-costs objective is NP-hard (Yu and LaValle,
2013; Surynek, 2010) and also determining the exis-
tence of a solution that differs from the optimum by a
factor less than 4/3 is NP-hard too (Ma et al., 2016).
Therefore designing algorithms based on search and
SAT for MAPF is justifiable.
2.1 Conflict-based Search
CBS is a representative of search-based approach.
CBS uses the idea of resolving conflicts lazily; that is,
a solution of MAPF instance is not searched against
the complete set of movement constraints that for-
bids collisions between agents but with respect to ini-
tially empty set of collision forbidding constraints that
gradually grows as new conflicts appear. The advan-
tage of CBS is that it can find a valid solution before
all constraints are added.
The high level of CBS searches a constraint tree
(CT) using a priority queue in breadth first manner.
CT is a binary tree where each node N contains a set
of collision avoidance constraints N.constraints - a
set of triples (a
i
,v,t) forbidding occurrence of agent
a
i
in vertex v at time step t, a solution N.paths - a set
of k paths for individual agents, and the total cost N.ξ
of the current solution.
The low level process in CBS associated with
node N searches paths for individual agents with re-
spect to set of constraints N.constraints. For a given
agent a
i
, this is a standard single source shortest path
search from α
0
(a
i
) to α
+
(a
i
) that avoids a set of
vertices {v ∈ V |(a
i
,v,t) ∈ N.constraints} whenever
working at time step t. For details see (Sharon et al.,
2015a).
CBS stores nodes of CT into priority queue OPEN
sorted according to ascending costs of solutions. At
each step CBS takes node N with the lowest cost from
OPEN and checks if N.paths represent paths that are
valid with respect to MAPF movements rules - that
is, N.paths are checked for collisions. If there is no
collision, the algorithms returns valid MAPF solution
N.paths. Otherwise the search branches by creating
a new pair of nodes in CT - successors of N. Assume
2
The notation path(a
i
) refers to path in the form of a
sequence of vertices and edges connecting s
0
(a
i
) and s
+
(a
i
)
while cost assigns the cost to a given path.
Algorithm 1: Basic variant of CBS algorithm for
MAPF solving.
1 CBS (G = (V,E),A,s
0
,s
+
)
2 N.constraints ←
/
0
3 N.paths ← {shortest path from s
0
(a
i
) to
s
+
(a
i
)|i = 1, 2,...,k}
4 N.ξ ←
∑
k
i=1
ξ(N.paths(a
i
))
5 insert R into OPEN
6 while OPEN 6=
/
0 do
7 N ← min(OPEN)
8 remove-Min(OPEN)
9 collisions ← validate(N.paths)
10 if collisions =
/
0 then
11 return N.paths
12 let (a
i
,a
j
,v,t) ∈ collisions
13 for each r ∈ {a
i
,a
j
} do
14 N
0
.constraints ←
N.constraints ∪ {(r,v,t)}
15 N
0
.paths ← N.paths
16 update(r, N
0
.paths, N
0
.constraints)
17 N
0
.ξ ←
∑
k
i=1
ξ(N
0
.paths(a
i
))
18 insert N
0
into OPEN
that a collision occurred between agents a
i
and a
j
in vertex v at time step t. This collision can be
avoided if either agent a
i
or agent a
j
does not re-
side in v at timestep t. These two options cor-
respond to new successor nodes of N - N
1
and
N
2
that inherit set of conflicts from N as fol-
lows: N
1
.con f licts = N.con f licts ∪ {(a
i
,v,t)} and
N
2
.con f licts = N.con f licts ∪ {(a
j
,v,t)}. N
1
.paths
and N
1
.paths inherit paths from N.paths except those
for agents a
i
and a
j
respectively. Paths for a
i
and a
j
are recalculated with respect to extended sets of con-
flicts N
1
.con f licts and N
2
.con f licts respectively and
new costs for both agents N
1
.ξ and N
2
.ξ are deter-
mined. After this, N
1
and N
2
are inserted into the pri-
ority queue OPEN.
The pseudo-code of CBS is listed as Algorithm 1.
One of crucial steps occurs at line 16 where a new
path for colliding agents a
i
and a
j
is constructed with
respect to the extended set of conflicts. N.paths(r)
refers to path of agent r.
The CBS algorithm ensures finding sum-of-costs
optimal solution. Detailed proofs of this claim can be
found in (Sharon et al., 2015a).
2.2 Highways
The planning part of Highway algorithm (HW) is de-
scribed in Algorithm 2. Lines 3-24 are plain A
∗
al-
gorithm. All notation is the same as in the CBS case
except the input H which is the heuristic to be used
for the in the A
∗
algorithm.
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
276

Algorithm 2: Highway algorithm.
1 HW (G = (V,E),H, A,s
0
,s
+
)
2 for each a
i
|i = 1, 2,...,k do
3 OPEN ← s
0
(a
i
)
4 for each v ∈ V do
5 v
CAMEFROM
← NAN
6 v
g
← ∞
7 v
f
← ∞
8 s
0
(a
i
)
g
← 0
9 while OPEN 6=
/
0 do
10 v ← o ∈ OPEN with smallest o
f
11 if v = s
+
(a
i
) then
12 path ←
path from s
0
(a
i
) to s
+
(a
i
)
13 traversing CAMEFROM
14 return path
15 remove v from OPEN
16 for each n: {v,n} ∈ E do
17 g
tentative
← v
g
+ 1
18 if g
tentative
< n
g
then
19 n
CAMEFROM
← v
20 n
g
← g
tentative
21 n
f
← n
g
+ H(n)
22 if n /∈ OPEN then
23 OPEN ← OPEN ∪ {n}
24 return failure
Unlike the CBS algorithm, the Highway algo-
rithm does not produce conflict-free plans. Therefore,
conflicts need to be resolved during the simulation
run. Details of our implementation of avoiding col-
lisions are described in the following section where
the whole experimental body of work is introduced
and described.
For the Highway algorithm to work, we need the
graph edges of the graph G = (V, E) to be oriented.
Otherwise, robots with conflicting plans can easily
block each other from executing the next step. This
might happen as well in the case of the Highway al-
gorithm in a pathological configuration of a graph and
number of agents. We observed this behaviour in the
second experiment described below. To avoid robots
blocking each other, we removed a couple of edges
from the underlying graph, the details are described
in the following sections and depicted in Figures 5
and 6.
In the Highway algorithm, we use as heuristics H
a zero vertex function H
0
defined the following way:
H
0
(v) = 0 ∀v ∈ V.
Let us think for now of Algorithm 2 as an actual
implementation of line 3 in Algorithm 1.
Furthermore, let us construct an oriented subgraph
G
HW
= (V
HW
,E
HW
) of the graph G = (V,E) and de-
fine the heuristics H
HW
the following way:
H
HW
(v) = min
π
∑
(s
i
,s
i+1
)∈π
=
(
1 if (s
i
,s
i+1
) ∈ E
HW
,
w otherwise,
where π = {v,...,s
+
(a
i
)} ∈ V is a path from vertex v
to a robot destination s
+
(a
i
) and w is a given constant.
If we use H
HW
as the the heuristics in Algorithm 2
for implementation of line 3 in Algorithm 1, we will
get the original algorithm from (Cohen and Koenig,
2016).
3 WAREHOUSE ABSTRACTION
For an abstraction of a physical world warehouse, we
use a rectangular planar graph as depicted in Figure
3. The graph can be either directed or undirected.
Whether we use directed or undirected edges depends
on the planning algorithm as described in the follow-
ing sections. Purple squares represent places where
an warehouse operator picks a single package from
a conveyor belt. Optical character recognition sys-
tem detects the nature and/or destination of the pack-
age, and then the sorting cage of the package is deter-
mined. When the unloaded agent arrives at the graph
node to the left of the loading spot, the operator loads
the package onto the sorting agent and the warehouse
system assigns the agent the proper destination cage.
Destination cages are depicted as yellow squares in
Figure 3. When the agent arrives at a graph node
above the destination cage, it unloads the package.
Then the agent destination is set to a loading spot.
Figure 3: Example of a planar graph used as an abstraction
of real-world warehouse where sorting agents can operate.
At each time step at every graph vertex, there can
be at most one agent. Moreover, one graph edge can
be used by only one agent at each time step, i.e.,
agents cannot swap locations in one step. Which
would make sense only in the case of undirected
graphs anyway.
Highways in Warehouse Multi-Agent Path Finding: A Case Study
277

Our model neglects several aspects of the real-
world scenario. We do not take into account any time
needed to load and unload the agent. In addition, ev-
ery agent move from one node of the graph to another
takes one time step. We are not taking into account ac-
celeration, deceleration, or direction change. Agents
need recharging from time, to time which is also not
in our consideration.
4 EXPERIMENTAL
COMPARISON
4.1 Agents.jl Implementation
We evaluated performance of the above-described
planning algorithms within the Agent-based mod-
elling paradigm where autonomous agents behave ac-
cording to a set of predefined rules inside a computa-
tional simulation environment.
We implemented the abstraction from Section 3 in
Agents.jl (Datseris et al., 2021). Agents.jl is a frame-
work for agent-based modelling written in Julia with
three basic building blocks:
1. model definition,
2. model step function,
3. agent step function.
Julia programming language was chosen because
it is a flexible programming language with perfor-
mance comparable to traditional statically-typed lan-
guages
3
.
Our warehouse abstraction can be defined in
Agents.jl as a straightforward application of the pre-
defined graph model block.
When CBS algorithm is employed, the model step
function finds a new plan every time a new destination
for any agent is determined. With HW, it does not
need to do anything.
In the case of CBS algorithm, the agent step func-
tion only makes the agent follow the central plan, i.e.,
move agent to the next vertex along the planned route.
In the case of HW, it finds the shortest path between
the starting point and the destination when a new des-
tination is determined and then follows the path. In
case of conflicting route with another agent, it makes
the agent wait at the current position in the present
time step.
The whole implementation is available from
GitHub
4
.
3
https://julialang.org/benchmarks/
4
https://github.com/voltej/warehouse sorting robots
4.2 Experiment Setup
Inspired by the real world application, we chose two
types of warehouse setup for experimental evaluation.
As representatives of the first type, we picked two
warehouse designs of size 17x15 (Experiment 1) and
51x51 (Experiment 2) building blocks. One building
block is a square planar graph with three vertices on
each edge and one vertex in the middle. The mid-
dle vertex can represent the loading spot or the des-
tination cage.To illustrate what we mean by a build-
ing block, we note that the planar warehouse graph in
Figure 3 consist of 3 x 3 building blocks. Therefore,
the overall grid dimensions in Experiments 1 and 2
are 35x31 and 103x103, respectively. The directed
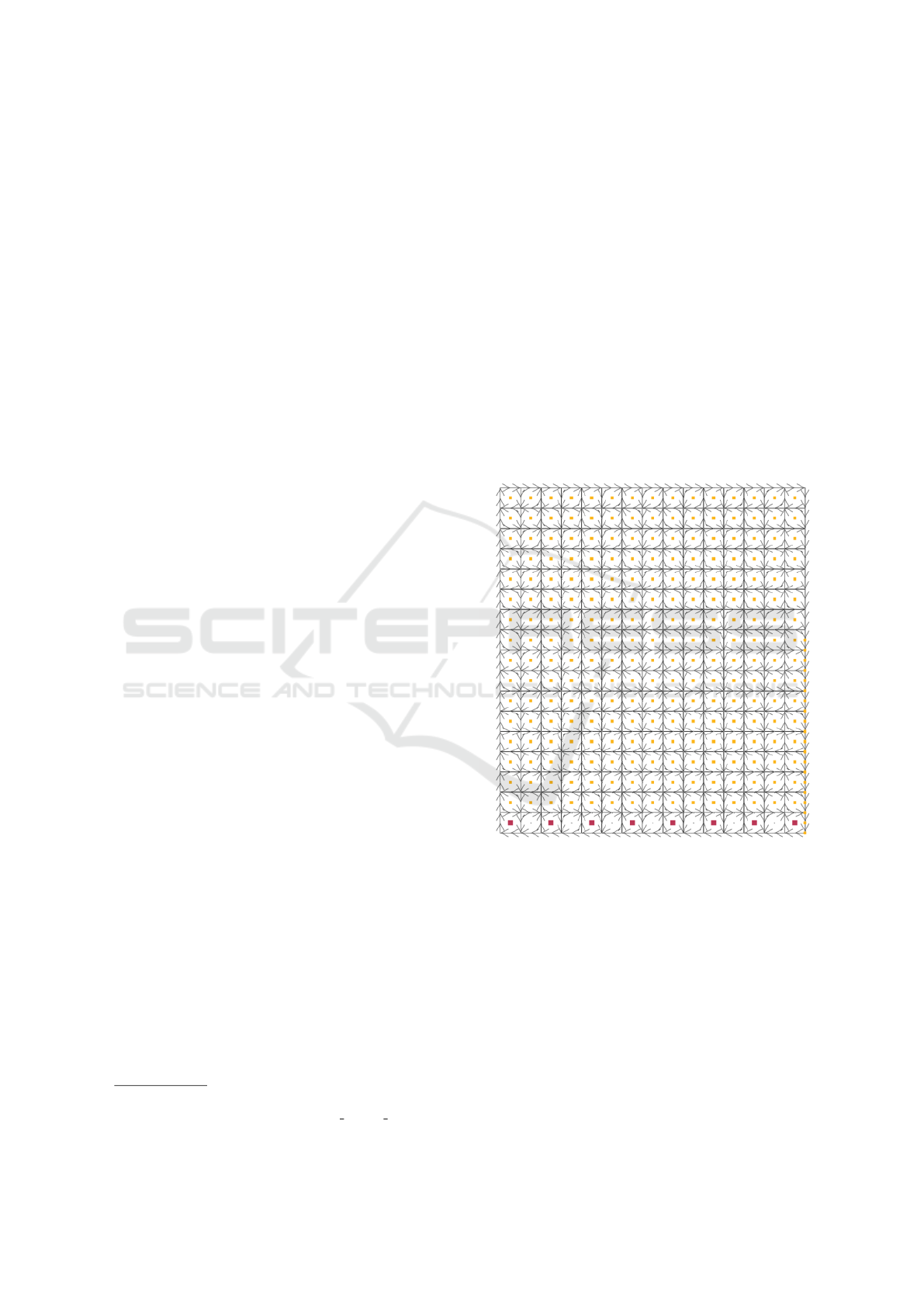
version of the warehouse design for Experiment 1 is
depicted in Figure 4 to show how the highways are
oriented.
Figure 4: Warehouse design for Experiment 1 with 17x15
building blocks.
For evaluation of another approach of warehouse
design, we prepared Experiment 3. The underlying
graph is depicted in Figure 5. To avoid agents block-
ing each others route to the extent that no agent can
make any movement, we needed to remove the hor-
izontal edges in the bottom of the graph as shown
in Figure 6. Again, only the directed version of the
CBSd algorithm is depicted in Figure 5. CBS was
evaluated on the same graph with the same edges, but
the edges were not oriented.
For all three warehouse designs, we initialized 100
random seeds to get 100 package destinations and run
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
278

Figure 5: Warehouse design for Experiment 3 with CBS and
CBSd algorithms.
Figure 6: Warehouse design for Experiment 3 adjusted for
the Highway algorithm.
simulations to see how many time steps are needed to
deliver all packages to their designed locations.
Number of packages and sorting robots for each
of the experiments is show in Table 1.
Table 1: Experimental setup.
Experiment
number
Number of
packages
Number of
robots
1 300 60
2 1000 100
3 100 20
We used the following three planning strategies:
1. CBS on undirected graph,
2. CBS on directed graph,
3. HW on directed graph.
The last possible combination, HW on an undirected
graph, does not make sense as agents can easily block
each other with their planned moves.
At the time of unloading, the robot is given a new
destination which is a loading spot that has dispatched
the smallest number of packages until the present time
step.
Since an agent is given a new location every time
it loads or unloads a package, the CBS solver must be
called at every time step when a loading or unloading
action occurs to create a new collision-free plan.
Therefore, CBS algorithm only need to produce
a conflict-free plan for the smallest number of time
steps that are needed for any robot to reach its desti-
nation or a loading spot. Stopping CBS algorithm at
such a time step allows it to solve much complicated
problems compared to the case when CBS is required
to find a conflict-free plan where all robots reach its
destinations.
4.3 Experimental Results
Results of the simulation runs described in the pre-
vious subsection are presented in Tables 2–4. In all
cases, all tracked parameters, i.e., minimal, maximal,
and average time span, CBS performs the best, fol-
lowed by CBS on a directed graph (CBSd) and HW.
To illustrate performance of the algorithms at ev-
ery time step we plot in Figures 7–9 how many pack-
ages had been delivered at each time step. Dim lines
presents the evolution of an simulation, bold lines
mean across all 100 simulations.
On the other hand, in case of Experiment 2 simu-
lations running on an average laptop, one simulation
run of HW takes, in general, about 0.05 second, CBSd
15 minutes, and CBS 1.5 hours.
Table 2: Times steps needed to deliver 300 packages in Ex-
periment 1.
Planning
Strategy
Min
Percentile
Max Mean Std
25 50 75
CBS 1107 1120 1130 1137 1158 1130 13
CBSd 1101 1130 1137 1146 1165 1137 13
HW 2167 2216 2234 2248 2313 2231 23
Table 3: Times steps needed to deliver 1000 packages in Ex-
periment 2.
Planning
Strategy
Min
Percentile
Max Mean Std
25 50 75
CBS 618 657 671 685 726 671 21
CBSd 634 676 689 709 738 690 23
HW 652 687 704 716 763 701 22
Highways in Warehouse Multi-Agent Path Finding: A Case Study
279

Figure 7: Mean of undelivered packages across all simula-
tions in Experiment 1. In this case the similar performance
of CBS and CBSd algorithms makes the red and green line
indistinguishable.
Figure 8: Mean of undelivered packages across all simula-
tions in Experiment 2. In this case the similar performance
of CBSd and Highway algorithms makes the green and blue
line indistinguishable.
Figure 9: Mean of undelivered packages across all simula-
tions for Experiment 3.
5 DISCUSSION
The results show that for Experiment 2, the average
difference in time needed to deliver 1000 packages
between a fast and simple algorithm and an optimal
one is about 5%.
A small difference between CBSd and HW might
suggest that the desired global conflict avoiding coor-
Table 4: Times steps needed to deliver 100 packages in Ex-
periment 3.
Planning
Strategy
Min
Percentile
Max Mean Std
25 50 75
CBS 194 205 210 215 227 209 7
CBSd 210 221 225 229 243 225 7
HW 349 356 359 364 372 360 6
dination is effectively introduced by imposing high-
ways in the graph.
Using CBS on the top of a directed graph im-
proves the average time span by 2-3 % while making
the simulation about 100 times slower.
With only about 5% difference in time span be-
tween a truly simple and fast algorithm and an optimal
one together with the rate by which every improve-
ment of the time span is prolonging the plan calcu-
lation, we conclude that it would be difficult to beat
the HW algorithm while maintaining its computation
time.
The same conclusions would have been true for
Experiment 1 if we would have run simulations with
20 sorting robots. But when we employed 60 sorting
robots, the time span resulting from the HW algorithm
is twice as long as in the CBS or CBSd case. This
might suggest that HW is not particularly suited for
higher traffic densities. Which turned to be true in the
last experiment as well.
In the case of Experiment 3, the difference in aver-
age time span is 7% between CBS and CBSd, but 70%
between CBS and HW. One would expect a difference
of such magnitude because route from the leftmost
loading spot the top left destination cage in the graph
in Figure 6 is more than twice as long as the route in
the graph in Figure 5. Carefully adding some of the
removed edges back to the graph depicted in Figure
6 could significantly improve the performance of the
HW algorithm. Such an approach may need to take
into account the number of robots in the warehouse
graph.
Evaluation of the results and their application to
real-world scenarios make us believe that the most
frugal next step would be to focus on enriching our
warehouse abstraction model by incorporating as-
pects we neglected in this stage, described in Sec-
tion 3.
With the model taking into account robot accel-
eration/deceleration and turning as well as charging
needs we would like to discover whether in ware-
house model with suitable size the results from this
case study still holds. Then it might make sense to try
to answer questions such as how many robots in the
warehouse performs the best, which planning algo-
rithm is the most suitable one for a given scenario, or
ICAART 2022 - 14th International Conference on Agents and Artificial Intelligence
280

how to design a warehouse space to achieve maximal
warehouse sorting capacity.
ACKNOWLEDGEMENTS
The presented work has been supported by GA
ˇ
CR -
the Czech Science Foundation under the grant regis-
tration number 22-31346S and by the Grant Agency
of the Czech Technical University in Prague, grant
registration number SGS20/213/OHK3/3T/18.
REFERENCES
Boyarski, E., Felner, A., Stern, R., Sharon, G., Tolpin,
D., Betzalel, O., and Shimony, S. E. (2015). ICBS:
improved conflict-based search algorithm for multi-
agent pathfinding. In Proceedings of the Twenty-
Fourth International Joint Conference on Artificial In-
telligence, IJCAI 2015, pages 740–746. AAAI Press.
Castiglione, F. (2009). Agent Based Modeling and Simula-
tion, Introduction to, pages 197–200. Springer New
York, New York, NY.
Cohen, L. and Koenig, S. (2016). Bounded suboptimal
multi-agent path finding using highways. In Kamb-
hampati, S., editor, Proceedings of the Twenty-Fifth
International Joint Conference on Artificial Intelli-
gence, IJCAI 2016, New York, NY, USA, 9-15 July
2016, pages 3978–3979. IJCAI/AAAI Press.
Datseris, G., Vahdati, A. R., and DuBois, T. C. (2021).
Agents.jl: A performant and feature-full agent based
modelling software of minimal code complexity.
Kautz, H. A. and Selman, B. (1999). Unifying sat-based
and graph-based planning. In Proceedings of the Six-
teenth International Joint Conference on Artificial In-
telligence, IJCAI 99, pages 318–325. Morgan Kauf-
mann.
Kornhauser, D., Miller, G. L., and Spirakis, P. G. (1984).
Coordinating pebble motion on graphs, the diame-
ter of permutation groups, and applications. In 25th
Annual Symposium on Foundations of Computer Sci-
ence, West Palm Beach, Florida, USA, 24-26 October
1984, pages 241–250. IEEE Computer Society.
Kornhauser, D., Wilensky, U., and Rand, W. (2009). De-
sign guidelines for agent based model visualization.
J. Artif. Soc. Soc. Simul., 12(2).
Lam, E., Bodic, P. L., Harabor, D. D., and Stuckey, P. J.
(2019). Branch-and-cut-and-price for multi-agent
pathfinding. In Proceedings of the Twenty-Eighth In-
ternational Joint Conference on Artificial Intelligence,
IJCAI 2019, pages 1289–1296. ijcai.org.
Ma, H., Tovey, C. A., Sharon, G., Kumar, T. K. S., and
Koenig, S. (2016). Multi-agent path finding with pay-
load transfers and the package-exchange robot-routing
problem. In Proceedings of the Thirtieth AAAI Con-
ference on Artificial Intelligence, 2016, pages 3166–
3173. AAAI Press.
Ryan, M. R. K. (2007). Graph decomposition for efficient
multi-robot path planning. In IJCAI 2007, Proceed-
ings of the 20th International Joint Conference on Ar-
tificial Intelligence, pages 2003–2008.
Sharon, G., Stern, R., Felner, A., and Sturtevant, N.
(2015a). Conflict-based search for optimal multi-
agent pathfinding. Artif. Intell., 219:40–66.
Sharon, G., Stern, R., Felner, A., and Sturtevant, N. R.
(2015b). Conflict-based search for optimal multi-
agent pathfinding. Artif. Intell., 219:40–66.
Sharon, G., Stern, R., Goldenberg, M., and Felner, A.
(2013). The increasing cost tree search for optimal
multi-agent pathfinding. Artif. Intell., 195:470–495.
Silver, D. (2005). Cooperative pathfinding. In Proceedings
of the First Artificial Intelligence and Interactive Dig-
ital Entertainment Conference, pages 117–122. AAAI
Press.
Surynek, P. (2009). A novel approach to path planning
for multiple robots in bi-connected graphs. In 2009
IEEE International Conference on Robotics and Au-
tomation, ICRA 2009, Kobe, Japan, May 12-17, 2009,
pages 3613–3619. IEEE.
Surynek, P. (2010). An optimization variant of multi-robot
path planning is intractable. In Proceedings of the
Twenty-Fourth AAAI Conference on Artificial Intelli-
gence, AAAI 2010, Atlanta, Georgia, USA, July 11-15,
2010. AAAI Press.
Surynek, P. (2019). Unifying search-based and
compilation-based approaches to multi-agent path
finding through satisfiability modulo theories. In
Kraus, S., editor, Proceedings of the Twenty-Eighth
International Joint Conference on Artificial Intelli-
gence, IJCAI 2019, pages 1177–1183. ijcai.org.
Surynek, P., Felner, A., Stern, R., and Boyarski, E. (2016).
Efficient SAT approach to multi-agent path finding un-
der the sum of costs objective. In ECAI 2016 - 22nd
European Conference on Artificial Intelligence, vol-
ume 285 of Frontiers in Artificial Intelligence and Ap-
plications, pages 810–818. IOS Press.
Wurman, P., D’Andrea, R., and Mountz, M. (2008). Coordi-
nating hundreds of cooperative, autonomous vehicles
in warehouses. AI Magazine, 29:9–20.
Yu, J. and LaValle, S. M. (2013). Structure and intractability
of optimal multi-robot path planning on graphs. In
Proceedings of the Twenty-Seventh AAAI Conference
on Artificial Intelligence, July 14-18, 2013, Bellevue,
Washington, USA. AAAI Press.
Highways in Warehouse Multi-Agent Path Finding: A Case Study
281