An Implemented System for Cognitive Planning

Jorge Fernandez

1 a

, Dominique Longin

2 b

, Emiliano Lorini

2 c

and Frédéric Maris

1 d

IRIT, Toulouse University, France

IRIT, CNRS, Toulouse University, France

Keywords:

Knowledge Representation, Epistemic Logic, Satisﬁability, Epistemic Planning, Cognitive Planning,

Persuasion.

Abstract:

We present a system that implements a framework for cognitive planning. The system allows us to represent

and reason about the beliefs, desires and intentions of other agents using an NP-fragment of a multiagent

epistemic logic. The system has three components: the belief revision, the planning and the translator modules.

They work in an integrated way to ﬁrstly capture new information about the world, secondly to plan a sequence

of speech acts aimed at achieving a persuasive goal and, ﬁnally, to verify satisﬁability of the formulas generated

at each step of the process. We illustrate how our system can be used to implement a persuasive artiﬁcial agent

interacting with a human user.

1 INTRODUCTION

Automated planning is at the center of AI research

with a variety of applications ranging from control

trafﬁc and robotics to logistics and services. Epis-

temic planning extends automated planning incorpo-

rating notions of knowledge and beliefs (Bolander

and Andersen, 2011; Löwe et al., 2011; Kominis

and Geffner, 2015; Muise et al., 2015; Cooper et al.,

2021). Cognitive planning is a generalization of epis-

temic planning, where the goal to be achieved is not

only a belief state but a cognitive state of a target in-

cluding not only beliefs but also intentions. More-

over, we are particularly interested in persuasive goals

of the planning agent, aimed at inﬂuencing another

agent’s beliefs and intentions.

The increasing number of applications in social

robotics, social networks, virtual assistants together

with sentiment analysis techniques allow us to col-

lect data related to humans’ beliefs and intentions. In

(Akimoto, 2019) a framework for modeling mental

attitudes of an agent, based on her narratives, is pro-

posed. In addition, cognitive models can be used to

predict agents’ decision-making by taking psycholog-

ical factors like motivation and emotions into account

(Prezenski et al., 2017). Nonetheless, few approaches

https://orcid.org/0000-0001-9328-1670

https://orcid.org/0000-0002-3138-2262

https://orcid.org/0000-0002-7014-6756

https://orcid.org/0000-0002-1084-1669

exist which leverage this information about humans’

cognitive states for changing their attitudes and be-

haviors through persuasion.

Our work aims to ﬁll this gap by introducing a

system

based on a simple framework detailed in

(Fernandez et al., 2021) in which we can represent

an agent’s cognitive state in a compact way, rea-

son about it and planning a sequence of speech acts

aimed at changing it. Our approach is based on an

epistemic logic introduced in (Lorini, 2018; Lorini,

2020), which allows us to represent an agent’s ex-

plicit beliefs, as the information in the agent’s belief

base, and the agent’s implicit beliefs, as the informa-

tion which is deducible from the agent’s belief base.

Given that the satisﬁability problem for the full logic

is PSPACE-hard, we focus on an NP-fragment that

makes the logic suitable for implementing real-world

applications.

The core components of the system are the belief

revision, the planning and the translator modules. The

formulas representing the rules and constraints for a

speciﬁc problem domain are loaded into the system.

We encode these rules using the NP-fragment pre-

sented in (Fernandez et al., 2021). The system takes

this information as the initial state and some actions

— which are of type speech act — to build a plan

that leads to the goal. An important feature is that

actions have preconditions that impose constraints on

their execution order. We illustrate the implementa-

https://github.com/CognitivePlanning/sw

492

Fernandez, J., Longin, D., Lorini, E. and Maris, F.

An Implemented System for Cognitive Planning.

DOI: 10.5220/0010846300003116

In Proceedings of the 14th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2022) - Volume 3, pages 492-499

ISBN: 978-989-758-547-0; ISSN: 2184-433X

tion of our system in a human-machine interaction

(HMI) scenario in which an artiﬁcial agent has to per-

suade a human agent to practice a sport based on her

preferences.

2 A LANGUAGE FOR EXPLICIT

AND IMPLICIT BELIEF

This section describes the basics of the Logic of Dox-

astic Attitudes (LDA) introduced in (Lorini, 2018;

Lorini, 2020). It is a multiagent epistemic logic which

supports reasoning about explicit and implicit beliefs.

Assume a countably inﬁnite set of atomic proposi-

tions Atm and a ﬁnite set of agents Agt = {1, . . . , n}.

We deﬁne the language in two steps.

We ﬁrst deﬁne the language L

(Atm, Agt) by the

following grammar in Backus-Naur Form (BNF):

α ::= p | ¬α | α

∧ α

| α

∨ α

| 4

α,

where p ranges over Atm and i ranges over Agt.

(Atm, Agt) is the language for representing agents’

explicit beliefs. The formula 4

α is read “i explicitly

believes that α”. The language L(Atm, Agt) extends

the language L

(Atm, Agt) by modal operators of im-

plicit belief and is deﬁned by the following grammar:

ϕ ::= α | ¬ϕ | ϕ

∧ ϕ

| ϕ

∨ ϕ

| 

ϕ | ♦

ϕ,

where α ranges over L

(Atm, Agt) and i ranges over

Agt. For notational convenience we write L

instead

of L

(Atm, Agt) and L instead of L(Atm, Agt), when

the context is unambiguous. The formula 

ϕ is read

“i implicitly believes that ϕ” and ♦

ϕ is read “ϕ is

compatible (or consistent) with i’s explicit beliefs”.

The other Boolean constructions >, ⊥, → and ↔ are

deﬁned in the standard way.

The language is interpreted with respect to a for-

mal semantics using belief bases whose details are

given in (Lorini, 2018; Lorini, 2020). Checking sat-

isﬁability of L formulas relative to this semantics is a

PSPACE-hard problem. For that reason, in (Fernan-

dez et al., 2021), we looked for an interesting NP-

fragment of L that we called L

Frag

ϕ ::= α | ¬ϕ | ϕ

∧ ϕ

| ϕ

∨ ϕ

| 

α | ♦

α,

where α ranges over L

and m is a special agent in Agt

called the ‘machine’. In L

Frag

, all agents have explicit

beliefs but only agent m has implicit beliefs. There-

fore, formulas including nesting implicit belief oper-

ators are not allowed (e.g., 

¬

p is not a well-

formed formula). Moreover the latter are restricted to

formulas of type α.

Agent m is the artiﬁcial planning agent. In order

to represent agents’ belief dynamics, language L

Frag

red

99K L

Frag

nnf

99K L

NNF

Frag

99K L

Mod

99K L

Prop

Figure 1: Summary of reduction process.

is extended by belief expansion operators. Such an

extension will allow us to represent the actions of

the planning agent in the cognitive planning prob-

lem. Speciﬁcally, we introduce the following lan-

guage L

Frag

ϕ ::=α|¬ϕ|ϕ

∧ϕ

|ϕ

∨ϕ

|

α|♦

α|[+

α]ϕ,

where α ranges over L

and i ranges over Agt. The

formula [+

α]ϕ is read “ϕ holds after agent i has pri-

vately expanded her belief base with α”. Event of

type +

α are generically called informative actions.

3 COGNITIVE PLANNING

The planning problem in the context of the logic L

Frag

is to ﬁnd a sequence of informative actions for agent

m of type +

α which guarantees that agent m will

knowingly achieve its goal. Let Act

= {+

α : α ∈

} be agent m’s set of informative actions and let the

elements of Act

be noted ε, ε

, . . . Agent m’s infor-

mative actions have executability preconditions that

are speciﬁed by the following function: P : Act

−→

Frag

. So, we can deﬁne the following operator of suc-

cessful occurrence of an informative action:

hhεiiϕ

def

= P (ε)∧ [ε]ϕ

with ε ∈ Act

. The formula hhεiiϕ has to be read

“agent m’s informative action ε can take place and ϕ

holds after its occurrence”.

Informative actions of type ‘speech act’ are of in-

terest here. In particular, we consider speech acts

of type ‘to inform’, where m is assumed to be the

speaker and j ∈ Agt such that j 6= m is assumed to be

the hearer. We deﬁne the speech act “agent m informs

agent j that α” as follows:

inform(m, j,α)

def

= +

α.

In (Fernandez et al., 2021) the planning problem

is deﬁned as a tuple hΣ, Op, α

i where:

• Σ ⊂ L

is a ﬁnite set of agent m’s available infor-

mation,

• Op ⊂ Act

is a ﬁnite set of agent m’s operators,

• α

∈ L

is agent m’s goal.

The planning problem has a solution if the formula



(

α∈Σ



α) → hhε

ii . . . hhε

ii



is unsatisﬁ-

able. Checking plan existence for a L

Frag

-planning

problem is in NP

= Σ

An Implemented System for Cognitive Planning

493

In Algorithm 1, plan

Frag

[k, i] (line 8) is the i can-

didate plan of size k, generated from the following

elements: the belief base, the i subset in the set of

combinations C of size k from Op and the goal.

Algorithm 1: Cognitive planning.

Data: Σ

base

, Op, α

Result: Plan

1 Begin

2 Function combinations (Op,k)

3 C = All subsets of size k from Op;

4 return C

5 Function generatePlans (k)

6 C ← combinations(Op, k);

7 for i ← 1 to |C| do

8 plan

Frag

[k, i] =

¬(

base

→ [+

C[i]]

)

9 plan

Prop

[k, i] =

Translator(plan

Frag

[k, i])

10 if TouIST(plan

Prop

[k, i]) =

UnSAT then

11 Print “Plan i of size k is

valid” ;

12 success ← true;

13 return

14 end if

15 end for

16 return

17 Main

18 k = 1 ;

19 success ← false;

20 while (k <= |Op| || not(success)) do

21 generatePlans(k);

22 k ++;

23 end while

24 if not(success) then

25 Print “Plan not found” ;

26 end if

27 exit

4 IMPLEMENTATION

The functionality of our integrated system for cogni-

tive planning is deﬁned by the use case presented in

Figure 2.

Its two core modules are belief revision and cog-

nitive planning which work in an integrated way.

Firstly, the belief revision module reads the input,

coming from the human through the graphical user

interface (GUI) for dialog, and veriﬁes that this input

does not contradict the core beliefs stored in the belief

Artiﬁcial Agent

include

GUI

Belief revision

Translations

Cognitive Planning

User

Figure 2: Use Case Artiﬁcial Agent.

base. Core beliefs are fundamental beliefs that never

change and are distinguished from volatile beliefs that

can change due to revision. If the input is in contra-

diction with the core beliefs, then the input is rejected

and the belief base is not updated. On the contrary, if

the input is not in contradiction with the core beliefs,

then the belief base is revised using a maximal con-

sistent subset (MCS) approach whereby the input has

priority over the old volatile beliefs.

Secondly, the planning module reads the initial

state, the set of actions, and the goal and starts to gen-

erate candidate plans of different size, starting with

size equal to one. During this phase, the planning

module calls the translator module which converts the

Frag

planning formula into its equivalent in propo-

sitional logic, following the sequence of reductions

detailed in Figure 1. After the reduction process per-

formed by the translator, the planning module exe-

cutes the SAT encoding tool TouIST (Fernandez et al.,

2020) to verify the validity of the propositional for-

mula. TouIST will encode the formula in CNF format

and send it to MiniSAT (this solver is set by default

in the application) for checking satisﬁability. TouIST

can work with external solvers that accept standard-

ized DIMACS as input language. Figure 3 shows the

proposed system architecture.

In order to probe the potential of our implemented

system for cognitive planning we applied it to a HMI

scenario detailed in (Fernandez et al., 2021). In this

scenario agent m is the artiﬁcial assistant of the hu-

man agent h. Agent h has to choose a sport to prac-

tice since her doctor recommended her to do a regular

physical activity to be in good health. Agent m’s aim

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

494

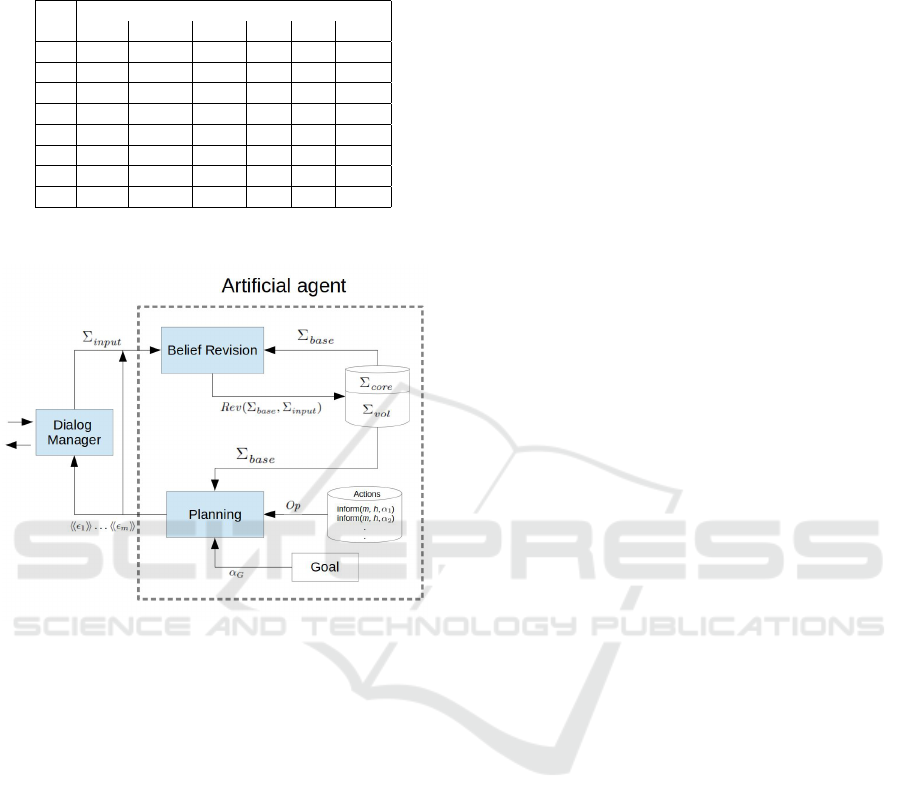
Table 1: Variable assignments. For every option o ∈ Opt

and variable x ∈ Var, we denote by v

o,x

the corresponding

entry in the table. For instance, we have v

sw,env

= water.

Opt

Var

env loc soc cost dan intens

sw water mixed single med low high

ru land outdoor single low med high

hr land outdoor single high high low

te land mixed mixed high med med

so land mixed team med med med

yo land mixed single med low low

di water mixed single high high low

sq land indoor mixed high med med

is to help agent h to make the right choice, given her

actual beliefs and desires.

Figure 3: System architecture.

In order to set the initial belief base, agent m has

to be provided with information about the possible op-

tions that the user can choose (Opt) and their proper-

ties (Var). For each pair (Opt,Var) we have a valu-

ation Val. In this example, we suppose that Opt in-

cludes the following eight elements: swimming (sw),

running (ru), horse riding (hr), tennis (te), soccer (so),

yoga (yo), diving (di) and squash (sq). Moreover,

there are exactly six variables in Var which are used

to classify the available options: environment (env),

location (loc), sociality (soc), cost (cost), dangerous-

ness (dan) and intensity (intens). The variable as-

signments are shown in Table 1.

Formulas representing the rules and constraints

are loaded as part of agent m’s belief base. For ex-

ample, the implementation of the formula represent-

ing the fact that agent h explicitly believes that a sport

cannot have two different values for a given property

is formalized as follows:

o∈Opt

x∈Var

∈Val

6=v



val(o, x 7→ v

) →

¬val(o, x 7→ v

)



The syntax for writing the formulas is based on

the TouIST language, with the extension of the modal

operators for explicit and implicit belief. For exam-

ple, we use {h} for representing 4

. Similarly we

use [m] for 

bigand

$o,$x,$v1,$v2

in $Opt,$Var,$Val($x),$Val($x)

when $v1 != $v2:

{h}val($o,ass($x,$v1))=>

{h}not val($o,ass($x,$v2))

end

Thus, this syntax allows us to represent functions

like the one included in the next formula, which states

that an option o is ideal for agent h if and only if the

option satisﬁes all agent h’s desires:

o∈Opt



ideal(h, o) ↔

Γ∈2

Des∗



des(h, Γ)∧

γ∈Γ

comp

(o, γ)





The function f

comp

speciﬁes, for every option o ∈

Opt and possible desire γ ∈ Des, the condition guar-

anteeing that o satisﬁes (or, complies with) γ:

comp

(o, a) = val(o, a),

comp

(o, ∼a) = ¬val(o, a),

comp



o, [d

, . . . , d

] d



= ¬ f

comp

(o, d

) ∨ . . . ∨

¬ f

comp

(o, d

) ∨ f

comp

(o, d).

The full implementation of the formula with the

function f

comp

included, requires the capture of the

human’s desires which together with the set of rules

and constraints are used to generate the machine’s be-

lief base.

$n1 =2

$n2 =1

$n3 =1

$Delta0 = [

"ass(env,land)",

"ass(intens,med)",

"not ass(loc,indoor)",

"ass(cost,high) => ass(soc,mixed)"

]

$Delta0_1(1) = ["ass(env,land)"]

$Delta0_1(2) = ["ass(intens,med)"]

$Delta0_2(1) = ["not ass(loc,indoor)"]

$Delta0_2(1,1) = ["ass(loc,indoor)"]

$Delta0_3(1) = ["ass(cost,high) =>

ass(soc,mixed)"]

$Delta0_3(1,1) = ["ass(cost,high)"]

$Delta0_3(1,2) = ["ass(soc,mixed)"]

$Opt = [sw, ru, te, hr, so, yo, di, sq]

$Var = [env, loc, soc, cost, danger, intens]

An Implemented System for Cognitive Planning

495

$Val(env) = [land,water]

$Val(loc) = [indoor, outdoor, mixed]

$Val(soc) = [single, team, mixed]

$Val(cost) = [low, med, high]

$Val(danger) = [low, med, high]

$Val(intens) = [low, med, high]

bigand

$o in $Opt :

ideal(h,$o) <=>

((bigand

$d0,$i,$e

in $Delta0, [1..$n1],

$Delta0_1($i)

when $d0 in $Delta0_1($i):

val($o,$e)

end) and

(bigand

$d0,$i,$e

in $Delta0, [1..$n2],

$Delta0_2($i,1)

when $d0 in $Delta0_2($i):

not val($o,$e)

end) and

(bigand

$d0, $i, $p, $c

in $Delta0, [1..$n3],

$Delta0_3($i,1),

$Delta0_3($i,2)

when $d0 in $Delta0_3($i):

not val($o,$p) or val($o,$c)

end))

end

The set of human desires is represented by

$Delta0 in the previous syntax. The counters

$n1, $n2, $n3 specify the number of positive desires,

negative desires and conditional desires respectively.

We conceive a positive desire as the human express-

ing a valuation for a variable assignment from Table

1 (e.g., environment is land). A negative desire is a

negative valuation for a variable assignment. Finally,

a conditional desire is a conditional valuation between

variable assignments (e.g., if the cost is high then so-

ciality level should be mixed).

Similarly, the goal to be achieved by the planning

agent is captured by the following formula:

def

o∈Opt

potIntend(h, o).

Moreover, we suppose that, for agent h to have

a potential intention to choose option o, denoted by

potIntend(h, o), she must have a justiﬁed belief that o

is an ideal option for her:

potIntend(h, o)

def

= 4

ideal(h, o) ∧ justif(h, o).

The latter is deﬁned using the same syntax and in our

case is expressed by the next formula:

bigor

$o in $Opt :

{h}ideal(h,$o) and justif(h,$o)

end

The set of actions are generated from Table 1. For

instance, inform(m,h,val_so_ass_env_land) is an in-

formative action. It is interpreted as the speech act

used by agent m to inform agent h that the valuation

of the property:environment for the option:soccer is

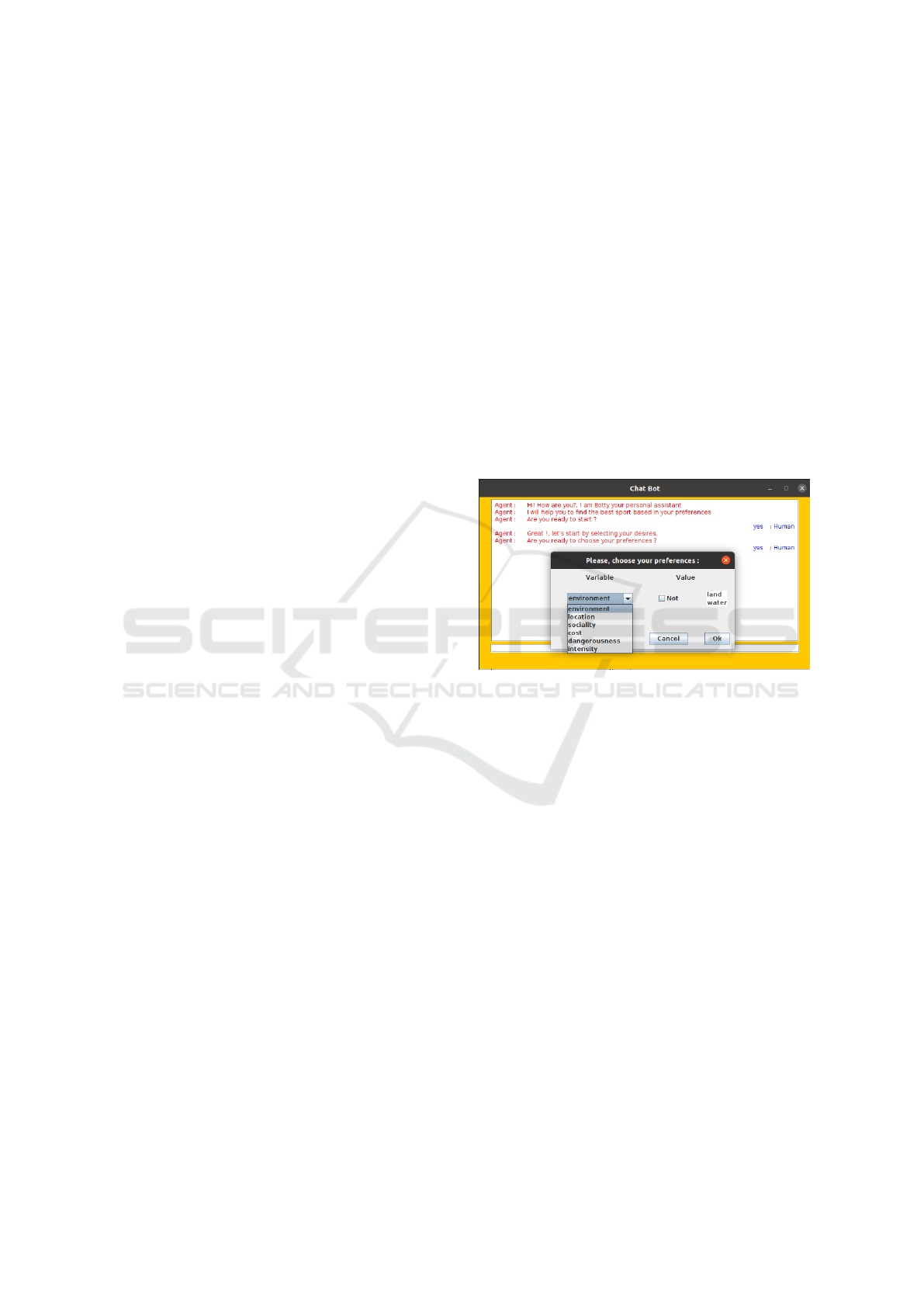
land. In order to help agent h to select an activ-

ity, agent m also needs information about h’s desires.

This information is gathered by agent m during its

interaction with agent h. The interaction interface

between h and m is shown in Figure 4. The belief

revision module is called after each agent h’s feed-

back and it restores consistency of the agent m’s be-

lief base, in case the incoming information is incon-

sistent with agent m’s pre-existent beliefs. In the ex-

Figure 4: Collecting agent h’s preferences.

ample, agent h would like to practice a land activity,

with medium intensity, which is not exclusively in-

door, and which can be practiced both in single and

team mode, if its cost is high. The next rule for

precondition states that agent h must be informed by

agent m about the dangerousness level of a sport, be-

fore presenting other properties for an option. For

a 6∈ Assign

dan



inform



m,h,val(o, a)





= 



val(o, a)∧

v∈Val

dan



val(o, dan 7→ v) → 4

val(o, dan 7→ v)





In the next lines we illustrate how the precondition

is assigned by the planning module together with its

α operator in order to specify the successful oc-

currence of an informative action:

[m]((val_te_ass_intens_med) and

(val_te_ass_danger_med =>

{h}val_te_ass_danger_med)) and

plus({h}val_te_ass_intens_med...

The planning module generates plans with the ele-

ments contained in the action ﬁle. It starts with plans

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

496

of length 1, and enters in a loop. At each interac-

tion the planning module asks the SAT solver to ver-

ify whether the plan allows to achieve the goal. If no

plan of length k is found, the program will increase

the counter in one and look for a plan of length k + 1.

An example of an abstract plan generated by the plan-

ning module is:

plus({h}(val_te_ass_danger_med)

plus({h}(val_te_ass_intens_med)

plus({h}(val_te_ass_soc_mixed)

plus({h}(val_te_ass_loc_mixed)

plus({h}(val_te_ass_env_land)

plus({h}(ideal_h_te)

The order of speech acts is determined by the pre-

conditions. Speciﬁcally, the planning module informs

ﬁrstly about the dangerousness level of the sport. Sec-

ondly, it provides explanation of why the user’s de-

sires are satisﬁed. Finally, it indicates the ideal sport

for the user, in this case tennis.

Figure 5: Plan shown by the chatbot to the human.

The chatbot writes both the sequence of speech acts

and its translation into natural language expressions.

We decided to display the abstract plan in the GUI, as

shown in Figure 5, for illustrative purposes oriented

to demonstrate how the GUI transforms it into natural

language using a simple function. The abstract plan

will not be displayed by the GUI in the end-user ver-

sion of the system.

5 EXPERIMENTS

In this section, we present the experiments conducted

in order to test the cognitive planning system in the

scenario described in the previous section. The ex-

periment was devoted to evaluate the performance of

the planning module in integration with the belief re-

vision module. The GUI was not used during the test,

therefore the procedure was carried out on command

line mode.

In order to perform the test we generate ﬁrstly a set

of desires of the human in different input ﬁles. These

input ﬁles are processed by the belief revision mod-

ule sequentially in order to generate the volatile side

of the belief base. Secondly, the translator module is

called to generate the initial state and the goal. Fi-

nally, the initial state, the set of actions (repertoire of

speech acts) and the goal are used to call the planning

module.

The set of options and variables described in Table

1 were used to test the performance of the system,

expanding the table in the number of sports available.

Similarly, we vary the number of the human’s desires.

Figure 6 shows the results of the computation. The

data plotted in the previous graph are shown in table

3 4

5 6

plan size

seconds

Opt = 3

Opt = 4

Opt = 5

Opt = 6

Opt = 7

Opt = 8

Figure 6: Processing time (in seconds) based on the number

of options.

Table 2: Processing time (in seconds) to achieve a plan

based of the number of Options.

Number of Options (Opt)

Plan

size

5 6 7 8

3 0.059

0.067 0.063 0.066 0.068 0.070

0.438 0.482

0.494

0.506

0.539

0.567

5 1.355 1.433 1.505 1.608 1.668 1.731

3.274 3.217 3.353

3.696

3.747 4.045

The experiments were conducted using an Ubuntu

64 bits linux virtual machine running on a core i7

processor with 8 gigabytes RAM. The belief revision

and cognitive planning module were implemented in

Ocaml version 4.10.0 and the chatbot interface was

programmed in Java openjdk version 1.8.0 with swing

components. The data ﬁles containing the belief base,

actions, goal and plan were stored as plain text ﬁles.

6 DISCUSSION

The architecture presented in Figure 3 works as an

integrated system. All the processes, interfaces and

An Implemented System for Cognitive Planning

497

exchange of data between the modules are working

according to the deﬁnition of the use cases displayed

in Figure 2.

The system dialogue capability is limited for the

moment. The human agent communicates her desires

to the machine, and the latter computes the most suit-

able plan. There is no feedback from the human af-

ter the sequence of speech acts performed by the ma-

chine.

The effectiveness of the computation is polyno-

mial with respect to the set of actions. Although the

algorithm for choosing the correct plan uses a brute

force technique, the experiments demonstrate that in

order to verify the validity of a single candidate plan,

the planning module takes around 66 ms on average.

The reason for choosing a brute force approach was to

allow the algorithm to be the most general as possible.

However, it would be possible to include a heuristic to

improve the performance of the general process. For

example, the planning module could consider the size

of the input (based on the human’s set of desires) as

the initial size of the plan. Thus, the planner will gen-

erate plans of that size at least. This prevents the plan-

ner from spending time to generate candidate plans of

smaller size than the number of human’s desires. In

addition, an optimization can be included in the al-

gorithm if we add a mechanism for giving priorities

to certain types of actions. For example, the actions

which are stated as preconditions should be priori-

tized to be included between the ﬁrst sets of combi-

nations to be tested by the planning module.

Despite the fact that the SAT encoding is efﬁcient

for solving the planning problem, we still need to gen-

erate one formula per candidate plan, which is time-

consuming, especially for the translation process and

the interface with the external tool TouIST. We want

to explore the possibility of using a QBF (quantiﬁed

boolean formulas) encoding of the planning problem

which will allow us to generate one single formula for

evaluating all possible candidate plans. In this case,

the preconditions are assigned if and only if there ex-

ists a plan that satisﬁes the goal. This alternative ap-

proach will allow us compare the efﬁciency of QBF

solvers against the SAT-based method in solving our

planning problem.

7 CONCLUSION

Our implementation demonstrates that the NP-

complete epistemic logic presented in (Fernandez

et al., 2021) and the cognitive planning problem for-

mulated in this logic are suitable for real-world appli-

cations in the domain of human-machine interaction.

In future work, we plan to extend the implemented

system by speech acts of type question to capture both

sides of interaction, from agent m to agent h (han-

dled by the actual implementation) and from agent

h to agent m. We expect to apply the same frame-

work to a joint activity scenario of type cooperative

boardgame (Bard et al., 2019; Longin et al., 2020)

involving the human and the machine in which they

have to exchange information and collaborate in or-

der to achieve a common goal.

We also plan to combine our implementation of

cognitive planning with machine learning and data

mining techniques, as presented in (Krzywicki et al.,

2016), in order to extract information about the hu-

man user from real data. In addition, we intend to

include a setting parameter in the artiﬁcial agent in

order to let the system select the most convenient ap-

proach (SAT or QBF) depending on the scenario. We

think that the SAT approach could be better when the

set of actions is not so big, while the QBF approach

will turn out to be well-suited for handling a large

repertoire of speech acts.

Last but not least, we intend to compare our

framework for cognitive planning with approaches

to epistemic planning closely related to ours (Muise

et al., 2015; Kominis and Geffner, 2015; Le et al.,

2018). None of these approaches presents a modular

architecture or an integration of planning and belief

revision. On the contrary, we have built our system

in a modular way by designing the different compo-

nents, including planning and belief revision, with the

interfaces that are necessary for the system working in

an integrated way. This feature allows the scalability

of the system. In fact, we are expecting to replace the

GUI with a more advanced web interface and add a

security module for granting access to the system in

a multi-user environment without altering the rest of

the modules.

ACKNOWLEDGEMENTS

This work is supported by the ANR project CoPains

(“Cognitive Planning in Persuasive Multimodal Com-

munication”). Support from the ANR-3IA Artiﬁcial

and Natural Intelligence Toulouse Institute is also ac-

knowledged.

REFERENCES

Akimoto, T. (2019). Narrative structure in the mind: Trans-

lating genette’s narrative discourse theory into a cog-

ICAART 2022 - 14th International Conference on Agents and Artiﬁcial Intelligence

498

nitive system. Cognitive Systems Research, 58:342–

350.

Bard, N., Foerster, J. N., Chandar, S., Burch, N., Lanctot,

M., Song, H. F., Parisotto, E., Dumoulin, V., Moitra,

S., Hughes, E., Dunning, I., Mourad, S., Larochelle,

H., Bellemare, M. G., and Bowling, M. (2019). The

hanabi challenge: A new frontier for AI research.

CoRR, abs/1902.00506.

Bolander, T. and Andersen, M. B. (2011). Epistemic plan-

ning for single- and multi-agent systems. Journal of

Applied Non-Classical Logics, 21(1):9–34.

Cooper, M. C., Herzig, A., Maffre, F., Maris, F., Perrotin,

E., and Régnier, P. (2021). A lightweight epistemic

logic and its application to planning. Artiﬁcial Intelli-

gence, 298:103437.

Fernandez, J., Gasquet, O., Herzig, A., Longin, D., Lorini,

E., Maris, F., and Régnier, P. (2020). TouIST: a

friendly language for propositional logic and more.

In Bessiere, C., editor, Proceedings of the Twenty-

Ninth International Joint Conference on Artiﬁcial In-

telligence, IJCAI-20, pages 5240–5242. International

Joint Conferences on Artiﬁcial Intelligence Organiza-

tion. Demos.

Fernandez, J., Longin, D., Lorini, E., and Maris, F. (2021).

A simple framework for cognitive planning. In Pro-

ceedings of the Thirty-Fifth AAAI Conference on Arti-

ﬁcial Intelligence (AAAI-21). AAAI Press.

Kominis, F. and Geffner, H. (2015). Beliefs in multiagent

planning: from one agent to many. In Brafman, R. I.,

Domshlak, C., Haslum, P., and Zilberstein, S., editors,

Proceedings of the 25th International Conference on

Automated Planning and Scheduling (ICAPS 2015),

pages 147–155. AAAI Press.

Krzywicki, A., Wobcke, W., Bain, M., Calvo Martinez, J.,

and Compton, P. (2016). Data mining for building

knowledge bases: Techniques, architectures and ap-

plications. The Knowledge Engineering Review, -1:1–

27.

Le, T., Fabiano, F., Son, T. C., and Pontelli, E. (2018).

EFP and PG-EFP: epistemic forward search planners

in multi-agent domains. In Proceedings of the Twenty-

Eighth International Conference on Automated Plan-

ning and Scheduling, ICAPS 2018. AAAI Press.

Longin, D., Lorini, E., and Maris, F. (2020). Beliefs, time

and space: A language for the y

okai board game. In

Uchiya, T., Bai, Q., and Marsá-Maestre, I., editors,

PRIMA 2020: Principles and Practice of Multi-Agent

Systems - 23rd International Conference, Nagoya,

Japan, November 18-20, 2020, Proceedings, volume

12568 of Lecture Notes in Computer Science, pages

386–393. Springer.

Lorini, E. (2018). In praise of belief bases: Doing epistemic

logic without possible worlds. In Proceedings of the

Thirty-Second AAAI Conference on Artiﬁcial Intelli-

gence (AAAI-18), pages 1915–1922. AAAI Press.

Lorini, E. (2020). Rethinking epistemic logic with belief

bases. Artiﬁcial Intelligence, 282.

Löwe, B., Pacuit, E., and Witzel, A. (2011). DEL planning

and some tractable cases. In Proceedings of the 3rd In-

ternational International Workshop on Logic, Ratio-

nality and Interaction (LORI 2011), pages 179–192.

Springer Berlin Heidelberg.

Muise, C., Belle, V., Felli, P., McIlraith, S. A., Miller, T.,

Pearce, A. R., and Sonenberg, L. (2015). Planning

over multi-agent epistemic states: A classical plan-

ning approach. In Proceedings of the 29th AAAI Con-

ference on Artiﬁcial Intelligence (AAAI 2015), pages

3327–3334. AAAI Press.

Prezenski, S., Brechmann, A., Wolff, S., and Russwinkel,

N. (2017). A cognitive modeling approach to strategy

formation in dynamic decision making. Frontiers in

Psychology, 8:1335.

An Implemented System for Cognitive Planning

499